1. Introduction

Tremendous advances in the understanding of complex systems have recently come from the availability of improved X-ray optics and imaging techniques [1]. Although in biophysics there is a general agreement that the spatial scale of the DNA (nanometers) as well as the one of the cell (microns), are of equal importance for the understanding of a unicellular living system, the advantages of a close connection between such different scales has only recently started to be included in the material design of condensed matter systems [2,3,4,5,6,7]. The race to attain sub-micron X-ray beam capacity is currently driving synchrotron radiation sources to thoroughly invest in ring upgrades [8]. While the identification of the real spatial disposition of defects in a condensed system has been considered merely from a material science perspective and mostly confined in the realm of applied physics, the broad use of X-ray microscopies has recently shown that from the visualization of defects and electronic order in a material, the underlying physical principles determining the emergence of the functionality can be clarified [9,10,11].

The role of defects and geometry in condensed matter physics has been theoretically and experimentally investigated in the dynamic melting of liquid crystals, vortex physics, fracturing process of materials, superconductors, and polymers [12]. However, in complex systems such as high temperature superconductors, which still constitute one of the biggest challenges in contemporary physics, the experimental difficulties to spatially visualize the structure were blurring the essential role of the heterogeneities into the microscopic mechanism explanation [13]. Progress on the imaging of defects with atomic scale resolution in condensed matter systems were made through the development of scanning tunneling microscopy. With this technique, it is possible to get spatial information to within few nanometers near the surface and within a region of a material no more than hundreds of nanometers [14]. Complementary to this technique, in the last five years, X-ray microscopies were applied to probe the k-space order in different spatial locations of the material structure. With the increased brilliance available in upgraded synchrotron radiation rings, the advances in X-ray optics and detectors, and the fast recording of thousands of X-ray patterns it has become possible to create a spatial imaging of nanoscale phase separation both in cuprates [15,16,17,18,19,20,21,22,23,24], pnictides families [18,25,26] of high temperature superconductors and in other magnetic parent compounds of the cuprate family [27].

The collection of massive amounts of data and the observation of local variations of disorder in real materials demanded the development of new mathematical tools for the description of the nanoscale electronic pattern observed. Fractals organization of nanoscale defects in high temperature superconductors was quantified and described up to the mesoscale, using two- dimensional correlation functions on scanning micro X-ray diffraction data [15,16,17]. The method enabled also the discovery of a fractal self-organization downwards to the atomic scale using scanning tunneling microscopy data [28,29]. We are therefore improving our current understanding of the material structure of high temperature superconductors, based on the spatial observation of the nanoscale electronic patterns in these materials. This will allow us to apply all the previous knowledge on nanoscale electronic systems [30] in the search for the essential material science ingredients for a stable high temperature superconductors at ambient pressure. Furthermore, the data coming from X-ray microscopies have provided and are providing a fresh perspective on nanoscale electronic systems themselves. Concomitantly, the opportunity and new understanding of materials, through the spatial visualization of defects and electronic orders, underlined the relevance of being able to control the defects in order to accurately displace dopants at the desired positions and attain novel functionalities. Especially the new generation of silicon electronics is currently providing promising examples of how defects, if efficiently controlled, can completely change the material functionalities [31,32].

It is the scope of this review therefore to show the contribution of advanced X-ray microscopies to the imaging of nanoscale electronic systems as an inspiration for their design up to the mesoscale. One particular case of a nanoscale electronic system that adopts a fractal organization, as probed by the micro X-ray diffraction technique will be reviewed. Finally, the review will discuss the data obtained from X-ray microscopies as useful leads in the design and realization of nanoscale electronic systems in devices with novel phase transitions. In particular, the design of nanoscale electronic systems with precisely tuned correlated disorder will be discussed.

2. Scanning Micro X-ray Diffraction: Applications to Granular Electronic Materials

The progress in X-ray beam focusing has given the opportunity to visualize structural aspects of the materials that were inaccessible before such as the grains self-organization and boundaries [33,34]. Grains and grain boundaries are of interest since they often possess unique electronic properties [35]. Lattice distortions (e.g. buckling, rotations, strain) have been resolved using scanning micro X-ray diffraction in ferroelectric ceramics such as BaTiO₃ [36]. The ferroelectric domains self-organize in alternating stripes along the c-axis, rotated by 90 degrees with a spatial separation of about 10 microns. Large strain can be created in BaTiO₃, accompanied by lattice distortions in the 90 degrees boundary as observed with micro X-ray diffraction [37]. In multiferroic systems, such as BiFeO, it has been observed, using micro X-ray diffraction, that vertical domain walls can be stabilized under the application of an electric field [38]. The orientation of the ferroelastic grains determines the local diffracted intensity distribution. In multilayer thin film, micro X-ray diffraction has been used to probe in depth both the thin film and the substrate [39]. Indeed, X-ray microdiffraction has shown that for thin film deposited on a substrate, the claim of a ‘perfect’ interface should be experimentally validated [40]. The approach was used to map the tilt mechanism of the thin film growth under different conditions (e.g. temperature). The grains orientation has been probed in metallic thin films using this technique [41]. Since the full width of an X-ray diffraction profile is a measure of the corresponding grain size, micro X-ray diffraction techniques can also be used to determine grains size distributions under different conditions (e.g. pressure) [42]. This is of relevance when designing novel nanoscale electronic structures, since strain engineering can often be used at the nanoscale to tailor material properties. In fact, micro X-ray diffraction can be used to image the strain fields around nanodots through reciprocal space mapping [43]. One clear advantage of this technique applied to nanoelectronics systems is that the experimental data can be obtained in a device that is still working.

Furthermore, an advantage of micro X-rays over more standard X-ray beams is that they allow us to collect more X-ray diffraction or X-ray spectra for the same sample. This provides the opportunity of imaging a k-space order as it varies point by point in the r-space. Considering the theoretical and experimental efforts to understand the nature of nanoscale electronic systems and the ‘strange metal’ in high temperature superconductors [44], this technique should be seen as an advantage in the difficult experimental task of determining the essential heterogeneities [45], nematicity [46] and superstripes [47] once the spatial distribution, orientation and the heterostructure at the atomic-limit of multiple phases have been considered. The essential role of the heterogeneities is well recognized, for example, by the observation that the local density of states is found to be strongly correlated with the quenched disorder to the impurity dopants [48,49]. In La₂CuO_4+y, a quenched disorder is introduced by electrochemically doping the system with oxygen. The quenched disorder is accompanied by an addition of charge carriers to an antiferromagnetic Mott insulator until the system becomes a superconductor [50]. Depending on the intrinsic misfit-strain of the material and the doping [51,52], the oxygen gets ordered in filamentary either two- or three dimensional stripes in the interstitial space left available by the rocksalt layer. The structural phase separation observed in La₂CuO_4+y between a dopant-poor and a dopant-rich phase [53] is linked to the electronic phase separation observed at low-temperatures with scanning tunneling microscopies and angle resolved photo emission experiments [54,55,56,57]. Since there is a large misfit strain between the layers (the Cu-O bonds are 4% shorter than their equilibrium value of 1.97 A [46]), the oxygen interstitials are mobile down to 200 K and they self-organize in metastable configurations like in many ionic conductors [58]. The mobility of the oxygen is also the origin of the extraordinary superconducting critical temperature dependence on the oxygen ordering and thermal treatments of the samples [59]. A decrease in the average oxygen ordering of the material, in fact, deeply influences its superconducting transition temperature. At optimal doping the critical temperature dependence on oxygen interstitial ordering is particularly evident since a macroscopic phase separation between oxygen poor and rich domains is present [15,16,17,60,61].

Generally, controlled thermal treatments reduce or increase the oxygen clusters size by few nanometers and concomitantly their spatial distribution. As a side effect, they modulate the holes concentration in the copper plane, therefore shaping the potential landscape and interactions of the quantum liquid. Although the signals of the oxygen interstitials are weak for a standard X-ray source, the satellite peaks, associated with a 3D nearly commensurate superstructure of the ordered oxygen interstitials dopants are still visible at the synchrotron radiation light source. It is a satellite which appears near the main crystal reflections displaced by the wavevector Q2-Oi with components ±l = 0.5c∗, ±k = 0.25b∗, ±h = 0.09a∗ with strong second and third harmonic components. The experiment is performed as follows; the crystalline sample is cleaved with a surface normal to the crystalline c axis. The crystal is mounted in a x-y mechanical translator for scanning parallel to the crystallographic (a, b) plane. The experimental set up allows the x-y translation of the sample with 22 µm steps in the x direction and 5 µm steps in the y direction, scanning a 350 × 600 µm² sample area. The integrated intensity of the satellite superstructure peaks recorded by a CCD detector at each microscale spot probes the square root of the volume of the ordered oxygen interstitials domains in a µm² spot area. Data have been normalized by recording the ratio of the Q2-Oi superstructure satellites integrated intensity on the tail of the main crystalline reflections, typically the (006) reflection, near the satellite spot.

The novel approach here is to apply statistical analysis on the weak k-space signal of a superstructure (e.g. oxygen interstitials) in order to quantify its variation in real space. The statistical analysis of X-ray diffraction signals is possible since the technological advances in X-ray optics [62] have made it possible to focus the X-ray beam down to few hundred nanometers and to scan the sample. Generally, a few thousand of X-ray diffraction images are sufficient to have a sufficiently solid collection of data for statistical analysis. Spatial correlation function and binning of the diffracted intensity of the superstructure signal have been shown to be the necessary mathematical tools to analyze the spatial variation of the signal in the sample. In the optimally doped La₂CuO_4+y, the analysis shows that the oxygen interstitial order is distributed in space following a power-law with all the characteristics of a scale-invariant system. It is worth to note that only the oxygen interstitials that get ordered in a striped phase can be clearly seen in X-ray diffraction. Oxygen interstitials, instead, that are disordered give no signal. However, as a complementary technique, scanning micro X-ray absorption near edge structures can be used in order to map the oxygen distribution in both the ordered and the disordered sample [21]. This is possible by mapping the shape resonance characteristics of the orbitals expected to be more influenced by the presence of oxygen interstitials like the L^III of the La atoms in the rock-salt layer. The results of this experiment showed that actually the oxygen concentration is homogeneous in the sample as one would expect on the basis of standard electrochemistry considerations, while the oxygen order is heterogeneous.

This order has a power-law distribution with an exponent measured a = 2.6 ± 0.1 with an exponential cut-off depending on the critical temperature of the sample. A scale-free pattern of oxygen rich puddles is forming a fractal with a spatial correlation length up to hundreds of microns. The fractal pattern emerges from the nanoscale phase separation between oxygen ordered and disordered puddles. The nanoscale phase separation is increasingly recognized both theoretically and experimentally not only as an intrinsic property of modern materials, but also as the origin of the granular electronic states between metallic or insulator behavior [63,64,65,66,67,68,69,70,71,72,73,74]. Furthermore, it has been pointed out that the quantum liquid fluctuations at the quantum critical point extend up to high temperature and the scale-invariance found for the oxygen interstitials order is the mesoscopic and classical manifestation of the intrinsic electronic quantum fluctuation of the system [10].

In addition to the quenched disorder, there is a further element of complexity in cuprate superconductors from nanoscale up to the mesoscale: the charge density waves. A charge density wave is known to be accompanied by a local distortion of the atomic lattice [75,76,77,78]. Charge density waves in cuprate superconductors were determined using X-ray absorption spectroscopies at synchrotron radiation facilities [79,80,81,82].

The X-ray absorption spectroscopies EXAFS (x-ray absorption fine structure) and XANES (x-ray absorption near edge structure) [57] probe the instantaneous pair distribution function and higher order correlation functions, i.e. local lattice geometrical symmetry, of the local structure with a range of 0.5 nm around a selected photo-absorbing Cu ion in the femtosecond time scale. These methods have provided the first measure of the amplitude of zero point lattice fluctuations in a double well potential providing a probe of the amplitude of periodic lattice distortions associated with short living and short range charge density waves. The EXAFS results have been supported by resonant X-ray diffraction at the Cu K-edge of the CuO₂ plane in Bi₂Sr₂CaCu₂O_8+y [83]. Recent advances in detector and soft X-ray diffraction beam lines have allowed the measurements of Cu L₃-edge resonant x-ray diffraction, while the improvement of hard x-ray energy diffraction beam lines has allowed to provide enough resolution to determine the universal presence of short range charge density waves [84,85,86,87,88,89,90,91] in all the cuprate families. Scanning X-ray microdiffraction using a focused sub-micron X-ray beam [16] has enabled the give the first observation of the inhomogeneous spatial distribution of the short range charge density wave accompanied by an incommensurate periodic lattice distortion with wavevector Q3-LLD = 0.21b∗ + 0.29c∗ in La₂CuO_4+y [16]. The temperature dependence of the charge density waves show a proliferation of quasi-two-dimensional puddles at low temperature. Indeed, the charge density wave peak reaches a maximum at around T = 100. The statistical analysis of the weak and diffuse charge density wave signals observed in different spot of the real space of the material, has given a power-law distribution with an exponent measured a = 2.6 ± 0.1. An exponential cut-off of the distribution is increasing as the critical temperature measured gets higher.

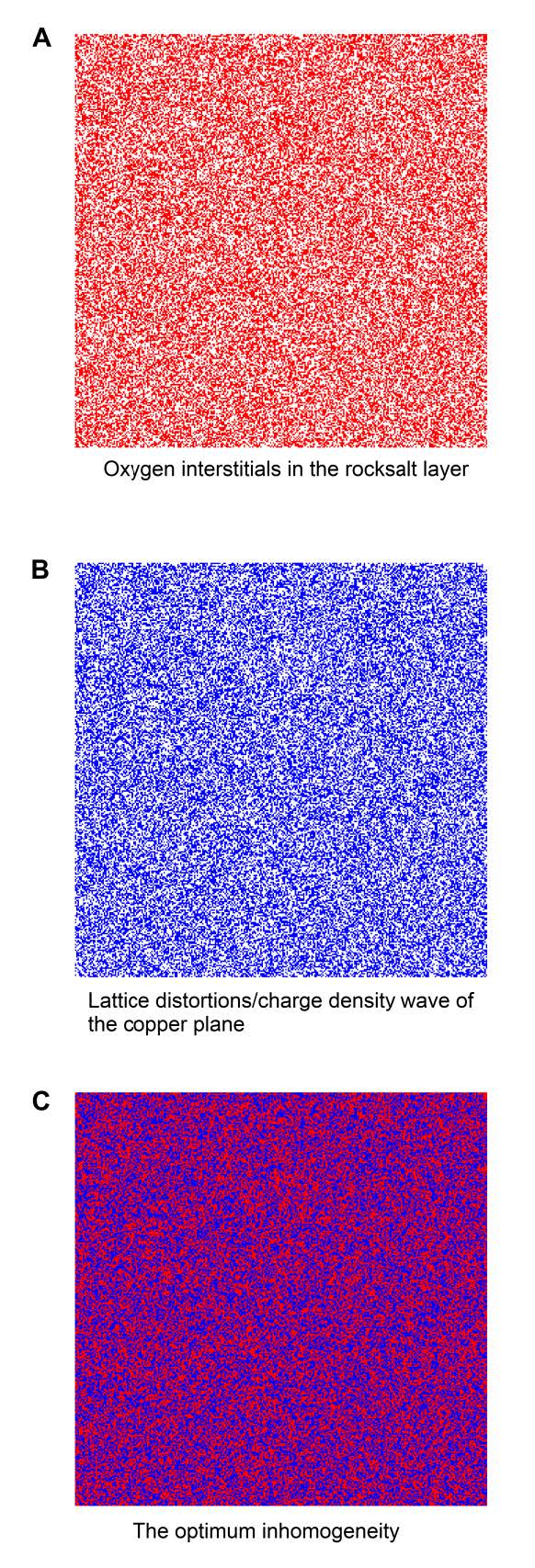
The detection in the same X-ray diffraction pattern of multiple weak signals in k-space can be used as an advantage in order to correlate their variation point-to-point in the real space of the sample. This has been shown to be an advantage when clarifying the nature of the ubiquitous competition and coexistence between charge density wave order and quenched disorder in cuprates. The Q2-Oi and Q3-LLD signals can be recorded in the same X-ray diffraction pattern, therefore their variation in the real space of the sample can be measured, scanning the nano X-ray beam in both the x-y real-space directions. It is observed in La₂CuO_4+y that the charge density wave accompanied by the local lattice distortions of the CuO₂ plane show a scale-free distribution. Although the quenched disorder is often described by a random organization, with this technique we were able to observe a fractal organization of oxygen interstitials decorating the fractal distribution of charge density wave puddles [16]. On the nanoscale therefore the system self-organizes into two competing and spatially separated fractal networks [23]. The fractal of lattice distortions occupies a space that is confined in the CuO₂ plane, while the anti-correlated fractal of oxygen interstitials is confined in the rock salt layer [16]. A scheme of the results is shown in Fig.1. The percolating oxygen interstitials (rock salt layer) and the charge density wave order accompanied by the local lattice distortions of the copper plane are shown respectively in Fig 1A as red dots and Fig.1B as blue dots. If we map both these orders on the same plane, we obtain what is shown in Fig.1C. This experimental observation shows an unexpected geometry of multilayer networks of defects and charge order in a media hosting superconductivity robust until 40 K.

Figure 1. A) Scheme of the oxygen interstitials ordered domains percolating in the rocksalt layer (red dots), B) and the charge density waves puddles of the copper plane accompanied by the lattice distortions of the atomic lattice (blue dots). C) Scheme of the charge density waves accompanied by the lattice distortions (blue dots), anti-correlated with interstitial dopants domains (red dots). See ref [16].

DownLoad: Full-Size ImgPowerPoint

The spatially anti-correlated two scale-free distributions of oxygen interstitials and charge density waves accompanied by lattice distortions are the definition of optimal inhomogeneity. In real materials, the power-law distribution shows an exponential cut-off. Although the manifestation of percolation in high temperature superconductivity has been reported in several works [92], the actual spatial characteristics of the phase separation in an optimally doped sample were less known. Further works in other cuprates compound with higher critical temperatures are needed to clarify the possible universality of this particular case of fractal nanoscale electronic materials made of two competing scale-free orders up to the mesoscale. However, this topic is not merely of interest for specialists working in high temperature superconductivity research. Multilayer networks applied at the structural and dynamical organization of graphs made of diverse relationships (layers) are also currently of central interest in the network science [93]. Furthermore, it is worth noticing that networksconstructed over hyperbolic spaces naturally possess heterogeneous scale-free degree distributions [94]. The spatial distribution of the charge density wave order and the quenched disorder in a different cuprate with a higher critical temperature (Tc = 95 K) has been recently reported [95], surprisingly showing the same spatial inhomogeneity of the La₂CuO_4+y [16]. The recurrence of this mesoscale pattern made by the same competing nanostructures in the cuprates is a fact already surprising in its own right. However, the application of a refined technique for big data analysis to unveil also the size distributions of the nanoscale electronic structure has given a more solid signature for a possible presence of a hyperbolic space for superconductivity. More detailed investigations with complementary techniques are needed in order to confirm the results for the currently explored superconductors and the benefit for nanoscale superconductivity of a hyperbolic space [96]. However, all these series of studies have definitely demonstrated that high temperature superconductors such as the cuprates are very far from systems with a structure that is homogeneous and where possibly only the electronic order is inhomogeneous. This is only a serious issue to be considered for practical application which could make use of these system, but is also a strong condition for theory. It is finally worth noting that the existence of hyperbolic dispersion equations in real materials is not just an academic curiosity, since it has been already shown to be an advantage for applications for example in photonic metamaterials [97,98,99]. In addition, it is intriguing that a seemingly unrelated field of science such as string theory has made a substantial effort to clarify the connection of scale invariants and hyperbolic geometries with the universal description of a strongly correlated electron systems [100].

The percolative nature of the phase separation in optimal doped cuprate superconductors can be used as an advantage for the control of the defects. The feasibility of permanent phase changes induced by prolonged exposure of the materials to X-rays has been shown by several groups. Using this approach, in 1997 it was shown that in manganese oxides of the general formula A_1-xB_xMnO₃ a transition can be driven from the insulating antiferromagnetic state to the metallic ferromagnetic state at low temperatures (<40 K) [101]. In La₂CuO4_+y, it has been shown that illumination by X-rays can control the ordering of oxygen interstitials in simple cuprate high temperature superconducting single crystals, intriguingly enhancing the superconducting critical temperature [11,59,102]. Hard X-ray exposure can give two remarkable phenomena also in manganite thin films, where an increase in the conductivity was observed simultaneously with an enhancement of the magnetic/orbital Bragg peak intensity as a function of the time of exposure [103]. X-rays induced insulator-to-metal transition through the formation of metallic percolation paths were also observed in VO₂ [104] and in TiO₂ [105].

In cuprate high temperature superconductors, nanoscale defects can be manipulated using a continuous X-ray beam. X-ray manipulation can be for example performed in a relatively simple high temperature cuprate superconductor like La₂CuO_4+y. At 370 K the diffraction signature (Q2-Oi) of the oxygen interstitial phase vanishes. Therefore, the oxygen interstitials domains become completely disordered. After this thermal treatment, by quenching the sample to low temperature, a poor superconducting order is also observed. On the other hand, if the same disordered sample is exposed to X-rays at room temperature, the nucleation and growth of ordered oxygen interstitials domains is observed, and a recovery of a robust high-T_c state [11,59].

The fact that several hours are required for the oxygen interstitials grains to grow while exposed to X-ray intensity indicates that X-ray illumination is the source. There is a threshold before the growth of the domains starts, After passing the threshold the oxygen interstitials domains in the rock salt layer first start to grow in-plane and subsequently accelerate out-of-plane when they have reached a further threshold, implying strain-mediated development through a coarsening process to the optimal inhomogeneity [11,59]. Furthermore, it is now understood that it is a particularly ordered phase of oxygen interstitials that hosts the highest temperature superconductivity. A typical sample will consist of ordered oxygen interstitials domains of sub-micrometer size embedded in a glassy matrix where the interstitials are disordered. When doped in the optimal range of 0.1 < y < 0.12, the optimal superconductivity occurs when conditions are such that the Q2 phase percolates into a fractal network. This has interesting connections to predictions that phase transitions in Josephson junctions array networks could be related to the scale-free and fractal nature of the physics of those systems [106] and the global phase coherence stabilized by a network of Josephson junctions [107,108] among the superconducting grains. In addition, during the exposure to X-rays, a hysteresis in the nucleation and growth of the oxygen interstitials domains was experimentally observed [97]. Although an application of this technique has not been found yet, it has been shown [11,59,102] that is possible to induce oxygen ordering with a dot and a line on the scale of 100 micrometers. Since the X-ray beam can be focused to a few hundred nanometres at the synchrotron facilities or to a few microns in recently developed laboratory X-ray sources [109], the manipulation can also be modulated laterally to obtain more complex geometries.

Experimental work has given a central role to the geometry and to defects in the emergence of novel phases of matter. The works were also of inspiration for recent theoretical predictions in network theory, claiming that the superconducting critical temperature is enhanced in networks with greater second moment of the degree distribution [66]. However, the search of the universal aspects (if any) for the description of quantum liquids in strongly correlated systems is often fogged by concomitant magnetic, charge, structural, or orbital orderings, as well as effects of disorder [92]. Today, state of the art nanotechnology provides new opportunities to treat each degree of freedom separately and realize artificial systems ad-hoc to explore the basic role of geometry in a condensed matter system. In the next section, it will be shown how the detection of novel nanostructured geometries of charge density wave order accompanied by lattice distortions and quenched disorder in the cuprate superconductors with X-ray microscopies, has partially motivated and guided the experimental realization of nanostructured superconductors exhibiting novel phase transitions.

3. From Granular electronic Systems towards Complex Materials with Precisely Tuned Correlated Disorder

The X-ray microscopy experiments in high temperature superconducting materials show that even in the best conditions of preparation of the material, the system is inhomogeneous and naturally nanostructured with correlated disorder (e.g. power law) extending from few nanometers up to hundreds of microns. Nanoscale systems properties are often determined by strong inhomogeneities and fluctuations. For example, local fluctuations of the average atomic positions in a lattice show up within an intrinsic nanoscale phase separation in a high temperature superconductor [110]. Structural deviations from the average structure, that are typical of nanoscale systems driven far-from equilibrum, require the development of both X-ray absorption [111] and neutron scattering techniques [112] to enable their observation.

Although the granular electronic systems are often intrinsically organized over multiple lenght scales [113], the actual term granular nanoelectronics was coined at the beginning of the 90s [114] to refer to a highly interdisciplinary branch of science interested in the manipulation of the single electron. It is therefore not surprising that a realistic route to the realization of a quantum computer was thereafter proposed [115]. In this respect, remarkable advancements in this field have been achieved [116]. However, superconductivity is not observed within an atom or at the single-electron level, but always requires a minimum size. The question therefore is which is the optimal inhomogeneity for the nanoscale structure in order to establish a global phase coherence up to the mesoscale, robust enough to spatial disorder and thermal fluctuations. An intrinsic nanoscale structured system that can sustain global phase coherence even at moderate temperatures up to the mesoscale is a high temperature superconductor, whose electronics and structural constituents are organized not only at the atomic scale, but also at the nanoscale, and show qualitatively different spatial organization up to the mesoscale. With this remarkable example of intrinsic multi-scale architecture clearly demonstrating the benefit for electronic transport, the design of nanoscale electronic materials by mimicking the patterns observed in these complex materials is therefore becoming a tantalizing opportunity for nanoelectronics. Promising strategies in order to realize the desired configuration of nanoscale electronic systems have been proposed with particular attention to the self-assembly of nanocrystals [117]. Notable examples of nanoscale electronic systems have been realized using state of the art electron beam lithography [118] where characteristics of superconducting temperature transitions were observed. In bulk materials, the superconducting critical temperature of nanoscale materials can be easily shifted by the dimensionality [119]. Dimensionality of a nanoscale electronic system, indeed, can be tuned by precisely controlling the spatial pattern and disorder which influences the electron transport [120]. In granular electronic and disordered superconducting systems, the spatial disorder is often modelled as a disordered array of Josephson junctions [121]. Spatial organization of the nanostructure determines the magnetic hysteresis effect in nanoscale systems since the inter-grain interaction plays a key role [122]. The spatial organization of the nanostructure is crucial for colossal magnetoresistance effects in non-multilayered systems [123]. Scattering at the interface among grains also produces anomalous hall effect in granular materials [124]. Thermal and magnetic effects in self-organized nanostructured materials are closely linked since a change in the thermal fluctuations of the system can determine a new regime in the transport [125]. Thermal transport is indeed influenced by the spatial organization of the nanostructure of a system [126,127]. Cellular automata models have also shown that self-organized nanostructured systems can have long tailed distribution of trapping times [128]. All these properties make nanostructured materials up to the mesoscale also interesting for technology, for example for the realization of strain sensors [129].

Since X-ray microscopies have shown that modern materials such as high temperature superconductors are not homogeneous, but nanoscale phase separated and with spatial correlation lengths that can reach even scales up to hundreds of microns [15,16,17,18,19,20,21,22,23,24,25,26,27], it is reasonable to expect that precisely spatially tuned correlated disorder in nanostructured electronic systems can determine emergent functionalities or enhance and reinforce the existing one. To address this question, the disorder found in cuprates and pnictides can be mimicked in more controllable devices, like thin film, which can be also nanostructured with the state of the art technique of electron beam lithography.

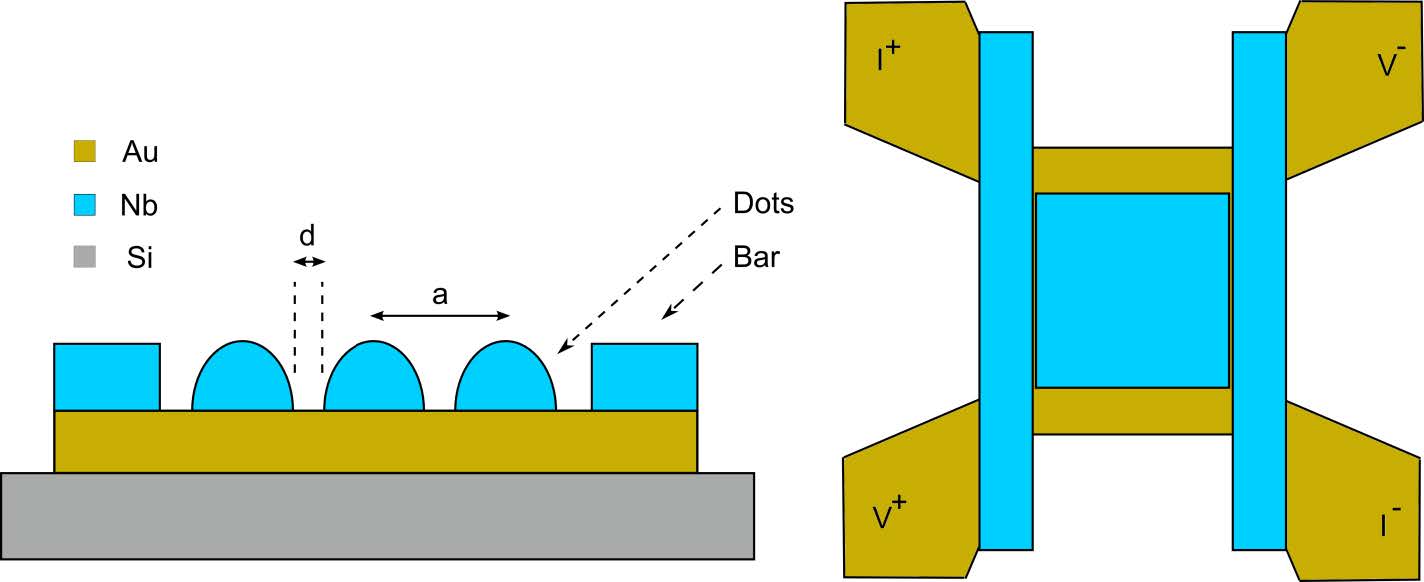
One of the possible strategies for the realization of a nanostructured electronic system with multi-scale controlled correlated disorder is made by an array of proximity-coupled nanoscopic superconducting islands (see Fig.2) [130]. This design relies also on the concept ofvortex-quantum particle mapping, which is a particular and important case of the general correspondence between classical statistical physics and quantum mechanics [131]. This concept was introduced in the course of studying vortex pinning by columnar defects. In quantum mechanical mapping T ħ and L ħ/T, where L is the size of the system along the vortex line [132,133]. Therefore, this implies that varying the physical temperature in a superconducting vortex array will change Planck’s constant i.e. the degree of “quantumness.”

Figure 2. Scheme of the nanoscale up to the mesoscale superconducting system.

DownLoad: Full-Size ImgPowerPoint

Based on this duality, it is possible to address questions about the nature of the Mott state [134], using vortex arrays. In condensed matter systems, a Mott insulator state forms when commensurate conditions for electron density win over strong repulsive interactions among electrons. The Mott insulator-to-metal transition critical region harbours diverse phases, exhibiting anomalous fluctuations and ordering in the spin, charge, and orbital degrees of freedom. The physics of the Mott state are at the heart of physics of stronglycorrelated systems, most notably underpinning the mechanism of high-temperature superconductivity in cuprates [135] and colossal magnetoresistance in manganites [136]. While much is understood about thermodynamic Mott transitions driven either by temperature or by one of the parameters controlling the electron density [137], the dynamic Mott transition driven by delocalizing electrons, remains mostly unexplored. Unveiling the physics of collective behaviour arising from Mott insulators can be of interest also for the search of macroscopic quantum objects that persist at room temperature, as shown by ground-breaking recent experiments in UO₂ [138,139]. The main obstacles hindering the understanding of dynamic collective behaviour in Mott insulators and its mechanism are structural defects in the materials hosting the Mott state. In standard electronic Mott insulators, such defects disguise the effects of Zener tunnelling [140], which is presumably behind the many-body transformation of the Mott insulator into the Mott metal.

Recently, an extensive theoretical study of the dynamic Mott transition in one dimension has been performed [141]. However, even for this simplest case, the progress relied upon mostly numerical studies due to the complexity of the many body dynamics of strongly correlated systems. Yet it has been reliably established that the dynamic destruction of the Mott state is likely to be governed by Landau-Zener tunnelling. Furthermore, the characteristic dielectric breakdown threshold for a Mott insulator could be estimated. Nevertheless, experiments point out that the dielectric breakdown occurs at fields much smaller than those predicted for dynamic Mott transitions [140]. This discrepancy was ascribed to the detrimental role of defects that trigger disorder-promoted avalanche-like breakdown along a percolation weak path, rather than a transformation of a gapped insulator spectrum into a metallic band (i.e. the Landau-Zener-based dynamic Mott transition). Indeed, in Mott insulators electric fields can actually induce structural transformation in a thin film that creates inhomogeneous landscapes at the nanoscale as shown by recent time resolved scanning X-ray microdiffraction [142]. Although in some circumstances the structural disorder can be neglected or even used as an advantage, it is still of the utmost importance that the correlated disorder to be controlled at will. Careful control of disorder and design of nanoscale up to the mesoscale geometries therefore is the challenge for experimentalists. The same approach was used to uncover features characteristic of a dynamic transition, using a dynamic scaling of the kind that was seen in the context of depinning of charge density waves and magnetic domain walls [143,144,145].

Substantial experience has been accumulated over decades for the study of vortex dynamics in patterned structures [144,145,146,147,148,149,150]. Characteristic matching effects, indicating the formation of the vortex Mott state have been reported [151], and the reversal of the peaks in the differential resistance, indicating the dynamic transition from a vortex Mott insulator to a vortex Mott metal have been observed [130]. The dip-to-peak reversal heralds a dynamic phase transition in the vortex system, jumping as a function of the applied current from a non-equilibrium Mott insulating state to a non-equilibrium metallic state. Actually, this dip-to-peak reversal, that is not present in the resistance, rules out the explanation of this phenomenon as depinning. These results strongly encourage the search for nanoscale up to the mesoscale electronic systems with novel phase transitions. Indeed, exploiting the dynamic vortex Mott transition physics in nanoscale up to the mesoscale superconductors that make use of the sharp switch in the character of the differential resistance is giving the fundamentals for applications in an emerging new generation of electronics based on stationary far-from equilibrium states.

4. Conclusion

Although these developments of dynamic vortex Mott transition are still in their infancy, it is already a promising example of how novel phase transitions can be attained with nanoscale superconductors once a correlated disorder is precisely tuned. Further encouraging experimental data come from nanoclusters [152] and the theory of networks [106,153]. Thus, a nanoelectronic system with precisely tuned correlated disorder is expected to improve our fundamental understanding of collective phenomena in complex networks by unveiling possible novel phenomena or novel reports of nanoscale superconductivity to high temperature. Finally, I expect that the synergy between nanotechnology, X-ray microscopies and free electron lasers techniques will provide in the future a unique combination for imaging and control of far from equilibrium dynamics and correlated disorder at multiple spatial scales in complex materials.

Acknowledgment

The work was partially supported by the Italian Ministry of Education and Research, by the Italian CNR, Dutch FOM and NWO foundations. N.P. acknowledges for partial financial support the Marie Curie IEF project FP7-PEOPLE-2012-IEF-327711-IMAX. The author is particularly grateful for the valuable discussions and work during these years with the experts in the fields of X-ray microscopies, nanoscale-mesoscale superconductivity and nanoelectronics listed here in alphabetical order: Gabriel Aeppli, Tatyana Baturina, Antonio Bianconi, Alexander Brinkman, Manfred Burghammer, Gaetano Campi, Daniele Di Gioacchino, Francesco Coneri, Francesco Giazotto, Alexander Golubov, Hans Hilgenkamp, Boby Joseph, Martijn Lankhorst, Augusto Marcelli, Alessandro Ricci, Naurang Saini, Elia Strambini, Valerii Vinokour, X. Renshaw Wang and the scientific staff of the XRD1 and ID13 beamlines respectively at the Elettra and European synchrotron radiation facility.

Conflict of Interest

The author declares that they have no competing financial interests.