Examining the relationship between public debt and private consumption in European OECD countries (2011–2020)

1.   Introduction

The variational inequality problem was first introduced independently by Fichera ^[1] and Stampacchia ^[2] to model optimization problems arising from mechanics. The concept of multi-time has been employed in optimization theory, namely in the framework of multi-time optimal control problem. This problem is a particular case of the multidimensional variational problems. Several problems, in science and engineering, can be modelled in terms of optimization problems, which are governed by $m$-flow type partial differential equations (multi-time evolution systems) and cost functionals expressed as path-independent integrals or multiple integrals. Apart from optimization theory, the concept of multidimensional parameters of evolution has also been applied in space theory, where the space coordinates are represented by two-dimensional time parameters $t = (t_1, t_2),$ where $t_1$ and $t_2$ represent the intrinsic time and the observer time, respectively. For more details and recent studies in this direction, interested readers are referred to the studies in ^[3,4,5] and the references therein.

The study of variational inequality problems in finite dimensional spaces was initiated independently by Smith ^[6] and Dafermos ^[7]. They set up the traffic assignment problem in terms of a finite dimensional variational inequality problem (VIP). On the other hand, Lawphongpanich and Hearn ^[8], and Panicucci et al. ^[9] studied traffic assignment problems based on Wardrop user equilibrium principle via a variational inequality model.

Lions and Stampacchia ^[10], and Brezis ^[11] independently introduced the time-dependent (evolutionary) variational inequality problem, and developed an existence and uniqueness theory of the problem. Daniele et al. ^[12] formulated a dynamic traffic network equilibrium problem in terms of an evolutionary variational inequality problem. Ever since then, several other economics related problems like Nash equilibrium problem, spatial price equilibrium problems, internet problems, dynamic financial equilibrium problems and environmental network and ecology problems have been studied via time-dependent variational inequality problem (see ^{[13,14,15,16]}).

Censor et al. ^[17] introduced a new split inverse problem called the split variational inequality problem (SVIP). The authors proposed iterative methods for estimating the solution of the problem, they and analysed the convergence of the proposed iterative schemes. The SVIP has several areas of applications, including network problems, image reconstruction, cancer treatment planning and many more.

Very recently, Singh et al. ^[18] introduced another split inverse problem, which they called evolutionary split variational inequality problem. The authors demonstrated the applicability of this new problem through the formulation of the equilibrium flow of dynamic traffic network models, which comprised two given cities. Moreover, they established the existence and uniqueness of equilibria for the proposed model.

However, Singh in ^[19] noted that in an economic problem, other parameters in addition to time may also affect the values of the constraints and arguments associated with the problem. Similarly, in a traffic network problem the flow of traffic depends on several economic parameters other than the time parameter. For instance, traffic flow data are known to be strongly influenced by both space (location) and time. In addition, parameters related to road capacity, safety measures for averting road accidents and several other economic parameters could affect traffic flow. Based on this observation, Singh ^[19] introduced a new split inverse problem, called the multidimensional split variational inequality problem (MSVIP). This new problem includes a multidimensional parameter of evolution. As an application, the author formulated the equilibrium flow within two different traffic network models, e.g., traffic networks for two given cities.

More recently, Alakoya and Mewomo ^[20] studied a new class of split inverse problems, known as split variational inequality problem with multiple output sets. This class of split inverse problems is designed such that multiple variational inequality problems are solved simultaneously. The authors proposed an iterative method for estimating the solution of this problem, and they further presented some numerical experiments to demonstrate the feasibility of the proposed iterative method.

We note that the results of Singh et al. ^[18] and Singh ^[19] are only capable of dealing with two different traffic network models simultaneously. In other words, their results are not applicable when the goal is to study multiple (more than two) traffic network models simultaneously. Moreover, we also note that in formulating the split inverse problems introduced in ^[18,19], the authors needed to define explicitly two inverse problems (one in each of the two spaces under consideration) such that the image of the solution of the first inverse problem under a bounded linear operator is the solution of the second inverse problem. This method of formulation made the proofs of the results in ^[18,19] lengthy and not easily comprehensible. To overcome these shortcomings, in this study we introduce and study a new class of split inverse problems, which we call the multidimensional split variational inequality problem with multiple output sets. This newly introduced problem also includes a multidimensional parameter of evolution. Moreover, in formulating our problem we demonstrate that the inverse problems involved in the formulation need not to be explicitly defined. Instead, by introducing an index set our problem could be formulated succinctly and the proofs of the results presented more concisely. To demonstrate its applicability in the economic world, we formulate the equilibrium flow of multidimensional traffic network models for an arbitrary number of locations, e.g., traffic network models for different cities. Moreover, we define a multidimensional split Wardrop condition with multiple output sets (MSWC-MOS), and establish its equivalence with the formulated equilibrium flow of multidimensional traffic network models. Furthermore, we establish the existence and uniqueness of equilibria for our proposed model. We propose a method for solving the introduced problem, which will be useful in evaluating the equilibrium flow of multidimensional traffic network models for different cities simultaneously. Finally, we validate our results using some numerical experiments. To further illustrate the utilization of our newly introduced problem, we apply our results to study the network model of a city with heterogeneous networks. More precisely, we consider a city, which comprises connected automated vehicles (CAVs) and legacy (human-driven) vehicles, alongside electricity network, e.g. for charging the CAVs, and we formulate the equilibrium flow of this network model in terms of our newly introduced multidimensional split variational inequality problem with multiple output sets. We note that the results in ^[18,19] cannot be applied to the numerical examples and application considered in our study.

2.   Preliminaries and problem formulation

In this section, we formulate our multidimensional split variational inequality problem with multiple output sets. First, we introduce some important notations and mathematical concepts, which are needed for the problem formulation. In what follows, except otherwise stated, the abbreviation "a.e." means "almost everywhere" and $\mathbb{R}^m_+$ denotes the set of non-negative vectors in $\mathbb{R}^m.$ We assume that our multidimensional traffic network model comprises a multi-parameter of evolution $v,$ which is the multidimensional parameter of evolution, i.e., $v = (v^\alpha)\in\Omega_{v_0, v_1},$ where $\alpha = 1, 2, \ldots, m.$ Geometrically, $\Omega_{v_0, v_1}$ is a hyper-parallelepiped in $\mathbb{R}^m_+$ with the opposite diagonal points $v_0 = (v_0^1, v_0^2, \ldots, v_0^m)$ and $v_1 = (v_1^1, v_1^2, \ldots, v_1^m),$ which by the product order on $\mathbb{R}^m_+$ is equivalent to the closed interval $v_0\le v\le v_1.$ Suppose that we have cities denoted by $C_i, i = 0, 1, \ldots, M.$ The traffic network of each city $C_i$ comprises the set of nodes $N_i,$ representing railway stations, airports, crossings, etc., the set of directed links $L_i$ between the nodes, the set of origin-destination pairs $W_i$ and the set of routes $V_i.$ Moreover, it is assumed that each route $r_i\in V_i$ connects exactly one origin-destination pair. We denote by $V_i(w_i)$ the set of all $r_i\in V_i,$ which connects a given $w_i\in W_i.$ Let $x_i(v)\in \mathbb{R}^{|V_i|}$ be the flow trajectory, and for each $r_i\in V_i,$ let $x_{r_i}(v)$ represent the flow trajectory of the route $r_i$ over the multidimensional parameter $v.$ We take our functional setting for the flow trajectories to be the reflexive Banach space $L^{p_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}), \; p_i > 1,$ with the dual space $L^{q_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}),$ where $\frac{1}{p_i}+\frac{1}{q_i} = 1, \; i = 0, 1, \ldots, M.$ We assume that every feasible flow satisfies the following multidimensional capacity constraints for each $i = 0, 1, \ldots, M$

and the multidimensional traffic conservation law/demand requirements

where $\lambda_i(v), \mu_i(v)\in L^{p_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|})$ are given bounds such that $\lambda_i(v)\le\mu_i(v)$ and $\rho_i(v)\in L^{p_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|W_i|})$ is the given demand such that $\rho_i(v)\ge 0,$ and $\Phi_i = (\phi_{r_i, w_i})$ is the pair-route incidence matrix, whose entries are equal to 1 if route $r_i$ links the pair $w_i$ and $0$ otherwise. It is also assumed that

This assumption implies the non-emptiness of the set of feasible flows

The canonical bilinear form on $L^{q_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|})\times L^{p_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|})$ is defined as

and

where $\langle \cdot, \cdot \rangle$ denotes the Euclidean inner product and $dv = dv^1dv^2\ldots dv^m$ denotes the volume element of $\Omega_{v_0, v_1}.$

Remark 1. It is clear that for each $i = 0, 1, \ldots, M,$ the feasible set $K_i$ is closed, convex and bounded. From this, it follows that each $K_i$ is weakly compact.

Moreover, for each $x_i(v)\in K_i, \; i = 0, 1, \ldots, M,$ the cost trajectory is denoted by the mapping $A_i:K_i\to L^{q_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}),$ and we let $T_i:L^{p_0}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_0|})\to L^{p_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}), \; \; i = 0, 1, \ldots, M$ be bounded linear operators, where $T_0 = I^{L^{p_0}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_0|})}$ is the identity operator on $L^{p_0}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_0|}).$

Now, we formulate our multidimensional split variational inequality problem with multiple output sets (MSVIP-MOS) as follows:

find $x_0(v) \in K_0$ such that

and such that

Alternatively, the problem can be formulated in a more compact form as follows:

find $\; x_0(v) \in K_0\;$ such that

We denote the solution set of the MSVIP-MOS by

where $C_0^*, C_i^*, \; \; i = 1, 2, \ldots, M$ are the solution sets of VIPs (2.1) and (2.2), respectively.

We have the following specials cases of our formulated MSVIP-MOS:

$1.$ if the multidimensional parameter of evolution $v = (t^\alpha), \alpha = 1, 2, \ldots, m,$ then the MSVIP-MOS reduces to a multi-time split variational inequality problem with multiple output sets.

$2.$ if $M = 1,$ then our formulated MSVIP-MOS reduces to the multidimensional split variational inequality problem introduced by Singh ^[19].

$3.$ if the multidimensional parameter of evolution $v = (v^\alpha)\in \Omega_{v_0, v_1}, \; \alpha = 1, \ldots, m,$ is a single or linear dimensional parameter of evolution, that is, $m = 1,$ then $\Omega_{v_0, v_1}$ is simply the closed real interval $[v_0, v_1]$ in $\mathbb{R}_+$ (set of non-negative real numbers). Moreover, for convenience we set $v_0 = 0$ and $v_1 = T,$ where $T$ denotes an arbitrary time. Thus, $\Omega_{v_0, v_1} = [0, T]$ (a fixed time interval). In this case, the MSVIP-MOS reduces to an evolutionary split variational inequality problem with multiple output sets. In addition, if $M = 1,$ then the MSVIP-MOS reduces to the evolutionary split variational inequality problem studied by Singh et al. ^[18].

$4.$ if all the functions are independent of the multidimensional parameter of evolution $v,$ then the MSVIP-MOS reduces to the split variational inequality problem with multiple output sets studied by Alakoya and Mewomo ^[20]. In addition, if $M = 1,$ then the MSVIP-MOS reduces to the split variational inequality problem introduced by Censor et al. ^[17].

In line with the definition of an equilibrium flow for a dynamic traffic network problem given by Danielle et al. ^[12], we put forward the following definition for a multidimensional traffic network model with multiple networks, in terms of the introduced MSVIP-MOS.

Definition 2.1. $x_0(v)\in K_0$ is an equilibrium flow if and only if $x_0(v)\in \Gamma.$

The equilibrium flow of a traffic network has been investigated by several authors in terms of the Wardrop condition. Danielle et al. ^[12] modelled the traffic network equilibrium problem as a classical variational inequality problem, thereby establishing an equivalent relationship between the Wardrop condition and the classical variational inequality problem. On the other hand, Raciti ^[21] examined the vector form of the Wardrop equilibrium condition. Motivated by these results, here we consider the following MSWC-MOS.

Definition 2.2. For an arbitrary $x_0(v)\in K_0$ and a.e. on $\Omega_{v_0, v_1},$ the MSWC-MOS is defined as follows:

Alternatively, we can recast the definition as follows:

Definition 2.3. For an arbitrary $x_0(v)\in K_0$ and a.e. on $\Omega_{v_0, v_1},$ the MSWC-MOS can be defined as

where $x_i(v) = T_ix_0(v)\in K_i, \; \; i = 0, 1, \ldots, M.$

3.   User-oriented multidimensional traffic network equilibria with multiple networks

In this section, we present an equivalent form of the equilibria of our multidimensional traffic network model with multiple networks via the MSWC-MOS. We note that because of the form of the MSWC-MOS, it is more responsive to the user. Hence, we can conclude that it is a user-oriented equilibrium.

Now, we state and prove the following theorem, which is the main result of this section.

Theorem 3.1. Let $x_0(v)\in K_0$ be an arbitrary flow. Then $x_0(v)$ is an equilibrium flow if and only if it satisfies the conditions of the MSWC-MOS.

Proof. First, we suppose that $x_0(v)\in K_0$ satisfies the conditions of the MSWC-MOS. For a given origin-destination pair $w_i\in W_i, \; i = 0, 1, \ldots, M,$ we define the following sets:

By the MSWC-MOS, it follows that

It follows from Eq (3.1) that there exist real numbers $a_i\in\mathbb{R}, \; i = 0, 1, \ldots, M$, such that

Suppose that $y_i(v)\in K_i, \; i = 0, 1\ldots, M,$ are arbitrary flows. Then, for a.e. on $\Omega_{v_0, v_1}$ we have

Note that if $r_i\notin R_i,$ then $(T_ix_0(v))^{r_i} = \mu^{r_i}(v)$ and $\big(y_i^{r_i}(v)-(T_ix_0(v))^{r_i}\big)\le 0, \; i = 0, 1, \ldots, M.$ Hence, it follows that $\big(A_i^{r_i}(T_ix_0(v))-a_i\big) \big(y_i^{r_i}(v)-(T_ix_0(v))^{r_i}\big)\ge 0, \; i = 0, 1, \ldots, M,$ a.e. on $\Omega_{v_0, v_1}.$ In a similar manner, for all $r_i\in V_i(w_i)$ such that $A_i^{r_i}(T_ix_0(v)) > a_i$ a.e. on $\Omega_{v_0, v_1},$ we also have that $\big(A_i^{r_i}(T_ix_0(v))-a_i\big) \big(y_i^{r_i}(v)-(T_ix_0(v))^{r_i}\big)\ge 0, \; i = 0, 1, \ldots, M,$ a.e. on $\Omega_{v_0, v_1}.$ Consequently, for each $i = 0, 1, \ldots, M,$ we get

Observe that in Eq (3.2), the value of the term $\sum\limits_{w_i\in W_i}\sum\limits_{r_i\in V_i(w_i)}\big(y_i^{r_i}(v)-(T_ix_0(v))^{r_i}\big), \; i = 0, 1, \ldots, M,$ is zero by the traffic conservation law/demand requirements, i.e., $\sum\limits_{r\in V(w)}x^r(v) = \rho_w(v)$ for all $x(v)\in K$ and $w\in W$ a.e. on $\Omega_{v_0, v_1}.$ Since each $y_i(v)\in K_i, \; i = 0, 1, \ldots, M$ is arbitrary, it follows from Eq (3.2) that

Consequently, $x_0(v)$ is an equilibrium flow.

Next, we prove the converse statement by contradiction, that is, we suppose that $x_0(v)$ is an equilibrium flow, but it does not satisfy the conditions of the MSWC-MOS. Then, it follows that there exists origin-destination pairs $w_0\in W_0, w_i\in W_i$ and routes

together with a set $\Psi\subset\Omega_{v_0, v_1}$ having a positive measure such that we have the following cases:

$1.$

$\text{and such that}$

$\text{satisfies}$

$2.$

$\text{and such that}$

$\text{satisfies}$

$3.$

$\text{and such that}$

$\text{satisfies}$

$4.$

$\text{and such that}$

$\text{satisfies}$

$5.$ Case 1. with $x_i(v) = T_ix_0(v)\notin K_i, \; i = 1, 2, \ldots, M.$

$6.$ Case 2. with $x_i(v) = T_ix_0(v)\notin K_i, \; i = 1, 2, \ldots, M.$

$7.$ Case 3. with $x_i(v) = T_ix_0(v)\notin K_i, \; i = 1, 2, \ldots, M.$

Starting with the Case 1., let

where $v\in\Psi.$ Then, $\delta_0(v) > 0$ and $\delta_i(v) > 0, \; \; i = 0, 1, \ldots, M,$ a.e. on $\Psi.$ Next, we construct a flow trajectory $y_0(v)\in L^{p_0}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_0|})$ as follows:

In the same manner, we can define a flow trajectory $y_i(v)\in L^{p_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}), \; i = 1, 2, \ldots, M$ as

Hence, it is obvious that $y_0(v)\in K_0$ such that $y_0(v) = x_0(v)$ outside of $\Psi$ and $y_i(v)\in K_i$ such that $y_i(v) = x_i(v), \; i = 1, 2, \ldots, M,$ outside of $\Psi.$ Moreover, we have

By a similar argument, $x_i(v) = T_ix_0(v)\in K_i, \; i = 1, 2, \ldots, M,$ satisfies

It follows that $x_0(v)$ is not an equilibrium flow. Using a similar argument, we can easily show that $x_0(v)$ is not an equilibrium flow for Case 2 and Case 3. Furthermore, by the fact that $x_i(v) = T_ix_0(v)\in K_i, i = 1, 2, \ldots, M,$ in Cases 4, 5, 6 and 7, it is clear that $x_0(v)$ is not an equilibrium flow. Consequently, we have a contradiction, and this completes the proof of the theorem. □

4.   Existence and uniqueness of equilibria of a multidimensional traffic network with multiple networks

Here, we establish the existence and uniqueness of equilibria of our multidimensional traffic network model with multiple networks, which is formulated as a MSVIP-MOS. To prove the existence and uniqueness theorem, we will employ the concept of graph theory of operators. First, we present the following definitions and lemma, which will be needed in establishing our results in this section (see ^[18,19,22]).

Definition 4.1. The graph of operator $T_i, \; i = 1, 2, \ldots, M$ is defined by

We assume that $K_i\cap T_iK_0\ne\emptyset$ for each $i = 1, 2, \ldots, M,$ where $T_iK_0 = \{y_i(v)\in L^{p_i}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}): \exists\; x_0(v)\in K_0\; \; \text{such that}\; \; y_i(v) = T_ix_0(v)\}.$ It can easily be shown that $\text{Gr}~~ T_i$ is a convex set. Since $T_i$ is a bounded linear operator for each $i = 1, 2, \ldots, M,$ it follows that $T_i$ is also continuous. Thus, by the closed graph theorem we have that Gr $T_i$ is closed w.r.t. the product topology. Consequently, Gr $T_i$ is a nonempty, closed and convex subset of $K_0\times K_i, \; i = 1, 2, \ldots, M.$ By Remark 1, we have that $K_0\times K_i, \; i = 1, 2, \ldots, M$ is a weakly compact set. Thus, Gr $T_i, \; i = 1, 2, \ldots, M$ is a weakly compact set.

Definition 4.2. The cost operator $A$ is said to be demi-continuous at the point $x(v)\in K_0$ if it is strongly-weakly sequentially continuous at this point, that is, if the sequence $\{A(x_n(v))\}$ weakly converges to $A(x(v))$ for each sequence $\{x_n(v)\}\subset K_0$ such that $x_n(v)\to x(v),$ where the symbol "$\to$" denotes strong convergence.

Definition 4.3. The cost operator $A$ is said to be strictly monotone if

Definition 4.4. The convex hull of a finite subset $\{(x^1(v), Tx^1(v)), (x^2(v), Tx^2(v)), \ldots, (x^n(v), Tx^n(v))\}$ of Gr $T$ is defined by

Remark 2. Observe that

Definition 4.5. (^[19]) A set-valued mapping $Q:\text{Gr}\; T\to 2^{K_0\times K_1}$ is said to be a KKM^* mapping if, for any finite subset $(x^1(v), Tx^1(v)), (x^2(v), Tx^2(v)), \ldots, (x^n(v), Tx^n(v))$ of $\text{Gr} ~~ T,$

^*Knaster–Kuratowski–Mazurkiewicz lemma

Lemma 4.6. (^[19] KKM-Fan theorem) Let $Q:\mathit{\text{Gr}}\; T\to 2^{K_0\times K_1}$ be a KKM mapping with closed set values. If $Q(x(v), Tx(v))$ is compact for at least one $(x(v), Tx(v))\in \mathit{\text{Gr}}\; T,$ then

We are now in a position to state and prove the existence theorem.

Theorem 4.7. Suppose that for $i = 1, 2, \ldots, M,$ the cost operators $A_0, A_i$ are demi-continuous, and that there exist $B_0\times B_i\subseteq\mathit{\text{Gr}}\; T_i$ nonempty and compact, and $D_0\times D_i\subseteq\mathit{\text{Gr}}\; T_i$ compact such that for all $(x_0(v), T_ix_0(v))\in \mathit{\text{Gr}}\; T_i\backslash B_0\times B_i$ there exists $(y_0(v), T_iy_0(v))\in D_0\times D_i$ with $\int_{\Omega_{v_0, v_1}}\langle A_0(x_0(v)), y_0(v)-x_0(v) \rangle dv < 0$ and $\int_{\Omega_{v_0, v_1}}\langle A_i(T_ix_0(v)), T_iy_0(v)-T_ix_0(v) \rangle dv < 0.$ Then, the MSVIP-MOS has a solution.

Proof. First, we define the following set-valued mappings:

● for all $x_0^*(v)\in K_0$, we define the mapping $P_0:K_0\to 2^{K_0}$ by

● for all $y_i^*(v)\in K_i, \; i = 1, 2, \ldots, M,$ we define $P_i:K_i\to 2^{K_i}$ by

● for all $(x_0(v), T_ix_0(v))\in \text{Gr}\; T_i, \; i = 1, 2, \ldots, M,$ we define the mappings $Q_i:\text{Gr}\; T_i\to 2^{K_0\times K_i}$ by

and

Clearly, $(x_0(v), T_ix_0(v))\in Q_i(x_0(v), T_ix_0(v)), \; i = 1, 2, \ldots, M.$ Therefore, $Q_i(x_0(v), T_ix_0(v))$ is nonempty for each $i = 1, 2, \ldots, M.$

Next, we prove that for each $i = 1, 2, \ldots, M, \; Q_i$ is a KKM mapping. We proceed by contradiction, i.e., by assuming that $Q_i$ is not a KKM mapping for each $i = 1, 2, \ldots, M.$ Then for each $i = 1, 2, \ldots, M,$ there exists a finite subset $\{(x^1(v), T_ix^1(v)), (x^2(v), T_ix^2(v)), \ldots, (x^n(v), T_ix^n(v))\}$ of $\text{Gr}\; T_i$ such that

By the definition of a convex hull, there exists the following, for each $i = 1, 2, \ldots, M,$

such that

where $\beta_i^j\in [0, 1]$ and $\sum_{j = 1}^n\beta_i^j = 1$ for each $i = 1, 2, \ldots, M.$ The expression (4.2) implies that

Consequently, for any $j = \{1, 2, \ldots, n\},$ we have the following cases:

$1.$ $\int_{\Omega_{v_0, v_1}}\langle A_0(\hat{y}_0(v)), x^j(v)-\hat{y}_0(v) \rangle dv < 0$ and $\int_{\Omega_{v_0, v_1}}\langle A_i(T_i\hat{y}_0(v)), T_ix^j(v)-T_i\hat{y}_0(v) \rangle dv < 0,$ $i = 1, 2, \ldots, M.$

$2.$ $\int_{\Omega_{v_0, v_1}}\langle A_0(\hat{y}_0(v)), x^j(v)-\hat{y}_0(v) \rangle dv\ge 0$ and $\int_{\Omega_{v_0, v_1}}\langle A_i(T_i\hat{y}_0(v)), T_ix^j(v)-T_i\hat{y}_0(v) \rangle dv < 0,$ $i = 1, 2, \ldots, M.$

$3.$ $\int_{\Omega_{v_0, v_1}}\langle A_0(\hat{y}_0(v)), x^j(v)-\hat{y}_0(v) \rangle dv < 0$ and $\int_{\Omega_{v_0, v_1}}\langle A_i(T_i\hat{y}_0(v)), T_ix^j(v)-T_i\hat{y}_0(v) \rangle dv\ge0,$ $i = 1, 2, \ldots, M.$

Case 1 implies that

Moreover, it is clear that $P_0(x_0^*)$ and $P_i(T_ix_0^*)$ are convex, for each $x_0^*\in K_0$ and $T_ix_0^*\in K_i,$ $i = 1, 2, \ldots, M.$ Consequently, we have

and

By the fact that

and by Remark 2, we have

which implies that $\hat{y}_0(v)\in P_0(\hat{y}_0(v))$ and $T_i\hat{y}_0(v)\in P_i(T_i\hat{y}_0(v)),$ $i = 1, 2, \ldots, M.$

Thus, we have

which are contradictions.

By a similar argument, we can easily show that the other cases also lead to contradictions. Hence, for each $i = 1, 2, \ldots, M, \; \; Q_i$ is a KKM mapping.

Next, we claim that for each $i = 1, 2, \ldots, M, \; \; Q_i$ is a closed set-valued mapping for each $(x_0(v), T_ix_0(v))\in \text{Gr}\; T_i$ w.r.t. the weak topology of $K_0\times K_i, \; i = 1, 2, \ldots, M.$ Let $(x_0(v), T_ix_0(v))\in \text{Gr}\; T_i$ be arbitrary and suppose that $\{(x_0^n(v), T_ix_0^n(v))\}_{n = 0}^\infty$ is a sequence in $Q_i(x_0(v), T_ix_0(v)),$ which converges strongly to $(y_0(v), T_iy_0(v)),$ $i = 1, 2, \ldots, M.$ Since for each $n\in\mathbb{N}, \; \; (x_0^n(v), T_ix_0^n(v))\in Q_i(x_0(v), T_ix_0(v)),$ $i = 1, 2, \ldots, M,$ we have the following for each $n\in\mathbb{N}$

Since $A_0, \; A_i\;, i = 1, 2, \ldots, M$ are demi-continuous and $T_0, \; T_i\;, i = 1, 2, \ldots, M$ are continuous, by taking the limit as $n\to\infty$ in Eq (4.3), we obtain

and

which implies that

for each $i = 1, 2, \ldots, M.$ Thus, $Q_i(x_0(v), T_ix_0(v))$ is closed (w.r.t. the strong topology) for each

By the hypothesis in Theorem 4.7, it follows that $Q_i(x_0(v), T_ix_0(v)), \; i = 1, 2, \ldots, M$ is compact (w.r.t. the strong topology) for each

Consequently, by the KKM-Fan theorem, we have

This implies that there exists

such that

for all

Now, we consider the subsets $F_0\subset K_0, \; F_i\subset K_i,$ $i = 1, 2, \ldots, M,$ such that

Then, we can write that there exists

such that

for all

Consequently, we have that for all $(x_0(v), T_ix_0(v))\in F_0\times F_i,$

Let

and observe that $x_0^*(v)$ and

are fixed in Eq (4.4). Thus, Eq (4.4) can be rewritten as $x_0^*(v) \in F_0$, such that

and such that

Hence, it follows that the MSVIP-MOS has a solution $x_0^*(v)\in F_0\subset K_0.$ □

Next, we present the result on the uniqueness of the solution of the MSVIP-MOS in the following corollary.

Corollary 1. If the cost operators $A_i, \; i = 0, 1, \ldots, M$ are strictly monotone on $K_i, \; i = 0, 1, \ldots, M,$ then the MSVIP-MOS has a unique solution.

Proof. Suppose to the contrary that the MSVIP-MOS does not have a unique solution. Let $x_0(v)\in K_0$ be a solution of the MSVIP-MOS. Then, we have

Let $\hat{x}_0(v)\in K_0$ be another solution of the MSVIP-MOS such that $x_0(v)\ne \hat{x}_0(v).$ Then, it follows that

We can rewrite Eq (4.5) as

By the strict monotonicity of the $A_i, \; i = 0, 1, \ldots, M,$ together with the fact that $x_0(v)\ne \hat{x}_0(v),$ we get

By adding Eqs (4.7) and (4.8), we obtain

which contradicts Eq (4.6). Therefore, it follows that $\hat{x}_0(v)$ is not a solution of the MSVIP-MOS. Consequently, the MSVIP-MOS has a unique solution. □

5.   Numerical experiments for the multidimensional traffic model with multiple networks

In this section, motivated by the work of Cojocaru et al. ^[23], we study our multidimensional traffic model with multiple networks by employing the theory of a projected dynamical system (PDS). Dupuis and Nagurney ^[24] were the first to introduce and study the PDS. Furthermore, they established the connections of PDS with the classical variational inequality problem. For more details about the various areas of applications of the PDS, we refer interested readers to ^[23,25].

Inspired by the results from the aforementioned works, here, we introduce and formulate a multidimensional split projected dynamical system with multiple output sets (MSPDS-MOS) for $p_i = 2, \; \; i = 0, 1, \ldots, M$ as follows:

where $A_i:K_i\to L^{2}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}), \; i = 0, 1, \ldots, M,$ are Lipschitz continuous vector fields and the operators $\Pi_{K_i}:K_i\times L^{2}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|}), \; i = 0, 1, \ldots, M$ are defined by

where $\text{proj}_{K_i}(\cdot)$ are the nearest point projection of a given vector onto the sets given by $K_i.$

Alternatively, the MSPDS-MOS can be formulated as follows:

Find $x_0(\cdot)\in K_0$ such that

For clarity, here we have represented the elements of the space $L^{2}(\Omega_{v_0, v_1}, \mathbb{R}^{|V_i|})$ at fixed $v\in\Omega_{v_0, v_1}$ by $x(\cdot).$ Observe that for all $v\in\Omega_{v_0, v_1},$ a solution of the MSVIP-MOS represents a static state of the underlying system and the static states define one or more equilibrium curves when $v$ varies over $\Omega_{v_0, v_1}.$ On the contrary, the time $\tau$ defines the dynamics of the system over the interval $[0, \infty)$ until it attains one of the equilibria on the curves. Clearly, the solutions to the MSPDS-MOS lie in the class of absolutely continuous functions with respect to $\tau,$ mapping $[0, \infty)$ to $K_i, \; i = 0, 1, \ldots, M.$ Before we describe the procedure to solve the MSVIP-MOS, we present the following useful definitions motivated by ^[26,27].

Definition 5.1. A point $\hat{x}_0(\cdot)\in K_0$ is called a critical point for the MSPDS-MOS if

and the point $\hat{y}_i(\cdot) = T_i\hat{x}_0(\cdot)\in K_i$ satisfies

Alternatively, the critical point for the MSPDS-MOS can be defined as follows: $\hat{x}_0(\cdot)\in K_0$ is called a critical point for the MSPDS-MOS if

Definition 5.2. The polar set $K^o$ associated with $K$ is defined by

Definition 5.3. The tangent cone to the set $K$ at $x(\cdot)\in K$ is defined by

where cl denotes the closure operation.

Definition 5.4. The normal cone of $K$ at $x(\cdot)\in K$ is defined by

Alternatively, we can express this as $\hat{T}_K(x(\cdot)) = [N_K(x(\cdot))]^o.$

Definition 5.5. The projection of $x(\cdot)\in L^{2}(\Omega_{v_0, v_1}, \mathbb{R}^{|V|})$ onto $K$ is defined by

Remark 3. The projection map $\text{proj}_K(\cdot)$ satisfies the following property for each $x(\cdot)\in L^{2}(\Omega_{v_0, v_1}, \mathbb{R}^{|V|}):$

We have the following results, which follow from Proposition 2.1 and 2.2 in ^[26].

Proposition 1. For all $x(\cdot)\in K$ and $y(\cdot)\in L^{2}(\Omega_{v_0, v_1}, \mathbb{R}^{|V|}), \; \Pi_K(x(\cdot), y(\cdot))$ exists and $\Pi_K(x(\cdot), y(\cdot)) = \mathit{\text{proj}}_{\hat{T}_K(x(\cdot))}(y(\cdot)).$

Proposition 2. For all $x(\cdot)\in K,$ there exists $n(\cdot)\in N_K(x(\cdot))$ such that $\Pi_K(x(\cdot), y(\cdot)) = y(\cdot)-n(\cdot), \; \; \forall y(\cdot)\in L^{2}(\Omega_{v_0, v_1}, \mathbb{R}^{|V|}).$

Now, we prove the following theorem, which establishes the relationship between solutions of MSVIP-MOS and the critical points of the MSPDS-MOS.

Theorem 5.6. The point $x_0^*(\cdot)\in K_0$ is a solution of the MSVIP-MOS if and only if it is a critical point of the MSPDS-MOS.

Proof. First, we suppose that $x_0^*(\cdot)\in K_0$ is a solution to the MSVIP-MOS, that is,

which implies that

From the last inequality, it follows that

By Proposition 2, we have

which implies that $x_0^*(\cdot)$ is a critical point of the MSPDS-MOS.

Conversely, suppose that $x_0^*(\cdot)$ is a critical point of the MSPDS-MOS. Then, Eq (5.1) holds. By Proposition 1, it follows that

Applying Remark 3, we obtain

which gives

From this, it follows that $x_0^*(\cdot)$ is a solution of the MSVIP-MOS. □

At this point, we present the method for finding the solution of the MSVIP-MOS. In our numerical experiments, we consider the case in which $v = (t^\alpha), \alpha = 1, 2, \ldots, m,$ that is, there are $m$-dimensional time parameters. We have established the existence and uniqueness of equilibria for the MSVIP-MOS in Section 4. Moreover, Theorem 5.6 guarantees that any point on a curve of equilibria in the set $\Omega_{v_0, v_1}$ is a critical point of the MSPDS-MOS and vice versa. Taking into consideration all of these facts, now we discretize the set $\Omega_{v_0, v_1}$ as follows: $\Omega_{v_0, v_1}:(v_0^1, v_0^2, \ldots, v_0^m) = (t_0^1, t_0^2, \ldots, t_0^m) < (t_1^1, t_1^2, \ldots, t_1^m) < \ldots < (t_j^1, t_j^2, \ldots, t_j^m) < \ldots < (t_n^1, t_n^2, \ldots, t_n^m) = (v_1^1, v_1^2, \ldots, v_1^m).$ Consequently, for each $t_j = (t_j^1, t_j^2, \ldots, t_j^m), \; j = 0, 1, \ldots, n,$ we obtain a sequence of the MSPDS-MOS on the distinct, finite-dimensional, closed and convex sets denoted by $K_{t_j}.$ After evaluating all of the critical points of each MSPDS-MOS, we obtain a sequence of critical points and from this, we generate the curves of equilibria by interpolation.

5.1.   Example 1

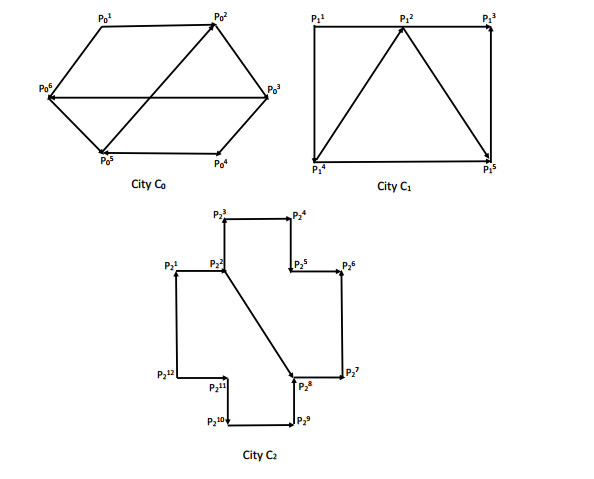
To demonstrate the implementation of this procedure, we consider the transportation network patterns of three cities $C_0, C_1$ and $C_2$ as shown in Figure 1 below.

We suppose that a bus company has stations at nodes $P_0^{1}$ and $P_0^{2}$ in City $C_0,$ at nodes $P_1^{1}$ and $P_1^{4}$ in City $C_1$ and at nodes $P_2^{1}$ and $P_{2}^{12}$ in City $C_2.$ In City $C_0,$ the buses from stations $P_0^{1}$ and $P_0^{2}$ have to deserve the locations $P_0^{3}$ and $P_0^{5},$ respectively. In City $C_1,$ the buses from stations $P_1^{1}$ and $P_1^{4}$ have to deserve the locations $P_1^{2}$ and $P_1^{3},$ respectively. While in City $C_2,$ the buses from stations $P_2^{1}$ and $P_{2}^{12}$ have to deserve the locations $P_2^{6}$ and $P_2^{8},$ respectively.

Hence, the network of City $C_0$ comprises six nodes and eight links, and we assume that the origin-destination pairs are $w_0^1 = (P_0^1, P_0^3)$ and $w_0^2 = (P_0^2, P_0^5),$ which are respectively connected by the following routes:

Let $\Omega_{v_0, v_1} = \Omega_{0, 3} = [0, 3]^2.$ The set of feasible flows, $K_0$, is given by

the cost function $A_0:K_0\to L^2(\Omega_{0, 3}, \mathbb{R}^4)$ is defined by

and the bounded linear operator

is defined by $T_0x(t) = (x_1(t), x_2(t), x_3(t), x_4(t)),$ where $x(t) = (x_1(t), x_2(t), x_3(t), x_4(t)).$

Moreover, the network of City $C_1$ is made up of five nodes and seven links, and we assume that the origin-destination pairs are $w_1^1 = (P_1^1, P_1^2)$ and $w_1^2 = (P_1^4, P_1^3),$ which are respectively connected by the following routes:

The set of feasible flows, $K_1$, is given by

the cost function $A_1:K_1\to L^2(\Omega_{0, 3}, \mathbb{R}^5)$ is defined as

and the bounded linear operator

is defined by

where

Also, the network of City $C_2$ is composed of twelve nodes and thirteen links, and we assume that the origin-destination pairs are $w_2^1 = (P_2^1, P_2^6)$ and $w_2^2 = (P_2^{12}, P_2^8),$ which are respectively connected by the following routes:

The set of feasible flows, $K_2$, is given by

the cost function $A_2:K_2\to L^2(\Omega_{0, 3}, \mathbb{R}^4)$ is defined by

and the bounded linear operator

is defined by

where

It can easily be verified that all the hypotheses of Theorem 4.7 are satisfied and that the cost operators denoted by $A_i, \; i = 0, 1, 2$ are strictly monotone on the sets of feasible flows denoted by $K_i, \; i = 0, 1, 2.$ Thus, the MSVIP-MOS has a unique solution. We select

Then, we have a sequence of MSPDS-MOS defined on the feasible sets

For evaluating the unique equilibrium, we have the following system at $t_j:$

After some computations, we obtain the equilibrium points which are presented in Tables 1–3. Then, we interpolate the points in Tables 1–3 to get the curves of equilibria displayed in Figures 2–4.

Table 1 displays the equilibrium points at each instant for City $C_0$ while the traffic network pattern of City $C_0$ is presented in Figure 2. We observe from Table 1 that at the beginning of the equilibrium flow in City $C_0,$ the flow on each of the routes connecting the origin-destination pair $w_0^2$ is about $1.5$ times the flow on each of the routes connecting the origin destination pair $w_0^1,$ and this factor increases gradually over the equilibrium flow time to about $1.9.$

Table 2 shows the equilibrium points at each instant for City $C_1$ and the traffic network pattern of the city is presented in Figure 3. We note from Table 2 that at the beginning of the equilibrium flow in City $C_1,$ the flow on each of the routes connecting the origin-destination pair $w_1^1$ is about $1.3$ times the flow on each of the routes connecting the origin destination pair $w_1^2,$ and this factor increases gradually over the equilibrium flow time to about $1.4.$

Table 3 presents the equilibrium points at each instant for City $C_2$ while the traffic network pattern of the city is presented in Figure 4. It is observed from Table 3 that at the beginning of the equilibrium flow in City $C_2,$ the flow on each of the routes connecting the origin-destination pair $w_2^2$ is about $1.8$ times the flow on each of the routes connecting the origin destination pair $w_2^1.$ Contrary to the observation in cities $C_0$ and $C_1,$ this factor decreases gradually over the equilibrium flow time to about $1.4.$ We observe from the results that when the system is in equilibrium every route in each of the three cities is in use. Moreover, routes connecting the same origin-destination pair in each city have an equal amount of flow at each instant $t$ within the equilibrium flow time.

5.2.   Example 2: Extension to models with heterogeneous networks

In this section, we illustrate how our results can be applied to study models with heterogeneous networks. For that purpose, we consider a City $C$, which comprises a traffic network of human-driven vehicles (HDVs), traffic network of connected automated vehicles (CAVs) and an electricity network as shown in Figure 5 below.

We denote the traffic network of human-driven vehicles by NHDV, while we denote the traffic network of connected automated vehicles by NCAV and the electricity network by EN. Here, it is assumed that the EN is analogous to the traffic network. Suppose that within the network coverage of CAVs, we have commuters such that some of them need to be transported from location $P^1$ to location $P^3$ and others from location $P^1$ to location $P^4$, using CAVs. On the other hand, we assume that within the network coverage of HDVs, we have commuters who need to be transported by HDVs from locations $Q^1$ and $Q^{12}$ to locations $Q^6$ and $Q^8,$ respectively. Also, we suppose that within the EN, electricity needs to be transmitted from point $R^1$ to point $R^4.$

Therefore, the NCAV consists of four nodes and six links, and we assume that the origin destination pairs are $w_p^1 = (P^1, P^3)$ and $w_p^2 = (P^1, P^4),$ which are connected respectively by the following routes:

The set of feasible flows $K_0$ is given by

the cost function is given by $A_0:K_0\to L^{q_0}(\Omega_{v_0, v_1}, \mathbb{R}^5)$ and the bounded linear operator $T_0: L^{p_0}(\Omega_{v_0, v_1}, \mathbb{R}^5)\to L^{p_0}(\Omega_{v_0, v_1}, \mathbb{R}^5).$

Similarly, the NHDV comprises twelve nodes and thirteen links, and we assume that the origin-destination pairs are $w_q^1 = (Q^1, Q^6)$ and $w_q^2 = (Q^{12}, Q^8),$ which are respectively connected by the following routes:

The set of feasible flows $K_1$ is given by

the cost function is given by $A_1:K_1\to L^{q_1}(\Omega_{v_0, v_1}, \mathbb{R}^4)$ and the bounded linear operator $T_1: L^{p_1}(\Omega_{v_0, v_1}, \mathbb{R}^4)\to L^{p_1}(\Omega_{v_0, v_1}, \mathbb{R}^4).$

On the other hand, the EN consists of six nodes and seven links, and we assume that the origin-destination pair is $w_r^1 = (R^1, R^4),$ which is connected by the following routes:

The set of feasible flows $K_2$ is given by

the cost function is given by $A_2: K_2\to L^{q_2}(\Omega_{v_0, v_1}, \mathbb{R}^3)$ and the bounded linear operator

Then, it follows that $x_0(v)\in K_0$ is an equilibrium flow if and only if

Therefore, by employing the model (5.2), we can determine the equilibrium flows of the NCAV, NHDV and EN simultaneously.

6.   Conclusion

We introduced and studied a new class of split inverse problem called the MSVIP-MOS. Our proposed model is finite-dimensional and essentially an assignment problem. It comprises a multidimensional parameter of evolution. To demonstrate the applicability of our proposed model in the economic world, we formulated the equilibrium flow of multidimensional traffic network models for an arbitrary number of locations. Moreover, we proposed a method for solving the introduced problem and validated our results with some numerical experiments. Finally, to further demonstrate the usefulness of our newly introduced model, we applied our results to study the network model of a city with heterogeneous networks that comprises CAVs and legacy (human-driven) vehicles, alongside the EN, e.g. for charging the CAVs, and we formulated the equilibrium flow of this network model in terms of the newly introduced MSVIP-MOS. However, we note that the problem investigated in this study belongs to the class of linear (split) inverse problems, and as such our results are not applicable to nonlinear traffic flow models. In our future study, we will be interested in extending our results to this class of models.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

This work was supported by the HEA (the Irish Higher Education Authority) North-South Research Programme 2021. The authors would like to thank the reviewers for their constructive comments and recommendations, which have helped to improve the quality of the manuscript. Vikram Pakrashi would like to also acknowledge Science Foundation Ireland NexSys 21/SPP/3756.

Conflict of interest

The authors declare that there is no conflict of interest.