Stability and implementation of a cycle-based max pressure controller for signalized traffic networks

1.   Introduction

This article investigates the design and stability of decentralized controller for vertical queueing networks. In a vertical queueing network, agents traveling across the network are stored in point queues that do not inhabit a "horizontal" position along the length of a network edge, but instead are considered to be stored in "vertical" stacks at each node. Such models are inherited from fields such as supply chain management or internet routing, but are also representative of signalized urban traffic networks and have recently regained popularity for use in applications of arterial traffic control [6,1,17,20]. The concept of a stabilizing network controller, or one which ensures that the mean length of all queues in the network remain bounded, is relevant to many applications such as communications networks [8,11,12] or industrial systems [7,4,10].

In the present work we examine a vertical queueing model in which only a finite set of non-conflicting flow movements (or phases) can be permitted to proceed simultaneously across each network node. Phase actuation is dictated by a controller, such as a traffic light signaling specific combinations of green lights. Specifically, we consider application of a maximum pressure controller.

Max pressure is a distributed network control policy derived from the concept of a "back-pressure" or "MaxWeight" controller, which was first studied in the context of routing packets through a multi-hop communications network [16]. It has since been introduced to many other networked applications including process scheduling [5], manufacturing [15], wireless networks [3] and general stochastic networks [14]. The idea was applied to road traffic management more recently by [18] as well as [19]. The concept is intuitive: at each controlled network node, priority is given to the control phase which will be able to service the most demand given knowledge of both available upstream demand and the subsequent feasibility of downstream queues. It is a particularly attractive concept for control of a signalized urban traffic network because it can be operated in a distributed manner on local controller hardware (such as locally-managed traffic lights) but still provides theoretical guarantees on network-wide performance. Therefore unlike existing adaptive signal control systems such as SCOOT [9] or SCATS [13], max pressure does not require communications between each node or central control infrastructure. Also, max pressure is a universal algorithm which does not have to be optimized and manually tuned for a given network geometry or expected flows. In fact it operates with no a-priori knowledge of demand beyond a basic requirement of serviceability. This presents a huge benefit over most existing traffic control systems which require a timely and expensive re-timing process in the event of changes in demand patterns.

The original adaptation of this controller in [18], however, does not fully consider the practical limitations on the rate of queue measurement and signal actuation in vehicle traffic networks. For example, it has no bound on the rate of signal switches which may occur relative to the rate of modeled queue formation and dissipation. In implementation, a traffic signal incurs a penalty upon every change in actuation in the form of capacity loss due to "intersection clearance time": a 2-3 second period where all movements are given a red light in order to allow traffic from the previous phase to clear the intersection before possibly conflicting traffic can be permitted to enter. Max pressure also lacks the ability to synchronize adjacent signals in a network by constraining the actuation periods of critical phases to fixed relative offsets. This feature is valued by traffic managers who wish to promote continuity of flow and limit vehicle stops on a preferred throughway. Furthermore, a standard max pressure implementation provides no explicit lower bound on the service rate of queues on minor approaches where demand may be very low relative to the main direction.

These limitations motivate a new extension of the max pressure algorithm which bounds signal switches and can maintain timed cyclical behaviors for signal coordination and queue service equity. While a similar concept was suggested in [18], the current work further extends a simple proportional phase controller to allow model dynamics to explicitly act at a faster rate than the controller update period. We then extend the stability proof of [18] to prove that our cycle-based max pressure (Cb-MP) controller still provides the desired guarantee of queue stability with a penalty to the theoretical bound on queue lengths due to the decreased rate of controller update.

The remainder of this article is organized as follows: Sections 2-3 describe the modeling framework and standard max pressure controller from [18]; Section 4 formulates an extended cycle-based max pressure controller; Section 5 proves that this extended controller stabilizes a vertical queueing network; finally, Section 6 presents numerical results provided by this controller using a microscopic traffic simulation running in the Aimsun platform.

2.   Network model dynamics

We consider a network of arterial roads with infinite storage capacity, modeled topologically as a graph with road segments (or links) being graph edges and intersections being nodes. We require that each link in the network has an exit path, or a continuous set of connected links on which vehicles can travel from the original link to eventually exit the network. This would in fact be the case in a practical road network.

An individual link $l\in\mathcal{L}$ can be either at the entry of the network $\left(l \in \mathcal{L}_{{\rm{ent}}}\right)$ or in the interior of the network $\left(l \in\mathcal{L}\backslash \mathcal{L}_{{\rm{ent}}} \right)$. The inflow on network entry links is defined entirely by a random network demand flow. We assume the expectation of this randomized boundary demand is known. The inflow on all other links (referred to as link demand) depends on observable queues on upstream links and the known set of constraints imposed by physical characteristics of the modeled network.

Each link in the network model can contain multiple queues, each of which correspond to separate movements: all vehicles in a single queue are intending to advance onto the same subsequent link. We describe the dynamics of network queues as a discrete time dynamical model using the following notation:

● A movement $(l, m)$ distinguishes an intention to travel from link $l$ to immediately downstream link $m$;

● A queue $x(l, m)(t)$ is the number of vehicles on link $l$ waiting to enter link $m$ at time step $t$, and $X(t)$ is the set (vector or matrix) of all the queue lengths on the network at time step $t$;

● A link capacity $C(l, m)(t)$ is the number of vehicles that can travel from link $l$ to link $m$ in time step $t$ given maximum demand on queue $x(l, m)$. To model heterogenous driver behaviors we assume that $C(l, m)(t)$ is a random variable, but it has known expectation $c(l, m)$.

● Random variable $R(l, m)(t) = \frac{x(l, m)(t)}{\sum_{k}x(l, k)(t)}$ is the turn ratio at time $t$. $R$ is assumed to have known expectation $r(l, m)\in[0, 1]$.

● The demand vector $d$ of dimension $|\mathcal{L}_{{\rm{ent}}}|$ specifies demands at network entry links;

● The flow vector $f$ of dimension $|\mathcal{L}|$ denotes flows on all links of the network such that $f_{l}$ is the flow in link $l$.

The expected flow through an entry link is defined to be equal to the expected demand on that link. Because we consider fixed turn ratios, the flow on an internal link is a weighted sum of the flows on the upstream neighboring links (with weights equal to the relevant expected turn proportions). Hence there is necessarily a linear relationship between the expected link flow $f$ and the boundary demand $d$:

where the (possibly non-unique) matrix $P$ depends only on observed routing proportions within the network.

Intersection signal controller. A road intersection is modeled as a node in our framework. Controllers (traffic signals) are placed at every node to limit the set of queues permitted to discharge at any given time. A set of movements that can be simultaneously actuated without flow conflicts is called a phase. Each permissible phase for a given intersection can be represented as a binary control matrix $S$ that is defined as follows:

We denote the known, finite set of permissible control matrices for a single node as $U$. Note that $U$ can be different for each node, as its construction depends on the number and physical arrangement of node entrances and egresses.

At each modeled time step $t$, a single control matrix $S(t)\in U$ encodes which single non-conflicting set of queues approaching the intersection are permitted to discharge during that time step. However in this work we consider a relaxed controller which operates on a finite set of contiguous time steps. This relaxed controller is defined as a matrix $\tilde{S}(t)$, which is populated with elements $\tilde{S}(l, m)\in [0, 1]$ that each represent the fraction of the relevant set of time steps that are allocated to the movement $\{l, m\}$. Such a relaxed controller must be able to be expressed as a convex combination of all $S\in U$,

This work will demonstrate how to optimally select $\lambda_S$ for a given set of time steps $\big(t+1, t+2, ..., t+\tau\big)$ based only on the state of the network queues at the previous time period $\big(t-\tau, t-(\tau-1), ..., t\big)$.

Queue dynamics. The evolution of network queue lengths $X(t)$ can be seen as a Markov chain: the state at time $(t+1)$ is a function of only the state at time $t$ and external demand $d$,

Define $[\, a \wedge b\, ]: = \min\{a, b\}$. To describe queue dynamics explicitly, we must make a distinction between entry links and internal links: if $l\in \mathcal{L}_{{\rm{ent}}}$,

and if $l\in \mathcal{L}\backslash\mathcal{L}_{{\rm{ent}}}$,

Demand feasibility. We focus on networks for which the boundary inflow demands are feasible——that is, the network is servicing a distribution of inflows for which it is possible to find a controller that allows in average more departures than arrivals at each link. Note that a stabilizing controller, defined as one that ensures that the mean length of all queues remains bounded, would not be possible by definition if demands were not feasible.

Define $\mathcal{C}(U)$ to be the convex hull of the set of permissible control matrices $U$. The following properties are then shown in [18]:

Property 1. A matrix $M$ is in $\mathcal{C}(U)$ iff $\exists$ a sequence of control matrices $\overline S = \{S(1), S(2), ..., S(t), ... \vert S(\cdot) \in U\}$ such that $\forall (l, m)$

The element $M(l, m)$ in (7) can be interpreted as the long-term average proportion of intersection capacity given to movement $(l, m)$. Hence define $M_{\overline{S}}$ to be the long-term control proportion matrix constructed as in (7) using a specific control sequence $\overline{S} = \{S(1), S(2), ..., S(t), ...\}$.

Property 2. A demand $d$ is feasible if and only if $\exists \; M_{\overline S} \in \mathcal{C}(U)$ and $ \varepsilon > 0$ such that

where $f = dP$ as in (1).

Define $D^0$ to be the set of all average demand vectors $d$ that satisfy (8) and are therefore feasible.

A network is stable if the following quantity is bounded:

where $\vert X\vert_{1} = \sum_{l, m} \vert x(l, m)\vert$ and the network state evolves according to dynamics under state dynamics (5)-(6).

3.   Max pressure controller

Consider a weight assigned to each queue $(l, m)$ as a function of all network queue lengths $X$:

where $Out(m)$ is the set of all links receiving flow from link $m$. The pressure $\gamma(S)$ that is potentially alleviated by a control action $S$ at time step $t$ is defined as follows:

At each time step $t$, the standard max pressure controller $u^{*}(X(t))$ explicitly choses the phase $S^*\in U$ that maximizes $\gamma(S)(X(t))$:

Reference [18] shows the following stability result for the standard max pressure controller:

Theorem 3.1. The max pressure control $u^{*}$ is stabilizing, i.e. the quantity in equation (9) remains bounded, whenever the average demand vector $d = \lbrace d_{l}\rbrace$ is within the set of feasible demands $D^0$.

We omit further explanation of the above theorem in this paper for brevity.

This theoretical guarantee is one of the many attractive qualities of max pressure for controlling vehicular traffic in urban road networks. Yet the controller as originally formulated is not practical for application on a signalized traffic network for three reasons:

a) it does not account for capacity reductions (lost time) due to excessive signal switching,

b) it cannot enforce coordination between subsequent intersections for purposes of maximizing flow continuity, and

c) it does not provide guarantees that low-demand queues will be served within a finite time period.

4.   Cycle-based max pressure (Cb-MP)

The above limitations motivate our extension of the standard immediate feedback max pressure control algorithm. In the following section, we define a new cycle-based max pressure (Cb-MP) controller which bounds the number of signal switches per fixed time period, provides capacity for standard signal coordination methods, and can easily guarantee a minimum service rate for all intersection phases.

For safety reasons, an intersection controller cannot switch signal phase actuation immediately. Instead, it must incorporate a pause of $R\approx2.5$ seconds in which all signal phases have a red light. This clearance time allows all vehicles in the previously actuated phase to clear the intersection before a conflicting phase can be permitted to use the intersection. In the standard formulation of max pressure, the controller chooses an appropriate action based feedback received at every time step of the modeled dynamics. To accurately capture queuing behaviors observed on arterial roadways, a model would need to operate with a time discretization of $\Delta t < 10$ seconds. A signal switch at every time step could therefore result in more than 25% loss of intersection service capacity, which is not considered in the theoretical examination presented in [18].

In this work, we explicitly specify the number of signal switches that occur in a fixed number of model time steps using the familiar concept of a signal cycle. As typical with modern traffic signals Cb-MP rotates through all available signal phases within a known time period. We define cycle time $\tau$ as a predefined number of model time steps and require that each controller phase $S$ must be green for some proportion $\lambda_S \geq \kappa_S$ of the $\tau$ steps, where the minimum green splits $\kappa_S \in (0, 1) \; \forall \; S \in U $ are parameters selected by a network manager to enforce equity in movement actuation.

The selection of a cycle time $\tau$ intuitively affects intersection capacity. Our proof of network stability in the following sections relies on the fact that road links are undersaturated: that is, the expected demand is served (on average) within a signal cycle. To avoid link saturation, we pose the following convex optimization problem (extended from that in [2]) to determine minimum constrained feasible actuation time $\Lambda^*$:

where $\kappa_S \in [0, 1] \; \forall S\in U$ and $\sum_S \kappa_S <1$. If $\Lambda^* > 1$, the demand is not feasible under the set of $\{\kappa_S\}$ for any cycle length. If $\Lambda^* < 1$, then we can define a cycle length for which flow is admissible without link saturation. However, this cycle length $\tau$ must be significantly greater than $\Lambda^*$ to account for clearance times. If we define $L = \lceil (\frac{R}{\Delta t} \cdot |U|) \rceil$ to be the total number of lost time steps per cycle, a feasible cycle length $\tau$ must satisfy the following condition:

Given an appropriate $\tau$ which satisfies (14), the cycle-based max pressure controller is a relaxed control matrix that is constructed as follows:

At time step $t = n\tau$ for integer $n$, the controller $u^{c*}$ uses feedback measurements $x(t)$ to select a relaxed control matrix $\tilde{S}^{*}$ with components $\lambda_S^*$ that satisfy (16). This relaxed controller is then applied for the subsequent $\tau$ time steps $\{t, t+1, \ldots, t+\tau-1\}$ before the controller is updated.

Note that this controller is modeled such that all phases in an intersection are simultaneously actuated at some proportion of their maximum flow capacity. This is not possible in practice, as many phases will have to make conflicting use of the same intersection resources. Hence individual phases $S$ will have to be actuated in series, with each having a duration corresponding to a number of "time units" that are equal to cycle proportions $(\lambda_S \tau\cdot \Delta t)$. Feedback measurements will then be a measure of "average" cycle queue length acquired over a set of measurements spanning the previous cycle. If the solution for (16) is not unique, one of the optimal solutions is chosen at random using a uniform probability distribution (or according to some practical actuation priority criteria chosen by the network manager). Because it can be implemented such that phases occur in a predictable order, a controller running Cb-MP can be synchronized with neighboring controllers to enforce a "green-wave progression" as is standard practice in existing traffic signal control design.

The Cb-MP controller formulated in (15)-(16) is fundamentally different from the standard max pressure formulation in [18] in two ways: first, it only updates the controller once every signal cycle (or $\tau$ model time steps); second, it applies a relaxed phase actuation (which is some convex combination of standard phase actuations). In the next section, we address how each of these modifications impact the resulting network dynamics, and ultimately show that the application of Cb-MP yields a similar stability guarantee to that shown by Varaiya for the standard max pressure controller given slightly weaker conditions on demand flow.

5.   Stability of Cb-MP

Define $\mathbb{C}_{\kappa}$ as the set of convex combinations of control matrices with coefficients larger than $\kappa$:

Also define a set of undersaturated admissible demands $D_{\kappa}$ with elements $d$ such that $f = dP$ and

This condition (also seen in (13)) ensures that a demand $d\in D_{\kappa}$ can in average be served within a single cycle by a relaxed control matrix that maintains a specified minimum time allocation for each phase.

Theorem 5.1. The cycle-based max pressure controller defined in (15)-(16) stabilizes a network whenever the demand is within a set of feasible undersaturated demands $D^{\kappa}$.

The remainder of this section proves Theorem 5.1 by finding a bound on (9) given a cycle-based max pressure controller. The structure of this proof is as follows:

1) First, we introduce the concept of a $\tau$-updated controller and we show that switching control only once every $\tau$ time steps does not impact the set of feasible demands.

2) Then we explain the mathematical structure used in [18] to derive a bound for the expected network state (9).

3) Next we define an intermediate "relaxed max pressure" formulation to demonstrate the impacts of expanding the domain of control actions to relaxed controllers which are convex combinations of allowable phase matrices.

4) We then demonstrate the intra-cycle queue dynamics given a $\tau$-updated relaxed controller.

5) We combine the above steps to show that queue stability holds given a Cb-MP controller with both relaxed actuation and $\tau$-updating.

6) Finally, we compare the our Cb-MP queue length bounds to those originally derived in [18] to illustrate the increase due to cycle-updating.

5.1.   Properties of a $\tau$-updated controller

Suppose that we impose that the control actuation $S^*(t)$ can only be updated every $\tau$ model time steps. A resulting $\tau$-updated control sequence is composed of a single control matrix repeated for $\tau$ time steps of the model dynamics:

In the Appendix of this paper, we prove that the set of demands that can be accommodated using $\tau$-updated control sequences is the same set of feasible flows as in (8). This equivalence becomes intuitive when one considers that our definition of feasible flows considers only the long-term (more precisely, infinite-term) average of both demand and service rates, and any infinite control sequence with limited admissible phases can be re-arranged to form a $\tau$-updated sequence for some $\tau$.

As will be shown in Section 5.6, occasional updating will also lead to an increased bound on queue lengths relative to the standard max pressure setting.

5.2.   Formulating a queue bound

Our ultimate goal is to derive a bound for the average expected queue state (9). The approach taken in this work follows that of [18]: we bound the incremental model-step queue increase $|X(t+1) - X(t)|$ and then recursively compute a bound on average queue lengths $\sum_{t\in [0, T]}\mathbb{E}\{|X(t)\}$ for an arbitrary time horizon $T$.

Begin by considering the expectation of the following function of queue state perturbation conditioned on the past queue state:

with $\delta(t) = X(t+1) - X(t)$, $\alpha(t) = X(t)^{T}\delta(t)$, and $\beta(t) = \vert \delta (t) \vert^{2}$. We continue by addressing bounds on $\beta$ and $\alpha$ separately.

First we consider $\beta(t) = \vert \delta (t)\vert^{2}$.

Lemma 5.2.

where $B = \max \left\{ \overline{C}(l, m), \sum_{k} \overline{C}(k, l), \overline{d}(l, m) \right\}$, $N$ is the number of queues in the network, $\overline{C} (l, m)$ is the maximum value of the random service rate $C(l, m)(t)$, and $ \overline{d}(l, m)$ is the maximum value of random demand $d(l, m)$.

The proof of Lemma 5.2 is exactly the same as presented in [18] and will therefore not be repeated here. Note that because these bounds hold for any arbitrary $S(l, m)(t) \in [0, 1]$, this bound on $\beta$ is trivially extended to any convex combination of control matrices; hence it is still valid in our extension.

Now we examine a bound on $\alpha (t) = X(t)^{T}\delta(t) $. Again following [18], we define additional sub-terms:

with

Lemma 5.3. For all $l$, $m$, $t$,

The proof of Lemma 5.3 again directly follows that presented in [18]; an extension from a binary controller $S\in \{0, 1\}$ to a relaxed controller $\tilde{S}\in [0, 1]$ is trivial.

In fact, the extension made here only affects the $\alpha_1 (t)$ term. To demonstrate a bound on $\alpha_1(t)$ given application of a cycle-based max pressure controller $u^{c*}$, we first examine the stability of a standard max pressure controller using relaxed controllers with minimum phase proportion constraints and a stricter limitation on network demands. We will then show that a $\tau$-updated cycle-based max pressure controller also stabilizes a network, but results in an increase in queue length bounds that is proportional to cycle length $\tau$.

5.3.   Effect of a relaxed controller

Define an intermediate "relaxed max pressure" policy in which relaxed controllers are applied at the standard max pressure update rate (once per time step of the model dynamics). This situation was suggested in [18] to simulate enforcing minimum phase proportions in a cycle formulation of max pressure. Yet this proposal unrealistically models "cycle" updates at the same rate as the model of queueing and discharging behaviors (hence the introduction of the $\tau$-updated formulation in this work). Nonetheless, we use this intermediate formulation to demonstrate that queue stability is still achieved upon use of a relaxed controller.

Lemma 5.4. If a "relaxed" max pressure control policy $\tilde{S}^{*}$ is updated and applied at each time step $t$ and the demand $d$ is in the set of feasible undersaturated demands $D^\kappa$, then there exists an $\varepsilon>0$, $\eta>0$ such that

Proof of Lemma 5.4. Consider the relaxed max pressure control matrix $\tilde{S}^{*}$ defined in (15) for $\tau = 1$. By construction, $ \forall \; \tilde{S} \in \mathbb{C}_{\kappa}$

with equality only if $\tilde{S} = \tilde{S}^{*}$. Thus $\forall \; (\tilde{S} \in \mathbb{C}_{\kappa}) \neq \tilde{S}^{*}$,

If the demand flow is admissible according to (18), then $\exists \; \hat{S} \in \mathbb{C}_{\kappa}$ and some small $\varepsilon>0$ such that

Therefore,

We assume that by our choice of $\hat{S}$, $f_{l}r(l, m) > \varepsilon$. Hence $\alpha_1(t) < -\varepsilon \sum_{l, m}w(l, m)(t)$. Given the linearity of (10) and the known properties of $r(l, m)(t)$, it can be show that $\sum_{l, m}w(l, m)(t) \geq \eta |X(t)|$ for some $\eta >0$. This completes the derivation of (26).

For ease of notation, now combine (21), (25) and (26) to obtain the following expression given application of the "relaxed max pressure" controller:

where $N$ and $B$ are as in (21).

5.4.   Intra-cycle queue bound

Next we establish a bound on queue growth in a single time step between controller updates.

Lemma 5.5. Assuming a cycle-based max pressure controller with an cycle steps $\tau$ beginning at time $t$, the following bound on state perturbation holds for all steps since update $p \in [0, \tau-1]$:

Proof of Lemma 5.5. As in Lemmas 5.2-5.4 above, begin by dividing the argument of (30) into three parts: $|X(t+ p + 1)|^{2} - |X(t + p)|^{2} = 2(\alpha_1(t + p)+\alpha_2(t + p)) + \beta(t + p)$, where $\beta$, $\alpha_{1}$ and $\alpha_{2}$ are quantities that depend on the controller applied at $(t + p)$:

Bounds on the expectations of $\beta(\cdot)$ and $\alpha_2(\cdot)$ were previously established for any binary or relaxed control matrix in (21) and (25), respectively. Thus we already know that:

The remainder of the bound proposed in (30) originates from the $2 \alpha_1 (t+p)$ term, which is directly dependent on the explicit form of the controller $S$. Rewrite $2\cdot\alpha_1$ from (34) as follows:

for

and

By Lemma 5.4 we know that $ \xi_1(t, S) < -2\varepsilon \eta \vert X(t) \vert $. Because $ \vert X(t) \vert = \vert X(t + p) - (X(t + p) - X(t)) \vert > \vert X(t + p) \vert - \vert X(t + p) - X(t) \vert$, we find that

So by (37) and (21),

To bound $\xi_2$, we study the term

By (21) and the fact that $w(\cdot)$ is linear,

Plugging (40) back into the definition of $\xi_2$, we obtain

Also note that

so (41) becomes

Substituting (38) and (43) into (36) yields (30).

5.5.   Network queue bound

Given Lemmas 5.2-5.5, we show that for a time $t$ within any number $K$ of $\tau$-updated cycles, the following quantity is bounded:

which, when taking the expectation, yields

Rearranging gives

By (9), the bound

establishes that the cycle-based max pressure controller $u^{c*}(X(t))$ defined in (15) will stabilize a vertical queueing network with dynamics $X(t)$ as in (5)-(6).

5.6.   Increase in queue bounds

The following bound on network queue state for a standard max pressure controller is derived in [18] (for $Y$ as in (31)):

Notice that by comparison between (47) and (46), the bound on the long-term sum of expected network queues in cycle-based max pressure is larger by a term that increases linearly in cycle length $\tau$:

6.   Numerical implementation

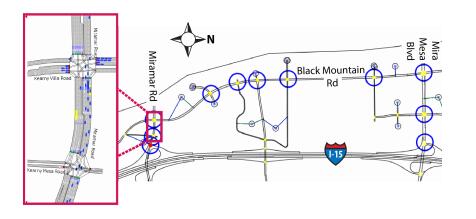
To demonstrate the effectiveness of ours algorithm, a cycle-based max pressure controller was implemented on a network of 11 signalized intersections modeled in the Aimsun, a commonly-used microsimulation platform. While microsimulation dynamics do not precisely represent the queuing behaviors represented above, the following results are provided as a valuable proof-of-concept of this controller in an environment that is actually more realistic and applicable than the vertical queueing model described in this work.

The specific model used in this work was generated as part of the I-15 Integrated Corridor Management project undertaken by the San Diego Association of Governments (SANDAG) in San Diego, CA. Demand and other model parameters are calibrated to match the morning peak period (5:00 AM to 10:00 AM).

This section of road is currently controlled using an offset-optimized actuated-coordinated control scheme. Under this system, each signal operates with a fixed cycle time of 100 seconds and a fixed phase ordering, but uses instantaneous feedback of intersection vehicle approaches to adjust cycle green splits (effectively $\lambda_i$) within fixed minimum and maximum green time constraints per cycle. This control algorithm is coded and calibrated in the SANDAG Aimsun model to represent realistic conditions and was therefore deemed an appropriate benchmark for performance comparison to Cb-MP.

Six variations of Cb-MP were implemented. First, a version with a cycle length of 100 seconds and minimum green time constraints of 10 seconds for each available signal phase was used to closely match the operational constraints of the existing fully-actuated controller. The relative offsets for the southbound coordination phases in this implementation were the same as those used in the actuated-coordinated system. We then ran variations which extended the cycle time for Cb-MP to 120, 140, 160, 180, and 200 seconds to demonstrate the effect of increased cycle time $\tau$ on observed queue lengths.

To compare performance, we calculated vehicle service rates, average delay, average number of stops and stopped time, and mean and maximum queue lengths that were modeled using each controller. These metrics were only calculated for vehicles and links corresponding to the southbound direction on Black Mountain Road as well as the short connections to the I-15 freeway on westbound Mira Mesa Blvd and eastbound Mirimar Rd. This pathway simulates a viable "freeway-alternative" in the congested direction during the morning peak period. During implementation, the Cb-MP algorithm most often chose to give actuation priority to this high-demand Southbound direction, as expected.

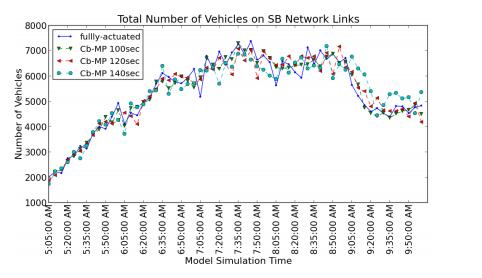
The comparison of network vehicle counts in Figure 2 suggests that Cb-MP is able to service approximately the same volumes as the optimized actuated-coordinated control when cycle times were comparable. The higher cycle length Cb-MP implementations are omitted from this plot for clarity; these controllers resulted in higher variations of vehicle service between 5-minute periods but ultimately only reduced total service rates slightly.

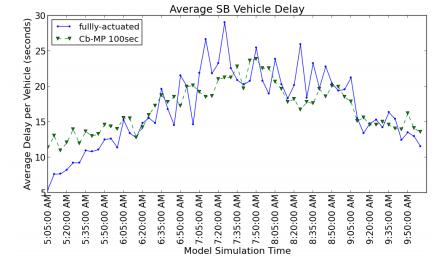
Yet distinct differences between the fully-actuated and Cb-MP controllers were observed in measurements of delays. Figure 3 compares the average vehicle delay given fully-actuated and max pressure control with the same cycle length. It is apparent that while the fully-actuated controller produces less delay when demand is far below network capacity, Cb-MP outperforms the existing controller given consistently high demand; it imposes less delay with a noticeably smaller variance. This may not be surprising given known deficiencies in actuated controllers, however it is important to point out that this implementation of max pressure produces very promising network delays with almost no controller parameters that require tuning.

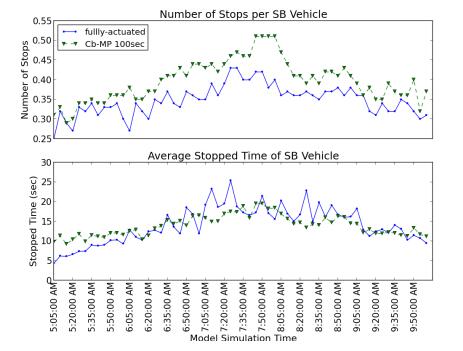
Despite maintaining the same relative offsets for actuation of the main (coordination) direction as the fully actuated controller, Cb-MP induced slightly more stops during a vehicle's south-bound journey across the network. Again, this may be expected given the stop-minimizing design objectives of the fully-actuated system: the small but consistent differences in average vehicle-stops shown in Figure 4 are likely caused by the on-demand service extensions provided for low density "back-of-queue" arrivals in the fully-actuated system. Notice that the average vehicle stopped time is actually lower in Cb-MP than with the fully actuated system during peak demand, which is consistent with the estimates of total delay demonstrated in Figure 3.

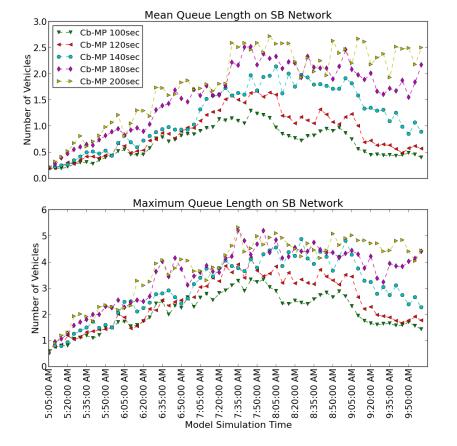
The higher cycle length Cb-MP implementations are again omitted from Figures 3-4 for clarity, yet it is important to note that higher cycle lengths predictably led the longer stops and more delay, as vehicles which encountered a red light would have to wait longer for the cycle to reach their desired green phase. This increase in wait time also corresponds to the predicted larger queues.

Figure 5 demonstrates the increase in mean queue lengths with increase in cycle length $\tau$. While the linear increase in maximum queue length derived in (48) is not explicitly depicted in the observations, these results appear to remain consistent with such an upper bound.

7.   Conclusion

The numerical implementation of cycle-based max pressure in Section 6 suggests a promising alternative for signal control in periods of high demand where the performance of existing actuated controllers is known to deteriorate. It is an intuitive and scalable control algorithm that is appealing because it maintains theoretical network-wide performance guarantees without the need for centralized communication or control centers. The cyclical operation of Cb-MP can still maintain the flow-progression benefits obtained from existing offset optimization algorithms along a prioritized route, as demonstrated by the fact that the average number of vehicle-stops on the southbound route only increases slightly using Cb-MP over an implementation of the optimized actuated system. Because the cycle splits are more predictable in Cb-MP than in current actuated-coordinated algorithms, it may even be possible to further optimize progression on multiple (conflicting) routes with additional linear constraints on cycle splits in (16).

Furthermore, Cb-MP is a widely-applicable algorithm which requires significantly less tuning and site-specific adjustment than the typical fully-actuated control system. For example, the timing parameters for a fully-actuation system deployed on networks such as the SANDAG site referenced above are often a result of many hours of both model-based and heuristic optimization procedures for a specific network geometry and expected demand. Yet in our implementation, the generalized Cb-MP algorithm with arbitrary reasonable minimum green parameters achieved approximately equal performance without requiring any knowledge of location or demand.

By addressing the practical problem of lost capacity due to frequent switching, our extension of the proofs of [18] brings the concept of max pressure closer to a realistic implementation. Yet it is important to point out that existing sensing infrastructure does not typically provide the capabilities necessary to accurately measure approaching link-counts, nor does it provide any measurement of downstream link state.

Future work should also address limitations of the unrealistic assumptions inherent in the vertical queueing model framework, such as the concept of infinite link buffer size. In practice, over-saturation could cause unmodeled instabilities in a traffic network if expected queue bounds exceed physical road storage.

One could also consider multiple ways in which the performance of Cb-MP could benefit from heuristic modification, such as enforcing a maximum value of the green split $\lambda_l$ as a function of queue measurement $x_l$ to prevent wasted green in a given cycle. Our extended proof of stability should hold for any additional linear constraints on $\lambda$ in (16) (which maintain the concept of a relaxed, $\tau$-updated controller) given that there exists any controller satisfying these constraints for which the network demand is feasible according to (18).

Appendix A. Feasible flows with a $\tau$-updated controller

Lemma A.1. All flows which satisfy Property 2 given a controller $u$ updated at every model time step will also satisfy Property 2 with a $\tau$-updated controller for some $\tau$.

Proof of Lemma A.1. Given the set admissible phases $U$, define:

● $\mathcal U$ is the set of control sequences with distinct elements

$\{S(1), S(2) \ldots S(t) \ldots | S(\cdot) \in U\} $,

● $\mathcal U_{\tau}$ is the set of $\tau$-updated control sequences

$\{S(1), S(1), \ldots, S(\tau + 1), S(\tau + 1), \ldots, S(n\tau + 1), S(n\tau + 1), \ldots | S(\cdot) \in U\} $,

Also define the following sets of long-term control proportion matrices, which are similar to the formulation in (7):

By Property 2, a demand $d$ is only feasible if there exists a control sequence $\overline {S}$ such that the corresponding long-term control proportion matrix $M_{\overline {S}}$ satisfies (8). Here we show $M_{\mathcal U} = M_{\mathcal{U_\tau}}$, and therefore any flows that are admissible given an unrestricted controller in $\mathcal U$ can also be accommodated using a $\tau$-updated controller in $\mathcal{U}_\tau$.

Obviously, $M_{\mathcal U_\tau} \subset M_{\mathcal U}$. To show equality, we must also demonstrate that $M_{\mathcal U} \subset M_{\mathcal {U}_\tau} $. Suppose there exists a control sequence $\hat{S} = \{ S(1), S(2), \ldots \} \in \mathcal{U}$. By definition,

Acknowledgments

The authors would like to thank Pravin Varaiya for his insights on this work, as well as Brian Peterson and Joe Butler for their support in the numerical implementation.