Does financial globalization uncertainty affect CO₂ emissions? Empirical evidence from some selected SSA countries

1.   Introduction

Due to the engineering backgrounds and strong biological significance, Babcock and Westervelt ^[1,2] introduced an inertial term into the traditional multidirectional associative memory neural networks, and established a class of second order delay differential equations, which was called as the famous delayed inertial neural networks model. Arising from problems in different applied sciences such as mathematical physics, control theory, biology in different situations, nonlinear vibration, mechanics, electromagnetic theory and other related fields, the periodic oscillation is an important qualitative property of nonlinear differential equations ^{[3,4,5,6,7,8,9]}. Consequently, assuming that the activation functions are bounded and employing reduced-order variable substitution which convert the inertial systems into the first order differential equations, the authors in ^[10,11] and ^[12] have respectively gained the existence and stability of anti-periodic solution and periodic solution for addressed inertial neural networks models. Manifestly, the above transformation will raise the dimension in the inertial neural networks system, then some new parameters need to be introduced. This will increase huge amount of computation and be attained hard in practice ^[13,14]. For the above reasons, most recently, avoiding the reduced order method, the authors in ^[15] and ^[16] respectively developed some non-reduced order methods to establish the existence and stability of periodic solutions for inertial neural networks with time-varying delays.

It has been recognized that, in neural networks dynamics touching the communication, economics, biology or ecology areas, the relevant state variables are often considered as proteins and molecules, light intensity levels or electric charge, and they are naturally anti-periodic ^[17,18,19]. Such neural networks systems are often regarded as anti-periodic systems. Therefore, the convergence analysis and stability on the anti-periodic solutions in various neural networks systems with delays have attracted the interest of many researchers and some excellent results are reported in ^{[20,21,22,23,24,25,26,27]}. In particular, the anti-periodicity on inertial quaternion-valued high-order Hopfield neural networks with state-dependent delays has been established in ^[28] by employing reduced-order variable substitution. However, few researchers have utilized the non-reduced order methods to explore such topics on the following high-order inertial Hopfield neural networks involving time-varying delays:

associating with initial value conditions:

where $\sum\limits_{j = 1}^{n}\bar{c}_{ij}(t)A_{j}(x_{j}(t)), \ \sum\limits_{j = 1}^{n}\bar{d}_{ij}(t)B_{j}(x_{j}(t- q_{ij}(t)))$ and $\sum\limits_{j = 1}^{n}\sum\limits_{l = 1}^{n}\theta_{ijl}(t)Q_{j}(x_{j}(t-\eta_{ijl} (t)))Q_{l}(x_{l}(t-\xi_{ijl}(t)))$ are respectively the first-order term and the second-order term of the neural network, $A_{j}, \ B_{j}$ and $Q_{j}$ are the nonlinear activation functions, $\tau_{i} = \max\limits_{1\leq l, j\leq n}\{\sup\limits_{t\in \mathbb{R}}q_{ij}(t), \ \sup\limits_{t\in \mathbb{R}}\eta_{ijl}(t), \sup\limits_{t\in \mathbb{R}}\xi_{ijl}(t) \},$ $J_{i}, \bar{c}_{ij}, \bar{d}_{ij}, \theta_{ijl}, \bar{a}_{i}, \bar{b}_{i} :\mathbb{R}\rightarrow \mathbb{R}$ and $q_{ij}, \ \eta_{ijl}, \ \xi_{ijl} :\mathbb{R}\rightarrow \mathbb{R}^+$ are bounded and continuous functions, $\bar{a}_{i}, \bar{b}_{i}, q_{ij}, \ \eta_{ijl}, \ \xi_{ijl}$ are periodic functions with period $T > 0$, the input term $J_{i}$ is $T$-anti-periodic $(J_{i}(t+T) = -J_{i}(t) \ \mbox{for all} \ t\in \mathbb{R})$, and $i, j, l\in D: = \{1, 2, \cdots, n\}$.

Motivated by the above arguments, in this paper, without adopting the reduced order method, we propose a novel approach involving differential inequality techniques coupled with Lyapunov function method to demonstrate the existence and global exponential stability of anti-periodic solutions for system (1.1). Particularly, our results are new and supplement some corresponding ones of the existing literature ^{[19,20,21,22,23,24,25,26,27,28]}. In a nutshell, the contributions of this paper can be summarized as follows. 1) A class of anti-periodic high-order inertial Hopfield neural networks involving time-varying delays are proposed; 2) Under some appropriate anti-periodic assumptions, all solutions and their derivatives in the proposed neural networks model are guaranteed to converge to the anti-periodic solution and its derivative, respectively; 3) Numerical results including comparisons are presented to verify the obtained theoretical results.

The remaining parts of this paper are organized as follows. In Section 2, we make some preparations. In Section 3, the existence and the global exponential stability of the anti-periodic solution are stated and demonstrated. Section 4 shows numerical examples. Conclusions are drawn in Section 5.

2.   Preliminaries

To study the existence and uniqueness of anti-periodic solutions to system (1.1), we first require the following assumptions and some key lemmas:

Assumptions:

$(F_{1})$ For $i, j, l \in D,$ $A_{j}(u), B_{j}(u), Q_{j}(u)$ are all non-decreasing functions with $A_{j}(0) = B_{j}(0) = Q_{j}(0) = 0$, and there are nonnegative constants $L^{A}_{j}$, $L^{B}_{j}$, $L^{Q}_{j}$ and $M^{Q}_{j}$ such that

and

$\mbox{for all} \ u, \ v \in \mathbb{ R}.$

$(F_{2})$ There are constants $\beta_{i} > 0$ and $\alpha_{i}\geq 0, \gamma_{i}\geq 0$ obeying

where

$(F_{3})$ For $i, j, l\in D,$ $q_{ij}$, $\eta_{ijl}$ and $\xi_{ijl}$ are continuously differentiable, $q_{ij}'(t) = \dot{q_{ij}} (t) < 1$, $\eta_{ijl}'(t) = \dot{\eta_{ijl} }(t) < 1$ and $\xi_{ijl}'(t) = \dot{\xi_{ijl}} (t) < 1$ for all $t\in \mathbb{R}$.

We will adopt the following notations:

Remark 2.1. Since (1.1) can be converted into the first order functional differential equations. In view of $(F_{1})$ and (^[29], p176, Theorem 5.4), one can see that all solutions of $(1.1)$ and (1.2) exist on $[0, \ +\infty).$

Lemma 2.1. Under $(F_{1})$, $(F_{2})$ and $(F_{3})$, label $x (t) = (x_{1}(t), x_{2}(t), \cdots, x_{n}(t))$ and $y (t) = (y_{1}(t), y_{2}(t), \cdots, y_{n}(t))$ as two solutions of system (1.1) satisfying

where $-\tau_{i} \leq s \leq 0, \ i\in D, \ \varphi^{x}_{i}, \psi^{x}_{i}, \varphi^{y}_{i}, \psi^{y}_{i}\in C([-\tau_{i}, 0], \mathbb{R}).$ Then, there are two positive constants $\lambda$ and $M = M(\varphi^{x}, \psi ^{x}, \varphi^{y}, \psi ^{y})$ such that

Proof. Denote $x (t) = (x_{1}(t), x_{2}(t), \cdots, x_{n}(t))$ and $y (t) = (y_{1}(t), y_{2}(t), \cdots, y_{n}(t))$ as two solutions of (1.1) and (1.2). Let $w_{i}(t) = y_{i}(t)-x_{i}(t)$, then

$\mbox{where } \ i, j\in D,$ $\widetilde{A}_{j}(w_{j}(t)) = A_{j}(y_{j}(t))- A_{j}(x_{j}(t))$ and

According to $(F_{2})$ and the periodicity in (1.1), one can select a constant $\lambda > 0$ such that

where

Define the Lyapunov function by setting

Straightforward computation yields that

It follows from $(F_{1})$ and $PQ \leq \frac{1}{2} (P^{2} + Q^{2}) (P, Q\in \mathbb{R})$ that

and

which, together with (2.4) and (2.5), entails that

This indicates that $K (t)\leq K (0)$ for all $t \in [0, +\infty)$, and

Note that

and

one can find a constant $M > 0$ such that

which proves Lemma 2.1.

Remark 2.2. Under the assumptions adopted in Lemma 2.1, if $y (t)$ is an equilibrium point or a periodic solution of (1.1), one can see $y (t)$ is globally exponentially stable. Moreover, the definition of global exponential stability can be also seen in ^[13,16].

3.   Anti-periodicity of system (1.1)

Now, we set out the main result of this paper as follows.

Theorem 3.1. Under assumptions $(F_{1})$–$(F_{3})$, system (1.1) possesses a global exponential stable $T$-anti-periodic solution.

Proof. Denote $\kappa(t) = (\kappa_{1}(t), \kappa_{2}(t), \cdots, \ \kappa_{n}(t))$ be a solution of system (1.1) satisfying:

With the aid of $(F_{1})$, one can see that

and

where $\ t\in \mathbb{R}$ and $i, j, l\in D$.

Consequently, for any nonnegative integer $m,$

Clearly, $(-1)^{m+1} \kappa (t + (m+1)T) \ (t+(m+1)T\geq 0)$ satisfies (1.1), and $v(t) = -\kappa (t + T)$ is a solution of system (1.1) involving initial values:

Thus, with the aid of Lemma 2.1, we can pick a constant $M = M(\varphi^{\kappa}, \psi ^{\kappa}, \varphi^{v}, \psi ^{v})$ satisfying

Hence,

Consequently,

and

Therefore, (3.3) suggests that there exists a continuous differentiable function $y (t) = (y_{1} (t), y_{2} (t), \cdots, y_{n} (t))$ such that $\{ (-1)^{m }\kappa (t + mT)\}_{m\geq 1}$ and $\{ ((-1)^{m }\kappa (t + mT))'\}_{m\geq 1}$ are uniformly convergent to $y (t)$ and $y'(t)$ on any compact set of $\mathbb{R}$, respectively.

Moreover,

involves that $y(t)$ is $T -$anti-periodic on $\mathbb{R}$. It follows from ($F_1$)-($F_3$) and the continuity on (3.2) that $\{(\kappa'' (t + (m+1)T) \}_{m\geq 1}$ uniformly converges to a continuous function on any compact set of $\mathbb{R}$. Furthermore, for any compact set of $\mathbb{R}$, setting $m \longrightarrow+\infty$, we obtain

which involves that $y(t)$ is a $T -$anti-periodic solution of (1.1). Again from Lemma 2.1, we gain that $y(t)$ is globally exponentially stable. This finishes the proof of Theorem 3.1.

Remark 3.1. For inertial neural networks without high-order terms respectively, suppose

and

the authors gained the existence and stability on periodic solutions in ^[10,11] and anti-periodic solutions in ^[12]. Moreover, the reduced-order method was crucial in ^[10,11,12] when anti-periodicity and periodicity of second-order inertial neural networks were considered. However, (3.4) and (3.5) have been abandoned in Theorem 3.1 and the reduced-order method has been substituted in this paper. Therefore, our results on anti-periodicity of high-order inertial Hopfield neural networks are new and supplemental in nature.

4.   Examples and numerical simulations

Example 4.1. Let $n = 2$, and consider a class of high-order inertial Hopfield neural networks in the form of

where $t\geq 0, \ A_{1}(u) = A_{2}(u) = \frac{1}{35} |u |, \ B_{1}(u) = B_{2}(u) = \frac{1}{48} u, \ Q_{1}(u) = Q_{2}(u) = \frac{1}{55} \arctan u.$

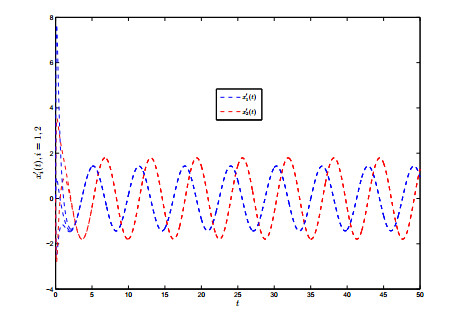
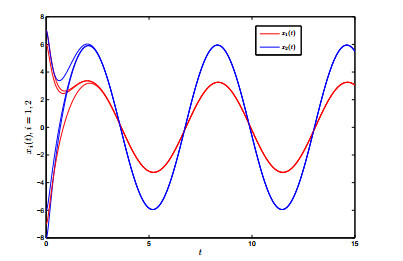
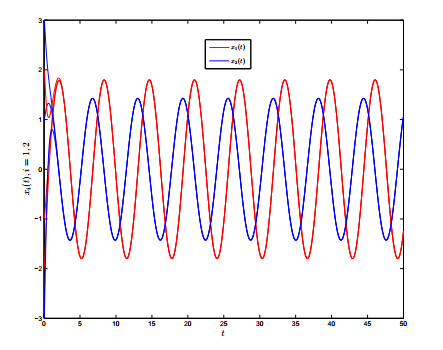
Using a direct calculation, one can check that (4.1) satisfies $(2.4)$ and $(F_{1})-(F_{3})$. Applying Theorem 3.1, it is obvious that system (4.1) has a globally exponentially stable $\pi$-anti-periodic solution. Simulations reflect that the theoretical anti-periodicity is in sympathy with the numerically observed behavior (Figures 1 and 2).

Example 4.2. Regard the following high-order inertial Hopfield neural networks involving time-varying delays and coefficients:

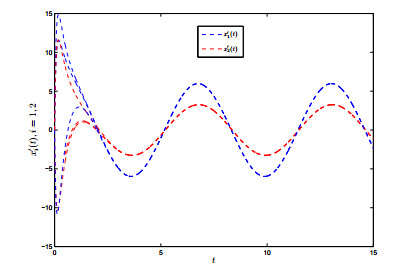
where $t\geq 0, \ A_{1}(u) = A_{2}(u) = \frac{1}{35} |u |, \ B_{1}(u) = B_{2}(u) = \frac{1}{48} u, \ Q_{1}(u) = Q_{2}(u) = \frac{1}{110} (|x+1| -|x-1|).$ Then, by Theorem 3.1, one can find that all solutions of networks (4.2) are convergent to a $\pi$-anti-periodic solution (See Figures 3 and 4).

Remark 4.1. From the figures 1–4, one can see that the solution is similar to sinusoidal oscillation, and there exists a $\pi$-anti-periodic solution satisfying $x (t+\pi) = -x (t)$. To the author's knowledge, the anti-periodicity on high-order inertial Hopfield neural networks involving time-varying delays has never been touched by using the non-reduced order method. Manifestly, the assumptions (3.4) and (3.5) adopted in ^[10,11] are invalid in systems (4.1) and (4.2). In addition, the most recently papers ^[10,11] only considered the polynomial power stability of some proportional time-delay systems, but not involved the exponential power stability of the addressed systems. And the results in ^{[35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74, 75,76,77,78,79,80,81,82]} have not touched on the anti-periodicity of inertial neural networks. This entails that the corresponding conclusions in ^{[10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48, 49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82]} and the references cited therein can not be applied to show the anti-periodic convergence for systems (4.1) and (4.2).

5.   Conclusion

In this paper, abandoning the reduced order method, we apply inequality techniques and Lyapunov function method to establish the existence and global exponential stability of anti-periodic solutions for a class of high-order inertial Hopfield neural networks involving time-varying delays and anti-periodic environments. The obtained results are essentially new and complement some recently published results. The method proposed in this article furnishes a possible approach for studying anti-periodic on other types high-order inertial neural networks such as shunting inhibitory cellular neural networks, BAM neural networks, Cohen-Grossberg neural networks and so on.

Acknowledgments

The authors would like to express the sincere appreciation to the editor and reviewers for their helpful comments in improving the presentation and quality of the paper.

Conflict of interest

The authors confirm that they have no conflict of interest.