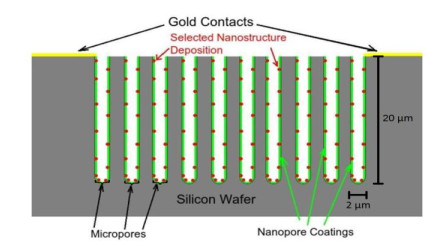
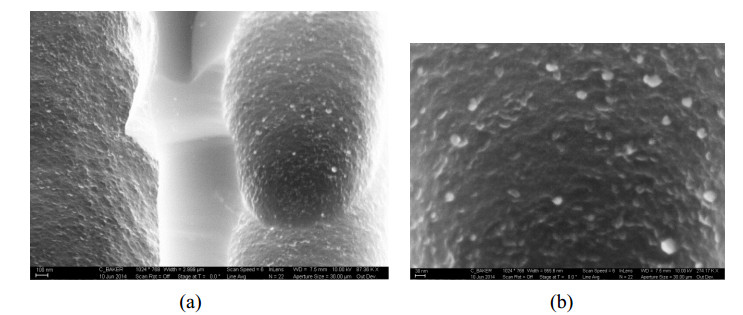
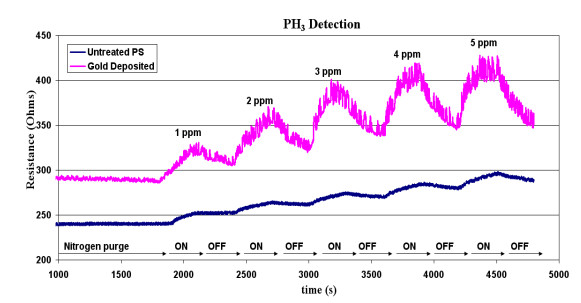
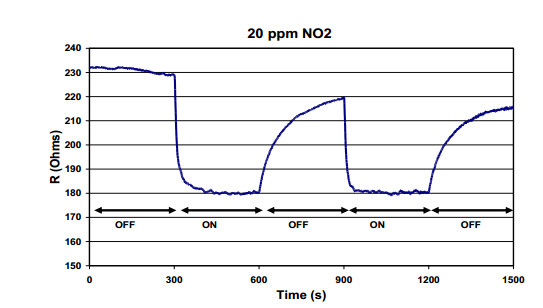
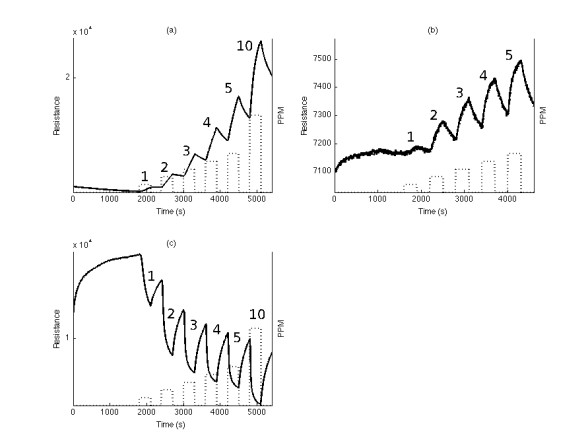
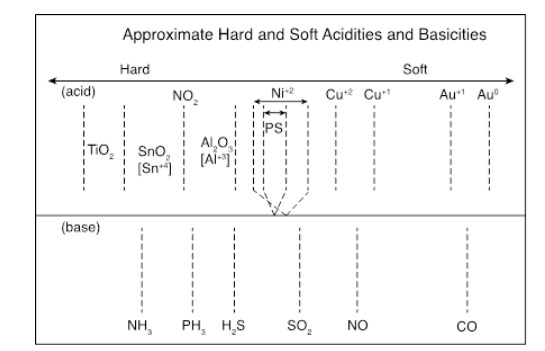
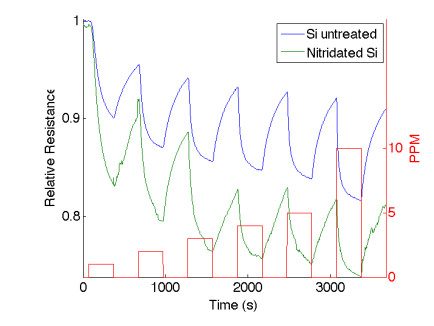
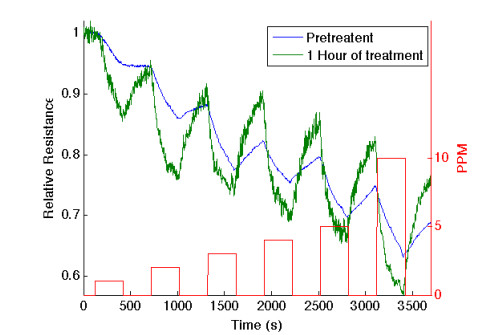
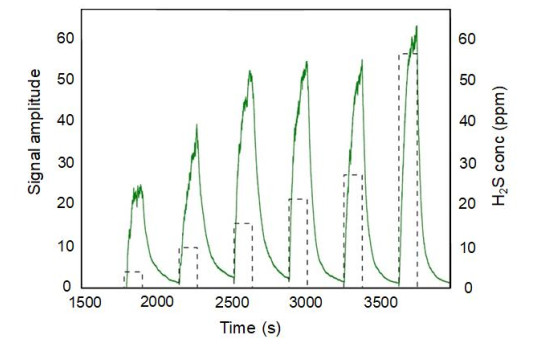
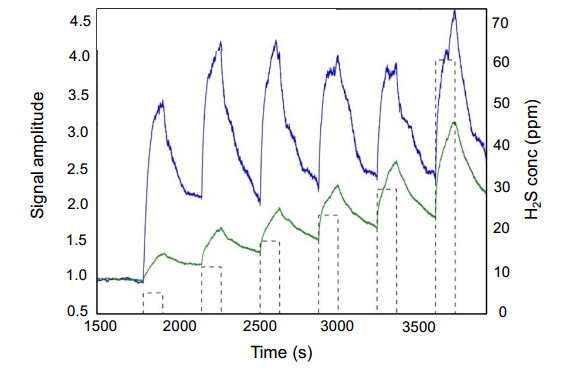
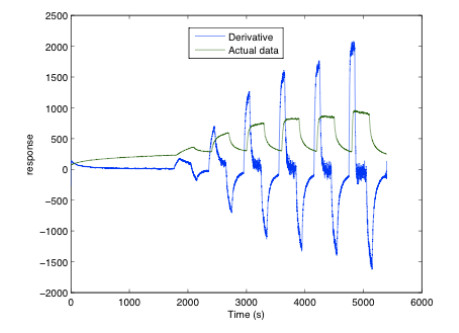
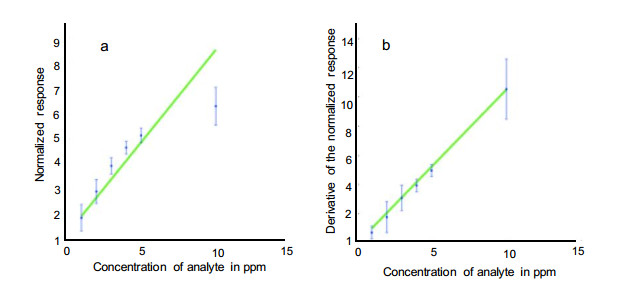
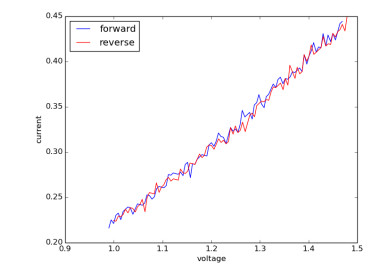
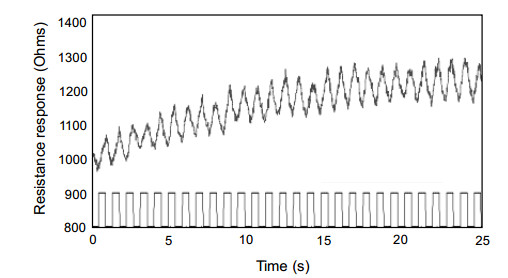
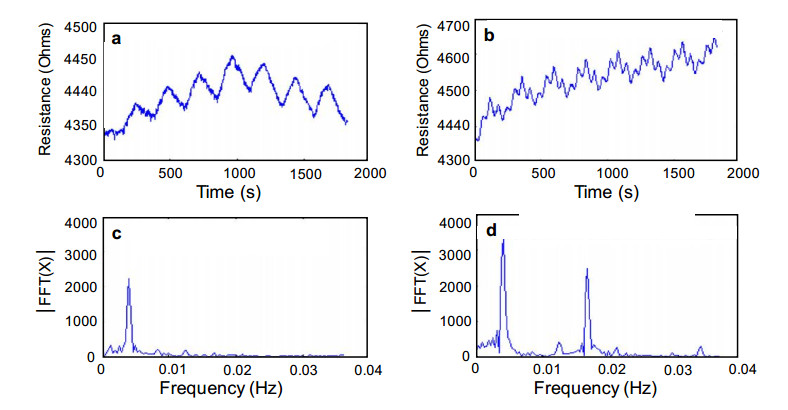
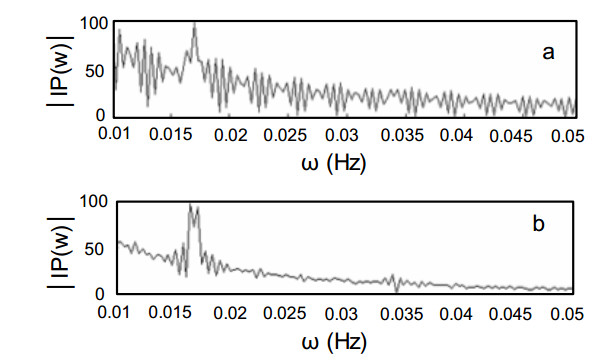
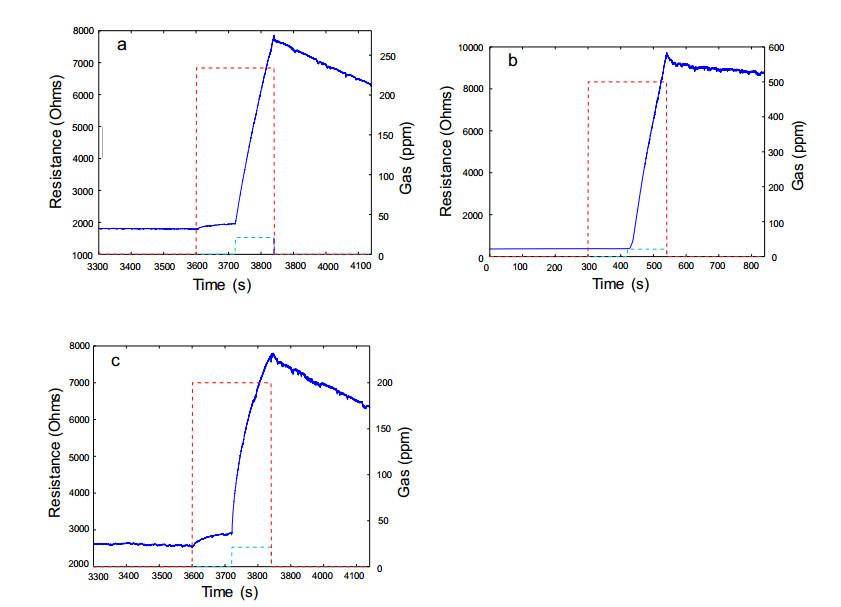
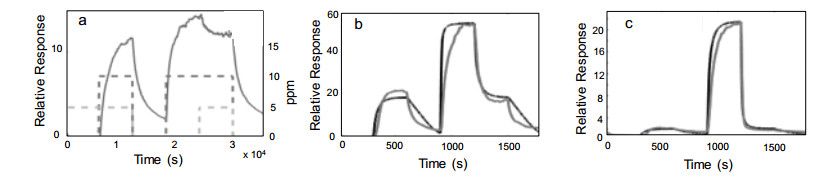
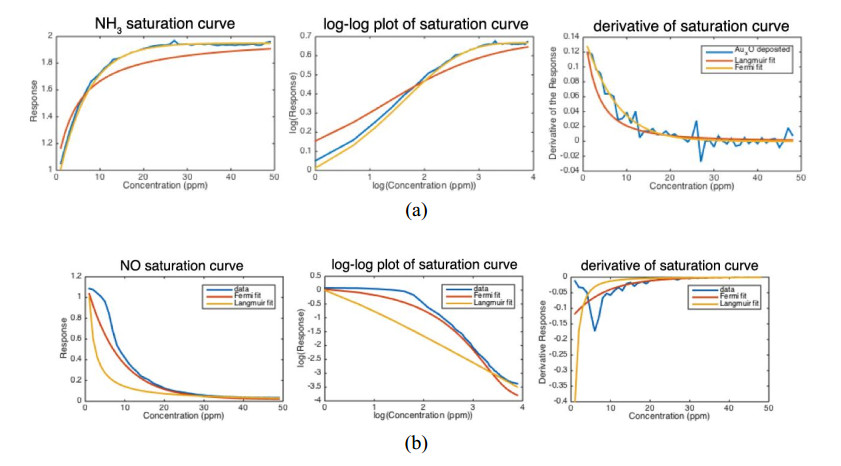
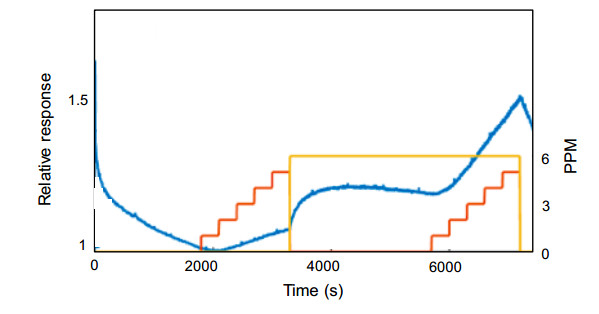
Key parameters of a nanostructure modified porous silicon (PSi) template that can affect the development and performance of PSi-based sensors are considered. The importance of pore selection and direct in-situ nitrogen functionalization are emphasized. Metal oxide nanostructured island sites deposited to select, well defined, and reproducible nano-pore walled, micron sized p and n-type silicon pores (0.7–1.5 μ diameter) provide enhanced selectivity. The micron-sized pores facilitate rapid Fickian analyte diffusion to these highly active sites. The metal oxide nanoparticles are trapped by a thin nanopored wall covering preventing their sintering at elevated temperatures. The varying sensitivities of the highly active metal oxide nanostructured sites are well predicted within the recently developed Inverse Hard/Soft Acid/Base (IHSAB) model. Nitrogen functionalization of the nanostructure decorated surfaces provides the conversion of these PSi interfaces from hydrophilic to hydrophobic character. The decrease of water interaction provides greatly enhanced stability. Selectivity can be extended to the measurement of multiple gases using a combination of nanostructured island site determined detection matrices, p and n-type charge carrier variation, time dependent diffusion response, and pore structure influenced sensitivity. The range of variable responses is dominated by the molecular electronic structure of the nanostructured island sites as evaluated using the IHSAB concept. Pulsed mode operation can facilitate low analyte consumption and high analyte selectivity and further provide the ability to assess false positive signals using Fast Fourier Transfer techniques. The modeling of the PSi sensor response with a new Fermi energy distribution –based response isotherm is found to be superior to other isotherms. The rate of sensor response, linearity of measurement, and hysteresis of response are also considered within the framework of the decorated micron sized pore structure.
The authors are honored to participate in this special issue and express their admiration to Professor Italo Capuzzo-Dolcetta for his mathematical work. The first author met Prof. Dolcetta for the first time at the end of his Ph.D. thesis more than 20 years ago during an extended visit to Roma. Prof. Dolcetta mentorship at that time influenced his career deeply and he is particularly grateful for this opportunity.
1.
Introduction
Mean-field games (MFG) is a tool to study the Nash equilibrium of infinite populations of rational agents. These agents select their actions based on their state and the statistical information about the population. Here, we study a price formation model for a commodity traded in a market under uncertain supply, which is a common noise shared by the agents. These agents are rational and aim to minimize the average trading cost by selecting their trading rate. The distribution of the agents solves a stochastic partial differential equation. Finally, a market-clearing condition characterizes the price.
We let (Ω,F,(Ft)0⩽t,P) be a complete filtered probability space such that (Ft)0⩽t is the standard filtration induced by t↦Wt, the common noise, which is a one-dimensional Brownian motion. We consider a commodity whose supply process is described by a stochastic differential equation; that is, we are given a drift bS:[0,T]×R2→R and volatility σS:[0,T]×R2→R+0, which are smooth functions, and the supply Qs is determined by the stochastic differential equation
with the initial condition ˉq. We would like to determine the drift bP:[0,T]×R2→R, the volatility σP:[0,T]×R2→R+0, and ˉw such that the price ϖs solves
with initial condition ˉw and such that it ensures a market clearing condition. It may not be possible to find bP and σP in a feedback form. However, for linear dynamics, as we show here, we can solve quadratic models, which are of great interest in applications.
Let Xs be the quantity of the commodity held by an agent at time s for t⩽s⩽T. This agent trades this commodity, controlling its rate of change, v, thus
At time t, an agent who holds x and observes q and w chooses a control process v, progressively measurable with respect to Ft, to minimize the expected cost functional
subject to the dynamics (1.1), (1.2), and (1.3) with initial condition Xt=x, and the expectation is taken w.r.t. Fr. The Lagrangian, L, takes into account costs such as market impact or storage, and the terminal cost Ψ stands for the terminal preferences of the agent.
This control problem determines a Hamilton-Jacobi equation addressed in Section 2.1. In turn, each agent selects an optimal control and uses it to adjust its holdings. Because the source of noise in Qt is common to all agents, the evolution of the probability distribution of agents is not deterministic. Instead, it is given by a stochastic transport equation derived in Section 2.2. Finally, the price is determined by a market-clearing condition that ensures that supply meets demand. We study this condition in Section 2.3.
Mathematically, the price model corresponds to the following problem.
Problem 1. Given a Hamiltonian, H:R2→R, H∈C∞, a commodity's supply initial value, ˉq∈R, supply drift, bS:R2×[0,T]→R, and supply volatility, σS:R2×[0,T]→R,
a terminal cost, Ψ:R3→R, Ψ∈C∞(R3), and an initial distribution of agents, ˉm∈C∞c(R)∩P(R), find u:R3×[0,T]→R, μ∈C([0,T]×Ω;P(R3)), ˉw∈R, the price at t=0, the price drift bP:R2×[0,T]→R, and the price volatility σP:R2×[0,T]→R solving
and the terminal-initial conditions
where b=(−DpH(x,w+ux),bS,bP), σ=(0,σS,σP), and the divergence is taken w.r.t. (x,q,w).
Given a solution to the preceding problem, we construct the supply and price processes
and
which also solve
with initial conditions
and satisfy the market-clearing condition
In [10], the authors presented a model where the supply for the commodity was a given deterministic function, and the balance condition between supply and demand gave rise to the price as a Lagrange multiplier. Price formation models were also studied by Markowich et al. [18], Caffarelli et al. [2], and Burger et al. [1]. The behavior of rational agents that control an electric load was considered in [16,17]. For example, turning on or off space heaters controls the electric load as was discussed in [13,14,15]. Previous authors addressed price formation when the demand is a given function of the price [12] or that the price is a function of the demand, see, for example [5,6,7,8,11]. An N-player version of an economic growth model was presented in [9].
Noise in the supply together with a balance condition is a central issue in price formation that could not be handled directly with the techniques in previous papers. A probabilistic approach of the common noise is discussed in Carmona et al. in [4]. Another approach is through the master equation, involving derivatives with respect to measures, which can be found in [3]. None of these references, however, addresses problems with integral constraints such as (1.7).
Our model corresponds to the one in [10] for the deterministic setting when we take the volatility for the supply to be 0. Here, we study the linear-quadratic case, that is, when the cost functional is quadratic, and the dynamics (1.1) and (1.2) are linear. In Section 3.2, we provide a constructive approach to get semi-explicit solutions of price models for linear dynamics and quadratic cost. This approach avoids the use of the master equation. The paper ends with a brief presentation of simulation results in Section 4.
2.
The model
In this section, we derive Problem 1 from the price model. We begin with standard tools of optimal control theory. Then, we derive the stochastic transport equation, and we end by introducing the market-clearing (balance) condition.
2.1. Hamilton-Jacobi equation and verification theorem
The value function for an agent who at time t holds an amount x of the commodity, whose instantaneous supply and price are q and w, is
where J is given by (1.4) and the infimum is taken over the set {\mathcal{A}}\left((t, T]\right) of all functions v:[t, T]\to {\mathbb{R}} , progressively measurable w.r.t. (\mathcal{F}_s)_{t{\leqslant} s {\leqslant} T} . Consider the Hamiltonian, H , which is the Legendre transform of L ; that is, for p\in {\mathbb{R}} ,
Then, from standard stochastic optimal control theory, whenever L is strictly convex, if u is C^2 , it solves the Hamilton-Jacobi equation in {\mathbb{R}}^3 \times [0, T)
with the terminal condition
Moreover, as the next verification theorem establishes, any C^2 solution of (2.3) is the value function.
Theorem 2.1(Verification). Let \tilde u:[0, T]\times {\mathbb{R}}^3 \to {\mathbb{R}} be a smooth solution of (2.3) with terminal condition (2.4). Let ({\bf X}^*, Q, \varpi) solve (1.3), (1.1) and (1.2), where {\bf X}^* is driven by the (\mathcal{F}_t)_{0{\leqslant} t} -progressively measurable control
Then
1). {\bf v}^* is an optimal control for (2.1)
2). \tilde u = u , the value function.
2.2. Stochastic transport equation
Theorem 2.1 provides an optimal feedback strategy. As usual in MFG, we assume that the agents are rational and, hence, choose to follow this optimal strategy. This behavior gives rise to a flow that transports the agents and induces a random measure that encodes their distribution. Here, we derive a stochastic PDE solved by this random measure. To this end, let u solve (2.3) and consider the random flow associated with the diffusion
with initial conditions
That is, for a given realization \omega\in\Omega of the common noise, the flow maps the initial conditions (x, \bar{q}, \bar{w}) to the solution of (2.5) at time t , which we denote by \left({\bf X}_t^\omega (x, \bar{q}, \bar{w}), Q_t^\omega (\bar{q}, \bar{w}), \varpi_t^\omega (\bar{q}, \bar{w})\right) . Using this map, we define a measure-valued stochastic process \mu_t as follows:
Definition 2.2. Let \omega\in \Omega denote a realization of the common noise W on 0{\leqslant} s {\leqslant} T . Given a measure \bar{m}\in {\mathcal{P}}({\mathbb{R}}) and initial conditions \bar{q}, \bar{w}\in {\mathbb{R}} take \bar \mu \in {\mathcal{P}}({\mathbb{R}}^3) by \bar \mu = \bar{m}\times \delta_{\bar{q}}\times \delta_{\bar{w}} and define a random measure \mu_t by the mapping \omega \mapsto \mu^\omega_t \in {\mathcal{P}}({\mathbb{R}}^3) , where \mu_t^\omega is characterized as follows:
for any bounded and continuous function \psi: {\mathbb{R}}^3\to {\mathbb{R}}
Remark 2.3. Because \bar \mu = \bar{m}\times \delta_{\bar{q}}\times \delta_{\bar{w}} , we have
Moreover, due to the structure of (2.5),
Definition 2.4. Let \bar{\mu}\in {\mathcal{P}}({\mathbb{R}}^3) and write
A measure-valued stochastic process \mu = \mu(\cdot, t) = \mu_t(\cdot) is a weak solution of the stochastic PDE
with initial condition \bar{\mu} if for any bounded smooth test function \psi: {\mathbb{R}}^3\times[0, T]\to {\mathbb{R}}
where the arguments for {\bf b} , {\boldsymbol \sigma} and \psi are (x, q, w, s) and the differential operators D and D^2 are taken w.r.t. the spatial variables x, q, w .
Theorem 2.5. Let \bar{m}\in {\mathcal{P}}({\mathbb{R}}) and \bar{q}, \bar{w}\in {\mathbb{R}} . The random measure from Definition 2.2 is a weak solution of the stochastic partial differential equation (2.6) with initial condition \bar{\mu} = \bar{m}\times \delta_{\bar{q}}\times \delta_{\bar{w}} .
Proof. Let \psi: {\mathbb{R}}^3\times [0, T]\to {\mathbb{R}} be a bounded smooth test function. Consider the stochastic process s \mapsto \int_{ {\mathbb{R}}^3}\psi(x, q, w, s)\mu^\omega_s(dx\times dq \times dw) . Let
be the flow induced by (2.5). By the definition of \mu^\omega_t ,
Then, applying Ito's formula to the stochastic process
the preceding expression becomes
where arguments of {\bf b} , {\boldsymbol \sigma} and the partial derivatives of \psi in the integral with respect to \bar{m}(dx) are ({\bf X}_s(x, \bar{q}, \bar{w}), Q_s(\bar{q}, \bar{w}), \varpi_s(\bar{q}, \bar{w}), s) , and in the integral with respect to \mu_t(dx\times dq \times dw) are (x, q, w, t) . Therefore,
Hence, (2.7) holds.
2.3. Balance condition
The balance condition requires the average trading rate to be equal to the supply. Because agents are rational and, thus, use their optimal strategy, this condition takes the form
where \mu_t^\omega is given by Definition 2.2. Because Q_t satisfies a stochastic differential equation, the previous can also be read in differential form as
The former condition determines b^P and \sigma^P . In general, b^P and \sigma^P are only progressively measurable with respect to (\mathcal{F}_t)_{0{\leqslant} t} and not in feedback form. In this case, the Hamilton–Jacobi (2.3) must be replaced by either a stochastic partial differential equation or the problem must be modeled by the master equation. However, as we discuss next, in the linear-quadratic case, we can find b^P and \sigma^P in feedback form.
3.
Potential-free linear-quadratic price model
Here, we consider a price model for linear dynamics and quadratic cost. The Hamilton-Jacobi equation admits quadratic solutions. Then, the balance equation determines the dynamics of the price, and the model is reduced to a first-order system of ODE.
Suppose that L(x, v) = \tfrac{c}{2}v^2 and, thus, H(x, p) = \tfrac{1}{2c}p^2 . Accordingly, the corresponding MFG model is
Assume further that \Psi is quadratic; that is,
3.1. Balance condition
Let
The balance condition is Q_t = -\tfrac{1}{c} \left(\varpi_t+\Pi_t\right) . Furthermore, Definition 2.2 provides the identity
Lemma 3.1. Let ({\bf X}^*, Q, \varpi) solve (1.3), (1.1) and (1.2) with {\bf v} = {\bf v}^* , the optimal control, and initial conditions \bar{q}, \bar{w}\in {\mathbb{R}} . Let u\in C^3({\mathbb{R}}^3\times[0, T]) solve the Hamilton-Jacobi equation (2.3). Then
where the arguments for the partial derivatives of u are ({\bf X}_t^*(x, \bar{q}, \bar{w}), Q_t(\bar{q}, \bar{w}), \varpi_t(\bar{q}, \bar{w}), t) .
Proof. By Itô's formula, the process t\mapsto u_x({\bf X}^*_t, Q_t, \varpi_t, t) solves
with {\bf v}^*(t) = -\tfrac{1}{c}(\varpi_t+u_x({\bf X}^*_t, Q_t, \varpi_t, t)) . By differentiating the Hamilton-Jacobi equation, we get
Substituting the previous expression in (3.3), we have
The preceding identity simplifies to
Using Lemma 3.1, we have
that is,
Thus,
3.2. Quadratic solutions to the Hamilton-Jacobi equation
If u is a second-degree polynomial with time-dependent coefficients, then
and
are deterministic functions of time. Accordingly, b^P and \sigma^P are given in feedback form by (3.4), thus, consistent with the original assumption. Here, we investigate the linear-quadratic case that admits solutions of this form.
Now, we assume that the dynamics are affine; that is,
Then, (3.4) gives
Because all the terms in the Hamilton-Jacobi equation are at most quadratic, we seek for solutions of the form
where a_i^j:[0, T]\to {\mathbb{R}} . Therefore, the previous identities reduce to
Using (3.6) and grouping coefficients in the Hamilton-Jacobi PDE, we obtain the following ODE system
with terminal conditions
While this system has a complex structure, it admits some simplifications. For example, the equation for a_2^1 is independent of other terms and has the solution
Moreover, we can determine a_2^2 and a_2^3 from the linear system
Lemma 3.1 takes the form
Therefore,
where
Replacing the above in the balance condition at the initial time, that is \bar{w} = -c\bar{q}-\Pi_0 , we obtain the initial condition for the price
where a_1^1 can be obtained after solving for a_2^1 , a_2^2 and a_2^3 .
Now, we proceed with the price dynamics using the balance condition. Under linear dynamics, we have
Thus, replacing the price coefficients for (3.6), we obtain
which determines the dynamics for the price.
4.
Simulation results
In this section, we consider the running cost corresponding to c = 1 ; that is,
and terminal cost at time T = 1
We take \bar{m} to be a normal standard distribution; that is, with zero-mean and unit variance. We assume the dynamics for the normalized supply is mean-reverting
with initial condition \bar{q} = 1 . Therefore, the dynamics for the price becomes
with initial condition \bar{w} given by (3.7), and a_2^2 and a_2^3 solve
with terminal conditions a_2^2(1) = 0 and a_2^3(1) = 0 . We observe that the coefficient multiplying Q_t in the volatility of the price is now time-dependent.
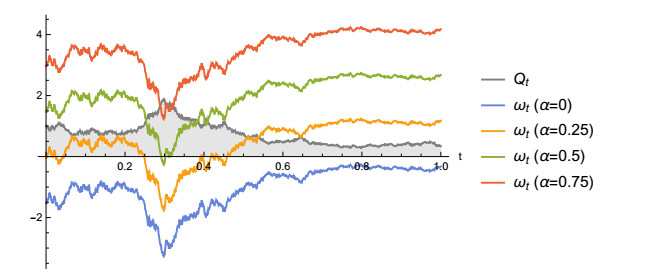
For a fixed simulation of the supply, we compute the price for different values of \alpha . Agents begin with zero energy average. The results are displayed in Figure 1. As expected, the price is negatively correlated with the supply. Moreover, as the storage target increases, prices increase, which reflects the competition between agents who, on average, want to increase their storage.
Acknowledgments
The authors were partially supported by KAUST baseline funds and KAUST OSR-CRG2017-3452.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: