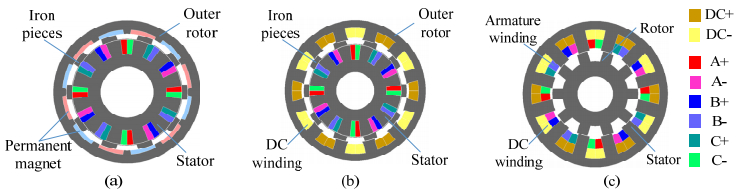
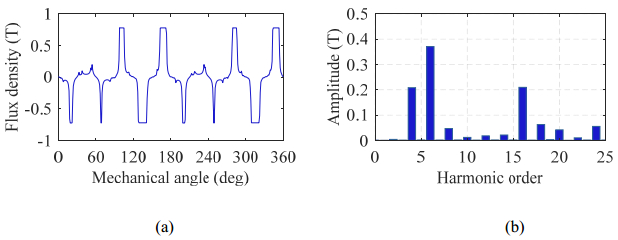
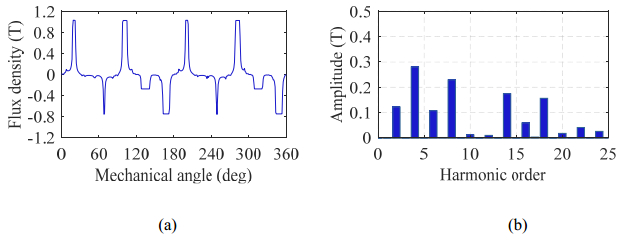
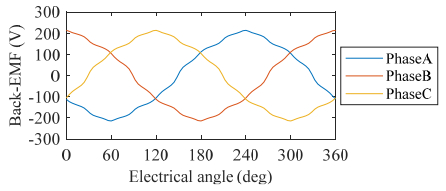
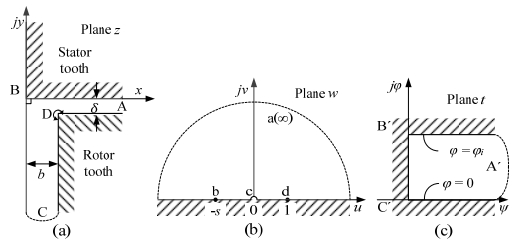
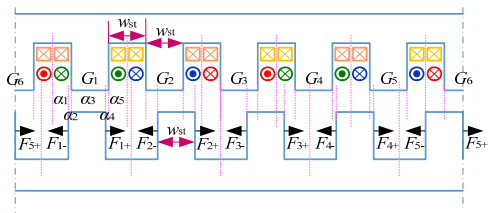
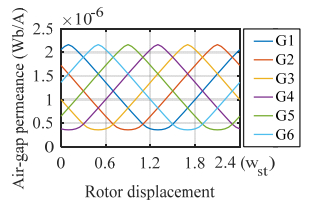
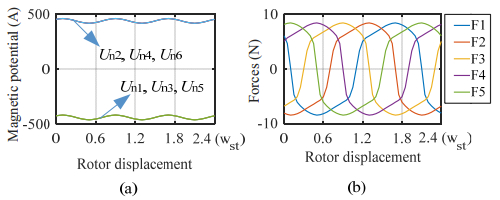
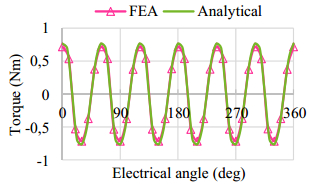
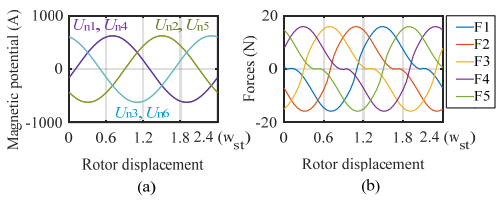
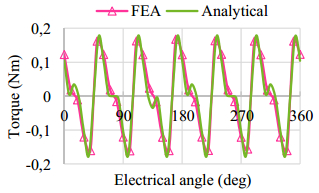
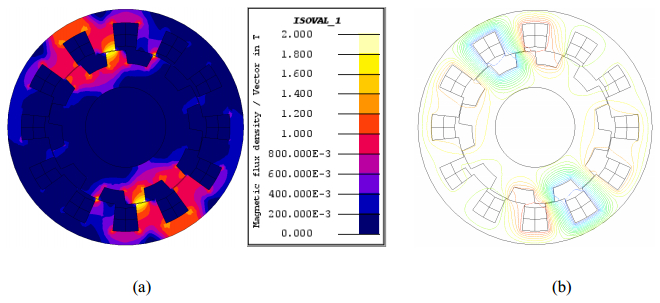
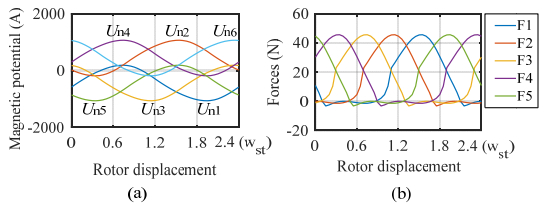
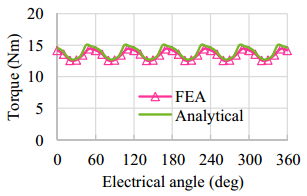
This paper presents a DC-excited flux-modulated (DCEFM) machine. It has one rotor with pr poles and two sets of windings on one stator. One of the windings has pf pole-pairs and is excited with DC current. The second winding has pa pole-pairs and is excited with AC sinusoidal current. The relationship between pr, pf and pa is pr = pf + pa. The purpose of this paper is to analyze the torque of the machine in order to optimize the slot regions assigned to the two stator windings for generating the highest torque at the admissible copper losses. Firstly, the torque equation of the machine is derived. The methods described in this paper are also feasible for other machine types such as variable flux reluctance machine, field excited flux-switching machine. By using the finite element analysis (FEA) the analytical results are verified. The results show that the magneto motive forces (MMFs) of the two windings need to be approximately equal to obtain optimal torque.
1.
Introduction and preliminaries
Recently, partial differential equations (PDEs) with fractional derivatives have gained significant attention of the research community in applied sciences and engineering. Such equations are encountered in various applications (continuum mechanics, gas dynamics, hydrodynamics, heat and mass transfer, wave theory, acoustics, multiphase flows, chemical engineering, etc.). Numerous phenomenon in Chemistry, Physics, Biology, Finance, Economics and other relevant fields can be modelled using PDEs of fractional order [1,2,3,4,5]. In literature a significant theoretical work on the explicit solution of fractional order differential equations can be found [6,7] and there references. Since the explicit solutions can be obtained for special cases and most of the time the exact/analytical solutions are cumbersome for differential equations of non-integer order, therefore an alternative way is to find the solutions numerically. Various computational methods have been developed for approximation of differential equations of fractional order. The authors in [8], for example, have analyzed the implicit finite difference method and proved its unconditional convergence and stability. In [9] approximate solution of fractional diffusion equation is obtained via compact finite difference scheme. Liu et al.[10] studied the sub-diffusion equation having non-linear source term using analytical and numerical techniques. In [11] a numerical scheme for the solution of turbulent Riesz type diffusion equation is presented. The authors in [12] have solved diffusion-wave equations of fractional order using a compact finite difference method which is based on its equivalent integro-differential form. Garg et al.[13] utilized the matrix method for approximation of space-time wave-diffusion equation of non-integer order. In [14] the authors solved multi-term wave-diffusion equation of fractional order via Galerkin spectral method and a high order difference scheme. Two finite difference methods for approximating wave-diffusion equations are proposed in [15]. Bhrawy et al. [16] utilized Jacobi operational matrix based spectral tau algorithm for numerical solution of diffusion-wave equation of non-integer order. In [4] the authors proposed numerical schemes for approximating the multi-term wave-diffusion equation. The Legendre wavelets scheme for diffusion wave equations is proposed in [17]. The authors [18] presented a numerical scheme which is based on alternating direction implicit method and compact difference method for 2-D wave-diffusion equations. Similarly a compact difference scheme [19] is utilized for approximation of 1-D and 2-D diffusion-wave equations. Yang et al. [20] proposed a fractional multi-step method for the approximation of wave-diffusion equation of non-integer order. A spectral collocation method and its convergence analysis are presented in [21] for fractional wave-diffusion equation.
Since all these methods are mesh dependent and in modern problems these methods have been facing difficulties due to complicated geometries. Meshfree methods, as an alternative numerical method have attracted the researchers. Some meshless methods have been devoloped such as element-free Galerkin method(EFG)[22], reproducing kernel particle method (RKPM)[23], singular boundary method [24], the boundary particle method [25], Local radial point interpolation method (MLRPI) [26] and so on.
Numerous meshless methods have been developed for the approximation of fractional PDEs. Dehghan et al. [27] analyzed a meshless scheme for approximation of diffusion-wave equation of non-integer order and proved its stability and convergence. In [28] the authors presented an implicit meshless scheme for approximation of anomalous sub-diffusion equation. Diffusion equations of fractional orders are apprximated via RBF based implicit meshless method in [29]. Hosseini et al. [26] developed a local radial point interpolation meshless method based on the Galerkin weak form for numerical solution of wave-diffusion equation of non integer order. In [30] the authors approximated distributed order diffusion-wave equation of fractional order using meshless method. The authors in [31] proposed a meshless point collocation method for approximation of 2−D multi-term wave-diffusion equations. In [32] the authors proposed a local meshless method for time fractional diffusion-wave equation. Kansa method [33] is utilized for numerical solution of fractional diffusion equations. Zhuang et al. [34] proposed an implicit MLS meshless method for time fractional advection diffusion equation. The numerical solution of 2D wave-diffusion equation is studied in [35] using implicit MLS meshless method. The mentioned methods are meshfree time stepping methods and these methods faces stability restriction in time, and in these methods for convergence a very small step size is required. To overcome the issue of time instability some transformations may be used.
In literature some valuable work is available on resolving the problem of time instability. The researchers have coupled the Laplace transform with other well known numerical methods. For example the Laplace transform with Kansa method [33,36], finite element method [37,38], finite difference method [39], RBF method on unit sphere [40] and the references therein. In the present work we have coupled the Laplace transform with local meshless method for approximating the solution of the multi-term diffusion wave equation of fractional order.
2.
Laplace transform based local meshless method
In our numerical scheme we transform the multi-term time fractional wave-diffusion equation to a time independent problem with Laplace transformation. The reduced problem is then approximated using local meshless method in Laplace space. Finally the solution of the original problem is obtained using contour integration. We apply the proposed method to multi-term fractional wave-diffusion equation of the form [14]
where
1<αm<...<α1<α<2, and dj≥0,j=1,2,...,m,m∈N are constants. Dαjτ is a Caputo derivative of order αj defined by
also for n=2, we have
The initial conditions for the above Eq (2.1) are
and the boundary conditions are
where L is the governing linear differential operator, and B is the boundary differential operator. By applying the Laplace transformation to Eq (2.1), we get
where
and
Similarly applying the Laplace transform to (2.5), we get
Hence, the system of time-independent equations is obtained as
In our method first we represent the solution U(χ,τ) of the original problem (2.1) as a contour integral
where, for Res≥ω with ω appropriately large, and Γ is an initially appropriately chosen line Γ0 perpendicular to the real axis in the complex plane, with Ims→±∞. The integral (2.10) is just the inverse transform of ˆU(χ,τ), with the condition that ˆU(χ,τ) must be analytic to the right of Γ0. To make sure the contour of integration remains in the domain of analyticity of ˆU(χ,τ), we select Γ as a deformed contour in the set ΣΥϕ={s≠0:|args|<ϕ}∪{0}, which behaves as a pair of asymptotes in the left half plane, with Res→−∞ when Ims→±∞, which force esτ to decay towards both ends of Γ. In our work we have used two types of contours, the first contour is the hyperbolic contour Γ1 due to [38] with parametric representation
where,
By writing s=x+ιy, we observe that Γ1 is the left branch of the hyperbola
the asymptotes for (2.13) are y=±(x−Υ−ℶ)cotη, and x-intercept at s=Υ+ℶ(1−sinη). The condition (2.12) confirms that Γ1 lies in the sector ΣΥϕ=Υ+Σϕ⊂Σϕ, and grows into the left half plane. From (2.11) and (2.10), we have the following integral
Finally to approximate Eq (2.14), the trapezoidal rule with step k is used as
The second contour employed in this work is the Talbot's contour [41], though ignored by many researchers, yet it is one of the best method for numerical inverting the Laplace transform [42]. The authors in [43] have optimized the Talbot's contour for approximating the solution of parabolic PDEs. Other works on Talbot's method can be found in [44,45] and there references. In our work we have employed the improved Talbot's method [46] for numerical inversion of Laplace transform. The Talbot's contour has parametric representation of the form
where the parameters σ,μ,ν, and γ are to be specified by the user. From (2.16) and (2.10) we have
We use M-panel mid-point rule with uniform spacing k=2πM, to approximate the integral (2.17) as
To obtain the solution Uk(χ,τ), first we must solve system of 2M+1 equations given in (2.8) and (2.9) for quadrature points sj,|j|≤M. For this purpose the local meshless method is used to discretize operators L,B.
2.1. Local meshless approximation
Given a set of points {χi}Ni=1inRd,whered≥1 the approximate function for ˆU(χ) using local meshless method has the form,
where λi={λij}nj=1 is the expansion coefficients vector, ϕ(r) is a kernel function, r=‖χi−χj‖ is the distance between the centers χi and χj. Ω, and Ωi are global domain and local domains respectively. The sub-domain Ωi contains the center χi, and around it, its n neighboring centers. Thus we obtain n×n linear systems
which can be written as,
the matrix Φi contains elements in the form bikj=ϕ(‖χik−χij‖),whereχik,χij∈Ωi, the unknowns λi={λij:j=1,...,n} are obtained by solving each of the N systems in (2.21). For the differential operator L we have the form,
the above Eq (2.22) can be expressed as a dot product
where νi is a n-row vector and λi is a n-column vector, entries of the n-column vector νi are given as
eliminating the co efficient λi from (2.21), and (2.23) we have the following expression
where,
thus at each node \mathit{\boldsymbol{\chi}}_i the approximation of the operator \mathcal{L} via local meshless method is given as
In (2.27) D is a sparse differentiation matrix obtained via local meshless method as an approximation to \mathcal{L}. The matrix D has order N \times N, it has n non-zero entries, and N-n zero entries, where N is number of centers in global domain, and n is the number of centers in local domain. The boundary operator \mathcal{B} can be discretized in similar way.
3.
Convergence and accuracy
In order to solve the multi-term time fractional diffusion wave equation using our proposed method, the local meshless method and Laplace transformation is used. In our numerical scheme first the Laplace transform is applied to time dependent equation which eliminates the time variable, and this process causes no error. Then the local meshless method is utilized for approximating time independent equation. The error estimate for local meshless method is of order O(\eta^{\frac{1}{\epsilon h}}) , 0 < \eta < 1 , \epsilon is the shape parameter and h is the fill distance. In the process of approximating the integrals (2.14) and (2.17) convergence is achieved at different rates depending on the paths \Gamma_1, and \Gamma_2 . In approximating the integrals (2.14) and (2.17) the convergence order rely upon on the step k of the quadrature rule and the time domain [t_{0}, T] for \Gamma_1. The proof for the order of quadrature error for the path \Gamma_1 is given in the next theorem.
Theorem 3.1 ([38], Theorem 2.1). Let \mathcal{U}(\mathit{\boldsymbol{\chi}}, \tau) be the solution of (2.1) with \hat{f}(\mathit{\boldsymbol{\chi}}, \tau) analytic in \Sigma^{\Upsilon}_{\phi}. Let \Gamma\subset \Omega_{r}\subset \Sigma^{\Upsilon}_{\phi}, and define b > 0 by coshb = \frac{1}{\theta \tau_{1} \sin(\eta)} , where \tau_{1} = \frac{t_0}{T} , 0 < \tau_0 < T , 0 < \theta < 1.0 and let \beth = \frac{\theta \overline{r}M}{bT}. Then for Eq (2.15), with k = \frac{b}{M}\leq \frac{\overline{r}}{log 2}, we have |\mathcal{U}(\mathit{\boldsymbol{\chi}}, \tau)-\mathcal{U}_{k}(\mathit{\boldsymbol{\chi}}, \tau)|\leq CQe^{\Upsilon \tau_{1}}l(\rho_{r}M)e^{-\mu M}\left(\|\mathcal{U}_{0}\|+\|\hat{f}(\mathit{\boldsymbol{\chi}}, \tau)\|_{\Sigma^{\Upsilon}_{\phi}}\right), for \mu = \frac{\overline{r}(1-\theta)}{b} , \rho_r = \frac{\theta \overline{r} \tau_{1} \sin(\eta-r_1)}{b} , \overline{r} = 2\pi r_1 , r_1 > 0 , \tau_0\leq \tau \leq T, C = C_{\eta, r_1, \beta} , and l(x) = \mathit{\mbox{max}}(1, log(\frac{1}{x})). Hence the error estimate for the proposed scheme is
The authors in [46] derived the optimal values of the parameters for the Talbot's contour (\Gamma_2) defined in (2.16) as given below
with corresponding error estimate as
4.
Stability
To investigate the stability of the systems (2.8) and (2.9), we represent the system in discrete form as
the matrix \mathit{\boldsymbol{\mathcal{M}}}_{N \times N} is sparse matrix obtained using local meshless method. For the system (4.1) the constant of stability is defined as
for any discrete norm \|.\| defined on R^{N} the constant \mathcal{C} is finite. From (4.2) we may write
Similarly for the pseudoinverse \mathit{\boldsymbol{\mathcal{M}}}^{†} of \mathit{\boldsymbol{\mathcal{M}}} , we can write
Thus we have
We can see that Eqs (4.3) and (4.5) confirms the bounds for the stability constant \mathcal{C} . Calculating the pseudoinverse for approximating the system (4.1) numerically be quite expansive computationally, but it confirms the stability. The MATLAB's function condest can be used to estimate \|\mathit{\boldsymbol{\mathcal{M}}}^{-1}\|_{\infty} in case of square systems, thus we have
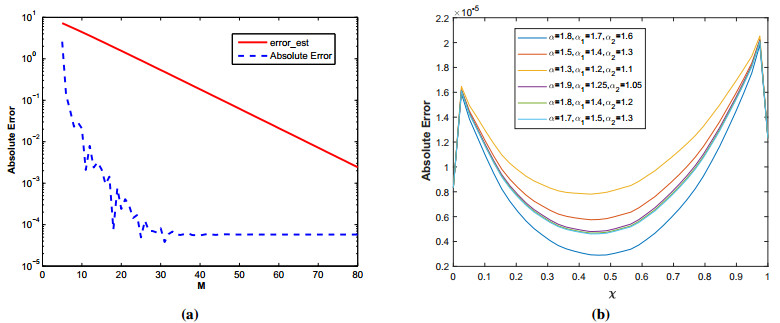
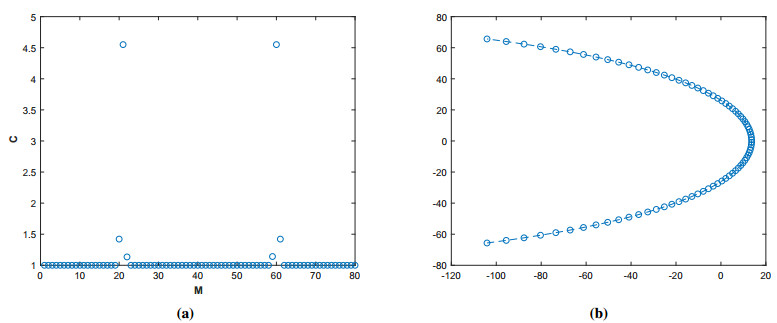
This work well with less number of computations for our sparse differentiation matrix \mathit{\boldsymbol{\mathcal{M}}} . Figure 1(a) shows the bounds for the constant \mathcal{C} of our system (2.8) and (2.9) for Problem 1 using the Talbot's contour \Gamma_2 . Selecting N = 80 , M = 80 , n = 15 , and \alpha = 1.8, \; \alpha_1 = 1.7, \; \alpha_2 = 1.6, \; c = 0.6 at \tau = 1 , we have 1.00\leq \mathcal{C} \leq 4.5501. It is observed that the upper and lower bounds for the stability constant are very small numbers, which guarantees that the proposed local meshless scheme is stable.
5.
Numerical results and discussion
The numerical examples are given to validate our proposed Laplace transform based local meshless scheme. In our computations we have considered different 1-D and 2-D linear multi term wave-diffusion equations. In our numerical examples we have utilized the multi-quadrics(MQ) kernel function \phi (r, \varepsilon) = (1+(\varepsilon r)^2)^{\frac{1}{2}} . We have used the uncertainty principal due to [47] for optimization of the shape parameter. The accuracy of the method is measured using L_{\infty} error defined by
is used. Here \mathcal{U}_{k} and \mathcal{U} are the numerical and exact solutions respectively.
5.1. Problem 1
In the first test problem we consider the following linear fractional equation
where
The exact solution of the problem is
The boundary and initial conditions are
and
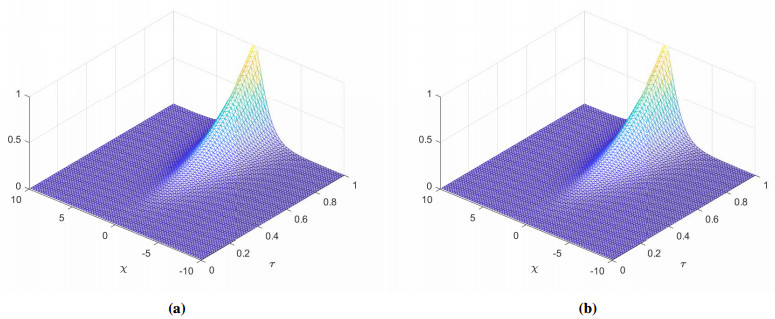
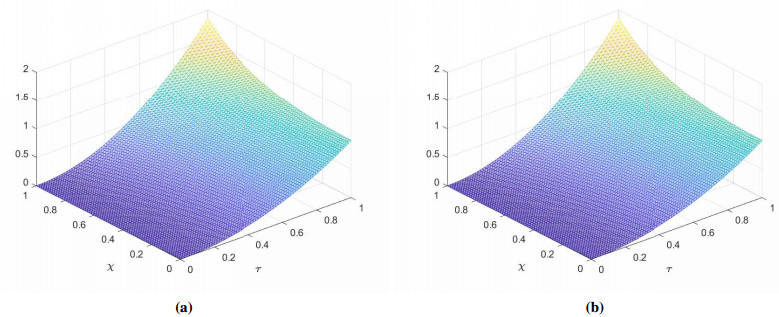
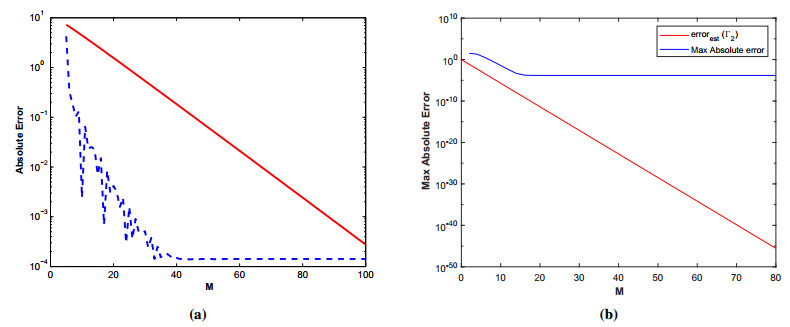
The points along the hyperbolic contour \Gamma_1 are calculated using the statement \xi = -M:k:M, and along Talbot's contour \Gamma_2 using the relation \xi_j = -\pi+(j-\frac{1}{2})k, \; \text{where}\; j = 1:M, \; \text{and}\; k = \frac{2\pi}{M}. The parameters used in our computations for the contour \Gamma_1 are \theta = 0.10, \; \eta = 0.15410, \; \tau_1 = \frac{t_0}{T}, \; r_1 = 0.13870, \; \bar{r} = 2r_1 \pi, \; \Upsilon = 2.0 The results obtained for the parameters \alpha, \; \alpha_1, \; \alpha_2, and c along the contour \Gamma_1 are displayed in Table 1, and along \Gamma_2 are displayed in Table 2. The exact and numerical spacetime solutions for the given problem is depicted in Figure 2(a) and in Figure 2(b) respectively. The absolute error and error estimate are displayed in Figure 3(a). Figure 3(b) shows error functions for various values of \alpha_j. The results confirms that our numerical scheme is accurate, stable and can solve multi-term time fractional wave-diffusion equations with less computation time.
5.2. Problem 2
As a second test problem we consider the following linear fractional equation
where
The exact solution of the problem is
This equation is considered on [0, 1] with boundary conditions
and initial conditions
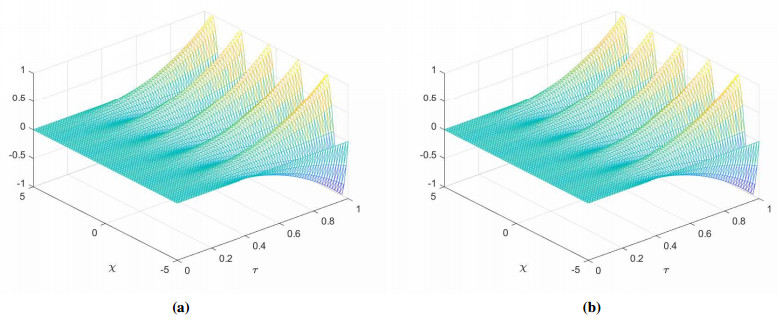
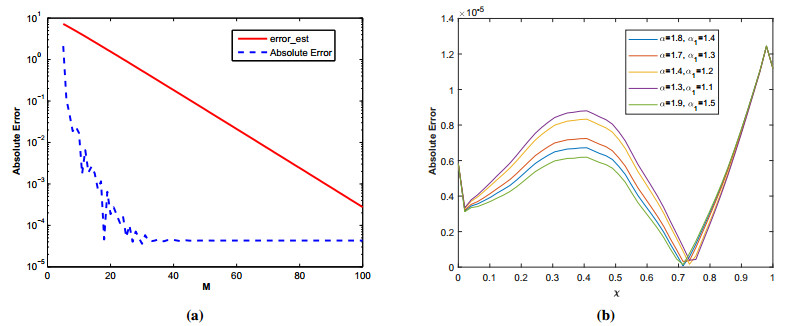
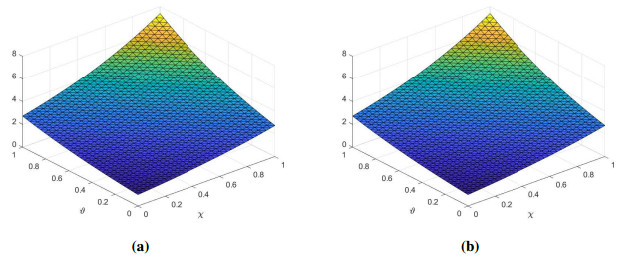
In this experiment we have utilized both the contours with the same set of optimal parameters. The numerical experiments are performed with different nodes N in the global domain n in the sub-domain. The results obtained for fractional orders \alpha , and \; \alpha_1. are displayed in Table 3 along the path \Gamma_1 , and in Table 4 along the path \Gamma_2 . The approximate and exact spacetime solutions are displayed in Figures 4(a) and Figure 4(b). The plot of absolute error and error estimate is displayed in Figure 5(a). Figure 5(b) shows the plot of error functions for various values of \alpha, and \alpha_1 . The results verifies the accuracy, stability and efficiency of the proposed local meshless scheme for multi-term time fractional wave-diffusion equations.
5.3. Problem 3
We consider the following fractional equation
where
The exact solution of the problem is
This equation is considered on [0, 1] with boundary conditions
and initial conditions
The results obtained for third test problem with fractional orders \alpha, and \alpha_1 along the hyperbolic contour \Gamma_1 are displayed in Tables 5, and along the Talbots contour are displayed in Table 6. From the Tables it can be seen the method has good results in accuracy. Figures 6(a) shows the exact spacetime solution and Figure 6(b) shows the numerical spacetime solution. Figure 7(a), and Figure 7(b) absolute error and error estimate for the contour \Gamma_1 and \Gamma_2 respectively.
5.4. Problem 4
We consider the two dimensional multi-term time fractional wave-diffusion equation
subject to zero initial conditions and the boundary conditions are generated from the exact solution
the given 2D test problem is solved with regular nodal points in rectangular, circular and complex domains.
5.4.1. Rectangular domain
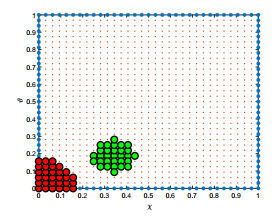
The rectangular domain [0, 1]^2 is descretized with N uniformly distributed points. For this problem also we have used the hyperbolic contour \Gamma_1 and Talbot's contour \Gamma_2 with the same set of optimal parameters used for Problem 1. The uniform nodes distribution with boundary stencil red and interior stencil green are shown in Figure 8. The graphs of exact and approximate solutions for the parameters \alpha = 1.3, \; \alpha_1 = 1.1, at \tau = 1 are shown in the Figure 9(a) and Figure 9(b). The results obtained for various values of N, \; n, and M along the path \Gamma_1 and \Gamma_2 are depicted in Table 7 and Table 8 respectively. From the results one can see that with large number of nodes the proposed method produced accurate results.
5.4.2. Circular Domain
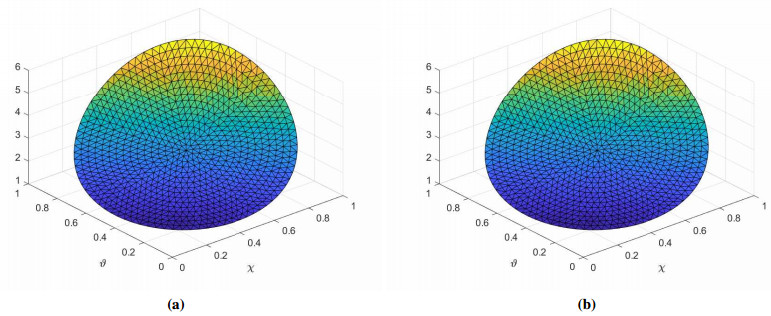
Here we solve the given problem in unit circle with center at (\chi, \vartheta) = (0.5, 0.5) . The domain is descretized with N uniform nodes. The computational results for different values of N, \; n, and M along \Gamma_1 and \Gamma_2 are depicted in Table 9 and Table 10 respectively. Figure 10(a) shows the uniform nodes in circular domain, whereas Figure 10(b) shows the absolute error computed along the hyperbolic path. The exact and approximate solutions are presented in Figures 11(a) and Figure 11(b). The proposed method produced results with good accuracy in circular domain.
5.4.3. Complex Shape Domain
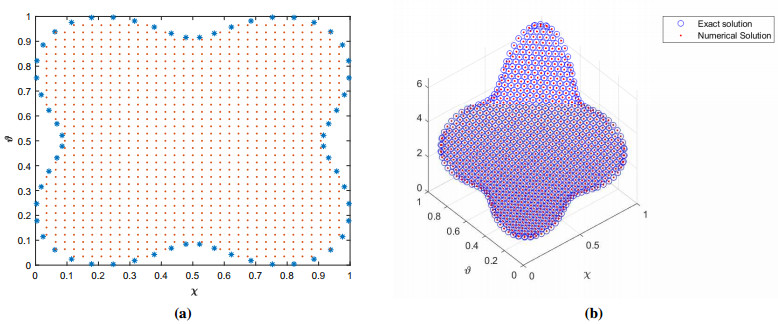
In the last test problem we have considered the complex shape domain. The domain is generated by r_d = \frac{1}{d}[1+2d+d^2-(d+1)\cos(d \theta)], d = 4. In this experiment also we have used the contours \Gamma_1 and \Gamma_2 with the same set of optimal parameters used in Problem 1. The results obtained for fractional orders \alpha = 1.5, \; \alpha_1 = 1.3 , and various nodes N in the global domain and n in the local domain and quadrature points along the contour \Gamma_1 and \Gamma_2 are shown in Table 11 and Table 12 respectively. The regular nodes distribution in the complex domain are shown in Figure 12(a), whereas the approximate and exact solutions are presented in Figures 12(b). Figure 13 shows the absolute error obtained using the Talbots contour. It can be seen that the proposed numerical method produced very accurate and stable results in the complex domain, this confirms the efficiency of the method for such type of equations.
6.
Conclusion
In this work, a local meshless method based on Laplace transform has been utilized for the approximation of the numerical solution of 1D and 2D multi-term time fractional wave diffusion equations. We resolved the issue of time-instability which is the common short coming of time-stepping methods using the Laplace transformation, and the issues of ill-conditioning due to dense differentiation matrices and shape parameter sensitivity with localized meshless method. The stability and convergence of the method are discussed. To verify the theoretical results some test problem in 1D and a test problem in 2D are considered. For the two dimensional problem we have considered rectangular, circular, and complex domains. For numerical inversion of Laplace transform we have utilized two types of contours the hyperbolic and the improved Talbot's contour. The results obtained using these two contours were accurate and stable. However, the results show that the Talbot's contour is more efficient computationally. The benefit of this method is that it can approximate such type equations very efficiently and accurately with less computation time, and without any time instability. The obtained results proves the simplicity in implementation, efficiency, accuracy, and stability of the proposed method.
Acknowledgment
This work was supported by “the Construction team project of the introduction and cultivation of young innovative talents in Colleges and universities of Shandong Province of China, 2019 (Project Name: Big data and business intelligence social service innovation team)” and “the Social Science Planning Project of Qingdao, China,2018 (Grant No. QDSKL1801229)”.
Conflict of interest
The authors declare that no competing interests exist.
First and second authors revised the paper, solved the examples and used software to compute and sketch the results. Third author did analysis and wrote the paper. Forth proposed the problem and verified the results.









 DownLoad:
DownLoad: