We formulate and study epidemic models with differential susceptibilities and
staged-progressions, based on systems of ordinary differential equations, for
disease transmission where the susceptibility of susceptible individuals vary
and the infective individuals progress the disease gradually through stages
with different infectiousness in each stage. We consider the contact rates to
be proportional to the total population or constant such that the infection
rates have a bilinear or standard form, respectively. We derive explicit
formulas for the reproductive number R0, and show that the infection-free
equilibrium is globally asymptotically stable if R0<1 when the infection
rate has a bilinear form. We investigate existence of the endemic equilibrium
for the two cases and show that there exists a unique endemic equilibrium for
the bilinear incidence, and at least one endemic equilibrium for the standard
incidence when R0>1.
1.
Introduction
Variable density and low Mach numbers flows have been widely investigated for the last decades. Indeed, they arise in plenty of physical phenomena in which the sound wave speed is much faster than the convective characteristics of the fluid : flows in high-temperature gas reactors, meteorological flows, combustion processes and many others. In this work, we are interested in a specific model derived from the usual low-Mach one for a calorically perfect gas, coming from an asymptotic expansion of the variables with respect to the Mach number M in the Navier-Stokes compressible equations (see [34]). For the usual low-Mach model, the local-in-time existence of classical solutions in Sobolev spaces is established in [23]. As observed in [33], a small perturbation of a constant initial density provides a global existence of weak solutions in the two-dimensional case. The originality of the model considered here relies on the dynamic viscosity of the fluid being explicitly given as a function of the temperature, as introduced in [4] and generalized in [5]. In this recent work, the authors establish the global existence of weak solutions in the three-dimensional case with no smallness assumption on the initial velocity.
Thanks to a change of variables, we obtain a system in which the velocity field is divergence-free, leading in return to the presence of a non linear and so-called "Joule term" in the mass conservation equation expressed in term of the temperature. In [8], some theoretical results are obtained on the local-in-time existence of strong solutions in the three-dimensional case. We mention also [19] where the authors study the local and global existence in critical Besov spaces, assuming that the initial density is close to a constant and that the initial velocity is small enough. The formulation of this model is close to the so-called ghost effect system, considered in [30,32], where a thermal stress term is added to the right-hand-side of the momentum equation. The local well-posedness of classical solutions is established in [32] for 2D or 3D unbounded domains. A local well-posedness result for strong solutions is proved in [30], where the authors give also the existence and uniqueness of a global strong solution for the two-dimensional case.
From a numerical point of view, many authors compute flows at low-Mach number regime. We refer only to the so-called pressure-based methods, widely used to compute incompressible flows (see e.g. [1,2,20,29,31]), but there exists also the so-called density-based methods widely used to compute supersonic or transonic flows, and recently adapted in the case of low-Mach regime (see [27,28]). In previous contributions on incompressible variable density flows [6,9,10] or on low-Mach flows with large variations of temperature [7], a combined finite volume - finite element scheme was proposed. Based on a time splitting, this combined method allows to solve the mass conservation equation by a finite volume method, whereas the momentum equation associated with the divergence free constraint and the temperature one are solved by a finite element method. It allows, in particular, to preserve the constant density states and to ensure the discrete maximum principle. In the present work, following the same idea, the nonlinear temperature equation is solved by a finite volume method, whereas the velocity equation associated with the divergence free constraint is solved by a finite element one.
The main contribution of this paper is twofold. First, we prove a discrete maximum principle on the temperature (see Theorem 3.1), similarly to the solution behavior at the continuous level. Second, we establish a footbridge between the finite volume fluxes and the finite element velocity field (see subsection 3.4), to ensure the good consistency of the method.
The outline of the paper is the following. Section 2 briefly introduces the model derivation. Section 3 details the proposed combined finite volume - finite element scheme. The maximum principle is established (Theorem 3.1), some variants of the original scheme are proposed (subsection 3.3), and the link between the finite volume fluxes and the finite element velocity field is carefully explained (subsection 3.4). Finally, section 4 proposes several numerical tests to illustrate the obtained theoretical results, and to investigate the behavior of the scheme on a physical benchmark corresponding to the convection of the temperature in a cavity.
2.
Model derivation
As already mentioned in the introduction, a low-Mach model is obtained by inserting the asymptotic expansions of the variables with respect to the Mach number M in the Navier-Stokes compressible equations (see for example [2,20,34]). One of the characteristics of the process is to consider the asymptotic expansion of the pressure π with respect to M. Denoting x∈Rd as the space variable and t∈R+∗ as the time one, we write
where P is called the thermodynamic pressure and q the dynamic pressure. Here, we assume that P(t)=P0>0 is constant for all t≥0. The other variables considered here are the velocity u(x,t), the density ρ(x,t) and the temperature θ(x,t).
Let Ω⊂Rd be an open polygonal domain with a boundary Γ and T a positive real. The continuity, momentum, temperature and state equations in QT=Ω×[0;T] for a calorically perfect gas are given by:
where ˜μ is the viscosity of the flow, κ is the heat conductivity which is assumed constant, R is the gas law constant and γ is the gas specific heat ratio. Here, Du=(∇u+∇Tu)/2 denotes the deformation tensor, I the identity matrix and g(x,t) the gravity field. In order to reduce the study to a system whose velocity is solenoidal, we define:
where λ=(γ−1)κγP0>0 is a fixed constant. In addition, the density is eliminated from the equations thanks to the state equation (2.1d). Following the idea introduced in [5] where a particular relation between the density and the viscosity in the combustion model was introduced, we assume moreover that
with
so that μ(θ) is strictly positive if and only if θ∈(0;1). If we denote by p the modified pressure, defined by:
we consequently obtain (see [8] for all details):
The system (2.2) needs to be completed with suitable initial and boundary conditions. We set ¯Γ=¯ΓD∪¯ΓN, with ΓD∩ΓN=∅. The initial conditions for the system (2.2) are given by:
with:
The boundary conditions on the temperature and the velocity are given by:
The local existence of a regular solution to the problem (2.2) has been shown in [8] in the case of dimension d=3, as well as the maximum principle for the temperature. Furthermore, the unique global strong solution can be proved in the case of dimension d=2 following the proof of Theorem 1.5 in [30] and assuming that for any fixed ˉθ>0, there exists a small constant δ(ˉθ)>0 such that
In this paper, we will prove that there exists at least one solution to the discretized temperature equation, and that this solution verifies the maximum principle. The questions of unicity and convergence of the numerical scheme will be addressed in a further work.
3.
A combined finite volume - finite element scheme
3.1. Spatial and temporal discretizations
3.1.1. The time splitting
The numerical scheme is based on a time splitting, allowing to solve the temperature equation with finite volumes, whereas the velocity equation is solved with finite elements, using the same strategy as in previous works [7,9].
Let Δt be the time step and tn=nΔt. Functions approximated at time tn will be identified with superscript n. Assuming that θn and vn are known:
1. We first compute the new temperature θn+1 by solving the temperature equation (2.2a) using an Euler implicit scheme:
with θn+1D(x)=θD(x,tn+1). The non-linearities of Equation (3.1) are treated thanks to Newton's method.
2. Then we compute the new velocity vn+1 and the new pressure pn+1 by solving the momentum equation (2.2b)-(2.2c) by:
Here and as usual, the nonlinear term in the momentum equation (3.2) is linearized.
3.1.2. Description of the mesh and notations
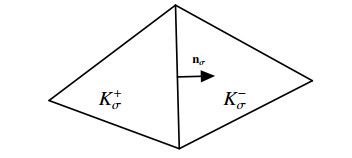
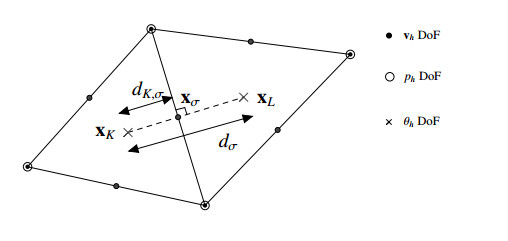
From now, we fix d=2, but our study can be easily extended to the three-dimensional case. The discretization in space is based on a triangulation T of the domain Ω⊂R2 (the elements of T are called control volumes), a family E of edges and a set P=(xK)K∈T of points of Ω defining an admissible mesh in the sense of Definition 3.1 in [25]. We recall that the admissibility of T implies that the straight line between two neighboring centers of cells xK and xL is orthogonal to the edge σ∈E such that ¯σ=¯K∩¯L (and which is noted σ=K|L) in a point xσ (see Figure 1). This condition is satisfied if all the angles of the triangles are less than π2.
The set of interior (resp. boundary) edges is denoted by Eint={σ∈E σ⊄Γ} (resp. Eext={σ∈E σ⊂Γ}). Among the outer edges, there are EN={σ∈E σ⊂ΓN} and ED={σ∈E σ⊂ΓD}. For all K∈T, we denote by EK={σ∈E σ⊂¯K} the edges of K, EintK=Eint∩EK, EextK=Eext∩EK, ENK=ENK∩EK and EDK=EDK∩EK.
The measure of K∈T is denoted by mK and the length of σ by mσ. For σ∈Eint such that σ=K|L, dσ denotes the distance between xK and xL and dK,σ the distance between xK and σ. For σ∈EextK, we note dσ the distance between xK and σ. For σ∈E, The transmissibility coefficient is given by τσ=mσdσ. Finally, for σ∈EK, we denote by nK,σ the exterior unit normal vector to σ. The size of the mesh is given by:
3.1.3. Spatial discretization
The piecewise constant temperature θh is computed with a cell-centered finite volume method described in section 3.2, so that θh∈X(T) with :
The velocity vh is discretized with P2-Lagrange finite elements, and the pressure ph with P1-Lagrange finite elements, so that they satisfy the usual LBB stability condition. The Degrees of Freedom of each variable are shown in the Figure 1.
The computation of the velocity and pressure by finite elements is usual, and we refer to our previous work for details [7,9]. One of the original points of the present work is the computation of the temperature by finite volumes. Indeed, we aim to develop a numerical scheme that ensures the discrete maximum principle property, see section 3.2. Another point of interest is the link between the two numerical methods, see section 3.4. Indeed, from the velocity field that has been computed by finite elements, we have to determine fluxes through the interfaces of the control volumes, which will be used for the computation of the temperature.
3.2. The finite volume scheme
Let v be a given velocity field and θn the previous approximate temperature, we aim at solving the temperature equation:
Since we want to ensure maximum principle properties, we favor a finite volume method. The main difficulty comes from the term |∇θn+1|2, called the Joule term in the context of the electrical conductivity, see for example A. Bradji and R. Herbin [3] or the works from C. Chainais and her collaborators [13,14]. Indeed, the definition of a discrete gradient is not straightforward, since the finite volume solution is piecewise constant. We can thus refer to the work of R. Eymard and his collaborators [24,26] for some definitions of discrete gradients on an admissible mesh. Alternatively, K. Domelevo and P. Omnes [21], and C. Chainais [13], used a discrete gradient reconstruction following the idea from the paper of Y. Coudière, J.-P. Vila and P. Villedieu [18]. The principle of these schemes, valid on very general meshes, consists in the double resolution of the equations, on primal and dual meshes. Moreover in [22], J. Droniou and R. Eymard propose a scheme whose unknowns are the function, its gradient and flows. Therefore, the definition of a discrete gradient by mesh is intrinsic to the scheme.
The respect of the bounds, and in particular of the lower bound, is another difficulty related to the Joule term. Indeed, if we consider "close" models, like the equation of porous media, see for example the work of C. Cancès and C. Guichard [12], or the convection-diffusion equation involved in Khazhikhov-Smagulov models-type, see for example C. Calgaro, M. Ezzoug and E. Zahrouni [11], the maximum principle is obtained quite easily for one order schemes. Nevertheless, adding the positive term |∇θn+1|2 in the temperature equation prevents the scheme from directly obtaining the lower bound. Consequently, we will have to particularly pay attention to the discretization of this term.
We are looking for θn+1h=(θn+1K)K∈T∈X(T) an approximated solution of θ(tn+1,.). The finite volume scheme is classically obtained by integrating equation (3.3) on a control volume K, that is:
with
Here, θn+1σ,+ is defined for σ∈EK by:
with
The numerical flux Fn+1K,σ is an approximation of the exact flux of the diffusive term through the edge σ and is given by:
where we define θn+1σ, an approximation of θn+1 at xσ, by:
Concerning the Joule term, JK(θn+1h) is an approximation of 1mK∫K|∇θ(tn+1,x)|2dx. We notice that |∇θ|2=∇⋅(θ∇θ)−θΔθ, and we propose the following definition:
where ¯θn+1σ is another approximation of θn+1 at xσ (this choice will be justified later) defined this time by:
Finally we obtain:
The rest of the section is devoted to the proof of the following result:
Theorem 3.1. We assume that
and:
Then the scheme (3.4) admits at least one solution that satisfies:
Proof. We start by studying the following intermediate scheme:
with the modified numerical flux
and
We underline that the definition (3.16) ensures that ˜θn+1σ≥0. With this choice in the scheme (3.14), the diffusion term has been a little "inflated" in order to compensate the Joule term and to increase the stability, as it will be seen later. Note moreover that if θn+1h is solution of (3.14) and satisfies (3.13), it is also solution of (3.4).
The schedule of proof is as follows. We first show in Lemma 3.2 that a solution of (3.14) satisfies the discrete maximum principle. Then, by an argument of topological degree, we prove the existence of a solution to (3.14) (see Lemma 3.3). As this solution satisfies the maximum principle, it is also a solution of (3.4) and this concludes the proof of Theorem 3.1.
Lemma 3.2. We assume that (3.11) and (3.12) are satisfied. Let θn+1h be a solution of (3.14). Then θn+1h satisfies (3.13).
Proof. For n=0, the property (3.13) clearly holds because of (3.11). Suppose now that (3.13) holds at step n and assume that there exists KM∈T such that:
We write (3.14) for the control volume KM and obtain:
The right hand side of (3.17) is negative, whereas the left hand side is non-negative (indeed, the treatment of the first term is classical, see for instance [25], and the sign of other terms is obvious). We thus obtain a contradiction.
Assume now that there exists Km∈T such that:
We write (3.14) on Km:
The right hand side of (3.19) is positive. Looking now at the left hand side, we notice that the first (see [25]) and third terms are non positive, whereas the second is non negative. Thus, to obtain a contradiction, we must reach a balance between the Joule term and the diffusive one. By noticing that:
a sufficient condition to obtain the contradiction is to show that for all σ∈EK, θn+1Km−θn+1Km,σ+˜θn+1σ≥0. Indeed it holds, because of (3.18) and Definition (3.16) of ˜θn+1σ, we have:
Lemma 3.3. We assume that (3.11) and (3.12) are satisfied. Then the scheme (3.14) admits at least one solution.
Proof. Lemma 3.3 is proved thanks to a topological degree argument (see for instance [25]). Let μ∈[0,1], we define θn+1h,μ=(θn+1K,μ)K∈T as the solution of the scheme: ∀K∈T,
where θn+1σ,+,μ and ˜Fn+1K,σ,μ are respectively defined by (3.6) and (3.15) by replacing θn+1K and θn+1L by θn+1K,μ and θn+1L,μ; also ¯Fn+1K,σ,μ is defined by (3.22) and ¯JK(θn+1h,μ) by (3.23):
Then (3.21) is equivalent to:
and consequently, we can show as in the proof of Lemma 3.2 that for all K∈T,
We now define K=[m−1;M+1]#T a compact of R#T, and H:[0,1]×R#T⟶R#T by: ∀K∈T,
Then, H∈C([0,1]×K,R#T) and thanks to (3.24),
admits no solution on ∂K. Consequently, its topological degree is independent of μ. As (3.21) admits a solution for μ=0 its topological degree is different from zero. We can now conclude that (3.21) has a solution for μ=1, and therefore (3.14) has at least one solution.
Lemma 3.2 and Lemma 3.3 conclude the proof of Theorem 3.1 since as already mentioned, if θn+1h is solution of (3.14) and satisfies (3.13), it is also solution of (3.4).
3.3. Variants of the scheme
In this subsection, several variants of the scheme (3.4), denoted in the following (SDmaxJcen), are presented. The scheme (SDmoyJup) (subsection 3.3.1) will also fulfill the discrete maximum principle without any condition, whereas the scheme (SDmoyJcen) (subsection 3.3.2) as well as (SDmaxJEGH) and (SDmoyJEGH) (subsection 3.3.3) will fulfill the discrete maximum principle under some restrictions on the temperature bounds m and M.
3.3.1. (SDmoyJup)
We propose here a first variant of (SDmaxJcen), which also leads to an unconditionally maximum principle. The idea is to consider the scheme (3.4), but with two differences compared to (SDmaxJcen). On the one hand, the diffusion term is centered, by defining now θn+1σ used in the definition of the diffusive flux Fn+1K,σ in (3.7) by:
instead of (3.8). On the other hand, an upwind in the Joule term gives us
instead of (3.10), where we use the notation a+=max(0,a). In that case, the maximum principle occurs. Indeed, the proof of Theorem 3.1 can easily be adapted by noticing that ((θn+1K−θn+1K,σ)+)2=0 if θn+1K≤θn+1K,σ. Let us note that the combination of (3.8) for the diffusion flux definition associated to (3.26) for the Joule term flux definition would also lead to a scheme with an unconditional maximum principle. Nevertheless, this choice would generate a loss of accuracy compared with (SDmaxJcen) and (SDmoyJup) which are both already unconditionally maximum-principle preserving. Since it is useless to upwind both the diffusion term and the Joule one, we did not considered it.
Remark 3.4. Note that we could also have considered the following definition in the diffusion term:
From the theoretical and numerical points of view, the cases (3.25) and (3.27) give similar results.
3.3.2. (SDmoyJcen)
A quite natural question, in order to increase the accuracy of the approximation, is to investigate the behaviour of the scheme when both flux are centered. Namely, it would consist in considering (3.25) for the definition of the diffusive flux Fn+1K,σ in (3.7), while using (3.10) for the Joule term flux definition. In that case, the upper bound can be obtained in the same way as in Lemma 3.2. Nevertheless, the obtention of the lower bound needs an additional assumption, so that the maximum principle can be ensured by a specific balance between the Joule term and the diffusion one. The definition of ˜θn+1σ in (3.16) has to be a little modified and given by :
so that the positivity of θn+1Km−θn+1Km,σ+˜θn+1σ (see (3.20)) is ensured provided that M≤3m. As it will be illustrated in the numerical test 4.1 below, such a condition is necessary. This can seem strange from the physical point of view. As we see in the proof, it is necessary for technical reasons, but could also be linked to the fact that the global solution in time of the continuous model is ensured if the initial datum is not too far from a constant state (see (2.3)). Anyway, even with this restriction in mind, (SDmoyJcen) could be used for cases where temperature variations are low, to expect a better accuracy of the solution compared to the one obtained by (SDmaxJcen) or (SDmoyJup).
3.3.3. (SDmaxJEGH) and (SDmoyJEGH)
Finally, two other schemes are investigated, considering another way to define the piecewise discrete gradient in each control volume given by (see [26]) :
while considering either (3.8) or (3.25) for the computation of θn+1σ arising in the definition of Fn+1K,σ given by (3.7), and leading respectively to the schemes denoted (SDmaxJEGH) and (SDmoyJEGH). Once again and in both cases, the maximum principle is ensured under a condition M≤C(T)m with C(T)∈(1,2), depending on geometrical characteristics of the mesh (see [17]).
In Section 4, we implement these different schemes and compare them on two main criteria: verification of the maximum principle and convergence rates. Table 1 summarizes the five considered schemes.
3.4. Coupling between finite elements and finite volumes
The resolution by a finite element method of (3.2) gives us the velocity field vn+1h which is P2 on each triangle K∈T. Let us denote by (vn+1σ)σ∈E the value of this velocity field at the center of edges. Thus, the local divergence constraint reads:
The sequence of reals (αK)K∈T is different from zero in general. Consequently, the velocity field (vn+1σ)σ∈E is not divergence-free in the Finite Volume sense, and can not be used for the resolution of the temperature equation. Here we can not follow the idea of [9], adapted in [7] for the projection method, which consists in defining a constant velocity per triangle. Indeed, the unknowns for the temperature are located at the center of the cells, and no more at the vertices of the mesh.
For σ∈Eint, we define arbitrarly K+σ and K−σ the two triangles such that σ=K+σ|K−σ. For σ∈Eext, we denote by K+σ the triangle such that σ⊂∂K+σ. Let nσ the unit normal vector to σ getting out of K+σ, see Figure 2.
We also define ∀K∈T and ∀σ∈EK:
By denoting (fσ)∈R#E the global numerical flux defined by:
equation (3.29) can be written as:
We now approximate (fσ)σ∈E by (˜fσ)σ∈E in order to obtain the local divergence-free constraint
Then the fluxes (˜fσ)σ∈E are used in the cell-centered Finite Volume scheme (3.4) for the computation of the temperature field, by setting:
Practically, (˜fσ)σ∈E is computed as an approximation of (fσ)σ∈E in the discrete least-mean-squares sense, which fulfills the divergence-free constraint on each finite volume control. It consists in solving the global optimization problem given by:
where (wσ)σ∈E is a sequence of strictly positive weights, which can be defined for example by wσ=1 or wσ=mσdσ, ∀σ∈E. Numerically, we observed similar behaviors for both possibilities. The solution of the problem (3.32) is given by the following theorem:
Theorem 3.5. Let M∈R#T×#T the M-matrix defined ∀K,L∈T by:
and A=(αK)K∈T∈R#T. Let Λ=(λK)K∈T∈R#T be the solution of:
Thus the solution of (3.32) can be defined ∀σ∈E by:
where for all σ∈Eext such that σ⊂∂K, we set λK−σ=0.
Proof. With the following change of variables:
problem (3.32) writes:
We define the lagrangian associated with (3.36) for (hσ)∈R#E and (μK)∈R#T by:
We will show the existence of a saddle point of L. Its first argument will therefore be the solution of the problem (3.36), while the second one corresponds to the Lagrange multiplier associated with the constraints, see for example [16]. We recall that if ((gσ),(λK)) is a saddle point of L, then:
We start with computing H((μK))=inf(hσ)L((hσ),(μK)). We easily verify that (gσ) (which depends on (μK)) defined by:
is solution of
We thus obtain:
with the notation
We now compute (λK)=argmax(μK) H((μK)) by solving:
which is equivalent, applying the notation (3.38) to λK,σ, to
Thus, (λK) is obtained by solving the linear system (3.33). We therefore deduce the expression of (gσ) thanks to (3.37) and then (˜fσ) with (3.35).
4.
Numerical simulations
4.1. Verification of the maximum principle
We previously proved that the schemes (SDmaxJcen) and (SDmoyJup) satisfy the maximum principle, without any restriction on m and M. This first experiment illustrates that if M is too large compared to m, the other schemes do not respect the maximum principle. In this perspective, we consider only the temperature equation (2.2a) and set:
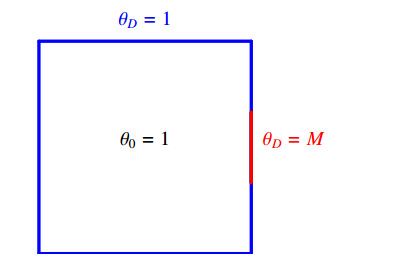
The initial temperature is defined on Ω=[0;1]2 by:
On all the boundaries, we impose Dirichlet conditions, see Figure 3. We denote by ΓH={1}×(0,3;0,7) and set ∀t∈[0;T]:
We run the simulations for different values of M on a triangulation T with mesh size h=7.25⋅10−2 and report the results in the Table 2. We find numerically the results shown previously. On the one hand, the schemes (SDmaxJcen) and (SDmoyJup) allow us to obtain the maximum principle whatever the value of M. On the other hand, the schemes (SDmoyJcen), (SDmoyJEGH) and (SDmaxJEGH) do not give a solution that satisfies the maximum principle if M is too large.
4.2. Analytical benchmark
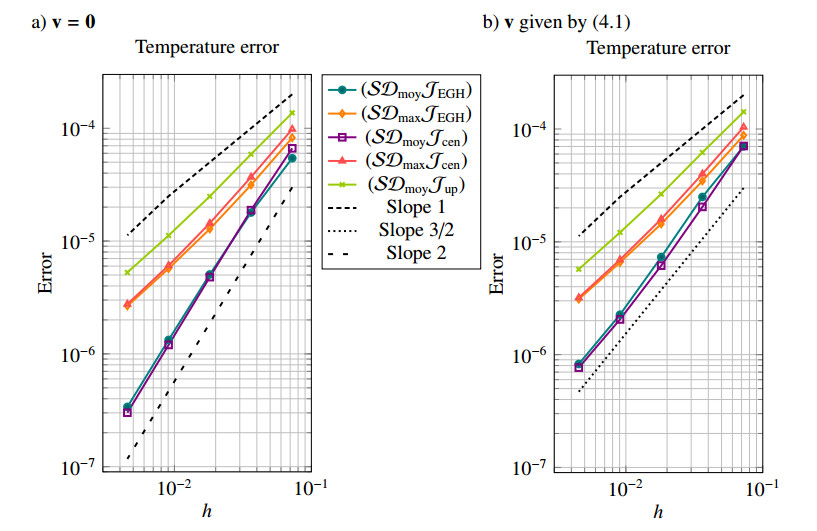
In this benchmark, we want to investigate the accuracy of the scheme described in section 3.2, depending on the discretization of the diffusive and Joule terms. We consider the domain Ω=[0;1]2. The simulations will be performed until the time T=0.1. The exact solution is defined for (x,y,t)∈Ω×[0;T] by:
with λ=2. In (3.3), a source term is added accordingly. For the velocity, two cases are considered:
a) v=0,
b) v defined by
Here, Dirichlet conditions are imposed on all the boundaries, so that ΓD=Γ. The temperature error in L∞(0,T;L2(Ω)) is plotted in Figure 4 as a function of the mesh size h, in log-log scale, for each scheme. We notice that without the convective term (case a)), the centered schemes (SDmoyJcen) and (SDmoyJEGH) converge at order two, whereas the others are only at order one. Thus, the upwind choice in the diffusion term (schemes (SDmaxJcen) and (SDmaxJEGH)) or in the Joule term (scheme (SDmoyJup) degrades the rate of convergence to order one, but is necessary to obtain the maximum principle. Adding the convective term (case b)), the centered schemes (SDmoyJcen) and (SDmoyJEGH) converge at order 3/2. This decrease of convergence rate can be explained by the upwind treatment of the convective term in order to ensure the stability.
4.3. The natural convection in a cavity
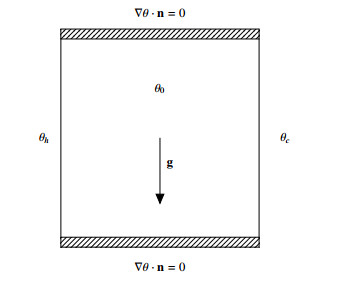
We will now validate the scheme (SDmaxJcen) by coupling the temperature equation with the velocity one on the benchmark introduced in [1,15,29,31] and used in [7] (slightly adapted because of the choice of the model (2.2)). We consider a square cavity Ω=[0,1]2 containing a calorifically perfect gas, see Figure 5. The gas is initially at rest with uniform temperature:
Note that the temperature has been scaled to be between 0 and 1. A temperature of θh=θ0(1+ε) (respectively θc=θ0(1−ε)) is imposed on the left (respectively right) wall with ε=0.01 as in [29]. For this small temperature amplitude, the thermodynamic pressure can be approximated by a constant, where the author verifies numerically that P(T)=P0 with an accuracy of 10−5). The horizontal walls are insulated. Denoting by ΓN=[0,1]×{0,1}, we thus have:
On all walls, the no-slip condition is imposed for the physical velocity u, which gives for the solenoidal one:
We set λ=4,76⋅10−2, which corresponds to a Rayleigh number of 10−5, as it is the case in [31].
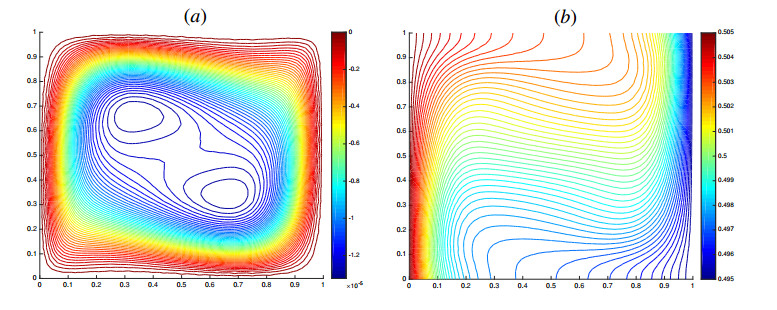
The time iterations are performed until the numerical steady state is reached, i.e. the relative errors for the solenoidal velocity and the temperature are less than 10−10. The steady state is obtained approximatively at T=100, using for instance a mesh T composed by 3584 triangles (corresponding to h=1.8⋅10−2) and a time step Δt of the order of 10−2. We represent in Figure 6 the streamlines of the velocity field and the contour lines of the temperature at steady state. The solutions obtained are close to the ones given in Figures 4 and 5 of [29]. We also verify that the maximum principle for the temperature is always respected.
Note that even though we have to solve a global optimization problem in order to obtain the fluxes used in the finite volume scheme, its cost is negligible. Indeed, the matrix of the linear system (3.33) is assembled a single time before the time loop. On the contrary, some matrices in the finite element step must be assembled at each time step. Note moreover that the cost of Newton's iterations for the temperature equation resolution is also negligible. Indeed, only two or three iterations are necessary in order to obtain the solution with an accuracy of 10−5. With this choice, approximatively only 10% of the overall computation time is devoted to the resolution of the temperature equation. This ratio in the computation cost is quite the same when we consider more coarse or more fine meshes.
5.
Conclusion
In this work we propose some finite volume schemes for the resolution of an unsteady convection-diffusion equation involving a Joule term. Several variants are investigated, depending on the way to discretize the diffusion term as well as the Joule one. A first main point is that two of these schemes verify the discrete maximum principle without any restriction on the data. Such schemes allow us to define a combined finite volume - finite element scheme for a low-Mach system, where the temperature is computed by the finite volume scheme whereas the velocity and pressure are approximated by a finite element one. The second point is that the finite volume velocity field, used for the convective term in the temperature equation, is computed from the finite element one by the resolution of a discrete least-mean-squares problem to ensure the local free divergence constraint. The numerical results illustrate the properties of the different schemes and confirm the relevance of the approach. The question of the convergence remains to be investigated, and will be addressed in a future work.
Acknowledgments
This work was supported in part by the Labex CEMPI (ANR-11-LABX-0007-01). The authors gratefully acknowledge Clément Cancès, Claire Chainais-Hillairet and Benoit Merlet for fruitful discussions about it.
Conflict of interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: