1.
Introduction
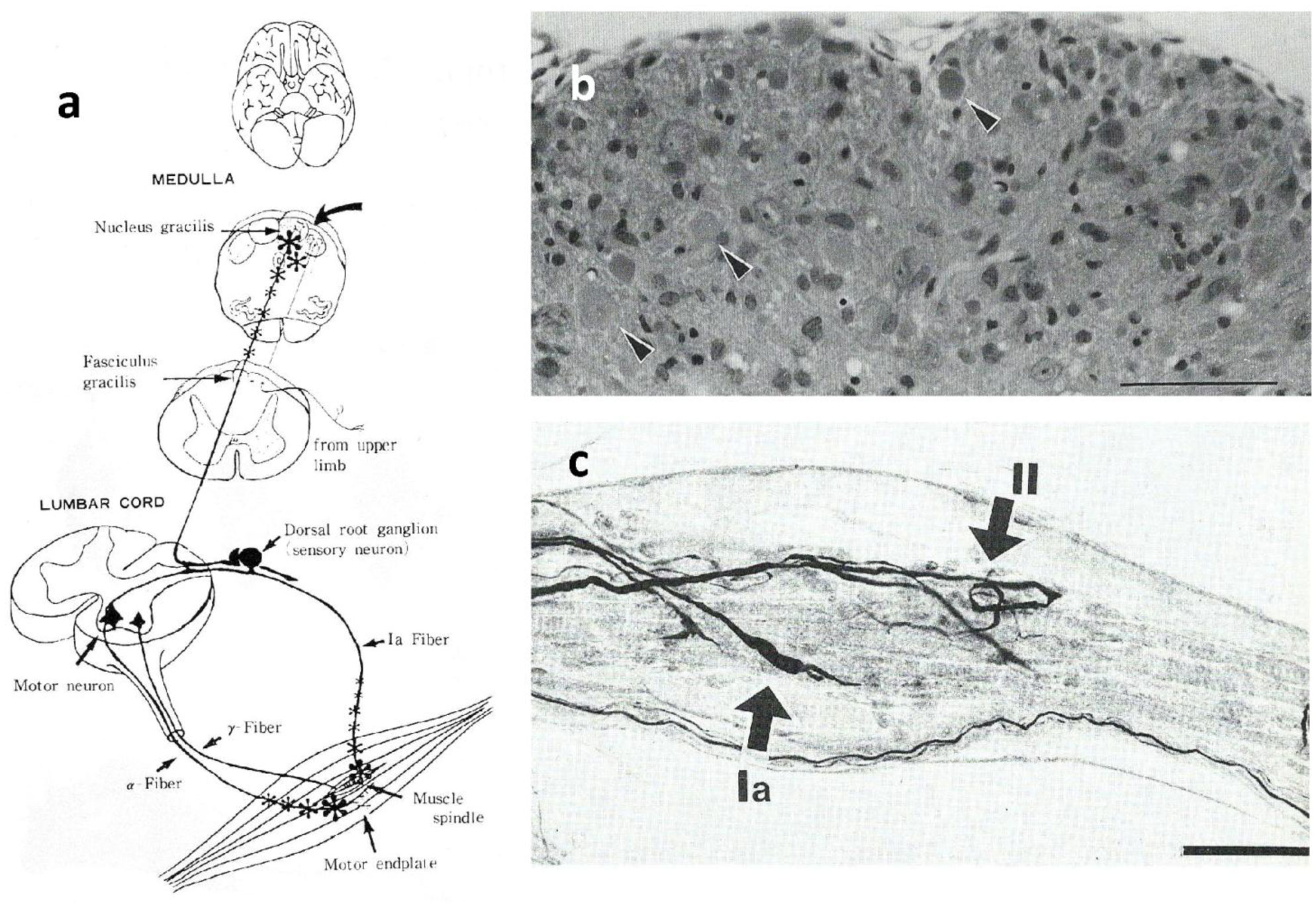
The primary sensory neurons that transmit information from muscle spindles in skeletal muscles of the limbs and trunk to spinal cord are clustered together in the dorsal root ganglion (DRG) located adjacent to spinal cord. The DRGs contain sensory neurons with central and peripheral branches projecting towards either terminate within spinal gray matter or ascends through gracile or cuneate funiculus along dorsal column and ends at the junctions of spinal cord with the medulla. The peripheral branches connect to motor neurons located in ventral grey matter. The central branches from hind limbs run a long way along gracile fasciculus and terminate in gracile nucleus, while those from fore limbs and upper trunk run in cuneate fasciculus and terminate in cuneate nucleus. The gracile and cuneate sensory tract is bundled up travel side by side within dorsal column of spinal cord (see a schematic view in Figure 1a) [1]. This review describes a mutant mouse showing abnormal behaviors due to severe sensory and motor neurological disorders.
In January 1984, abnormally suffering gaits were found in three 80-day-old mice, two females and one male, in the Laboratory of Genetics, Nagoya University [2]. The clinical and pathological examinations were made promptly in the National Institute of Neuroscience in NCNP, Tokyo. The homozygous mice were not identified from normal controls until 30-day-old. The first sign of abnormal behavior was confirmed when they were suspended by tail. Although normal mice extend their limbs out from the trunk, the hind limbs of homozygotes are initially stretched spasmodically and then become flexed and folded tightly towards the trunk (sensory ataxia stage), By about 80-day-old, the hindlimb weakness and tremor, muscle atrophy became apparent (motor paresis stage). The neurological signs were progressively severe, and most of death occur by about 5 to 6 months of age. The inheritance followed autosomal recessive mode. Linkage tests showed that the genetic mutation located on chromosome 5 linking to Pgm-1 and W [3].
2.
The gracile axonal dystrophy (gad) mouse
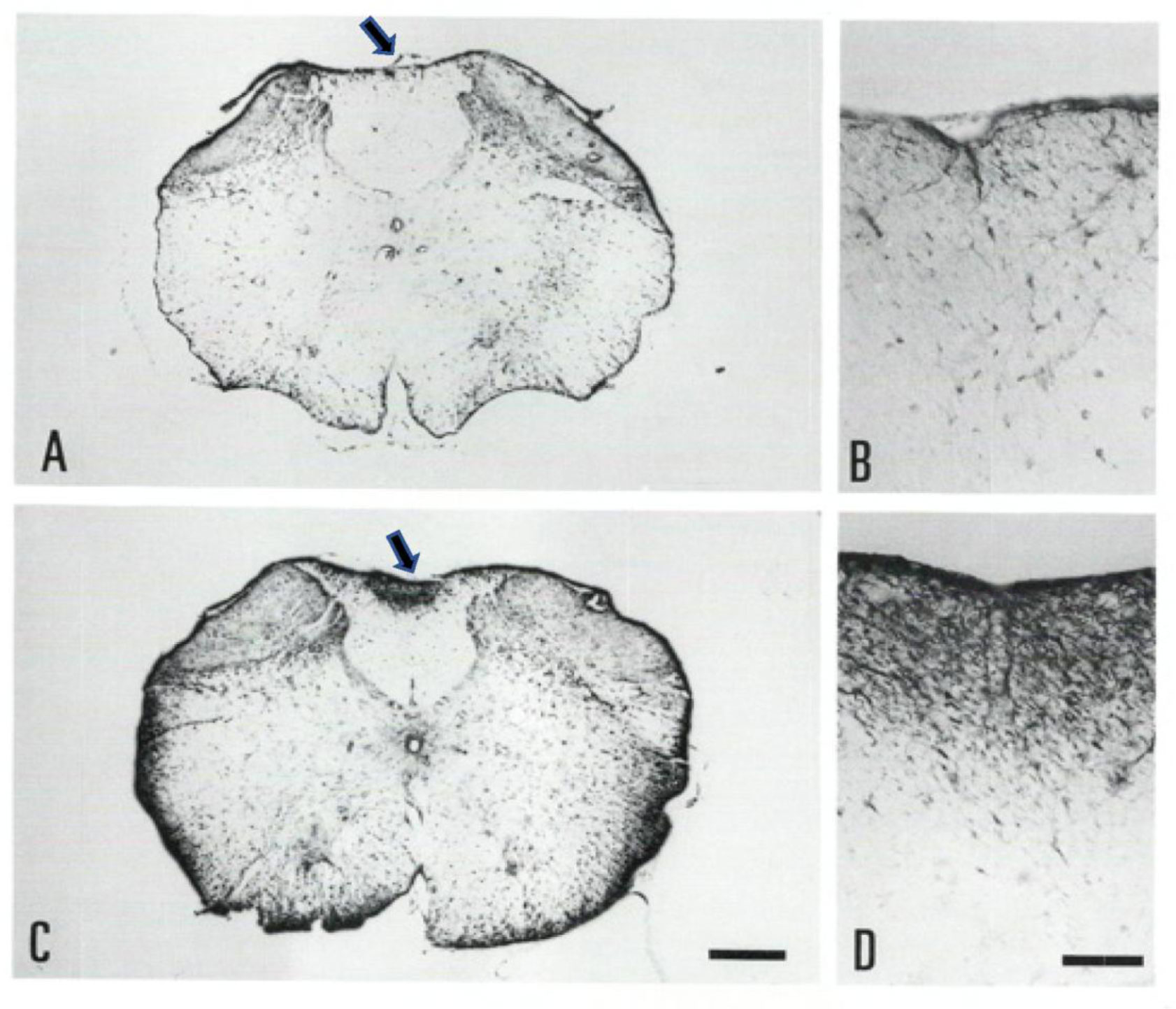
This mutant mouse was named originally “gracile axonal dystrophy (GAD)”, but, since etiology became clear, a gene symbol (gad) came to be used widely. The earliest pathological sign was detected as early as 40-day-old in gracile nucleus at the junction of spinal cord with medulla oblongata. The swollen eosinophilic axons called “spheroid” scatter over this nucleus (Figure 1b). The spheroids are also called “dystrophic axons” showing enormous enlargement most striking in the terminal segment of affected axons that appear just distal to the normal termination of the myelin sheath [6],[7]. They are often filled a number of neurofilaments, dense bodies, mitochondria with dark matrix, and multiple-vesicles which often surround a whirlpool towards the center. Abundant astrocytic processes are often seen around spheroids in lesioned sites [4],[8].
The ultrastructural observations revealed the first signs of spheroids in gad mice at 10 to 20-day-old after birth. Spheroids varying in size are identified by slight presynaptic boutons which are facing to secondary neurons contact to and ascend to thalamus, or by thin myelin sheath surrounding them. They maintain a synapse-complexes containing electron dense bodies, mitochondria at their axonal ends. With progress of axonal degeneration, the cytoplasmic neurofilaments and thicker filament-like structures with 40 nm gathered intensely, moreover, few lysosomes contained amorphous substances seen in some places which make electron density in cytoplasm darker than usual, and finally loose presynaptic boutons. The filament-like structures gather keeping in line complicatedly and rarely branched off [4].
The anterograde transports from DRGs are often very long-distance. Many intracellular proteins and organelles have to be transported down them after synthesis in neuron body. The retrograde transport from axonal ends to neuron body is also necessary to degrade proteins, clear useless aggregates, and provide a signaling mechanism from the synapse side to the cell body [9]. The kinesin and dynein families move along tracks of cytoskeletal filaments, termed microtubules [10]. Any disturbance of axonal transport may have severe consequences for neuronal function causing generally known as axonal traffic jams that are the consequence of an aberrant axonal transport, and usually lead to local swellings and accumulations of needless organelles [10]. However, it is not clear enough what mechanism(s) and substances do cause the deficits in axonal transportation in long axons derived far away from the neuron cell body.
The incidence of spheroids shifts from gracile nucleus to fasciculus with the disease progress, suggesting that the degenerating axonal terminals of DRG neurons back from the distal presynaptic parts in the gracile nucleus, toward the cell bodies in the DRGs. These results indicate that axonal degeneration is age dependent and follows a “dying-back” process of the primary sensory axons [4],[5].
3.
Axonal dystrophy and substance P
Axonal dystrophy, which shows the unique pathological feature including axonal swelling (spheroids) localized throughout the central nervous system (CNS) and peripheral nervous systems (PNS), occurs under many pathological and physiological conditions. It has been observed in the infantile neuroaxonal dystrophy in mutant mouse [11] and Hallervorden-Spatz disease [12], and in the vitamin E deficiency in rats [13],[14]. In addition, physiological ageing is known to accompany the formation of spheroids in dorsal column nuclei in humans [15],[16]. The swelling axons occur at preterminal or presynaptic portions of sensory axons in a progress of axonal dystrophy. However, why these axons in ascending spinal tract are vulnerable still remain enigmatic [17].
During the course of our study on gad mice, it was speculated that a similar lesion seen in CNS may also occur in the opposite PNS derived from DRG neurons which have sensory axon ending in muscle spindle, and motor endplates on every muscle fiber. The axonal pathology was studied by using a method of combining acetylcholine-esterase and silver impregnation method [5],[18]. The sensory axons in gad mice show axonal degeneration and swelling at their distal ends in muscle spindles as early as around 20-day-old (Figure 1c). Similar degeneration occurs in the distal motor ends little later than that in sensory endings [18]. The progressive degeneration of motor nerves was recently confirmed in UCH-L1 knockout mouse model [19],[20]. There are several differences in spheroid formation in gad mice between CNS and PNS. Axonal dystrophy in ascending gracile tract are accompanied by marked swollen axons, whereas sensory and motor axons in PNS swell only slightly (Figure 1c) [5],[18]. The DRG neurons are morphologically intact until later stages as far as examined [5],[21]. Although motor neurons in the spinal ventral horn are morphologically normal even at advanced stages, the dying-back degeneration is seen at nerve terminals in the distal endplate zone. In pathological concepts, the distal spheroids with myelin loss develops first in the most distal parts of the axons, and, if abnormality persisted, the formation of spheroids is mostly limited at the tip of axons retained other parts intact and continue dying-back degeneration [22],[23]. The dying-back axonopathy seen in CNS of gad mice resembles Wallerian degeneration which shows spheroids and myelin loss [24]. It is important to understand mechanisms underlying axonal dystrophy in gad mice which may be caused by impaired axonal transport resulting inability to keep up with the metabolic demands of axon.
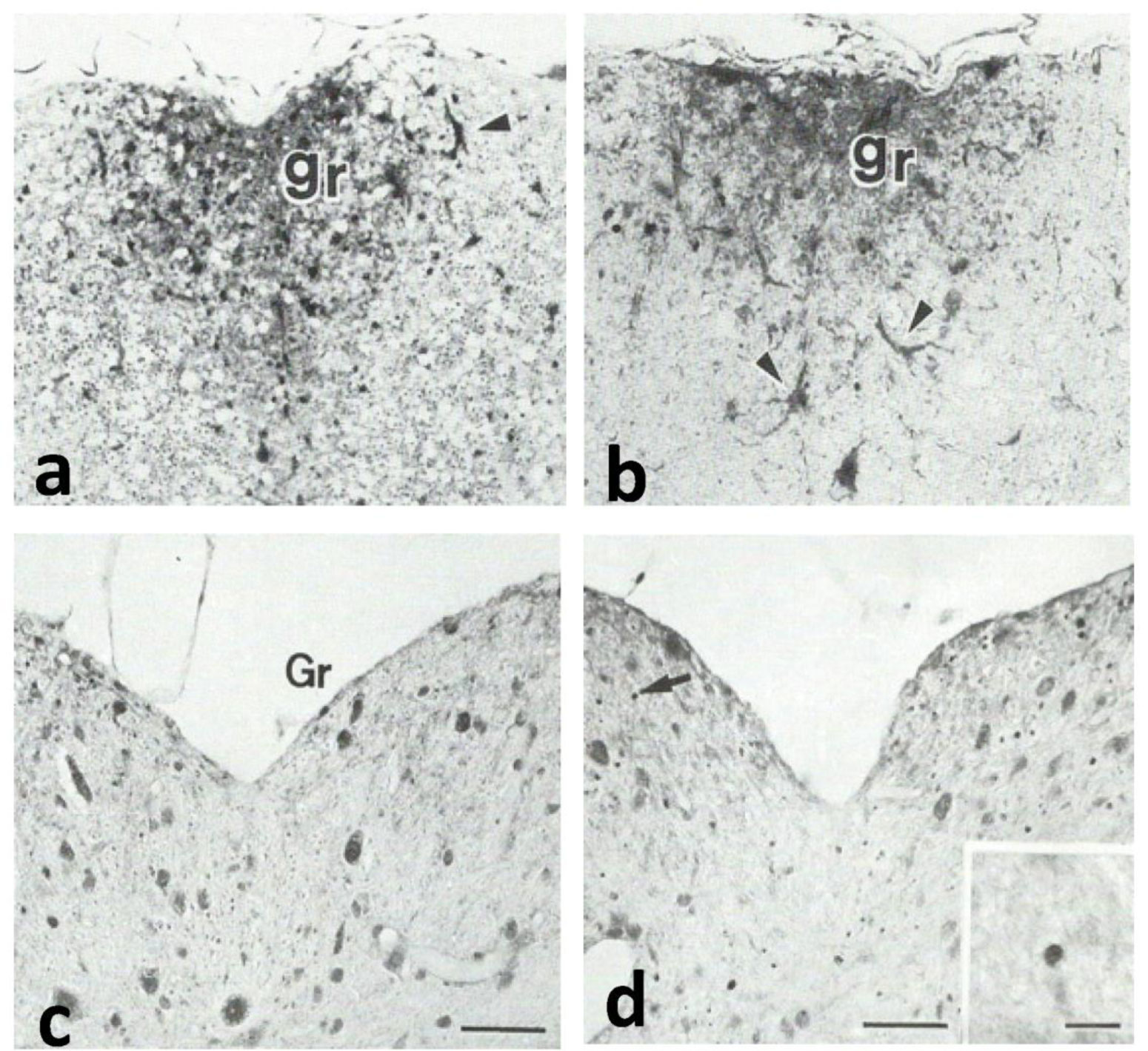
The enhancement of substance P (SP)-like immunoreactivity was observed in axonal profiles of gracile nucleus and fasciculus in 13-month-old normal mice [25] and ageing rat [16], but no SP-positive axons were detected in gracile ascending tract of young 3- and 5-month-old mice. Although partial arrest of axonal transport of SP and/or enhanced SP-synthesis in DRG neurons are ascribable, the true reason is still unclear [26]. It was reported that some of spheroids in gracile nucleus contain cholecystokinin (CCK) which is one of neuropeptides thought to be a somatosensory neurotransmitter or neuromodulator [27]. Authors suggested that CCK may be partly involved in the formation of dystrophic axons in this region. Since axonal dystrophy of gracile sensory neurons in gad mice are likely to those in aged mice mentioned earlier [4],[20], it was expected that SP reactivity is enhanced in lesioned sites of gad mice.
The SP reaction in gad mice is more intense throughout gracile tract, and is already visible by earlier stages than in normal aged mice (Figure 2a and 2b). As mentioned in chronic pain, reactive astrocytes are involved in the regulation of chronic pain [28]. Interestingly, the astrocytes in lesioned sites of gad mice are stained with both GFAP and SP, and are characterized by astrocytic hypertrophy and proliferation [29],[30]. Dacil N, et al. (2015) reported recently that, although SP detected within cytoplasm of astrocytes is taken in through SP-receptors, the preprotachykinin mRNA (precursor of SP) and SP are shown to be localized in reactive astrocytes around senile plaques, moreover, SP expression increases angiogenesis of brain vessels associated with β-amyloid plaques [31]. Application of SP prevents β-amyloid-induced impairment of cognitive processes through inhibition of β-amyloid-induced overexpression of potassium channel subunits [32]. It seems likely that astrocytes are stimulated to proliferate and grow rapidly by unknown factor(s) released from axons and/or other cells degenerating in nearby tissues to prevent triggering a perivascular inflammation. Noguchi et al. (1995) reported that the peripheral nerve axotomy of primary afferent neurons results in de novo expression of preprotchykinin mRNA in rat DRG neurons, and, after 2 weeks, an increase of SP immunoreactivity is observed in axons and their terminals of large myelinated fibers in gracile nucleus [33].
From these reports, we postulated that the loss of peripheral nerve endings of gad mice may lead to abnormal pain sensations and other sensory abnormalities as with in peripheral nerve axotomy. The SP has both neuroprotective and neurodegenerative properties which are related to proper development of CNS and changes in progressive neurodegenerative diseases [34]. In this context, we remark a report that SP induces α-secretase-mediated amyloid precursor protein (APP) cleavage and to protect cerebellar granule neurons from attenuating amyloid-β protein (AβP) production, without modifying the steady state level of its precursor APP [35],[36]. Kowall et al. (1991) added a fact that SP prevents β-amyloid induced neuronal loss when coadministered it into cerebral cortex [37]. Moreover, the cognitive impairment of rat by AβP brain infusion was prevented by SP administration [38].
4.
Amyloid precursor protein and amyloid β-protein
From several pathological features in gad mice, we thought that abnormal expression of APP may be involved in axonal dystrophy along the gracile tract, following an accumulation of AβP which appears to be generated by aberrant proteolytic cleavage of APP, and deposits as an insoluble form mainly in the extracellular matrix surrounded by activated astrocytes [39],[40]. Yamaguchi et al. (1990) proposed a “diffuse plaque” as a pathological term to define the early and immature stage of the senile plaque formation, and demonstrated that the majority of senile plaques in AD brain are diffuse rather than the classic-core plaques [40]. A striking feature of APP-IR and AβP-IR in gad mouse is a diffuse and intracellular distribution of the immunoreacted products, suggesting that there is an intracellular deficit to accumulate these proteins within the cytoplasm (Figure 3a and 3b) [41],[42]. It was also reported that APP accumulates within the swollen axons in the human brain lesions [43] and in ageing rat brain [44]. The APP synthesized in DRG neurons moves along axon by the fast-anterograde transport to the distal ends [45] and distributes in almost all neuron cytoplasm and some glial cells in the nervous system [46]. The astrocytes are known to express APP and AβP following experimentally induced neuronal damage [47]–[49] and in cell cultures [50]. The distribution and expression of SP in transgenic mice overexpressing human APP indicated that SP-immunoreactive β-amyloid plaques dramatically increased after 12 months, thereafter SP was expressed in a number of reactive astrocytes [51]. Furthermore, the morphological abnormalities at synapses in the cerebral cortices of aged macaques preceded the accumulation of APP within neurites and reactive astrocytes and microglia [52]. Indeed, aberrant processing of APP into AβP by these cells is implicated as the initiating factor in the formation of senile plaques [53]. Another finding that astrocytic cells are immunoreacted with both APP and AβP, leads to an idea that similar mechanism may function along the gracile tract of the gad mouse.
5.
Ubiquitin, ubiquitination for substrates
The Ubiquitin (Ub) is a 76 amino acid polypeptide involved in an ATP-dependent and non-lysosomal degradation of abnormal and short-lived normal proteins [54], and in the pathogenesis of cellular inclusions, many of which have a fibrillar structure and contain cytoskeletal proteins [55]. The Ub also plays an important role in the proteolysis of abnormal proteins in aberrant cells [56].
The gracile axonal dystrophy in gad mice is mainly represented by swelling of axonal ends and “dying-back” degeneration of afferent neurons [57], and by an accumulation of APP and AβP along gracile ascending tract [41],[42]. These abnormalities are first observed at the most distal ends of afferent axons in gracile nucleus as early as 20-day-old [4]. Despite a modest filamentous accumulation in swollen axons, Ub-positive products are not found in the cytoplasm by 4 weeks of age. This raises the possibility that there may not be enough abnormal filaments for their selective degradation by cytoplasmic Ub and/or a lysosomal proteolysis may already be activated to function cooperatively with Ub-proteolysis. The axonal terminals are not always Ub-positive in the earliest stages, even if they reveal an initial sign of the structural alterations due to axonal degeneration. Thereafter, when axons are filled with an excess amount of aberrant neurofilaments, the Ub immunoreactivity increases and becomes to be detected in these axonal terminals (Figure 3c and 3d) [58],[59].
The distribution of ubiquitinated deposits in gracile tract of gad mice is closely related to the severity of axonal degeneration progressing retrogradely from distal ends of primary sensory neurons, followed by axonal dystrophy in the nervous tracts of the secondary sensory neurons in Clarke's nucleus and gracile nucleus [30]. Similar Ub distribution extents further throughout the thalamus to the sensory areas in cerebral cortex [59]. In contrast, The Ub deposits in the descending motor neuron system are seen in the grey matter surrounding motor neurons in the ventral horn of spinal cord, followed by an increase in the order of lumbar, thoracic, and cervical spinal cord. The axonal degeneration in the motor neuron system in gad mice starts from the distal axonal ends toward the upper cerebral cortex, especially in cortex motor areas [59]. Together, the transneuronal degeneration beyond PNS to the lower CNS extends further to the upper CNS [58],[59].
6.
Ubiquitin c-terminal hydrolase-L1 (UCH-L1); Arriving at one goal is the starting point to another
In eleven years after the first report on gad mice, Saigoh et al. (1999) revealed gad mutation which is caused by an in-frame deletion including exons 7 and 8 of Uchl1 gene, encoding ubiquitin carboxy-terminal hydrolase (UCH) isozyme L1 (UCH-L1) selectively expressed in nervous system and testis/ovary. UCH-L1 is a 24.8 kDa, consisting of 223 amino acids and encoded by 9 exons with a transcript of 1172 bps in length, and located on human chromosome 4(4p14) [60]. UCH-L1 (originally known as PGP 9.5 or PARK5) plays a key role in ubiquitin turnover through its C-terminal hydrolase activity. Several functions of UCH-L1 were proposed including ubiquitin hydrolyze activity, ubiquitin ligase activity and stabilization of the mono-ubiquitin. Mutations in human UCH-L1 gene are associated with PD and other neurodegenerative disorders [62]. The gad mutation with approximately 3.5 Kb deletion exists at genomic DNA level, encoding a truncated Uch-L1 gene lacking a segment of 42 amino acids containing a catalytic residue.
The UCH-L1 is, as mentioned above, a member of deubiquitinating enzymes which functions as a Ub ligase and also a role in stabilizing Ub monomers in vivo [61]. As a deubiquitinating enzyme activity, UCH-L1 facilitates Ub recycling and regulates the cellular pool of available Ub, giving the capacity to modulate many ubiquitin-dependent cellular processes. Thus, the lack of UCH-L1 expression in mice results in gad phenotype. Down-regulation and extensive oxidative modification of this enzyme are observed in the brains of AD patients as well as PD patients [63]. It is unclear which human diseases are related to the pathogenesis of gad mice.
An isoleucine 93 to methionine amino acid mutation (I93M) of UCH-L1 was identified as a cause of autosomal dominant PD [64]. To make sure whether this I93M mutation occurs due to a gain of toxic function in vivo, a transgenic mice (Tg) expressing human UCH-L1I93M were cleated [65]. The midbrains of Tg mice contain increased amounts of insoluble UCH-L1 as compared with those of non-Tg mice, perhaps due to a toxic gain of function. Authors also revealed one of typical pathological phenotypes of human PD, namely “dopaminergic neuron loss” in the substantia nigra, but did not detect α-synuclein in dystrophic spheroids [65],[66] and a sign of “Lewy body formation” [62]. These observations suggest that the molecular mechanism of β- and γ-synuclein accumulation in gad spheroids is different from that in Lewy bodies. Alzheimer's disease (AD) is characterized by amyloid plaques (Senile plaques) composed of β-amyloid (Aβ) peptide surrounded by swollen presynaptic dystrophic neurites consisting of dysfunctional axons and terminals that accumulate the amyloid precursor protein (APP) required for Aβ generation. The primary lesions observed in gracile nucleus of gad mice, are characterized by dystrophic swollen axons, and surrounded by the projections of astrocytes. As mentioned earlier, swollen axonal dystrophy with a dying back-type degeneration occurs from both central and peripheral distal ends of DRG neurons.
Leaving secondary neurons in gracile nuclei behind, axonal dystrophy gradually retreats towards parent DRG neurons. The secondary neurons then continue to ascend the midline of medulla and cross to the other side and ascend to thalamus. Since Ubiquitin accumulation is often seen in thalamus neurons in advanced stages, the functional and metabolic deficits in secondary neurons occur already to some extent, resulting in partial synaptic loss of 3rd order neurons in thalamus. The 3rd neurons project their axons to somatosensory cerebral cortex, where somatosensory stimuli are processed.
On the other hand, the motor nerve fibers descend through corticospinal tract to motor neurons in spinal grey matter. The UCH-L1 in maintaining corticospinal motor neurons keeps viability and cellular integrity. Such motor neurons with a long distance from cortex, show early, selective, progressive, and profound cell loss in the absence of UCH-L1 [67],[68]. From the results that maintenance of memory in a passive avoidance test and exploratory behavior in an open field test is reduced, and the long-term potentiation (LTP) of field synaptic responses from Schaffer collaterals to CA1 pyramidal cells in hippocampal slices is also impaired in gad mice [69],[70], a collapse of the synapse-axon circulation around CNS from PNS seems to take place. Thus, the true mechanism(s) and functions to cause axonal dystrophy in gad mice should be clarified more.









 DownLoad:
DownLoad: