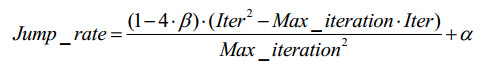Quantum codes from $\sigma$-dual-containing constacyclic codes over $\mathfrak{R}_{l, k}$

1.   Introduction

Global competition and the demand for integration among enterprises have been pushing the development of the supply chain network (SCN). SCN has been applied in many fields in reality, which is generally composed of different members and materials flowing between the members, such as electronics ^[1] and the food industry ^[2]. The common members of SCN include suppliers, warehouses, distributors and so on ^[3,4]. The main purpose of supply chain network design is to maximize the profit of the whole network and to meet the demands of different facilities at the same time.

Recently, the researchers have paid more attention to the closed-loop supply chain (CLSC) under the background of the deepening environmental awareness and the development of remanufacturing industry ^[5]. A CLSC network consists of the forward and reverse networks that consider both production and recycling ^[6]. The forward supply chain concentrates on delivering products for customers effectively. In contrast, the reverse supply chain aims to decrease the cost of customers and lower pollution by helping the collection and distribution of the recycling products to the appropriate facilities. Therefore, the CLSC model has great practical application foreground. Mosallanezhad et al. ^[7] proposed a shrimp CLSC model to meet the growing market demand for fresh food and to minimize the total cost, which also considers the balance for demands of poultry and livestock food market at supplying the shrimp products. Salehi-Amiri et al. ^[8] designed a sustainable CLSC network for the walnut industry, which considers meeting the demand of different markets and provides the channel of returned products for the second use. Cheraghalipour et al. ^[9] proposed a bi-objective CLSC model for citrus fruits, which aims to minimize the total cost of the whole CLSC network and satisfy the customers' demands as much as possible. The uncertainty generally exists in CLSC due to various factors, such as the economy or environment ^[10,11]. Chouhan et al. ^[12] developed a CLSC network with uncertain demands. The line balancing strategy is addressed to handle uncertainty. Fathollahi-Fard et al. ^[13] proposed a dual-channel CLSC network under uncertainty for the tire industry, and a fuzzy approach called Jimenez's method is applied to tackle the uncertain parameters.

The network design of CLSC is proved to be an NP-hard problem ^[14], and therefore it is hard for most traditional approaches to get the satisfied solutions for this problem. Moreover, commercial software such as CPLEX and GAMS usually require a lot of time or even are unsolvable when they solve the large-scale and complex mathematical CLSC models. As intelligent algorithms have a good global searching ability, many intelligent algorithms are used for solving this kind of problem and specific methods can be designed according to the specific problem ^{[15,16,17,18]}.

Genetic algorithm (GA) as a popular and efficient intelligent algorithm has been widely applied in CLSC problems. HJ et al. ^[19] proposed a GA-based heuristic algorithm that was based on the dynamic integrated distribution network and simplex transshipment algorithm, and this method was used to optimize the integrated network for third-party logistics providers. Hamed et al. ^[20] proposed a new hybrid algorithm that used the operators of particle swarm optimization (PSO) to improve the performance of GA for solving the large-scale CLSC problems. Abir et al. ^[21] constructed a multi-objective CLSC model to minimize both carbon emission and the total cost, and the multi-objective GA and the weight sum method were used to solve the proposed problem. Besides, other heuristic algorithms are also applied to the CLSC problems, such as PSO ^[22,23,24], ant colony optimization (ACO) ^[25], red deer algorithm ^[26], and hybrid heuristic algorithms ^[27,28].

For the optimization of CLSC network design, the solution encoding is an important part of a competitive algorithm. However, few researches focus on it. Gen et al. ^[29] proposed an improved GA to solve the supply chain problem, and developed an improved priority-based encoding method for chromosomes. A freight matrix is used to calculate the transportation route's priority, and the gene information is composed of corresponding priority. The advantage is that the chromosomes can contain more information with fewer genes. However, if there are many constraints to satisfy, encoding and decoding operations will be time-consuming due to the constraint verification. In addition, the CLSC problem often has multiple complex constraints, and the complexity of the problem would increase significantly with large scale networks ^[30]. Therefore, how to deal with multiple constraints and obtain high-quality solutions is also a key problem for an intelligent algorithm to solve the CLSC problem.

This paper focuses on the proposed model of the CLSC and develops a genetic algorithm with two-step rank-based encoding (GA-TRE) to solve the multi-constrained and large-scale CLSC problem. According to the characteristics of the CLSC problem and GA operators, a new encoding method is proposed, called two-step rank-based encoding. Since, the main problems of the proposed model are the decision of route planning and delivery volume, this encoding scheme decomposes the encoding process into two steps, and different encoding steps are used to solve different subproblems. The first step encoding is used to determine the alternative transportation routes, and the second step encoding is to determine the specific route and the delivery volume among the CLSC network. Moreover, a rank-based method is used to achieve greedy solutions in the second step encoding. The two-step encoding mechanism can help to relieve the multi-constrained challenges, since the feasibility of the transportation routes will be predicted according to the relevant constraints after the first step of encoding. In this way, the constraints can be verified separately according to different subproblems, which can reduce the difficulty of solving the problem and find illegal solutions as soon as possible.

Besides, for the canonical GA, it is difficult to obtain legal solutions after genetic operators and time-consuming to handle large-scale constrained problems. Therefore, in this paper, the genetic operators are only used for the chromosome of the route for reinforcing the exploring ability of GA to tackle this kind of problem. Since the chromosome of the transportation route can be represented by binary encoding, it involves fewer constraints than the complete problem. This method will help to reduce the probability of generating illegal solutions. To reduce the chance of the population being trapped into the local optimum and explore the solution space, a new mutation operator which is called stage-mutation, and an adaptive population disturbance mechanism are designed. Stage-mutation can increase the diversity of chromosomes based on the characteristics of the CLSC problem, and the adaptive population disturbance mechanism can effectively explore more search space by adding new individuals in different periods of the algorithm. Comprehensive validation of the proposed algorithm is conducted by comparing it with other algorithms in the different scales of instances. The experimental results show that GA-TRE has a better performance on the CLSC problem.

In conclusion, the main contributions of the proposed algorithm are as follows:

1) A two-step rank-based encoding scheme for the CLSC problems is proposed to handle the constraints and increase the algorithm efficiency, which is also used for improving the crossover and mutation operators;

2) The constraints handling and greedy solutions achieving are considered on different encoding steps;

3) A new mutation operator based on CLSC problems and an adaptive population disturbance mechanism are designed to improve the population diversity of the GA-TRE algorithm.

The rest of this paper is organized as follows. Section 2 outlines the problem description and the detailed model formulation. Section 3 describes the proposed encoding method and algorithm, respectively. Section 4 shows the exhaustive experiment which is conducted to validate the performance of the GA-TRE, and the conclusion follows in Section 5.

2.   CLSC problem definition

2.1.   Problem description

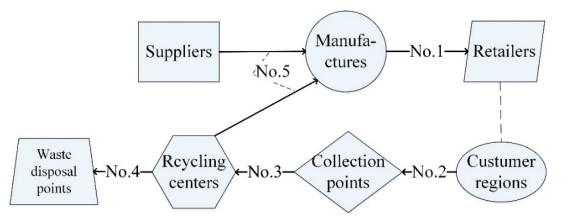
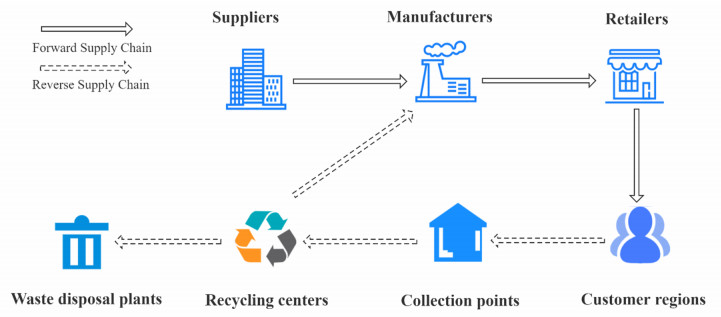
Nowadays, environmental protection has attracted increasing attention. A variety of closed-loop supply chains have been designed for recycling, such as the recycling of plastic products, tires ^[31], and leather products ^[32]. However, the design of the CLSC network for different industries and different scenarios will bring burden on manpower and material resources, especially for small and medium-sized enterprises. Hence, this paper aims to propose a CLSC model to match more application scenarios. The proposed CLSC network contains seven kinds of members: suppliers (S), manufacturers (M), retailers (R), customer regions (CR), collection points (CP), recycling centers (RC), and waste disposal plants (WDP). The proposed CLSC network structure is shown in Figure 1.

In this model, certain facilities have their capacity/demand (${c}_{◻}^{◻}/{d}_{◻}$), opening fixed cost (${f}_{◻}^{◻}$), and variable cost (${x}_{◻}$). The transportation cost (${m}_{jk}{, cr}_{vl}$, etc.) exists when a certain quantity of raw materials or products are transported among different facilities (${q}_{◻}^{◻}$). Moreover, to be closer to reality, the customers in the model do not refer to a single buyer but represent a not fixed customer region, and the total customer demands in this model must be met. In the process of customers buying products from retailers, the specific number of customers, positions, and quantity of commodities are difficult to determine. Therefore, the concept of customer region is used in this model, and the route from retailers to customer regions is not planned. The demand of retailers comes from the demand of the customer, and therefore the sum of all the retailer demand must be met by the manufacturers.

Because the products exceed the service cycle or are damaged, customers will discard them. At present, the used product collection points have been set up in most cities in China. Each point will receive the used products and transport them to the recycling center after centralized sorting (S). For customers, they will get a certain amount of subsidy (${p}_{2}$). Besides, because the government supports the environmental protection industry, the price of raw materials from the recycling center is cheaper than from manufacturers, which contributes to the smooth flow of the reverse supply chain to a certain extent. The minimal recycling rate of customer regions (${\mu }_{v}$) is preset in this model. The used products are transported from the collection points to the recycling centers for recycling and processing. During the whole process, most parts of products can be recycled as raw materials and be transported to the manufacturers. Some parts which cannot be recycled will be disposed of by the waste disposal plant for burning or landfills. The maximal disposal rate (φ) is also preset in this model.

Some assumptions are applied in this model.

1) Recycled materials from the recycling centers have the same quality as the materials from suppliers.

2) There are no products or materials to flow among the members from the same level.

3) The maximum manufacturing capacity and storage capacity of each member are fixed.

4) In the first time, the supply chain flows after the customer purchases the product, and the recycling center receives the used product. In this way, the manufacturer can receive raw materials from both suppliers and recycling centers.

2.2.   Model formulation

The notations of indices, parameters, and decision variables about this model are shown as follows:

Indices

i  index of suppliers, $i \in\{1, 2, \ldots, I\}$

j  index of manufacturers, $j \in\{1, 2, \ldots, J\}$

k  index of retailers, $k \in\{1, 2, \ldots K\}$

v  index of customer regions, $v \in\{1, 2, \ldots V\}$

l  index of collection points, $l \in\{1, 2, \ldots L\}$

m  index of recycling centers, $m \in\{1, 2 \ldots M\}$

w  index of waste disposal plants, $m \in\{1, 2 \ldots W\}$

Parameters

$c_{i}^{s}$  capacity of supplier i

$c_{j}^{m}$  capacity of manufacturer j

$c_{l}^{c p}$  capacity of collection point l

$c_{m}^{r c}$  capacity of recycling center m

$d_{k}$  demand of retailer k

$d_{v}$  demand of customers in customer region v

$s_{i j}$  unit cost of transportation from supplier i to manufacturer j

$m_{j k}$  unit cost of transportation from manufacturer j to retailer k

$c r_{v l}$  unit cost of transportation from customer region v to collection point l

$c p_{l m}$  unit cost of transportation from collection point l to recycling center m

$r c_{m j}$  unit cost of transportation from recycling center m to manufacturer j

$r c_{m w}$  unit cost of transportation from recycling center m to waste disposal plant j

$f_{j}^{m}$  fixed cost of manufacturer j

${f}_{l}^{c p}$  fixed cost of collection point l

$f_{m}^{r c}$  fixed cost of recycling center m

s  unit cost of sorting out the used products

x₀  unit cost of producing new products

x₁  unit cost of purchasing raw materials from suppliers

x₂  unit cost of purchasing recycled materials from recycling center

x₃  unit cost of disposing the material which cannot be recycled

x₄  unit cost of decomposing the used products in recycling centers

p₁  unit price of new products

p₂  unit cost that collection point pay to customers for the used products

μ_v  the minimal recycling rate of customer region v

φ  the maximal disposal rates

Decision variables

$q_{i j}^{s}$  number of raw materials shipped from supplier i to manufacturer j

$q_{j k}^{m}$  number of products from manufacturer j to retailer k

$q_{v l}^{c r}$  number of used products from customers region v to collection point l

$q_{l m}^{c p}$  number of used products from collection point l to recycling center m

$q_{m j}^{r c}$  number of recycled materials from recycling center m to manufacturer j

$q_{m w}^{r c}$  number of waste materials from recycling center m to waste disposal plant w

$q_{j}^{ {new }}$  number of new produced products in manufacturer j

Objective function

The objective function of the proposed closed-loop supply chain problem is to maximize the total profit which is equal to the total income minus total expenditure as shown in Eq (1).

The total income is the sum of the cost of all new products, which is displayed in Eq (2).

The total expenditure consists of the total transportation cost, the total fixed cost, and total processing cost as represented by Eq (3).

Equation (4) shows the total transportation cost.

Equation (5) shows the total fixed costs of the manufacturers, collection points, and recycling centers.

Maintaining the operation of the closed-loop supply chain also needs some necessary costs. Eq (6) shows the total processing cost which is equal to the sum of seven parts, including the cost of obtaining used products to pay customers in collection points, the cost of sorting out and classifying used products in collection points, the cost of recycling used products in the recycling centers, the cost of dealing with non-recyclable waste, the cost of producing new products, and the cost of purchasing materials in manufacturers.

Subject to

Constraints (7) and (8) make sure the quantity of raw materials between manufacturers and suppliers should not exceed the capacity of each supplier and manufacturer.

Constraint (9) shows the quantity of products supplied by each manufacturer to retailers should not exceed the capacity of the manufacturer. Constraints (10) and (11) restrict that the demand of retailers and customers must be satisfied.

Constraint (12) guarantees the number of used products provided by each customer region must be more than minimum collection rates. Constraint (13) shows the capacity limitation of collection points.

Constraints (14) and (15) formulate the quantity of used products between collection points and recycling centers should not violate the capacity limitation of collection points and recycling centers, respectively.

Constraint (16) shows the capacity limitation between manufacturers and recycling centers. Constraint (17) restricts suppliers and recycling centers providing raw materials for each manufacturer should be equal to the quantity of transporting to retailers.

Constraints (18) and (19) restrict the inflow and outflow quantity of collection points, recycling centers, and manufacturers.

Constraint (20) restricts the total quantity of new products should be equal to the total quantity of products transported from manufacturers to retailers.

Constraint (21) restricts the quantity of recycled materials and the waste materials of each recycling center should be less than the quantity of used products from collection points to the recycling centers. Constraint (22) shows the quantity of waste materials from recycling centers to waste disposal plants should be less than the maximum value preset.

Constraints (23) and (24) show the value ranges of decision variables.

3.   The proposed GA

Compared with the traditional optimization method based on mathematical analysis, heuristic algorithms have the advantages of optimizing black-box problems, have a good global search capability, and are simple to implement and use. Therefore, heuristic algorithms are widely applied for various challenging optimization problems, such as scheduling ^[33,34], vehicle routing ^[35], online learning ^[36], multi-objective optimization ^[37,38], and feature selection ^[39,40]. In this paper, an improved GA was designed to optimize the proposed CLSC problems.

3.1.   Two-step rank-based encoding

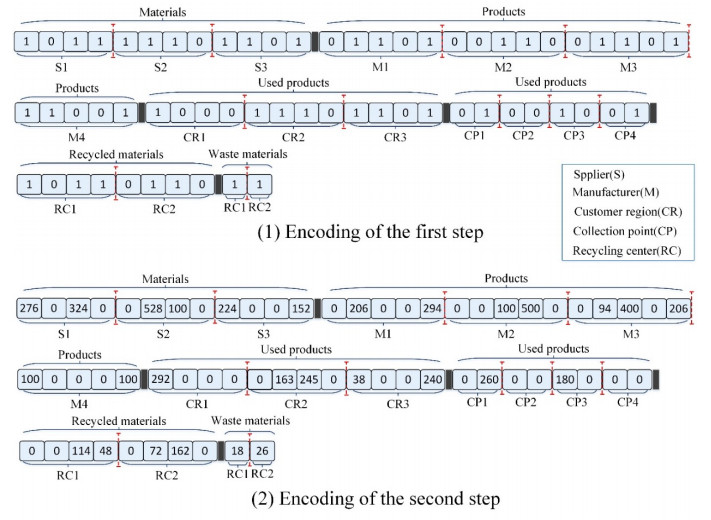
Due to the complexity of the CLSC optimization problem proposed in this paper, it is important to propose a new encoding method in GA. Firstly, according to the definition of the problem model, the chromosome should contain the information of the transportation routes, the quantity of materials or products among the facilities, and the open state of the facilities. Secondly, the encoding should be helpful to generate feasible solutions. Thirdly, the design of chromosomes needs to be convenient for genetic operators. This paper proposes a two-step rank-based encoding method to solve the above problems. Figure 2 shows the chromosome in the encoding of each step with the numerical example of I = 3, J = 4, K = 5, V = 3, L = 4, M = 2, W = 1.

The first step of encoding is only to determine the transportation route. The chromosome can use binary encoding to express the information of the route and each gene is generated randomly. For the binary number, 1 means this route can be used, and 0 means not. As shown in Figure 2(1), the chromosome has six sections corresponding to different stages of CLSC. In the first section, 12 (3 $\times$ 4) genes represent the route information of suppliers supplying raw materials to manufacturers. For example, the first four genes (1, 0, 1, 1) represent that supplier 1 can supply raw materials to manufacturers 1, 3 and 4, but not supply materials to manufacturer 2. In the second section, 20 (4 $\times$ 5) genes represent the route information of the manufacturer supplying new products to the retailers. For example, the first five genes (0, 1, 1, 0, 1) represent that manufacturer 1 can supply products to retailers 2, 3 and 5, but not provide products to retailers 1 and 4 and so on. The length of a chromosome can be calculated as $I \times J+J \times k+V \times L+L \times M+M \times J+M \times W$. It should be noted that the route of retailers to customer regions is not considered as mentioned before in the problem description.

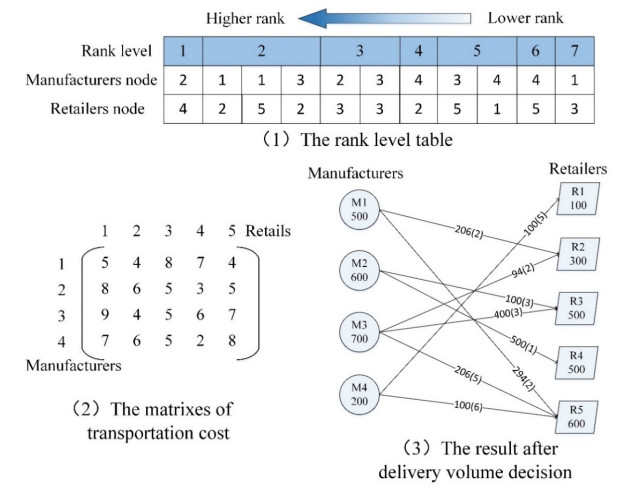
After the first step, a chromosome representing the transportation route has been established. The second step encoding is to decide the quantity of transportation materials or products according to the route, which is called delivery volume decision. As shown in Figure 2(2), the chromosome of the second encoding remains the same structure as the first step encoding, but the content has been changed. For example, the first four genes (276, 0,324, 0) in the first section represent that supplier 1 provides 276 and 324 units of raw materials to manufacturers 1 and 3, respectively but provides nothing to manufacturers 2 and 4. In order to explain the encoding process of the second step clearly, Figure 3 shows the details of delivery volume decision in the stage of manufacturers to retailers, which uses the numerical example of Figure 2. Figure 3(1) shows the rank level table, and the lowest value means the highest rank. The rank level of the routes is built according to the transportation cost, and the lower cost corresponds to the higher rank. The transportation route will be allocated from the higher rank to the lower rank. Figure 3(2) shows the matrixes of transportation cost. Figure 3(3) shows the result after the delivery volume decision, and the numbers in parentheses are the rank level of the route. The numbers in the circles and parallelograms are the capacity of the manufacturer and demand of the retailer, respectively. The detailed methods of second step encoding are as follows:

Step 1: Build a rank table by using the matrixes of transportation costs.

Step 2: Set the routes of the top rank level as the current allocation routes. For example, in Figure 3(3), the route from manufacturer 2 (M2) to retailer 4 (R4) is the first to allocate.

Step 3: Check whether the current allocation routes only have one route. If yes, go to Step 4a. Otherwise, go to Step 4b.

Step 4a: Compare the provider's capacity and receiver's demand of the route, and the delivery volume can be set as the smaller one. Update the capacity and demand value of the corresponding facilities. For example, in Figure 3(3), the capacity of manufacturer 2 (M2) is 600 units and the demand of retailer 4 (R4) is 500 units, and therefore the route's delivery volume will be 500 units. The remaining capacity of manufacturer 2 is updated as 100, and the demand of retailer 4 is updated as 0.

Step 4b: Multiple routes with the same rank level will be classified into three situations.

Situation 1: If the route's provider and receiver facility are all different from other routes in this level, allocate the delivery volume as step 4a until all routes in this situation have been allocated.

Situation 2: If the route's provider facility is the same as other routes in this level, then let N denote the number of these routes. Randomly generate a number $x_{i}(i = 1, 2 \cdots N-1)$ that ranges from 0 to the value of provider's capacity as provider's 'temporary capacity' for the random route and allocate the delivery volume as step 4a. Repeat this step for all the first (N-1) routes, and let $x_{N}$ be the provider's remaining capacity and allocate the delivery volume as Step 4a for the last route.

For example, in rank level 2 in Figure 3(3), the routes manufacturer 1 (M1) to retailers 2 and 5 (R2 and R5) have the same provider facility and rank level, and therefore randomly generate a number 206 as the 'temporary capacity' of the manufacturer 1 and randomly select one route which is the route of M1 to R2. The remaining capacity of M1 is updated as 294 (500–206) units and the remaining demand of R2 as 94 (300–206) units after allocated. Then, M1 allocates 294 units to R5 as the last route in this situation. The remaining capacity of M1 is updated as zero units and the demand of R5 as 306 (600–294) units.

Situation 3: If the route's receiver facility is the same as the other route in this level, the allocation method is the same as situation 2.

Step 5: Update the rank level table, and then repeat Steps 2 to 5 until the encoding of this stage of CLSC ends.

The customer demand must be satisfied in this model. Therefore, the second step encoding starts from manufacturer to retailer and ends from supplier and recycling center to manufacturer, and the detailed encoding sequence is shown in Figure 4. It should be noted that the procedure of the encoding is simultaneously in the section of supplier and recycling center to the manufacturer. Therefore, the routes of suppliers to manufacturers and recycling centers to manufacturers need to be ranked together.

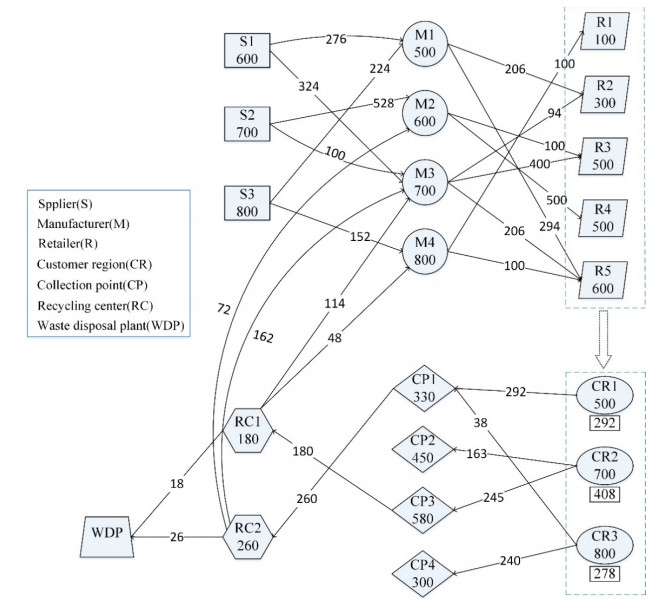
The diagram of the final encodes of the proposed problem model is shown in Figure 5, which corresponds to Figure 2(2). The numbers below the abbreviation of CLSC network members represent the capacity. The numbers in the routes represent the delivery volume. The numbers in the rectangular box under the customer regions represent the final delivery volume to the collection points.

3.2.   Constraint check

There are many constraints in the proposed model, and therefore the constraints checking step is necessary. Constraints check is not only used for the legitimacy examining of newly generated chromosomes, but also for the offspring after the operators of GA such as crossover and mutation. In this paper, constraints check includes the capacity check of routes and delivery volume check.

The purpose of the delivery volume check is to test whether the chromosome satisfies the constraints (7) to (22) after the second step encoding. Capacity check of routes aims to check whether binary chromosome satisfies the capacity constraints after the first step encoding. If the chromosome fails to pass the capacity check, it means that no matter how the delivery volume is allocated, it will violate the constraints finally. Therefore, the route that violates the constraint will be regenerated. The details of the capacity check are shown below.

1) The total capacity of active manufacturers must be able to satisfy the total demand of all retailers.

2) The total capacity of active recycling centers and suppliers must be able to satisfy the total demand of all customers.

3) The quantity of products of each customer to recycling centers cannot be zero simultaneously, which means the customer must return the used products.

4) If the used products are transported to an active recycling center, then the delivery volume of the recycling center to waste disposal plants should not be zero simultaneously.

3.3.   GA operators

3.3.1.   The overall procedure of the proposed GA

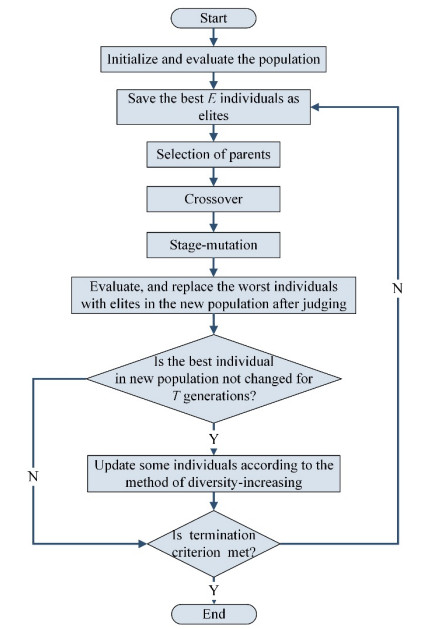
In this paper, for preserving high-quality solutions, an elite strategy is used. The best E individuals of the parent are saved as the elites. If the best E individuals of the next generation are changed, the E elites will replace the worst individuals of the current population to avoid losing high-quality solutions, and E can be set according to the problem scale. The flowchart of the proposed algorithm shows in Figure 6.

3.3.2.   Initialization and selection

An initial population includes a certain number of chromosomes generated based on two-step rank-based encoding and verified by constraint check. In this way, there are all feasible solutions in the initial population, since it is difficult for GA without the initialization based on the two-step rank-based encoding to generated feasible solutions, which is verified in the experiment in Sections 4.2 and 4.4. In the iteration of GA-TRE, the roulette selection is used as the selection operator ^[41].

3.3.3.   Crossover

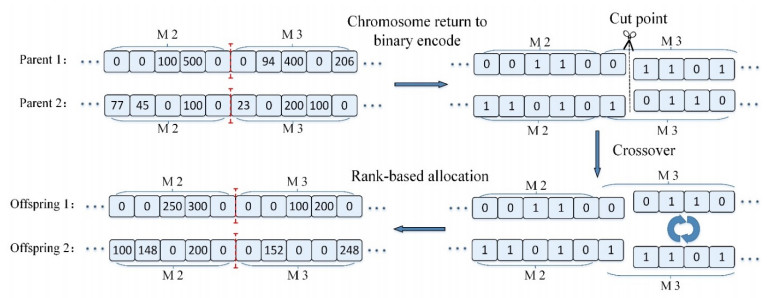
For the proposed encoding method in this paper, the value of genes and their positions in the chromosome represent different information. It is difficult for the new individuals after crossover to satisfy the constraints. Hence, dramatic changes in the parent chromosomes are unfavorable for the preservation of the promising part of solutions. In this paper, the genes in the parent chromosome will degrade to binary encoding, and the single point crossover operation is implemented to minimize the change of the parent chromosomes. The position of the crossover point is random. The rank-based method of the second step encoding is used to reallocate delivery volume for child chromosomes. The offspring needs to be checked for constraints after crossover, and the crossover operator will be executed again if constraints are not met. An example of the crossover process and the pseudo-code of the crossover are shown in Figures 7 and 8, respectively.

3.3.4.   Stage-mutation

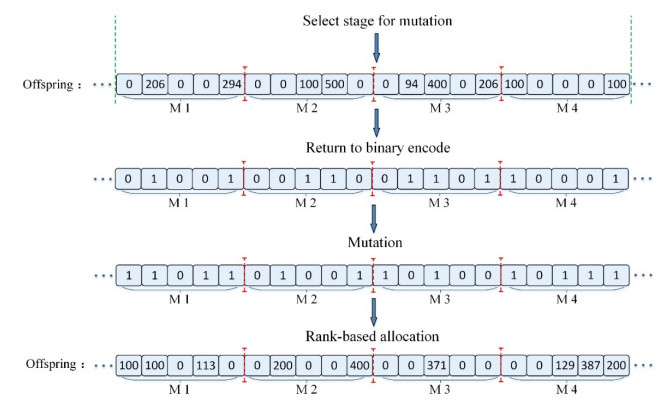
Stage-mutation is designed by combining with the characteristics of the problem in this paper, which aims to reduce the probability of population trapped into the local optimum. In the stage-mutation, the chromosomes degrade to binary and one section of the chromosome is randomly selected which corresponds to a kind of member of the CLSC, such as manufacturers to retailers. The binary encoding of the selected section is randomly generated. If the new chromosome with binary representation passes the capacity check, the rank-based method of the second step encoding is used for reallocation. Moreover, the constraints check is used for the new chromosome. The mutation operator will be executed again if constraints are not met. The pseudo-code of stage-mutation and an example of the process are shown in Figures 9 and 10, respectively.

3.3.5.   The diversity-increasing method

To enhance the diversity of individuals in the population and explore more solution space, if the best X individuals remain unchanged after T iterations, X new solutions will be generated to replace the worst X solutions in the population. T can be set according to the problem scale, and X can be changed adaptively according to different periods of population iteration. In detail, at the initial stage of the iteration, the population aims to explore, and therefore it is better to have a smaller X. In the middle of the iteration, the population will gradually converge. To prevent premature convergence and search for better solutions, X needs to be larger. At the later stage of iteration, the algorithm needs fast convergence. Therefore, X is not suitable for too large. To obtain different values of X in different periods of the iteration, an adaptive method of setting X is designed:

where Jump_rate is the proportion of the population, X is the number of individuals updated in the population, Iter is the current number of iterations, Max_iteration is the maximum number of iterations, α is the minimum value of Jump_rate, and β is the maximum value of Jump_rate, and N_pop is the number of individuals in the population.

4.   Experimental results and analysis

4.1.   Experimental setting

To evaluate the performance of the proposed algorithms for solving the CLSC problem, three different scales are used. Each scale includes three instances. There are 3(scales) $\times$ 3(instances) = 9 instances in total. Moreover, the dimension of the problem-scale Ⅲ is up to 292, and the range of each dimension is zero to hundreds, which is large-scale for an integer programming problem. The instance data are generated randomly according to the reality ^[29]. The details of each problem scale are reported in Tables 1 and 2.

Six algorithms were compared and implemented, including the classical algorithm GA, DE (differential evolution) ^[42], CSO (competitive swarm optimizer, which is designed for the large-scale optimization) ^[43], the current relatively new algorithms MPA (marine predators algorithm) ^[44], RDA (red deer algorithm) and SLPSO (social learning particle swarm optimization) ^[45,46]. For a fair comparison, the solution structure is the same as GA-TRE for the compared algorithms as Figure 2 (2), and the variables are generated randomly from zero to the corresponding boundary value. The penalty function method is used on infeasible solutions in these compared algorithms for meeting the constraints. GA uses single-point crossover and mutation, and DE uses the binomial crossover in Reference ^[42]. The specific parameters of the algorithms are shown in Table 3.

Each instance was tested with 30 replications, and the best, the worst, the average, and the standard deviation (std) values were recorded. All the algorithms were implemented in python 3.8 and run on a PC with the Intel Core i7-11700 and 16.0-GB memory.

4.2.   Experimental comparisons with other algorithms

The experimental results of the algorithms for different scales and instances are shown in Tables 4–6. The results in italic type mean that the global optimal solution is illegal and the results in bold type are the best solutions among all the algorithms.

As it is seen in Table 4, GA-TRE obtains the maximum profit results on all the tested instances, and its mean result is 2000 higher than other algorithms at least. On account of the problem scale being small, most algorithms can obtain feasible solutions. SLPSO and MPA have similar results on instance 1, and SLPSO performs better than other algorithms on the rest of the instances. The results of DE, MPA, CSO, and SLPSO do not have a dramatic gap in general. In addition, RDA and GA cannot obtain feasible solutions on all the instances. In Table 5, the results show that GA-TRE yields the maximum profit results on all the tested instances with an obvious advantage. With the problem-scale increasing, GA, DE, CSO, and RDA cannot obtain feasible solutions in all the tested instances. MPA and SLCSO sometimes can obtain feasible solutions in some instances. From the observation of Table 6, the performance of GA-TRE does not deteriorate in the largest problem-scale, and all results are still the best on all the tested instances. Besides, all the compared algorithms cannot obtain feasible solutions in this problem scale.

From the perspective of solution quality, GA-TRE obtains the best results in different problem scales, and therefore it shows an absolute advantage over the compared algorithms. DE and the three recent popular algorithms—MPA, CSO and SLPSO can also obtain promising results on a small problem scale. However, with the problem scale increasing, these algorithms cannot obtain feasible solutions. It indicates that these algorithms are ineffective to handle multi-constraints when facing large-scale problems. Besides, GA and RDA cannot obtain feasible solutions on all the problem scales. The reason may be that the randomly generated initial population of GA and RDA almost do not have feasible solutions, and it is difficult to improve the feasibility of the infeasible solutions with the classical genetic operators, such as crossover and mating commander.

The standard deviation values were recorded to evaluate the reliability of the algorithms, as shown in Tables 4–6. The results show that GA-TRE achieves the minimal value in different instances with three problem scales, which means it has a better robust ability. SLPSO, MPA and DE have near results in the small problem scale and outperform the rest algorithms. As for the algorithms achieving the unfeasible solutions, the standard deviation value seems to have little effect on the evaluation of the performance.

Furthermore, the relative percentage deviation (RPD) is used to evaluate and compare the performance of the algorithms. For the maximization problem, RPD can be defined as follows:

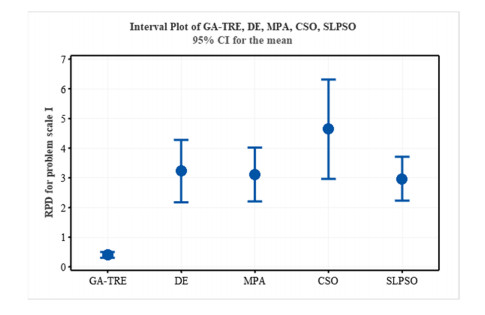
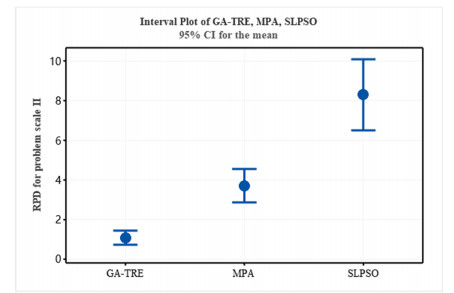
where ${Alg}_{sol}$ is the value of the objective function in individual trials and ${Max}_{sol}$ depicts the best solution among trials. To intuitively observe the difference of algorithms' performance based on the RPD, the interval plots for different problem scales at 95% confidence limit are shown in Figures 11 and 12. It should be noticed that this analysis only includes the algorithms which can achieve feasible solutions, and therefore, GA-TRE, DE, MPA, CSO, and SLPSO for the problem scale Ⅰ are drawn in Figure 11, and GA-TRE, MPA, and SLPSO for the problem scale Ⅱ are drawn in Figure 12. As shown in Figure 11 for the problem scale I, GA-TRE outperforms all other algorithms, and there is a minor difference among DE, MPA, and SLPSO. Figure 12 demonstrates that GA-TRE still maintains the best performance among the algorithms with the problem scale increasing.

Finally, the one-way analysis of variance (ANOVA) is applied to verify the statistical validity of the results (based on standard deviation). The three problem scales have been all included in this analysis. The crucial measure parameter in ANOVA analysis is the p value, if it is lower than 0.05 that means the algorithms exist different. The results were calculated by the Minitab, and the obtained p value is equal to zero. Therefore, it proves that there are obvious differences between the performances of algorithms.

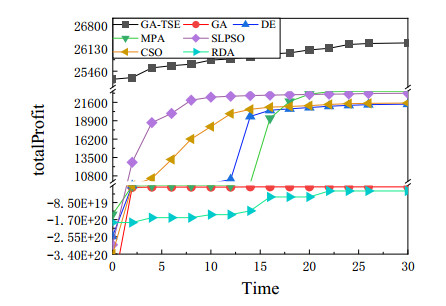
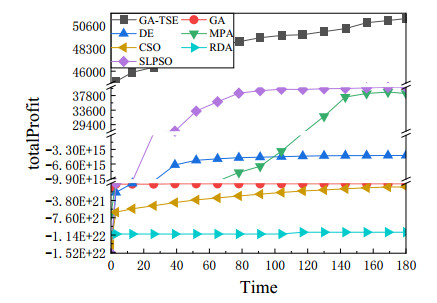
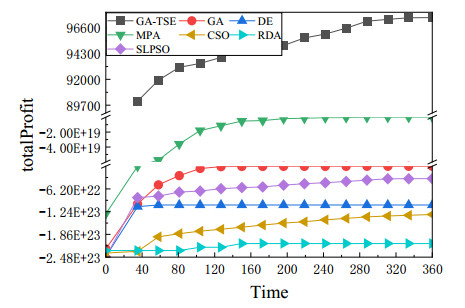
4.3.   Analysis of convergence speed

To analyze the convergence speed of algorithms, the convergence curves are drawn for different scales, as shown in Figures 13–15. From the observation of figures, the convergence curves of GA-TRE are rising gradually under different scales. Other algorithms will stagnate after several generations of iteration. Therefore, GA-TRE can obtain better solutions than other algorithms. The convergence speed of MPA is the slowest on all scales, and GA is the fastest on the contrary. That is because MPA has three different phases for exploration and exploitation, but the first two phases for exploration consume too much time for the complex constraints, and GA can firstly obtain its best solutions. SLPSO, CSO, and DE have similar convergence speed in scales Ⅰ and Ⅲ, and RDA and GA have similar convergence speeds in scales Ⅱ and Ⅲ. In addition, with the problem scale increasing, the first iteration time of the GA-TRE is different from other algorithms as shown in Figure 15. The reason is that the individuals in the initial population are all feasible solutions, but it will take more time to initialize the population.

4.4.   Effectiveness of two-step rank-based encoding

To validate the effectiveness of the two-step rank-based encoding, this encoding method is combined with other algorithms and tested on different problem scales. Since the proposed encoding is designed for the GA, only GA and DE (which has similar evolutionary operators to GA) are combined with the proposed encoding. It should be noticed that GA still uses single-point crossover and mutation. The experimental results are shown in Table 7.

From the comparison of Table 7, it can be seen that GA-e (which is GA with two-step rank-based encoding) can obtain promising feasible solutions on all problem scales, and DE-e (which is DE with two-step rank-based encoding) also can obtain feasible solutions on scales Ⅱ and Ⅲ. The important reason why GA-e and DE-e can obtain feasible solutions at different scales is that the initial population and new individuals of these algorithms are generated based on the two-step rank-based encoding and pass the constraint checking. The advantage of the initialization is that all solutions are legal after the initialization. However, it will consume more time to initialize the population and generate new individuals with the increase of the problem scale. The comparison between GA-e and DE-e in Table 7 shows that GA-e is better than DE-e on different scales and instances. It indicates that the vector difference strategy of DE is not suitable for the proposed encoding method. Moreover, from the comparison between GA-TRE and GA-e in Table 7, it can be seen that GA-TRE obtains better results on different scales and instances. Therefore, it also proves the proposed operators including stage-mutation, elite strategy, and the adaptive population disturbance mechanism in this paper are effective for the proposed CLSC problems.

4.5.   Analysis of Parameters

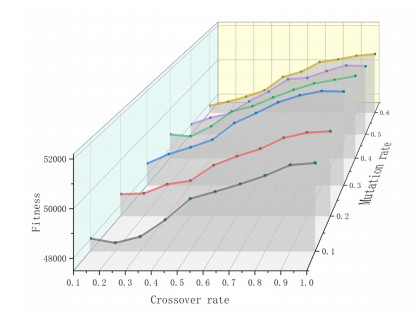
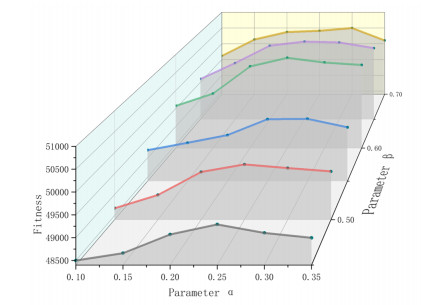
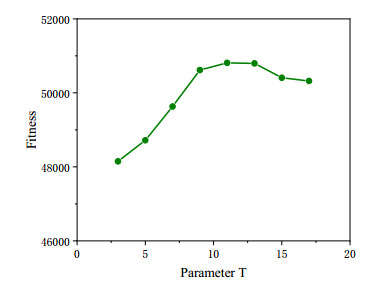
There are five key parameters of the GA-TRE algorithm to be investigated, including the crossover rate, mutation rate, parameter T of the diversity-increasing method and parameters α and β in (25). In this part, these parameters will be taken by a series of different values for observing the impact of the results, which aims to find a better combination of parameters. Specifically, the crossover rate is set by ten values from 0.1 to 1 (interval for 0.1), the mutation rate is set by six values from 0.1 to 0.6 (interval for 0.1), α is set from 0.1 to 0.35 (interval for 0.05), β is set from 0.45 to 0.7 (interval for 0.05), and T is set from 3 to 17 (interval for 2). Also, the instances of problem scale Ⅱ are selected for the test problem, and the results are presented in Figures 16–18.

It can be observed from Figure 16, the results become better with the increase of crossover rate under different mutation rates and get relatively stable when the crossover rate is about 0.9. It indicates that the frequent crossover operations can promote sharing of excellent solutions in the population. The change of mutation rate seems to have a relatively smaller effect on the fitness, and the fitness value shows an upward to downward trend with the increase of mutation rate. Because mutation operation brings better diversity for the population, it also needs to take the algorithm consuming more time. As seen in Figure 17, the increase of parameters α will lead to near parabola shape changes for the fitness curve. The reason may be that if parameter α is too big, it will bring relatively large population changes in the early stage of the algorithm, which affects the exploitation ability. Also, the fitness value shows an increasing trend with the increase of parameter β, but it will get worse results when β is higher than about 0.6, and the reason is similar to the former. Besides, parameter T is not suitable for setting too large from the observation in Figure 18.

From the above comparisons and analysis, the five parameters crossover rate, mutation rate, parameter α, β and T are set as 0.9, 0.2, 0.25, 0.6 and 10 for the GA-TRE algorithm under problem scale Ⅱ, respectively. In addition, the same analysis method is also applied to the other problem scales, the results of parameters combination for scale I and scale III are set as (0.9, 0.1, 0.25, 0.6 and 6) and (0.9, 0.25, 0.3, 0.65 and 10), respectively.

4.6.   Sensitivity analysis

In this section, sensitivity analysis for the key parameters of the proposed CLSC model is conducted. The problem scale II experimental instance 1 was selected as a test problem and GA-TRE was selected as the optimizer. There are three scenarios created for sensitivity analysis to investigate the behavior of the objective function under the change of different CLSC members' capacity/demand, and recycling/disposal rate.

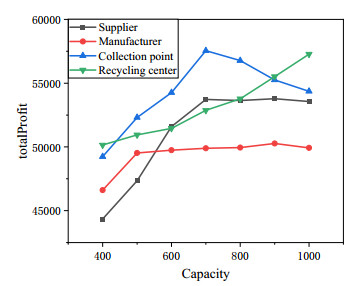
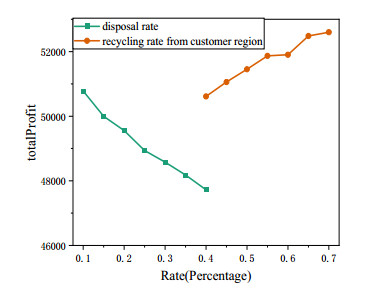
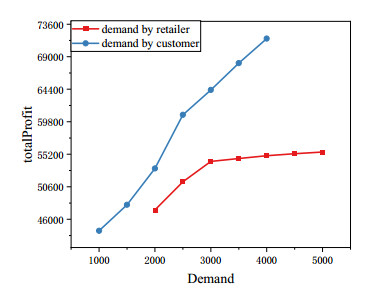
The first scenario discusses the changes in the capacity of supplier (${c}_{i}^{s}$), manufacturer (${c}_{j}^{m}$), collection point (${c}_{l}^{cp}$), and recycling center (${c}_{m}^{rc}$), and each parameter varies between 400 to 1000 units. The second scenario explores the effect of changes in the minimal recycling rate of customer region (${\mu }_{v}$), and the maximal disposal rate (φ). The last scenario investigates the influence of demand of customer (${d}_{v}$) and retailer (${d}_{k}$). Moreover, other parameters remain unchanged when one parameter is tested. The performance of the objective function for the different scenarios is shown in Figures 19–21.

As seen from the results in Figure 19, the capacity of the considered CLSC members is positively associated with an increase in the objective function. But notably, the capacity of the collection center exceeds a certain threshold, it will have a negative impact on the objective function. The reason may be that excessive recycled products lead to an increase in consumer subsidies, but the operation capacity of the recycling center is limited. Therefore, the supply chain decision-makers should consider carefully to avoid decreasing profit in the process of recycling products. According to Figure 20, the value of the objective function decreases with the increase of the disposal rate. It indicates that a bigger disposal rate in the recycling center brings more cost to deal with waste and affects the quantity of product recycling to a certain extent. In contrast, a higher recycling rate will provide cheaper recycled materials for manufacturers to increase the total profit. As shown in Figure 21, with the increase in the demand of retailers and customers, there is a significant increase in the objective function. However, the demand of customers has a greater impact on the supply chain network than the demand of retailers. The above analysis of the important parameters of the model can provide a basic reference for decision-makers who are willing to use the proposed model in this paper.

5.   Managerial insights

In this paper, a CLSC network is designed to maximize the total profits of the supply chain. The goal of the proposed model is to match more application scenarios under considering the development of sustainability. It can significantly help in providing the guidelines on how to take strategic decisions for the industries which have products with recyclable value, such as electronics and plastic.

The important managerial insights are generated by the sensitivity analyses of the model as given in Figures 19–21. The decision-makers should carefully plan the capacity of recycling centers, and each supplier and manufacturer can also avoid waste of production capacity (shown in Figure 19). In the reverse supply chain, it is crucial to balance the recycling rate from customers and disposal rate in the recycling center by under considering both increasing profits and environmental protection (shown in Figure 20). According to Figure 21, the demand of retailers and customers are positively associated with profits. In addition, the customer does not refer to a single buyer but represent a not fixed customer region for more closing the reality. The relationship between the demand of customer regions and retailers needs more detailed investigation for decision-makers.

As validated in the experiment, the proposed CLSC problem can be well solved by the GA-TRE algorithm, and the validation is presented in section 4. It can provide decision-makers to solve their similar or specific network design problems. Moreover, the key parameters tuning of GA-TRE refers to Figures 16–18.

6.   Conclusions

Increasing environmental, legislative, and social concerns are forcing companies to take attention to green development, and therefore the CLSC model has become more and more popular. This paper solves an important practical issue considering the design and optimization of a general CLSC model. Due to the complexity of the problem, a novel genetic algorithm named GA-TRE is proposed. For handling the complex constraints and facilitating genetic operators, two-step rank-based encoding is proposed. Besides, for increasing the diversity, a new mutation operator and an adaptive population disturbance mechanism are designed. To validate the proposed algorithm, nine test problems are produced in three scales, and the performance and reliability of the proposed algorithm are evaluated in comparison with other heuristic algorithms. The experimental results demonstrate that GA-TRE outperforms all the compared algorithms on all the instances for the proposed CLSC problem.

For future studies, the CLSC model can extend as the multi-objective by considering sustainability and service quality to improve the versatility ^[3], and the proposed algorithms can be improved further to solve multi-objective problems. Moreover, the model with uncertain factors could be designed ^{[10,11,12,13,22]}. Finally, the evolutionary multitasking algorithm as a new search paradigm can also be used to solve supply chain problems as a promising direction for future research ^[47,48].

Acknowledgments

The work described in this paper was substantially supported in part by the National Natural Science Foundation of China under Grant No. 62106088, in part by the High-level personnel project of Jiangsu Province (JSSCBS20210852), and in part by the Fundamental Research Funds for the Central Universities, Jiangnan University (JUSRP121070), and Jilin University (93K172021K15).

Conflict of interest

The authors declare there are no conflicts of interest.