Mediterranean diet and health in the elderly

1.   Introduction

The biomechanical characterization of biological soft tissues was initially developed by Y.C. Fung on his classical biomechanical treatments ^[1,2]. He was one of the firsts, together with Fronek, to used a ``new kind'' of elasticity to describe the mechanical behavior of the soft tissues ^[3], they called this new behavior as pseudo-elasticity. A few years later a new generation of researchers continued on this sense, one of the most know is Holzapfel that together with Gasser and Ogden proposed a new constitutive framework for arterial wall mechanics behavior ^[4], basically based in a non linear elastic theory introduced by Ogden ^[5]. In 2004 this group of research realized a comparison of a multi-layer structural model for arterial walls applying a Fung type model, i.e. viscoelasticity. They explored the problematic that emerge on the material stability, in the convergence sense and others problems relatives to the viscoelastic formulation, then in 2010 Holzapfel and Ogden proposed a constitutive modeling of arteries ^[6] that originated a whole new constitutive frame, named hyperelasticity. Based on strain-energy functions and that represents a huge step on the task of arteries biomechanical characterization, and a great variety of progress was developed and published, like the modeling of biomechanical effects originated by an aneurysm ^[7,8], the 3D modelling of the human aorta ^[9,10] or the visco/hyperelastic model that simulate the nonlinear dynamics of atherosclerotic coronary arteries used to predict the initiation of heart attack ^[11,12].

No often it is not the original Fung's propose for modeling arteries biomechanical behavior, he originally describe the mechanical behavior of the artery as a viscoelastic material. In general, this behavior may be imagined as a spectrum with elastic deformation in one limit case and viscous flow in the other, with varying combinations of the two spread over the range between. Thus, valid constitutive equations for viscoelastic behavior embody elastic deformation and viscous flow as special cases and at the same time provide for response patterns that characterize behavior blends of the two. Intrinsically, such equations will involve not only stress and strain, but time-rates of both stress and strain as well ^[13]. As mentioned before this kind of materials models, has a great inconvenient related with the convergence on the finite element method software, frequently used to solve this mathematical models ^[8,6,14,15]. To avoid this situation we can use a prony series and the relaxation function, but again to obtain an accurate solution we need to use a large number of prony series that elevates the computer time on the task of solution finding.

At recent times the fractional calculus theory has been used to modeling viscoelastic materials ^[16,17,18], consequently some researchers used to model biological soft tissues ^[19,20], like the use of Kelvin-Voigt fractional viscoelastic model employed to determinate the biomechanical properties of the human liver tissue or the pancreas by Wex ^[21,22], using stress relaxation test to articular cartilage ^[23], and even the human calcaneal fat pad ^[24] using fractional derivatives kernels. Recently this material models are used to estimate the biological changes of the mechanical behavior due to the presence of tumors ^[25]. Craiem et al ^[26,27,28] use a fractional viscoelastic constitutive model to describe the arterial biomechanics response, using uniaxial relaxation test.

One of the greatest advantages consist on that many of the basic viscoelastic ideas can be introduce within the context of a one-dimensional state of stress. Once the relaxation modulus, the creep compliance and the complex modulus are obtained, its functions can be included by a subroutine on a FEM software, with the necessary geometry restrictions ^[29] and the viscoelastic relaxation modifications, or by an finite element model specially develop for fractional differential and integral operators ^[30].

Viscoelastic fractional models have taken a recent boom in the task of modeling the mechanical behaviour of polymers and soft tissues. Due to the fact that the definition of the fractional derivative provide a new formulation to describe the mechanical behaviour of a material that exhibits a behavior that oscillates between the hooke solids model and the Newtonian fluids ^[31]. That is one of the principal characteristics of the soft tissues.

2.   Materials and method

2.1.   The circulatory system

The circulatory system is basically composed of the heart and blood vessel system. At the time, the blood vessel system are composing of arteries, arterioles and veins. Arteries are basically conform of three internal layers, known as Tunica Intima, Tunica Media and Tunica Externa or Adventicia, with a semi-cylindrical form and mainly compose of collagen, elastin and muscular fibers ^[32]. In young humans, the intima is an extremely thin layer (80nm) like a membrane separate to the media for a lay of elastin, the media are form of soft muscular cells merge on a collagen and elastin cellular matrix, finally the externa is the thick layer compose of collagen and fibroblasts ^[33].

This particular conformation brings the artery a mixed mechanical material behavior know as viscoelasticity ^[1]. In general, viscoelastic behavior may be imagined as a spectrum with elastic deformation as one limiting case and viscous flow the other extreme case, with varying combinations of the two spread over the range between. Thus, valid constitutive equations for viscoelastic behavior embody elastic deformation and viscous flow as special cases and at the same time provide for response patterns that characterize behavior blends of the two.

Intrinsically, such equations will involve not only stress and strain, but time-rates of both stress and strain as well ^[13].

2.2.   Mechanical background

We first develop the mathematical and mechanical background that support the present research, with the finality that those readers interested on the topics be familiarized with the basic concepts.

2.2.1.   Linear viscoelasticity

Linear viscoelasticity is a common theory to approximate the time-dependent behaviour of polymers, and materials that exhibit similar characteristics at relatively low temperatures and stress.

The development of the mathematical theory of linear viscoelasticity is based on the principle that the mechanical stress on a certain period of time is directly proportional to the strain rate. In that way, if we have that stress and stress rate are infinitesimal and the stress-strain relation depend on time, that relationship can be expressed by a differential equation with constant coefficients.

The stress-strain relationship can be described, assuming that the Maxwell-Boltzmann principle are satisfied, by the constitutive equation:

or

were $G(t)$ and $J(t)$ are the stress relaxation modulus and the creep compliance respectively. These important functions are commonly employing on material characterization, and are describing above.

2.2.2.   Creep compliance and stress relaxation tests

The creep test consists of instantaneously subjecting the material to a simple shear stress of magnitude $\mathsf{σ}_0$ and maintaining that stress constant thereafter while measuring the shear strain as a function of time. The resulting strain is called the creep. In the stress relaxation test, and instantaneous shear strain of magnitude $\mathsf{ε}_0$ is imposed on the material sample and maintained at the value while the resulting stress, is recorded as a function of time. The decrease in the stress values over the duration of the test is referred to as the stress relaxation.

2.2.3.   Oscillatory experiments

The behavior of viscoelastic materials when are subject to harmonic stress or strain is an important part of the theory of viscoelasticity and sustains a fundamental part of the research. Cyclic experiments are used to identify the mechanical behavior of the material and to determine the values of the elastic and viscous plots of this, maintaining a balance between complexity and simulation capacity of the phenomena. Data processing could be carried out in the same way for a non-cyclic signal, but it would have to be extensive in time to have enough information to fit the model and its processing would be complex.

Consider the response of the material, when is applying a harmonic shear strain of frequency $\omega$ as:

At the same time the strain rate changes with the same frequency $\omega$ with a translation $\phi$ with respect to the stress,

replacing equation 2.4 on equation 2.1, will be able to obtain the constitutive equation:

with

and

where $G^{\prime}(\omega)$, $G^{\prime\prime}(\omega)$ are known as the storage and loss modulus respectively. Expressing the harmonic functions on the complex plane we have

where $G^{\ast}$ are define as the complex modulus, and is simply the norm of the loss and storage modulus contributions.

2.3.   Fractional viscoelastic model

At recent times the fractional calculus theory, has used to formulate a wide range of new models on the biomechanics and mechanobiology field ^[20], the fractional differential and integral equations have a great development specially in the task of characterize the mechanical behavior of soft tissues ^[19] like the brain ^[25], liver ^[21], arteries ^[27,28,34] and even the human calcaneal fat pad ^[24].

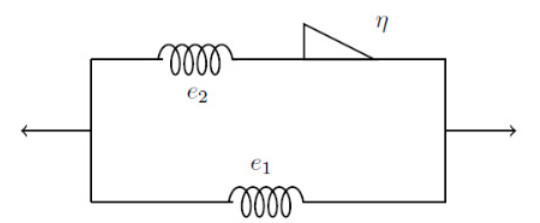
We now consider the fractional generalization of the Standard Linear Solid (FSLS), show on Figure 1. For this purpose, is sufficient to replace the first order derivative with the fractional Caputo ^[35] derivative of order $\nu\in (0, 1)$ in their constitutive equations. We obtain the following stress-strain relationship and the corresponding material functions are described latter.

The equation 2.9 is basically the same that in integer order, but here we replace the first derivative with the Caputo fractional differential operator

applying the Laplace transform to both sides of the equation 2.9 we obtain,

solving for $\bar{\mathsf{ε}}(s)$

where $\alpha = \frac{e_2}{\eta}$ and $\beta = \frac{e_1e_2}{\eta}$, applying the Laplace inverse transform and the convolution law, we have the analytical solution for FSLS model,

where $\delta(t)$ is the traditional Dirac's delta, $*$ is a convolution and $\zeta = \dfrac{\beta}{e_1}$.

3.   Results

Now we proceed to the implementation of the FSLS to the artery modeling process, first we describe the relaxation modulus, the creep compliance and the complex modulus, all necessary for the mechanical one dimensional characterization on the material ^[36]. Next we briefly shown the process to the creation of the vectorized image and the exportation to CAD software that aloud to be treating like a solid with the mechanical properties and restrictions.

3.1.   Artery characterization

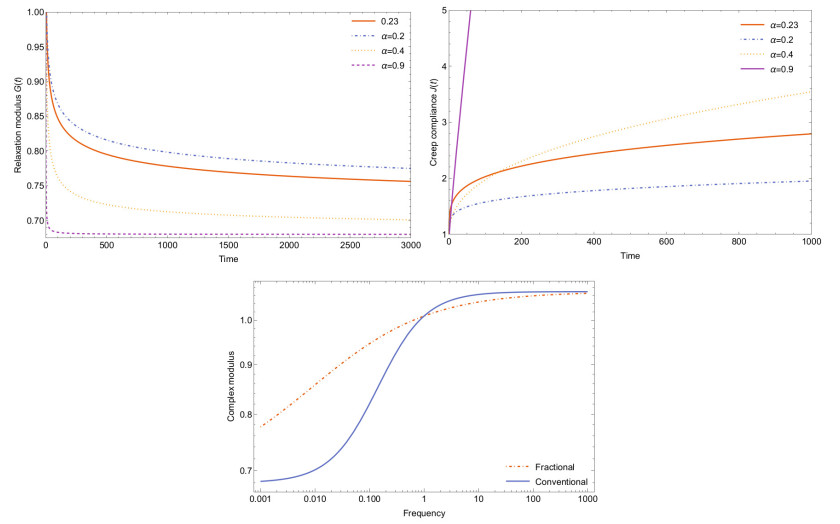
The values of the constants used on the research are taking for experimental creep relaxation test realized on ^[27] and are $e_1 = 0.68$, $e_2 = 0.39$, $\eta = 2.14$ and $\nu = 0.23$. Now we describe the material model functions like the relaxation modulus, creep compliance and complex modulus. The relaxation modulus for the FSLS has the form,

where

is the Mittag-Lleffler function ^[20] with $\nu, \varphi\in\mathbb{R}^{+}$ and $\dfrac{e_1}{\eta} \in\mathbb{R}$. On Figure 2 are plot the relaxation modulus function for four fractional order values, and the constants value mentioned before.

In the same way, we obtain and plot the creep compliance function, for different fractional values $\nu$, the creep compliance function $J(t)$ have the form:

where $\mu = \dfrac{1}{e_1+e_2}$.

The complex modulus, present on Figure 2, complete the set of basic functions required for the mechanical characterization.

3.2.   Three-dimensional construction

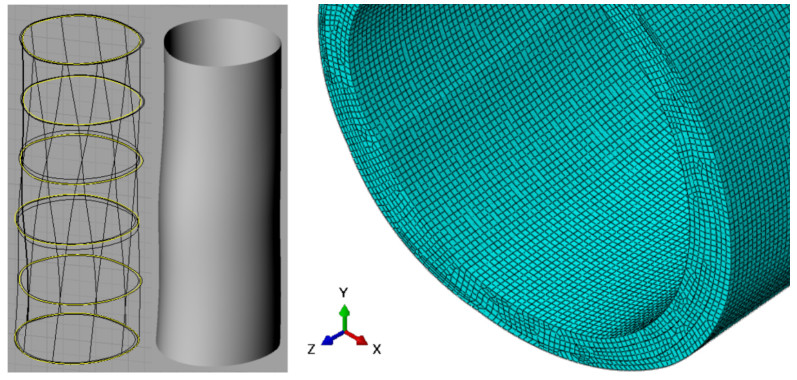
The axial dicom images are used to obtain a 2D geometry for every one of the slices, taking care on identify properly witch points generate each one of the segments, to do that its necessary to establish a consistent metric respect the patient's measure and an appropriate Hounsfield scale. The coordinates are localized and saved on a csv file. Now a spline curve can be generated through the geometric pattern, this way the cloud of points on each slice are limit by a close contour. This processes are repeat for the creation of each one of the slices and each one of the respective segments of the artery, the intima, the media and the adventicia. This procedure is illustrated in the left side of Figure 3.

Once the geometric patterns are due in all the set of axial images. Again a spline is applied to the set of slices, now to generate the 3D artery segment representation. Therefore this geometry is save on.iges format and export to CAD software, for the three layer solid representation. Now this is able to function properly in finite element method analysis software as see on the right side of Figure 3.

Like in all the others numerical methods, the precision of the method consist basically on the size of the step. If the element is the sufficient small the method converge to the require solution with minimal error. For that reason we need to do the finest mesh that can be possible in function that the processor is able to work.

The artery have a total volume of 0.2865 cm$^3$ and are meshed with 654,977 eight node brick elements, i.e. the mesh consist on 2,000,000 element for cubic centimeter. This size of the mesh it's necessary to are secure that the finite element method converge to the require solution, because in other way the software can enter on a infinity loop or brings an non sense solution, from this number of elements the convergence is the same. The mechanical properties of the three segments are shown in table 1.

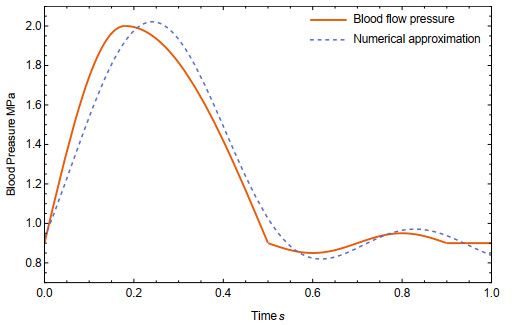
The finite element method software are configured to realize the viscoelastic material routine by the property implementation of the frequency data test. Once the data are introduced on the software, we need to apply a load on the internal intima surface, simulating the pressure caused by a blood flow rate of 120/80 mmHg as shown on Figure 4 ^[37], and a constant load pressure on the exterior externa surface due to muscular compression originated by the muscles that round the artery, the temperature of the body will be consider constant, the extremes of the aorta are fixed by a constraint option and for last the interaction between the layers is set as a tie restriction.

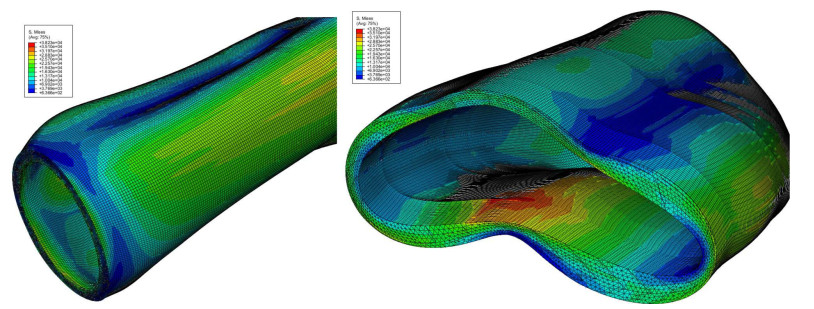
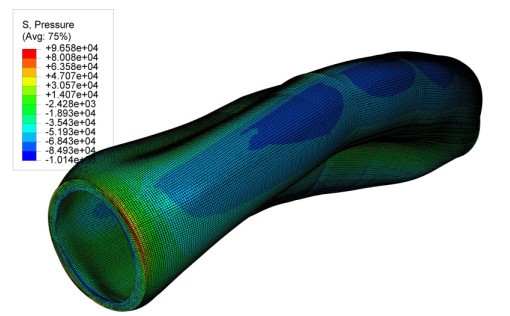
The result of the solid's deformation is shown on top of Figure 5, where the simulation exhibit a tendency or pattern of the deformation route and not necessarily the real deformation, the behavior showed by the artery concord with those founded and predicted previously by ^[24,19].

In Figure 5 the efforts of von Mises also known as equivalent efforts are show since these are obtained from a relationship that combines the main efforts in an equivalent effort that can be used to compare with the effort of transfer of the analyzed material. The values of the von Mises stress obtained in this research are consistent with previously developed investigations in the experimental field where values of 0.213 MPa for blood pressure of 120mmHg are reported, which coincides with the results obtained by simulation using the viscoelastic fractional method.

In previous research it is founded that the area where the maximum stress values are presented, is distributed in the intimate layer of the artery and is located in the place where it changes its geometry, that is, where there is a change in artery curvature ^[40].

Finally, Figure 6 shows the distribution of internal pressure caused by blood flow where 0.03MPa pressure zones are identified in general and some 0.098MP maximum pressure zones, which is consistent with the results previously published by Holzapfel ^[41]

The results obtained were compared with experiments carried out in 2014, where fractional models have been used to characterize various soft tissues, showing that the parameters determined in the research are within the range of those previously found ^[24,25,19].

The stress distribution and the maximum values funded in the research concords with those previously reported by Holzapfel ^[40,41], using an hyperelastic model with prony series.

4.   Conclusion

First we obtained the reconstruction of a segment of the aortic artery based on medical images obtained from a computerized axial tomography scanner, using the Hounsfield scale we could identify each of its three constituent layers (intima, media and adventitia). In addition, the process of exporting the medical image in a vectorized geometry was carried out with which it was possible to export to a solid form, that could be manipulated in a finite element software.

Compared with previous works where simulations of the biomechanical effects of the artery were performed using geometric idealizations, considering the layers of the artery as perfect cylinders, it was observed that when doing this what is had for the state of stress consists of a distribution perfectly symmetrical of the stresses, and in the case of the state of deformations in the same way there is a constant deformation in all directions of the solid. However, the geometry of the artery does not consist of a series of cylinders, so it was found in the development of the investigation that the distribution of stress has its local maximum, speaking of von Mises stress, at the point where the artery presents a change in curvature that generates a great deformation at that point, unlike to a uniform deformation, will end up affecting more to one end of the artery.

In this paper we shown that viscoelastic fractional models represents properly the mechanical behavior of the aortic artery, based on a uniaxial simple model.

In addition, it has been proven that with the viscoelastic fractional model, values similar to those previously provided in the literature are obtained without the use of prony series, which considerably reduces the computation time required.

Acknowledgments

We want to thankful the institutions that supported the present research project, Tecnológico Nacional de México / Instituto Tecnológico Superior de Cajeme, the Biomechanics Investigation Group from Universidad Tecnológica de la Habana, La Habana, Cuba and the Pontificia Universidad Católica de Valparaíso, Chile.

Conflict of interest

All authors declare no conflicts of interest in this paper.