Support vector machine optimization via an improved elephant herding algorithm for motor energy efficiency rating

1.   Introduction

Statistics from the World Energy Agency show that the energy consumption of the industrial sector accounts for nearly 1/3 rd of the global primary energy supply and produces approximately 36% of energy-related CO$_{2}$, and that the electricity consumption of the motor system accounts for more than 50% of the total electricity consumption. Therefore, improving the energy efficiency of the motor system is of great significance for reducing energy consumption, improving cost efficiency, reducing pollution emission and responding to demands for national energy conservation and emission reduction. Cui et al. proposed that a correct rating of the motor energy efficiency is the best way to improve the energy efficiency of motor systems ^[1].

In recent years, there have been many advances in artificial intelligence technology in various fields ^[2,3,4,5,6], whereas there are few types of research on the energy efficiency classification of electric motors. In 2012, guo biao (GB) specifies the minimum energy efficiency values for small and medium-sized motors at rated efficiency and provides initial motor energy efficiency standards ^[7]. However, in the actual production process, the motor is always operating under variable working conditions due to the power quality, load characteristics, and other influential factors. So the motor energy efficiency standard reported in ^[8] cannot be effectively applied to an actual situation. Luo et al. conducted a comprehensive analysis of the factors affecting the motor energy efficiency and developed a motor energy efficiency evaluation index system ^[8]. Li has performed an in-depth study of the main factors affecting motor efficiency and used analytic hierarchy process (AHP) to obtain the weight of each index ^[9]. These studies provide ideas for research on motor energy efficiency rating.

In this paper, the three aspects of power quality, load characteristics and the characteristics of the motor itself are used as the first-level evaluation indicators, also, there are seven second-level indicators that have a greater impact on the energy efficiency of the motor that have been selected and divided into 10-grade intervals. For electrical energy efficiency classes, Ma and Lv used a support vector machine model for classification and achieved an accuracy of 94% with a small number of test samples ^[10]. The accuracy rate decreased with increasing sample data.

Currently, SVM theory has unique advantages in terms of solving classification and target recognition problems ^[11], but the key parameters in SVM i.e., the penalty factor $c$ and kernel parameter $\sigma$, are determined by empirical assignment or cross-validation, which are not only inefficient but they are also susceptible to the local optima problem. Metaheuristic algorithm are widely used for the optimization of various complex problems due to their non-derivative mechanism, flexibility, simplicity and ease of implementation. Classical examples of metaheuristics include particle swarm optimization, ant colony optimization, evolutionary algorithms, and simulated annealing. Inspired by more natural biological behavior, the development of this field has recently experienced something similar to a gold rush in terms of a proliferation of similar new or improved algorithms of all kinds. The more recent metaheuristic algorithms are monarch butterfly optimization ^[12], the whale optimization ^[13], satin bowerbird optimization ^[14] the moth search algorithm ^[15], hunger games search ^[16], harris hawks optimization ^[17], the slime mould algorithm ^[18], runge kutta method ^[19], the colony predation algorithm ^[20] the weighted mean of vectors algorithm ^[21].

The optimization search process for these algorithms has a common feature of using both exploration and development. The exploration phase should utilize and enhance the stochastic operator capability as much as possible to diversify the search in the feature space; the development phase usually follows the exploration phase and should enhance the local search in the vicinity of the more optimal solution. A good optimization algorithm should be able to make a reasonable and fine balance between exploration and exploitation. Otherwise, it is prone to falling into local optimality and premature maturity. Most metaheuristic algorithms have the disadvantage of being insensitive to the tuning of user-defined parameters and not always converging to the global optimum.

In 2015, wang et al. proposed elephant herd optimization (EHO) inspired by the nomadic behavior of elephant herds ^[22]. Elephant herds have two special behaviors: 1) the herd is composed of multiple clans and led by the female, and 2) adult males will leave the herd to live alone. Therefore two mechanisms have been developed to mimic the nomadic behavior of elephant herds their, clan renewal mechanism and their separation mechanism. EHO has been shown to be effective at finding optimal solutions ^[23]. EHO differs from other metaheuristic algorithms in that EHO can generate multiple clans, each of which is a group, and it is a multiple group collaboration mechanism. However, the original EHO only addresses the position update of one clan and does not consider the collaboration of the whole elephant group. The performance of EHO may be significantly improved if the multiple group collaboration approach can be fully utilized and applied.

The accurate evaluation of motor energy efficiency under off-condition operation can provide an important basis for the energy-saving upgrade of the motor and the elimination of backward motors. In the past, research on motor energy efficiency mainly focused on the rated operating condition, and there were few studies on motor energy efficiency under off-conditions.

1) In this article, we present seven evaluation indexes that have a great influence on motor energy efficiency from the three aspects of power quality, load characteristics, as well as motor characteristics, and establish a quantitative classification standard to achieve an accurate grade of the motor energy efficiency.

2) Moreover, we developed an improved EHO (IEHO) algorithm to optimize the motor energy efficiency rating model of SVMs.

3) In order to improve the superior seeking ability of the EHO algorithms, we propose five improvements and compare them with other algorithms.

The organization of this paper is as follows: Section 2 introduces the principle and the optimization search of the standard EHO, and Section 3 introduces the improved EHO, which first analyzes the shortcomings of the standard EHO; we then propose five improvement strategies. Section 4 presents a comparison of the IEHO with other optimization algorithms which was achieved via testing and experimental analysis. Section 5 introduces the model of the energy efficiency evaluation system of electric machines based on the IEHO combined with SVM (IEHO-SVM) algorithm, and experiments and analyses are discussed. The conclusion and future works are discussed in Section 6.

2.   Elephant herding optimization

The EHO algorithm was inspired by the nomadic behavior of the elephant herd ^[22]. Elephants live in groups and consist of multiple clans under the leadership of one of the best female elephant ministers. Each clan will select an excellent female elephant to serve as the matriarch, and the matriarch will lead the female elephants or baby elephants who have a direct or indirect blood relationship with her. Male elephants will leave the group to live alone once they become adults. Although male elephants are far away from their family, they can keep in touch with the elephants in the family through low-frequency vibrations.

To make the elephant herding behavior solve global optimization problems, we have established the following idealized rules: 1) An elephant tribe consists of multiple clans and an optimal female elephant female minister, and each clan has a fixed number of elephants. 2) Each clan in each generation elects a superior matriarch, and then a fixed number of male elephants leave, followed by an equal number of new ones.

2.1.   Clan updating operator

The position of each elephant in the clan is affected by the matriarch. For the elephant $j$ in the clan $ci$, the position is updated as follows:

where $a\in[0, 1]$ represents the scaling factor, $x^{new}_{ci, j}$ represents the new position of Elephant $j$ in the clan $ci$, $x_{ci, j}$ represents the old position of Elephant $j$ in the clan $ci$, $x_{best, ci}$ represents the matriarch in the clan $ci$ and $r\in[0, 1]$ is a random number.

The position of the matriarch has a specific update formula, and the updated position is as follows:

where $\beta\in[0, 1]$ represents a control parameter that determines the factor of $x_{center, ci}$ influence on $x_{best, ci}$. $x_{center, ci}$ represents the center position of the clan $ci$. It can be determined by the following equation.

where $d\in[1, D]$ represents the $d$ th dimension, $D$ is the total number of dimensions and $n_{ci}$ represents the number of elephants of Clan $ci$.

2.2.   Separating operator

In the elephant group, the male elephant in adulthood prefers to leave the group to live alone. To simulate this process, the adult elephant is regarded as the least adaptive elephant in the algorithm. At the same time, to make the algorithm have greater searchability, it is assumed that the elephant with the worst fitness work the separation operator shown in Eq 2.4 in each generation:

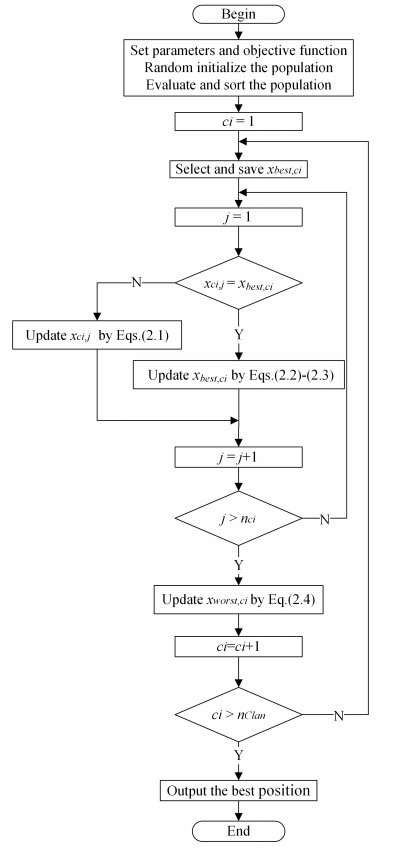
where $x_{max}$ and $x_{min}$ respectively represent the maximum and minimum values of the search space, $x_{worst, ci}$ represents the position of the worst elephant in the clan $ci$. The EHO algorithm flowchart is shown in Figure 1.

3.   Improved Elephant herding optimization algorithm

The standard EHO algorithm updates the position of each elephant by using clan update and separation operations. Its position update method is singular and has the following disadvantages:

1) The initial position of the elephant is randomly generated, which affects the efficiency of elephant swarm optimization.

2) It only utilizes the position variable and ignores the fact that the moving speed will affect the convergence speed of the elephant group.

3) In the clan update process, the position update of the best female elephant in the entire elephant group is not considered. For ordinary elephants, the position is updated according to the position of themselves and that of the matriarch. The matriarch position is updated by the middle position of the clan, makeing it easy to form the local optimal position.

4) In the iteration process, the optimal solution of the clan is updated and not retained. Equation 2.4 was used in the separation process to replace the worst elephant in each generation of the clan, simulating the adult male elephant leaving and producing a new baby elephant. Although the ethnic diversity was preserved, as a newborn baby elephant, it would be protected by other elephants and should have a good position.

Based on these shortcomings, we propose the following improvement strategies.

3.1.   Strategy 1: Chaotic mapping and opposition-based learning population initialization

The distribution and initial value of the initial position of the population affect the optimization efficiency of the population. It is evenly distributed in the solution space, which is beneficial to improve the population diversity and global searching ability.

This paper introduces a population initialization strategy based on chaotic mapping ^[24] and opposition-based learning ^[25]. The strategy initializes the population by using better randomness, spatial ergodicity and non-repetition of chaotic mapping; it also uses the opposition-based learning method to generate its corresponding opposite individuals. Then, it compares and selects individuals with good fitness values as the initial individuals to improve the overall performance of the algorithm optimization efficiency.

Chaotic mapping is used to generate chaotic sequences and random sequences are generated by simple deterministic systems. Table 1 shows several chaotic mapping functions in common use.

According to the analysis of the study presented in ^[26], when $\lambda = 4$, the distribution of a logistic mapping chaotic sequence is unevenly distributed, and the optimization speed and efficiency are slow. When the initial value is 0 or is fixed, the ICMIC mapping function cannot continue to iterate. Chebyshev mapping has higher requirements for functions. The chaotic sequence of tent mapping is evenly distributed, the optimization is faster and the search efficiency is higher. Tent mapping has been applied in this study to generate the initial population of a chaotic sequence.

The initialization steps are as follows:

Step 1: Generate random numbers:

where $d$ represents the dimension $d = 1, 2, …, D$; $K$ represents the number of current iterations.

Step 2: Calculate the tent function chaotic map:

Step 3: Generate $N$ positions, which gives the original population $X = (x_{ci, j, 1}, x_{ci, j, 2}, …, x_{ci, j, D})$ and $N$ = $ci \times j$:

where $x_{max, d}$ and $x_{min, d}$ represent the upper and lower limits of elephants in the $D$ dimension.

Step 4: Perform opposition-based population initialization $OX = (ox_{ci, j, 1}, ox_{ci, j, 2}, …, ox_{ci, j, D})$ based on opposition-based learning:

where $ox_{ci, j, d}$ represents the individual opposing $x_{ci, j, 1}$ and $X$ and $OX$ are opposing populations.

Step 5: Merge the original population and the opposing population, calculate the individual fitness, and take the first $N$ positions with high fitness as the initial population.

3.2.   Strategy 2: Speed

Inspired by the PSO algorithm ^[27], the individual elephants were given a speed to simulate elephant motion; additionally a global speed strategy is proposed, which can accelerate the convergence speed of the elephant herd and balance the convergence speed by introducing inertia weights to avoid premature population maturity.

Speed is also initialized by chaotic mapping and opposition-based learning, taken as $v_{max, d} = 0.2(x_{max, d} - x_{min, d})$ and $v_{max, d} = -v_{min, d}$. The elephant's position is updated as follows:

where $x^{new}_{ci, j}$ and $v^{new}_{ci, j}$ represent the updating position and speed of Elephant $j$ in Clan $ci$ respectively, and $\omega^{k}$ represents the linearly decreasing inertia weight in the iterative process.

where $\omega^{begin}$ and $\omega^{end}$represent the weight at the beginning and end of the iteration respectively, taken as $\omega^{begin} = 0.9$ and $\omega^{end} = 0.4$; $K_{max}$ represents the maximum number of iterations.

3.3.   Strategy3: Adaptive learning step size

In the above equation, $a$ represents the step size from the current position of the elephant to the optimal position. When the value of $a$ is large, the global optimization ability is strong, while the local optimization ability is poor; when the value of $a$ is small, the global optimization ability is poor, while the local optimization ability is strong. In the standard EHO algorithm, the value of $a$ is fixed and the superior and inferior individuals in the clan have the same search range, which does not match the actual situation. The actual situation is that the better individual is close to the optimal solution, so a smaller learning step size should be used to enhance the local optimization ability; altternatively, the less fit individual is far away from the optimal solution, so a larger learning step size should be used to enhance the global optimization ability. Therefore, an adaptive learning step size strategy is proposed.

1). The optimal solution $x_{mbest}$ of the clan requires less learning, learning step take $a$ fixed value and taken as $a_{1} = 0.2$.

2). The optimal solution $x_{cbest, ci}$ of the clan is learned from the optimal solution $x_{mbest}$ of the clan.

Learning step $a_{cbest, ci}$ is expressed as follows:

where $f(x_{cbest, ci})$ and $f(x_{mbest})$ represent the fitness values of $x_{cbest, ci}$ and $x_{mbest}$ respectively.

3). Other elephants $x_{otherci, j}$ of the clan learn from the matriarch $x_{cbest, ci}$ of the clan. Learning step $a_{otherci, j}$ is expressed as follows:

where $f(x_{otherci, j})$ and $f(x_{cbest, ci})$ represent the fitness values of $x_{otherci, j}$ and $x_{cbest, ci}$ respectively and $a_{1} < a_{2} < a_{3}$ are constants.

3.4.   Strategy 4: Group learning

In a large elephant herd tribe, each individual has a unique level of fitness. There are excellent female ministers and matriarchs and males and other ordinary elephants, so the elephants have been divided into four groups, and different groups of elephants have different learning styles. The first group is the best female elephant of the tribe, represented by $x_{mbest}$. The second group is the best matriarch of the clan, represented by $x_{cbest, ci}$. The third group is the other female elephants and young elephants, represented by $x_{otherci, j}$. The fourth group is the worst individual of the clan, represented by $x_{worst, ci}$.

The learning mode of the first group $x_{mbest}$ is as follows:

As the best female elephant in the herd, her position and speed should be updated according to the matriarch information of all clans. The update mode is as follows:

where $x^{new}_{mbest}$ and $v^{new}_{mbest}$ respectively represent the update position and speed of $x_{mbest}$, $x_{center}$ represents the central location for all matriarchs and $n_{ci}$ represents the total number of clans.

The learning mode of the second group $x_{cbest, ci}$ is as follows:

The best matriarch of the clan should learn from the best female elephant of the tribe to achieve a larger search area. The update mode is as follows:

where $x^{new}_{cbest, ci}$ and $v^{new}_{cbest, ci}$ respectively represent the update position and speed of $x_{cbest, ci}$.

The learning mode of the third group $x_{otherci, j}$ is as follows:

The other female elephants and young elephants should learn from the best matriarch of the clan to achieve a faster learning speed. The update mode is as follows:

where $x^{new}_{otherci, j}$ and $v^{new}_{otherci, j}$ respectively represent the update position and speed of $x_{cbest, ci}$.

In order to optimize the learning of the elephants in the clan, a mutual learning strategy is proposed. The ordinary elephants in the clan learn from the matriarch first, and then from others who are better than themselves.

Elephant $p$ is randomly selected from Clan $ci$; then, its new fitness value is calculated. If the fitness value of Elephant $j$ is better than that of Elephant $p$, Elephant $p$ needs to learn from Elephant $j$. If it is the opposite Elephant $j$ needs to learn from Elephant $p$. If the fitness values of Elephants $j$ and $p$ are equal, then there is no need to learn from each other. The update mode is as follows:

where $x^{new}_{otherci, j}$ and $v^{new}_{otherci, j}$ respectively represent the position and speed of Elephant $p$ after learning.

3.5.   Strategy 5: Elite retention

In the standard EHO algorithm, the separation operator is used to replace the worst solution in the clan. At the same time, the clan optimal solution continuously updated during the iteration, and not preserved. Therefore, an elite retention strategy was developed. The worst elephants in the fourth group directly learned from the matriarch and replaced the worst solution with the clan optimal solution. At the same time, the fitness values for each elephant before and after updating were compared, and the positions of elephants with high fitness values were retained. The method preserves the optimal solution for each generation's clan and the optimal solution for individual elephants, which can effectively accelerate the optimization speed of the elephant group.

The IEHO algorithm flowchart is shown in Figure 2.

The learning mode of the fourth group $x_{worst, ci}$ is as follows: the worst male elephant learns directly from the matriarch. The update mode is as follows:

3.6.   Computational complexity analysis

Standard EHO mainly includes initialization, fitness evaluation, sorting and optimal selection, a clan updating operator and a separating operator. In the associated formula, $M$ indicates the number of clans, $N$ indicates the number of elephants in each clan, $D$ is the number of dimensions of the problem and $T$ represents the maximum number of iterations. The complexity of the initialization stage is $O(1)$. In the main part of the algorithm, the complexity of the sorting algorithm is $O(N*Mlog(N*M))$. The clan updating operator is $O(M*N)$; the separating operator is $O(N)$. The overall complexity of the algorithm is $O(1+T*(N*MlogN*M+M*N+M))$.

The proposed IEHO algorithm mainly includes the following parts: initialization, fitness evaluation, sorting and optimal selection, position and speed updating and a fitness comparison. During the initial stage, the complexity of initializing the individuals in each dimension based on dyadic learning is $O(M*N*D)$. In the main part of the algorithm, the complexity of the sorting algorithm is $O(N*Mlog(N*M))$, the complexity of updating the speed and position of the individuals is $O(M*N)$ and the complexity of adaptive comparison is $O(M*N)$. From the above analysis, we can acquire the complexity of the whole algorithm: $O(M*N*(D+T*(log(M*N)+2)))$.

4.   Testing and experimental analysis

4.1.   Experiment design

To verify the effectiveness of the IEHO algorithm, 12 typical reference functions proposed in ^[28] were selected for testing, as is shown in Table 2. $f_{1}-f_{6}$ are unimodal functions with only one global optimal point, which is used to test the convergence accuracy of the algorithm. $f_{7}-f_{12}$ are multi-peak functions with multiple local optimal points, which are used to test the algorithm's global search capability, local development and ability to jump out of local optima.

Due to the fact that five improved strategies are proposed, to prove the effectiveness of the final five strategy combinations of IEHO, we did not consider partial strategies based on the EHO algorithm that are stronger than the IEHO algorithm, and a strategy combination comparison experiment was conducted. First, a comparison experiment of strategy combinations was conducted, and $Schwefel2.22$ and $Qing$ were selected as the benchmark test functions; the experimental results are shown in Figure 3. EHO + S1 is the combination of EHO with Strategy 1; EHO + S12 is the combination of EHO with Strategy 1 and Strategy 2; EHO + S123 is the combination of EHO with Strategy 1, Strategy 2 and Strategy 3; EHO + S1234 is the combination of EHO with Strategy 1, Strategy 2, Strategy 3 and Strategy 4; EHO + S12345 is the combination of EHO with 5 strategies. Furthermore, to prove the convergence speed, convergence accuracy and stability of IEHO, the IEHO algorithm has been compared with the multi-mechanism hybrid EHO (MCEHO) algorithm proposed in ^[21], original EHO algorithm ^[22], the PSO algorithm ^[29] and the artificial bee colony (ABC) algorithm ^[30,31].

To ensure fairness and accuracy of the algorithm comparison, the parameters of the five algorithms were set to be the same, the population size was set as 50 and the maximum number of iterations was set to be 500. For EHO, MCEHO and IEHO, we set $nclan = 5$ and $nci = 10$. Each algorithm ran the optimal value independently 30 times on each test function in 30D and 100D. The mean value and standard deviation were calculated to evaluate the convergence accuracy and stability of each algorithm. The simulation environment was a Windows 10 operating system equipped with an i5-6500 CPU, 3.2 GHz main frequency, 8 GB of memory, and MATLAB 2016a simulation software.

4.2.   Experimental results and analysis

It can be seen in Figure 3 that with the increase of strategy combinations, the EHO performance gradually improved, the speed and adaptive learning step size can effectively improve the convergence speed, group learning and elite retention can effectively improve the convergence accuracy and the IEHO performance from the combination of five strategies was optimal. The IEHO still follows the nomadic behavior of the elephant herd, IEHO is an improvement on the standard EHO, only its search method is improved during the iterative process so that the elephant herd becomes more intelligent; essentially, it is still EHO. These five strategies are also useful for improving the performance of other optimization algorithms.

Table 3 shows the means and standard deviations of the fitness values for the 12 test functions calculated by the five algorithms under the conditions of fixed iteration times for the low dimension $(30)$ and high dimension $(100)$, respectively. The performance of each of the five algorithms on each test function is shown in Figure 6, and the three-dimensional mathematical model of each of the 12 test functions is also presented.

The left plots in Figures 4–6 show the three-dimensional search spatial distributions for the 12 test functions. $X_{1}$ and $X_{2}$ are function search intervals, and the vertical axis is the function value. The graphs on the right are the convergence curves for the intelligent algorithms for optimizing the test functions. The horizontal axis is the number of iterations, and the vertical axis is the logarithm of the optimal values.

As can be seen in Figures 4–6, after 500 iterations, all five algorithms were able to converge to the extreme value of the test function with different convergence speeds and convergence accuracies; however, PSO resulted in the worst performance. For the unimodal functions $f_{1}-f_{6}$, in the beginning, the convergence rates of EHO and IEHO were faster and better than that of MCEHO. This shows that the initial population initialization strategy based on chaotic mapping and opposition-based learning can facilitate a better position and fitness value for the initial population and improve the global searching ability. The convergence speed of the IEHO algorithm improved after 100 iterations, while that of the MCEHO algorithm improved after 150 iterations. The convergence speeds of the EHO and ABC is similar, but slightly higher than ABC. The IEHO algorithm was able to converge to the minimum value after about 100 iterations, and the convergence accuracy was higher than that of other algorithms, indicating that the addition of a speed strategy can effectively accelerate the population optimization speed. Regarding the unimodal function $f_{3}$, the IEHO algorithm was able to converge to 0 and the standard deviation was 0.

For the multimodal functions $f_{7}-f_{12}$, the convergence speed and convergence precision of EHO were better than those for PSO, indicating that EHO has obvious advantages over PSO when it comes to solving multi-extremum problems. The EHO and ABC algorithms had similar convergence accuracies, except for the test functions $f_{6}$ and $f_{10}$. Regarding the other functions, EHO was found to be superior to ABC optimization, as it resulted in a faster convergence speed and higher convergence accuracy. However, EHO is susceptible to the local optima problem; MCEHO can jump out of partial local optima but it is still hard to find global optima. The IEHO algorithm's optimization speed and precision were found to be superior to those of the MCEHO algorithm, indicating that adaptive step grouping learning and an elite retention strategy can effectively improve the algorithm's ability to develop global optimal and jump out of local optima.

As can be seen in Table 3, for the unimodal and multi-peak test functions, the IEHO algorithm had the lowest means and standard deviations among all of the algorithms. Its mean value was closest to the theoretical value and able to find the minimum point. As the number of dimensions of the test function increases, the model complexity exponentially grows and increases the difficulties of optimization. To further validate IEHO performance on complex high-dimensional problems, we added a 100D high-dimensional test function experiment; the parameter settings are the same as those for lower dimensions. According to the data in Table 3, the IEHO algorithm performed poorly for $f_{6}$ with low convergence accuracy. Regarding the other test functions, it was able to maintain good optimization stability and was found to be superior to the other four algorithms, which fully verified the advantages of IEHO as a tool to solve high-dimensional problems. From the above analysis, it can be seen that the IEHO algorithm presented in this paper has a better convergence effect for both in terms of mean and standard deviation, on low- and high-dimensional test functions, as well as a stronger ability to find the optima as compared with the algorithms based on PSO, ABC, EHO and MCEHO.

5.   Motor system energy efficiency rating

5.1.   Motor energy efficiency evaluation index system model

In a motor system, the transmission process for the current from the power supply to the motor to the load will generate energy loss, and the energy efficiency of the motor is affected by many factors ^[32]. In this study, the power quality, motor characteristics and load characteristics of the motor system were considered as the first-level indexes. From these three aspects, seven secondary indexes that have a greater impact on motor energy efficiency were selected to obtain the motor energy efficiency rating system as shown in Figure 7.

The motor energy efficiency has been divided into 10 grades according to the national standards, the upper and lower limits of each indicator's deviation and the impact on the motor energy efficiency. The quantified motor energy efficiency grading standards are based on the parameter values of various indicators at different levels, as shown in Table 4.

The data of the training model were randomly generated. A total of 1000 samples were randomly generated in each indicator interval and marked as$\left\{(x^{i}_{1}, x^{i}_{2}, …, x^{i}_{7}), y^{i}\right\}$, where $x^{i}_{j}$ represents the random number, $j = 1, 2, …, 7$ represents the seven characteristic index components of the corresponding sample, $i = 1, 2, … 1000$ represents the corresponding 1000 sample quantity and $y^{i} = 1, 2, …, 10$ represents the corresponding sample label. First, the training set and test set data were divided and preprocessed; then, the IEHO-SVM model was trained with the training data; finally, the model was verified with the test data.

5.2.   Improved elephant herding optimization and support vector machine rating model

The SVM is a two-class classification model ^[33], and it defined as a linear classifier with the maximum interval in the feature space. Different from the perceptron SVM, the learning strategy is to find the separation hyperplane with the maximum interval, which is essential in solving the optimal problem of convex quadratic programming. For one-class classification models, support vector data description is usually used ^[34,35].

There is no completely linearly separable data. By introducing a "soft interval", incomplete linearly separable data can be solved by allowing partial error points. For some linear indivisible problems, it may be nonlinearly divisible by using nonlinear kernel functions to map the original feature space to the higher-dimensional Hilbert space ^[36]; a nonlinear SVM can be obtained by using a linear SVM, so the nonlinear separable problem is transformed into a linearly separable problem.

Taking a nonlinear SVM as an example, the learning algorithm is as follows:

Input: Training set $T = \left\{(x_{1}, y_{1}), (x_{2}, y_{2}), …, (x_{n}, y_{n})\right\}$, where $x_{i} \in R, y_{i} \in\left\{-1, 1\right\}.$ Output: Separation hyperplane and classification decision function.

Step 1: Select a proper Gaussian kernel width $\sigma$ and penalty factor $c$ and construct and solve convex quadratic programming problems.

Get the optimal solution $a^{\ast} = (a^{\ast}_{1}, a^{\ast}_{2}, …, a^{\ast}_{n})^{T}$.

Step 2: Select the $a$ component of $a^{\ast}$, $a^{\ast}_{i}$ and calculate $w^{\ast}$ and $b^{\ast}$:

Step 3: Compute the separation hyperplane:

Step 4: Compute the classification decision function:

According to the above analysis, the main parameters affecting SVM learning ability are the penalty factor $c$ and Gaussian kernel width $\sigma$. The selection of the parameters has an important influence on the running result of the SVM model, which determines its learning ability and generalization ability. The penalty factor $c$ represents the tolerance of error, where a larger $c$ means a higher likelihood of overfitting, and a smaller $c$ means a higher likelihood of underfitting. The Gaussian kernel width $\sigma$, which is inversely proportional to the number of support vectors, affects the model training and prediction speed. Traditional parameter selection methods include manual selection and grid optimization, which are more suitable for small data. When the amount of data increases, the amount of computation and calculation time will also increase and it becomes easier to fall into local optimization.

In this study, the IEHO algorithm was used to optimize SVM parameters $c$ and $\sigma$, and the algorithm was applied to the motor energy efficiency rating. The specific algorithm process is shown in Figure 7. The position vector for each elephant corresponds to a group of specific parameter combinations. The evaluation function for its location fitness is defined as follows:

where $N$ represents the number of samples; $Y_{i}$ and $Y^{\ast}_{i}$ represent the actual value and the predicted value of SVM, respectively.

5.3.   Example simulation and result analysis

In order to evaluate the performance of the algorithm and its robustness on the training data, the following two strategies were performed.

1) A stratified sampling method was used to divide the data set into four different proportions: (80%, 20%), (70%, 30%), (60%, 40%) and (50%, 50%).

2) Using the same data, the IEHO-SVM algorithm proposed in this paper was compared with the original SVM and k-nearest neighbor ^[37] algorithms.

The classification accuracies of the three algorithms on different training sets and test sets are shown in Table 5. The classification results for the three algorithms on the 50% training sets and test sets are shown in Figure 8.

As we can see in Table 5 and Figure 9, the accuracy of the IEHO-SVM algorithm on different training sets and test sets was higher than 98%, whereas that of the KNN algorithm was around 91% and that of the original SVM algorithm was around 87%. This experiment demonstrates that the robustness of the IEHO-SVM algorithm on training data is not limited to a particular training-test set combination, but that better results can be achieved in all these cases. So, we found that the IEHO-SVM algorithm can accurately grade the motor energy efficiency with high accuracy and reliability.

6.   Conclusions and future prospects

In the past, research on motor energy efficiency mainly focused on the rated operating condition, but there were few studies on motor energy efficiency performed under off-conditions. The correct grade of the motor energy efficiency can provide scientific guidance for motor energy-saving upgrades, fault damage and the elimination of backward motors. To determine an accurate grade of the motor energy efficiency, we selected seven evaluation indexes that have a great influence on motor energy efficiency from the three aspects of power quality, load characteristics, and motor characteristics, and established a quantitative classification standard.

Aiming to eliminate disadvantages of the original EHO algorithm, such as a slow convergence speed, a low convergence accuracy and susceptibility to the local optima problem, and developed five improvement measures. A new EHO algorithm, i.e., the IEHO algorithm, was designed and compared with other algorithms. The results show that the IEHO algorithm has a higher convergence precision and faster convergence speed than other algorithms, can jump out of local optima and exhibits better performance for optimization.

The IEHO algorithm was used to optimize the SVM parameters, and the IEHO-SVM model was established; it was subsequently applied to the motor energy efficiency rating system. Compared with the KNN and original SVM algorithms, the experimental results show that the IEHO-SVM algorithm can accurately grade the motor energy efficiency with an accuracy higher than 98%, which was better than the KNN and original SVM algorithms.

The IEHO algorithm and IEHO-SVM model proposed in this paper has strong portability, and it can not only be used for motor energy efficiency rating, but also for other optimization problems. The motor energy efficiency grading model established in this paper is simple and easy to realize, has a high practical value and is of great significance for realizing energy conservation and emission reduction and improving energy utilization.

Possible opportunities and future proposals are as follows. Initialization strategies for orthogonal learning can be attempted next, and location updates can be attempted for quantum computing, parallel computing, and co-evolutionary approaches. The IEHO algorithm presented in this paper been demonstrated to effectively solve static optimization problems, and the development of dynamic optimization and variants of multi-objective optimization methods that can handle more kinds of optimization problems can be attempted next.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.