Association of cerebral infarction with vertebral arterial fenestration using non-Newtonian hemodynamic evaluation

Abbreviations: VBA: vertebrobasilar artery; VA: vertebral artery; PCA: posterior cerebral artery; SCA: superior cerebellar artery; WSS: wall shear stress; OSI: oscillatory shear index; TAWSS: time-averaged wall shear stress

1.   Introduction

Fenestration of an intracranial artery involves a segmental duplication of cerebral arteries, and the lumen is divided into two separate endothelium-lined channels that rejoin distally ^[1]. This luminal division often impacts the endothelial layer and the tunica media, and in some instances affects the adventitia ^[2,3]. Fenestration is a rare but well-known congenital anatomical abnormality of blood vessel development that results from the incomplete fusion of primitive embryologic vessels during embryogenesis, but this etiology is thought to be controversial since it is related to the fenestration site. Fenestration is different from duplication, which is also a congenital developmental anomaly but fuses separately during the course of the artery ^[4,5]. Fenestration was firstly found in a vertebral artery during an autopsy reported in 1866 ^[6]. Thereafter, fenestrations were mostly detected through cadaveric dissection and imaging examinations in recent decades ^[6,7,8]. However, the actual fenestration incidence is hard to define. Firstly, numerical studies reported that intracranial arterial fenestrations were discovered incidentally revealing that they were asymptomatic in the clinic. On the other hand, a large proportion of fenestrations are unable to be visible in angiograms owing to the tiny size. The growing size and number of researches and series of case reports indicate that intracranial fenestration has been reported to be a predisposing factor to other vascular malformations, such as aneurysm, ischemic stroke, moyamoya disease, and venous malformations, among which aneurysms were reported most extensively ^{[7,9,10,11,12]}.

The blood supply to vital structures of the brain, such as the cervical spinal cord, brainstem, thalamus, cerebellum, and occipital lobes, relies on the vertebrobasilar system ^[13]. A morphological variation of the vertebral artery or basilar trunk leads to the change of hemodynamic condition, such as the flow pattern, mass flow rate and pressure, etc. which has been reported as a critical factor in vascular diseases. Computational fluid dynamics has revealed its powerful effectiveness in the investigation and applications on disease initiation, progression, and treatment outcomes. The blood property in the majority of hemodynamic simulations is regarded as Newtonian viscosity model, but the blood flow in small arteries often exhibits non-Newtonian characteristics ^[14,15,16]. High blood viscosity results in blood stagnation and subsequent pathological thrombotic events, leading to the evolution of ischemic stroke. Therefore, the viscosity information derived from the modeling of non-Newtonian flow is necessary for excavating the underlying mechanism of infarction.

The pathogenic relationship between fenestration and other vascular abnormalities remains unclear, the understanding of which has become necessitated and has a suggestive effect on the decision-making of vascular interventional therapy. The association between fenestration and other vascular abnormalities has only recently come into prominence and the correlated hemodynamic studies are even less. The purpose of this study is to explore reasons for cerebral infarction in patients with fenestration structure from the perspective of hemodynamics.

2.   Materials and methods

2.1.   Study design and participants enrollment

This study aims to explore the association between cerebral infarction and the fenestration structure by analyzing hemodynamic characteristics, investigating indicating factors for the early warning of a stroke. Between March 2018 to October 2020, a total of eight patients with fenestration located at the base of the vertebral basilar artery were recruited from the radiology department of Hongqi Hospital affiliated with Mudanjiang Medical University. The MRA scanning system is Philips Medical Systems (PHILIPS-CT04LKC), and the slice thickness is 2 mm. The data of collection and analysis comply with the guidelines of the local ethics committee.

Figure 1.  Volume rendering three-dimensional reconstruction showing different locations of cerebral artery fenestrations and reconstructed 3D models for hemodynamic simulation.

DownLoad: Full-Size Img PowerPoint

2.2.   Model reconstruction and morphological measurement

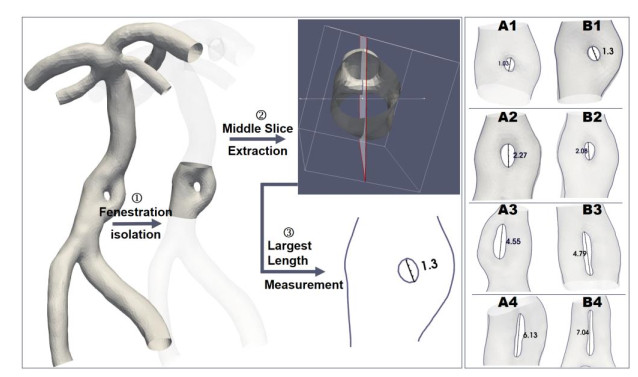
The 3D fenestration models were reconstructed by the initiatory thresholding function and a series of manual segmentation operations in Mimics 19.0 (Materialise, Belgium). Surface smoothing procedures were then conducted. The datasets were classified into four groups referring to the fenestration size (Table 1). In each group, one patient suffered cerebral infarction (named as Case B-series) and one patient was set as the control subject (named as Case A-series). The measurement method of fenestration size follows the operation procedure shown in Figure 2. Firstly, the fenestration segment is isolated from the entire model to expose the fenestration structure like the endoscope mode. Secondly, a slice inserted at the middle of fenestration needs to be extracted. The largest length of fenestration is defined as the fenestration size and computed from the outline of fenestration on the slice. The corresponding measurement results of eight models are displayed on the right column in Figure 2 and listed in Table 1. VA inlets and outlets at the bifurcation of VBA were truncated perpendicular to the centerline using Geomagic Studio 2012 (North Carolina). Wherein, the B2 case has three superior cerebellar arteries. For the B1 case, the diameter of the branch derived from the right posterior cerebral arteries is relatively large, therefore, was kept for the subsequent hemodynamic simulation.

Table 1.  Demographics and geometrical information of Fenestration.

Case	Sex	Age	Fenestration			Cerebral Infarction
			Location	Type	Size [mm]
A1	F	50	Proximal VBA	convex-lens-like	1.03	N
B1	F	69			1.30	Y
A2	F	65			2.27	N
B2	M	81			2.08	Y
A3	M	51		slit-like	4.55	N
B3	M	58			4.79	Y
A4	M	66	VA		6.13	N
B4	F	63	VBA junction		7.04	Y
VBA: vertebrobasilar artery; VA: vertebral artery

---

 | Show Table

DownLoad: CSV

Figure 2.  Flow chart of fenestration size measurement and the corresponding results of eight models.

DownLoad: Full-Size Img PowerPoint

2.3.   Hemodynamic analysis with non-Newtonian behavior

The mesh discretization of all 3D models was performed in ICEM CFD (ANSYS Inc.). The core region was filled with tetrahedral elements and five boundary layers close to the wall were reserved to generate prismatic grids. The grid resolution ranges from 1.57 to 2.02 million elements which are able to satisfy the accuracy requirement, and the grid refinement study was conducted in our previous paper ^[17]. The governing incompressible Navier-Stokes equations are given as

where u denotes the velocity vector, $\rho$ represents the density and $p$ is the pressure. T, i.e., stress tensor, is expressed as

where D = $0.5*(\nabla \boldsymbol{u}+\nabla {\boldsymbol{u}}^{T})$, $\dot{\gamma }$ is the shear rate, and η is a function of $\dot{\gamma }$ representing the viscosity of the blood. In this study, the shear-thinning behavior of blood was considered and the flow was modeled as Non-Newtonian flow. The power law model, the Casson model, and the Carreau-Yasuda model are commonly employed in simulating hemodynamic properties of Non-Newtonian flow. However, the power law model and the Casson model have shortcomings in aspect of high gradient and the range of shear rates, respectively ^[18]. Blood flow dynamic analyses applied to ideal models and anatomical models suggested that the Carreau-Yasuda model was the most suitable model in simulating the blood properties of cerebral arteries ^[18,19]. Here the constitutive model this study used is expressed as

which is the Carreau-Yasuda B model, and the values for ${\mu }_{\infty }$, ${\mu }_{0}$, $\lambda$, a, and n are 0.0022 Pa·s, 0.022 Pa·s, 0.110 s, 0.644, and 0.392 employed from an experimental study of the non-Newtonian properties of blood ^[15,20]. Solution of governing equations and constitutive model was accomplished in the commercial solver ANSYS CFX 19.2 (ANSYS Inc.), which uses cell-vertex finite volumes to discretize the domain and the flow variables are stored at the vertices of the elements. Besides, the blood was assumed as an incompressible flow with a constant density of 1066 kg/m³. For the arterial wall, it was assumed to be rigid, no-slip, and no-penetration conditions were imposed. The inlet flow and outlet pressure were pulsatile with waveforms taken from the software @neufuse which possesses the database of a 1D model of the human vascular tree ^[21]. One cardiac cycle was set as 0.8s discretized into 100 time-steps. Three cycles were simulated to ensure periodic flow conditions, and the results of the third cycle were adopted for data evaluation. For case B2, it has two instinctive right superior cerebellar arteries, these anatomical variations are reported to be common, where the velocity boundary condition was computed in accordance with a flow-splitting-based computation method ^[22]. The data post-processing and visualization were accomplished through CFD-post (ANSYS Inc.) and ParaView software. Frequently-used hemodynamic parameters were calculated to describe flow patterns and mechanical environment. The flow pattern and special flow division induced by the fenestration structure were analyzed. Besides, two most extensively used hemodynamics indicators, wall shear stress (WSS) and oscillatory shear index (OSI), normally linking to disease mechanism were calculated. The time-averaged WSS (TAWSS) calculated the average amplitude value of the wall shear stress during a cardiac cycle which is expressed as

where $\tau$ denotes the WSS and T mean the cardiac cycle period. And the OSI is calculated as

which represents the degree of the reversal flow during on cardiac cycle.

3.   Results

3.1.   Flow division going through fenestration

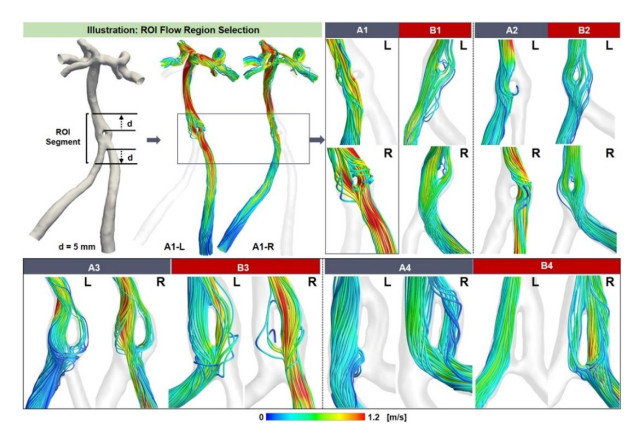
The flow division induced by fenestration structure undoubtedly impacts the hemodynamic environment, but it has not been investigated using the computational modelling analysis. For the sake of looking into the way that the blood flowing through the fenestration, streamlines were started from the left and right VA separately. Here, an ROI region around fenestration was selected to show the flow pattern more explicitly and the intact flow was plotted in Figure S1 (see supplementary material). The upper and lower bounds of ROI region were defined as a 5 mm distance to the fenestration top and the connection root of VAs, and the graphical representation using Model A1 as an illustration model was shown in Figure 3. Results showed that the blood flow pattern was relatively separated along two channels of fenestration in series A compared with series B cases in Group 1-2, i.e., small fenestration sizes. And there was a short distance between fenestration and the junction of the left and right VA in series B cases but these two structures were connected directly in series A cases. This distance leads to the mixture of blood flow before the fenestration (Figure 3 B1-B2) which might have an impact on the re-allocation of blood flow and the flow division consequence of fenestration. As to Group 3, the geometrical characteristics between A and B are significantly different. The area of the left channel of Model A3 is approximately 2.52 folds larger than the right channel at the fenestration, resulting in a large proportion of blood going through this channel (flow rate ratio: 4.28). The fenestration was located at the distal VA of Model B4 and a narrow pipeline beneath the fenestration is easy to generate the vortex caused by the confluence of blood flow. Blood from the left VA directly went through the left fenestration channel without flow exchange, while the flow from the right VA was split into two parts with one part passed through the aforementioned narrow pipeline.

Figure 3.  Flow streamlines going through the ROI region defined by an illustration model (A1 model) were shown. The velocity legend is limited to 0–1.2 m/s to clearly show the flow pattern differences among cases. Flow streamlines started from the left and right VA respectively are displayed in Figure S1 (see supplementary material).

DownLoad: Full-Size Img PowerPoint

3.2.   Quantitative comparison of two channels of fenestrations

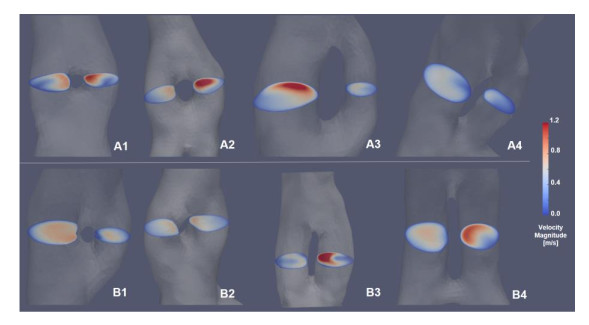
Besides the qualitative analysis of the flow division behavior through fenestrations (Figure 3), the quantitative calculation was performed to further explore the differences between infarction cases and control cases. As shown in Figure 4, a slice was cut in the neutral position of each fenestration showing the in-plane velocity. Blood flow with high velocity was normally going close to the inner side of fenestration and one side was performed as the dominant flow channel. To be more specific, the area and the flow rate were measured for each channel and listed in Table 2. Due to the unbalanced geometrical features between two fenestration channels, an index named the ratio was calculated as the flow rate divides by the area. In Group 1-2, the right side is the dominant flow channel for control cases (series A) while the dominant side was the opposite for infarction cases (series B). For cases with a larger fenestration size (Group 3-4), the dominant flow side was left in control cases and right in infarction cases, which was converse compared with the other two groups.

Figure 4.  Planes were cut in the middle of fenestrations and embedded with the peak systolic velocity distribution information. The velocity legend is limited to 0-1.2 m/s to compare differences between the infarction cases and control cases and maintain consistency with the streamline illustration.

DownLoad: Full-Size Img PowerPoint

Table 2.  Area and flow rate data calculated from the middle plane of fenestrations.

Case No.	Side	Area [mm2]	Flow Rate [ml/s]	Ratio	Case No.	Side	Area [mm2]	Flow Rate [ml/s]	Ratio
A1	L	6.08	4.11	0.676	B1	L	10.19	5.59	0.548
	R	4.01	3.14	0.783		R	4.46	1.50	0.336
A2	L	6.76	2.82	0.417	B2	L	8.12	3.36	0.414
	R	6.50	4.33	0.667		R	9.34	3.83	0.410
A3	L	10.69	6.14	0.574	B3	L	7.05	2.37	0.336
	R	3.00	1.04	0.347		R	7.82	4.81	0.615
A4	L	14.46	5.74	0.397	B4	L	7.76	3.58	0.461
	R	6.13	1.34	0.219		R	6.24	3.59	0.575
L: left; R: right; ratio = Flow rate/Area [mm/s]

---

 | Show Table

DownLoad: CSV

3.3.   Arterial mechanical properties

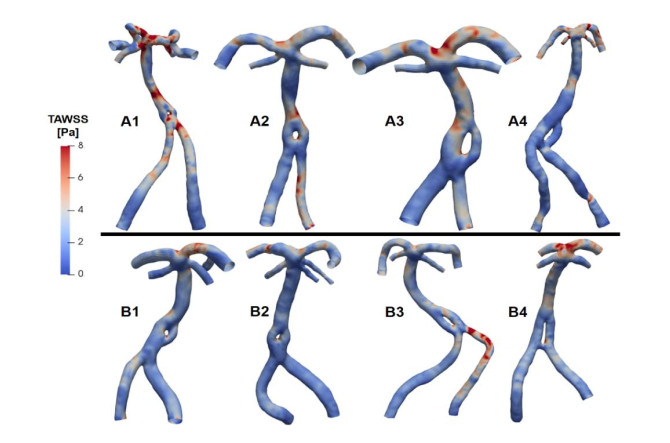
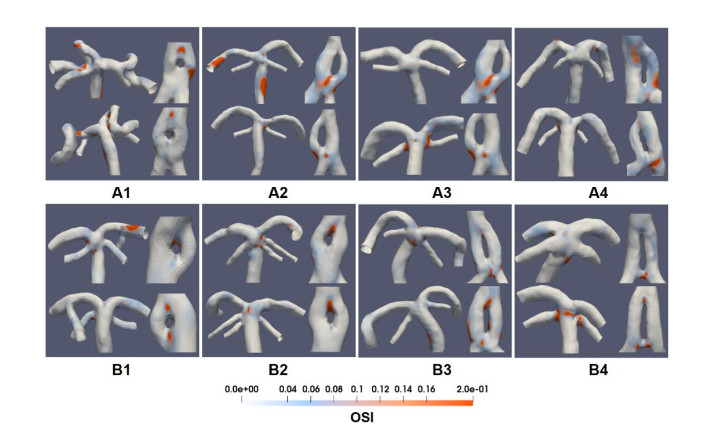
Apart from the flow dividing analysis, the mechanical force imposing on arterial wall has been considered as a critical role playing in the pathological progress of vascular disease, e.g., atherosclerosis and aneurysm. Figure 5 displayed the TAWSS distribution for each case and the legend rage was constrained to 0–8 Pa. High TAWSS region were mostly concentrated around the fenestration and the basilar tip.

Figure 5.  TAWSS distribution during on cardiac cycle was displayed for each model and the color bar was limited to 0–8 Pa.

DownLoad: Full-Size Img PowerPoint

Similar to the TAWSS distribution, the high OSI regions were mostly located in the vicinity of the bifurcation and fenestration (Figure 6). However, results showed that the surface areas with high OSI (>0.1) were generally corresponding to the areas with low TAWSS values, suggesting the great probabilities of recirculation and stagnation of blood components that forms the thrombus.

Figure 6.  OSI distributions of the bifurcation section and fenestration for all cases from the anterior and posterior view, respectively. To clearly show the distribution characteristics, the range of legend was limited to 0–0.2.

DownLoad: Full-Size Img PowerPoint

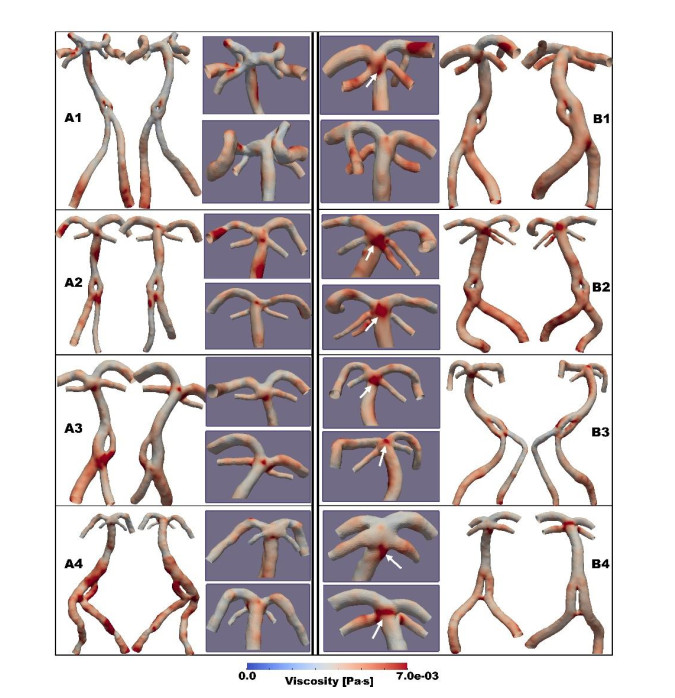
3.4.   Viscosity distribution

The viscosity distribution on the vascular wall was extracted from the result files and illustrated in Figure 7 from the view of both anterior and posterior. Concentrated viscosity regions were located around the fenestration, artery with larger curvatures, and the basilar bifurcation region where the flow was normally disturbed. By comparing these regions, larger areas with high viscosity at basilar bifurcation were shown in the infarction cases noted with white arrows in Figure 7. Meanwhile, the locations were closer to superior cerebellar arteries which seemed to show higher viscosity as well.

Figure 7.  Time-averaged viscosity distribution during on cardiac cycle was displayed for each model in anterior and posterior view, respectively. Specifically, the corresponding distribution of basilar bifurcation was magnified to explicitly demonstrate the high viscosity concentration region (white arrows).

DownLoad: Full-Size Img PowerPoint

3.5.   Quantitative analysis

Section 3.3 and 3.4 provided the visual presentation of wall mechanics induced by flow and the viscosity distribution, referring to the formation and destruction mechanism of atherosclerotic plaque. Here, six significant segments of each model were extracted for the further quantitative data analysis, i.e., posterior cerebral artery (PCA), superior cerebellar artery (SCA), fenestration and top region. (definitions and segmentation models see supplementary material Figure S2).

The maximum and mean values of WSS, OSI, viscosity were calculated. Besides, the area ratio is defined as the area distributed with specific variable in a given range divided by the area of the corresponding location model. The comparison of two significant locations was listed in Table 3 and the data of other four locations was presented in Table S1 (see supplementary material). For the top region, results showed that the maximum and mean TAWSS in Group B was lower than that in Group A, and the area with low TAWSS (0–2 Pa) exhibited that same condition. And the OSI and viscosity performed the similar trend, i.e., values and area ratio were both greater in Group B, except in Group A3 and B3. However, there was no clear regulation shown in the fenestration region and other locations.

Table 3.  Comparison of hemodynamic data on top and fenestration locations.

Location	Parameters		A1	B1	A2	B2	A3	B3	A4	B4
Top	TAWSS [Pa]	max	14.349	8.377	8.039	6.051	13.327	6.584	12.336	9.737
		mean	5.990	2.986	3.228	2.222	3.401	2.565	3.532	3.553
		ratio(0-2)	2.39%	23.59%%	26.69%	59.12% %	31.27%	34.66%	22.69% %	37.61%
	OSI	max	0.298	0.374	0.325	0.357	0.380	0.336	0.310	0.441
		mean	0.018	0.029	0.027	0.034	0.039	0.034	0.027	0.048
		ratio(0.2-0.5)	0.05%	0.76%	1.50%	2.20%	1.93%	0.52%	0.75%	6.37%
	viscosity# [Pa$\cdot$s]	max	5.717	8.466	8.527	10.945	9.999	11.425	8.826	9.318
		mean	3.581	4.575	4.435	5.298	4.698	4.847	4.407	4.715
		ratio(5-11)	0.88%	19.96%	26.19%	56.56%	28.01%	31.21%	19.72%	34.47%
fenestration	TAWSS [Pa]	max	23.715	10.381	8.671	7.536	10.285	12.168	6.967	8.373
		mean	4.342	2.406	2.866	2.061	2.670	2.552	1.451	2.389
		ratio(0-2)	19.06%	44.72%	40.10%	56.23%	42.11%	46.83%	80.92%	30.86%
	OSI	max	0.446	0.436	0.441	0.428	0.441	0.440	0.398	0.458
		mean	0.030	0.019	0.050	0.023	0.032	0.036	0.039	0.018
		ratio(0.2-0.5)	0.35%	0.29%	2.01%	0.13%	0.93%	0.41%	0.26%	0.35%
	Viscosity# [Pa$\cdot$s]	max	7.649	7.568	11.542	11.941	10.666	9.097	9.419	10.055
		mean	4.184	4.697	4.609	5.163	4.869	4.761	5.892	4.588
		ratio(5-11)	16.75%	26.84%	28.66%	49.88%	32.77%	31.28%	69.40%	14.21%
viscosity# = viscosity $\times$ 10−3

---

 | Show Table

DownLoad: CSV

4.   Discussion

A study that reviewed 280 cerebrovascular fenestrations reported fenestrations located in the VA were more likely to coexist with cerebrovascular diseases and the proportion of patients complicated with ischemic stroke was 64.3% ^[23]. The correlation between fenestration and cerebrovascular diseases has raised increasing attention recently, and most researches were focusing on the statistical analysis from clinical symptoms and imaging scans. From the view of etiology, fenestration at any VA segment is caused by the absence of obliterations of two intersegmental vessels which fuse, or by segmental arteries which become short or disappear while a portion of the dorsal aorta remains against the vertebral artery ^[24]. The exact underlying mechanism of fenestrated-related infarction remains unknown, but it may be related to dissection and local embolism ^[25]. In fact, the evaluation of the cause-to-effect relationship is hard which needs interdisciplinary research to involve in, like biomechanics, microscopic and histopathological examination. One study found that the limbs have shown irregularities in the lateral and medial wall structure by histopathological research ^[24,26]. These irregularities may alter the hemodynamics of blood flow at the proximal and distal end of the fenestrated segment causing transient ischemic attacks.

In this study, patients with cerebrovascular fenestration were classified into four groups according to the fenestration size. In each group, there was one who suffered infarction and one was set as control. The non-Newtonian flow simulations were conducted to investigate the potential reasons which might lead to the infarction. A critical variation brought by the fenestration structure is the flow division phenomenon. Dan Ye et al. have reported the various flow condition from the left and right VA respectively with the consideration of different fenestration sites, bifurcations, and curvatures using schematic diagrams ^[23]. The flow distribution results in this study showed that the blood flow around the fenestration site was found relatively separate in control patients but mixed in front of the fenestration in infarction patients for small fenestration cases (Group 1-2). It's not too difficult to spot that this phenomenon was consistent with morphological characteristics, i.e., a short distance existed between the fenestration and the bifurcation of bilateral VAs. However, for case B4, the fenestration located at the VBA junction determined a narrow and flat channel beneath the fenestration, which brought more high curvature structures and disturbed flow there. Hence, we supposed that this type of structure may contribute to platelet aggregation and accumulation.

Quantitatively, we measured the area and flow rate data calculated from the middle plane of fenestrations at systolic peak and the ratio was calculated as the flow rate divides by the area to eliminate the morphological impact. Results showed that the dominant side of blood supply was different in control and infarction cases and this phenomenon was reversed in smaller and larger fenestration groups. We hypothesize that the dominant blood supply plays a role in the progression of infarction since the blood of high velocities is often going close to the inner side of fenestration where has irregular geometry.

Early in 1974, Erwin O. indicated that high blood viscosity impairs hemodynamic conditions in the cerebral microvasculature, leading to poor collateral circulation ^[27]. A series of studies have reported that the high blood viscosity may contribute to the ischemic stroke, and the blood viscosity and the plasma viscosity were both elevated in the population with stroke or at high risk for stroke ^[28,29,30]. An experimental study using an electromagnetic spinning sphere viscometer found that blood viscosity at the date of admission was significantly higher in the small artery occlusion group than in the control group ^[28]. The blood viscosity as a function of shear rate is dependent on the aggregation of red blood cells in the lumen of small vessels which is closely related to the endothelial remodeling and luminal occlusion. Microscopically, one trunk of the fenestrated segment was composed of a large muscular layer without elastic fibers and the other one was composed of a less developed muscular layer with an irregular and sparse aspect of elastic fibers ^[31]. In this study, the time-averaged viscosity distributions results suggested that concentrated viscosity regions were located around the fenestration, artery with larger curvatures, and the basilar bifurcation region. Morphologically, the basilar junction is subjected to the greatest stresses of flow and turbulence from the bilateral vertebral artery below ^[32]. Besides, a high viscosity concentrated region was located on the basilar bifurcation close to the superior cerebellar arteries in the infarction patients. This high concentration region was in conformity with the flow condition, i.e. the flow in superior cerebellar arteries was less and more disturbed. Moreover, the diameter of the superior cerebellar artery is significantly narrower than inferior cerebellar arteries, resulting in higher risks for arterial occlusion. The quantitative data analysis of wall mechanics and viscosity showed that the top region was distributed with lower TAWSS, higher OSI and viscosity values and area in the infarction group. This result suggests that the top region might be a hatchery of thrombosis components where often suffers the jet flow. It imposes the impact force there thus dissociating the thrombus to flow with blood to downstream branches, leading to cerebral infarction consequently.

This study has a few limitations. First, the number of enrolled patients is small and a further study with a larger dataset of the same inclusion criterion needs to be conducted to verify the conclusion in this study. Secondly, the spatial quantification of significant hemodynamic parameters is relatively weak. However, our results provide the rationale for future prospective observational studies that might confirm the cause-effect relationship. Thirdly, the rigid wall was employed in the hemodynamic simulation, the compliant property of the arterial wall could affect the hemodynamic parameters and the risk factors of cerebral infarction in patients with intracranial arterial fenestrations. In our next study, the comparison of different wall properties would be conducted and determined whether the compliant property could be neglected.

5.   Conclusions

In summary, we investigated the hemodynamics of VBA fenestrations in the cerebral infarction group and control group with the non-Newtonian flow model. The qualitative flow division analysis and quantitative flow measurement showed that the flow pattern in the infarction group has specific characteristics, but is not typical in the larger fenestration cases. Interestingly, the high blood viscosity region was larger and concentrated and located basilar bifurcation close to the superior cerebellar arteries for the cerebral infarction cases, which is consistent with the low-velocity and disturbed flow there. These results suggest that computational hemodynamic analysis has the potential to be a useful tool in identifying the risk factors for cerebral infarction, specifically, associated with fenestration structure in this study. Meanwhile, the non-Newtonian flow model is necessitated in the investigation of vascular disease, especially for the cerebral blood vessels.

Acknowledgments

We are grateful for the funding provided by the National Natural Science Foundation of China (82001938, 82171966), the Doctoral Scientific Research Foundation of North Sichuan Medical College (CBY21-QD03), Heilongjiang Applied Technology Research and Development Program (GZ20C01), basic business cost scientific research project of provincial colleges and universities in Heilongjiang Province (2020-KYYWF-0795).

Conflict of interest

All authors declare no conflicts of interest in this paper.