Transmission dynamics of varicella before, during and after the COVID-19 pandemic in Japan: a modelling study

1.   Introduction

In response to the coronavirus disease 2019 (COVID-19) pandemic, which has been globally widespread since early 2020, public health and social measures (PHSMs), including physical distancing measures, the use of personal protective equipment and mobility restrictions, have been implemented to suppress the transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection across the world ^[1]. PHSMs for COVID-19 have also affected the seasonal transmission patterns of endemic infectious diseases, such as influenza and respiratory syncytial virus (RSV) ^[2,3]. These viral infectious diseases favor winter weather conditions; however, the historical lowest epidemic activity was recorded in the 2020/21 winter in many parts of the world ^[4]. Japan has not been an exception. During the 2020/21 winter season, the number of influenza-like illness cases reported per sentinel per week never exceeded 1.0 per week, traditionally used as an indicator of the start of the influenza season ^[5]. In the case of RSV, the epidemic peak was observed in week 37 in 2018 and 2019, and the number of reported RSV cases per week/sentinel was 2.46 and 3.45, respectively, but during the 2020 season, this value was as low as 0.05, meaning the typically evident epidemic pattern was not seen ^[6].

Once the activity of COVID-19 is recognized to be gradually waning, global human mobility and contact behaviors may be restored to levels similar to those during the pre-pandemic period. To attain an objective reopening (or the science-based reopening), it is vital to project potential scenarios in which the adverse impact of reopening is captured. A published modeling study from the United States indicated the possible future outbreak of endemic infections ^[7], including RSV and influenza, following periods under PHSMs, due to the increasing number of susceptible individuals who avoided contracting these infections during the pandemic. A similar quantitative forecast has been made in Japan ^[8], and in fact, an increased number of RSV infections were reported across the country in 2021 ^[9]. Such an increase may not be limited to influenza and RSV, but also a variety of other viral infectious diseases.

Here, we specifically consider varicella (also referred to as chickenpox), a vaccine-preventable disease caused by varicella-zoster virus (VZV). The causative agent, VZV, is a human alphaherpesvirus that causes varicella and herpes zoster. Varicella was a common childhood disease worldwide before the implementation of varicella vaccination programs ^[10]. In the last two decades, one- or two-dose universal varicella vaccination has been implemented in more than 50 countries ^[11], and vaccination programs have reduced the varicella incidence by 81 and 92% for one-dose and two-dose regimens, respectively ^[12]. Published modeling studies have shown that varicella vaccination successfully induced substantial indirect effects and is cost effective, substantially reducing the incidence and elevating the age at infection ^[13–22]. A two-dose routine varicella vaccine regimen for children aged 12–36 months was introduced in 2014 in Japan, and the vaccination coverage has reached approximately 90% (received at least one-dose of varicella vaccine) ^[23]. Although routine immunization programs have successfully reduced the overall varicella incidence over time, we have observed that the annual risk of infection among adolescents has increased ^[24]. In addition to that observation, it is plausible that ceasing PHSMs after the COVID-19 pandemic could fuel future outbreaks of varicella due to the accumulation of susceptible individuals to be infected during the pandemic.

Here we aimed to quantify the transmission dynamics of varicella before, during and after the COVID-19 pandemic in Japan, investigating the impact of restored contact on post-pandemic transmission scenarios. We devised a new but simplistic modeling approach to tackle this issue and estimated infections in three periods, namely, pre-vaccination, pre-pandemic vaccination and during the COVID-19 pandemic. We then projected the epidemiological dynamics of varicella after the pandemic.

2.   Materials and methods

2.1.   Epidemiological data

We analyzed three pieces of information: i) weekly number of notifications of varicella cases; ii) vaccination coverage; and iii) number of newborns. Notification data of varicella were derived from the National Epidemiology Surveillance for Infectious Diseases (NESID) that rests on the Communicable Disease Prevention Law until March 1999 and the Infectious Diseases Control Law thereafter. A case of varicella is defined as a patient presenting with following symptoms: 1) sudden generalized development of serous papules and vesicles and 2) co-existence of rashes in different stages (papules, vesicles, and crusts) ^[25]. Varicella is a disease monitored using a sentinel surveillance program. That is, cases are notified to NESID on a weekly basis from approximately 3000 pediatric sentinel sites, which represent approximately 10% of pediatric medical facilities in Japan.

Routine vaccination since 2014 has been conducted among children aged from 12–36 months. Vaccination coverage was derived from the National Epidemiological Surveillance of Vaccine-Preventable Diseases (NESVPD) ^[26] after 2014. Before the initiation of routine immunization, varicella vaccination coverage was not routinely monitored. Thus we used the vaccination coverage calculated as annual sales of varicella vaccine divided by the number of newborns in the previous year before 2014 ^[27] (Figure A2A). We imposed a simplifying assumption that birth events were evenly distributed over the year and the weekly number of newborns was calculated as the annual number of newborns divided by 52 weeks. To project future varicella dynamics, the annual number of newborns after 2021 was extracted from the Population Projections for Japan (2017) from 2016 to 2065 ^[28] (Figure A2B).

2.2.   Mathematical model

Here we consider the type of susceptible-infectious-recovered model that is dealt with in a discrete timescale and may be regarded as a type of balance equation for the entire population of Japan. To reconstruct the epidemiological dynamics of varicella, we made the following assumptions: i) all susceptible individuals contract varicella during their lifetime; ii) lifelong immunity following natural infection or vaccination (we did not differentiate between one- and two-dose vaccination); and iii) recruitment of susceptible individuals occurs only through births. Under these assumptions, the balance equation can be described as follows:

where t = 1, 2, 3… denotes the calendar week starting from week 1 of 2010 (i.e., pre-vaccination period). ${S}_{t}$, ${v}_{t}$, ${B}_{t}$ and ${I}_{t}$ represent the estimated number of susceptible individuals, vaccination coverage (expressed as a fraction), the number of newborns and the estimated number of new varicella infections in calendar week t, respectively. The weekly number of notifications of varicella cases, was defined as:

where is the parameter that represents biases associated with ascertainment and reporting (i.e., weekly number of notifications $\left({C}_{t}\right)$ divided by estimated number of varicella infections in the total population $\left({I}_{t}\right)$). The calculation using $\delta$ involves an assumption that all children are born as susceptible and become immune once vaccinated or infection, and this estimation procedure was conducted elsewhere ^[24] following an convention of time-series SIR (TSIR) modelling (see Appendix). ${\alpha }_{k}$ (where k = 1, 2 and 3) is the multi-year component of the force of infection during Jan. 2010–Dec. 2014 (k = 1), Jan. 2015–Mar. 2020 (k = 2) and Apr. 2020–Sep. 2021 (k = 3), respectively. Each period represents the pre-vaccination period, pre-pandemic vaccination period and the COVID-19 pandemic period, respectively. Although the routine immunization program was initiated from Oct. 2014, we chose the pre-pandemic vaccination period starting from Jan. 2015 because it took a certain amount of time for spreading the immunization program. is the within-year component of the force of infection at week t. To capture the seasonality of varicella transmission, we decomposed the time series of varicella notification data into a multi-year trend, within-year variation and noise (Figure A3). A clear bimodal seasonal pattern of incidence was seen in Japan, which we modeled by using a trigonometric function. Accordingly, ${\gamma }_{t}$ was described as

where n is the order of the trigonometric function to capture within-year variations and ${a}_{0}$, ${a}_{l}$, ${b}_{l}$ are parameters that govern the trigonometric function. To incorporate the trend in force of infection into the model, we examined the following definitions of ${\gamma }_{t}$ as alternative:

Equations (4) and (5) assume that the trend effect would influence the within-year pattern and was fully independent of within-year variation, respectively, with the coefficient of time, $\beta$.

We examined three types of models: i) model1: a trigonometric function only (using Eqs (1)–(3)); ii) model 2: a trigonometric function with additive linear trend (using Eqs (1), (2) and (4)) and iii) model 3: a trigonometric function with multiplicative linear trend (using Eqs (1), (2) and (5)). By using these equations, we fitted three models to the weekly number of varicella notifications respectively and estimated parameter values $\left(\delta, {{\alpha }_{1}, {\alpha }_{2}, {\alpha }_{3}, a}_{0}{, a}_{l}, {b}_{l}, \beta \right)$ for each model, employing a maximum likelihood method. A gaussian distribution was used to describe the variation in weekly notification rates for the entirety of Japan.

where ${\mu }_{t}$, ${\sigma }_{t}^{2}\; {{\rm{a}}{\rm{n}}{\rm{d}}}\; r_{t}$, refer to the expected number of varicella notifications (i.e., E(C_t)), the associated variance and the number of varicella notifications (i.e., observed number of cases) in week t, respectively. We chose the best model by comparing the Akaike information criterion (AIC) as well as conducting visual inspections. Using the selected model, we reconstructed the epidemiological dynamics in Japan from 2010 to 2021. Further details of the parameter estimation and the model selection process were described in Appendix.

In addition, we projected the future dynamics of varicella up until 2027.We assumed that the force of infection of varicella in 2022 would be the same level as that of the period between Apr. 2020 to 2021, because COVID-19 infection continues to spread as of early 2022 in Japan. We investigated five scenarios for the future force of infection from 2023 onwards: i) pre-pandemic level; ii) 25% increase from pre-pandemic level; iii) 50% increase from pre-pandemic level; iv) 25% decrease from pre-pandemic level and v) 50% decrease from pre-pandemic level. Scenario i) represents the full restoration of epidemic activity to pre-pandemic levels after COVID-19. Because our modelling approach does not capture non-linear dynamic increases nor international human migrations, scenarios ii) and iii) were investigated as the possible alternative scenarios following the recovery of contact. Moreover, scenarios iv) and v) were considered, assuming the possibility of continued inhibition of social activities during the waning stages of the COVID-19 pandemic (e.g., voluntary restriction of contact in new normal life). We calculated the mean number of years to varicella infection among susceptibles as the inverse of the force of infection. To adjust the change in number of susceptibles over time, we also calculated the mean number of years to varicella infection as the inverse of the force of infection multiplied by the ratio of the number of susceptibles to that of the beginning of 2010 $\left({S}_{0}\right)$. All analyses were performed with R software (version 4.0.2).

2.3.   Ethical considerations

This study used publicly available information. The analysis of publicly available data without private information did not require ethical approval.

3.   Results

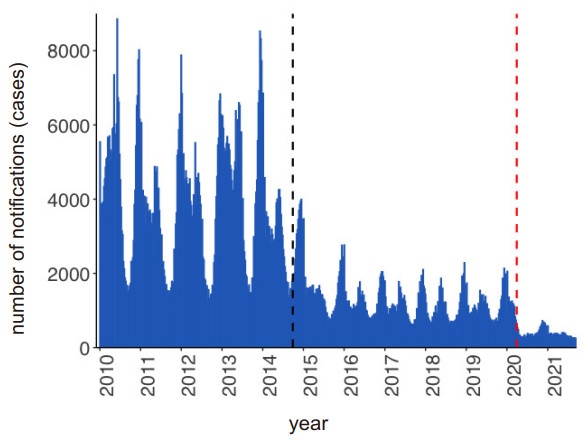
Figure 1 shows the epidemic curve for the weekly number of notifications of varicella from Jan. 2010 to Sep. 2021. The epidemic curve shows a bimodal yearly pattern that yields a bigger peak in the winter and another peak in the spring. The incidence remains small during the summer. This seasonal pattern might reflect not only the seasonal preference of the virus but also contact activities among school children with long vacations during spring and summer seasons in Japan. Following the start of a routine varicella immunization program from Oct. 2014, the varicella incidence swiftly started to decline; subsequently, continued transmission of VZV at similar levels was observed from 2016 to spring 2020. However, varicella incidence declined drastically after the declaration of the state of emergency in light of the COVID-19 pandemic in Apr. 2020.

Figure 1.  Weekly number of notifications of varicella cases to NESID from sentinel sites in Japan, 2010–2021. Black dashed line indicates the initiation of the national varicella immunization program (Oct. 2014) while the red dashed line indicates the first state of emergency in Japan (Apr. 2020). Ticks on the x-axis indicate the first week of each year. Numbers on the vertical axis represent the absolute number of notifications from sentinel medical facilities.

DownLoad: Full-Size Img PowerPoint

To compare model uncertainties associated with the within-year component of the force of infection (${\gamma _t}$), we first examined the first order trigonometric function; however, the first order trigonometric function was insufficient for describing the bimodal yearly pattern. We then employed second and third order trigonometric functions; the third order trigonometric function barely improved model fit as measured using the AIC. Consequently, we chose the second order trigonometric function for models 1–3. Secondary, we examined three models (models 1–3) to choose the best fit model by comparing AIC as well as conducting the visual inspection. (Table A1 and FigureA1). Model 1 yielded the smallest AIC and fitted best to the observational data. Therefore, we adopted model 1 as the best-fit model for our analysis. Figure 2 shows ${\alpha }_{1}, {\alpha }_{2}$ and ${\alpha }_{3}$ (multi-year component of the force of infection) for Jan. 2010–Dec. 2014 (pre-vaccination), Jan. 2015–Mar. 2020 (pre-pandemic vaccination period) and Apr. 2020–Sep. 2021 (during the COVID-19 pandemic), respectively. The parameter values and its 95% CI for ${\alpha }_{1}, {\alpha }_{2}$ and ${\alpha }_{3}$ were $6.37\times {10}^{-2}\left(95{\rm{\%}}{\rm{ }}{\rm{ }}{\rm{ }}{\rm{ }}{\rm{ }}{\rm{ }}{\rm{C}}{\rm{I}}:5.71\times {10}^{-2}, 7.04\times {10}^{-2}\right)$, $2.40\times {10}^{-2}\left(95{\rm{\%}}{\rm{ }}{\rm{C}}{\rm{I}}:2.15\times {10}^{-2}, 2.65\times {10}^{-2}\right)$ and $7.95\times {10}^{-3}\left(95{\rm{\%}}{\rm{ }}{\rm{C}}{\rm{I}}:7.04\times {10}^{-3}, 8.86\times {10}^{-3}\right)$, respectively. Ratio ${\rm{o}}{\rm{f}}{\alpha }_{2}$ to ${\alpha }_{1}$ and of ${\alpha }_{3}$ to ${\alpha }_{1}$ were 0.38 and 0.12, respectively.

Figure 2.  Multi-year component of the force of infection over time. Black vertical lines and black shaded areas show the parameter values for multi-year component of the force of infection and their 95% confidence intervals (CIs). * Jan. 2010–Dec 2014 (pre-vaccination), ** Jan. 2015–Mar. 2020 (pre-pandemic vaccination), *** Apr. 2020–Sep. 2021 (during the COVID-19 pandemic).

DownLoad: Full-Size Img PowerPoint

Comparison of the number of varicella notifications to NESID and estimated number of notifications using model 1 are shown in Figure 3. Our model successfully captured the bimodal seasonal pattern, as well as the long-term temporal dynamics covering three distinct periods: Jan. 2010–Dec. 2014, Jan. 2015–Mar. 2020 and Apr. 2020–Sep. 2021.

Figure 3.  Comparison of observed and estimated number of notifications. Black dots indicate the weekly number of notifications while the blue line shows the estimated number of notifications (cases). The blue shaded area represents the 95% confidence interval (CI) for the fitted line.

DownLoad: Full-Size Img PowerPoint

Figure 4A shows the susceptible dynamics from 2010 to 2027, assuming the force of infection after 2023 is restored to pre-pandemic levels. Similarly, Figure 4B shows varicella dynamics under identical assumptions. The number of susceptible individuals has continued to decline since 2010; however, the decline was slowed during the pandemic. In the post-pandemic period, the number of susceptible individuals was continued to start smoothly declining again. The varicella incidence dropped drastically during the pandemic, and the incidence will reach a similar level to that of the pre-pandemic period.

Figure 4.  Temporal varicella dynamics in Japan, 2010–2027. A. Estimated number of susceptibles (1,000). = 8,224,245. B. Estimated weekly number of notifications. Black shaded area shows the 95% confidence intervals (CIs). * Jan. 2010–Mar. 2020 (before COVID-19 pandemic), ** Apr. 2020–Dec. 2022 (during COVID-19 pandemic), *** Jan. 2023–Dec. 2027 (post COVID-19 pandemic).

DownLoad: Full-Size Img PowerPoint

Figure 5A shows the predicted number of varicella notifications from 2022 to 2027 under five scenarios for the future force of infection after 2023: i) pre-pandemic level, ii) 25% increase from pre-pandemic level, iii) 50% increase from pre-pandemic level, iv) 25% decrease from pre-pandemic level, and v) 50% decrease from pre-pandemic level. Even if the force of infection increases by 50% from the pre-pandemic level, a major outbreak may not be observed by 2027; the highest number of weekly notifications will remain around 2000 cases. Figure 5B shows the mean number of years to varicella infection, simply the inverse of the force of infection, from 2010 to 2027. After initiation of the universal varicella vaccination, the mean number of years to varicella infection substantially increased, and that increase became more prominent during the pandemic. Because the pandemic has lasted only for 2 years by the present day, the actual elevation in the age at infection is not seen, and rather, the incidence abruptly decreased. After the pandemic, the mean number of years to varicella infection is expected to return to a similar level to that in the pre-pandemic period.

Figure 5.  Predicted number of notifications from 2022–2027 and the mean number of years to varicella infection. A. The solid line indicates the estimated number of notifications (cases) when the force of infection is at a similar level to that in the pre-pandemic period. Dashed and dotted lines show the estimated number of reported cases, if the force of infection has a 25% increase, 50% increase, 25% decrease and 50% decrease from the pre-pandemic level. B. The solid line indicates the mean number of years to varicella infection ($1/{\alpha }_{k}{\gamma }_{t}$). The dotted line indicates the mean number of years to varicella infection adjusted by the change in the number of susceptible individuals over time $\left(\left(1/{\alpha }_{k}{\gamma }_{t}\right){\rm{*}}\left({S}_{t}/{S}_{0}\right)\right)$.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

The present study explored the impact of PHSMs for COVID-19 on the post-pandemic dynamics of varicella in Japan. Epidemiological data have indicated that there was a drastic decline in varicella incidence during the COVID-19 pandemic similar to that observed in other respiratory infections, such as influenza and RSV. First, we estimated the within-year and multi-year component of the force of infection and the parameters associated with reporting and ascertainment in three periods, pre-vaccination (Jan. 2010–Dec. 2014), pre-pandemic vaccination (Jan. 2015–Mar. 2020) and during the COVID-19 pandemic (Apr. 2020–Sep. 2021), using a trigonometric function. Second, by using estimated parameter values, we reconstructed and calculated the varicella dynamics in Japan from 2010 to the present day. Third, the models were extended to project post-pandemic scenarios, and our analysis indicated that the increase in varicella incidence would be relatively small in the post-pandemic era and a large varicella outbreak may not occur easily, mainly due to the steady decline in the number of susceptible individuals as a result of the vaccination program.

One important point that should be noted from our study is that there has been a major impact of universal immunization on varicella dynamics. Despite the disruption of seasonal patterns of varicella infection during the COVID-19 pandemic, the change in susceptible dynamics was relatively small during the corresponding period. The accumulation of susceptible individuals during the pandemic that was expected for endemic respiratory infections, such as influenza and RSV, was not observed in the case of varicella in Japan. Our analysis projects that the number of susceptible individuals will continue to decrease gradually in the post-pandemic period.

In our previous study, we reported that the initiation of the routine immunization left a substantial number of unvaccinated individuals who were born in pre-vaccination era susceptible during their adolescence, suggesting the possibility of future varicella outbreaks among middle and high school children ^[24]. Although our results showed the impact of PHSMs for COVID-19 on varicella dynamics was relatively small, careful monitoring of surveillance data, as well as seroepidemiological data, would be required to take necessary countermeasures, such as supplementary vaccination for adolescents.

Three limitations for the present study should be discussed. First, our study did not consider the age-specific force of infection. Varicella has mainly been a childhood infectious disease, and at least in the present day, most reported cases were in children younger than 15 years old. Since the current study evaluated the population level impact of PHSMs on varicella dynamics, we have assumed a uniform force of infection across all age groups. Second, we did not explore the causes or mechanisms of the seasonal pattern of varicella, even though our model successfully captured the bimodal within-year pattern. A published study investigated the seasonal pattern of measles in England and Wales revealed that the regular bimodal pattern corresponded to the cycle of primary school openings ^[28]. The major and minor bimodal epidemic cycle of varicella in Japan is also close to the cycle of school opening after the summer and spring vacation. To confirm the reasons for the seasonal pattern of varicella infection, we need additional data analysis of human mobility patterns. Last, we did not consider the effects of human mobility across countries. Global travel is likely to be accelerated during the post-pandemic period, and the epidemiological dynamics of endemic infectious diseases, such as varicella, may be affected by imported cases from abroad. This is an important topic that we need to investigate in future works, although it is out of the scope of the present study.

5.   Conclusions

The present study quantitatively examined the impact of PHSMs for COVID-19 on the epidemiological dynamics of varicella in Japan. Immunization with the universal varicella vaccination was shown to be sufficient to avoid an increase in the number of susceptible individuals during the pandemic, and varicella incidence during the post-pandemic period might remain at most similar to the level before the pandemic. Although the risk of a devastating varicella epidemic may not be high, there are still uncertainties, including age-dependent susceptibility and imported cases from abroad, that were not taken into account in the present study. Careful monitoring of cases would be vital to swiftly take necessary countermeasures to prevent future outbreaks.

Acknowledgments

This study was supported by funding from Health and Labor Sciences Research Grants (19HB1001, 19HA1003, 20CA2024, 20HA2007, and 21HB1002 to H.N.), the Japan Agency for Medical Research and Development JP20fk0108140 and JP21fk0108612 to H.N.), the Japan Society for the Promotion of Science KAKENHI (A.S: 19K24159, H.N: 17H04701 and 21H03198), the Inamori Foundation, the GAP Fund Program of Kyoto University, the Japan Science and Technology Agency CREST program (JPMJCR1413 to H.N.), and the SICORP program (JPMJSC20U3 and JPMJSC2105 to H.N.). The funders played no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. We thank John Holmes, MSc, from Edanz (https://jp.edanz.com/ac) for editing a draft of this manuscript.

Conflict of interest

The authors declare no conflicts of interest.

Appendix

To estimate the initial condition (the number of susceptibles in the first week of 2010), we used the weekly number of notifications of varicella cases from 1990 to 2009. The vaccination rate was relatively low, around 20–35%, from 1990–2009, (Figure A1), and we assumed that the force of infection remained the same level during this period. We also assumed that the proportion of the susceptible is 10% of the total population in Japan in 1990 $\left({\rm{12,361}}\times {10}^{4}\right)$. We set the initial value of $\delta$ as 0.2 that derived from the previous estimation by using linear regression analysis of the yearly number of newborns and cumulative number of varicella notifications in corresponding birth cohort ^[24]. First, we estimated the number of susceptibles in the first week of 2010 $\left({S}_{0}\right)$ for three models (model1, model2 and model3) by fitting each model to the number of notifications of varicella from 1990 to 2009, employing a maximum likelihood method. Second, we estimated the parameter values ($\delta, {{\alpha }_{1}, {\alpha }_{2}, {\alpha }_{3}, a}_{0}{, a}_{l}, {b}_{l}, \beta)$ during Jan 2010 to Sep 2021 by using the same method as the first step. We calculated the Akaike information criterion (AIC) for each model (Table A1). We also conducted the visual inspection of the comparison of the estimated number of varicella notifications and the observed number of varicella notifications. Finally, we chose the model 1 as the best model, because the model 1 yielded the smallest AIC and the visual inspection showed the best fit to the model 1. All parameter values we estimated for model 1 were presented in Table A2.

Table A1.  Akaike information criteria (AIC) for model 1, model 2 and model 3.

Model assumption	AIC
Model 1 (Second order trigonometric function)	2390
Model 2 (Second order trigonometric function with additive linear trend)	2577
Model 3 (Second order trigonometric function with multiplicative linear trend)	2792

---

 | Show Table

DownLoad: CSV

Table A2.  All parameter values estimated for model 1.

Parameter values for model 1 (95% CI)
$\delta$	${\alpha }_{1}$	${\alpha }_{2}$	${\alpha }_{3}$	${a}_{0}$	${a}_{1}$	${a}_{2}$	${b}_{1}$	${b}_{2}$
$2.31\times {10}^{-1}$ $\left(2.29\times {10}^{-1}, 2.33\times {10}^{-1}\right)$	$6.37\times {10}^{-2}$ $\left(5.71\times {10}^{-2}, 7.04\times {10}^{-2}\right)$	$2.40\times {10}^{-2}$ $\left(2.15\times {10}^{-2}, 2.65\times {10}^{-2}\right)$	$7.95\times {10}^{-3}$ $\left(7.04\times {10}^{-3}, 8.86\times {10}^{-3}\right)$	$7.31\times {10}^{-2}$ $\left(6.54\times {10}^{-2}, 8.08\times {10}^{-2}\right)$	$1.10\times {10}^{-2}$ $\left(1.00\times {10}^{-2}, 1.22\times {10}^{-2}\right)$	$-6.83\times {10}^{-3}$ $\left(-7.56\times {10}^{-3}, -6.11\times {10}^{-3}\right)$	$6.31\times {10}^{-3}$ $\left(5.64\times {10}^{-3}, 6.98\times {10}^{-3}\right)$	$1.14\times {10}^{-2}$ $\left(1.02\times {10}^{-2}, 1.26\times {10}^{-2}\right)$

---

 | Show Table

DownLoad: CSV

Figure A1.  Comparison of observed and estimated number of notifications for A. model 1, B. model 2 and C. model 3.

DownLoad: Full-Size Img PowerPoint

Figure A2.  A. Estimated varicella vaccination coverage in Japan, 1990–2021. The solid line shows estimated varicella vaccination coverage and dotted horizontal lines show the 5–year average used for data analysis. B. Number of newborns in Japan, 1990–2027. The solid line shows the number of newborns from 1990 to 2020. The dotted line shows the estimated number of newborns from 2021 to 2027 extracted from the Population Projections for Japan (2017) from 2016 to 2065 ^[28].

DownLoad: Full-Size Img PowerPoint

Figure A3.  Decomposition of additive time series of varicella incidence. Decomposed time series as a combination of level trend, seasonal and random components.

DownLoad: Full-Size Img PowerPoint