Solving reduced biquaternion matrices equation $\sum\limits_{i = 1}^{k}A_iXB_i = C$ with special structure based on semi-tensor product of matrices

1.   Introduction

Throughout this paper, the following notations are used. $\mathbb{R},$ $\mathbb{RB}_Q$ represent the set of real number and reduced biquaternion, respctively. $\mathbb{R}^{t}$$(\mathbb{R}_t)$ represent the set of all real column(row) vectors with order $t$. $\mathbb{R}^{m\times n}$, $\mathbb{RB}_Q^{m\times n}$ represent the set of all $m\times n$ real matrices, reduced biquaternion matrices, respectively. $\mathbb{RB}_{HQ}^{n\times n}$, $\mathbb{RB}_{AQ}^{n\times n}$ represent the set of all $n\times n$ Hermitian reduced biquaternion matrices and Anti-Hermitian reduced biquaternion matrices, respectively. $I_k$ represents the unit matrix with order $k$, $\delta_k^i$ represents the $i$th column of unit matrix $I_k$. $\delta_k[i_1, \ \cdots, \ i_s]$ is a abbreviation of $[\delta_k^{i_1}, \ \cdots, \ \delta_k^{i_s}]$. $A = A_1+A_2{{\bf i}}+A_3{{\bf j}}+A_4{{\bf k}}\in\mathbb{RB}_Q^{m\times n}$, where $A_i\in\mathbb{R}^{m\times n}, \ (i = 1:4)$ and define $\overline{A} = A_1-A_2{{\bf i}}-A_3{{\bf j}}-A_4{{\bf k}}$ to be conjugate of $A$. $A^T, \ A^H, \ A^\dagger$ represent the transpose, conjugate transpose, Moore-Penrose$(MP)$ inverse of matrix $A$. $\otimes$ represents the Kronecker product of matrices. $\ltimes$ represents the semi-tensor product of matrices. $\left \|\cdot\right \|$ represents the Frobenius norm of a matrix or Euclidean norm of a vector.

The concept of quaternion was proposed by Hamilton in 1843, which is an extension of complex number. It consists of four parts, i.e.

where $a_r, \ a_i, \ a_j, \ a_k$ are real numbers and ${{\bf i}}, \ {{\bf j}}, \ {{\bf k}}$ satisfy

As can be seen from the product rule above, quaternion is not commutative with respect to multiplication. Owing to this reason, quaternion becomes more complicated in some operations, and it will have great trouble in application to practical problems. This also promotes the generation of reduced biquaternion to some extent. Reduced biquaternion is similar to quaternion in form, but it has a different product rule.

Definition of reduced biquaternion [1]

where $a_r, \ a_i, \ a_j, \ a_k$ are real numbers and

$e_1 = \frac{1+j}{2}$, $e_2 = \frac{1-j}{2}$ are two special numbers in reduced biquaternion. Obviously,

Therefore, $e_1$ and $e_2$ are both idempotent elements and divisors of zero. Any reduced biquaternion with the form $k_1e_1$ or $k_2e_2$ is also a divisor of zero and does not have a multiplicative inverse, where, $k_1, \ k_2$ are arbitrary complex numbers. By means of $e_1$ and $e_2$, we can uniquely express the reduced biquaternion $a = a_r+a_i{{\bf i}}+a_j{{\bf j}}+a_k{{\bf k}}$ as $a = a_1e_1+a_2e_2$, where $a_1 = (a_r+a_j)+(a_i+a_k){{\bf i}}$, $a_2 = (a_r-a_j)+(a_i-a_k){{\bf i}}$.

The conjugate of a reduced biquaternion $a$ is denoted by $\overline{a}$ and $\overline{a} = a_r-a_i{{\bf i}}-a_j{{\bf j}}-a_k{{\bf k}}$. The norm of a reduced biquaternion $a$ is

Then, the Frobenius norm of $A\in\mathbb{RB}_Q^{m\times n}$ is defined as follows

The concept of reduced biquaternion was first defined by Sch$\ddot{u}$tte and Wenzel in 1990 [2]. It can be seen that the product of reduced biquaternions has commutability compared with quaternion. Thus, many operations of reduced biquaternion are simpler than those of quaternion. Such as, the implementations of the discrete reduced biquaternion Fourier transform, convolution, correlation. Therefore, it is of importance to study the theoretical knowledge and numerical calculation of reduced biquaternions. Many good results on reduced biquaternions have obtained. For example, Pei et al. investigated digital signal and image processing using reduced biquaternion in 2004 [1] and gave the algorithms for calculating the eigenvalues, the eigenvectors, and the singular value decomposition of a reduced biquaternion matrix in 2008 [3]; Isokawa et al. studied two types of multistate Hopfield neural networks using reduced biquaternion in 2010 [4]. At the same time, scholars also focused on the solution of specific reduced biquaternion matrix equations because matrix equations have a wide range of applications in control theory, stability and other fields. Hidayet derived the expressions of the minimal norm least squares solution for the reduced biquaternion matrix equation $AX = B$ using the $e_1-e_2$ form in 2019 [5]; Yuan studied the Hermitian solutions of the reduced biquaternion matrix equation $\left(AXB, CXD\right) = \left(E, F\right)$ using complex representation [6].

In this paper, we study the least squares problems of the reduced biquaternion matrix equation

Since Hermitian and Anti-Hermitian matrices are very useful in engineering problems and linear system theory. So many researchers turn on the problems of (Anti)-Hermitian matrix equations, for example, [7,8] derived explicit determinantal representation formulas of the general, Hermitian, and Anti-Hermitian solutions to the system of two-sided quaternion matrix equations $A_1XA_1^{*} = C_1$ and $A_2XA_2^{*} = C_2$ in 2018 and the Sylvester type matrix equation $AXA^*+BYB^* = C$ in 2019 using determinantal representations of Moore-Penrose inverse, respectively. [9] proposed a recursive algorithm for calculating the inversion of the confluent Vandermonde matrix that with consecutive powers devoted just to the Hermite type interpolation and derived an explicit analytic formula for the calculation of the inverse of the confluent Vandermonde matrix in 2013. [10] considered the quaternion matrix equation $X-A\widehat{X}B = C$ and studied its minimal norm least squares solution, $j$-self-conjugate least squares solution and anti-$j$-self-conjugate least squares solution by means of real representation matrices of quaternion matrix in 2020.

We determine our research objective as the least squares Hermitian solution and the least squares Anti-Hermitian solution as follows:

Problem 1. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{p\times q}$, $C\in \mathbb{RB}_Q^{m\times q}$, and

Find out $X_Q\in S_Q$ such that

Problem 2. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{n\times q}$, $C\in \mathbb{RB}_Q^{m\times q}$, and

Find out $X_{HQ}\in S_{HQ}$ such that

Problem 3. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{n\times q}$, $C\in \mathbb{RB}_Q^{m\times q}$, and

Find out $X_{AQ}\in S_{AQ}$ such that

The semi-tensor product(STP) of matrices was proposed initially by Cheng to solve linearization problem of nonlinear systems, which is a generalization of traditional matrix product for the case when the two factor matrices do not meet the dimension matching condition. It has been proved to be a power tool in many fields such as game theory [11], graph coloring [12], logic systems [13] and so on. In this paper, we will convert the least squares problem of reduced biquaternion matrix equation to the corresponding real problems by using the semi-tensor product of matrices.

This paper is organized as follows. In Section 2, some basic knowledge of semi-tensor product of matrices is introduced. In Section 3, a new kind of real vector representation of a reduced biquaternion matrix and the main properties are proposed. In Section 4, the solutions of Problems 1–3 are studied by using the real vector representation of reduced biquaternion matrix, the special structure of solutions and semi-tensor product of matrices. In Section 5, two examples are illustrated to demonstrate the Algorithms. Finally the present thesis is summarized.

2.   Semi-tensor product of matrices(STP)

In this section, we will recall some basic knowledge of semi-tensor product of matrices. Please refer to [14,15] for more details.

Definition 2.1. Let $A\in \mathbb{R}^{m\times n}, \ B\in \mathbb{R}^{p\times q}$, the semi-tensor product of $A$ and $B$, denoted by

where $t = lcm(n, p)$ is the least common multiple of $n$ and $p$. If $n = p,$ the semi-tensor product reduces to the traditional matrix product.

Next, a simple numerical example is used to explain the semi-tensor product of matrices.

Example 2.1. Suppose $A = \left[\begin{matrix}2 & -2 & -1 & 1\\1 & 0 & 3 & -3\\-2 & -3 & 2 & 1\end{matrix}\right]$, $B = \left[\begin{matrix}1 & 2\\-2 & -1\end{matrix}\right]$, then

Lemma 2.1. Assume that $A, \ B, \ C$ are real matrices with appropriate sizes, $a, \ b\in\mathbb{R}$.

(1) (Distributive law) $A\ltimes (aB\pm bC) = aA\ltimes B\pm bA\ltimes C,$ $(aA\pm bB)\ltimes C = aA\ltimes C\pm bB\ltimes C.$

(2) (Associative law)$(A\ltimes B)\ltimes C = A\ltimes (B\ltimes C).$

(3) (Transpose)$(A\ltimes B)^T = B^T\ltimes A^T.$

(4) (Inverse)$(A\ltimes B)^{-1} = B^{-1}\ltimes A^{-1}$, where $A$ and $B$ are invertible square matrices.

(5) Assume that $x\in \mathbb{R}^m, \ y\in \mathbb{R}^n$, then $x\ltimes y = x\otimes y.$

It can be seen from the Definition 2.1 that semi-tensor product of matrices is a generalization of traditional matrix product. A large part of the properties of traditional matrix product are preserved by semi-tensor product of matrices. Here, only (3) of Lemma 2.1 is simply proved and the other properties of Lemma 2.1 are similarly proved.

Proof. Suppose $A\in\mathbb{R}^{m\times n}$, $B\in\mathbb{R}^{p\times q}$, $t = lcm(n, p)$, we can obtain

The semi-tensor product of a matrix and a vector has the following property of quasi-commutativity.

Definition 2.2. A swap matrix $W_{[m, n]}$ is a $mn\times mn$ matrix, which is defined as

We use the following example to briefly illustrate the construction of swap matrix.

Example 2.2. Suppose $m = 2, \ n = 3$, then

Remark 2.1. When $m = n$, we denote $W_{[m, n]} = W_{[n]}$.

The function of a swap matrix is to exchange the order of two vectors in vector multiplication.

Lemma 2.2. Let $x\in \mathbb{R}^m$ and $y\in \mathbb{R}^n$ be two column vectors. Then $W_{[m, n]}\ltimes x\ltimes y = y\ltimes x$.

Example 2.3. Suppose $x = \left[\begin{matrix}x_1\\x_2\end{matrix}\right]$, $y = \left[\begin{matrix}y_1\\y_2\\y_3\end{matrix}\right]$. Using the swap matrix constructed in Example 2.2, we can obtain

Lemma 2.3. Assume $A\in\mathbb{R}^{m\times n}$ is given, $x\in \mathbb{R}^t$, $\omega\in \mathbb{R}_t$. Then

Proof. Suppose $x = \left[\begin{matrix}x_1, x_2, \ldots, x_t\end{matrix}\right]^T\in\mathbb{R}^t$, $A = \left[\begin{matrix}a_{11} & \ldots&a_{1n}\\ \vdots & & \vdots\\a_{m1} & \ldots&a_{mn}\end{matrix}\right]\in\mathbb{R}^{m\times n}$, thus

When $\omega$ is a row vector, we use the transpose property of the semi-tensor product of matrices to derive the transformation.

Definition 2.3. Let $W_i \ (i = 0, 1, \cdots, n)$ be vector spaces. The mapping $F: \Pi_{i = 1}^n W_i\rightarrow W_0$ is called a multilinear mapping, if for any $1 \leq i\leq n, \ \alpha, \ \beta\in\mathbb{R},$

in which $x_i\in W_i, 1\leq i\leq n, y_i\in W_i.$ If $dim(W_i) = k_i, \ (i = 0, 1, \cdots, \ n),$ and $(\delta_{k_i}^1, \ \delta_{k_i}^2, \ \cdots, \ \delta_{k_i}^{k_i})$ is the basis of $W_i$. Denote

in which $j_t = 1, \ \cdots, \ k_t, \ t = 1, \ \cdots, \ n.$ Then

are called structure constants of $F.$ Arranging these structure constants in the following form

$M_F$ is called the structure matrix of $F$.

3.   A new kind of real vector representation of a reduced biquaternion matrix and its properties

In this section, we will propose the concept of real vector representation of a reduced biquaternion matrix and study its properties.

Definition 3.1. Let $x = x_1+x_2{{\bf i}}+x_3{{\bf j}}+x_4{{\bf k}}\in \mathbb{RB}_Q$, denote $v^R(x) = \left[x_1, x_2, x_3, x_4\right]^T$, $v^R(x)$ is called as the real vector representation of $x$.

Theorem 3.1. Let $x, y\in\mathbb{RB}_Q$, then

where

$M_Q$ is the structure matrix of multiplication of reduced biquaternions.

Proof. Suppose $x = x_1+x_2{{\bf i}}+x_3{{\bf j}}+x_4{{\bf k}}$, $y = y_1+y_2{{\bf i}}+y_3{{\bf j}}+y_4{{\bf k}}$, we can obtain

thus the left hand side of (3.1) is

Since the right hand side of (3.1) is

(3.1) can be obtained.

Combined the real vector representation of a reduced biquaternion with vec operator of a real matrix, we propose a new kind of real vector representation of a reduced biquaternion matrix. For this purpose, we first propose the real vector representation of a reduced biquaternion vector as follows.

Definition 3.2. Let $x = \left[x^{1}, \cdots, x^{n}\right], \ y = \left[y^{1}, \cdots, y^{n}\right]^T$ be reduced biquaternion vectors. Denote

$v^R(x)$ and $v^R(y)$ are called as the real vector representation of reduced biquaternion vectors $x$ and $y$.

Now we define the concepts of the real vector representation of a reduced biquaternion matrix $A$.

Definition 3.3. For $A = (A^{ed})\in \mathbb{RB}_Q^{m\times n}, \ e = 1, \cdots, m, \ d = 1, \cdots, n$, denote

$v^R_c(A)$ and $v^R_r(A)$ are called the real column stacking form and the real row stacking form of $A$, respectively. Real column stacking form and real row stacking form of $A$ are collectively called real vector representation of $A$.

We can prove that this real vector representation has the following properties with respect to vector or matrix operations.

Theorem 3.2. Let $x = \left[x^{1}, x^{2}, \cdots, x^{n}\right], \ \check{x} = \left[\check{x}^{1}, \check{x}^{2}, \cdots, \check{x}^{n}\right], \ y = \left[y^{1}, y^{2}, \cdots, y^{n}\right]^T, \ a\in \mathbb{R}, \ x^i, \ \check{x}^i, \ y^i\in\mathbb{RB}_Q$, then

Proof. By simply computing, we know (1), (2) hold. We only give a detailed proof of (3). Using Theorem 3.1, we have

By using Theorem 3.2, we can drive the following results on the real vector representation of multiplication of two reduced biquaternion matrices.

Theorem 3.3. Let $A, \ \check{A} \in \mathbb{RB}_Q^{m \times n}, \ B\in \mathbb{RB}_Q^{n \times p}, \ {\alpha} \in \mathbb{R}$, then

in which

and $F = M_Q\ltimes \sum^n\limits_{i = 1}(\delta_n^i)^T\ltimes \left(I_{4n}\otimes(\delta_n^i)^T\right).$

Proof. We still only prove the first equality in (3). We block $A$ and $B$ with its rows or columns as follows

Then we have

The second equality can be proved similarly.

4.   Algebraic solutions of Problems 1–3

In this section, we study Problems 1–3. By means of the real vector representation of reduced biquaternion matrix and STP, we first convert Problems 1–3 into the corresponding real least squares problems. And then we obtain their solutions.

Lemma 4.1. [16]The matrix equation $Ax = b$, with $A\in\mathbb{R}^{m\times n}$ and $b\in\mathbb{R}^m$, has a solution $x\in \mathbb{R}^n$ if and only if

In that case it has the general solution

where $y\in \mathbb{R}^n$ is an arbitrary vector. The minimal norm solution of the linear system of equations $Ax = b$ is $A^{\dagger}b$

Theorem 4.2. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{p\times q}$, $C\in \mathbb{RB}_Q^{m\times q}$, denote

where $G_1$ has the same structure as $G$ in Theorem 3.3 excepting the dimension. Hence the set $S_Q$ of Problem 1 is represented as

And then, the minimal norm solution $X_Q$ of Problem 1 satisfies

Proof.

For the real matrix equation

by Lemma 4.1, its solutions can be represented as

Thus we get the formula in (4.1).

Notice

According to the previous proof of this theorem, we have that the minimal norm solution $X_Q\in S_Q$ of Problem 1 satisfies

Therefore, (4.2) holds.

By Theorem 4.2, we can get the sufficient and necessary condition of compatibility of the reduced biquaternion matrix equation $\sum\limits_{i = 1}^n A_iXB_i = C$ and the expression of the solution when $\sum\limits_{i = 1}^n A_iXB_i = C$ is compatible.

Corollary 4.3. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{p\times q}$, $C\in\mathbb{RB}_Q^{m\times q}$, $M$ is given in Theorem 4.2. Then the following statements are equivalent:

(a) Problem 1 has a solution $X\in S_Q$;

(b) $(MM^\dagger-I_{4mq})v_r^R(C) = 0$.

Moreover, if (b) holds, the solution set of (1.1) over $\mathbb{RB}_Q^{n\times p}$ can be represented as

Proof.

In order to study Problem 2, we define $v_s^R(X)$ and give the relation of $v_s^R(X)$ and $v_c^R(X)$ for an Hermitian matrix.

Theorem 4.4. Let $X = \left[\begin{matrix}x_{11} & \cdots&x_{1n}\\\vdots & \vdots & \vdots\\x_{n1} & \cdots&x_{nn}\end{matrix}\right]\in \mathbb{RB}_{HQ}^{n\times n}$, $x_{ij} = x_{ij}^1+x_{ij}^2{{\bf i}}+x_{ij}^3{{\bf j}}+x_{ij}^4{{\bf k}}\in\mathbb{RB}_Q$, denote

where, $\gamma = \frac{(m-1)(8n+2-4m)}{2}$, $\eta = 4(r-m-1)$, $\lambda = \frac{(r-1)(8n+2-4r)}{2}$, $\theta = 4(m-r-1)$. Then

Remark 4.1. It can be seen from the structural characteristics of matrix $X$ that only part of the elements in matrix $X$ can be used to represent the whole matrix $X$. So we need to find all the non-zero and non-repeating elements in $X$, which reduces the number of elements in $v^R_c(X)$. $J$ is a correspondence between the real vector representation of the matrix $X$ and the real vector representation of the independent elements of the matrix $X$.

Theorem 4.5. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{n\times q}$, $C\in \mathbb{RB}_Q^{m\times q}$, denote

where $G_3$, $G_4$ have the same structure as $G$ in Theorem 3.3 excepting the dimension. Hence the set $S_{HQ}$ of Problem 2 is represented as

And then, the minimal norm solution $X_{HQ}$ of Problem 2 satisfies

Proof.

Using Theorem 4.4, we can obtain

For the real matrix equation

we can obatin $v_s^R(X) = \tilde{M}^\dagger v_r^R(C)+\left(I_{2n^2-n}-\tilde{M}^\dagger \tilde{M}\right)y$ by using Lemma 4.1. Thus we get the formula (4.3).

Notice

we obtain that the minimal norm reduced biquaternion Hermitian solution $X_{HQ}\in S_{HQ}$ of Problem 2 satisfies

Therefore, (4.4) holds.

Corollary 4.6. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{n\times q}$, $C\in\mathbb{RB}_Q^{m\times q}$, $\tilde{M}$ is given in Theorem 4.5. Then the following statements are equivalent:

(c) Problem 2 has a solution $X\in S_{HQ}$;

(d) $(\tilde{M}\tilde{M}^\dagger-I_{4mq})v_r^R(C) = 0$.

Moreover, if (c) holds, the solution set of (1.1) over $\mathbb{RB}_{HQ}^{n\times n}$ can be represented as

Remark 4.2. When $X$ is a Hermitian matrix, Theorem 4.4 can be used to transform the reduced biquaternion matrix equation $\sum\limits_{i = 1}^nA_iXB_i = C$ into real matrix equation $\tilde{M}v^R_s(X) = v^R_r(C)$. Corollary 4.6 can be obtained by a proof method similar to Corollary 4.3.

Similar to Theorem 4.4, we can give the relationship between $v_s^R(X)$ and $v_c^R(X)$ in the reduced biquaternion Anti-Hermitian matrix for studying Problem 3.

Theorem 4.7. Let $X = \left[\begin{matrix}x_{11} & \cdots&x_{1n}\\\vdots & \vdots\\x_{n1} & \cdots&x_{nn}\end{matrix}\right]\in \mathbb{RB}_{AQ}^{n\times n}$, $x_{ij} = x_{ij}^1+x_{ij}^2{{\bf i}}+x_{ij}^3{{\bf j}}+x_{ij}^4{{\bf k}}\in\mathbb{RB}_Q$, denote

where, $\sigma = \frac{(m-1)(8n+6-4m)}{2}$, $\tau = \frac{(r-1)(8n+6-4r)}{2}$, $\xi = 4(r-m)$.Then

Theorem 4.8. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{n\times q}$, $C\in \mathbb{RB}_Q^{m\times q}$, denote

where, $G_3$, $G_4$ are defined in Theorem 4.5. Hence the set $S_{AQ}$ of Problem 3 is represented as

And the minimal norm reduced biquaternion Anti-Hermitian solution $X_{AQ}\in S_{AQ}$ of Problem 3 satisfies

Corollary 4.9. Let $A_i\in \mathbb{RB}_Q^{m\times n}$, $B_i\in \mathbb{RB}_Q^{n\times q}$, $C\in\mathbb{RB}_Q^{m\times q}$, $\hat{M}$ is given in Theorem 4.8. Then the following statements are equivalent:

(e) Problem 3 has a solution $X\in S_{AQ}$;

(f) $(\hat{M}\hat{M}^\dagger-I_{4mq})v_r^R(C) = 0$.

Moreover, if (f) holds, the solution set of (1.1) over $\mathbb{RB}_{AQ}^{n\times n}$ can be represented as

5.   Algorithm and numerical experiments

Based on the algebraic solutions in Section 4, we now present the numerical algorithms and numerical examples for finding solutions of Problems 1–3 in this section.

To simplify the process of checking the algorithms, in the following numerical examples, we use the reduced biquaternion matrix equation $A_1XB_1+A_2XB_2 = C$. To ensure that Problem 1 under testing has a solution, we suppose $A_i$, $B_i$, $C$, $X$ are known reduced biquaternion matrices.

Example 5.1. Let $m = n = p = q = 3$, and $A_i = A_{i1}+A_{i2}{{\bf i}}+A_{i3}{{\bf j}}+A_{i4}{{\bf k}}\in\mathbb{RB}_Q^{m\times n}$, $B_i = B_{i1}+B_{i2}{{\bf i}}+B_{i3}{{\bf j}}+B_{i4}{{\bf k}}\in\mathbb{RB}_Q^{p\times q}$(i = 1, 2), $X = X_{1}+X_{2}{{\bf i}}+X_{3}{{\bf j}}+X_{4}{{\bf k}}\in\mathbb{RB}_Q^{n\times p}$. We take

Compute

Denote $\varepsilon_1 = log_{10}\|MM^{\dagger}-I_{4mq}\|$, we obtain

According to Algorithm 5.1, the reduced biquaternion matrix equation (5.1) has a unique solution $X_{Q}\in S_Q$, we can get $\varepsilon_2 = log_{10}\|X_Q-X\| = -11.3929$.

Example 5.2. $A_i$ and $B_i$ $(i = 1, 2)$ are defined in Example 5.1. Suppose

Compute (5.1). we can get $\varepsilon_3 = log_{10}\|\tilde{M}\tilde{M}^{\dagger}-I_{4mq}\| = -10.7394$ and $rank(\tilde{M}) = 15$. The reduced biquaternion matrix equation (5.1) has a unique solution $X_{HQ}$ by using Algorithm (5.2). So we can get $\varepsilon_4 = log_{10}\|X_{HQ}-\widetilde{X}\| = -13.5758$.

Example 5.3. $A_i$ and $B_i$ $(i = 1, 2)$ are defined in Example 5.1. Suppose

Similarly, Compute (5.1). we can get $\varepsilon_5 = log_{10}\|\hat{M}\hat{M}^{\dagger}-I_{4mq}\| = -9.6723$ and $rank(\tilde{M}) = 21$. The reduced biquaternion matrix equation (5.1). has a unique solution $X_{AQ}$ by using Algorithm 5.3. So we can get $\varepsilon_6 = log_{10}\|X_{AQ}-\overline{X}\| = -12.6248$.

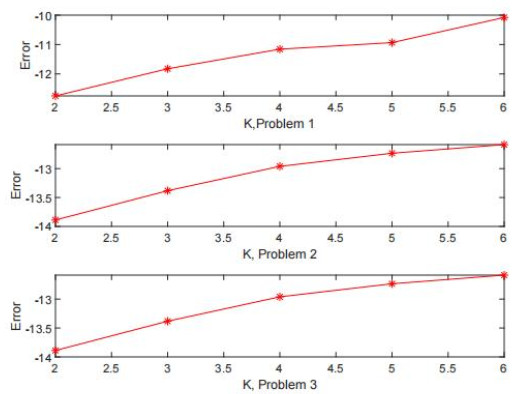
Example 5.4. For $m = n = p = q = 2K$, $A_i$ and $B_i$ generated randomly for $K = 2:6$. Consider the reduced biquaternion matrix equation (1.1), we record the errors in the three Problems in Figure 1.

Examples 5.1–5.4 are used to show the feasibility of Algorithms 5.1–5.3.

6.   Conclusions

In this paper, we proposed a real vector representation of reduced biquaternion matrix, which preserves the relative positions of the elements in the original reduced biquaternion matrix. For every element in reduced biquaternion, the real and three imaginary parts are remained as a whole. Combined this real vector representation with semi-tensor product of matrices, we solved the Problems 1–3.

Acknowledgments

This work was supported by National Natural Science Foundation of China 62176112; Science and Technology Project of Department of Education, Shandong Province ZR2020MA053; the science foundation of Liaocheng University under grants 318011921.

Conflict of interest

The authors declare that they have no competing interests.