On threshold dynamics for periodic and time-delayed impulsive systems and application to a periodic disease model

1.   Introduction

The basic reproduction number (ratio) $\mathcal{R}_{0}$ is an important parameter in epidemiology and within-host pathogen dynamics. $\mathcal{R}_{0}$ is defined as the expected number of secondary cases produced by a single (typical) infection in a completely susceptible population in epidemiology. $\mathcal{R}_{0}$ determines whether an infectious disease will break out usually. If $\mathcal{R}_{0} > 1$, it means that an individual can produce more than one individuals on average, then the population persists, if $\mathcal{R}_{0} < 1$, an individual can produce less than one individual on average, thus the population becomes extinct. Diekmann et al. ^[1] first introduced the next generation matrix approach to $\mathcal{R}_{0}$ and Van den Driessche et al. ^[2] established the theory of $\mathcal{R}_{0}$ for autonomous compartmental epidemic models. These two works have been widely used in various infectious disease models. For epidemic models with periodic coefficients, Bacaër et al. ^[3] presented a general definition of $\mathcal{R}_{0}$, that is, $\mathcal{R}_{0}$ is the spectral radius of an integral operator on the space of continuous periodic functions. Since then, there has been a lot of research on $\mathcal{R}_{0}$ in epidemic models. Wang et al. ^[4] proved that $\mathcal{R}_{0}$ is a threshold parameter for the local stability of the disease-free periodic solution of periodic compartmental ODE models. Liang et al. ^[5] and Zhao ^[6], proved similar results for a class of time-delay evolution equations, respectively. Bai et al. ^[7] generalized the above results to impulse differential equations. Further, Thieme ^[8] characterized the relationship between spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity. Bacaër et al. ^[9] obtained a more biological interpretation of $\mathcal{R}_{0}$ for periodic models, and Inaba ^[10] used the concept of a generation evolution operator to give a new definition of $\mathcal{R}_{0}$ in heterogeneous environments.

In population biology and epidemiology, more and more people adopt impulsive delay differential equations. For instance, Huo et al. ^[11] studied the global attractivity of positive periodic solutions for an scalar impulsive differential equations. Gourley et al. ^[12] evaluated the effectiveness of the age-structure culling strategies for controlling the vector-borne diseases by pulse model with two delays. Shen et al. ^[13] studied the positive periodic solutions of a predator-prey model with impulsive harvest and time delays. Motivated by the recent works of Liang et al. ^[5], Zhao ^[6], especially Bai et al. ^[7], by using a method similar to Bai et al. ^[7], we show that $\mathcal{R}_{0}-1$ determines the stability of the zero solution of the associated periodic linear impulsive system and there are no special requirements for the period of the model coefficients and pulse time of the model coefficients.

This paper is organized as follows. In Section 2, we introduce the definition of the basic reproduction ratio $\mathcal{R}_{0}$ for impulse delay periodic compartmental model and prove a stability equivalence result (Theorem 2.1). In Section 3, we apply the developed theory to an impulsive model of parasitic diseases in aquaculture with time delay, and establish a threshold type result in terms of $\mathcal{R}_{0}$. A brief discussion section then completes the paper.

2.   The model formulation

Let $\tau \geq 0$ be a given number, denote

where $\phi(t^{+}) = \text{lim}_{s\rightarrow t^{+}}\phi(s)$ and $\phi(t^{-}) = \text{lim}_{s\rightarrow t^{-}}\phi(s)$. We equip the linear space $PC([-\tau, 0], \mathbb{R}^{m})$ with the norm $\parallel\cdot\parallel_{\tau}$ defined by $\parallel\phi\parallel_{\tau} = \text{sup}_{-\tau\leq\theta\leq0}|\phi(\theta)|$, where $|\cdot|$ is any convenient norm on $\mathbb{R}^{m}$ (for example the Euclidean norm). For a left continuous function $u:\mathbb{R}\rightarrow \mathbb{R}^{m}$ and $u(t^{+}) = u(t) \text{ for all but at most finite number of points within a limited interval}$, define $u_{t}\in PC([-\tau, 0], \mathbb{R}^{m})$ by

Let $F:\mathbb{R}\rightarrow \mathcal{L}(PC([-\tau, 0], \mathbb{R}^{m}), \mathbb{R}^{m})$ be a map and $V(t)$ be a continuous $m \times m$ matrix function on $\mathbb{R}$. Assume that $F(t)$ and $V(t)$ are $\omega-$periodic in $t$ for some real number $\omega > 0$, and for each fixed $\phi$, $F(t)\phi$ is a measurable function of $t$, continuous in $\phi$ for each fixed $t$ and there exists $M > 0$ such that

We consider a linear impulsive and periodic functional differential system

where $P_{n}$ is $m\times m$ matrix such that $\text{det}(P_{n}+I)\neq 0\ (n\in \mathbb{N})$, $I$ is the identity matrix, $t_{k}:\mathbb{N}\rightarrow \mathbb{R}^{+}$ and there exists an integer $q\geq1$ such that $t_{n+q} = t_{n}+\omega, \ P_{n+q} = P_{n}, \text{ }n\in \mathbb{N}.$

Let $\tilde{J} = [-\tau, 0)\cap\{t_{i}+n\omega:n\in \mathbb{Z} \text{ and } i = 1, ..., q\}$ (possibly empty), and $J = [-\tau, 0)\backslash\tilde{J}$. Denote the space $PC_{J}$ by

It is easy to see that $PC_{J}\subset PC([-\tau, 0], \mathbb{R}^{m})$, and $PC_{J}$ is a Banach space endowed with the norm $\parallel\cdot\parallel_{\tau}$. Given $\phi\in PC_{J}$ we consider the following initial condition

A function is said to be a solution of (2.1) with initial conditions (2.2) if the following condition are satisfied:

$\rm(i)$ $u(t)$ is absolutely continuous on each interval $(t_{n}, t_{n+1}], \ n\in \mathbb{N}$.

$\rm(ii)$ $u(t^{+}_{n}), \ u(t^{-}_{n})\ {\rm{exist \; and }}\; u(t^{-}_{n}) = u(t_{n}), \ n\in \mathbb{N}.$

$\rm(iii)$ $u(t)$ satisfies (2.1a) for almost everywhere in $[0, +\infty)\setminus\{t_{n}\}$ and $u(t)$ satisfies (2.1b) for every $t = t_{n}, \ n\in \mathbb{N}$.

By the general theory of impulsive delay differential equations ^[14], it follows that for any $\phi\in PC_{J}$, system (2.1) has a unique solution $u(t, \phi)$ on $[0, +\infty)$ with $u_{0} = \phi$.

The internal evolution of individuals in the infectious compartments (e.g., natural and disease-induced deaths, movements among compartments and recovery) is governed by the linear impulsive ordinary differential system:

By the theory of impulsive differential equations [15,Sect.1.2], we denote by $U_{n}(t, s)(n\in \mathbb{Z}, t, s\in(t_{n-1}, t_{n}])$ the fundamental matrix for the linear equation

Then the evolution matrices associated with (2.3) can be written as

A straightforward verification shows that

In order to introduce the basic reproduction ratio for system (2.1), we need the following assumptions.

(H1) For any given $t\in \mathbb{R}$, operator $F(t):PC([-\tau, 0], \mathbb{R}^{m})\rightarrow \mathbb{R}^{m}\;$ is positive in the sense that $F(t)PC([-\tau, 0], \mathbb{R}^{m}_{+})\subseteq \mathbb{R}^{m}_{+}$.

(H2) For any given $t\in \mathbb{R}$, matrix $-V(t)$ is cooperative, and $r(W(\omega, 0)) < 1$,

(H3) $P_{n}+I$ is nonnegative for every $n\in \mathbb{N}$, which means all entries of $P_{n}+I$ are nonnegative,

where $r(W(\omega, 0))$ represents the spectral radius of $W(\omega, 0)$. By the theory of impulsive delay differential equations [15,Remark 3.5] with (H2), we can conclude that there exists $K\geq 1$ and $\alpha > 0$ such that

In view of the periodic environment, we suppose that $v(t),$ $\omega-$periodic in $t$, is the initial distribution of infectious individuals. For any $t\geq s$, $F(t-s)v_{t-s}$ is the distribution of newly infected individuals at time $t-s$, which is produced by the infectious individuals who were introduced over the time interval $[t-s-\tau, t-s]$. Then $W(t, t-s)F(t-s)v_{t-s}$ is the distribution of those infected individuals who were newly infected at time $t-s$ and remain in the infected compartments at time $t$. It follows that

is the distribution of accumulative new infections at time $t$ produced by all those infectious individuals introduced at all previous times to $t$.

By the definition of $W(t, s)$, for any given $s\geq 0$, $W(t, t-s)v_{t-s}$ is the distribution of those infectious individuals who were introduced at time $t-s$ and remain in the infected compartments at time $t$, then $w(t): = \int_{0}^{\infty}W(t, t-s)v_{t-s}ds$ is the distribution of accumulative infectious individuals who were introduced at all previous times to $t$ and remain in the infected compartments at time $t$. Thus, the distribution of newly infected individuals at time $t$ is

Let the Banach space $X_{\omega}$ be given by

with the norm $\|v\|_{X_{\omega}} = \text{sup}_{t\in [0, \omega]}|v(t)|$, where $|\cdot|$ is any convenient norm on $\mathbb{R}^{m}$ and the positive cone $X_{\omega}^{+}: = \left\{v\in X_{\omega}:v(t)\geq 0, \, \forall t\in \mathbb{R}\right\}.$ According to the above analysis, we define two linear operators on $X_{\omega}$ by

and

Moreover, let $A$ and $B$ be two bounded linear operators on $X_{\omega}$ defined by

It then follows that $L = A\circ B$ and $\hat{L} = B\circ A$, and hence, $L$ and $\hat{L}$ have the same spectral radius. Motivated by the concept of next generation operators in ^[7], we define the spectral radius of $L$ and $\hat{L}$ as the basic reproduction ratio

for periodic system (2.1).

In view of the previous assumptions and conclusions, one can verify that $L$ and $\hat{L}$ are well defined. To see this, we introduce the following operator.

For any given $\lambda\in \mathbb{R}$, let $E_{\lambda}$ be a linear operator on $PC([-\tau, 0], \mathbb{R}^{m})$ defined by

It is easy to see that $\|E_{\lambda}\|\leq \text{max}\{1, e^{-\lambda\tau}\}$ for any $\lambda\in \mathbb{R}$. Then we introduce a family of linear operators $L_{\lambda}$ on $X_{\omega}$:

Obviously, $L_{0} = L$, and $L_{\lambda}$ is well defined for all $\lambda > -\alpha$. Further, we can prove the following assertion.

Lemma 2.1. For each $\lambda > -\alpha, \, L_{\lambda}$ is positive, continuous and compact on $X_{\omega}$.

Proof. Let $\lambda > -\alpha$ be given. Clearly, $E_{\lambda}$ is a positive linear operator on $PC([-\tau, 0], \mathbb{R}^{m})$. By hypothesis (H1), (H2) and (H3), $F(t)$ and $W(t, s)(t\geq s)$ are positive linear operators. Then it is easy to see that $L_{\lambda}$ is positive on $X_{\omega}$. In view of

for any given $t\in \mathbb{R}$, $s\in[0, +\infty)$ and $v\in X_{\omega}$, we have

Thus,

That means $L_{\lambda}$ is bounded, and hence, continuous on $X_{\omega}$

Let $v\in X_{\omega}$ and $\forall \underline{t}, \; \overline{t}\in(0, \omega]$ with $\underline{t} < \overline{t}$. Note that

we have

Thus $|[L_{\lambda}v](\bar{t})-[L_{\lambda}v](\underline{t})\mid\rightarrow 0$ as $|\bar{t}-\underline{t}|\rightarrow0$, and hence $[L_{\lambda}v](t)$ is quasiequicontinuous. Therefore, by applying [15,Lemma 2.4], $L_{\lambda}$ is compact on $X_{\omega}$.

In order to study the properties of the solution of the equation (2.1), we need the following auxiliary system. For any given $\lambda\in[0, +\infty)$, consider the linear impulsive system:

For any $\phi\in PC_{J}^{+}$, [14,Corollary 3.1] implies that system (2.6) admits a unique solution $u^{\lambda}(t, \phi)$ on $[0, +\infty)$ satisfying $u^{\lambda}_{0} = \phi$. In addition, the following statements are valid.

Lemma 2.2. $\rm(i)$ For any $\phi\in PC_{J}^{+}$, the solution $u^{\lambda}(t, \phi)$ of (2.6) with $u^{\lambda}_{0} = \phi$ is positive.

$\rm(ii)$ Let $u^{\lambda_{1}}(t, \phi)$ and $u^{\lambda_{2}}(t, \phi)$ be two solutions of (2.6) with $0\leq\lambda_{1} < \lambda_{2}$. Then $u^{\lambda_{1}}(t, \phi)\leq u^{\lambda_{2}}(t, \phi)$ for all $t\geq0$.

Proof. ${\rm{(i)}}$For $\epsilon > 0$, we consider the following small perturbations of system (2.1)

where $e = (1, 1, ..., 1)^{T}\in\mathbb{R}^{m}$. For any $\psi\in PC^{+}_{J}$, we define

Let $u^{\lambda, \epsilon}(t, \phi)$ be the solution of (2.7) with initial condition $u^{\lambda, \epsilon}_{0} = \phi\in PC_{J}^{+}$. Now we show that $u^{\lambda, \epsilon}(t, \phi)\gg 0$ for $t > 0$ whenever $\phi\geq0$. Due to $u^{\lambda, \epsilon}(0, \phi) = \phi(0)\geq0$ and $(u^{\lambda, \epsilon})'_{+}(0, \phi) = f(0, \phi)+\epsilon > 0$, where $(u^{\lambda, \epsilon})'_{+}(0, \phi)$ is the right derivative with respect to (2.7). It is easy to see that there exist a positive number $\ell > 0$ such that $u^{\lambda, \epsilon}(t, \phi)\gg0 \; \text{ for }\; 0 < t < \ell$. Therefore, if the result is false, we can assume that there exists $\hat{t} > 0$ such that

Then we get $(u_{i}^{\lambda, \epsilon})'_{\_}(\hat{t}, \phi)\leq 0,$ where $(u_{i}^{\lambda, \epsilon})'_{\_}(\hat{t}, \phi)$ is the left-hand derivative of $u_{i}^{\lambda, \epsilon}$ at $t = \hat{t}$. However, $u_{\hat{t}}^{\lambda, \epsilon}\in PC([-\tau, 0], \mathbb{R}_{+}^{m})$ and by (H1), (H2) and (2.7),

which is a contradiction. By (H3) the positivity of $u^{\lambda, \epsilon}(t, \phi)$ doesn$\text{'}$t change at impulsive points, thus $u^{\lambda, \epsilon}(t, \phi)\gg 0$ for $t\in(0, +\infty)$. Let $\epsilon\rightarrow 0,$ then $u^{\lambda, \epsilon}(t, \phi)\rightarrow u^{\lambda}(t, \phi)$, and hence $u^{\lambda}(t, \phi)\geq0$ for $t\in[0, +\infty).$

(ⅱ) Note that (2.6) is a linear equation, (ⅱ) is a corollary of (ⅰ).

Let $U(t, \lambda)$ be the solution maps of system (2.6) from $PC_{J}$ to $PC([-\tau, 0], \mathbb{R}^{m})$ that is,

where $u^{\lambda}(t, \phi)$ is the unique solution of (2.6) with $u_{0}^{\lambda} = \phi\in PC_{J}.$ It is easy to see that $U(\omega, \lambda)$ is an operator from $PC_{J}$ to $PC_{J}$. The basic reproduction number of (2.6) is represented by $R(\lambda): = r(\lambda L) = \lambda \mathcal{R}_{0}$. For convenience, we write $U: = U(\omega, 1)$ for $\lambda = 1$. Then we have the following result.

Lemma 2.3. The existence of fixed point of $U$ in $PC_{J}$ is equivalent to that of $\omega$-periodic solution of (2.1).

Proof. Suppose that $u(t, \phi^{*})$ is a periodic solution of (2.1), that is, $u(t+\omega, \phi^{*}) = u(t, \phi^{*})$ for $t\in[-\tau, +\infty)$. Note that $U$ is the Poincaré map of system (2.6) with $\lambda = 1$, the proof is obvious.

Conversely, assume that $\phi^{*}\in PC_{J}$ and $U\phi^{*} = \phi^{*}.$ Let $u(t): = u(t, \phi^{*})$ be the solution of (2.1) with $u_{0} = \phi^{*}.$ Let $v(t): = u(t+\omega), \; \forall t > 0$. Then Consider the derivative of $v(t)$ we get

and at the impulsive points $v(t_{n}^{+}) = u(t_{n+q}^{+}) = (I+P_{n+q})u(t_{n+q}) = (I+P_{n})v(t_{n}), \; n\in \mathbb{N}$. In addition, $v(\theta) = u(\theta+\omega) = u_{\omega}(\theta) = u_{0}(\theta) = \phi^{*}(\theta)$ for all $\theta\in[-\tau, 0]$. Thus the uniqueness of solutions of (2.1) imply that $u(t+\omega) = u(t)$ for all $t\geq-\tau.$ Clearly, $u(t_{n}^{+}) = u(t_{n+q}^{+}), \; \forall n\in \mathbb{N}$. Hence, $u(t)$ is a periodic solution of (2.1).

Lemma 2.4. For each $n > \frac{\tau}{\omega}$, $U^{n}$ is positive and compact on $PC_{J}$.

Proof. Let $u(t, \phi)$ be the unique solution of (2.1) with $u_{0} = \phi\in PC_{J}$. By Lemma 2.2(ⅰ), $U^{n}, \, n\in\mathbb{N}$ is positive on $PC_{J}$. Under the assumption that $n\omega > \tau$, $U^{n}\phi$ can be written as follows

where $t_{k}$ is the impulsive point on $[0, n\omega+\theta)$. Let $B$ be the bounded subset of $PC_{J}$. Obviously, for any $\phi\in B$, $u(s, \phi)$ is bounded for $s\in[0, n\omega]$, and hence, $U^{n}(B)$ is bounded.

Next, we prove that the set $U^{n}(B)$ is quasiequicontinuous whenever $n\omega > \tau$. Then, with [15,Lemma 2.4], we can deduce that $U^{n}$ is compact for $n\omega > \tau$.

Note that $V(t)$ is continuous and periodic, then $\|V(t)\|\leq N$ and $\|F(t)\|\leq M$ for $t > 0$, Thus

for $0\leq\alpha\leq\beta\leq n\omega$, where $B'\geq \text{max}_{0\leq s\leq n\omega}|u(s, \phi)|$ with $\phi\in B$. Suppose that the interval $(n\omega-\tau, n\omega)$ has $p$ impulsive points, denote by $\theta_{i}^{(n)}, \; 1\leq i\leq p.$ Let $\theta_{0}^{(n)} = n\omega-\tau$ and $\theta_{p+1}^{(n)} = n\omega$. Then for any $\bar{t}, \underline{t}\in(-\tau, 0]$ with $n\omega+\bar{t}, n\omega+\underline{t}\in (\theta_{i}^{(n)}, \theta_{j}^{(n)}]$ for some $i, j$, we have

which implies that $|[U^{n}\phi](\bar{t})-[U^{n}\phi](\underline{t})|\rightarrow0$ as $|\bar{t}-\underline{t}|\rightarrow0$. Hence, $U^{n}(B)$ is quasiequicontinuous. The proof is completed.

Lemma 2.5. If $r(U) = 1$, then $\mathcal{R}_{0}\geq1$.

Proof.Fix an integer $n_{0} > 0$ such that $n_{0}\omega > \tau$. Then the operator $U^{n_{0}}: = U(n_{0}\omega)$ is compact and positive by Lemma 2.4. The Krein-Rutman theorem [16,Theorem 1.1] implies that there is $\phi\in PC_{J}^{+}\backslash\{0\}$ such that $U^{n_{0}}\phi = r(U^{n_{0}})\phi = \phi$. Note that

from the positivity of $U$, we get that $\phi^{*}\in PC([-\tau, 0], \mathbb{R}_{0}^{m})\backslash\{0\}$ and $U\phi^{*} = \phi^{*}$. It follows from Lemma 2.3 that $u^{*}(t): = u(t, \phi^{*})$ with $u^{*}_{0} = \phi^{*}$ is an $\omega$-periodic solution of (2.1). We extend $u^{*}(t)$ to the entire $\mathbb{R}$ in the following way

It is easy to see that $\hat{u}_{*}(t)$ is an $\omega$-periodic solution of system (2.1). By the constant-variation formula,

Letting $t_{0}\rightarrow -\infty$ in (2.8), together with (2.5) and the boundedness of $\hat{u}^{*}(t)$ on $\mathbb{R}$, we have

Thus 1 is an eigenvalue of $L$ on $X_{\omega}$, and hence, $\mathcal{R}_{0}\geq1$.

Lemma 2.6. If $\mathcal{R}_{0} = 1$, then $r(U)\geq1.$

Proof. If $\mathcal{R}_{0} = 1$, then there exists $\varphi^{*}\in X_{\omega}$ such that

It is easy to see that

At the impulsive points $t_{n}$, (2.4) indicates that $\varphi^{*}(t_{n}^{+}) = (I+P_{n})\varphi^{*}(t_{n}), \; n\in \mathbb{Z}$. Thus, $u^{*}(t): = \varphi^{*}|_{t\in[-\tau, +\infty)}$ is a periodic solution of (2.1). Lemma 2.3 implies that $Uu^{*}_{0} = u^{*}_{0}$, hence, $r(U)\geq1$.

Lemma 2.7. $r(U) > 1$ if and only if $\mathcal{R}_{0} > 1$.

Proof.(Necessity) If $0 < \lambda_{1} < \lambda_{2}$, then $U(\omega, \lambda_{1})(\phi)\leq U(\omega, \lambda_{2})(\phi)$ for any $\phi\in PC^{+}_{J}$ by Lemma 2.2(ⅰ). Note that $U(\omega, \lambda)$ is a positive and bounded linear operator on $PC_{J}$, then [17,Theorem 1.1] implies that $U(\omega, \lambda)$ is a nondecreasing function of $\lambda$ on $(0, +\infty)$. By Lemma 2.3, there exists $n_{0}\in \mathbb{N}$ such that $U^{n_{0}}$ is compact. Since $r(U) = r(U(\omega, 1)) > 1$ and $\text{lim}_{\lambda\rightarrow0^{+}}r(U(\omega, \lambda)) = r(W(\omega, 0)) < 1$, By the continuity of spectral radius for compact linear operators [18,Theorem 2.1(a)] and $U$ and $U^{n_{0}}$ have the same spectral radius, we can conclude that there exists $\lambda_{0}\in(0, 1)$ such that $r(U(\omega, \lambda_{0})) = 1$. Thus $R(\lambda_{0})\geq1$ by Lemma 2.5. Then $\mathcal{R}_{0} = \frac{R(\lambda_{0})}{\lambda_{0}} > 1$.

(Sufficiency) It is easy to see that $R(\frac{1}{\mathcal{R}_{0}}) = 1$ since $R(1) = \mathcal{R}_{0} > 1$. Then $r(U(\omega, \mathcal{R}_{0}^{-1}))\geq 1$ due to Lemma 2.6. Note that $r(U(\omega, \lambda))$ is nondecreasing in $\lambda\in[0, +\infty)$, we have $r(U(\omega, 1)\geq r(U(\omega, \mathcal{R}_{0}^{-1}))$.

Suppose, by contradiction, that $r(U(\omega, 1)) = 1$. Then $r(U(\omega, \lambda)) = 1$ for all $\lambda\in[\mathcal{R}_{0}^{-1}, 1]$. By the proof of Lemma 2.5, we see that $1$ is an eigenvalue of $\lambda L$ with positive eigenvector for all $\lambda\in[\mathcal{R}_{0}^{-1}, 1]$. Thus $\lambda^{-1}$ is an eigenvalue of $L$ with positive eigenvector for all $\lambda\in[\mathcal{R}_{0}^{-1}, 1]$. But this is impossible since the compact linear operator $L$ has only countablely many eigenvalues. This shows that $r(U(\omega, 0)) > 1$. The proof is completed.

In fact, we have proved the main theorem of this section.

Theorem 2.1. $\mathcal{R}_{0}-1$ has the same sign as $r(U)-1$.

The following result is about the numerical calculation of $\mathcal{R}_{0}$ (see, e.g., ^[7]). For completeness, here we list the main steps.

Theorem 2.2. If $\mathcal{R}_{0} > 0$ then $\lambda = \mathcal{R}_{0}^{-1}$ is the unique solution of $r(U(\omega, \lambda)) = 1$.

Proof. The proof is essentially the same as that of Bai ^[7], we omit it here.

Remark 2.1. With Theorem 2.2, we can numerically compute $\mathcal{R}_{0}$ according to the following three steps:

With Theorem 2.2, we can numerically compute $\mathcal{R}_{0}$ according to the following three steps:

$\rm(i)$ Choose initial function $v_{0}\in \text{Int}(PC_{J}^{+})$.

$\rm(ii)$ For any given $\lambda\in[0, +\infty)$, let $a_{n} = \|U(\omega, \lambda)v_{n-1}\|_{\tau}$ and $v_{n} = \frac{U(\omega, \lambda)v_{n-1}}{\|U(\omega, \lambda)v_{n-1}\|_{\tau}}$ for all $n\geq 1$. By Liang et al. [5,Lemma 2.5], it follows that

Moreover, if $\text{lim}_{n\rightarrow \infty}a_{n}$ exists, then $r(U(\omega, \lambda)) = \text{lim}_{n\rightarrow +\infty}a_{n}.$

$\rm(iii)$ Compute the numerical solution $\lambda_{0}$ to $r(U(\omega, \lambda)) = 1$ via the bisection algorithm, and hence, $\mathcal{R}_{0} = \frac{1}{\lambda_{0}}$.

3.   An application

Mathematical methods have been used to study infectious diseases for a long time and certain results have been obtained. People have added various factors to the model by analyzing the actual situation to better reflect the actual problem. For example, Sharma et al. ^[19] considered the incubation period of the disease and used the time-delayed model, Gupta et al. ^[20] used a time-delay SEIRD model to analyze the spread of COVID-19 infection in a population. Church et al. ^[21] considered the vaccination situation and used the impulse model, etc.

The non-impulsive system has been studied in ^[6] and non-delayed system has been studied in ^[22], In this section, inspired by the above work, we combine a variety of factors and apply the theory developed in the previous section to an impulsive model of parasitic diseases in pork farming with time delay. Parasites can cause a decrease in feed conversion rate and weight gain, and there is a risk of pig-to-human transmission in pork and various organs after slaughter. This has caused huge economic losses to the global pork industry ^[23]. Concentrated breeding makes the treatment of parasitic diseases easier to achieve. The purpose of treatment is achieved by adding to the feed and spraying the corresponding drugs on the body surface. The timely removal of feces and other potential sources of infection can effectively reduce the infection rate of parasitic diseases. However, there are few researches on the above strategies in mathematics. The following simulation of the above methods by applying the method of infectious disease dynamics has some reference significance for when and how to control parasitic diseases in reality.

Let $S(t), E(t)$ and $I(t)$ be the total numbers at time t of the susceptible, exposed, and infective populations, respectively. For simplicity, we assume that the latent period of the disease is $\tau$, and the incidence rate function $f (t, S, I)$ depends on time $t$ and variables $S$ and $I$. Let $\mu(t)$ be the natural death rate of the population. It then follows that the rate of entry into the infective class from the exposed one at time $t$ is

As discussed in ^[24], $E(t)$ can be represented as

It is easy to show that

Then, we obtain the following non-autonomous SEI model with impulses:

Here $\delta(t)$ is the recruitment rate, $\theta$ represents the treatment rate of parasite drugs.

According to ^[25], we need to impose the following compatibility condition:

Assume that $f (t, S, I)$ and all these time-dependent coefficients are $\omega$-periodic in $t$ for some real number $\omega > 0$. Obviously the function

is also $\omega$-periodic, and hence, model (3.1) is an $\omega$-periodic and time-delayed system with impulses. To study the dynamic behavior of system (3.1), we make the following assumptions, which are natural considering the biological background of the system (3.1):

(A1) $\delta(t)$ and $\mu(t)$ are all non-negative and continuous functions with $\delta(t) > 0$ and $\int_{0}^{\omega}\mu(t)dt > 0$.

(A2) $f (t, S, I)$ is a $C^{1}$-function with the following properties:

$\rm(i)$ $f (t, S, 0)\equiv0, f (t, 0, I)\equiv0,$ and $\frac{\partial f (t, S, 0)}{\partial I}$ are positive and non-decreasing for all $S > 0$.

$\rm(ii)$ $\frac{\partial f (t, S, I)}{\partial S}\geq 0$ and $f (t, S, I)\leq \frac{\partial f (t, S, 0)}{\partial I}I$ for all $(t, S, I)\in \mathbb{R}\times \mathbb{R}^{2}_{+}$.

By virtue of (A1), the scalar linear periodic equation

has a unique positive $\omega$-periodic solution $S^{*}(t)$, which is globally stable in $\mathbb{R}$. Linearizing system (3.1) at its disease-free periodic solution $(S^{*} (t), 0, 0)$, we obtain the following periodic linear impulsive differential equation for the infective variable $I$:

where

Take $m = 1$, $F(t)\phi = a(t)\phi(-\tau)$, and $V(t) = \mu(t)$. Then system (2.1) becomes system (3.4), and

where

From the definition of the basic reproduction number, we get $\mathcal{R}_{0} = r(L)$ for the system (3.4)

By the general theory of impulsive delay differential equations ^[14], it follows that for any $\phi\in PC_{J}$, system (3.1) has a unique solution $u(t, \phi) = (S(t), E(t), I(t))$ on $[0, +\infty)$ with $u_{0} = \phi\in D$.

Let $N(t) = S(t)+ E(t)+ I(t)$. Then we have

Thus, the global stability of $S^{*}(t)$ for (3.3) implies that solutions of system (3.1) with initial data in $D$ exist globally on $[0, +\infty)$ and are ultimately bounded.

Just like the procedure in Sect. 2, we take $m = 1$ and let $U(t):PC_{J} \rightarrow PC([-\tau, 0], \mathbb{R})$ be the solution maps of (3.1), that is,

where $u(t, \phi)$ is the unique solution of (3.1) satisfying $u_{0} = \phi\in PC_{J}$. Then $U : = U(\omega)$ is the Poincar$\acute{e}$ (period) map associated with (3.1) on $PC_{J}$. Let $r(U)$ be the spectral radius of $U$. Then the following assertion holds true.

Lemma 3.1. Let $\mu = \frac{lnr(U)}{\omega}$. Then there exists a positive and $\omega$-periodic function $v^{*}(t)$ such that $e^{\mu t}v^{*}(t)$ is a solution of (3.1).

Proof. Since the proof is essentially the same as that of [7,Lemma 8], we omit it here.

Theorem 3.1. Let (A1) and (A2) hold. Then if $\mathcal{R}_{0} < 1$, then the disease-free periodic solution $(S^{*}(t), 0, 0)$ of (3.1) is globally attractive.

Proof. Let $P(t)$ be the solution maps of the impulsive delay differential equations (3.4) on $PC_{J}$, that is, $P(t)\phi = I_{t}(\phi), t\geq0$, where $I(t, \phi)$ is the unique solution of (3.4) satisfying $I_{0} = \phi\in PC_{J}^{+}\setminus\{0\}$. Put $P: = P(\omega)$ is the Poincaré (period) map associated with system (3.4). We have $sign(\mathcal{R}_{0}-1) = sign(r(P)-1)$ due to Theorem 2.1.

Let $\phi\in PC_{J}^{+}\backslash \{0 \}$. We assert that there exists $t^{*}\in[0, \tau]$ such that $I(t^{*}) > 0$. If that's not correct, it means $I(t) = 0$ for all $t\in[0, \tau]$. Then the first equation of (3.4) implies

but $a(t) > 0$, which contradicts the assumption that $\phi > 0$. In view of

we have

This means that $P^{n}$ is strongly positive on $PC_{J}$ whenever $n\omega\geq2\tau$. By a method similar to the proof of Lemma 2.4, we can show that $P^{n}$ is compact when $n\omega\geq2\tau$. Since $P^{n} = P(n\omega)$, [26,Lemma 3.1] implies that $r(P)$ is a simple eigenvalue of $P$ with a strongly positive eigenvector, and the modulus of any other eigenvalue is less than $r(P)$.

Since $R_{0} < 1$, we have $r(P) < 1$. Let $P_{\epsilon}$ be the Poincaré map of the following perturbed impulsive delay differential system

Note that $\text{lim}_{\epsilon\rightarrow0} r(P_{\epsilon}) = r(P) < 1$, we can fix a sufficiently small number $\epsilon > 0$ such that $r(P_{\epsilon}) < 1$. By Lemma 3.1, there is positive $\omega$-periodic function $v_{\epsilon}(t)$ such that $u_{\epsilon}(t) = e^{\mu_{\epsilon}t}v_{\epsilon}(t)$ is a positive solution of (3.6), where $\mu_{\epsilon} = \frac{lnr(P_{\epsilon})}{\omega} < 0$. For any given $\phi\in D$, let $v(t, \phi) = (S(t), E(t), I(t))$. Due to (3.5) and the global stability of $S^{*}(t)$ for (3.3), there exists a sufficiently large integer $n_{1} > 0$ such that $n_{1}\omega\geq\tau$ and $S(t) < S^{*}+\epsilon, \forall t\geq n_{1}\omega-\tau$. In view of assumption (A2), we have

for all $t\geq n_{1}\omega$. Choose a sufficiently large number $K > 0$ such that $I(t)\leq K u_{\epsilon}(t), \, \forall t\in [n_{1}\omega-\tau, n_{1}\omega]$. Thus, the same method as in [7,Theorem 3] shows that

and hence, $\text{lim}_{t\rightarrow \infty}I(t) = 0$. Thus, for any given $\kappa\in \mathbb{R}$, by the continuity of $f(t, S, I)$ and $f(t, S, 0) = 0$, there is $T_{1} > 0$ such that $f (t, S(t), I(t))-e^{-\int_{t-\tau}^{t}\mu(t)dr}f (t-\tau, S(t-\tau), I(t-\tau)) < \kappa$,

By the second and fifth equations of (3.1), we have

Consider the following impulsive differential equation

By virtue of (A1), we see that the system (3.7) has a unique positive $\omega$-periodic solution $x^{*}$ which is globally stable in $\mathbb{R}$.

Let $\kappa\rightarrow0$ and $t\rightarrow \infty$, then $x^{*}(t)\rightarrow0$. Thus the comparison theorem for impulsive differential equations and the global stability of $x^{*}(t)$ for (3.7) implies that $E(t)\rightarrow0$ as $t\rightarrow \infty$. Note that $S(t)+E(t)+I(t) = S^{1}(t)$, where $S^{1}(t)$ is the solution of (3.1) satisfying $S^{1}(0) = \phi_{1}(0)+\phi_{2}(0)+\phi_{3}(0)$ It is easy to see that $\text{lim}_{t\rightarrow \infty}(S^{1}(t)-S^{*}(t)) = 0$ then $\text{lim}_{t\rightarrow \infty}(S(t)-S^{*}(t)) = 0$.

Theorem 3.2. Let (A1) and (A2) hold. If $\mathcal{R}_{0} > 1$, then there exists a real number $\eta > 0$ such that the solution $u(t, \phi) = (S(t), E(t), I(t))$ satisfies $\liminf_{t \to \infty}I(t)\geq\eta$ for any $\phi\in D$.

Proof. Let $P_{\delta}$ be the Poincaré map of

on $PC_{J}$. Since $\text{lim}_{\delta\rightarrow0}r(P_{\delta}) = r(P) > 1$, we can fix a small number $\delta > 0$ such that $r(P_{\delta}) > 1$. It then follows that there is a small number $\eta_{0} > 0$ such that

We claim that $\text{lim sup}_{t\rightarrow \infty}I(t) > \eta_{0}, \; \forall\phi\in D.$ Suppose, by contradiction, that there is a $\hat{t} > 0$ such that $I(t) \leq\eta_{0}$ for all $t\geq\hat{t}$. Then system (3.6) becomes

Choose a sufficiently small real number $\hat{k}$ such that

Note that $\mu_{\delta} > 0$, let $t\rightarrow \infty, \; \text{then } I(t)\rightarrow \infty,$ which is a contradiction. Then there are only two possibilities: (ⅰ) for all large $t$, $I(t)\geq \eta_{0}$; (ⅱ) $I(t)$ oscillates around $\eta_{0}$. Obviously, we only need to consider the second case. Put $\underline{t}$ and $\overline{t}$ are sufficiently large such that

If $\overline{t}-\underline{t}\leq\tau$, then the system (3.1) implies that

Because $\mu(t)$ is $\omega$-periodic and $t_{n+q} = t_{n}+\omega$, it is obvious that $e^{-\int_{\underline{t}}^{t+\tau}\mu(s)ds}$ and $\prod_{k:t_{k}\in[\, \underline{t}, \, \underline{t}+\tau \, )}$, for any given $\tau$, have a minimum value which is independent of $\bar{t}$ and $\underline{t}$, denoted by $c$. Then $I(t)\geq\eta_{0}c = q,$ if $\overline{t}-\underline{t}\leq\tau$.

If $\overline{t}-\underline{t} > \tau$, then for $t\in[\underline{t}, \underline{t}+\tau]$,

For $t\in(\underline{t}+\tau, \overline{t}\, ]$, we consider the following comparison equation

Note that $v(t)$ is $\omega$-periodic, let $m$, $M$ be the minimum and maximum of $v(t)$, respectively, then choose a sufficiently small real number $k > 0$ such that

where $q'$ is a constant independent of $\underline{t}$ and $k$. Then combined with the principle of comparison, we conclude that

due to $I(t) > ke^{\mu_{\delta}t}v_{\delta}(t) > q'$. Consequently, we get $I(t) > \eta$ for $t\in[\, \underline{t}, \overline{t}\, ]$, where $\eta = \text{min}\{q, q'\}$. Since this kind of interval $[\, \underline{t}\, , \, \overline{t}\, ]$ is chosen arbitrarily, we get $\text{lim inf}_{t\rightarrow \infty}I(t)\geq\eta.$

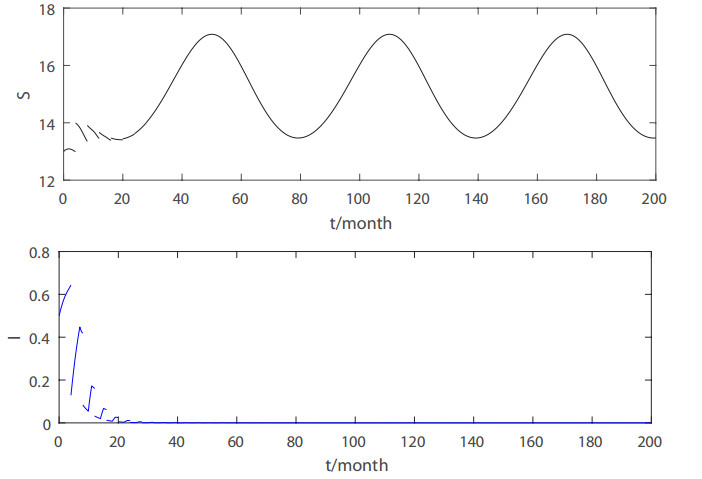
From the above theorem, we find that $\mathcal{R}_{0}$ is the threshold parameter for the extinction of the disease. Now we verify the theoretical results through numerical simulations. According to ^[27], we set $\delta(t) = 3+0.2\times sin(\pi t/30), \; \mu(t) = 0.2\times(1+0.2\times sin(\pi t/30)), \; f = \frac{\beta S(t)I(t)}{1+0.5\times I(t)}, \; \tau = 3, \; t_{n} = 4n, \, n\in\mathbb{N}, \; \theta = 0.8,$ When $\beta = 0.055$, then $\mathcal{R}_{0} = 0.9665 < 1$. Figure 1 shows that the disease-free periodic solution is globally attractive. When $\beta = 0.2$, then $\mathcal{R}_{0} = 3.5148 > 1$. Figure 2 shows that the non-zero solution is uniformly persistent.

4.   Discussion

In this paper, we develop the basic reproduction ratio $\mathcal{R}_{0}$ of more general periodic and time-delayed impulsive model. Note that the period of model coefficients is not same as that of fixed impulsive moments. We extend some known results of Bai et al.^[7]. We show that $\mathcal{R}_{0}$ is the threshold parameter for the stability of the zero solution of the associated linear system.Furthermore, We use the developed theory to a swine parasitic disease model with pulse therapy and obtain threshold results on its global dynamics in terms of $\mathcal{R}_{0}$. We hope that our method can also be applied to more general population models or epidemic model with impulse.

In the early stage of the disease outbreak, the corresponding measures have not been implemented. If the time of the outbreak of the infectious disease can be known, preparing in advance is of great significance for controlling the spread of the infectious disease. Turkyilmazoglu ^[28] proposed a explicit formulae for the peak time of SIR model. Kröger et al. ^[29] compared different forecasting methods and this is a very meaningful but challenging task for non-autonomous impulsive systems.

Acknowledgments

We are grateful to the anonymous referees and the editors for their valuable comments and suggestions which improved the quality of the paper. This work is supported by the NNSF of China (11861044), the NSF of Gansu of China(21JR7RA212 and 21JR7RA535) and the HongLiu first-class disciplines Development Program of Lanzhou University of Technology.

Conflict of interest

The authors declare there is no conflict of interest.