Socio-technical transitions and innovation niches: the case of the virtual and augmented reality in Europe

1.   Introduction

The fuzzy set ($\mathbb{FS}$) ^[1] is a useful mathematical approach for dealing with uncertain situations. It focuses on the membership grade of an individual in the sample space. The $\mathbb{FS}$ has several limitations, as it cannot discuss the parametrization tool, which results in uncertainty when inquiring about solutions to various problems. To conquer such types of issues, there is a need for the development of some mathematical mechanisms. The soft set ($\mathbb{SS}$) ^[2] was created to address such constraints. The $\mathbb{SS}$ is a parameterized collection of subsets of $\mathbb{U}$, the universal set. Ali et al. ^[3] discussed operations for $\mathbb{SS}$s. Fuzzy soft set ($\mathbb{FSS}$) ^[4] is facilitated $\mathbb{FS}$ with the inclusion of a parameterization tool. Yang et al. ^[5] intermingled $\mathbb{SS}$ with interval-valued fuzzy set ($\mathbb{IVFS}$) ^[6] to form interval-valued fuzzy soft set ($\mathbb{IVFSS}$) for interval-type data. Many researchers used the concept of $\mathbb{IVFSS}$ to solve real-world problems, particularly the work of Peng and Yang ^[7], Peng and Garg ^[8], Chetia and Das ^[9], Qin and Ma ^[10], and Ma et al. ^[11,12]. Sebastian and Ramakrishnan ^[13] initialized the multi-fuzzy set ($\mathbb{MFS}$) as an extension to $\mathbb{FS}$. The novel concept of interval-valued multi-fuzzy soft set ($\mathbb{IVMFSS}$) was initiated by Zhou et al. ^[14] as the unification of multi-fuzzy soft set ($\mathbb{MFSS}$) ^[15] and $\mathbb{IVFSS}$. Dey and Pal ^[16] generalized $\mathbb{MFSS}$. The contributions of the researchers like Gergin et al. ^[17], Riaz & Farid ^[18], Ashraf et al. ^[19] and Das & Granados ^[20] are worth noting about the use of various decision making techniques for discussing multidisciplinary applications in fuzzy hybrid structures. In dealing with real-world scenarios, the $\mathbb{DM}$ is sometimes affected when the decision-makers ignore sub-attributes and fully rely on attributes. This may distract decision-makers and lead to misunderstandings. So to make the decision more consistent, parameters need to be sub-classified in the form of sub-parametric-valued sets. The inclusion of approximate mapping with multi-argument ($\mathbb{MAAM}$) in the Hypersoft set ($\mathbb{HSS}$) ^[21] model easily handles such situations. Abbas et al. ^[22] discussed the basic operations of $\mathbb{HSS}$ and $\mathbb{HS}$-point. Elementary notions of $\mathbb{HSS}$ were discussed by Saeed et al. ^[23]. Rahman et al. ^[24,25,26] initiated the modification of the $\mathbb{HSS}$ for not only complex structures but also convex and concave structures. Debnath ^[27] used weight operators in fuzzy hypersoft sets ($\mathbb{FHSS}$) $\mathbb{DM}$. Yolcu & Öztürk ^[28] discussed various properties and operations of $\mathbb{FHSS}$ and explained them with examples. They ^[29] also developed topological structures based on the theory of $\mathbb{FHSS}$ and discussed the various properties of these structures. Rough hypersoft sets ($\mathbb{RHSS}$s) were developed by ^[30] along with their application in the selection of chemical materials. The hybrid structure of $\mathbb{HSS}$ with rough set was initiated by Kamacı ^[31]. Yolcu et al. ^[32] developed intuitionistic fuzzy hypersoft set by extending their own concept of $\mathbb{FHSS}$. Similarity measures for $\mathbb{SS}$, $\mathbb{FSS}$, and $\mathbb{IVFSS}$ were discussed by Majumdar, Samanta, and Peng et al. ^[33,34,35]. The entropy of $\mathbb{IVFS}$s on the basis of similarity measure and distance measure was initiated by authors ^[36,37]. $\mathbb{DM}$ with multi-argument for neutrosophic hypersoft sets based on aggregations and similarity measures was instigated by Rahman et al. ^[38].

1.1.   Relevant literature, research gap and motivations

It is a well-known fact that any evaluation or optimization problem based on parameterization-like approximations cannot be solved by simply taking parameters into account. This problem thus creates a different circumstance that necessitates careful parameter observation. Each parameter in this scenario is further divided into a set of related sub-parametric values. This classification helps decision-makers make reliable and consistent decisions by providing their approximate opinions with the right to multiple arguments at the same time. By substituting the single set of parameters in the domain of soft sets with the cartesian product of sub-parametric valued disjoint sets, one can create such a multi-argument domain. The absence of this particular setting, known as a "hypersoft setting", could result in a biased conclusion. It is important to note, after reading through the literature on fuzzy soft sets, that the researchers ^{[39,40,41,42,43,44,45,46,47,48,49,50,51,52]} have previously examined a number of decision-making applications and proposed methods based on $\mathbb{IVFSS}$. The Table 1 presents a brief review of these references with descriptions of their adopted applications. Although they make great contributions in the case of a soft setting, their contributions are insufficient in the substantial decision-making scenario indicated above, which is a hypersoft setting. Therefore, motivated by this shortcoming of the existing literature, the purpose of this study is to characterize the novel model "$\mathbb{IVFHSS}$" that is capable of coping with this shortcoming. The wide scope and flexibility of this model can be estimated from the fact that it generalizes most of the previous soft set-like models. This additional feature makes this model more adaptable and comprehensive in dealing with hesitant data. Moreover, the notions of similarity measures based on $\mathbb{IVFHSS}$, are also introduced and then applied to the decision-making problem of "recruitment process" through a pattern recognition-based robust algorithm.

1.2.   Major contributions of the study

The main contributions of this research article are described below:

${\bf{(1)}}$ The concept of similarity measures for $\mathbb{IVFHSS}$ is discussed, and one of its important results, is generalized.

${\bf{(2)}}$ A decision-support system is designed by using the formulations of similarity measures and aggregation operations of $\mathbb{IVFHSS}$ with the proposal of a robust algorithm. The computational steps are made easy for all kinds of multidisciplinary audiences.

${\bf{(3)}}$ The suggested algorithm is tested using a decision-making application, or recruitment process that helps decision-makers choose the best applicant for the open position in an institution by using pattern recognition based on similarity measures of $\mathbb{IVFHSS}$.

${\bf{(4)}}$ By structurally comparing the proposed decision-support system and model to existing models and taking into consideration appropriate evaluation indicators, the flexibility and reliability of both are evaluated.

The outlines of the paper are as follows: In Section 2, some definitions of "fundamental nature" are recalled from literature to make the paper understandable to the readers. In Section 3, similarity measures based on $\mathbb{IVFHSS}s$ are formulated and their relevant theorems and results are proved. In Section 4, the formulations of similarity measures between $\mathbb{IVFHSS}s$ are then applied in designing a decision-support system for recruitment based pattern recognition. Moreover, the computed results are compared with already developed models to judge the advantageous features of the proposed study. Lastly, the paper is summarized in Section 5 with discussion on managerial implications and future directions.

1.3.   Abbreviation

Full names of the used abbreviations are presented in Table 3.

2.   Preliminaries

Let $\mathbb{U}, \, \mathbb{P}(\mathbb{U}), \, \mathbb{C}(\mathbb{U})$ represent the universe of discourse, the collection of all subsets of $\mathbb{U}$ and the collection of all fuzzy sets of $\mathbb{U}$ respectively, and $\mathcal{W}$ be the set of attributes.

Definition 2.1. ^[1] A fuzzy set $\mathbb{F}$ over $\mathbb{U}$ is characterized by a membership function $f_\mathbb{F}$, where $f_\mathbb{F}:\mathbb{U}\, \to\, [0, 1]$ is given by

which assigns a real value within $[0, 1]$ to each $z\, \in\, \mathbb{U}$ and $f_\mathbb{F}(z)$ is the membership grade of $z \in \mathbb{U}$.

Definition 2.2. ^[6] An interval-valued fuzzy set ($\mathbb{IVFS}$) $\mathbb{V}$ over $\mathbb{U}$ is given by a function $\mathfrak{I}_{\mathbb{V}}:\mathbb{U} \to \mathbb{I}([0, 1]),$ where $\mathbb{I}([0, 1])$ denotes the set containing all sub-intervals of $[0, 1]$, $\mathfrak{I}_{\mathbb{V}}(z)$ for all $z \in \mathbb{U}$ is an interval $[\sigma, \nu], 0 \le\sigma\le\nu\le1, \sigma$ and $\nu$ denote the lower and upper membership-grades of an element, respectively.

For convenience, say $a = [\sigma, \nu]$ an interval-valued fuzzy number $\mathbb{IVF}$-number and the set of all $\mathbb{IVFS}$s over $\mathbb{U}$ is represented by $\Gamma(\mathbb{U}).$

Definition 2.3. ^[2] A soft set $\mathbb{S}_S$ over $\mathbb{U}$ is stated as $\Lambda_{\mathbb{S}_S}:\mathcal{W'} \to \mathbb{P}(\mathbb{U}),$ and $\mathcal{W'} \subseteq \mathcal{W}$ and is given by

The value $\Lambda_{\mathbb{S}_S}(\theta)$ is called $\theta$-approximate element of soft set $\mathbb{S}_S$.

Definition 2.4. ^[4] A fuzzy soft set ($\mathbb{FSS}$) $\mathbb{F}_{\mathbb{S}_S}$ over $\mathbb{U}$ is defined as $\Delta_{\mathbb{F}_{\mathbb{S}_S}}:\mathcal{W'} \to \mathbb{C}(\mathbb{U})$ and is given by $\mathbb{F}_{\mathbb{S}_S} = \left\{ (\theta, \Delta_{\mathbb{F}_{\mathbb{S}_S}}(\theta)):\theta \in \mathcal{W'}\right\}, \Delta_{\mathbb{F}_{\mathbb{S}_S}}(\theta) \in \mathbb{C}(\mathbb{U})$ for $\mathcal{W'} \subseteq \mathcal{W}$, $\Delta_{\mathbb{F}_{\mathbb{S}_S}}(\theta) = \phi$ for $\theta \notin \mathcal{W'}$ and

for all $\theta \in \mathcal{W'}$ is a $\mathbb{FS}$ over $\mathbb{U}$, where $\Delta_{\mathbb{F}_{S_\mathcal{W'}}}$ is approximate function of $\mathbb{F}_S$, $\Delta_{\mathbb{F}_S}(z)$ is a $\mathbb{FS}$ with condition that if $\Delta_{\mathbb{F}_{S_\mathcal{W'}}}(\theta) = \phi$, then $(\theta, \Delta_{\mathbb{F}_{S_\mathcal{W'}}}(\theta)) \notin \mathbb{F}_{S_\mathcal{W'}}$.

Definition 2.5. ^[5] The pair $(\mathcal{\tilde{F}}_{S}, \mathcal{W})$ is called an "interval-valued fuzzy soft set ($\mathbb{IVFSS}$) over $\mathbb{U}$ and is given by $\mathcal{\tilde{F}}_{S}:\mathcal{W} \to \mathbb{P}(\mathbb{U})$. In other words, $\mathbb{IVFSS}$ is parameterized collection of $\mathbb{IVF}$-subsets of $\mathbb{U}$ and is defined as

where $\mathcal{\tilde{F}}_{S}(\theta)$ represent the $\mathbb{IVF}$ membership degree of $\tau \in \mathbb{U}, \theta \in \mathcal{W}$. $\mathcal{\tilde{F}}_{S}(\theta)$ will become fuzzy set if $\xi^-_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau) = \xi^+_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ for all $\tau \in \mathbb{U}, \theta \in \mathcal{W}$.

Definition 2.6. ^[5] The compliment $(\mathcal{\tilde{F}}_{S}, \mathcal{W})^c$ of $\mathbb{IVFSS}$ $(\mathcal{\tilde{F}}_{S}, \mathcal{W})$ is given by $(\mathcal{\tilde{F}}_{S}, \mathcal{W})^c = (\mathcal{\tilde{F}}^c_{S}, \mathcal{W})$ and is given by $\mathcal{\tilde{F}}^c_{S}(\theta) = [1-\xi^+_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau), 1-\xi^-_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)]$ for all $\tau \in \mathbb{U}, \theta \in \mathcal{W}$.

Definition 2.7. ^[7] Based on Definition 2.6, distance measure between interval-valued fuzzy numbers ($\mathbb{IVFN})$ $\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ and $\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)$ is given by

Definition 2.8. ^[53] The score function $s(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau))$ of $\mathbb{IVFSS}$ $(\mathcal{\tilde{F}}_{S}, \mathcal{W})$ for all $\tau \in \mathbb{U}, \theta \in \mathcal{W}$ is defined as

where $s(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)) \in [-1, 1]$.

Definition 2.9. ^[53] The accuracy function $a(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau))$ of $\mathbb{IVFSS}$ $(\mathcal{\tilde{F}}_{S}, \mathcal{W})$ for all $\tau \in \mathbb{U}, \theta \in \mathcal{W}$ is defined as $a(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)) = \xi^-_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau) - \xi^+_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)+1$, where $a(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)) \in [0, 1]$.

Peng et al. ^[35] developed comparative laws for $\mathbb{IVFSS}$s on the basis of the score function and accuracy function.

Definition 2.10. ^[35] The following laws hold for any two $\mathbb{IVF}$-numbers $\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ and $\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)$: If $s(\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)) \ne s(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau))$, then

(1) $\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ is superior to $\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)$ if $s(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)) > s(\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau))$;

(2) $\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)$ is superior to $\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ if $s(\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)) > s(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau))$.

If $s(\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)) = s(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau))$, then

(3) $\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ is superior to $\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)$ if $a(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)) > a(\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau))$;

(4) $\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)$ is superior to $\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ if $a(\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)) > a(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau))$;

(5) $\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)$ and $\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau)$ are equivalent if $a(\xi_{\mathcal{\tilde{F}}_{S}(\theta)}(\tau)) = a(\xi_{\mathcal{\tilde{J}}_{S}(\theta)}(\tau))$.

Definition 2.11. ^[21] The pair $(\mathbb{\tilde{H}}_{S}, \mathcal{Q})$ defined by $\mathbb{\tilde{H}}_{S}:\mathcal{Q}\to \mathbb{P}(\mathbb{U})$ is called hypersoft set ($\mathbb{HSS}$) over $\mathbb{U}$ with $\epsilon_1, \epsilon_2, \ldots, \epsilon_n$ are distinct attributes belonging to disjoint attribute valued sets $\mathcal{Q}_1, \mathcal{Q}_2, \ldots, \mathcal{Q}_n$, respectively and $\mathcal{Q} = \mathcal{Q}_1\times\mathcal{Q}_2\times\cdots\times\mathcal{Q}_n$ be cartesian product of non-overlapping attribute valued sets.

Definition 2.12. ^[21] Let $\epsilon_1, \epsilon_2, \ldots, \epsilon_n$ are distinct attributes belonging to disjoint attribute valued sets $\mathcal{Q}_1, \mathcal{Q}_2, \ldots, \mathcal{Q}_n$ such that for $i, j = 1, 2, \ldots, n, i \ne j, \mathcal{Q}_i \cap \mathcal{Q}_j = \phi$, then $(\mathcal{\tilde{F}_H}, \mathcal{Q})$, the fuzzy hypersoft set ($\mathbb{FHSS}$) over $\mathbb{U}$ is given by ordered paired sets

where $\mathcal{\tilde{F}}:\mathcal{Q} \to \mathbb{C}(\mathbb{U})$ and $\mathbb{C}(\mathbb{U})$ be collection of all $\mathbb{FS}$s over $\mathbb{U}$ with $\sigma\in\mathcal{Q} = \mathcal{Q}_1\times\mathcal{Q}_2\times\cdots\times\mathcal{Q}_n$, then

is a $\mathbb{FS}$ over $\mathbb{U}$.

Definition 2.13. ^[23] Let $\epsilon_1, \epsilon_2, \ldots, \epsilon_n$ are distinct attributes belonging to disjoint attribute valued sets $\mathcal{Q}_1, \mathcal{Q}_2, \ldots, \mathcal{Q}_n$ such that for $i, j = 1, 2, \ldots, n, i \ne j, \mathcal{Q}_i \cap \mathcal{Q}_j = \phi$, then $(\mathbb{\tilde{F'}_H}, \mathcal{Q})$, the interval-valued fuzzy hypersoft set ($\mathbb{IVFHSS}$) over $\mathbb{U}$ is given by ordered paired sets

where $\mathbb{\tilde{F'}}:\mathcal{Q} \to \mathbb{C}(\mathbb{U})$ and $\mathbb{C}(\mathbb{U})$ be collection of all $\mathbb{IVFS}$s over $\mathbb{U}$ with $\sigma\in\mathcal{Q} = \mathcal{Q}_1\times\mathcal{Q}_2\times\cdots\times\mathcal{Q}_n$, then

is $\mathbb{IVFS}$ over $\mathbb{U}$.

3.   Formulations of similarity measure for $\mathbb{IVFHSS}$

In this section, the similarity measure for $\mathbb{IVFHSS}$ is discussed.

Definition 3.1. Let $\mathcal{\tilde{F}}$, $\mathcal{\tilde{J}}$ and $\mathbb{\tilde{H}}$ be three $\mathbb{IVFHSS}$s over $\mathbb{U}$. A mapping $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$ is the similarity measure given by $\Lambda: ivfs(\mathbb{U}) \times ivfs(\mathbb{U}) \to \mathbb{IVFN}$ if the following conditions hold:

(1) $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$ is $\mathbb{IVF}$-number;

(2) $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}}) = [1, 1]$ if and only if $\mathcal{\tilde{F}} = \mathcal{\tilde{J}}$;

(3) $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}}) = \Lambda (\mathcal{\tilde{J}}, \mathcal{\tilde{F}})$;

(4) If $\mathcal{\tilde{F}} \subseteq \mathcal{\tilde{J}} \subseteq \mathbb{\tilde{H}}$, then $\Lambda (\mathcal{\tilde{F}}, \mathbb{\tilde{H}}) \subseteq \Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$ and $\Lambda (\mathcal{\tilde{F}}, \mathbb{\tilde{H}}) \subseteq \Lambda (\mathcal{\tilde{J}}, \mathbb{\tilde{H}})$.

Theorem 3.2. Let $\mathcal{\tilde{F}}$ and $\mathcal{\tilde{J}}$ are $\mathbb{IVFHSS}$s over $\mathbb{U}$, then $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$ is a similarity measure given by

where $\sum\limits_{l = 1}^n {\mu _l} = 1$ such that $\mu _l$ is weight of $l$th $\mathbb{IVF}$-number.

Proof. To show that $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$ is a similarity measure for $\mathbb{IVFHSS}$s, it must satisfy four conditions.

Condition Ⅰ: As

so $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$ is $\mathbb{IVF}$-number.

Condition Ⅱ: If $\Lambda(\mathcal{\tilde{F}}, \mathcal{\tilde{J}}) = [1, 1]$, then

and

So $\left| {\sigma _{il}^ - - \sigma _{jl}^ - } \right| \ge 0$ and $\left| {\sigma _{il}^ + - \sigma _{jl}^ + } \right| \ge 0$ which means $\sigma _{il}^ - = \sigma _{jl}^ -$ and $\sigma _{il}^ + = \sigma _{jl}^ +$ and hence $\mathcal{\tilde{F}} = \mathcal{\tilde{J}}$.

Conversely, If $\mathcal{\tilde{F}} = \mathcal{\tilde{J}}$, then $\sigma _{il}^ - = \sigma _{jl}^ -$ and $\sigma _{il}^ + = \sigma _{jl}^ +$, so $\left| {\sigma _{il}^ - - \sigma _{jl}^ - } \right| \ge 0$ and $\left| {\sigma _{il}^ + - \sigma _{jl}^ + } \right| \ge 0$, which means

and

and hence $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}}) = [1, 1]$.

Condition Ⅲ: It can be easily shown that $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}}) = \Lambda (\mathcal{\tilde{J}}, \mathcal{\tilde{F}})$.

Condition Ⅳ: If $\mathcal{\tilde{F}} \subseteq \mathcal{\tilde{J}} \subseteq \mathbb{\tilde{H}}$, then $\sigma _{1l}^ - \le \sigma _{2l}^ - \le \sigma _{3l}^ -$ and $\sigma _{1l}^ + \le \sigma _{2l}^ + \le \sigma _{3l}^ +$. Also one can write $\left| {\sigma _{1l}^ - - \sigma _{3l}^ - } \right| \ge \left| {\sigma _{1l}^ - - \sigma _{2l}^ - } \right|$ and $\left| {\sigma _{1l}^ + - \sigma _{3l}^ + } \right| \ge \left| {\sigma _{1l}^ + - \sigma _{2l}^ + } \right|$. Therefore,

and

Hence, $\Lambda (\mathcal{\tilde{F}}, \mathbb{\tilde{H}}) \subseteq \Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$.

Similarly it can be shown that $\Lambda (\mathcal{\tilde{F}}, \mathbb{\tilde{H}}) \subseteq \Lambda (\mathcal{\tilde{J}}, \mathbb{\tilde{H}})$.

4.   Recruitment pattern recognition based decision-support system

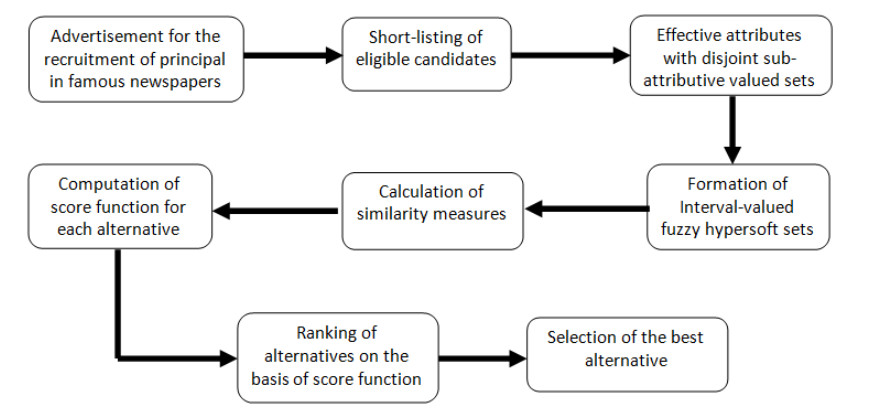
It is easier to focus on parameters and sub-parameters in real-world scenarios. As a result, parameters are sub-classified into disjoint attribute valued sets to investigate their impact on selecting the best alternatives during the recruitment process. Another important factor that affects the $\mathbb{DM}$ process in real-world problems is that the data is not taken in the form of intervals, so when interval-valued fuzzy values are assigned to parameters or sub-parameters, this makes the selection process more competent and reliable as its results become more precise and accurate. The process of $\mathbb{DM}$ based on similarity measures in $\mathbb{IVFHS}$ environments considers non-overlapping attribute-valued sets instead of attributes, making this selection process more reliable and result-oriented. The model of similarity pattern recognition for recruitment is displayed in Figure 1.

4.1.   Statement of the problem

In this section, the recruitment process is done based on similarity measures. An ideal case with specific criteria forms the basis of the model. All the alternatives that fall within the minimum eligibility criteria are taken into consideration. The similarity is measured among the other options and ideal cases. The alternative with maximum similarity will be selected.

Example 4.1. The college's administrative staff is looking for qualified candidates to fill the position of principal. There is a set of four decision-makers from four different fields, each with more than 20 years of experience. The recruitment process for the post of principal of a college is done based on a proposed algorithm. An advertisement is published in three famous newspapers, specifying the basic qualifications and minimum experience of candidates. There were 18 applicants who applied for the job. Only five candidates meet the specified criteria and are chosen for an interview. A team of decision-makers consisting of four experts is given the task of recruiting the best candidate for the post. This team specifies other criteria for the recruitment process that are not mentioned in the advertisement. The chairman of the committee sets criteria for the decision-makers and fixes a model. The interviewing committee assigns specific values in the form of intervals. The similarity measure is performed using $\mathbb{IVFHSS}$s.

4.2.   Effective attributes with their attributive valued sets

In this section, effective attributes and their disjoint attribute-valued sets are discussed.

(1) Experience Type: The principal is the head of an educational institution. He must know all the intricacies of the organization. Previous experience in an institution, especially an educational institution, is very helpful in dealing with such complexities. Experience is mainly of three types, depending on the level of the institution. 1. Teaching Experience: Experience in teaching secondary and higher classes. 2. Office management experience: experience in office management, including the account and data management branches. 3. Managerial experience: experience in managing educational institutions. Managerial experience is preferred over the other two types due to the nature of the job. Similarly, teaching experience weighs less compared to office management experience. So while assigning values to sub-attributes and transforming those values into fuzzy values, preference is taken into consideration. That is why teaching experience, office management experience, and managerial experience have been assigned fuzzy interval values of 0-0.33, 0.34-0.66, and 0.67-1, respectively, and displayed in Tables 3 and 4.

(2) Experience period: Five years of experience are required for eligibility for the post of principal, so five years of experience will act as the baseline. Experience is more than what is categorized into four levels. Level Ⅰ$=$ more than 5 years of experience, up to a maximum of 10 years. Level Ⅱ$=$ more than 10 years of experience, up to a maximum of 15 years. Level Ⅲ$=$ more than 15 years of experience, up to a maximum of 20 years. Level Ⅳ$=$ more than 20 years. Based on preference, experience periods are arranged in ascending order and assigned fuzzy values in such a way that a smaller fuzzy value corresponds to a less experienced period and a greater fuzzy value corresponds to a more experienced period, as displayed in tables 3 and 4.

(3) Higher qualification: Sixteen years of education are the basic educational criteria for a candidate to be eligible for the post of principal. Higher qualification is preferred, which is categorized into three levels. Level Ⅰ$=$ MS (eighteen years of education). Level Ⅱ$=$ Ph.D. (21 years of education). Level 3$=$ Post-doctoral. Fuzzy values corresponding to higher qualifications are given in Table 3 and Table 4.

(4) Extra qualification: Besides academic qualifications, professional qualifications such as degrees in educational planning and management, assessment, leadership learning, etc. enhance the leadership competencies and the $\mathbb{DM}$ power of an individual. So candidates with professional degrees have greater abilities to manage and control educational institutions. The candidates with extra qualifications are given preference over the candidates with no qualifications.

(5) Communication skills: communication skills are the ability of an individual to share information effectively. Being the head of an institution, the principal should be good at giving and taking information from his subordinates and leaders of other institutions. There are mainly three types of communication skills. 1. Verbal communication (VC): Verbal communication exploits spoken words. VC is necessary for most interactions, but there are other nods that facilitate extra circumstances beyond the expressions of their own. 2. Nonverbal communication (NVC): Nonverbal communication offers some insight into a spokesperson's word selection. NVC includes derision, gratification, and legitimacy, which are communicated not only through posture but also through body gestures, facial expressions, and physical appearance. A disheveled presenter with unironed clothes and a pitiable posture would depict low confidence or proficiency. On the other hand, a well-suited speaker, who spoke clearly, came out to be more serious and well-informed. 3. Visual communication (VIC): Visual communication consists of signs, graphic designs, and drawings. Vi-aids help a spokesperson memorize important points and facilitate the listener's easy understanding of the message. Individuals with dominant communication skills are preferred over others.

(6) IT skills: A principal must have basic IT knowledge. He must have a keen knowledge of his surroundings. He must be aware of what is happening around the globe. A principal is a role model for his institution, so he must have the latest knowledge and IT skills. An individual having dominant IT skills is preferred over others lacking such qualities.

(7) Leadership skills: There are some specific qualities that the principal of an educational institution must have. He is responsible for every aspect of the institution. He has to manage six levels of people, including students, teachers, clerical staff, support staff, parents, and community members. He should have the ability to deal with all levels. Creativity, flexibility, motivation, and self-awareness are the qualities of Principle that dominate him over others.

Effective attributes with their disjoint attributive value sets are summarized in Table 3, where values corresponding to attributes and transformed fuzzy values are displayed in Table 4.

4.3.   Problem description

Let $\mathbb{U} = \left\{z_1, z_2, \ldots, z_p\right\}$ be the sample space and $(\mathcal{\tilde{F}}, \mathcal{Q})$ be $\mathbb{IVFHSS}$ over $\mathbb{U}$ where $\epsilon_1, \epsilon_2, \ldots, \epsilon_q$ are distinct attributes belonging to disjoint attribute valued sets $\mathcal{Q}_1, \mathcal{Q}_2, \ldots, \mathcal{Q}_q$ such that for $i, j = 1, 2, \ldots, q, i \ne j, \mathcal{Q}_i \cap \mathcal{Q}_j = \phi$ with weight of each $\theta_i \in \mathcal{W} : \mathcal{W} = \mathcal{Q}_1\times\mathcal{Q}_2\times\cdots\times\mathcal{Q}_q$ is $\mu_i$ and $\sum\limits_{l = 1}^q {\mu _l} = 1$. $\mathbb{IVFHSS}$ $(\mathcal{\tilde{F}}, \mathcal{Q})$ can be expressed in the form of Table 5.

4.4.   Decision-support system based on similarity measures of $\mathbb{IVFHSS}$s

There are a lot of applications of similarity measures in fields like coding theory, image processing, pattern recognition, etc. The concept tells us whether two pictures are alike or how much they are similar. The concept of a similarity measure for $\mathbb{SS}$s, $\mathbb{FSS}$s, and generalized $\mathbb{FSS}$s was initiated by Majumdar, and Samanta ^[33,34]. Similarity measures between two $\mathbb{IVFHSS}$s adopted from Majumdar & Samanta ^[33,34] and Peng et al. ^[35] with slight variations. An easier and more accepted set-theoretic approach has been utilized in computations. $\mathbb{DM}$ based on an extended form of the similarity measure, is done with the proposed model under an $\mathbb{IVFHSS}$ environment. This section introduces a new method for solving $\mathbb{DM}$ real-world problems based on a proposed similarity measure. The "ideal point" concept is utilized to select the best option among the given alternatives. Even though the existence of an ideal alternative is impossible in practical problems, it is possible to construct a theoretical alternative to perfection. Therefore, let $\rho^I$ be an ideal alternative as $\mathbb{IVF}$-number $\rho^I_j = [1, 1]$ for all values of $j$. Therefore, by using Eq 3.1, the similarity measure $\Lambda (\mathcal{\tilde{F}}, \mathcal{\tilde{J}})$ between alternative ${\rho_i}$ and ideal alternative $\rho^I$ is represented by $\mathbb{IVFHSS}$ is given by

4.5.   Proposed Algorithm and Implementation on Similarity measure method ($\mathbb{SM}$-method)

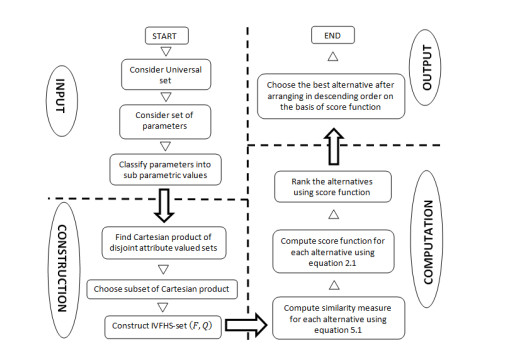
In this section, the $\mathbb{SM}$-method for $\mathbb{IVFHSS}$ is applied in $\mathbb{DM}$. $\mathbb{SM}$ is calculated for $\mathbb{IVFHSS}$ after developing the proposed algorithm.

The flow chart of algorithm is displayed in Figure 2.

Example 4.2. Consider Example 4.1. The five candidates who fulfill the criteria for the job vacancy are shortlisted for an interview.

(1) Input Stage(Step 1–Step 3): The five candidates (alternatives) form the universal set $\mathbb{U} = \left\{\rho_1, \rho_2, \rho_3, \rho_4, \rho_5\right\}$. Let $\ddagger = \left\{\ddagger_1, \ddagger_2, \ddagger_3, \ddagger_4\right\}$ be the set of four experts, including $\ddagger_1$, the chairman of the recruitment committee. The process of recruitment is done on the basis of the proposed algorithm. The committee specifies other criteria for the recruitment process that are not mentioned in the advertisement. The chairman of the committee sets criteria for the decision-makers and fixes a model. The interviewing committee assigns specific values in the form of intervals. The similarity measure is done on the basis of $\mathbb{IVFHSS}$s. Let $\left\{ \right.$Experience type, Experience period, Higher qualification, Extra qualification, Communication skills, IT skills, Leadership skills$\left. \right\}$ be the set of attributes selected by the recruitment committee. Mathematically, this set can be written as $\Delta' = \left\{\Delta_1, \Delta_2, \Delta_3, \Delta_4, \Delta_5, \Delta_6, \Delta_7\right\}$. These attributes are sub-categorized into non-overlapping attribute valued sets, which are described as follows:

(2) Construction Stage (Step 4, Step 5): Now,

where $t = 3 \times 4 \times 3 \times 2 \times 2 \times 2 \times 2 = 576$, and each $\hat{d}_i$ is a seven-tuple element of $\Delta$. Consultation with education experts, $\delta_{11}$ and $\delta_{12}$ is preferred in $\Delta_1$, $\delta_{23}$ and $\delta_{24}$ are preferred in $\Delta_2$, $\delta_{31}$ and $\delta_{32}$ are preferred in $\Delta_3, \delta_{42}$ is preferred in $\Delta_4, \delta_{52}$ is preferred in $\Delta_5$, $\delta_{62}$ is preferred in $\Delta_6, \delta_{72}$ is preferred in $\Delta_7$. Therefore, the set $\bigwedge \subset \Delta$ has eight elements. So $\bigwedge = \left\{\wedge_1, \wedge_2, \wedge_3, \wedge_4, \wedge_5, \wedge_6, \wedge_7, \wedge_8\right\}$ where each $\wedge_i$ is again a seven tuple element. $(\mathcal{\tilde{F}}, \mathcal{Q})$, the $\mathbb{IVFHSS}$ is constructed, and its matrix formation is demonstrated in Table 6.

(3) Computation Stage(Step 6–Step 8): The weights as assigned to sub-parametric tuples by the expert committee are $(0.14, 0.09, 0.17, 0.06, 0.21, 0.10, 0.15, 0.08).$

As $\rho^I$ is an ideal alternative, utilizing Eq (4.1), similarity measure $\Lambda_{\rho_1}(\mathbb{F}, \mathcal{J})$ for $\rho_1$ can be calculated as follows:

So, $\Lambda_{\rho_1}(\mathbb{F}, \mathcal{J}) = \left[0.493, 0.691\right].$

In the same way, similarity measures $\Lambda_{\rho_2}(\mathbb{F}, \mathcal{J})$, $\Lambda_{\rho_3}(\mathbb{F}, \mathcal{J})$, $\Lambda_{\rho_4}(\mathbb{F}, \mathcal{J})$, $\Lambda_{\rho_5}(\mathbb{F}, \mathcal{J})$ for $\rho_2, \rho_3, \rho_4, \rho_5$ respectively can also be calculated as follows:

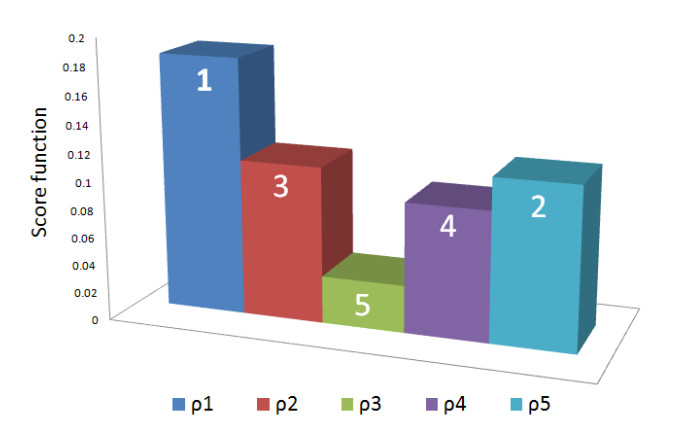
The score function for the alternative, $\rho_1$ can be calculated using Eq (2.1) as $S_{\rho_1} = 0.493+0.691-1 = 1.184-1 = 0.184$. Similarly, the score function for the remaining alternatives can be calculated as follows:

As it is clear that $S_{\rho_1} > S_{\rho_5} > S_{\rho_2} > S_{\rho_4} > S_{\rho_3}$, so on the basis of this score function, the alternatives are ranked in the following way:

$(4)$ Output Stage(Step 9): The score function clearly shows that alternative $rho_1$ is preferred over other alternatives due to its highest ranking. As a result, candidate $rho_1$ is chosen for the position of principal. The pictorial form of ranking is shown in Figure 3.

4.6.   Discussion and comparison analysis

The recruitment process as a MADM problem has been studied in uncertain environments by many researchers, but the most relevant work is the contributions of Tripathy et al. ^[40] who have discussed the recruitment process as a MADM problem in $\mathbb{IVFSS}$ environment. We now compare our computed results and ranking of the candidates with the computed results and ranking made by Tripathy et al. ^[40]. Although they have computed scores in terms of discrete values like 17, 16, 12, 6, and 9 for five candidates that are compatible with our structure, these scores are first converted to relevant fuzzy values by dividing each scoring value by the highest score, i.e., 17, and we obtain 1.000, 0.941, 0.705, 0.352, and 0.529, respectively. This comparison is presented in Table 7. The table clearly states that the score values computed through our proposed algorithm are more reliable and consistent because it is an admitted fact of numerical mathematics that "the smaller the values, the more reliable and precise the results are considered". Next, we compare our proposed model with some relevant existing models to assess its advantageous aspects by considering some important evaluating indicators like interval-valued settings, fuzzy membership grades, $\mathbb{SAAM}$ = single-argument approximate mapping, and $\mathbb{MAAM}$ = multi-argument approximate mapping. This comparison is usually known as structural comparison and is meant to judge the flexibility of the model. From Table 8, it is clear that most of the existing models are particular cases of our proposed model, which proves the flexibility of our model.

5.   Conclusions

In order to tackle the interval type of data and the partitioning of parameters into sub-parametric disjoint sets, a generalized model $\mathbb{IVFHSS}$ is characterized first, and then the notions of similarity measures between $\mathbb{IVFHSS}s$ are formulated. Some significant results and theorems are proved by using the properties of $\mathbb{IVFHSS}s$. Afterward, using the formulations of similarity measures of $\mathbb{IVFHSS}s$, a robust decision-support framework is designed which is accompanied by an intelligent algorithm that helps the decision makers to evaluate the suitability of a candidate for an advertised post through pattern recognition method. The computed results are then compared with the most relevant models to understand the advantages of the proposed study by considering some significant evaluation features. To cover the uncertain and vague nature of data, this model uses intervals with upper and lower bounds and fuzzy values. Using the $\mathbb{MAAM}$ model, data can be stored in fuzzy-valued intervals. The main benefit of this study is that it can handle a large amount of data in the form of intervals by taking into account the disjoint partitioning of parameters in the form of the multi-argument domain of $\mathbb{MAAM}$. It is also helpful for handling ambiguity and information-based uncertainties while approximating the alternatives using sub-parametric tuples. As far as the managerial implications and limitations of the proposed study are concerned, there are some real-world scenarios in which some special settings are required to be applied. Such scenarios may include:

${\bf{(1)}}$ The periodic nature of data in a complex plane which demands the entitlement of phase and amplitude terms,

${\bf{(2)}}$ The rough types of data which demand the concepts of lower and upper approximations,

${\bf{(3)}}$ The uncertain nature of parameters and their sub-parametric tuples demands the use of fuzzy parameterization settings. In such settings, a particular fuzzy membership grade is attached to each parameter or sub-parametric tuple to assess its vagueness.

The research covers almost the entire mainstream line of artificial intelligence, soft computing, and pattern recognition. In future directions, many structures, like intuitionistic fuzzy sets, neutrosophic sets, Pythagorean fuzzy sets, picture fuzzy sets, and refined fuzzy sets, can be hybridized with hypersoft sets to form new structures with their application in $\mathbb{DM}$. Similarly, other $\mathbb{DM}$ methods like TOPSIS, VIKOR, and AHP can also be applied to extend this study for addressing various $\mathbb{DM}$ problems.

Conflicts of interest

Authors declare no conflicts of interest.

Acknowledgments

This work was supported by the Technology Innovation Program (20018869, Development of Waste Heat and Waste Cold Recovery Bus Air-conditioning System to Reduce Heating and Cooling Load by 10%) funded By the Ministry of Trade, Industry & Energy (MOTIE, Republic of Korea).