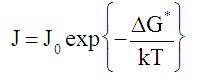1. Introduction

The use of nucleic acids as “drugs” to modify cellular functions was first proposed in the 1970s [1]. In the intervening period, nucleic-acid based therapies were developed where DNA and siRNA are used for the relief of diseases including cystic fibrosis and some types of cancer [2,3,4,5,6,7,8,9,10,11,12,13,14]. Critically, these carriers need to condense and stabilize the nucleic acid, which is otherwise vulnerable to be delivered “naked”. In addition, carriers must bind to the cell surface, transport into the cell cytosol, escape from the endosome and release the nucleic acid [2,3,4,5,6,7,8,9,10,11,12,13,14]. DNA carriers must import it into the nucleus for transcription, and siRNA carriers need to target specific tissues. In vivo systemic intravenous administration requires, in addition, the ability to circulate in the bloodstream for a prolonged period of time while resisting degradation by immune-agents. Combined, these specifications mean that carriers must be responsive to the biological environment to be functional [15,16,17,18].

Several formulations emerged as potential nucleic acid carriers; Viral-based systems are highly efficient delivery agents, but require complex processing, and their use in vivo can pose health risks [19]. Polymer-based synthetic carriers (polyplexes) are benign [20], but the strong bonding between the carrier cationic polymers and their cargo nucleic acid hinders necessary steps such as gene unpackaging (see, for example, [21]).

Complexes between nucleic acids and cationic lipids—lipoplexes—are a well-suited synthetic alternative to viral carriers [22,23,24,25,26]. The majority of studies to date focused on gene delivery, and thus, DNA-based lipoplexes. However, the potential therapeutic advantages of RNA interference shifted recently to small interfering (si) RNA vehicles, which were found to be similar in structure and properties to the DNA complexes [14,27,28,29,30].

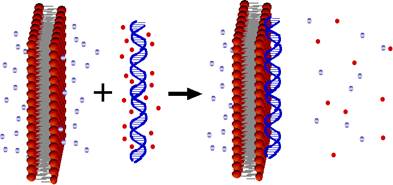
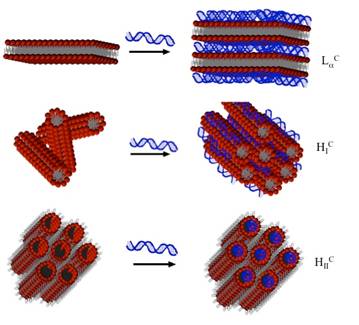
The local microstructure of lipoplexes, on length scales of order 100-500 nm, has been widely studied and is known to be set by equilibrium thermodynamic processes. This allowed constructing a “phase diagram” that links the lipid properties and the charge ratio (defined by the ratio between the cationic lipid and DNA charges −L/D, +/−) to structural features [31,32,33,34,35]. It has been shown that the preferred local geometry depends on the lipid properties, as sketched in Figure 1: Lipoplexes based on bilayer forming lipids are composed of a multi-lamellar structure where lipid bilayers intercalate with nucleic acid layers characterized by a regular spacing. Lipoplexes utilizing lipids that favor hexagonal arrays are composed of an underlying hexagonal structure. However, since lipoplex formation is driven by electrostatic attraction between the oppositely charged nucleic acid and lipids, detailed aggregate features vary with parameters such as the charge ratio or the interactions between nucleic acid molecules (hydrophobic end-to-end and electrostatic) [36,37,38,39,40,41].

Larger features of lipoplexes are less well defined. Irreversible processes such as flocculation lead to structural heterogeneity on length scales of order 1 mm or larger [42,43]. Since they depend on kinetic driven, rather than equilibrium, processes, global aggregate features are only weakly correlated with system parameters such as the charge ratio. Indeed, recent studies using microfluidics showed that the macroscopic features of lipoplexes (size, polydispersity) can be controlled by such parameters as the flow rates of the constituent solutions in both DNA and RNA systems[44,45,46].

The kinetics of the assembly process depend on additional parameters, such as the overall concentration of the components and system temperature [18]. Complex kinetics also depends on the initial form of the components (e.g. vesicle size) and complex preparation route (e.g. order and rate of mixing) [47,48,49]. Thus, while the ultimate local molecular lipoplex structure may be set by equilibrium, the route and rate by which the structure would be obtained, and larger scale lipoplex features, are set by the kinetics. Furthermore, some complexation rates have been found to be extremely long, on the order of hours or even days; as a result, studies conducted on moderately short time scales may be examining kinetically trapped structures rather than equilibrium systems.

Understanding the kinetics of lipoplex self-assembly is of fundamental and practical interest: Lipoplex formation is a multi-stage, multi-time scale and multi-length-scale process that encompasses many aspects of self-assembly relevant to various other systems (e.g. polyelectrolyte-amphiphile complexes). Many transfection steps, such as the release of the nucleic acid in the cell environment, are themselves a kinetic processes that would be better understood if the kinetics of assembly are known. Even more important is the correlation between the global lipoplex structure (size, shape, surface charge, etc.) and its efficacy [50,51,52,53] which control the circulation in vivo or interactions with cellular membranes. These properties are dominated by kinetics rather than equilibrium, so that controlling them requires control of the kinetic process.

Reviews of lipoplexes emphasize the properties of equilibrium structures and their effect on transfection efficiency and biological performance [31,32,33,34,35,50,51,52,53]. Few consider the kinetic aspects of assembly [18]. Yet, the link between biological function and global structure may confuse the correlation between local properties and efficacy.

The present review is focused on the kinetics of complex formation, suggesting that the process is similar to both adsorption of polyeletcrolytes on oppositely charged colloidal particles, and to cluster nucleation and growth. To put the process in context, we first briefly discuss the equilibrium features of lipoplexes, and in particular the local structure of the nucleic-acid/lipid assemblies. We next examine the kinetics of lipoplex formation, and conclude with a discussion section.

2. Equilibrium Lipoplex Structures

Lipid aggregation is driven by their amphiphilic structure. Aggregate geometry is set by the lipid molecular properties: Most favor bilayers/lamellae—manifested in the form of vesicles (liposomes) on large length scales (see, for example, [54]). However, some lipids may form hexagonal phases [55,56], as sketched in Figure 1.

Mixing cationic lipid assemblies with negatively charged nucleic acids leads to complex formation. Complexation is driven by electrostatics, and resembles polyelectrolyte adsorption on oppositely charged surfaces (see, for example, [57]): As any charged surface, lipid assemblies trap a fraction of their counterions in an “electrical double layer” whose thickness is of order 1/k, the Debye screening length [58]. A somewhat similar effect is known to occur in highly charged, rigid polyelectrolytes—a category that includes nucleic acids. In this “Manning condensation” some of the counterions of the charged polymer do not fully dissociate, so that the effective charge density is reduced [57]. Binding between the macroion and the lipid aggregate allows the release of these counterions, thereby increasing significantly the system entropy [57,59].

The adsorption of polyelectrolytes is dominated by the polymer molecular weight (MW) and its charge density. Due to the chain high MW, the number of segments that attach to the surface is large, so that the adsorption energy per segment may be as low as 0.3 kT (where k is the Boltzmann constant and T the temperature) [60], and still compensate for the entropy loss due to the immobilization of the polymer on the surface. The probability of any one segment detaching may be high (of order e^−Q/kT, where Q is the binding energy per segment), allowing local rearrangement via thermal fluctuations. However, polymer binding to the surface is irreversible since the large number of parallel binding events per chain means the overall binding energy is much higher than thermal energy or configurational entropy loss. The strength of the adsorption energy per segment, and the resultant adsorbed layer structure, depend on the solution ionic strength [61].

Similarly, in lipoplexes the binding free energy gain per nucleotide charge is rather small, of order ~kT or less, but complexes are stable due to the high number of binding sites per nucleic acid molecule. Theoretical predictions linking counterion release to lipoplex formation (see, for example, [39]) were later confirmed by calorimetry analysis of DNA interactions with both single lipids and lipid mixtures [47,62,63]. More recently, Cuomo, et al. found that the association between oligo and poly nucleotides depends on both the length of the chain and the charge density.

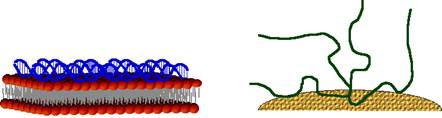
Despite similarities, two significant differences between polyelectrolyte adsorption and lipoplex formation must be considered. The first is due to the nature of the adsorbing macroion: The persistence length of DNA is of order 50nm, a value that is insensitive to the solution ionic strength [58]. This value is an order of magnitude larger than the lipid bilayer or hexagonal phase thickness [58]. In contrast, the typical rigidity of polyelectrolytes is of order 1nm, and is highly sensitive to the solution conditions [57]. As a result, adsorbed polyelectrolytes display “loops and trains”, and the layer thickness depends on the ionic strength [61], as sketched in Figure 3. In contrast, nucleic acid adsorbs onto the lipid surface in a flat layer whose thickness is the same order of magnitude as the nucleic acid diameter, insensitive to the solution ionic strength [23,35]. The ordered arrays are characterized by a regular spacing (see, for example, [22,23,35,39,41]).

The second significant difference between the two systems is the nature of the surface with which the macroion interacts. In the case of polyelectrolytes, the surface is rigid so that rearrangements in the adsorbed layer configuration occur only through local desorption and re-adsorption of polymer segments. The rigidity of nucleic acids limits (or even eliminates) rearrangement in this manner; however, the lipid surface can rearrange in response to external forces, such as those induced by the nucleic acids. Thus, while in polyelectrolyte adsorption the layer structure is set by the polymer rearrangement, in lipoplexes the dominant process is that of lipid reconfiguration.

As noted, some lipid species favor other geometries such as hexagonal or bicontinuous phases [55,56,58]. Theoretical calculations and coarse-grained simulations investigated the structure and thermodynamic stability of DNA-containing lipoplexes [36,37,38,39,40,41]. They predicted that complex structure should generally match that of the lipid phase (i.e. lamellar or hexagonal) [41]. However, since the presence of DNA affects the lipid packing, local “buckling” can occur [39], as indeed verified later by experiments [23,35]. Experimental studies also show that nucleic acid properties have only a weak effect on the local structure of lipoplexes: Similar arrays were reported for both linear lambda-phage DNA and circular plasmid DNA [23,35].

Lipoplexes may be based on a single component (cationic) lipid phase, or on a mixture of cationic and non-ionic species. The structure of complexes formed by DNA and bilayer-favoring lipids, whether pure cationic lipid systems e.g., dioleoyl-trimethylammonium propane (DOTAP) or mixtures of this lipid with the neutral lipid (dioleoyl-phosphadtidycholine, DOPC), was identified as a lamellar L_α^C phase [22,23,35,64] with the DNA strands within a layer organized in a two-dimensional liquid-crystal smectic array [22,35,36,37,38,40,47,65,66]. Characteristic dimensions for L_α^C lipoplexes are membrane thickness of ≈ 40 Å, and water gap accommodating a DNA monolayer between lipid bilayers ≈ 25 Å. Unlike the overall geometry, the typical spacing between DNA strands within a monolayer varies, e.g., between 25-50 Å for isoelectric complexes, depending on membrane charge density and L/D ratio (the ratio between the cationic lipid and DNA charges) [22,35].

In mixtures of bilayer-forming lipids with micellar-favoring lipids, other types of structures may form. Complexes containing dioleoyl-phosphadtidylethanolamine (DOPE), a non-ionic lipid with a relatively small headgroup that favors the inverse hexagonal mesophase, were found by Koltover et al. to display a rich phase behavior that was not observed in the lamellae-favoring DOPC [23]. Mixtures of DOTAP, DOPC and DOPE yielded L_α^C lipoplexes when the fraction of DOTAP was high. However, in mixtures where DOPE dominated (fraction of 0.7-0.85), complexes formed a two-columnar, inverted hexagonal phase, H_II^C—a honeycomb phase. In this structure DNA is coated by an inverse lipid monolayer into cylindrical micelles, which, in turn, are arranged to a hexagonal lattice, similar to the inverted hexagonal H_II phase of pure DOPE in water [67]. Typical diameter of the inverse micelles in H_II^C lipoplexes is ≈ 28 Å [23,35].

The structure of equilibrium L_α^C and H_II^C lipoplexes may be manipulated by changes in the environment. Studies demonstrated a dynamic transition from lamellar to hexagonal lipoplexes in isoelectric complexes of DNA and mixed neutral and cationic lipids, in response to an osmotic stress exerted by polyethylene glycol (PEG) [68]. The process was shown to be reversible by, for example, Scarzello et al. [69], so that H_II^C lipoplexes converted back to lamellar ones upon PEG dilution. In another study, of mixtures of N-methyl-4-(dioleoyl)methylpyridinium (SAINT) and DOPE, complexes exhibiting a lamellar phase were converted to stable non-lamellar H_II structures at high temperatures when suspended in a salt solution of physiological concentration.

Several other local symmetries were also reported: Complexes of DNA with mixtures of the multivalent cationic lipid MVLBG2 (dendritic headgroup with +16 charges) and DOPC were found by Ewert et al. [70] to exhibit the lamellar L_α^C phase at low MVLBG2 fraction. However, in a narrow range of compositions, a dual-lattice structure was detected of hexagonally arranged normal cylindrical lipid micelles surrounded by DNA, forming a continuous substructure with a hexagonal symmetry (H_I^C) [70]. At larger mole fractions of MVLBG2 a distorted hexagonal H_I^C phase was found by Zidovska et al. [71]. Similarly, in sugar-based Gemini surfactants, lamellar DNA complexes transitioned into H_I^C phase upon acidification [34,72]. Another phase, the bicontinuous cubic phase (termed Q_II and sometimes V_II), was found by Bilalov et al. in DNA complexes with lecithin and dodecyltrimethylammonium (DTA) in a narrow composition range [73]. Cubic bicontinuous structures are known to be intermediates of membrane fusion thus it was envisioned that complexes with this symmetry will present better biological activity, as indeed was recently indicated. Complexes formed between short DNA and mixtures of DOTAP and the nonionic lipid monoolein (GMO, a low water-solubility nonionic lipid known to extensively form non-lamellar mesophases—hexagonal and bicontinuous cubic [74]) were also found to form cubic bicontinuous phases with short DNA. These phases could reversibly transition to the inverted hexagonal phase by change in temperature, as found by Leal at al. [75].

The local structure of lipoplexes is defined not only by the local packing, or geometry of the lipids, but also by the properties of the associated nucleic acid array. The packing density of DNA in lamellar phases was predicted to increase monotonically with the cationic lipid content when the DNA concentration is low [36,37,38,39,40,41]. However, in higher DNA packing densities, we [39] predicted potential coexistence between closely packed and more dispersed domains, which was indeed observed later by Farago et al. [76].

The discovery of RNA interference (RNAi) as a post-transcriptional gene-silencing pathway by Fire et al. [77] led to exploration of complexes between small-interfering RNA (siRNA) and cationic lipids (or cationic polymers) for gene therapy of numerous chronic diseases and cancer [78,79,80,81]. Qualitatively, it is expected that siRNA lipoplexes would be similar to the DNA-lipid complexes. Indeed, numerous studies indicated that like for DNA-lipid systems, the lipid composition and L/D charge ratio are primary factors affecting the siRNA-lipid structures. Desigaux et al. [30] reported on lamellar lipoplexes formed in mixtures of custom-made aminoglycoside derivatives and siRNA. Small lipoplexes (<200 nm) formed in excess of one of the components, siRNA or cationic lipid, and large and unstable complexes at concentrations near charge neutralization (~700 nm) [30]. Two main lamellar morphologies were detected - of concentric multilamellar structures and of ordered lamellar microdomains, depending on the class of the aminoglucoside derivative. Importantly, both were shown to form also in DNA lipoplexes. Like for DNA, the presence of GMO induced formation of multiple siRNA lipoplex structures [35,82,83]. Lipoplexes displayed layered structure (Lα^siRNA) in mixtures of DOTAP and GMO at very low GMO concentrations [35], and a two-dimensional hexagonal array of inverse cylindrical micelles decorating siRNA (H_II^siRNA) at higher GMO concentrations. The transition between these two phases took place at a given GMO concentration, where both phases coexisted [35,82]. In mixtures containing a pentavalent cationic lipid and high excess of GMO the bicontinuous, Leal et al. found that a double gyroid cubic phase formed, with the siRNA molecules incorporated in the water channels [83]. Characteristic multilamellar siRNA lipid lipoplexes were also found by Aytar et al. [84] in mixtures containing the reduced form of the cationic lipid BFDMA (bis(11-ferrocenylundecyl) dimethylammonium bromide). Interestingly, lipoplexes of oxidized BFDMA and siRNA showed primarily amorphous structures.

While the similarities are striking, there are some key differences between DNA and siRNA lipoplexes [85]. First, siRNA is two orders of magnitude shorter than DNA, which can influence the carrier size. Second, siRNA’s high sensitivity to enzymatic degradation stimulated various modification to its backbone and conjugation strategies for improved stability [27,86,87]. In addition, challenges associated with the need to target specific tissues led to further modifications such as the addition of targeting ligands, addition of PEG moieties for steric stabilization in circulation, and inclusion of pH-sensitive groups to promote siRNA release (reviewed recently in [20]), all of which affect siRNA complex design and structure.

3. The Kinetics of Lipoplex Formation

The kinetics of lipoplex formation may be put in context by examining both the kinetics of cluster nucleation and growth, and of polyeletrolyte adsorption. All are multi-step processes, where a rapid initial complex (or cluster) formation stage is followed by growth and rearrangement steps that occur on much longer timescales.

The nucleation of nano-clusters from a supersaturated medium is well understood: In either homogeneous or heterogeneous processes, the nucleation rate depends only on thermodynamic equilibrium properties [88], and tends to be relatively rapid if there are strong attractive interactions between the molecular species composing the cluster. The rate of nuclei formation J, defined by the number of nuclei formed (per unit volume) per time, is given by [88]

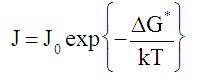(1)

where DG is the energy barrier to the formation of a critical cluster, and the pre-exponential rate factor J₀ is a function of the atomic vibration frequency, temperature and the properties of the critical cluster size [59]. The combination of terms in equation (1) leads to a non-monotonic dependence of the rate on temperature, where a maximum is achieved at a particular critical value [59,88].

Polyelectrolyte adsoprtion onto oppositely charged surfaces is also a complex process. Initially, the rate can be approximated by that of any adsorption process similar to equation (1), where DG represents the energy gain associated with the release of some of the surface and polyeletrolyte counterions. This energy gain will depend on the solution ionic strength, as well as the charge density of the surface and the polyelectrolyte, and the polymer molecular weight: For example, Filippova found that increasing the chain MW from 12 to 142 Kg/mol decreased the characteristic adsorption time from order 130 to 3 min [89]. However, the pre-exponential factor should be sensitive to species concentration and mobility. Furthermore, as the polymer layer builds on the surface, the driving force for adsorption (as defined by DG) decreases roughly as ln(1-f), where f is the fraction of total polymer adsorbed [59]. As a result, one of the models used to predict the rate of polyelectrolyte adsorption uses a collision probability expression that is proportional to both the concentration of the polyelectrolyte chains and the colloidal particles [59] with an associated rate constant that is given by the Smoluchowski expression [59], where the rate constant is inversely proportional to the medium viscosity. This approach is in good agreement with experimental studies [90,91,92,93,94].

The initial step in cluster formation is followed by stages of growth that are complex and variable. One growth mechanism is through the flocculation of clusters, where the rate depends on the frequency of cluster collision and the probability of adhesion upon collision [59]. The former depends on the concentration of clusters and their mobility, and the latter on the direct interaction between clusters [59]. Flocculation can also take place in systems of polyelectrolyte adsorption on colloidal particles, where the adsorbed layer affects colloid stability. Although in dilute colloidal suspensions the adsorbed chains can impart steric stability [10], the polymers can also cause flocculation owever, in Howin dense suspensions and/or [95] by either bridging or charge neutralization. Bridging occurs at low polymer surface coverage, where a single chain binds to two adjacent colloidal particles. Charge neutralization and charge inversion can take place when the surface coverage is high [96]. The charge inversion can lead to aggregation between colloidal particles with the original charge and ones where charge inversion took place [97,98]. The kinetics of flocculation depend on the kinetics of polyelectrolyte adsorption: In dilute suspensions where the adsorption rate may be of order minutes due to the low probability of collision between particles and polymers, the onset of flocculation will occur after an appreciable period of time. In contrast, when the polymer is in excess, flocculation may occur rapidly [59]. Another growth mechanism for clusters is the addition of new molecules. Models such as the Johnson-Mehl-Avrami-Kolmogorov (JMAK) equation relate systems properties to the addition-type rate of growth (i.e. the addition of new molecules to a cluster) [88]. Typical time scales for the growth stage vary greatly, but are usually much slower than those associated with the initial nucleation.

In both types of systems (polymers and clusters) binding or flocculation is a random process that gives rise to fractal-like structures that may not be optimal. As a result, local rearrangement can take place over long time scales, until equilibrium is reached. As noted in Section (2), the randomly adsorbed polyelectrolyte chains adjust by local desorption and re-adsorption of segments. While the time scale for any segment rearrangement may be of order seconds, the lack of long-range coordination (even between segments along the same chain) means that this stage may require timescales of order hours or even days [59]. Similarly, in cluster flocculates an internal rearrangement stage where the external features of the larger aggregate remain unchanged but internal re-ordering takes place has been found to occur on timescales of order hours [99,100].

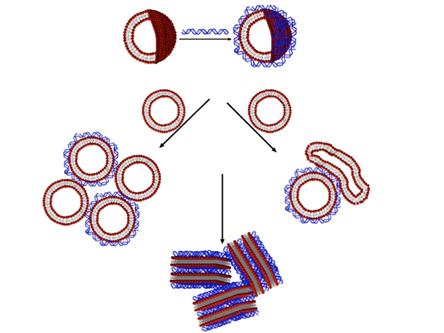
Lipoplex formation is expected to follow similar stages: A relatively rapid “adsorption” or complexation stage where the rate depends on the segmental binding energy, followed by slower stages of growth and rearrangement. Indeed, the first kinetic step in lipoplex formation is relatively rapid, an electrostatically-driven binding between DNA’s negatively charged phosphates and the lipid cationic charges (similar to polyelectrolyte adsorption onto oppositely charged surfaces). This initial step is followed by a second stage where clusters grow and condense, characterized by longer timescales. On even longer time scales, the large-scale lipoplex structure remains unchanged, but internal changes may occur.

It should be noted that most studies of lipoplex formation kinetics focused on DNA L_α^C complexes, where DNA (typically plasmid) is mixed with cationic vesicles. However, it is expected that the kinetics of other lipoplex phase formation (e.g. the hexagonal H_II^C), or complexes with siRNA, will follow the same steps (although potentially with different rate constants).

Lai and van Zanten [101] examined lipoplex formation from mixtures of monovalent cationic lipids (1-[2-(9-(Z)-octadecenoyloxy)ethyl]-2-(8-(Z)-heptadecenyl)-3-(hydroxyethyl)imidazolinium chloride (DOTIM), and 1,2-dimyristoyl-sn-glycero-3-ethylphosphocholine (EDMPC) with two neutral lipids (cholesterol and diphytanoyl phosphatidylethanolamine -DipPE). Time-resolved multi-angle laser light scattering (TR-MALLS) indicated L/D charge ratio as the primary factor determining both the initial rate of lipoplex formation kinetics, and the final lipoplex size, mass and density. These properties were found to increase with concentration, and were maximal, for a given system concentration, at charge ratios near unity. Quite surprisingly, though, the rate at 2:1 charge ratio was not the same as for the 1:2 system, an asymmetry attributed to the smaller number of complexes formed at excess DNA when compared to the number of complexes formed at excess lipid [101]. It was noted that only the charge ratio, but not the type of cationic or nonionic lipid, affected the kinetics.

While complexes formed in solutions with high or low charge ratio were found to reach a steady-state quickly, complexes formed in mixtures with a charge ratio close to unity displayed a continued growth for order 10 min following the initial complexation [102]. These findings are qualitatively consistent with early work by Minsky [103] on DOTAP/DNA systems, showing that complexes that form in excess lipid or excess DNA (charge ratios of 0.5 and 1.5) are stabilized within seconds, while lipoplexes of nearly equal charge ratios (1.1) become stable only after 40 min. Lai and van Zanten [102] interpreted the growth as aggregation of the initial (primary) complexes. The growth stage was thought to be associated with (the lack of) electrostatic repulsion between complexes: In highly asymmetric charge composition, excess charge stabilizes lipoplexes and prevents their aggregation; Isoelectric aggregates are more likely to flocculate and coalesce. Indeed, Lai and van Zanten [101] find that decreasing the effects of electrostatic repulsion by using DMEM/F-12 media (a commonly used cell growth and transfection medium which contains, among other components, divalent Ca²⁺ and Mg²⁺ ions) led to increase in lipoplex size when compared to systems immersed in dextrose.

Pozharski and MacDonald [48] examined the effect of vesicle characteristics (extruded vs. vortexed) and mixing methodology on the kinetics, using flow fluorometry. Consistent with other reports [101], they identified the first, rapid lipoplex formation step as that of DNA coating cationic lipid vesicles, followed by a longer stage where rearrangement leads to the multilamellar structure of DNA layers alternating with lipid bilayers. However, the initial vesicle coating step occurred on time scales shorter than the method’s threshold of 1 min. In equal-charge ratio mixtures of DNA and dioleoyl-O- ethylphosphocholine (EDOPC), DNA-coated vesicles from uniform, extruded vesicles were found to be stable over periods of order hours, while vortexed large vesicles converted to multilamellar lipoplexes within several minutes. In systems where lipid charges were in excess (charge ratio of 2:1), the stability of the coated vesicles was reduced compared to that of isoelectric (1:1) complexes. It was further suggested that in excess DNA, competition between vesicle rupture and vesicle coating determines the amount of lipid that converts into multilamellar lipoplex.

Zhang et al. [104] studied lipoplex formation between DOTAP-DOPE and DOTAP-cholesterol mixtures and plasmid DNA using fluorescence resonance energy transfer (FRET). As in previous studies, they find that DNA binding to the cationic vesicles occurs on time scales below 1min. However, a subsequent reorganization stage required time scales on order of several hours, although the most significant changes occurred within the first 60 min. The time scale for the second stage varied with the charge ratio: Increasing the ratio of cationic lipid to DNA charges reduced the time required to reach stability. The effect of the charge ratio, however, was found to differ between complexes containing cholesterol and those containing DOPE. In cholesterol-containing systems, the effect of charge ratio was weaker than in those containing DOPE, suggesting that the uncharged bilayer component in lipoplexes may play an active role in complex formation kinetics.

The kinetics of lipoplex formation by dimethyldioctadecylammonium bromide (DDAB) and DOTAP with plasmid DNA was studied by Braun el al. [105] as a function of temperature. Two sequential steps were distinguished for the assembly: One thought to be a binding/dehydration step, and the second a condensation one. The initial rate constant, of the association step, was found to decrease with temperature in both DDAB and DOTAP; indeed, above 40 °C it became too rapid for measurement for both systems. However, the sensitivity of the rate constant to temperature was much weaker in DDAB (0.086 s at 10 °C and 0.061 s at 30 °C) than in DOTAP (0.25 s at 10 °C to 0.05 s at 30 °C). This was translated to activation energy for DOTAP that is nearly 5 times higher than that of DDAB. The time scales for the second, condensation stage, also decreased with temperature; however, the activation energy was three times higher for DDAB than for DOTAP. Unlike other studies, however, the time scales found were similar for the two stages. These measurements also suggested that DOTAP condenses DNA more than DDAB, most likely due to differences between the lipid headgroup interactions with DNA.

Contrary to the two-stage process discussed above, Lindman [49,106] suggested a three-step mechanism that follows first-order reactions for the formation of multilamellar lipoplexes. At first, over a period of order milliseconds, DNA adsorbs onto the oppositely charged membrane surface (process is controlled by electrostatic interactions). This process is similar to the nucleation stage in cluster formation. In the next stage DNA-lipid complexes aggregate and grow at time scales of seconds (possibly by another cationic bilayer surrounding the DNA molecule), as in the flocculation of clusters. During these two stages, the secondary structure of the DNA becomes more compact, so that tertiary folding exposes more binding sites to the cationic bilayer. The third, final stage, which occurs over long time scales (ranging from 100 seconds to hours), involves further changes in DNA conformations, and rearrangement of complexes, probably into multilamellar structures. Time constants from stopped-flow turbidity and fluorescence experiments [49] were found to vary with the DNA to lipid charge ratio and the lipid composition (extruded vesicle mixtures of the cationic dioctadecyldimethylammonium bromide (DODAB) and DOPE).

In systems with a fixed lipid composition, the time constant for the initial complex formation was shown to depend on the charge ratio: Complexes formed with excess DNA (0.24 and 0.75 charge ratio) have a time constant that is about twice as much as that of complexes with the same lipid composition but excess lipids (1.5, 3 and 5) [49]. This is in agreement with the expectation that this stage represents the initial clustering, or complexation between the DNA and the lipid phase. Excess DNA reduces the rate at which the highly charged nucleic acid binds to the lipid surface. The time constant for the second stage, however, decreases with increasing L/D charge ratio. In contrast, both first and second stage constants increase with the fraction of cationic lipid, DODAB (under excess cationic lipid conditions). This was attributed to the fact that increasing DODAB fraction increases the cationic charge density and decreases the bilayer fluidity, thereby hindering rearrangement (pure DODAB bilayers are in the gel state). The rate constant for the third stage is almost independent of both charge ratio and lipid composition [49].

Neutron scattering experiments by Barreleiro et al. of DODAB/DOPE lipoplexes supported the 3-step model, extending the 3^rd time scale of complexes reorganization into multilamellar structures to order of ~10 min. The authors correlated the second step to the formation of an intermediate complex with a locally cylindrical structure developing via vesicle rupture events and rolling up of the cationic bilayers around the DNA double helix axis [106]. The third step was explained by further layer-to-layer association of previously ruptured vesicles leading to continuous aggregation and growth of the complexes into, eventually, multilamellar structures [106].

As noted, the last stage of lipoplex formation requires significant rearrangement of the lipids and nucleic acid within the aggregate. Leal et al. [107] investigated the mobility of lipids and DNA in lipoplexes, using both solid state and diffusion NMR in systems composed of cationic and zwitterionic lipids. They find that the zwitterionic lipid displayed diffusion coefficients typical for lipids in bilayers, while the cationic species diffusion rate was an order of magnitude slower. The DNA was found to be relatively static [107]. Their findings suggest that the DNA induced lipid segregation within the bilayer, resulting in regions of pure lipid (mostly the zwitterionic component) with typical mobility, and regions of DNA-bound (cationic) lipids, where the DNA is immobilized, and the lipid mobility is suppressed.

4. Discussion

The kinetics of any complex formation can be broken into three steps: An initial “nucleation” one where binding between the components occurs. This step is dominated by the complexation driving force, i.e. the binding energy, as described by an Arrhenius dependence. The process is relatively rapid, and may also depend on the concentration and mobility of the components. Next is a growth stage where the initially formed clusters flocculate or aggregate into larger, irregular structures. This process requires longer time scales and depends on a variety of system parameters. Last is an internal rearrangement stage where although the external properties of the complex do not change, local fluctuations cause rearrangement on short lengthscales until equilibrium is reached. This step (which is absent in systems composed of irreversibly bound rigid bodies) may take extremely long timescales.

Similarly to polyelectrolyte adsorption or to cluster nucleation and growth, lipoplex formation follows these same kinetic steps. It should be noted that studies of the kinetics of lipoplex formation focused on lamellae-forming lipid mixtures that yield L_α^C liquid crystalline complexes. However, it is expected that the initial step in the formation of hexagonal H_II^C and other non-lamellar types of complexes will be qualitatively similar.

The initial stage is rapid and irreversible, occurring on timescales significantly less than 1 min, most likely of order seconds [48,101,104,105]. It is driven by electrostatic binding between the anionic nucleic acid and the cationic lipid assembly. The rate can be captured by equation (1), found to display an Arrhenius-like dependence on temperature with an activation energy that depends on lipid type [105]. The pre-factor setting the rate in this stage depends on the concentration of binding species, i.e. nucleic acid and lipid charges, and the charge ratio [49]. As expected, increasing the concentration of species increases the rate linearly (for fixed L/D ratio and temperature) [101]. However, the rate of binding is a function of the charge concentration rather than the species concentration. In lipid bilayers, the charges in the inner leaflet of the bilayer are not available for binding, however, so that increasing the lipid concentration increases the rate by a factor of ½ when compared to a similar increase in the concentration of nucleic acid, as does mixing cationic and nonionic lipids, even if the charge ratio is held fixed [24,108,109]. The type and properties of the nucleic acid also affect complex formation, since the decrease in diffusion rate of chain molecules with increasing chain length [57] will reduce the rate of association to some degree via the exponential pre-factor of equation (1), although the time scales are still expected to be of the same order of magnitude.

The next kinetic step in lipoplex formation is one where the initially-formed DNA-lipid complexes aggregate and grow, and is typically of order minutes to hours [102,104]: The adsorption of nucleic acid on the lipid assemblies in the first step leaves exposed binding sites (either nucleic acid or lipid), that act as focal points for clustering. The process is highly heterogeneous and depends on the preparation route, although, surprisingly, this issue is under-emphasized in the literature in the context of lipoplexes. The fact that the rate depends on the charge ratio [102,104] indicates that complex growth depends on the local “environment” at any given time point, set by the overall concentration and mass transfer. Indeed, it has been shown that the rate depends on the method used. Therefore, rapid mixing of vesicle solutions with nucleic acid solutions will display different rates and larger-scale structures than those obtained by the drop-wise addition of one component to the other. When solutions are mixed together, the local nucleic acid and lipid concentrations are similar to the global, end-result values. However, when using drop-wise addition of the solution of one component to the solution of the other (a commonly applied protocol), complexation starts with highly asymmetric, and potentially inhomogeneous conditions. Although there is no explicit study comparing lipoplexes formed using the two kinetic routes, such differences were found in polyelectrolyte adsorption onto colloidal particles [110]. Indeed, a recent microfluidic study by Balbino, et al. [45] found similar sensitivity of the lipoplex properties to the method of mixing.

In addition, the properties of the vesicles themselves—such as size and polydispersity—may significantly affect the kinetics: under identical complexation conditions, DNA-coated vesicles from uniform, extruded vesicles were found by Pozharski et al. to be stable over periods of order hours, while large (and likely polydispersed) vortexed vesicles converted to multilamellar lipoplexes within several minutes [48].

Another factor that can affect the growth stage is the rigidity of the bilayer. Highly cohesive bilayers that resist rupture will aggregate in the same manner as that of cluster flocculates: DNA binds to the lipid, but the vesicles remain intact and complexes grow but do not re-arrange to an ordered mesophase over long timescales [24]. In contrast, membranes which undergo rupture readily form ordered, uniform structures, relatively rapidly [106].

In the last final stage of lipoplex formation, the local, equilibrium order of the nucleic acid develops. In this stage, which can occur on the order of hours, the global characteristics of the lipoplex remain unchanged but their local organization evolves. The rate constant was found to be insensitive to both charge ratio and lipid composition [49], much shorter than for polyelectrolytes adsorbed onto solid colloidal particles [59,110] since rearrangement occurs via lipid reconfiguration: The nucleic acid must rearrange into the two-dimensional, long range ordered array. As found by Leal et al. [107], the close binding between DNA and the cationic lipids inhibits the mobility of the DNA in the complex, and slows the diffusion rate of the associated cationic lipids. However, rearrangement of the uncharged lipid in the bilayer plane can still lead to the equilibrium order relatively quickly (on time scales similar to the lipid two-dimensional diffusion), as indeed found by Maier and Radler [111]. In bilayers with low fluidity, or that are in the gel phase, this reorganization stage may be significantly slowed down or even suppressed.

As previously noted, the kinetics of non-lamellar complexes is expected to follow the same three-step process: First, DNA adsorption onto the lipid aggregates, followed by aggregate-aggregate condensation, and then by internal rearrangement. Thus, the time scales for the first two steps should be relatively similar regardless of the end-complex geometry. However, the time scale for the third stage may differ greatly, depending on the type of lipids and the end-phase: The transition from the nucleic-acid adsorbed onto vesicle surfaces obtained in the second stage, to hexagonal or bicontinuous cubic structures, requires more radical reorganization than the formation of the multi-lamellar complexes. The bilayer must bend, locally, to “wrap” around the nucleic acid. In the case of the hexagonal arrays, a decoupling of the two monolayers composing the bilayer is also required. Indeed, rigid membrane would require extremely long time scales to reach such equilibrium structure, or may even be kinetically trapped in an intermediate form.

5. Conclusion

The modification of cellular functions through delivery of nucleic acids, transfection, promises to be an effective therapy route. Lipid based carriers, lipoplexes, could be developed to be efficient delivery agents for nucleic acids in vitro and in vivo. Understanding the kinetics of lipoplex self-assembly will enable understanding how to control essential steps in the delivery process such as the release of the nucleic acid into the cell environment. Transfection efficacy has been clearly linked to both the internal, nano-scale organization of the complexes (e.g. lamellar vs. hexagonal arrays), as well as to more global characteristics such as the complex size and net charge. While the local structure is dominated by equilibrium, thermodynamic processes, the latter properties are controlled by kinetics rather than equilibrium, so that controlling them requires understanding and control of the kinetic process.

Compilation of the studies examining lipoplex kinetics shows a three-step process. Initially, the nucleic acid adsorbs onto the surface of the cationic vesicles. This step is rapid (occurring within less than a minute in all systems studied), and largely insensitive to system parameters. The second step is one where the nucleic-acid carrying vesicles flocculate to form larger aggregates. This step occurs on intermediate time scales, and is sensitive to both the charge ratio and lipid properties. In particular, the rate and type of lipoplex formed depend on the propensity of the lipid bilayer to rupture. In the third step, local rearrangement occurs, while the global properties of the lipoplex remain constant. This process may require hours (or even longer), and is largely set by the bilayer characteristics. Fluid membranes with a tendency to rupture would allow rapid rearrangement, while rigid, gel-like ones may potentially be permanently trapped in a non-equilibrium structure. As a result, time scales may vary greatly.

Distinguishing between the flocculation stage and the rearrangement rate also requires understanding of the measurement type: Methods that track the size and mass of aggregates measure flocculation (aggregation). As a result, “steady-state” under such conditions indicates reaching the end of overall complex growth, namely the second stage. However, such methods cannot distinguish the third stage, which may continue beyond the time frame of complex growth. In contrast, molecular-type probes can distinguish and follow rearrangement, and thus the third stage, but are not sensitive to the second step flocculation and growth. This explains the large discrepancy in time scales reported for the second/third steps. It should also be emphasized that, although the three-stage process is expected to be universal, the specific rates are highly sensitive to the lipid properties, as discussed.

Understanding the kinetics of lipoplex formation is not limited to improving the (arguably broad) efficiency of nucleic-acid transfection. Similar complexes are currently being investigated for addressing challenges of current medicine, e.g., fighting microbial resistance to antibiotics [112,113,114], or treating genetic diseases (e.g., cystic fibrosis (CF) and Duchenne muscular dystrophy (DMD)) caused by alterations in the genetic code that lead to the production of non-functional proteins. These lipoplexes formed by the positively charged aminoglycoside antibiotic gentamicin and the anionic lipid DOPS (dioleoyl phosphatidylserine), drug/lipid lipoplexes formed spontaneously, into concentric and multilamellar lipoplexes resembling in morphology and order nucleic acid/lipid lipoplexes, and guided by the same interactions that lead to the creation of nucleic acid/lipid lipoplexes.

The behavior of lipoplexes in cellular environments depends on both global and local complex properties. Although this review focused on the kinetics of complex formation in vitro, better understanding of lipoplex kinetics will allow better design of effective nucleic acid carriers. Furthermore, it could shed light on methodologies for controlling the characteristics- and thus improving- any type of similar lipid complexes, thereby opening exciting opportunities for new applications in biotechnology and nanomedicine. The rapid advances in microfluidic methodologies promise the potential for production of homogeneous, small, uniform and effective carriers [14,115,116] thereby overcoming heterogeneity and reproducibility difficulties of traditional preparation routes.

Acknowledgments

Thanks to Dagnit Danino for her advice and help.

Conflict of Interest

The author declares that there is no conflict of interests regarding the publication of this paper.