Analysis of the effectiveness of the treatment of solid tumors in two cases of drug administration

1.   Introduction

Applied mathematics did not only appear because of an objective purpose, but also thanks to the human desire of always getting to know more. It is known that a quantitative description of a phenomenon observed with the formulation of laws is not enough if it does not make a qualitative study of the model along with the corresponding phenomenon. Mathematical modeling of a real problem is sometimes a difficult, long-term and very detailed process. An effective or at least close to an effective solution represents the final target of any problem. The theory of differential equations and some software packages are important tools for solving several actual problems from different real-world domains.

There are known various contributions to the investigation of solid tumor growth and chemotherapeutic scenarios. Thus, the effects of drug administration in chemotherapy are studied in the papers of R.B. Martin et al. ^[1] and S.T.R. Pinho et al. ^[2]; the fail of chemotherapy, in S.T.R. Pinho et al. ^[3] and D.S. Rodrigues et al. ^[4]; problems of optimal control of drug administration, in J.C. Panetta and K.R. Fister ^[5], L.G. de Pillis and A. Radunskaya ^[6], L.G. de Pillis et al. ^[7], A. D'Onofrio et al. ^[8]; multi-scale simulations, in G.S. Stamatakos et al. ^[9]; Monte Carlo models, in L.G. Marcu and E. Bezak ^[10]; models based on ordinary differential equations, in S.T.R. Pinho et al. ^[11], D.S. Rodrigues and P.F. de Arruda Mancera ^[12], M. Mamat et al. ^[13], J. Malinzi ^[14] and P. Unni and P. Seshaiyer ^[15]; and stochastic dynamic models, in W. L. Duan ^[16], W. L. Duan and H. Fang ^[17] and W. L. Duan et al. ^[18]. For some reviews on mathematical models for tumor growth and treatment, we refer the reader to P.M. Altrock et al. ^[19], A. Fasano et al. ^[20] and A. Yin et al. ^[21].

In paper ^[22], the mathematical model for solid tumors has been the self-limiting equation

involving three positive parameters $a, b, c.$ The same equation has been used in ^[23,24,25] for modeling cell proliferation in leukemias.

Alternatively, one can use the generalized logistic equation or Richards' growth model ^[26],

Such an approach is given by H.M. Byrne in ^[27], where the following dynamic system is suggested as a model for tumor chemotherapy:

We will adopt this model for the study which follows. In this model, $N(t)$ represents the number of the tumor cell population from a solid tumor that changes in time, $A(t)$ is the drug concentration within the tumor at time $t,$ and $\ \alpha (t)$ represents the rate at which the drug is injected in the body.

Parameter $r$ represents the nonrestrictive growth rate of the tumor cell population giving the proliferative capacity of the cells, $K$ stands for the tumor carrying capacity, $\theta$ measures how quickly the tumor reaches its carrying capacity, $\mu$ is the rate at which the drug kills malignant cells, $\lambda$ represents the decreasing rate of the concentration of the drug, and $\gamma$ gives the rate at which the drug is consumed significantly within the tumor. We emphasize the role of the parameter $\theta$ for the adequacy of the logistic equation to the real clinical data obtained on each type of tumor. A method for determining the value of this parameter is described in paper ^[28], where the criterion of best fit was the mean square error between the observed and predicted tumor values. For breast cancer, the best overall fit to the clinical data was obtained with $\theta = 1/4.$

According to the clinical practice, two cases have to be considered: (a) the case of continuous infusion, when $\alpha (t)$ is a constant $\alpha _{\infty },$ and (b) case of periodic infusion, when the drug is delivered as a series of interrupted continuous infusions, and thus $\alpha (t)$ is only piecewise constant.

The scope of this paper is to perform a complete analysis of the stability of the equilibrium or stationary solutions of the Eq (1.2), as a theoretical basis of the chemotherapeutic protocols. Our results extend to a general exponent $\theta$ and some of the conclusions established in [27, Chapter 4]. The theory is illustrated and complemented by a number of numerical simulations with MATLAB and MAPLE software, using real data from the medical literature. A part of the numerical simulations was carried out on the Kotys HPC (High Performance Computing) infrastructure of Babeş-Bolyai University, Cluj-Napoca ^[29].

2.   The generalized logistic growth model for a solid tumor

Before starting to discuss the model of chemotherapy given by the Eq (1.2), in this first section, for comparative purposes, we remind the reader of some well-known basic results regarding the generalized logistic Eq (1.1) here considered as a model for tumor cell dynamics and the stability of its equilibrium solutions.

The solution of Eq (1.1) satisfying the initial condition $N\left(0\right) = N_{0}$ can be given explicitly, namely

The equation admits two equilibrium solutions, $N_{1}^{\ast } = 0$ and $N_{2}^{\ast } = K.$ Their stability properties can be easily established and are given by the next result.

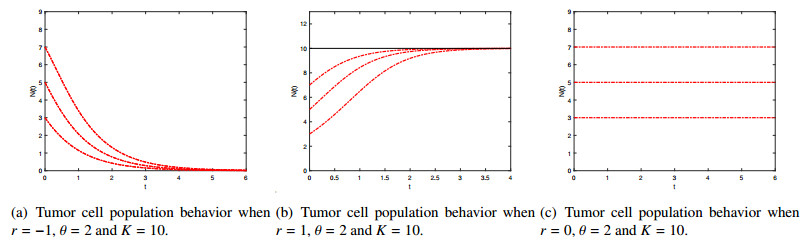
Theorem 2.1. (a) If $r < 0$ and $N_{0} < K,$ then $N(t)\rightarrow 0$ as $t\rightarrow +\infty,$ thus $N_{1}^{\ast } = 0$ is the only one equilibrium solution which is locally asymptotically stable.

(b) If $r > 0,$ then $N(t)\rightarrow K$ as $t\rightarrow +\infty,$ thus $N_{2}^{\ast } = K$ is the only one equilibrium solution which is locally asymptotically stable.

(c) If $r = 0,$ then $N(t)\equiv N_{0},$ thus the solution $N(t)$ remains constantly equal with the initial value $N_{0}.$

From a biological point of view, we can say that in the case of a negative nonrestrictive growth rate, as in situation (a) from the previous theorem, the population of tumor cells will be eliminated in time, see Figure 1(a). On the contrary, in the case of a positive nonrestrictive growth rate, as in situation (b), the population of tumor cells reaches its carrying capacity $K,$ see Figure 1(b). In the case when the nonrestrictive growth rate is equal to zero, as in situation (c), the population of tumor cells remains constant in time, see Figure 1(c).

The aim of this paper is to study the influence of chemotherapy over the dynamics of the tumor cell population, in the case $r > 0,$ when, in the absence of the treatment, the tumor cell population approaches $K.$ We are looking for conditions for the treatment to be effective, i.e. to make the transition from the bad situation $N\left(t\right) \rightarrow K$ to the good one $N\left(t\right) \rightarrow 0$ as $t\rightarrow +\infty$.

3.   Treatment of homogeneous solid tumors

Consider that a tumor grows according to the generalized logistic model, where $r > 0,$ that a drug is used to destroy the malignant cells, and that the mathematical model of the therapeutic dynamics is given by Eq (1.2).

We take into consideration two methods of treatment administration: by continuous infusion and by periodic infusion.

3.1.   Continuous infusion

When the tumor is in a continuously mode exposed to cytostatic medicine, the concentrations of tumor cells and of the drug can evolve to equilibrium values. To study the impact produced by the continuous infusion of the drug, we will find and classify the equilibrium solutions of the Eq (1.2), by taking into consideration how they both depend on $\alpha _{\infty }$ and therefore on the amount of medicine administered.

We consider two cases: Case Ⅰ of continuous infusion when the medicine keeps its efficiency effect (which means is not consumed within the tumor), that is $\gamma = 0;$ Case Ⅱ of continuous infusion when the drug does not keep its efficiency effect (which means is consumed significantly within the tumor), that is $\gamma \neq 0.$

Case Ⅰ:Assume that the drug keeps its efficiency effect, that is, $\gamma = 0.$ Then Eq (1.2) has the following form

The equilibrium points are the solutions of the algebraic system

By direct calculation, we find two equilibrium points $X_{1}\left(N_{1}^{\ast }, A^{\ast }\right)$ and $X_{2}\left(N_{2}^{\ast }, A^{\ast }\right),$ where

We say that an equilibrium point is admissible (from a biological point of view) if its components are nonnegative. The discussion which follows is about the admissibility and local stability of the above equilibrium points.

Clearly, the equilibrium $X_{1}$ is admissible. As regards $X_{2}, \ $observe that if $r > \frac{\mu \alpha _{\infty }}{\lambda },$ then $N_{2}^{\ast } > 0,$ that is the equilibrium point $X_{2}$ is admissible, while if $r < \frac{\mu \alpha _{\infty }}{\lambda },$ then $N_{2}^{\ast } < 0$ and so $X_{2}$ is not admissible, without biological relevance.

Next, by the method of the first approximation (for details about the method see ^[30,31]), we study the stability of the equilibrium solutions. The Jacobian matrix associated to Eq (3.1) is

For $X_{1}\left(N_{1}^{\ast }, A^{\ast }\right)$ we have

and its eigenvalues are

Hence, if $r < \frac{\mu \alpha _{\infty }}{\lambda },$ then the equilibrium solution $X_{1}\left(0, \frac{\alpha _{\infty }}{\lambda }\right)$ is locally asymptotically stable, while if $r > \frac{\mu \alpha _{\infty }}{ \lambda },$ then it is unstable.

For $X_{2}\left(N_{2}^{\ast }, A^{\ast }\right),$ the Jacobian matrix is

and its eigenvalues are

Hence, if $r\lambda -\left(\theta +1\right) \left(r\lambda -\mu \alpha _{\infty }\right) < \mu \alpha _{\infty },$ or equivalently $r > \frac{\mu \alpha _{\infty }}{\lambda },$ then the equlibrium point $X_{2}\left(N_{2}^{\ast }, A^{\ast }\right)$ is locally asymptotically stable, while if $r < \frac{\mu \alpha _{\infty }}{\lambda },$ then it is unstable.

If we put together the above results, we can state the following theorem about the local asymptotic stability of the equilibrium points of Eq (3.1).

Theorem 3.1. Let $r, K, \theta, \mu, \alpha _{\infty }$ and $\lambda$ be positive parameters. Then Eq (3.1) has the following admissible equilibrium points:

(a) If $r < \frac{\mu \alpha _{\infty }}{\lambda },$ then there is only one admissible equilibrium point $X_{1}\left(N_{1}^{\ast }, A^{\ast }\right)$ which is locally asymptotically stable.

(b) If $r > \frac{\mu \alpha _{\infty }}{\lambda },$ then there are two admissible equilibrium points: $X_{1}\left(N_{1}^{\ast }, A^{\ast }\right)$ unstable, and $X_{2}\left(N_{2}^{\ast }, A^{\ast }\right)$ locally asymptotically stable.

From a medical point of view, conclusion (a) of the above theorem says that the treatment is successful leading to the elimination of the cancer cells provided that the amount $\alpha _{\infty }$ of drug infused is large enough as the inequality $\alpha _{\infty } > \frac{r\lambda }{\mu }$ shows. If on the contrary $\alpha _{\infty } < \frac{r\lambda }{\mu },$ then the treatment can only guarantee a reduction of the limit value for the tumor cell population from $K$ to $K\left(1-\frac{\mu \alpha _{\infty }}{r\lambda } \right) ^{\frac{1}{\theta }}.$

Numerical simulations in Case Ⅰ of continuous infusion

The results of our study cover all the positive values of the parameters. For clinical applications, however, it is necessary to determine the specific values of these parameters. This aspect is intensely analyzed in the literature (see, for example ^{[15,32,33,34]}) and is not the subject of our research. Here, for the numerical simulations, we use the values of the parameters presented in Table 1.

Next, we simulate numerically the Eq (3.1) to investigate the behavior of the tumor cell population after the continuous infusion of the chemotherapy treatment when the drug is not consumed within the tumor, that is when $\gamma = 0.$

The initial number of tumor cells $N_{0}$ was calculated by dividing up the initial tumor volume to the individual volume of a typical tumor cell. For the initial tumor volume, we took the median value of all breast tumor volumes $V_{t} = 407 \ mm^{3}$ as estimated by mammography in a series of $448$ patients see J.A. Spratt et al. ^[28]. The individual volume of a tumor cell $V_{c} = 1760 \ \mu m^{3}$ was taken from M.P. Gamcsik et al. ^[35], which measured breast cancer cells in culture. It appears reasonable to approximate the size of actual tumor cells in vivo by the size of the lab-grown cells. This leads to an initial number of cells equal to:

We chose a value for $\gamma$ such as the consumption of the drug within the tumor $(-\gamma NA)$ equals the elimination of the drug by first-order kinetics such as excretion via kidneys $(-\lambda A),$ when the tumor is large ($N$ approaches the carrying limit $K$). That is, $\lambda = \gamma K,$ or

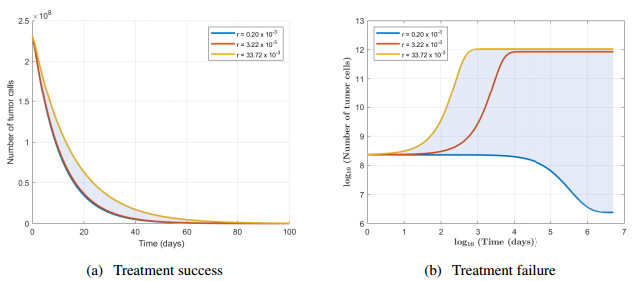
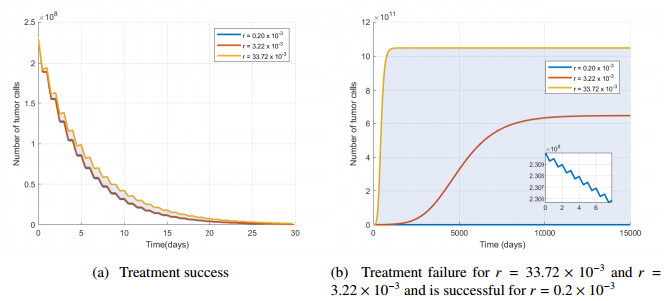
In a previous study on a sample of $448$ patients diagnosed with breast tumors, see J.A. Spratt et al. ^[28], the growth rate $r$ was calculated for each individual case by regression analysis. Centrality (the median, $3.22\times 10^{-3}$/day) and dispersion measures ($1\%$ and $99\%$ percentiles, $0.2\times 10^{-3}$/day, and $33.72\times 10^{-3}$/day, respectively) were then computed for the set of growth rates. We have employed these three values for $r$ across all our simulations. They characterize synthetically the spectrum of disease severity, spanning from the slowest growing tumors (low $r$) to the most agammaessive (high $r$). The shaded area between the curves in the simulations using time-series representations corresponds to values of $r$ between the above limits.

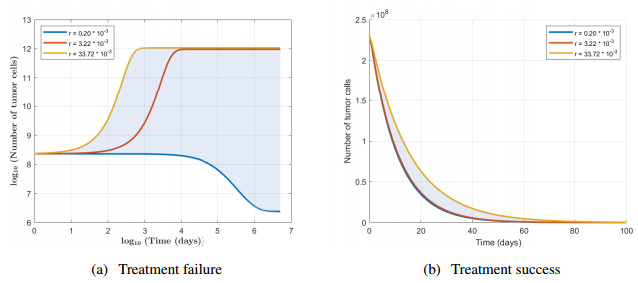
Case Ⅰ of continuous infusion: In this case, the drug is not consumed within the tumor, that means $\gamma = 0$. Figure 2(a) shows the behavior in time ($t = 100$ days) of the breast tumor cell population for the corresponding parameter values from Table 1, values that correspond to treatment success, when $r < \mu \alpha _{\infty }/\lambda.$ The breast tumor cell population $N(t)$ and the drug concentration $A(t)$ becomes arbitrarily close to the values $N_{1}^{\ast } = 0$ and $A^{\ast } = \alpha _{\infty }/\lambda,$ that means the equilibrium point $X_{1}\left(N_{1}^{\ast }, A^{\ast }\right)$ is locally asymptotically stable. Figure 2(b) shows the behavior in time ($t = 5\times 10^{6}$ days) of the breast tumor cell population for the corresponding parameter values from Table 1, values that correspond to treatment failure, when $r > \mu \alpha _{\infty }/\lambda.$ The breast tumor cell population $N(t)$ and the drug concentration $A(t)$ tend toward $N_{2}^{\ast }$ and $A^{\ast }$, respectively. In this case, the equilibrium $X_{1}\left(N_{1}^{\ast }, A^{\ast }\right)$ is unstable and $X_{2}\left(N_{2}^{\ast }, A^{\ast }\right)$ is locally asymptotically stable.

Case Ⅱ:Assume that the drug does not keep its efficiency effect. Then $\gamma \neq 0$ and for the determination of the equilibrium points of the Eq (1.2), we need to solve the algebraic system

Direct calculation yields the equilibrium point

and possible additional equilibrium points of the form $X\left(N^{\ast }, A^{\ast }\right),$ where $\left(N^{\ast }, A^{\ast }\right)$ solves the system

and consequently, $N^{\ast }$ is a solution of the equation

To discuss the solvability of Eq (3.3) and the number of its solutions, it is convenient to look at the functions $\varphi _{1}, \varphi _{2}:[0, +\infty)\rightarrow \mathbb{R},$

Both functions are decreasing and

In addition, the function $\varphi _{2}$ is convex, while $\varphi _{1}$ is concave if $\theta > 1,$ and convex if $\theta < 1.$ Then, elementary geometric considerations yield the following conclusions about Eq (3.3):

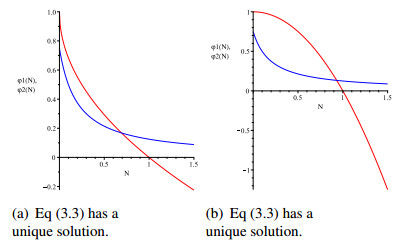
(a) If $r > \frac{\mu \alpha _{\infty }}{\lambda },$ then Eq (3.3) has a unique solution $N^{\ast }\in (0, K)$ and Eq (1.2) admits the equilibrium point $X\left(N^{\ast }, \frac{\alpha _{\infty }}{\lambda +\gamma N^{\ast }}\right).$

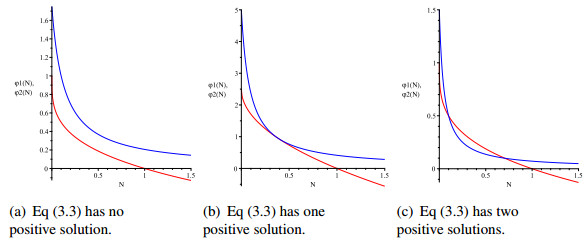
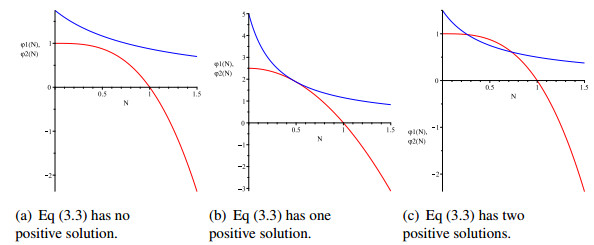
(b) If $r < \frac{\mu \alpha _{\infty }}{\lambda },$ then Eq (3.3) may have no positive solution, one positive solution, or two positive solutions, and any positive solution belongs to the interval $(0, K).$

(c) If $r\left(1+\frac{\gamma K}{\lambda }\right) \leq \frac{\mu \alpha _{\infty }}{\lambda },$ then Eq (3.3) has no solution in $\left(0, K\right).$

We can prove assertion (c) assuming the contrary, i.e., the existence of a solution $N$ in $\left(0, K\right).$ Then we would have

or equivalently

which yields a contradiction.

Numerical simulations for Eq (3.3)

Figures 3(a)–(b), 4(a)–(c) and 5(a)–(c) illustrate the number of solutions of Eq (3.3).

We now go to study the stability of the equilibrium solutions. The Jacobian matrix is in this case

For $X_{1}\left(0, \frac{\alpha _{\infty }}{\lambda }\right),$ one has

and the eigenvalues are

Therefore, the equilibrium point $X_{1}\left(0, \frac{\alpha _{\infty }}{ \lambda }\right)$ is locally asymptotically stable if $r < \frac{\mu \alpha _{\infty }}{\lambda },$ and unstable if $r > \frac{\mu \alpha _{\infty }}{\lambda }.$ Notice the same stability behavior of the equilibrium point $X_{1}\left(0, \frac{\alpha _{\infty }}{\lambda }\right)$ as in the case $\gamma = 0.$

Assume now that there exists a solution $N^{\ast }\in \left(0, K\right)$ of the Eq (3.3). Then

and using the equality

we obtain

The corresponding characteristic polynomial is

From the Hurwitz principle, we have that $Re\ \eta < 0$ if and only if all coefficients of the characteristic polynomial are positive. Thus, the equilibrium point $X\left(N^{\ast }, A^{\ast }\right)$ is locally asymptotically stable if and only if

Replacing

we obtain the equivalent condition in terms of $A^{\ast },$ namely

We can summarize the conclusions about the local asymptotic stability of the equilibrium points of Equation (1.2) in this case as follows.

Theorem 3.2. Let $r, K, \theta, \mu, \alpha _{\infty }, \lambda$ and $\gamma$ be positive parameters. Then Eq (1.2) has the following admissible equilibrium points:

(a) If $r > \frac{\mu \alpha _{\infty }}{\lambda },$ then there are two admissible equilibrium points: $X_{1}\left(0, \frac{\alpha _{\infty }}{ \lambda }\right)$ unstable, and $X\left(N^{\ast }, A^{\ast }\right)$ locally asymptotically stable if and only if condition Eq (3.4) or equivalently Eq (3.5) holds.

(b) If $r < \frac{\mu \alpha _{\infty }}{\lambda },$ then there is at least one admissible equilibrium point, namely $X_{1}\left(0, \frac{\alpha _{\infty }}{\lambda }\right)$ which is locally asymptotically stable. Additionally, one or two other equilibrium points of the form $X\left(N^{\ast }, A^{\ast }\right)$ could exist depending on the number of positive solutions of Eq (3.3), and they are locally asymptotically stable provided that condition Eq (3.4) or equivalently Eq (3.5) holds.

In the case of one equilibrium point, the treatment succeeds, but in the case of multiple equilibrium points the dynamics is sensitive to the initial conditions since it is possible that one of the equilibrium points $X\left(N^{\ast }, A^{\ast }\right)$ is locally asymptotically stable if the condition Eq (3.4) (or Eq (3.5)) is satisfied. So, to make sure that the treatment succeeds, it is necessary to have $r < \; \frac{\mu \alpha _{\infty }}{\lambda }$ and that the Eq (3.3) has no positive solution.

Numerical simulations in Case Ⅱ of continuous infusion

In the following, we will simulate numerically the Eq (1.2) in order to investigate the behavior of the tumor cell population after the continuous infusion of the chemotherapy treatment when the drug is consumed significantly within the tumor, that is when $\gamma \neq 0.$ For the numerical simulations, we use the values of the parameters presented in Table 1.

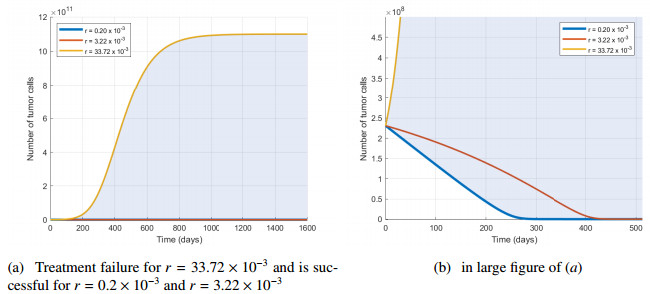
Case Ⅱ of continuous infusion: In this case, the drug is consumed significantly within the tumor, that means $\gamma \neq 0.$ Figure 6(a) shows the behavior in time ($t = 5\times 10^{6}$ days) of the breast tumor cell population for the corresponding parameter values from Table 1, values that correspond to treatment failure, when $r > \mu \alpha _{\infty }/\lambda.$ The breast tumor cell population $N(t)$ and the drug concentration $A(t)$ tend toward $N^{\ast }$ and $A^{\ast },$ respectively. In this case, there exists two admissible equilibrium $X_{1}\left(0, \frac{ \alpha _{\infty }}{\lambda }\right)$ unstable and $X\left(N^{\ast }, A^{\ast }\right)$ locally asymptotically stable. Figure 6(b) shows the behavior in time ($t = 100$ days) of the breast tumor cell population for the corresponding parameter values from Table 1, values that correspond to treatment success, when $r < \mu \alpha _{\infty }/\lambda.$ The breast tumor cell population $N(t)$ and the drug concentration $A(t)$ becomes arbitrarily close to the values $N_{1}^{\ast } = 0$ and $A_{1}^{\ast } = \alpha _{\infty }/\lambda.$ In this case the Eq (3.3) has no positive solution, so $X_{1}\left(0, \frac{ \alpha }{\lambda }\right)$ is locally asymptotically stable. This case is similar to the Case Ⅰ when $\gamma = 0,$ see the treatment success from the Figure 2(a).

In the Figure 7(a), (b) (enlarged Figure 7(a)), we can see the behavior in time ($t = 1600$ days respectively $t = 500$ days) of the breast tumor cell population for the corresponding parameter values from Table 1. Under the condition $r < \mu \alpha _{\infty }/\lambda,$ both treatment success and treatment failure are possible outcomes. As we can see, for the value of the nonrestrictive growth rate $r = 33.72\times 10^{-3}$ the breast tumor cell population $N(t)$ and the drug concentration $A(t)$ tend toward $N_{3}^{\ast }$ and $A_{3}^{\ast },$ respectively. For the values $r = 3.22\times 10^{-3}$ and $r = 0.2\times 10^{-3}$ of the growth rate, the breast tumor cell population $N(t)$ and the drug concentration $A(t)$ become arbitrarily close to the values $N_{1}^{\ast } = 0$ and $A_{1}^{\ast } = \alpha _{\infty }/\lambda.$ In this case the Eq (3.3) has two positive solutions $N_{2}^{\ast }$ and $N_{3}^{\ast },$ so $X_{1}\left(0, \frac{\alpha _{\infty }}{\lambda }\right)$ is locally asymptotically stable, $X_{2}\left(N_{2}^{\ast }, \frac{\alpha _{\infty }}{\lambda +\gamma N_{2}^{\ast }}\right)$ is unstable and $X_{3}\left(N_{3}^{\ast }, \frac{ \alpha _{\infty }}{\lambda +\gamma N_{3}^{\ast }}\right)$ is locally asymptotically stable.

Numerical simulations of the dependence on parameters

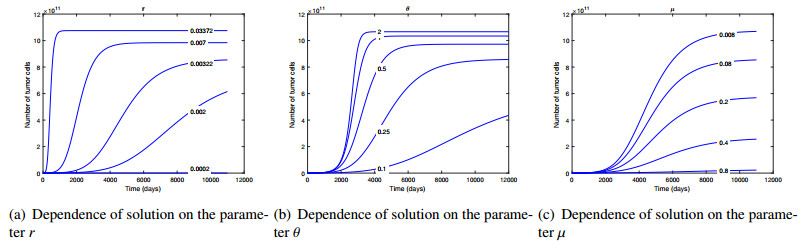
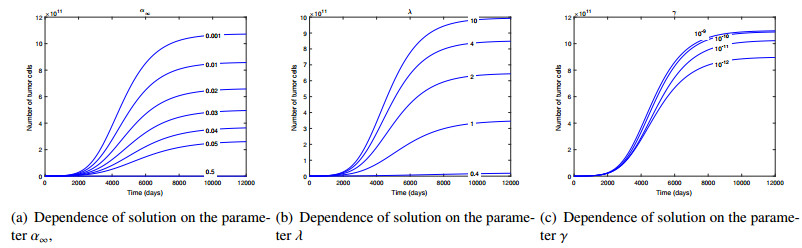
To illustrate the dependency of solution on the parameters, we have performed numerical sweeps for each of the six system parameters: $r, \ \theta, \ \mu, \ \alpha_{\infty}, \ \lambda$ and $\gamma$, see Figures 8 and 9. We have excluded from the analysis the carrying capacity K, as it has only a trivial effect on the solution (scaling). Except for the swept parameter, the fixed values are: $r = 3.22 \times 10^{-3}, \ \; \theta = 0.25, \ \; \mu = 8 \times 10^{-2}, \ \; \alpha_{\infty} = 0.01, \ \; \lambda = 4.16, \ \; \gamma = 0, \ K = 1.1 \times 10^{12}$. The initial conditions are: $N_{0} = 2.31 \times 10^{8}, \ A_{0} = 0$.

3.2.   Periodic infusion

In real situations, secondary effects reveal that continuous infusion is not usually considered a viable method to administrate the drug. Administered systematically, the drug can have an adverse effect on the vital organs (i.e., the liver). As a result, the chemotherapeutic drug is usually delivered as a series of continuous infusions, so that the health of the patient's organs can recover between the successive treatments. Unfortunately, this kind of method can have as a result the regeneration of the tumor.

Next, we will investigate the impact of periodic infusion considering that the tumor cell population grows according to the generalized logistic model with a nonrestrictive growth rate $r > 0$. Thus, we assume that the cell population develops under treatment according to the model

where this time the function which describes the chemotherapeutic drug infusion $A\left(t\right)$ is only piecewise continuous, more exactly it has the form

Here, $\tau$ denotes the duration of each period of treatment in which the drug is administered, and it is assumed that $\tau < 1.$ Therefore, on a time interval $\left[n; n+\tau \right],$ the drug is continuously infused at the constant rate $\alpha _{\infty },$ while on the time interval $\left[n+\tau; n+1\right],$ no drug is administered. By integration, we find the expression of $N(t)$ on $[n, n+1],$ namely

where $\ \Lambda = 1-\frac{\mu \alpha _{\infty }}{r}$ and $N_{t}: = N\left(t\right).$ Then

and we find that the values $N_{n}$ satisfy the following recurrence relation

where $h$ is the function

The equilibrium points of the discrete dynamic process Eq (3.8), that is the solutions $N_{\infty }$ of the equation $\ N_{\infty } = h\left(N_{\infty }\right)$ are $N_{\infty }^{1} = 0$ and

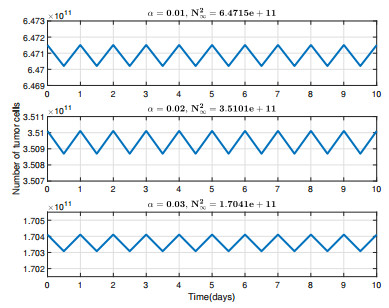
in case that $r-\tau \mu \alpha _{\infty } > 0.$ Obviously, if the initial condition is $N\left(0\right) = N_{\infty }^{1} = 0,$ then $N\left(t\right) \equiv 0$ meaning that tumor cannot develop in the absence of cancer cells. By contrary, if the initial condition is $N\left(0\right) = N_{\infty }^{2},$ then $N\left(t\right)$ becomes a nontrivial periodic function $N_{per}$ because $N_{n+1} = h\left(N_{n}\right) = N_{\infty }^{2},$ see the Figure 10.

We now study the stability of the equilibrium points for the discrete dynamic process Eq (3.8). One has

Therefore, we can state the following theorem.

Theorem 3.3. (a) If $r-\tau \mu \alpha _{\infty } < 0,$ then $h^{\prime }\left(N_{\infty }^{1}\right) < 1,$ which implies that $N_{\infty }^{1} = 0$ is locally asymptotically stable; so if $N_{0}$ is in a neighbourhood of $N_{\infty }^{1}$ then $\ N_{n}\rightarrow N_{\infty }^{1} = 0\ $as$n\rightarrow +\infty$ and therefore $N\left(t\right) \rightarrow 0$ as $t\rightarrow +\infty.$

(b) If $r-\tau \mu \alpha _{\infty } > 0,$ then $h^{\prime }\left(N_{\infty }^{1}\right) > 1$ and $h^{\prime }\left(N_{\infty }^{2}\right) < 1,$ which implies that $N_{\infty }^{1} = 0$ is unstable and $N_{\infty }^{2}$ is locally asymptotically stable, so if $N_{0}$ is in a neighbourhood of $N_{\infty }^{2}$ then $\ N_{n}\rightarrow N_{\infty }^{2}$ as $n\rightarrow +\infty$ and therefore $N\left(t\right) \rightarrow \; N_{per}\left(t\right)$ as $t\rightarrow +\infty.$

Under the conditions of the previous theorem, in case (a), we have $N\left(t\right) \rightarrow 0$ as $t\rightarrow +\infty,$ which means that the malign cells are eliminated in time, and so the treatment succeeds; in case (b), we have $N\left(t\right) \rightarrow \; N_{per}\left(t\right),$ which shows that the graph of tumor cell population stabilizes at the graph of a periodic function. Thus, when a periodic infusion takes place, the system can develop to a nontrivial periodic solution for which $N\left(t\right) = N\left(1+t\right).$ Applying numerical simulation, we will see how $N_{\infty }^{2}$ and the limit function $N_{per}$ depend on the drug dose. In the simulations, the graphs show us the way that $N_{\infty }^{2}$ decreases as the drug dose $\alpha _{\infty }$ increases. If the drug dose is high enough, then the eradication of the tumor occurs. Obviously, with periodic infusion, the dose required to achieve eradication is greater than that required for continuous infusion. This conclusion holds because with periodic infusion, tumor cells are exposed to chemotherapy for short periods of time.

Numerical simulations in the case of periodic infusion

Next, we will simulate numerically the Eq (3.6) when the chemotherapeutic drug infusion $A(t),$ given by Eq (3.7) is a piecewise continuous function, in order, to investigate the behavior of the tumor cell population after the periodic infusion of the chemotherapy treatment. For the numerical simulations, we use the values of the parameters presented in Table 1.

In Figure 11(a) we can see the behavior in time ($t = 30$ days) of the breast tumor cell population after the periodic infusion of the drug, for the corresponding parameter values from Table 1, values that correspond to treatment success, when $r-\tau \mu \alpha _{\infty } < 0.$ The breast tumor cell population $N(t)$ becomes arbitrarily close to the values $N_{\infty }^{1} = 0,$ that means the equilibrium $N_{\infty }^{1}$ is locally asymptotically stable. Figure 11(b) shows the behavior in time ($t = 15000$ days) of the breast tumor cell population for the corresponding parameter values from Table 1, values that correspond to treatment failure, when $r-\tau \mu \alpha _{\infty } > 0$ and to treatment success, when $r-\tau \mu \alpha _{\infty } < 0.$ As we can see, when the treatment fails, for the values of the nonrestrictive growth rate $r = 33.72\times 10^{-3}$ and $r = 3.22\times 10^{-3}$ the breast tumor cell population $N(t)$ tend toward a periodic solution $N_{per}.$ For the value $r = 0.2\times 10^{-3}$ of the growth rate, the breast tumor cell population $N(t)$ becomes arbitrarily close to the value $N_{\infty }^{1} = 0.$ In the case when the treatment fails, the equilibrium points of the equation with differences Eq (3.8) are $N_{\infty }^{1} = 0$ unstable and $N_{\infty }^{2}$ locally asymptotically stable, and when the treatment is successful, the only admissible equilibrium point is $N_{\infty }^{1} = 0$, locally asymptotically stable.

4.   Conclusions

It is natural that due to the limitations imposed by the biological environment, the mathematical models of the growth of homogeneous solid tumors should be based on self-limited equations, particularly on the logistic equation. In this paper, we worked with the generalized logistic equation of Richards. Without any medical intervention, if the nonrestrictive growth rate is positive ($r > 0$), the tumor cell population will tend to the carrying capacity constant\ $K.$ In order to destroy the tumor a medical treatment is necessary.

We study the dynamics of the tumor cell population in two cases of chemotherapy, the case of continuous infusion when the medicine keeps its efficiency ($\gamma = 0$) and when the medicine does not keep its efficiency ($\gamma \not = 0$), and the case when the chemotherapeutic drug is administrated as a series of continuous infusions, so that the health of the patient's organs can recover between successive treatments. The mathematical model is given by the dynamic Eq (1.2), where $\alpha _{\infty }\left(t\right)$ is constant in case of continuous infusion of the drug and piecewise continuous when the drug administration is periodic. In the first case the system is autonomous, while in the second case it is nonautonomous.

From the stability analysis of the equilibrium solutions of the system, it turns out that it is necessary that the parameters satisfy the condition $r < \frac{\mu \alpha _{\infty }}{\lambda }$ in order to have a successful treatment, but in the case when the medicine does not keep its efficiency this is not sufficient. In addition, it is necessary that the value of $\frac{\mu \alpha _{\infty }}{\lambda }$ to be big enough - more exactly $\frac{\mu \alpha _{\infty }}{\lambda }\geq r\left(1+\frac{\gamma K}{\lambda }\right)$ - so that the system has only one positive equilibrium point $X_{1}\left(0, \frac{\alpha _{\infty }}{\lambda }\right),$ i.e.. Eq (3.3) has no positive solutions. If Eq (3.3) has a positive solution $N^{\ast },$ then it is possible that the corresponding equilibrium point $X\left(N^{\ast }, \frac{\alpha _{\infty }}{\lambda +\gamma N^{\ast }}\right)$ be asymptotically stable, and the cell dynamics becomes sensitive to the initial conditions: if the initial value is in the attraction basin of $X_{1}, \ $then the treatment succeeds, while if it is in the attraction basin of $X,$ then the treatment fails.

A more realistic chemotherapy treatment is that when the drug is administrated as a series of continuous infusions separated by rest periods. Then the dynamics is described by a nonautonomous system. In this case, in addition to the trivial null periodic solution, a non trivial periodic solution appears, which biologically means that the tumor cells can remain in the body. However, if the null periodic solution is asymptotically stable, then the treatment succeeds. Our result is that this happens if the condition $r < \tau \mu \alpha _{\infty }$ holds. Otherwise, i.e., if $r > \tau \mu \alpha _{\infty },$ then the non trivial periodic solution is asymptotically stable and the treatment proves unsuccessful.

It is noteworthy that the conditions for successful treatment never depend on the exponent $\theta.$ That is, from a treatment standpoint, the generalized logistic model behaves exactly like a plain logistic variant. In biological terms, the speed of tumor cell proliferation may modify the growth curve towards the plateau phase of tumor growth, but has no bearing whatsoever on the success or failure of chemotherapy. This interesting and counterintuitive finding may have implications for adjuvant antiangiogenic therapy, even modeled without an explicit description of tumor vascular network. However, our study highlights a certain dependence on the parameter $\theta,$ namely the value of $N$ representing residual cancer (in the case of incomplete elimination of the disease). Therefore, we can conclude that, for the same dose, the size of the residual cancer also depends on the speed of proliferation of the tumor cells.

The mathematical analysis performed provides the necessary conditions for the success of chemotherapy, in the form of precise mathematical relationships given in terms of system parameters. Practically, the determination by theoretical and laboratory methods of the values of these parameters becomes essential for anticipating the effectiveness of treatment.

Acknowledgments

The authors would like to express their gratitude to the three anonymous reviewers for their time and effort for a careful reading of the manuscript and valuable comments and suggestions which have led to an improved version of the article.

Conflict of interest

The authors declare that they have no conflicts of interest.