Biochar: an organic amendment to crops and an environmental solution

1.   Introduction

As history indicated, infectious diseases have been becoming a main enemy affecting human's health and economic development. Mathematical modelling is an useful tool to investigate the mechanisms of transmission of diseases and make optimal control measures ^[1]. There are many ways to suppress the disease transmission, such as media propagation, vaccination, quarantine and so on ^[2]. As we know, vaccination is one of effective methods to control and prevent disease prevalence. Indeed, vaccination has succeeded in slowing down transmission of diseases such as tuberculosis, hepatitis, and some children diseases ^[3]. However, it has been reported that vaccination immunity waning has caused some diseases reemergence such as measles, rubella and pertussis. There is no doubt that vaccine waning has great effects on understanding the evolution of diseases. Based on the epidemic compartment knowledge in Kermack and McKendrick ^[4,5,6], an SIVS epidemic model can be written as follows ^[7]:

where the total population is splited into four classes (Susceptible, Infected, Recovered and Vaccinated). $b$ is the birth rate, $\mu$ is the natural death rate, $\beta$ is the transmission rate, $\gamma$ is the recovery rate, $p$ is the vaccinated rate, $\epsilon$ is the vaccine waning rate. In ^[7], Li and Yang investigated two vaccine strategies consisting of continuous and impulsive styles, and they obtained the global stability of equilibria by constructing Lyapunov functionals. Zaleta and Hernández proposed an SIVS model with a standard incidence rate and a disease-induced death rate ^[8]. They showed that their model exhibits a backward bifurcation. Based on model (1), many researchers have evolved many different structures and successfully captured the key characters of diseases transmission and evaluated the risk of their prevalence (see, for examples, ^[9,10,11]).

We note that all models mentioned above are based on the homogeneous assumptions for host population. However, host heterogeneity plays an important role in exploring their dynamics. Many diseases such as tuberculosis, hepatitis C, HIV/AIDS and so on infect their host for a long time and sometimes for the duration of lifespan. During the long infectious period, the variability of infectivity with age-since-infection has been studied most extensively in HIV infection ^[12]. The immunity waning process of pertussis satisfies Gamma distributions ^[13], which can be expressed by the vaccinated age. In this case, the densities of the infected and vaccinated in time $t$ and age $a$ are denoted by $i(t, a),$ and $v(t, a)$, respectively. The parameters $\beta, \gamma,$ and $\epsilon$ in system (1) are associated with age $a$. Based on system (1), the model can be described as follows:

where $\mathbb R_+ = (0, +\infty),$ and $L_+^1(\mathbb R_+)$ denotes the space of all the integral functions in $L^1$ and maintaining positivity after integral. Obviously, system (2) is a hybrid system combining an ordinary differential equation and two partial differential equations. Global dynamics of such a system has been becoming a challenging issue due to lack of well posed mathematical techniques.

On the other hand, some diseases such as mumps, measles, gonorrhea, HIV/AIDS etc exhibit heterogeneity in host populations. Groups can be geographical such as counties, cities, communities, or epidemiological as different infectivity and multi-stain agents. Many authors introduced an irreducible matrix and summing elements of the matrix together as a kernel function to describe the inter-group and intra-group infections. In ^[14], Lajmanovich and Yorke proposed the earliest multi-group model for gonorrhea spread in a community and investigated the global stability. They assumed that the total size of population doesn't change and maintain a constant. Under this assumption their model can be simplified to just consider the infected classes. Since then, many multi-group epidemic models have been studied (see, for example ^[15,19,20]). In ^[21], Guo et al proposed a multi-group SIR epidemic model and used the graph-theoretic approach to investigate the global stability of endemic equilibrium. This method combining with nonnegative irreducible matrix is an effective tool in solving the global behavior of endemic equilibrium. In ^[20], Kuniya considered a multi-group SVIR model to explore the global behavior of equilibria by constructing Lyapunov functional and using a developed graph-theoretic method. There are few literatures incorporating age structure into multi-group epidemic models ^[15].

Motivated by the discussions above, we separate the total population into $n$ groups and four compartments: susceptible, infected, and vaccinated, recovered, denoted by $S_k(t), i_k(t, a)$ and $v_k(t, a)$ and $R_k(t)$, respectively. $i_k(t, a)$ denotes the infected individuals at time $t$ and infection age $a$ in group $k$. $v_k(t, a)$ denotes the vaccinated individuals at time $t$ and vaccinated age $a$ in group $k$. $R_k(t)$ represents the recovered individuals at time $t.$ Susceptible individuals in group $k$ can be infected by infected individuals in group $j$ at rate $\beta_{kj}(a)$. Hence, we denote the incidence rate in group $k$ in the form of

Susceptible individuals in group $k$ can be vaccinated at rate $p_k$ and become vaccinated individuals with immunity. The vaccinated individuals in group $k$ lose its immunity at rate $\epsilon_k(a)$ and become susceptible individuals. A multi-group SIRVS epidemic model is formulated by the following differential equations:

where $b_k$ denotes the birth rate, $\gamma_k$ is the recovery rate with respect to infection age $a$, $\mu_k$ is the natural death rate in group $k$. In order to satisfy the biological meaning, all the parameters are assumed to be nonnegative and $b_k>0$ and $\mu_k>0.$ Note that the total population $N_k(t) = S_k(t)+\int_0^\infty i_k(t, a)da+R_k(t)+\int_0^\infty v_k(t, a)da$ satisfies the following equation:

which yields $\lim\limits_{t\rightarrow\infty}N_k(t) = \frac{b_k}{\mu_{k}}$. Without loss of generality, we assume that the total population is $N_{k} = \frac{b_k}{\mu_{k}}$. Since the first four equations in (3) do not contain the variable $R_k$, we can consider the following closed subsystem:

Once behaviors of $S_k(t)$, $i_k(t, a)$ and $v_k(t, a)$ are known, those of $R_k(t)$ can be derived from the fourth equation in (3). For convenience, we make the following assumption:

Assumption 1.1. For system (5), we assume

(ⅰ) For each $j, k\in\{1, 2, \cdots, n\}$, $\beta_{jk}(a), \gamma_k(a), \epsilon_k(a)\in L^\infty_+(0, \infty)$. That is, there exist positive constants $\beta_{jk}^+$ and $\epsilon_k^+$ such that

(ⅱ) For each $j, k\in\{1, 2, \cdots, n\}$, $\beta_{jk}(a)$ satisfies the following property:

(ⅲ) For each $j, k\in\{1, 2, \cdots, n\}$, there exists an $\varepsilon_0>0$ such that for almost all $a\in[0, +\infty), \beta_{jk}(a)\ge\varepsilon_0.$

(ⅳ) For each $j, k\in\{1, 2, \cdots, n\}$, the matrix $(\beta_{jk})_{n\times n}$ is irreducible.

The assumptions above on the parameters in system (5) are naturally satisfied for some real diseases. Evidence exists that the infectivity $\beta_{jk}(a)$ has been addressed by Gamma and Log-normal distributions for smallpox ^[16,17], Weibull distribution for Ebola ^[18]. It is easy to find that all of these probability distribution functions have peak values and they are continuous. Hence, (ⅰ) and (ⅱ) in Assumption 1.1 readily hold. As for (ⅲ) in Assumption 1.1, we can modify it in a more generalized form:

(ⅲ)' There exists a positive constant}$a_\beta$ such that $\beta_{jk}(a)(k, j\in\mathbb N)$ is positive in a neighbourhood of $a_\beta$.

Obviously, the distribution functions mentioned above have this property. If we assume that every group keeps up close exchanges in mutual contact, then the generated graph is strongly connected. (ⅳ) in Assumption 1.1 is satisfied automatically.

2.   Well-posedness of the problem

In order to investigate the dynamic behavior of system (5), define the functional spaces

and

with the norm

where $\psi_i = (\psi_{i1}, \psi_{i2}, \cdots, \psi_{in})^T\in\mathbb R^n$ or $L^1(\mathbb R_+, \mathbb R^n) (i = 1, 2, 3)$. In addition, denote $X_+, Y_+$ and $Z_+$ as the positive cones of $X, Y$ and $Z$. We define

Under Assumption 1.1 we see that the set

is invariant, where ${\bf S} = (S_1, S_2, \cdots, S_n)^T$, ${\bf i} = (i_1, i_2, \cdots, i_n)^T$ and ${\bf v} = (v_1, v_2, \cdots, v_n)^T$. In the following, we just assume that all the initial values are taken from $\Omega$.

Next, we will show that system (5) has a globally classic solution in $\Omega.$ Let $b, p, \mu, \gamma(a),$ and $\epsilon(a)$ be diagonal matrixes given by

Then let us define a linear operator $\mathcal A_i:D(A_i)\subset X\rightarrow X$ as

and

where $D(A_j) = \{(0, \psi)\in X_0| \psi \textrm{ is obsolutely continuous}, \psi'\in L^1(\mathbb R_+, \mathbb R^n), \psi(0) = 0\}$, $j = i, v$. If $\lambda\in\rho(A_i)$ ($\rho(A_i)$ denotes the resolvent set of $A_i$), for any initial value $\left(\theta_i, \phi_i \right)^T\in X$, we have

Similarly, for any $\lambda\in\rho(A_v)$ and any initial value $\left(\theta_v, \phi_v \right)^T\in X$, we have

Furthermore, define two nonlinear operators as

where $B_i(\phi) = S\sum\limits_{j = 1}^n\int_0^\infty\beta_{j}(a)\phi_{ij}(a)da$ and $B_v(\phi) = p\phi_S$. We further define another nonlinear operator

If we set $u = \left(S, \left(\begin{array}{c} 0 \\ i \\ \end{array} \right), \left(\begin{array}{c} 0 \\ v \\ \end{array} \right) \right)^T\in Z$, $\mathcal A = \textrm{diag}(-\mu, \mathcal A_i, \mathcal A_v)$, and $F = (F_s, F_i, F_v)$, (5) can be rewritten as the following abstract Cauchy problem

Proposition 2.1. There exists a uniquely determined semiflow $\{\mathcal U(t)\}_{t\geq 0}$ on $Z_{0+}$ such that, for each $u = \left(S(t), \left(\begin{array}{c} 0 \\ i(t, \cdot) \end{array} \right), \left(\begin{array}{c} 0 \\ v(t, \cdot) \end{array} \right) \right)\in Z_{0+}$, there exists a unique continuous map $\mathcal U\in C(\mathbb{R}_+, Z_{0+})$ which is an integral solution of the Cauchy problem (9), that is, for all $t\ge 0$,

Proof. By the definition of $\mathcal A$ and equations (7) and (8), $\mathcal A$ is dense in part of $X_0$ (see Page 1117, , ^[22]), and the resolvent operator is bounded. From Proposition 3.2 in, ^[23], we need only to verify that $F$ satisfies Lipschitz condition. Denote

and

By calculation, we have

Similarly, we have $\|F_{lk}(x_k)-F_{lk}(\bar x)\|\le L_{lk}\|x-\bar x\|, l = i, v,$ where $L_{ik} = \frac{b_k}{\mu_k}\sum\limits_{j = 1}^n\beta^+_{kj},$ and $L_{vk} = p_k$. Therefore, $\|F(x)-F(\bar x)\|\leq\sum\limits_{k = 1}^n\|F_k(x_k)-F(\bar x_k)\|\leq L\|x-\bar x\|,$ where $L = \max\{L_{Sk}, L_{ik}, L_{vk}\}$.

In order to prove the positivity of the solution of (5), we first rewrite the operator $\mathcal A_v$ and the nonlinear function $F_{vk}$ as follows:

and

Denote $\mathcal A' = \textrm{diag}(\mu, \mathcal A_i, \mathcal A_v')$, and $F' = (F_{S}, F_{i}, F'_{v})$. Then system (9) can be written as

It is obvious that $e^{\mathcal A' t}u_0\in \Omega_+$ if $u_0\in\Omega_+$, where $\Omega$ is the positive cone of $\Omega.$ Then we need to show that

For any $\psi_{lk}\in\mathbb R$ and $\phi_{lk}\in \Omega_+$, it follows from the definitions of $\mathcal A'$ and $F'$ that

On the other hand, choose a $\kappa_k\in\mathbb R_+$ and redefine the operator in (12) as follows: $\mathcal A_{\kappa_k} = \textrm{diag}(-(\mu_k+\kappa_k), \mathcal A_{i\kappa_k}, \mathcal A_{v\kappa_k})$, where

and

The nonlinear functions in (12) are defined as $F_{l\kappa_k}(\phi) = F_{lk}+\kappa_k\|\phi_k\| (l = S, i, v)$ for any $\phi\in Z.$ Hence, we have

and

If we choose $\kappa_k>\max\{p_k+\sum\limits_{j = 1}^n\beta^+_{kj}\|\phi_{ij}\|, \epsilon^+_k\},$ it follows from (14)-(16) that

From what has been discussed above, we have the following result.

Proposition 2.2. If Assumption 1.1 holds, system (5) has a unique positive solution in $\Omega.$

3.   The basic reproduction number

In this section, we show the computation process of the basic reproduction number $\mathcal R_0$, which is the average number of secondary cases produced by a classical infected individual during its infectious period in a fully susceptible population. Many literatures have given different methods to solve this problem. In this paper, it follows from the renewal process mentioned in Diekman et al in ^[24] that its value is determined by a next generation operator. Note that $E_0 = (\bf \hat S^0, 0, 0, 0, \hat v^0(a))$ is the disease-free equilibrium of system (5) where ${\bf\hat S^0} = (S^1_0, S_2^0, \cdots, S_n^0)$ and ${\bf\hat v^0(a)} = (v_1^0(a), v_2^0(a), \cdots, v_n^0(a))$ with $S_k^0 = \frac{b_k}{\mu_k+p_k(1-K_k^1)}, v_k^0(a) = p_kS_k^0\pi_k^1(a),$ and $\pi_k^1(a) = e^{-\int_0^a(\mu_k+\epsilon_k(s))ds},$ $K_k^1 = \int_0^\infty\epsilon_k(a)\pi^1_k(a)da.$ Linearizing system (5) at the disease-free equilibrium $E_0$, the subsystem (5) can be rewritten as

where

and

Let $\mathcal B: D(\mathcal B)\subset X\rightarrow X$ be a linear operator defined by

where $\mu$ and $\gamma$ are defined in (6). Based on the above definition, (7) can be rewritten as the following linear Cauchy problem in $Z_0$:

Let $u(t) = e^{t\mathcal B}$ be the $C_0$ semigroup generated by the generator $\mathcal B$. By the variation of constants formula, we have

Mapping $S^0\Lambda$ on both sides of the above equation yields

where $v(t) = S^0\Lambda I$ denotes the density of newly infectives in the linear invasion phase, $f(t) = S^0\Lambda u(t)I_0$ and $\Psi(s) = \Lambda S^0 u(s)$. Then the next generation operator is defined by

where we used the relation $(z-\mathcal B)^{-1} = \int_0^\infty e^{-zs}V(s)ds,$ for $z\in\rho(\mathcal B)$($\rho(\mathcal B)$ denotes the resolvent set of $\mathcal B$) and $0\in\rho(\mathcal B).$ In fact, the next generation operator is calculated as follows:

where

Based on Diekmann et al ^[24], the basic reproduction number $\mathcal R_0 = r(\mathcal K)$ is the spectral radius of the next generation operator $\mathcal K$, where $r(A)$ denotes the spectral radius of a bounded operator $A$. It follows from Inaba ^[25] that Malthusian parameter or asymptotic growth rate of infectives is positive if $\mathcal R_0>1$, otherwise it is negative.

4.   Existence of endemic equilibria

In this section, we focus on the existence of the endemic equilibrium $E^*$ of system (5). It follows from Section 2 that equilibria of system (5) satisfy $\mathcal Au^*+F(u^*) = 0$. Actually, it satisfies the following equations

From the last two equations of (23), we have

Substituting (24) into the first equation of (23) yields

It follows from the second and the third equations of (23) that

Note that

where $K_{kj} = \int_0^\infty\beta_{kj}(a)\pi_j(a)da.$ Hence, we can define a nonlinear operator

where

In fact, it follows from (26) that the endemic equilibrium of (23) is a positively nontrivial fixed point of the operator $H$. Note that the Fréchet derivative of $H$ at $\phi = 0$ is given by

Let

where

Consequently, $H'[0]$ is equal to the next generation operator $\mathcal K$ defined by (21).

Next, we show that $\mathcal R_0$ determines the existence of the positive fixed point of operator $H$. Under Assumption 1.1, the following lemma holds.

Lemma 4.1. Let $\mathcal K$ be defined by (21). We have

(a) $\quad\mathcal K$ is compact.

(b)$\quad\mathcal K$ is nonsupporting.

Proof. Assume that $B_0$ is an arbitrary bounded subset of $\mathbb R$. Then there exists a positive constant $c_0$ such that $\|\phi\|\le c_0$ for all $\phi\in B_0$. Note that

(28) implies that the operator $\mathcal K$ is bounded. It follows from Fréchet-Kolmogorov Theorem ^[31] that the operator $\mathcal K$ is compact. It is obvious that $\mathcal K$ is nonsupporting under (ⅲ) or (ⅲ)' of Assumption 1.1.

Lemma 4.1, together with the monotonicity of the operator $H$ with respect to $\phi$ manifests that the following lemma holds.

Lemma 4.2. Let $H$ be defined (27). $H$ is compact and $H(\mathbb R_{+})$ is bounded.

Employing Theorem 4.11 in ^[26] (Krasnoselskii fixed theorem) and Krein-Rutman Theorem in ^[27], Lemma 4.2 implies that $r(\mathcal K)$ is the uqiue eigenvalue of the operator $\mathcal K$ associated with a positive eigenvector and there is no eigenvector of $\mathcal K$ associated with eigenvalue $1$. As a consequence of Corollary 5.2 in ^[15], the following result is immediate.

Proposition 4.1. If $\mathcal R_0>1,$ then $H$ has at least one nontrivial fixed point in $Z_{0+}$.

Corollary 4.1. If $\mathcal R_0>1,$ then system (5) has at least one positive endemic equilibrium $E^* = ({\bf S^*, 0, i^*, 0, v^*})\in Z_{0+}$, where ${\bf S}^* = (S_1^*, S_2^*, \cdots, S_n^*), {\bf i}^* = (i_1^*, i_2^*, \cdots, i_n^*), {\bf v}^* = (v_1^*, v_2^*, \cdots, v_n^*)$.

In order to determine the uniqueness of the solution of system (23), we define two operators by (ⅱ) and (ⅲ) of Assumption 1.1 as follows:

and for a small positive value $\delta$

For convenience, define

and

It is obvious that $0\le H^-(\phi){\bf e}\le H(\phi){\bf e}\le H^+(\phi){\bf e}$, where ${\bf e} = (1, 1, \cdots, 1)^T$.

Theorem 4.3. If $\mathcal R_0>1$, then the operator $H$ defined in (27) has at most one nontrivial fixed point in $Z_{0+}$.

Proof. By Proposition 4.1, we assume that there are two different nontrivial fixed points in $\mathbb R_+$, denoted by $\phi^*$ and $\hat\phi^*$. Borrowing the definitions of $H^-$ and $H^+$, we have

Hence, there exists a positive constant $q = \sup\{r\ge0, \phi^*\ge r\hat\phi^*\}>0.$ Suppose $0 < q < 1$, for all $\phi\in \mathbb R_+$ and $k\in\mathbb N$, then

where $\xi_k(\phi, q) = q(1-q)\sum\limits_{j = 1}^n\frac{b_j\phi_j}{(\mu_j+p_j(1-K_j^1)+\phi_j)(\mu_j+p_j(1-K_j^1)+q\phi_j)}K_{kj}$. It follows from $0 < q < 1$ and (ⅲ) of Assumption 1.1 that $\xi_k$ is positive for all $k\in\mathbb N_+$ and $\phi\in \mathbb R_+$. Furthermore,

Inequality (30), together with the monotonicity of $H$ implies that

This contradicts the definition of $q$. Therefore, $q\ge1$ and $\phi^*\ge q\hat\phi^*\ge\hat\phi^*$. Exchanging the role of $\phi^*$ and $\hat\phi^*$, we can prove $\phi^*\le\hat\phi^*$. This implies that $\phi^* = \hat\phi^*$.

5.   Asymptotic smoothness

In this section, we will show the relative compactness of the positive orbit $\{\mathcal U(t, u_0)\}_{t\ge0}$ defined by (5). This process is spurred by Lemma 19 in ^[28] and Theorem 2.46 in ^[29]. To apply them, we define

and

Then we can divide the solution of semigroup $\mathcal U(t)$ into two parts:

and

where

This implies that $\mathcal U(t)u_0 = \mathcal V(t)u_0+\mathcal W(t)u_0$.

Theorem 5.1. The semiflow $\mathcal U: \mathbb R_+\times X_{0}\rightarrow X_{0}$ is asymptotically smooth if there are maps $\mathcal V(t), \mathcal W(t): \mathbb R_+\times X_{0}\rightarrow X_{0}$ such that $\mathcal U(t)u_0 = \mathcal V(t)u_0 + \mathcal W(t)u_0,$ and the following statements hold for any bounded closed set $\Omega$ that is forward invariant under $\mathcal U:$

($i$) For any $u_0\in\Omega$, there exists a function $\delta:\mathbb R_+\times\mathbb R_+\rightarrow\mathbb R_+$ such that for any $r>0$ $\lim\limits_{t\rightarrow+\infty}\delta(t, r) = 0$ with $\|u_0\|_\Omega\le r$, then $\|\mathcal V(t, u_0)\|_\Omega\le\delta(t, r)$;

($ii$) there exists a $t_\Omega \ge0$ such that $\mathcal W(t)(\Omega)$ has a compact closure for each $t\ge t_\Omega$.

Lemma 5.2. There exists a function $\delta:\mathbb R_+\times\mathbb R_+\rightarrow\mathbb R_+$ such that for any $r>0$,

and

Proof. Integrating $i_k$ and $v_k$ equations along the characteristic line $t-a =$ const. yields

for all $k\in\mathbb N$. Hence for any $u_0\in Y$ and $\|u_0\|_Y\le r$,

where $\delta(t, r) = e^{-\underline\mu t}r$ and $\underline\mu = \min\limits_{k\in\mathbb N}\{\mu_k\}.$ Obviously, $\|\mathcal V(t)u_0\|_\Omega$ approaches $0$ as $t$ goes to infinity.

Lemma 5.3. $\mathcal W(t)$ maps any bounded subsets of $\Omega$ into sets with compact closure in $Y$.

Proof. It follows from the first equation of (5) that $S_k(t)$ remains in the compact set $\{\phi\in\mathbb R_+^n|0\le\phi_k\le\frac{b_k}{\mu_k}, k\in\mathbb N\}$ for all $t\ge0$. Therefore, we need to show that $\tilde i$ and $\tilde v$ still remain in pre-compact subsets of $Y_0$ which is independent of $u_0$. Note that

Since for all $k\in\mathbb N_+,$ $0\le\tilde i_k(t, a) = i_k(t-a, 0)\pi_k(a)\le\frac{b_k}{\underline\mu^2}\sum\limits_{j = 1}^n\beta_{kj}^+b_je^{-\underline\mu a}: = \Delta_ke^{-\underline\mu a}$ where $\Delta_k = \frac{b_k}{\underline\mu^2}\sum\limits_{j = 1}^n\beta_{kj}^+b_j$, and $0\le\tilde v_k(t, a)\le \frac{b_kp_k}{\mu_k}e^{-\underline\mu a}.$ It is easy to see that (ⅰ) - (ⅲ) of Theorem B.2 in ^[29] hold.

In what follows, we need to show that (iv) of Theorem B.2 in ^[29] also holds. Assume that $h\in(0, t)$ without loss of generality. Then

Similarly,

Obviously, both (36) and (48) uniformly converge to $0$ as $h\rightarrow0$ which is independent of $u_0$.

Lemmas 5.2 and 5.3, together with $\|\mathcal U(t)u_0\|_{Z_0}\le\sum\limits_{k = 1}^n\frac{b_k}{\mu_k}$, imply that $\mathcal U(t)$ has compact closure in $Z$ for $u_0\in\Omega$. It follows from Proposition 3.13 in ^[32] that the solution orbit is relatively compact and the semiflow $\mathcal U(t)$ is asymptotically smooth.

Proposition 5.1. The semiflow $\mathcal U(t)$ defined in (10) is asymptotically smooth.

6.   Uniform persistence

In this section, we establish the uniform persistence of (5) when $\mathcal R_0>1.$ This property guarantees the well-definition of the Lyapunov functionals in Section 7. For some $k\in\mathbb N,$ define $\rho_k: \Gamma\to \mathbb{R}_+$ and $u_{0} = ({\bf S_{0}, {\bf 0}, i_0(\cdot), {\bf 0}, v_0(\cdot)})\in \Omega_0$ by

Let

Obviously, if $u_0\in \Omega\setminus \Omega_0$, then $({\bf S}(t), {\bf0, i}(t, \cdot), {\bf0, v}(t, \cdot))\to E_0$ as $t\to\infty$. Hence, if $\mathcal U$ has a global compact attractor in $\Omega_0,$ then it also has a global compact attractor in $\Omega$.

Assumption 6.1. The support of the initial age-since-infection value $i_{k0}(a)\in L^1(\mathbb R_+)$ lies to the right of the support the infectivity function $\beta_{kj}$ for all $k, j\in\mathbb N.$

Proposition 6.1. If $\mathcal {R}_0>1$ and Assumption 6.1 hold, then system (5) is uniformly weakly $\rho$-persistent for some $k\in\mathbb N.$

Proof. Since $\mathcal{R}_0>1$, there exists an $\eta_{j0}>0$ and $\phi_j\in \mathbb R_+$ for $k, j\in\mathbb N$ such that

where $\tilde S_k^0(\eta_{k0}) = \frac{b_k}{\mu+\eta_{k0}+p_k(1-K_k^1)}-\eta_{k0}(>0)$ and $\widehat{K_{kj}(\cdot)} = \int_0^\infty e^{-\lambda a}\beta_{kj}(a) \pi_k(a)da.$

Suppose that, for any $\eta_{k0}>0$, there exists an $u_{0}\in \Omega_0$ such that

and show a contradiction. Therefore, there exists a $t_0\in\mathbb{R}_+$ such that $\rho_k(\mathcal U(t, u_0))\le \eta_{k0}$ for $t\ge t_0$ and all $k\in\mathbb N.$ Without loss of generality, we shift the time to $t_0 = 0$. Then $\lambda_k(t)\le \eta_{k0}$ for $t\ge t_0 = 0$ and $k\in\mathbb N.$

Next, we show that $S_{k{\infty}} \ge S^0_k(\eta_{k0}): = \frac{b_k}{\mu_k+\eta_{k0}+p_k(1-K_k^1)}$, where $S_{k{\infty}} = \liminf\limits_{t\rightarrow\infty}S_k(t).$ By the Fluctuation Lemma ^[35], we can pick up a sequence $\{t_n\}$ such that $S_k(t_n)\to S_{k{\infty}}$, $\frac{dS_k(t_n)}{dt}\to 0$ as $n\to\infty$. Then from the first equation of (5), it follows that

This, combined with (40), gives

Letting $n\to\infty$ leads to

This implies that $S_{k\infty}\ge S_k^0(\eta_{k0})$.

Finally, since $S_{k\infty}\ge S_k^0(\eta_{k0})$, there exists a $t_1\in\mathbb{R}_+$ such that $S_k(t)\ge \tilde S_k^0(\eta_{k0})$ for $t\ge t_1$. Again, without loss of generality, we can assume $t_1 = 0$. Solving $i_k(t, a)$ by the characteristic line method yields

where $b_k(t) = S_k(t)\lambda_k(t).$ Then

Taking Laplace transforms on both sides of the above inequality gives

This inequality holds for any $\xi$ and $\eta_{k0}.$ If we take $\xi$ and $\eta_{k0}$ small enough, then this is a contradiction with (38). This completes the proof.

Clearly, for all $k\in\mathbb N$, $\rho_k$ is a continuous function on $\mathbb R_+.$ Proposition 5.1 implies that $\{\mathcal U\}_{t\ge0}$ has a global attractor. From Theorem A.34 in ^[34], we need to show that for any bounded total orbit $h(t+s) = \mathcal U(s, u(t))$ of $\mathcal U_t$ such that $\rho_k(h(t))>0$ for all $t\in\mathbb R$ and $s\in\mathbb R_+.$ For the total trajectory, we have

for $t\in\mathbb R$ and $a\in\mathbb R_+.$ In order to prove the strongly uniform persistence, the following lemma is helpful.

Lemma 6.1. Let $({\bf S}(t), {\bf 0, i}(t, \cdot), {\bf0, v}(t, \cdot))$ be a solution of (5). Then $S_k^{\infty}\le S_k^0$, where $S_k^{\infty} = \limsup\limits_{t\rightarrow\infty}S_k(t)$ for $k\in\mathbb N.$

Proof. By Fluctuate Lemma in ^[35], there exists $\{t_n\}$ such that $t_n\to\infty$, $S_k(t_n)\to S_k^{\infty}$, and $\frac{dS_k(t_n)}{dt}\to 0$ as $n\to\infty$. Integrating $v_k$ equation in (5) along the characteristic equation $t-a = \mathrm{const.}$, we have

Substituting $v_k$ into $S_k$ equation yields

Applying Fluctuate Lemma, we immediately obtain

or $S_k^{\infty}\le \frac{b_k}{\mu_k+p_k(1-K_k^1)} = S_k^0$ as required. This completes the proof.

Lemma 6.2. Let us define $\Theta(b(t)) = \sum\limits_{k = 1}^nb_k(t)$. Suppose that Assumption 6.1 holds, then $\Theta(b(t))$ for total trajectory $h(t)$ is identically zero on $\mathbb R$, or it is strictly positive on $\mathbb R$.

Proof. Suppose that there exists a $t_1>0$ such that $b_k(t) = 0$ for all $t\le t_1$. By the definition of $\lambda_k$, we have

where $\bar \beta = \max\limits_{j, k\in\mathbb N}\{\beta_{kj}^+\}.$ Summing $k$ from $1$ to $n$ on both sides of (41) yields

for all $t> t_1.$ It follows from Gronwall inequality that $\Theta(b(t)) = 0$ for all $t\ge t_1.$

Suppose there doesn't exist a $t_1$ such that $\Theta(b(t)) = 0$ for all $t\le t_1.$ Thus, there exists a sequence $\{t_m\}$ towards $-\infty$ such that $\Theta(b(t_m))>0$ for each $m.$ That means that $b_{k}(t_m)>0$ for each $m$. Moreover, there exists a sequence $a_m$ such that $i_k(t_m, a_m) = i_k(t_m-a_m, 0)\pi_k(a_m)>0$ for each $m.$ In view of the first equation, with the dissipative property of system (5), we obtain

Hence, there exists a positive constant $\zeta>0$ such that $S_k(t)>\zeta>0$ holds for all $t\in\mathbb R$. Let $b_{km}(t) = b_k(t+t_m^*)$ for each $n$, where $t_m^* = t_m-a_m.$ Recalling equation (41), we arrive at

where $\varepsilon_0$ is defined in (ⅲ) of Assumption 1.1 and

Consequently,

Since $\tilde\Theta_m(0) = \sum\limits_{k = 1}^n\sum\limits_{j = 1}^n\int_0^\infty \beta_{kj}(a) i_{jm0}(a)da>0$ and $\tilde\Theta_m(t)$ is continuous at $t = 0$, it follows from Assumption ^[29] and Gronwall inequality that $\Theta(b_m(t))$ and $\tilde\Theta_m(t)$ are positive for sufficiently small $t$. Furthermore, from Corollary B.6 ^[29], we conclude that there exists a constant $l>0$ such that $\Theta(b_m(t))>0$ for all $t>l$. Since $\Theta(b_m(t))$ is a time shift of $\Theta(b(t))$ by $t_m^*$ with $t_m^*\rightarrow-\infty$ as $m\rightarrow\infty,$ it follows that $\Theta(b(t))>0$ for all $t\in\mathbb R.$ This completes the proof.

Corollary 6.1. Suppose that Assumption 6.1 holds. Then for all $k\in\mathbb N,$ $b_k(t)$ for the total trajectory $h(t)$ is strictly positive for every $t\in\mathbb R$.

From Propositions 5.1 and 6.1, together with Corollary 6.1, we apply Theorem 5.2 in ^[29] to illustrate the $\rho-$ strongly uniform persistence of system (5).

Lemma 6.3. Suppose that $\mathcal R_0>1$ and the assumption of Corollary 6.1 hold. Then system (5) persists uniformly strongly, in this sense, there exists some $\eta_{k0}$ such that

for some $k\in\mathbb N$ and $\lambda_k(0)\neq0.$

Proof. From Corollary 6.1, we readily see that $\inf \lambda_k(0)>0$ for some $k\in\mathbb N.$ Applying Theorem A.34 in ^[34], we conclude that there exists a constant $\eta_{k0}>0$ such that $\liminf\limits_{t\rightarrow+\infty}\rho_k(\mathcal U(t, u_0))>\eta_{k0}.$

By Lemma 6.3, we present the following theorem to state the uniformly strong persistence of system (5).

Theorem 6.4. Suppose that $\mathcal R_0>1$ and Assumption 6.1 hold. There exist some positive constants $\eta_{k0}>0(k\in\mathbb N)$ such that for all $t\in\mathbb R$ and $a\in\mathbb R_+$

7.   Global attractivity of the equilibria

In this section, we will show the global behavior of the equilibria of system (5). To achieve this goal, we employ a Volterra type functional defined by $g(x) = x-1-\ln x$ in ^[22], which is positive and attains minimum value $0$ at $x = 1$. In what follows, we check this Volterra type functional is well-defined in infinite dimension and make the following assumption.

Assumption 7.1. For all $j\in\mathbb N_+$, $S_{j0}\in \mathbb R_+,$ $\displaystyle\int_0^\infty|\ln h_{j0}(a)|da < +\infty$, $h = i, v.$

Lemma 7.1. If Assumption 7.1 holds, then $\displaystyle\int_0^\infty v_j^0(a)\ln\frac{v_j(t, a)}{v_j^0(a)}da$ is bounded.

Proof. For $t>a$,

For $t\le a$,

It follows from (44) - (45) that

Therefore, it follows from Assumption 7.1 that $\displaystyle\int_0^\infty v_j^0(a)\ln\frac{v_j(t, a)}{v^0_j(a)}da$ is bounded.

Theorem 7.2. Let Assumption 7.1 hold. If $\mathcal R_0 = r(\mathcal K) < 1$, the disease-free equilibrium $E^0$ is a global attractor in $\Omega.$

Proof. For $j\in\mathbb N$, define

where $\alpha_{kj}(a) = \int_a^\infty\beta_{kj}(s)\frac{\pi_j(s)}{\pi_j(a)}ds$ and $\delta_k(a) = \int_a^\infty\varepsilon_k(s)v^0_k(s)da.$ Lemma 7.1 ensures $V_j(t)$ is well-defined. Then

From Lemma 7.1, together with 6.4, $V_j(t)$ is well-defined. Deviating it along the solution of (5) yields

Note that $\mathcal R_0 = r(\mathcal K) < 1$ implies that $\sum\limits_{k = 1}^nS_k^0K_{jk} < 1$. Therefore, $V'_j(t)\le0$ and it is easy to see that the equality holds if and only if $({\bf S}(t), {\bf 0}, {\bf i}(t, \cdot), {\bf 0}, {\bf v}(t, \cdot)) = ({\bf S^0}, {\bf 0}, {\bf 0}, {\bf 0}, {\bf v^0}(\cdot))$. This implies that the largest positive invariant subset of $\{u(t)\in \Omega|V'_j(t) = 0\}$ is the singleton $\{({\bf S}^0, {\bf 0}, {\bf 0}, {\bf 0}, {\bf v^0}(\cdot))\}$. This shows that the disease-free equilibrium $E_0$ is a global attractor.

In the following, we give a lemma to show the boundedness of the Lyapunov functional for proving the global attractivity of the endemic equilibrium $E^*.$

Lemma 7.3. If Assumption 7.1 holds, then $\displaystyle\int_0^\infty h^*_j(a)\ln\frac{h_j(t, a)}{h^*_j(a)}da$ $(h = i, v)$ is bounded.

Proof. Prior to this proof, denote $\beta_j^+ = \max\limits_{k\in\mathbb N}ess.\sup\limits_{a\in\mathbb R_+}\beta_{jk}(a)$ for all $j\in\mathbb N.$ For $t>a$, it follows from $b_j(t)\le\beta^+_j\frac{\Lambda_j^2}{\mu_j^2}$ that

For $a>t$,

Then,

By the assumption, it follows that $\displaystyle\int_0^\infty i^*_j(a)\ln\frac{i_j(t, a)}{i^*_j(a)}da$ is bounded.

Similarly, $\displaystyle\int_0^\infty v^*_j(a)\ln\frac{v_j(t, a)}{v^*_j(a)}da$ is also bounded.

Assume that $f(t, a)\in\mathbb R\times L^1(\mathbb R_+)$ is a solution of the following system

where $m(a), \eta(a)\in L^1(\mathbb R_+)$ and $L(t)\in\mathbb R.$ Obviously, the nontrivial equilibrium $E_1^*$ of system (52) satisfies the following equations:

Define a Lyapunov functional $V_1(t) = \int_0^\infty M(a)g\left(\frac{f(t, a)}{f^*(a)}\right)da,$ where $M(a) = \int_a^\infty\beta(s)$ $f^*(s)ds.$

Lemma 7.4. Suppose that $\displaystyle\int_0^\infty|\ln f_0(a)|da$ is bounded. There exists a positive value $\eta_0>0$ such that $f(t, a)>\eta_0e^{-\int_0^am(s)ds},$ then

where $M(a) = \displaystyle\int_a^\infty\eta(s)f^*(s)da.$

Proof. Note that

where we denote $h'_l(s, l) = \frac{\partial h(s, l)}{\partial l}.$

It follows from the proving process of Lemma 7.3, together the assumption of Lemma 7.4 that $V_1(t)$ is well-defined. Deviating it along the solution of (52), we obtain

Observing (55), we have

With the help of integral by parts, we obtain

here we used the fact $M(0) = \int_0^\infty\eta(a)f^*(a)da,$ and $M'(a) = -\eta(a)f^*(a).$

Next, we will give the global attractivity of the endemic equilibrium $E^*$.

Theorem 7.5. Suppose $\mathcal R_0>1$, ($iv$) of Assumption 1.1 and Assumption 7.1 hold. Then the endemic equilibrium $E^*$ is a global attractor in $\Omega_0.$

Proof. Define

where $\alpha_j(a) = \sum\limits_{k = 1}^n\int_a^\infty\beta_{jk}(s)i^*_k(s)da$ and $\delta_j(a) = \int_a^\infty\varepsilon_j(s)v^*_j(s)ds.$ $\kappa_j$ will be determined later and considered as a weighted coefficient. The well-definition of $V(t)$ follows from Lemma 7.3. From the definitions of $\alpha_j(a)$ and $\delta_j(a)$, it follows that

and

Assisting with Lemma 7.4 and deviating $V(t)$ along the solution of (5) yield

Note that

Equation (60) implies that

Noting that $\int_0^\infty\epsilon_k(a)v_k^*(a)da = p_kS_k^*\int_0^\infty\epsilon_k(a)\pi_k^1(a)da = p_kS_k^*K_k^1$, it follows from (60) and (61) that

where $H_j(i) = \displaystyle\frac{i_j(t, a)}{i^*_j(a)}-\ln\frac{i_j(t, a)}{i^*_j(a)}$. Define $\Theta_{jk} = S_j^*\int_0^\infty\beta_{jk}(a)i_k^*(a)[H_k(i)-H_j(i)]da$, $(j, k = 1, 2, \cdots, n)$ and a Laplacian matrix

By Lemma 2.1 in ^[21], we have that the solution space of the linear system $\Theta\kappa = 0$ is 1 and one of its basis is given by

where $c_{jj}>0 (j = 1, 2, \cdots, n)$ denotes the cofactor of the $j-$th diagonal element of matrix $\Theta$. This implies that $\sum\limits_{k = 1}^n\theta_{jk}\kappa_j = \sum\limits_{j = 1}^n\theta_{kj}\kappa_k$ and

Employing the graph-theoretic approach mentioned in ^[21], (63) is equal to zero. Therefore, $V'(t)\le0$. The equality holds if and only if $\frac{i_k(t, a)}{i_k^*(a)} = \frac{i_j(t, 0)}{i_j^*(0)} = \frac{i_j(t, a)}{i_j^*(a)}$. This implies that $\mathbf i = \mathbf ci^*$. It follows from the first equation of (5) with respect to the monotonicity of $\mathbf c$ that $\mathbf c = \mathbf 1$. Hence, the largest invariant set of $\{u(t)\in \Omega_0| V'(t) = 0\}$ is the singleton $E^*$. Combining the relative compactness of the solution orbit (see Lemma 5.3) with the invariance principle (see [Theorem 4.2, ^[30]]), we see that the endemic equilibrium $E^*$ is a global attractor in $\Omega_0.$

8.   Simulations

In this section, we perform some numerical experiments to illustrate our theoretical results. For the experimental operability, we set $a_{max} = 10$ instead of infinity. For simplicity, we assume system (5) describes some sexually transmission diseases, such as Zika, Ebola and genital warts etc, which consist of two groups - male group and female group. As some news reported in ^[33], human papillomaviruses (HPV) is an effective and safe vaccine to control some sexually transmitted diseases inducing by virus. In order to illustrate system (5), we firstly fix the demographic parameters as follows:

Hence the total male population maintains the size $N_1(t) = 2050$ and the size of the total female population is $N_2(t) = 4050.$ It has been reported that nearly half of newly infections are diagnosed as females in age range between $15$ to $24.$ Therefore, we assume that the vaccination rates $p_1 = 0.21$ for male and $p_2 = 0.22$ for female. Other parameters are associated with infection age in the form of

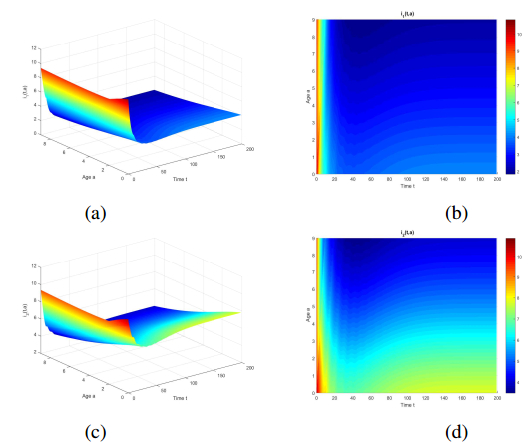
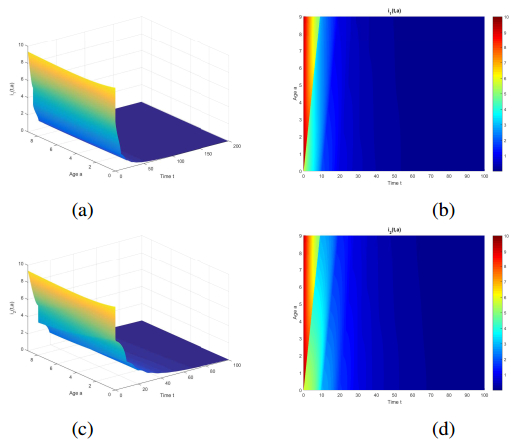
where $\Gamma(n) = (n-1)!,$ or $\Gamma(z) = \int_0^\infty x^{z-1}e^{-x}dx (z\in\mathbb N).$ Obviously, $y(x, A, B)$ satisfies (ⅲ)' of Assumption 1.1. We fix $\gamma(a) = y(a, 2, 5),$ $\varepsilon(a) = y(a, 1, 1)$ and verify the transmission rate $\beta(a) = y(a, 6, B)$. If we choose $B = 9$, this implies that the mean of the transmission function is $54$ and the variance is $486.$ It follows from Figure 1 that the disease-free equilibrium $E_0$ is asymptotically stable. Then we decrease $B = 8$ associated with the variance changed as $384$. Figure 2 shows that the endemic equilibrium $E^*$ is asymptotically stable.

Comparing infected male and female populations in Figure 2, we find that the total infected number for female population is larger than that for male population. However, the first peak time for female population is later than the time for male population. Although the vaccination rate for female designed is higher than such rate for male, the level of infected peak and the total number for female population are still larger than those for male population. Consequently, the government should pay more attentions to female population.

9.   Discussion

In this paper, we proposed a multi-group SIVS epidemic model with age-since-infection. We calculated the basic reproduction number $\mathcal R_0$ by the renewal equation, which is the spectral radius of the next generation operator $\mathcal K$. From Theorems 7.2 and 7.5, we see that the global attractivity of system (5) is totally determined by $\mathcal R_0$. This implies that the basic reproduction number is a sharp threshold determining that the disease prevails or vanishes. Implicit Euler method performed illustrates the theoretical results. Numerical experiment shows that the number of the infected females is larger than the number of the infected male although the vaccination rate for female group is higher than that for male group. The government should pay much more concerns on female group for suppressing sexual diseases prevalence.

Irreducibility of the transmission matrix $\beta_{jk}, j, k\in\mathbb N$ has been highly influential in analyzing the global stability of equilibria. This assumption is still a basic assumption of epidemics spreading on scale free networks. Therefore, we hope our analysis method proving theoretical results and numerical method can be generalized to investigate the dynamics of some epidemic models on complex networks ^[36]. Besides, oscillation is one of the important phenomena in diseases transmission. What mechanisms resulting in oscillation has been becoming an increasing trend in investigating epidemic models with age-since-infection ^[37]. We leave this for our future work.

Acknowledgements

The authors are very grateful to the Editor-in-Chief, Professor Yang Kuang, and the anonymous referees for their valuable comments and suggestions, which helped us to improve the presentation of this work significantly.

This work was supported by the National Natural Science Foundation of China (Nos. 61573016, 11871316), Shanxi Scholarship Council of China (2015-094), Shanxi Scientific Data Sharing Platform for Animal Diseases, and Startup foundation for High-level Personal of Shanxi University.

Conflict of interest

The authors declare there is no conflict of interest.