Retinal blood vessel segmentation from fundus image using an efficient multiscale directional representation technique Bendlets

1.   Introduction

A topological index is a mathematical measure that can be computed from chemical structures and can be depicted as simple graphs. They play an important role in the study of QSPR and QSAR. In theoretical chemistry, molecular structure descriptors (also called topological indices) are used for modeling physico-chemical, pharmacological, toxicological, biological and other properties of chemical compounds. Chemoinformatics is an active area of research where quantitative pattern behavior and structure-property relations detect biological processes and other properties ^[].

The chemical graph theory is a branch of graph theory that is concerned with analyses of all consequences of connectivity in a chemical graph. A structural formula of a chemical compound can be represented by a molecular graph which is used to characterize a molecule by depicting the atoms as the vertices of the graph and the molecular bonds as the edges. In chemistry, molecular topological indices, also known as topological indices, are utilized. Wiener ^[2] was the first to demonstrate that the Wiener index is strongly connected to the boiling points of alkanes. Feng et al. ^[3] provided a necessary criterion for a graph to be '$l$-connected' in 2017 using the well-known Wiener index and Harary index. Su et al. ^[4] discussed the sufficient condition used with the forgotten topological index.

To predict physico-chemical properties and bioactivity of chemical compounds in QSPR/QSAR investigation, topological indices are employed. Zagreb indices ^[5,6] are among the most effective for identifying physical attributes and chemical processes of chemical compounds. Gutman and Trinajstic ^[7] considered the first Zagreb index $M_{1}(G)$ and the second Zagreb index $M_{2}(G)$ for the first time in 1972. Ghobadi and Ghorbaninejad ^[8] developed accurate formulae for the Zagreb and Hyper-Zagreb indices of some molecular graphs in 2018. They defined the Forgotten topological index or super F-index, a novel distance-based Zagreb index. Estrada et al. ^[9] developed the Atom-Bond Connectivity $(ABC)$ index, while Vukicevic and Furtula ^[10] introduced the geometric-arithmetic index. Gutman ^[11] proposed a novel graph-based topological index, the Sombor index. The index was initially used in chemistry, but it quickly piqued the curiosity of mathematicians ^[12]. Randic index is one of the oldest, most often used and most successful topological indices in QSPR and QSAR. Bollabas and Erdos ^[13] later proposed the generalized Randic index. The Harmonic index is a version of the Randic index, which was initially presented by Fajtlowicz ^[14].

The physico-chemical properties and biological activities of a compound are crucial in the development of pharmaceutical drugs. Many researchers are working on the QSPR analysis of various chemical compounds ^[15,16], since it is an economically efficient approach to test a compound instead of testing the compounds in a wet lab. Gupta, Singh and Madan ^[17] proposed a unique graph invariant for predicting biological and physical features using the eccentric distance sum index (EDS). This topological index has a wide range of possible applications in the structure activity/property interactions of molecules, and it has a high discriminating power for both biological activities and physical characteristics. Hua, Xu and Shu ^[18] obtained a strong lower bound on the EDS index of n-vertex cacti. Yu, Feng and Ili'c ^[19] investigated the lower and upper bounds of the EDS index in terms of other graph invariants such as the Wiener index, the degree distance index, the eccentric connectivity index and so on.

Chemical qualities, physical properties, pharmacological properties and biological properties of medications are all important in medical research for drug creation. Topological indices can be used to identify these features ^[20]. Recently, researchers have started researching topological indices and COVID-19 medications. In addition, the following studies are notable in the investigation of medications repurposed against SARS-CoV-2 ^[21]. Kirmani et al. ^[22] established QSPR models with linear regression between physico-chemical properties of potential antiviral drugs and some topological indices for various antiviral drugs used in the treatment of COVID-19 patients. Shirkol et al. ^[23] investigated the predictive power of degree-distance and distance-based topological indices through QSPR analysis. Similarly, Lučić et al. ^[24] performed QSPR analysis using novel distance-related indices.

Deutsch and Klavžar ^[25] defined the M-Polynomial in 2015. Using the edge partition technique, $M-$ Polynomial is employed to perform degree based computations. It is crucial in calculating the exact expressions of several degree-based topological indices. The Neighborhood $M-$ polynomial ($NM-$ Polynomial) was introduced by Mondal et al. ^[26]. It performs the same functions as the $M-$ polynomial for neighborhood degree sum-based indices. It is used to make computations related to neighborhood degree sum-based indices easier. These polynomials are determined by the sum of neighboring vertex degrees. The $RNM-$ polynomial is used to evaluate several forms of reduced neighborhood indices ^[27].

In this paper, we have considered some antiviral drugs that are used for the treatment of COVID$-19$ patients, namely, Arbidol, Chloroquine, Hydroxy-Chloroquine, Lopinavir, Remdesivir, Ritonavir, Thalidomide and Theaflavin. We have introduced a new type of vertex degree called Diameter Eccentricity Based vertex degree and employed it to introduce a new polynomial called $\mathscr{D}\varepsilon$-polynomial. We use the newly introduced polynomial to derive our proposed topological indices. We further check the applicability of our indices by deriving the $\mathscr{D}\varepsilon$-polynomials for the eight afore-mentioned COVID-19 drugs. We perform Quantitative Structure-Property Relationship (QSPR) analysis by arriving at the best fit curvilinear and multilinear regression models based on our topological descriptors for 8 physico-chemical properties of the COVID-19 drugs. We also perform Quantitative Structure-Activity Relationship (QSAR) analysis and identify the best fit multilinear regression model to predict the $IC_{50}$ values of the eight COVID-19 drugs.

Let $G$ be a simple, finite and connected graph with vertex set as $V(G)$ and edge set as $E(G)$. Let $d_{p}$ denote the degree of a vertex $p$ in $G$ and $\varepsilon_{p}$ the eccentricity of the vertex $p$. Let $\Delta(G)$ denote the maximum degree and $\delta(G)$ denote minimum degree among the vertices of $G$, respectively.

Definition 1.1. ^[28] The eccentricity index for a graph $G$ is defined as

where $\varepsilon_{p}$ denotes the eccentricity of the vertex $p$.

Definition 1.2. ^[29] The Ediz eccentric connectivity index $E\mathscr{E}^{c}(G)$ of $G$ is defined as

where $S(v)$ is the sum of degrees of all vertices adjacent to vertex $v$ and $\varepsilon(v)$ is the eccentricity of the vertex $v$.

The Revan vertex degree of $p$ in $G$ is defined as $r_{p} = \Delta(G) + \delta(G) - d_{p}$. Based on the Revan vertex degree, Revan indices were introduced by Kulli ^[30,31]. He has studied oxide networks, honeycomb networks, drugs and antibiotic structures with the help of Revan and Banhatti indices ^[32]. Inspired by this definition, we have introduced and defined a new type of vertex degree called Diameter Eccentricity Based vertex degree of $p$ in $G$ as

where $D(G)$ denotes the diameter of the graph $G$.

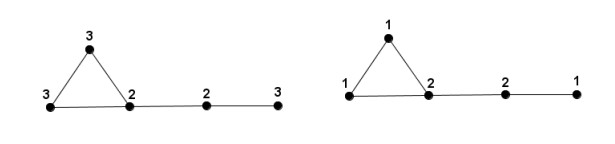
Figure 1 shows the eccentricity and diameter eccentricity based vertex degrees $(d\varepsilon-$values) of the Tadpole Graph $T(3, 2)$.

Eccentricity of a vertex is a measure of the centrality of a vertex. Diameter, on the other hand, is a global entity with respect to the graph, that can be considered as a measure of the spread of the graph. Our diameter eccentricity based vertex degree captures both these measures and determines the importance of a vertex with respect to the whole graph..

Based on this new vertex degree definition, we define diameter eccentricity based and hyper diameter eccentricity based indices for any connected graph $G$ by introducing a new polynomial called $D\varepsilon-$polynomial as

where $r\rho_{(i, j)}$ denotes the number of edges in the edge partition and $\alpha, \beta$ are variables. Our $\mathscr{D}\varepsilon-$ Polynomial is a function of $\alpha$ and $\beta$. It is dependent on the diameter eccentricity based vertex degrees of the end vertices of the edges of the graph. The $M-$ polynomial, $NM-$ polynomial and $RNM-$ polynomial can be used to derive degree based, neighborhood degree based and reverse neighborhood degree based indices. Our polynomial is novel and the first of its kind related to eccentricity based indices.

In Table 1, we introduce our new indices as functions of $d\varepsilon_{p}$ and $d\varepsilon_{q}$

Our diameter eccentricity based indices, that is $\mathscr{D}R_{1}\varepsilon$ and $\mathscr{D}R_{2}\varepsilon$ and the Hyper Diameter Eccentricity Based indices, that is $H\mathscr{D}R_{1}\varepsilon$ and $H\mathscr{D}R_{2}\varepsilon$ indices can be derived using our $\mathscr{D}\varepsilon$-polynomial.

Table 2 shows the formulae for deriving our indices using the $\mathscr{D}\varepsilon$-polynomial In Table 2,

The chemical structures (molecular graphs) of the drugs which we have considered in this paper are given in Figures 2 to 5.

2.   Methodology

We use the method of edge partitions and the newly introduced $\mathscr{D}\varepsilon$-polynomial to compute our proposed indices. Edge partitioning is the process of grouping (partitioning) edges based on the appropriate vertex degrees of the end vertices of the edges of a graph. By "appropriate", we refer to the type of vertex degrees used to compute the topological indices. For example, in order to partition the edges for computing our proposed indices, we make use of the diameter eccentricity based vertex degrees of the end vertices of the edges.

In Tables 3 to 10, we present the distance eccentricity based edge partitions for the eight COVID-19 drugs. Here, $r\rho_{(p, q)}$ is the number of edges in the edge partition $(d\varepsilon_{p}, d\varepsilon_{q})$ in a graph $G$. From Table 3 we observe that the edges of Arbidol can be partitioned into 8 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Arbidol. From Table 4 we observe that the edges of Chloroquine can be partitioned into 7 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Chloroquine. From Table 5 we observe that the edges of Hydroxy-Chloroquine can be partitioned into 7 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Hydroxy-Chloroquine. From Table 6 we observe that the edges of Lopinavir can be partitioned into 9 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Lopinavir. From Table 7 we observe that the edges of Remdesivir can be partitioned into 11 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Remdesivir. From Table 8 we observe that the edges of Ritonavir can be partitioned into 13 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Ritonavir. From Table 9 we observe that the edges of Thalidomide can be partitioned into 7 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Thalidomide. From Table 10 we observe that the edges of Theaflavin can be partitioned into 10 partitions based on the distance eccentricity based vertex degrees of the end vertices of the edges of the molecular graph of Theaflavin.

3.   Main results

In this section, we compute $\mathscr{D}\varepsilon$-polynomial of the molecular graphs of the mentioned COVID-19 drugs and obtain our proposed topological indices values.

3.1.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ Indices for Arbidol

Theorem 3.1. Let $A$ be the molecular graph of Arbidol. Then, we have,

Proof. Let $A$ be the molecular graph of Arbidol represented in Figure 2. It has $29$ vertices and $31$ edges. Consider

Using the edge partitions given in Table 3, it is clear that $r\rho_{(1, 2)} = 4$, $r\rho_{(2, 3)} = 6$, $r\rho_{(3, 3)} = 1$, $r\rho_{(3, 4)} = 6$, $r\rho_{(4, 5)} = 5$, $r\rho_{(5, 5)} = 1$, $r\rho_{(5, 6)} = 5$ and $r\rho_{(6, 7)} = 3$.

Applying these values in $\mathscr{D}\varepsilon(A)$, we get the $\mathscr{D}\varepsilon$-polynomial for Arbidol as follows:

□

Proposition 3.2. Let $A$ be the molecular graph of Arbidol. Then, we have,

1) $\mathscr{D}R_{1}\varepsilon(A) = 239.$

2) $\mathscr{D}R_{2}\varepsilon(A) = 546.$

3) $H\mathscr{D}R_{1}\varepsilon(A) = 2133.$

4) $H\mathscr{D} R_{2} \varepsilon (A) = 13594.$

Proof. Using the derivation formula given in Table 2 and the $\mathscr{D}\varepsilon$-polynomial for Arbidol from Theorem 3.1, we have

Similarly, the other three indices can be obtained as follows:

□

3.2.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ Indices for Chloroquine

Theorem 3.3. Let $C$ be the molecular graph of Chloroquine. Then, we have,

Proof. Let $C$ be the molecular graph of Chloroquine represented in Figure 2. It has $21$ vertices and $23$ edges. Consider

Using the edge partitions given in Table 4, it is clear that $r\rho_{(1, 2)} = 3$, $r\rho_{(2, 3)} = 4$, $r\rho_{(3, 4)} = 5$, $r\rho_{(4, 5)} = 4$, $r\rho_{(5, 6)} = 3$, $r\rho_{(6, 7)} = 3$ and $r\rho_{(7, 7)} = 1$.

Applying the values in $\mathscr{D}\varepsilon(C)$, we get the $\mathscr{D}\varepsilon$-polynomial for Chloroquine as follows:

□

Proposition 3.4. Let $C$ be the molecular graph of Chloroquine. Then, we have,

1) $\mathscr{D}R_{1} \varepsilon (C) = 186.$

2) $\mathscr{D}R_{2} \varepsilon (C) = 435.$

3) $H\mathscr{D}R_{1} \varepsilon (C) = 1762.$

4) $H\mathscr{D}R_{2} \varepsilon (C) = 12869.$

Proof is similar to that of proposition $3.2$.

3.3.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ Indices for Hydroxy-Chloroquine

Theorem 3.5. Let $HC$ be the molecular graph of Hydroxy-Chloroquine. Then, we have,

Proof. Let $HC$ be the molecular graph of Hydroxy-Chloroquine represented in Figure 3. It has $22$ vertices and $24$ edges. Consider

Using the edge partitions given in Table 5, it is clear that $r\rho_{(1, 2)} = 2$, $r\rho_{(2, 3)} = 4$, $r\rho_{(3, 4)} = 6$, $r\rho_{(4, 5)} = 4$, $r\rho_{(5, 6)} = 3$, $r\rho_{(6, 7)} = 2$ and $r\rho_{(7, 8)} = 3$.

Applying the values in $\mathscr{D}\varepsilon(HC)$, we get the $\mathscr{D}\varepsilon$-polynomial for Hydroxy-Chloroquine as follows:

□

Proposition 3.6. Let $HC$ be the molecular graph of Hydroxy-Chloroquine. Then, we have,

1) $\mathscr{D}R_{1} \varepsilon (HC) = 208.$

2) $\mathscr{D}R_{2} \varepsilon (HC) = 522.$

3) $H\mathscr{D}R_{1} \varepsilon (HC) = 2092.$

4) $H\mathscr{D}R_{2} \varepsilon (HC) = 18252.$

Proof is similar to that of proposition $3.2$.

3.4.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ Indices for Lopinavir

Theorem 3.7. Let $L$ be the molecular graph of Lopinavir. Then, we have,

Proof. Let $L$ be the molecular graph of Lopinavir represented in Figure 3. It has $46$ vertices and $49$ edges. Consider

Using the edge partitions given in Table 6, it is clear that $r\rho_{(1, 2)} = 5$, $r\rho_{(2, 3)} = 6$, $r\rho_{(3, 4)} = 8$, $r\rho_{(4, 5)} = 7$, $r\rho_{(5, 6)} = 7$, $r\rho_{(6, 7)} = 6$ and $r\rho_{(7, 8)} = 4$.

Applying the values in $\mathscr{D}\varepsilon(L)$, we get the $\mathscr{D}\varepsilon$-polynomial for Lopinavir as follows:

□

Proposition 3.8. Let $L$ be the molecular graph of Lopinavir. Then, we have,

1) $\mathscr{D}R_{1} \varepsilon (L) = 487.$

2) $\mathscr{D}R_{2} \varepsilon (L) = 1454.$

3) $H\mathscr{D}R_{1} \varepsilon (L) = 5865.$

4) $H\mathscr{D}R_{2} \varepsilon (L) = 73468.$

Proof is similar to that of proposition $3.2$.

3.5.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ Indices for Remdesivir

Theorem 3.9. Let $R$ be the molecular graph of Remdesivir. Then, we have,

Proof. Let $R$ be the molecular graph of Remdesivir represented in Figure 4. It has $41$ vertices and $44$ edges. Consider

Using the edge partitions given in Table $7$, it is clear that $r\rho_{(1, 2)} = 5$, $r\rho_{(2, 3)} = 4$, $r\rho_{(3, 3)} = 1$, $r\rho_{(3, 4)} = 4$, $r\rho_{(4, 5)} = 5$, $r\rho_{(5, 6)} = 7$, $r\rho_{(6, 6)} = 1$, $r\rho_{(6, 7)} = 7$, $r\rho_{(7, 8)} = 4$, $r\rho_{(8, 9)} = 4$ and $r\rho_{(9, 10)} = 2$.

Applying the values in $\mathscr{D}\varepsilon(R)$, we get the $\mathscr{D}\varepsilon$-polynomial for Remdesivir as follows:

□

Proposition 3.10. Let $R$ be the molecular graph of Remdesivir. Then, we have,

1) $\mathscr{D}R_{1} \varepsilon (R) = 460.$

2) $\mathscr{D}R_{2} \varepsilon (R) = 1423.$

3) $H\mathscr{D}R_{1} \varepsilon (R) = 5734.$

4) $H\mathscr{D}R_{2} \varepsilon (R) = 72245.$

Proof is similar to that of proposition $3.2$.

3.6.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ Indices for Ritonavir

Theorem 3.11. Let $Ri$ be the molecular graph of Ritonavir. Then, we have,

Proof. Let $Ri$ be the molecular graph of Ritonavir represented in Figure 4. It has $50$ vertices and $53$ edges. Consider

Using the edge partitions given in Table 8, it is clear that $r\rho_{(1, 1)} = 1$, $r\rho_{(1, 2)} = 4$, $r\rho_{(2, 3)} = 3$, $r\rho_{(3, 3)} = 1$, $r\rho_{(3, 4)} = 5$, $r\rho_{(4, 5)} = 5$, $r\rho_{(5, 6)} = 5$, $r\rho_{(6, 7)} = 6$, $r\rho_{(7, 8)} = 6$, $r\rho_{(8, 9)} = 7$, $r\rho_{(9, 10)} = 4$, $r\rho_{(10, 11)} = 4$, $r\rho_{11, 12)} = 2$.

Applying the values in $\mathscr{D}\varepsilon(Ri)$, we get the $\mathscr{D}\varepsilon$-polynomial for Ritonavir as follows:

□

Proposition 3.12. Let $Ri$ be the molecular graph of Ritonavir. Then, we have,

1) $\mathscr{D}R_{1} \varepsilon (Ri) = 629.$

2) $\mathscr{D}R_{2} \varepsilon (Ri) = 2502.$

3) $H\mathscr{D}R_{1} \varepsilon (Ri) = 10059.$

4) $H\mathscr{D}R_{2} \varepsilon (Ri) = 188762.$

Proof is similar to that of proposition $3.2$.

3.7.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ Indices for Thalidomide

Theorem 3.13. Let $T$ be the molecular graph of Thalidomide. Then, we have,

Proof. Let $T$ be the molecular graph of Thalidomide represented in Figure 5. It has $19$ vertices and $21$ edges. Consider

Using the edge partitions given in Table 9, it is clear that $r\rho_{(1, 1)} = 1$, $r\rho_{(1, 2)} = 3$, $r\rho_{(2, 3)} = 4$, $r\rho_{(3, 3)} = 1$, $r\rho_{(3, 4)} = 7$, $r\rho_{(4, 5)} = 4$ and $r\rho_{(5, 5)} = 1$.

Applying the values in $\mathscr{D}\varepsilon(T)$, we get the $\mathscr{D}\varepsilon$-polynomial for Thalidomide as follows:

□

Proposition 3.14. Let $T$ be the molecular graph of Thalidomide. Then, we have,

1) $\mathscr{D}R_{1} \varepsilon (T) = 132.$

2) $\mathscr{D}R_{2} \varepsilon (T) = 229.$

3) $H\mathscr{D}R_{1} \varepsilon (T) = 934.$

4) $H\mathscr{D}R_{2} \varepsilon (T) = 3471.$

Proof is similar to that of proposition $3.2$.

3.8.   $\mathscr{D}\varepsilon$-polynomial and $\mathscr{D}\varepsilon$ indices for Theaflavin

Theorem 3.15. Let $Th$ be the molecular graph of Theaflavin. Then, we have,

Proof. Let $Th$ be the molecular graph of Theaflavin represented in Figure 5. It has $41$ vertices and $46$ edges. Consider

Using the edge partitions given in Table 10, it is clear that $r\rho_{(1, 2)} = 8$, $r\rho_{(2, 3)} = 4$, $r\rho_{(3, 4)} = 6$, $r\rho_{(4, 5)} = 7$, $r\rho_{(5, 6)} = 8$, $r\rho_{(6, 6)} = 1$, $r\rho_{(6, 7)} = 7$, $r\rho_{(7, 7)} = 1$, $r\rho_{(7, 8)} = 3$ and $r\rho_{(8, 8)} = 1$.

Applying the values in $\mathscr{D}\varepsilon(Th)$, we get the $\mathscr{D}\varepsilon$-polynomial for Theaflavin as follows:

□

Proposition 3.16. Let $Th$ be the molecular graph of Theaflavin. Then, we have,

1) $\mathscr{D}R_{1} \varepsilon (Th) = 415.$

2) $\mathscr{D}R_{2} \varepsilon (Th) = 1103.$

3) $H\mathscr{D}R_{1} \varepsilon (Th) = 3944.$

4) $H\mathscr{D}R_{2} \varepsilon (Th) = 40589.$

Proof is similar to that of proposition $3.2$.

4.   Curvilinear regression analysis of COVID-19 drugs

In this section, we analyze the topological indices given in Table 1 for the following physico-chemical properties of the 8 COVID-19 antiviral drugs: Boiling point $(BP)$, Enthalpy $(E)$, Flash point $(FP)$, Molar refraction $(MR)$, Polar Surface Area $(PSA)$, Polarizability $(P)$, Surface Tension $(T)$, Molar Volume $(MV)$.

Experimental values of physico-chemical properties of the antiviral drugs presented in Table 11 were obtained from Kirmani et al. ^[22]. In Table 12 we have presented the values of the proposed indices calculated in Section 3.

We performed curvilinear regression analysis for our proposed indices aganist the physico-chemical properties.

The general form of the curvilinear regression model is

where $P$ is the physico-chemical property (dependent variable), $\tilde{\gamma}$ is the regression model constant, and $\tilde{\alpha_{i}}$ are the coefficients corresponding to topological descriptors (TI), $i = 1, 2, \ldots, n$.

We performed a comparative analysis of the linear, quadratic, cubic and fourth order curvilinear regression models. The models for which $R^{2} \geq 0.8$ (as per International Academy of Mathematical Chemistry Guidelines) were considered for further analysis. We observed the following:

● From Table 13, it can be seen that the $R^{2}$ values for the following properties: boiling point $(BP)$, enthalpy $(E)$, flash point $(FP)$, molar refraction $(MR)$, polarizability $(P)$ and molar volume $(MV)$, are higher for the cubic models and they can be used to predict these properties. However, polar surface area $(PSA)$ and surface tension $(T)$ could not be predicted using the cubic models.

● All the eight physico-chemical properties could be predicted using fourth order regression models.

4.1.   Best fit fourth order regression models

In this subsection, we present the fourth order regression models for the eight physico-chemical properties. Based on the $R^{2}$ and $RMSE$ values we obtained the following best fit fourth order regression models for the physico-chemical properties.

From Table 13, it is clear that the mentioned indices can be used to predict all the physico-chemical properties of the COVID-19 drugs. From our analysis of the proposed indices, we observe that

● $\mathscr{D} R_1 \varepsilon$ index can be used to predict the Boiling Point $(BP)$, Enthalpy of Vaporization $(E)$, Molar Refraction $(MR)$, Polar Surface Area $(PSA)$, Polarizability $(P)$ and Molar Volume $(MV)$ with the corresponding $R^{2}$ values as $0.9995$, $0.9978$, $0.9776$, $0.9583$, $0.9777$ and $0.9634$, respectively.

● $H\mathscr{D}R_{1} \varepsilon$ index can be used to predict the Flash Point $(FP)$ with the corresponding $R^{2}$ value as $0.9704$.

● $H\mathscr{D}R_{2} \varepsilon$ index can be used to predict the Surface Tension $(T)$ with the corresponding $R^{2}$ value as $0.9996$.

Figure 6 to Figure 8 show the plots of the fourth order regression equations for Boiling Point $(BP)$, Enthalpy of Vaporization $(E)$, Molar Refraction $(MR)$, Polar Surface Area $(PSA)$, Polarizability $(P)$ and Molar Volume $(MV)$ with respect to $\mathscr{D}R_{1} \varepsilon$ index. Figure 9 shows the plots for Flash Point $(FP)$ and Surface Tension $(T)$ with respect to $H\mathscr{D}R_{1} \varepsilon$ and $H\mathscr{D}R_{2}\varepsilon$ indices, respectively.

4.2.   Ediz eccentric connectivity index

In this section, we compare the predictive capability of our proposed indices against the ediz eccentric connectivity index. Table 15 shows the comparison of fourth order regression models of ediz eccentric connectivity index $(E\mathscr{E}^{c}I)$ aganist the fourth order regression models based on our proposed indices.

From Table 15, based on $R^{2}$ and $RMSE$ values it can be observed that the fourth order regression models based on our proposed indices provide the best fits for the eight physico-chemical properties.

5.   Multilinear regression analysis of COVID-19 drugs

In this section we present the Multilinear regression analysis performed for the eight physico-chemical properties aganist our proposed indices. The general form of Multilinear regression is

where $P$ is the physico-chemical property (dependent variable), $\tilde{\gamma}$ is the regression model constant and $\tilde{\alpha_{i}}$ are the regression coefficients for the topological descriptors.

5.1.   Best fit multilinear regression models

In this subsection we present the Multilinear regression models and the analysis for the eight physico-chemical properties.

From Table 16, it can be observed that except for Polar Surface Area with $R^{2} < 0.8$, all other properties are well predicted using the multilinear regression models.

5.2.   QSAR analysis

The most generally used and useful indicator of a drug's effectiveness is its half-maximal inhibitory concentration $IC_{50}$. It is a quantitative metric that shows how much of a certain inhibitory substance (such as a medicine) is required in vitro to inhibit a specific biological process or biological component by $50$ percent ^[33].

We fitted the Multilinear regression model given in Eq ($5.10$) to predict the $IC_{50}$ values for the COVID-19 drugs.

The predicted $IC_{50}$ values for the seven COVID-19 drugs, for which the experimental values are available, are presented in Table 17. It can be seen that the proposed multilinear regression model can be used to predict $IC_{50}$ values.

6.   Conclusions

In this article, we proposed and computed the Diameter Eccentricity Based and Hyper Diameter Eccentricity Based topological descriptors for eight COVID-19 drugs, namely, Arbidol, Chloroquine, Hydroxy-Chloroquine, Lopinavir, Remdesivir, Ritonavir, Thalidomide and Theaflavin through $\mathscr{D}\varepsilon$-Polynomial. The indices were computed using our newly introduced $\mathscr{D}\varepsilon$- polynomial.

From the QSPR analysis using the curvilinear regression models, we conclude that the best fit fourth order regression models based on our proposed index $DR_{1}\varepsilon$ predict Boiling Point, Enthalpy of Vaporization, Molar Refraction, Polar Surface Area, Polarizability and Molar Volume. The fourth order regression models based on $DHR_{1}\varepsilon$ and $DHR_{2}\varepsilon$ can be used to predict Flash Point and Surface Tension, respectively.

We computed the Ediz Eccentric Connectivity index for COVID-19 drugs. Based on $R^{2}$ and $RMSE$ values, it can be observed that the fourth order regression models based on our proposed indices provide good predictions for the eight physico-chemical properties of the 8 COVID-19 drugs compared to the fourth order regression models based on the Ediz Eccentric Connectivity index.

Our proposed multilinear regression models provide good predictions for the physico-chemical properties expect the Polar Surface Area.

Multilinear regression model is best suited for predicting the 50% inhibitory concentration $(IC_{50})$ values with $R^{2}$ value 0.947.

The proposed indices can be used in designing new drugs to combat COVID-19 and other diseases.

Acknowledgement

The authors would like to thank the editor and reviewers for their helpful remarks in improving this manuscript. In addition, the authors would like to express their gratitude to the management of Vellore Institute of Technology, Chennai, India, for their encouragement and assistance in carrying out this research. This research work is financially supported by Vellore Institute of Technology, Chennai, India.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.