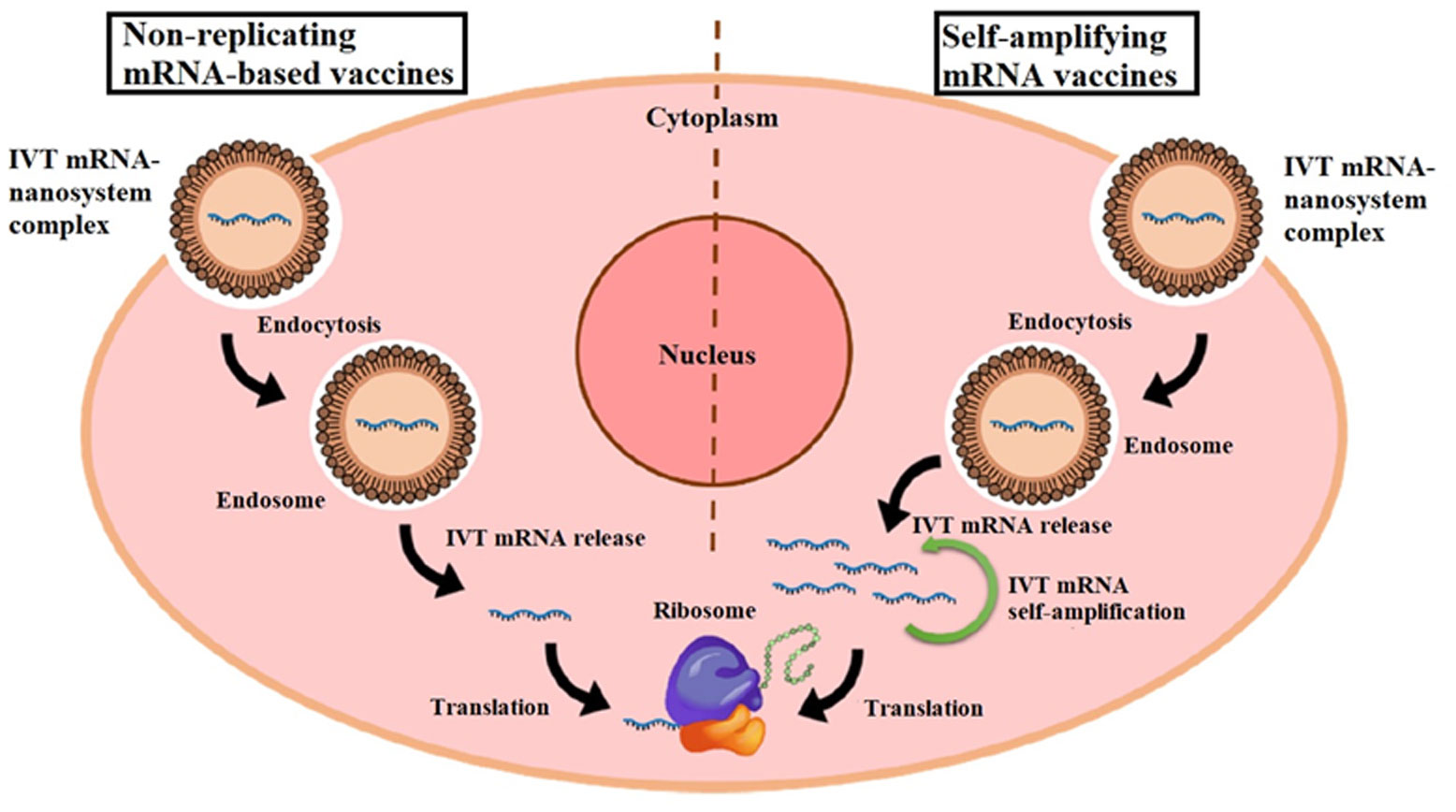
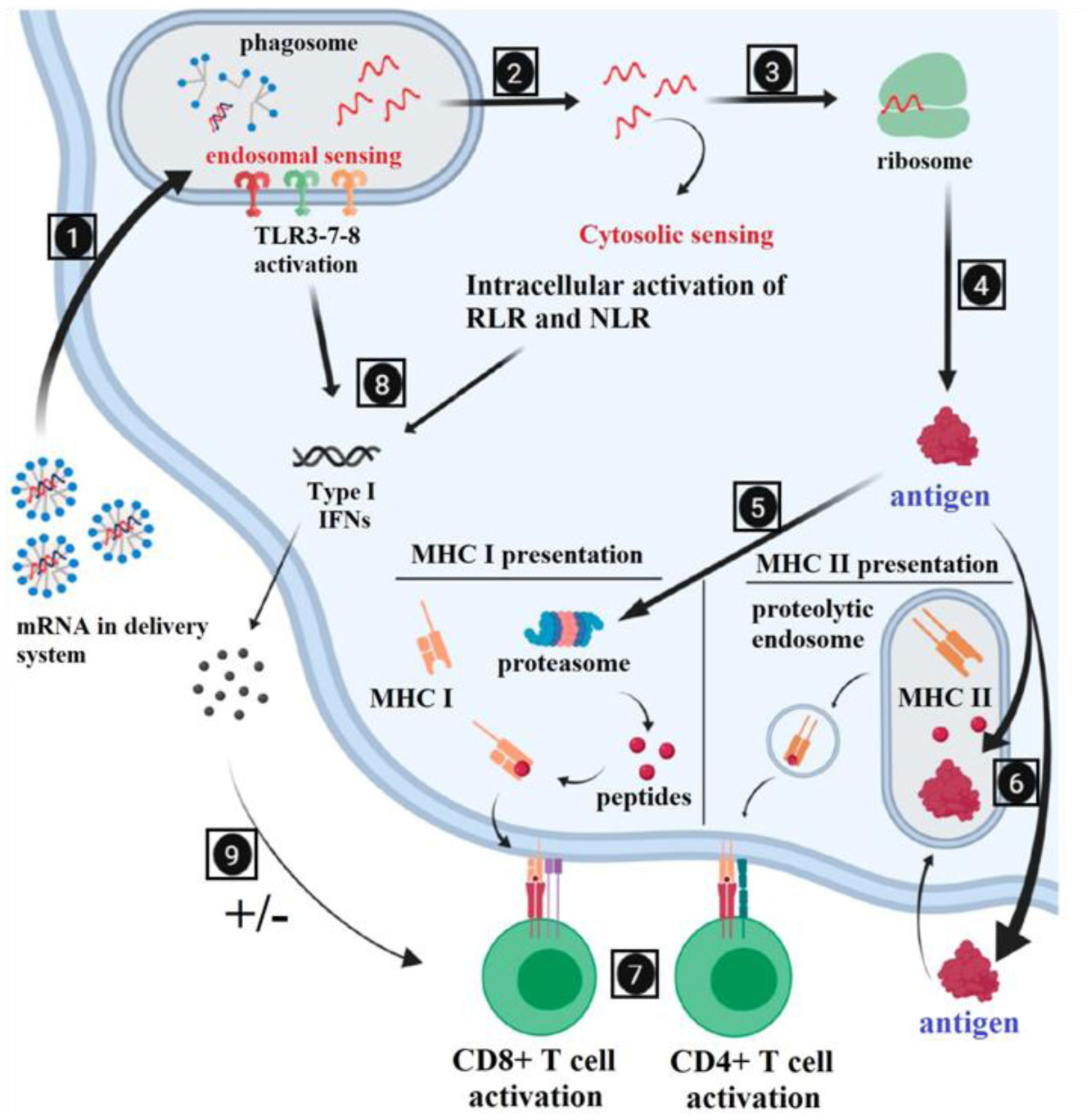
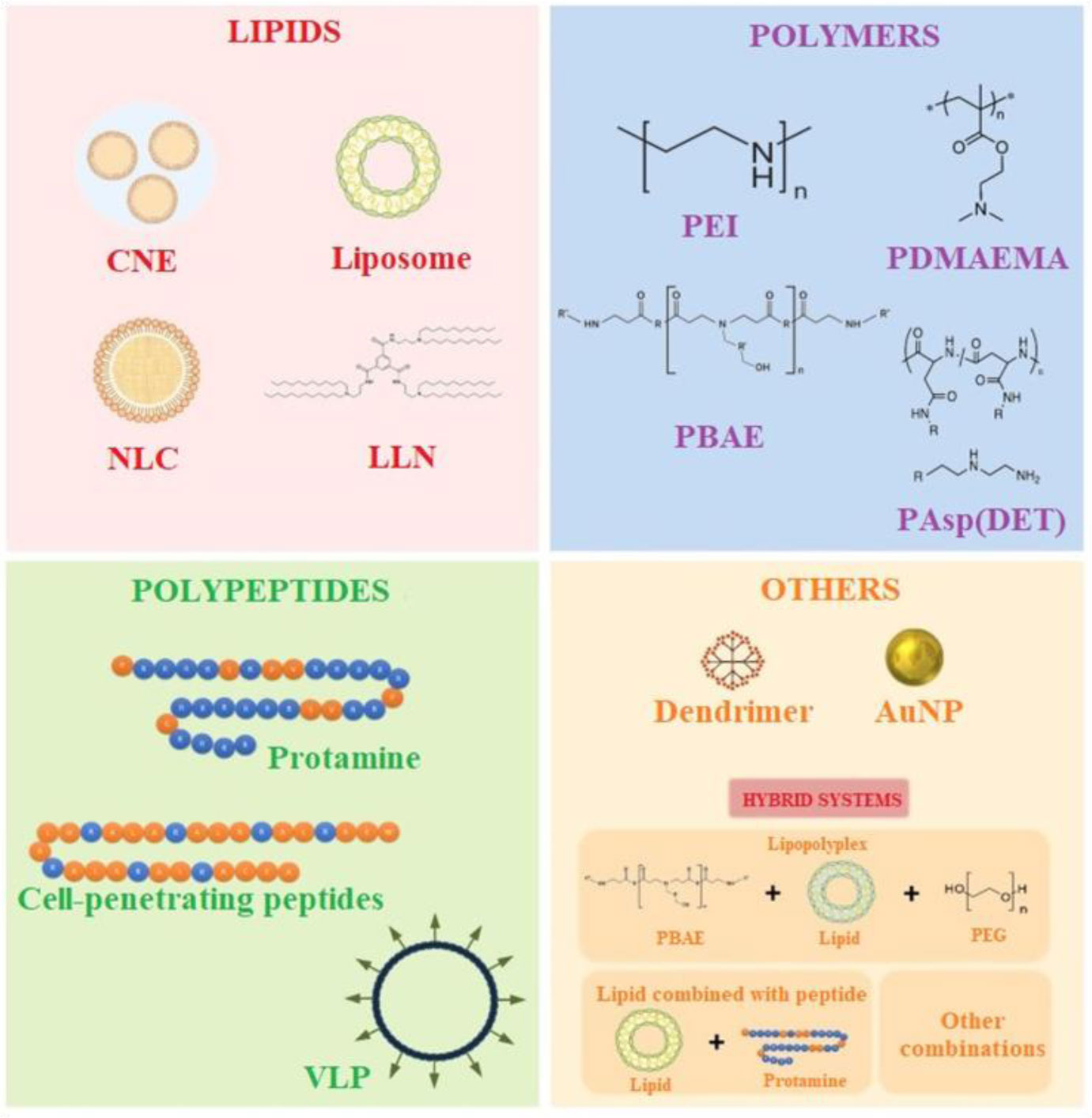
Conventional vaccines have saved millions of lives, and new vaccines have also been developed; however, an urgent need for an efficient vaccine against SARS-CoV-2 showed us that vaccine development technologies should be improved more to obtain prophylactic agents rapidly during pandemic diseases. One of the next-generation vaccine technologies is utilization of mRNA molecules encoding antigens. The mRNA vaccines offer many advantages compared to conventional and other subunit vaccines. For instance, mRNA vaccines are relatively safe since they do not cause disease and mRNA does not integrate into the genome. mRNA vaccines also provide diverse types of immune responses resulting in the activation of CD4+ and CD8+ T cells. However, utilization of mRNA molecules also has some drawbacks such as degradation by ubiquitous nucleases in vivo. Nanoparticles (NPs) are delivery platforms that carry the desired molecule, a drug or a vaccine agent, to the target cell such as antigen presenting cells in the case of vaccine development. NP platforms also protect mRNA molecules from the degradation by nucleases. Therefore, efficient mRNA vaccines can be obtained via utilization of NPs in the formulation. Although lipid-based NPs are widely preferred in vaccine development due to the nature of cell membrane, there are various types of other NPs used in vaccine formulations, such as virus-like particles (VLPs), polymers, polypeptides, dendrimers or gold NPs. Improvements in the NP delivery technologies will contribute to the development of mRNA vaccines with higher efficiency.
1.
Introduction
According to the definition of [1], mutualism is the interaction of two/many species that benefits both/each other. As a common occurrence in nature, the mutualism interaction has an important impact and is well documented in many types of communities. Mutualism can be obligate or facultative, more specifically, an obligate mutualist is a species which requires the presence of another species for its survival [2] while a facultative mutualist is one which benefits in the same way from the association with another species but will be survive in its absence [3]. In recent years many mutualism models have been studied intensively and some good results have been obtained, for details to see stability and bifurcation [4,5,6,7,8,9,10,11,12], persistence and extinction [5,7,8,11,13,14,15,16,17,18,19,20], periodic solution and almost periodic solution [20,21,22,23,24], optimal control [25,26], and stationary distribution [27,28].
Recalling many of the above studies, we can see that the distributed delay does't been taken into account. In fact the evolution of a species may reply on an average over past population or the cumulative effect of the past history, and distributed delays are often incorporated into populations models, for details to see references [30,31,32,33,34,35,36,37,38,39,40]. Particularly, the following Gamma distribution initially given by MacDonald [32]
is usually used for the delay kernels. It is well known that there exist two types of kernels: weak kernel and strong kernel, which respectively, represented by
Both weak kernel and strong kernel own different biological meanings: the former implies that the maximum weighted response of the growth rate is due to current population density while past densities have exponentially decreasing influence, and the latter indicate that the maximum influence on the growth rate response at some time is due to population density at the previous time (see [41]).
On the other hand, the deterministic models may be necessary to incorporate the environmental noises into these models. Nisbet and Gurney [42] and May[43] suggested that the growth rates in population systems should own stochasticity and emerge random fluctuation to a certain degree. Thus, some noise sources were incorporated and then corresponding stochastic models were established. However, in many excellent investigations the authors assumed that one noise source only had an effect on the intrinsic growth rate of one species. Obviously, a reasonable idea is to consider that one noise source has influence not only on the intrinsic growth rate of one species but also on that of other species.
Inspired by the above arguments, in the next section we introduce a stochastic facultative mutualism model with distributed delays and strong kernels (see model (2.3)). Survival analysis and stationary distribution will become two topics of our whole research because the survival analysis reveals the persistence or extinction of one or more species in random environment and the stationary distribution is concerned with the stochastic statistical characteristic of the long-term behaviours of the sample trajectories. To the best of our knowledge, there are few published papers concerning model (2.3). The rest of this work is organized as follows. In Section 3, we present the main results including extinction exponentially, persistence in the mean, permanent in time average. In Section 4, we devote to investigating the existence and uniqueness of stationary distribution. In Section 5, numerical simulations are given to support our findings. A brief discussion on the biological meanings is shown in Section 6.
2.
Model and preliminaries
For the final export of the model we will discuss, let us first introduce the following facultative mutualism model with saturation effect which corresponds to a deterministic competitive model proposed by Gopalsamy [29]
where xi (i=1,2) are the densities of two species, ai>0 denote the intrinsic growth rates, bi>0 are the intraspecific competition rates, ci>0 are the interspecific mutualism rates and the nonlinear term c1x2/(1+x2) (or c2x1/(1+x1)) reflects a saturation effect for large enough x2 (or x1).
With the idea of distributed delays and strong kernels, model (2.1) becomes a delayed version
Similar to [44], we use two coupling noise sources to model the random perturbations and derive a new stochastic model
with initial values xi(s)=ϕi(s)≥0, s∈(−∞,0] and ϕi(0)>0, where ϕi are continuous bounded functions on (−∞,0]. Bi(t) are standard independent Brownian motions defined on a complete probability space (Ω,F,{Ft}t≥0,P) with a filtration {Ft}t≥0 satisfying the usual conditions. And α21i, α22i denote the coupling noise intensities.
Assign
With the help of chain techniques, the delayed stochastic facultative mutualism model (2.3) is transformed into an equivalent undelayed stochastic six-dimensional system
with initial value (x1(0),x2(0),m1(0),m2(0),n1(0),n2(0)), where
To show the novelty of our work, we explicate the following two facts:
(I) Zuo et al. [36] recently investigated the following stochastic two-species cooperative model with distributed delays and weak kernels
Obviously, there exists a limitation in model (2.6): with the increase of one cooperator's density, its cooperative capacity will increase and tend to infinity (see ci∫t−∞σje−σj(t−s)xj(s)ds). But in real life, this interaction between different species should be upper-bounded (a similar argument can be seen in [45]). In our model (2.3), the interspecific mutualism terms ci∫t−∞(t−s)σ2ie−σi(t−s)xj(s)1+xj(s)ds show saturation effects. Also, by the chain techniques, model (2.6) can be transformed into an equivalent four-dimensional system (see model (2.2) in [36]) whose dimension is lower than the above six-dimensional system (2.5). Finally, we must point out that there are two noise sources in model (2.6), but one noise source only has an effect on one species. It is easy to see that one noise source affects two species at the same time in model (2.3).
(II) In a recent investigation, Ning et al. [40] discussed a stochastic competitive model with distributed delays and weak kernels
Clearly, there exists a remarkably different mechanism of action between model (2.3) and model (2.7) because the former is interspecific mutualism (see the positive feedback parameters ci) and the latter is interspecific competition (see the negative feedback parameters −ci). The strong kernel functions of our model (2.3) differs distinctly from the weak kernel functions of the above model (2.7) (also see Eq (1.1)). By the chain techniques, an equivalent undelayed six-dimensional system to model (2.3) is also different from that of the undelayed four-dimensional system to model (2.7) (see model (3) in [40]).
As a continuation of previous work [40], our main purpose of this contribution is to investigate the effects of both coupling noise sources on the long-time behaviors of facultative mutualism model (2.3) with distributed delays and strong kernels by analyzing its equivalent system (2.5). For the convenience of the subsequent analysis, we list the following two definitions.
Definition 2.1. Signals and abbreviations are defined in Table 1.
Definition 2.2. Survival results of species are defined in Table 2.
3.
Survival analysis
This section is determined to analyze the survival of system (2.5). For the convenience of the subsequent discussion, we first estimate mi(t) and ni(t).
Lemma 3.1. mi(t), ni(t)≤1 and limt→+∞mi(t)/t=limt→+∞ni(t)/t=0, i=1,2.
Proof. We first consider the upper bound of mi(t). It follows from Eq (2.4) that
Also, we obtain from Eq (2.4) that
Obviously, Eqs (3.1) and (3.2) imply that limt→+∞mi(t)/t=0, limt→+∞ni(t)/t=0, i=1,2.
We continue to give the following fundamental lemma on the global existence and uniqueness of positive solution to system (2.5).
Lemma 3.2. For any initial value X(0)=(x1(0),x2(0),m1(0),m2(0),n1(0),n2(0))>0, system (2.5) admits a unique global solution X(t)=(x1(t),x2(t),m1(t),m2(t),n1(t),n2(t))>0 for t≥0 a.s.
Proof. Using Itô's formula, we obtain from system (2.5) that
Define a C2-function U(X(t)) by
Applying Itô's formula to Eq (3.4) leads to
where
and
It follows from Lemma 3.1 that m1≤1 and m2≤1, and then K is bounded when x1,x2∈(0,+∞). As a consequence, LU(X(t)) is bounded. The rest proof is similar to that of Theorem 2.1 in [46], and hence we omit it.
Assign ξ1=0.5(α211+α212), ξ2=0.5(α221+α222). The following Theorems 3.1-3.4 focus on the survival results of both species.
Theorem 3.1. Both species are extinct exponentially if a1+c1<ξ1 and a2+c2<ξ2.
Proof. An integration of Eq (3.3) over [0,t] leads to
Dividing by t and using Lemma 3.1, one has
The strong law of local martingales [47] states limt→+∞t−1Bi(t)=0, and moreover, we derive from Eq (3.6) that
Thus, both species are extinct exponentially by the assumptions of Theorem 3.1.
Theorem 3.2. Assume that a1+c1<ξ1 and a2>ξ2, then species x1 goes to exponential extinction while species x2 is persistent in the mean and limt→+∞⟨x2(t)⟩=(a2−ξ2)/b2 a.s.
Proof. If a1+c1<ξ1, then we obtain from Theorem 3.1 that species x1 will be extinct exponentially and lim supt→+∞t−1lnx1(t)<0. Thus, we further derive that
An integration of the last four equations of system (2.5) on both sides results in
Consequently, we have
furthermore, it follows from Lemma 3.1 that limt→+∞mi(t)/t=0 and limt→+∞ni(t)/t=0. And limt→+∞mi(0)/t=0, limt→+∞ni(0)/t=0. So we have
Next, by Eq (3.7) one gets for arbitrarily small ε>0, there is T>0 such that for t≥T,
which together with Eq (3.8) leads to
Let −ε<t−1lnx2(0)<ε/2 for t≥T. We obtain from Eqs (3.5) and (3.9) that for t≥T,
An application of Lemma 4 in [48] to the above two inequalities gives that
Thus
is acquired by the arbitrariness of ε.
Theorem 3.3. Suppose that a1>ξ1 and a2+c2<ξ2, then species x2 goes to exponent extinction while species x1 is persistent in the mean and limt→+∞⟨x1(t)⟩=(a1−ξ1)/b1 a.s.
Proof. The proof is similar to that of Theorem 3.2, and hence we omit it.
Theorem 3.4. Assume that a1>ξ1 and a2>ξ2, then both species will be permanent in time average and (a1−ξ1)/b1≤⟨x1⟩∗≤⟨x1⟩∗≤(a1−ξ1+c1)/b1, (a2−ξ2)/b2≤⟨x2⟩∗≤⟨x2⟩∗≤(a2−ξ2+c2)/b2 a.s.
Proof. Recalling Eq (3.5) and Lemma 3.1, we have
It follows from Lemma 4 in [48] that
So the desired conclusion is obtained.
4.
Stationary distribution
In this section, to discuss the stationary distribution of system (2.5) we make some preliminaries. Consider the following integral equation
Lemma 4.1. [49]. Assume that the coefficients of Eq (4.1) are independent of t and satisfy the following conditions for a constant κ:
in OR⊂Rd+ and there exists a nonnegative C2-function V(x) in Rd+ satisfying LV(x)≤−1 outside some compact set. Then Eq (4.1) exists a solution which has a stationary distribution.
Remark 4.1. [36]. The condition in Lemma 4.1 may be replaced by the global existence of the solution to Eq (4.1) according to Remark 5 in Xu et al. [50].
We first give Lemma 4.2 which is important for the subsequent discussions.
Lemma 4.2. Assume that X(t) is a solution to system (2.5) with initial value X(0)>0. Then there is a positive constant Qq such that for q>0,
Proof. Let
Applying Itô's formula to Eq (4.2), one can derive that
in which
Obviously, we get, by Young's inequality, that
It follows from Lemma 3.1 that m1≤1 and m2≤1. By Eq (4.3) we have
For a constant η>0, we have
Choosing the above constant η small enough such that biη/(2σi)−bi/2<0, and noting that biη/(2σi)nq+1i≤biη/(2σi) (see Lemma 3.1, ni≤1), we further obtain
where
Integrating Eq (4.4) from 0 to t and then taking the expectation, one has
which together with the continuity of V(X(t)) and the boundedness of e−ηtV(X(0)) and G1/η, implies that there exists a constant G2>0 such that for all t≥0
We further obtain from Eq (4.2) that E[xqi/q]≤E[V(X(t))]≤G2, and hence
Also, it follows from Eq (4.2) that E[mq+1i]≤2σiG2/bi. And by the Young's inequality, there exist A1i>0 such that
Similarly, we can prove there exist A2i such that
Let
then for q>0,
The proof is complete.
Lemma 4.3. Suppose that X(t) is a solution to system (2.5) with X(0)>0, then almost every path of X(t) to system (2.5) will be uniformly continuous.
Proof. First let us consider x1(t). For any 0≤t1≤t2, an integration of the first equation of system (2.5) yields
Let p>2, by the elementary inequality |a+b+c|p≤3p−1(|ap+bp+cp|), one has
Recalling Lemma 4.2 (see Eq (4.5)) and using the Hölder inequality result in
In addition, using the Moment inequality and Lemma 4.2 leads to
Substituting Eqs (4.8) and (4.9) into Eq (4.7), we have
where
Next, we continue to consider m1(t). For any 0≤t1≤t2, integrating the third equation of system (2.5) from t1 to t2 yields that
Similar to Eq (4.7), we have from the Hölder inequality and Lemma 4.2 that
where F2=2p(t2−t1)p2σp1Qp.
Finally, we investigate n1(t). For any 0≤t1≤t2, by integrating the fifth equation of system (2.5) one has
Similar to Eq (4.11), one obtains
Repeating the same analysis method as above, we obtain that x2, m2 and n2 own similar results as those of Eqs (4.10)-(4.12), respectively. Thus, it follows from Lemma 3.4 in [50] that almost every sample path of X(t) is uniformly continuous.
Lemma 4.4. [51]. Let h(t) be a nonnegative function defined on [0,+∞) such that h(t) is integrable on [0,+∞) and is uniformly continuous on [0,+∞). Then limt→+∞h(t)=0.
Lemma 4.5. If b1b2−c1c2>0, then the solution X(t)=(x1(t),x2(t),m1(t),m2(t),n1(t), n2(t))>0 to system (2.5) is globally attractive, that is, for any solution ˉX(t)=(ˉx1(t),ˉx2(t), ˉm1(t),ˉm2(t),ˉn1(t),ˉn2(t)) to system (2.5) with ˉX(0)>0, there exist limt→+∞|xi(t)−ˉxi(t)|=0, limt→+∞|mi(t)−ˉmi(t)|=0, limt→+∞|ni(t)−ˉni(t)|=0 a.s., i=1,2.
Proof. It follows from the last two equations of system (2.5) that
Integrating both sides of Eq (4.13) over the interval [0,t] yields that
As a consequence, one has
Note that
we have
from which we conclude that
Similarly, one has
Assign
A direct calculation of the right differential D+M(t) of M(t) leads to
from which and Eqs (4.15) and (4.16) one can obtain
Rearranging the above inequality leads to
from which one gets |xi(t)−ˉxi(t)|∈L1[0,+∞). Similarly, it follows from Eqs (4.15) and (4.16) that |mi(t)−ˉmi(t)|,|ni(t)−ˉni(t)|∈L1[0,+∞). Thus, we obtain from Lemmas 4.3 and 4.4 that
which confirms Lemma 4.5.
Theorem 4.1. If a1−ξ1−c1>0, a2−ξ2−c2>0 and b1b2−c1c2>0, then system (2.5) admits a unique stationary distribution.
Proof. To finish this proof, we will consider the following two steps.
Step 1: We first prove the existence of stationary Markov process.
It follows from Lemma 4.1 and Remark 4.1 that we only need to find a nonnegative C2-function W(X(x1,x2,m1,m2,n1,n2)) and a closed set U⊂R6+ such that LW(X)≤−1 on X∈R6+∖U. Let q>1 and
where δi=2λimax{2,Hi},λi=ai−ξi−ci,i=1,2, and the constants Hi>0 will be given later. An application of Itô's formula and Lemma 3.1 gives
Choose ϵ>0 sufficiently small such that
i=1,2, where the constant H3>0 is supplied later. A bounded closed set is defined by
Assign
To prove that LW(X)≤−1 for X∈R6+∖Uϵ, we will consider the following six cases.
Case 1. When X∈Uϵ1, one has from Eq (4.19) that
where
We have from δ1=2λ1max{2,H1} that δ1λ1/4≥1. Then
Similarly, for X∈Uϵ2 and δ2=2λ2max{2,H2}, one has
where
To discuss the following Cases 2-6, we reconsider Eq (4.19) and obtain
where
Case 2. When X∈Uϵ3, it follows from Eq (4.20) that LW(X)≤H3+5−12b1ϵ−(q+1)≤−1. Similarly, if X∈Uϵ4, then LW(X)≤H3+5−12b2ϵ−(q+1)≤−1.
Case 3. When X∈Uϵ5 and X∈Uϵ6, one has LW(X)≤H3+5−m2i4<H3+5−14ϵ4≤−1.
Case 4. When X∈Uϵ7 and X∈Uϵ8, then LW(X)≤H3+5−3n2i4<H3+5−34ϵ4≤−1.
Case 5. When X∈Uϵ9 and X∈Uϵ10, we get LW(X)≤H3+5−12mini<H3+5−12ϵ3ϵ2≤−1.
Case 6. When X∈Uϵ11 and X∈Uϵ12, then LW(X)≤H3+5−1nixi1+xi<H3+5−1ϵ2ϵ1+ϵ≤−1.
From the above discussions we know the closed set Uϵ satisfying supX∈R6+∖UϵLW(X)≤−1.
Step 2: When b1b2−c1c2>0, we know from Lemma 4.5 that the solution X(t) is globally attractive.
Combining Step 1 and Step 2, we complete the proof of Theorem 4.1.
5.
Numerical simulations
In this section, we will employ several specific examples to simulate the solutions to system (2.5), and verify the analytical results of the previous section.
For system (2.5), we first fix the parameter values as follows: a1=0.295, a2=0.3, b1=0.75, b2=0.65, c1=0.05, c2=0.05, σ1=0.1, σ2=0.2 and initial value x1(0)=0.1 and x2(0)=0.12. We will reveal how two coupling noise sources influence the long-time behaviors by choosing different noise intensities α211, α212, α221 and α222.
Choose α211=0.652, α212=0.752, α221=0.642, α222=0.742. A calculation gives that a1+c1=0.3<ξ1=0.4925 and a2+c2=0.35<ξ2=0.4786, which surely satisfies Theorem 3.1. Thus, both species will be EE (see Figure 1).
Choose α211=0.652, α212=0.752, α221=0.032, α222=0.022. By calculating we have a1+c1=0.3<ξ1=0.4925 and a2=0.3>ξ2=0.00065, it then follows from Theorem 3.2 that species x1 is EE while x2 is PM (see Figure 2).
Choose α211=0.032, α212=0.022, α221=0.652, α222=0.752. Since a1=0.295>ξ1=0.00065 and a2+c2=0.35<ξ2=0.4925, Theorem 3.3 indicates that species x1 is PM while x2 is EE (see Figure 3).
Choose α211=0.032, α212=0.022, α221=0.022, α222=0.012. Together with Theorem 3.4, we have from a1=0.295>ξ1=0.00065 and a2=0.3>ξ2=0.00025 that both species are PTA (see Figure 4).
Furthermore, taking the same noise intensities as in Figure 4, a calculation shows that a1−ξ1−c1=0.24435>0, a2−ξ2−c2=0.24975>0 and b1b2−c1c2=0.485>0. So we know, by Theorem 4.1, that system (2.5) owns a unique stationary distribution (see Figure 5).
6.
Discussion
This paper is concerned with a stochastic facultative mutualism model with saturation effect and distributed delays, in which strong kernel functions are incorporated (see model (2.3)). By analyzing a corresponding equivalent system (2.5), a set of easily verifiable sufficient conditions for the survival results and stationary distribution of system (2.5) is established. Note that ξ1=0.5(α211+α212) and ξ2=0.5(α221+α222) and from the above theoretical results, we have the following conclusions:
● Theorems 3.1-3.4 imply that large coupling noise intensities are harmful for the survival of both species while suitably small coupling noise intensities are advantage for them (see Figures 1-4).
● It follows from Theorems 3.2 and 3.3 that if the intrinsic growth rate of one species is small, the coupling noise intensities are large amplitude and the cooperation from the other species is not enough, then one species will be extinct exponentially (see Figures 2-3). However, if the other species only owns large intrinsic growth rate and relatively small coupling noise intensities, then it will be persistent in the mean (see Figures 2-3).
● Compared with the conditions of Theorems 3.1, 3.4 and 4.1, that is, ai+ci<ξi, ξi<ai and ξi<ai−ci (i=1,2), we find that the intrinsic growth rates ai are larger and larger while the coupling noise intensity ξi is smaller and smaller, then both species go from exponent extinction (see Figure 1) to permanence in time average (see Figure 4) to the existence of a unique stationary distribution (see Figure 5). In addition, b1b2−c1c2>0 reveals that the effect of interspecific mutualism is less than that of intra-specific competition.
Acknowledgments
The authors thank the editor and referees for their careful reading and valuable comments. The work is supported by the College Innovation Team Project of Hubei Provincial Department of Education (No.T201812).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: