Noninvasive fetal ECG extraction using doubly constrained block-term decomposition

1.   Introduction

The abdominal fetal electrocardiogram (fECG) is the electrical activity of the fetal heart that is recorded by abdominal electrodes. It is a very important tool for monitoring and evaluation of fetal cardiac activity. This signal is generated from a small heart, so the signal amplitude is low and it is morphologically quite similar to the adult ECG, with a higher heart rate. Non-invasive fECG extraction means extracting a clean fECG signal from the abdominal mixed signals, which is an interesting issue for several reasons ^[1]. The fECG provides useful information about fetal health for clinicians and helps them in better diagnosis. It also provides more precise data on fetal heart rate compared to ultrasonic Doppler techniques ^[2]. Nevertheless, there are limitations in non-invasive fECG extraction, due to the presence of interference signals such as the much stronger maternal ECG as the main interference source, muscle noise, motion artifacts, and etc. Moreover, since fECG and maternal ECG have temporal and spectral overlap, fECG separation from the abdominal mixture is complicated ^[3]. These limitations could be considered as the major difficulties in fECG extraction, which have turned it to one of the major challenges in biomedical signal processing.

In the field of non-invasive fECG extraction, there are many mathematical based methods such as Kalman Filter ^[4,5,6], wavelet transform ^{[7,8,9,10,11]}, blind source separation ^{[12,13,14,15,16,17]}, and matrix decomposition ^[18,19]. These methods attempt to detect R-peaks or extract the fECG from either abdominal or abdominal and thoracic recordings. In recent years, an approach has been developed in which, tensor decompositions have been employed for signal processing and fECG extraction, whereby promising results have been achieved ^[20]. An effective solution for the extraction and separation of sources from tensorized observations could be obtained by constrained tensor decomposition and modified cost function. In addition, a correct selection of decomposition type and the method of constructing tensors from observation data are very important in achieving significant results.

In ^[21], a tensor decomposition-based algorithm for fECG extraction is introduced by adding fetal periodicity constraint to Tucker decomposition. Because of the low-amplitude of the fetal signal compared to the high-amplitude of the maternal signal, the drawback of this method, especially in Low SNRs, is the use of only the fetal periodicity constraint.

Block-term decomposition (BTD) decomposes a tensor into tensors with a rank greater than one. In the application of fECG extraction, by changing the cost function and applying constraints on it, the structure of the BTD can be modified to decompose the tensor into three blocks containing maternal, fetal, and noise subspaces. In this paper, by using some source separation methods (πCA or ICA), the fECG peaks are first extracted and then, by using the extracted subspace from the observation matrix (abdominal mixed signals), the observation tensor is formed, and finally by applying periodicity constraints on BTD, the fECG signal could be extracted. In fact, by utilizing the useful information of the ECG signal, the semi-periodicity property, is the objective of constraining the BT decomposition. Regarding the semi-periodicity of both the maternal ECG (mECG) and fECG signals, we apply two constraints on the BTD, simultaneously.

The remainder of this paper is organized as follows. Section 2 presents the concepts and relations of BTD. Section 3 involves how to construct the observations tensor and the proposed constrained BTD. Finally, the results and conclusion are presented in sections 4 and 5, respectively.

2.   Block term decomposition

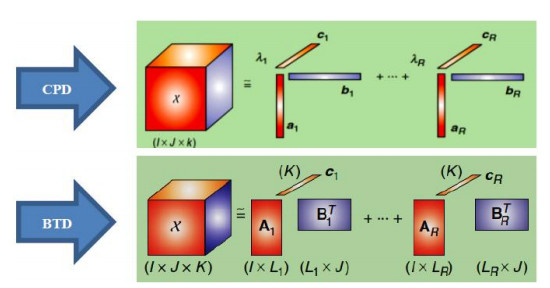
A tensor is a multidimensional array, which is the higher-order generalization of vector and matrix ^[22]. Decompositions of tensors have applications in many fields such as signal processing and image processing. CP (Canonical Polyadic) decomposition approximates a tensor by a sum of Rank-1 tensors.

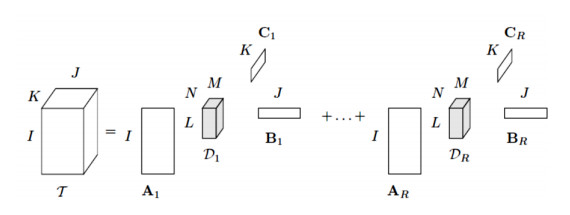
In many applications, e.g. blind source separation (BSS), a given tensor should be decomposed into tensors of rank higher than one. BTD has been introduced for this purpose. In contrast to the CPD, BTD approximates a tensor by a sum of higher-rank terms (Figure 1). In this section, definitions and characteristics of BTD are represented. A block term decomposition of a tensor $x \in \mathbb{R}^{I \times J \times K}$ is a decomposition of X of the form

where the main tensor $x \in \mathbb{R}^{I \times J \times K}$ is decomposed to a sum of Rank$-\left(L_{r}, M_{r}, N_{r}\right)$ terms; $\mathrm{A}_{r} \in\mathbb{R}^{I \times L_{r}}, {B}_{r} \in \mathbb{R}^{J \times M_{r}}$, and $\mathrm{C}_{r} \in \mathbb{R}^{K \times N_{r}}$ are the factor matrices where $I \geq L_{r}, J \geq M_{r}, K \geq N_{r}$, $1 \leq r \leq R$ and $\mathcal{D}_{r} \in \mathbb{R}^{\mathrm{L}_{r} \times M_{r} \times N_{r}}$ are the core tensors. A visual representation of a third-order tensor is shown in Figure 2.

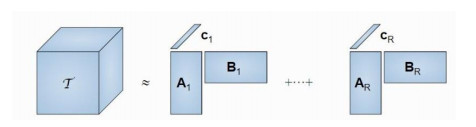
Another type of BT decomposition writes a third-order tensor as a sum of R Rank-(L_r, L_r, 1) terms. Each of these terms can be written as the outer product of a matrix and a vector

The matricized form of BT decomposition based on factor matrices could be expressed as follows

where A, B and C are more general matrices and considered as ${\rm{A}} = \left[{{{\rm{A}}_1}{{\rm{A}}_2} \ldots {\rm{}}{{\rm{A}}_R}} \right], {\rm{B}} = \left[{{{\rm{B}}_1}{{\rm{B}}_2} \ldots {\rm{}}{{\rm{B}}_R}} \right]$, and ${\rm{C}} = \left[{{{\rm{c}}_1}{{\rm{c}}_2} \ldots {\rm{}}{{\rm{c}}_R}} \right]$. Figure 3 shows this decomposition.

The optimal estimate of the factor matrices A_r, B_r and C_r could be obtained by solving the optimization problem (4) by using the alternating least square method ^[23].

Other tensor decomposition methods and more details of BTD are presented in ^{[22,23,25,26]}.

3.   Proposed method: DoCoBT decomposition

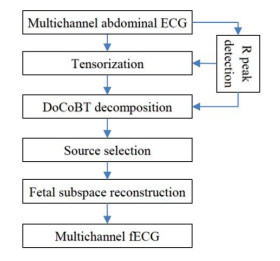
In this section, the proposed method for fECG extraction based on tensor decomposition is explained in two parts: The doubly periodicity constraints and the DOCoBT decomposition.

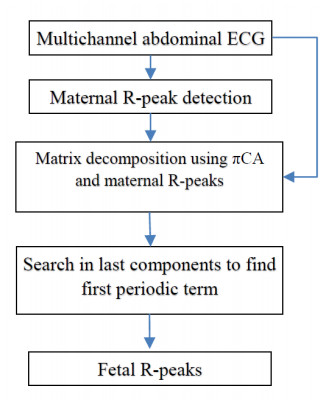
Figure 4 shows the block diagram of the proposed method and contains tensor construction by using maternal abdominal signals, constrained BT decomposition by using maternal and fetal periodicity constraints, detection, and selection of fetal sources and reconstruction of fECG in the sensor space.

3.1.   Tensor construction

The tensor used in this study is a third-order one ${\cal X} \in \mathbb{R}^{L \times N \times K}$ with channel × time × subspace structure (L = number of channels, N = number of time indecis, K = number of subspaces).

In order to create this tensor, the abdominal signals and fECG subspace obtained by using a source separation methods (ICA or πCA) are placed in the first and second slice of the third mode of the tensor, respectively. Figure 5 shows the structure of these tensors.

3.2.   Fetal R-peak detection

To eliminate user interference and to speed up processing for fECG extraction, it is important to automatically identify the type of sources (maternal, noise and fetal sources) obtained from source separation methods. The type of sources can be determined by employing the maternal and fetal R-peaks and using correlation analysis. In order to extract fetal R-peaks, a πCA-based algorithm is proposed in this section (Figure 6). Due to the dominance of mECG signals, at first, the maternal R-peaks are extracted using one of the common peak detection methods ^[27,28]. Then, the observation matrix is decomposed into its sources using πCA and maternal R-peaks. In the πCA algorithm, the extracted sources are ranked according to their synchronization degree (periodicity) with a vector of peaks impulse train. Therefore, since the maternal R-peaks are used as the impulse train in the πCA method, the extracted sources are ordered based on their similarity to the mECG. So, the most similar sources to the mECG could be observed in the source matrix from the first to the last extracted component. Consequently, the last signals have the least similarity to the mECG, and accordingly, the fetal components could be observed in the last rows. Since the average beat-rate for mother and fetus are different significantly, after extracting the R-peaks of the last signals, we calculate average RR interval and compare it with a threshold T = 0.5 sec (the average RR interval for mother and fetus are about 0.9 sec and 0.45 sec respectively). The first semi-periodic source with average RR interval less than 0.5 sec is recognized as fetal signal and its R-peaks are utilized as fetal R-peaks.

3.3.   Periodicity constraint

Biomedical signals usually contain information that could be employed for separation and extraction of desired sources. The semi-periodicity of ECG and fECG signals could be considered as the mentioned information.

In ^[29], the cost function (5) has been introduced as a criterion of periodicity for semi-periodic signals. Thus, the maximization of the following cost function could be used as a means of extracting the semi-periodic signal s(t)

where E_t{} represents averaging over time index t, and τ_t is the time-varying period of s(t). This maximization problem could be reformed as a minimization problem:

In ^[21], the penalty (5) has been used in order to force Tucker decomposition (called it πTucker) to extract fetal components as periodic signals. In this method, the mother's ECG as a strong periodic interference has been ignored.

3.4.   DoCoBT decomposition

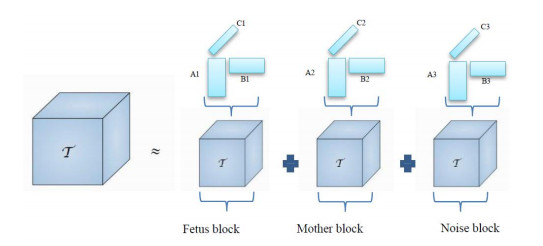
In order to extract the fECG from abdominal signals, we first construct an observation tensor and then decompose it into three blocks or tensors using BTD. The first and second blocks are constrained by fetal and maternal ECG periodicity constraints, respectively, and the third one is considered as a noise block (Figure 7).

By considering the BTD for three blocks, Eq 2 for observation tensor ${\cal X} \in \mathbb{R}^{L \times N \times K}$ could be written as

The matricized form of Eq 7 could be represented as

where, A, B and C contain the factor matrices and A and C are obtained by closed equations ^[26]

Consider the tensor $\mathcal{X} \in {\mathbb{R}^{L \times N \times K}}$ has the structure of channel × time × subspace. Therefore, ${\text{A}} = \left[{{{\text{A}}_1}{{\text{A}}_2}{\text{}}{{\text{A}}_3}} \right]\left({{{\text{A}}_1} \in {\mathbb{R}^{L \times {R_1}}}, {{\text{A}}_2} \in {\mathbb{R}^{L \times {R_2}}}, {{\text{A}}_3} \in {\mathbb{R}^{L \times {R_3}}}} \right)$, ${\text{B}} = \left[{{{\text{B}}_1}{{\text{B}}_2}{\text{}}{{\text{B}}_3}} \right]\left({{{\text{B}}_1} \in {\mathbb{R}^{N \times {R_1}}}, {{\text{B}}_2} \in {\mathbb{R}^{N \times {R_2}}}, {{\text{B}}_3} \in {\mathbb{R}^{N \times {R_3}}}} \right)$ and ${\text{C}} = \left[{{{\text{c}}_1}{\text{}}{{\text{c}}_2}{\text{}}{{\text{c}}_3}} \right]\left({{{\text{c}}_1} \in {\mathbb{R}^{K \times 1}}, {{\text{c}}_2} \in {\mathbb{R}^{K \times 1}}, {{\text{c}}_3} \in {\mathbb{R}^{K \times 1}}} \right)$ contain channel, temporal and subspace components, respectively. Thus, the penalty (6) could be written for B₁ and B₂ factor matrices that are initialized with R₁ fetal and R₂ maternal sources, extracted from a BSS algorithm such as ICA

where τ_if and τ_im are the fECG and mECG time-varying periods, respectively. B₁(i, :) and B₂(i, :), as ith rows of the factor matrices B₁ and B₂, contain the ith time index of fetal and maternal components, respectively. Moreover, B₃ is initialized with R₃ noise components extracted from the BSS algorithm. Finally, to estimate matrix B (sources matrix), the following optimization problem with doubly periodicity constraints could be obtained

where λ_f and λ_m are the penalty coefficients of fECG and mECG periodicity constraints, respectively.

Now, by using ${\rm{B}}\left({i{\rm{, }}:} \right) = {e_i}^T{\rm{B}}$ and defining ${{\rm{W}}_1} = {\rm{}}{E_i}\left\{ {{e_i}{e_{i + {\tau _{im}}}}^T - {e_i}{e_i}^T} \right\} = {\rm{}}\frac{1}{N}{\rm{}}\mathop \sum _{i = 1}^N {e_i}{e_{i + {\tau _{im}}}}^T - {e_i}{e_i}^T$ and ${{\rm{W}}_2} = {\rm{}}{E_i}\left\{ {{e_i}{e_{i + {\tau _{if}}}}^T - {e_i}{e_i}^T} \right\} = {\rm{}}\frac{1}{N}{\rm{}}\mathop \sum _{i = 1}^N {e_i}{e_{i + {\tau _{if}}}}^T - {e_i}{e_i}^T$, Eq 12 could be rewritten as

Thus, the cost function in (13) could be considered as $J = {J_{\rm{t}}} + {\lambda _f}{J_f} + {\lambda _m}{J_m}$ where ${J_{\rm{t}}} = {\left\| {{{\rm{X}}_{\left(3 \right)}} - \left({{{\rm{C}}_1} \otimes {{\rm{A}}_1}} \right).{{\rm{B}}_1}^T - \left({{{\rm{C}}_2} \otimes {{\rm{A}}_2}} \right).{{\rm{B}}_2}^T - \left({{{\rm{C}}_3} \otimes {{\rm{A}}_3}} \right).{{\rm{B}}_3}^T} \right\|^2}$, ${J_f} = {\left\| {{{\rm{B}}_1}^T{{\rm{W}}_1}{{\rm{B}}_1}} \right\|^2}$ and ${J_m} = {\left\| {{{\rm{B}}_2}^T{{\rm{W}}_2}{{\rm{B}}_2}} \right\|^2}$.

Since the optimization problem (13) does not have a closed-form solution, one can use the gradient descent algorithm to update the factor matrices B₁, B₂ and B₃, alternatively. So the derivatives $\frac{{\partial J}}{{\partial {{\rm{B}}_1}}} = {\rm{}}\frac{{\partial {J_t}}}{{\partial {{\rm{B}}_1}}}{\rm{}} + {\rm{}}{\lambda _f}\frac{{\partial {J_{\rm{f}}}}}{{\partial {{\rm{B}}_1}}}$, $\frac{{\partial J}}{{\partial {{\rm{B}}_2}}} = {\rm{}}\frac{{\partial {J_t}}}{{\partial {{\rm{B}}_2}}}{\rm{}} + {\rm{}}{\lambda _m}\frac{{\partial {J_{\rm{m}}}}}{{\partial {{\rm{B}}_2}}}$, and $\frac{{\partial J}}{{\partial {{\rm{B}}_3}}} = {\rm{}}\frac{{\partial {J_t}}}{{\partial {{\rm{B}}_3}}}$ are calculated as follows:

Using Eq 15 we introduce Algorithm 1 to estimate matrices A, B, C and to extract the fetal ECG using doubly constrained block term decomposition. We named this algorithm as "doubly constrained block term (DoCoBT)"

Eventually, the fetal subspace is achieved via updated factor matrices A₁, B₁ and c₁ as

4.   Results

In this section, we present the datasets and evaluation measures at first. Then, the proposed method using both synthetic and real data is evaluated.

4.1.   Dataset and evaluation criterion

4.1.1.   Synthetic dataset

In order to evaluate the proposed method, we use a synthetic dataset that resembles real fECG signals. These data must contain mECG as the main interference and other noises such electrode movement and clear fECG to compute signal to noise ratio. The open-source electrophysiological toolbox (OSET) contains the required functions for generating synthetic maternal-fetal ECG datasets, using the following data model for modeling maternal abdominal signals ^[30].

In this model, x_m is the maternal ECG as interference and x_f is the fetal ECG. η and n represent colored and white noises respectively. Therefore, parameter α controls the signal-to-interference ratio (SIR) and the parameters β and γ control the signal-to-noise ratio (SNR). In order to evaluate the quality of the extracted fECG, the signal-to-interference and noise ratio (SINR) is calculated for the extracted fECG (output) signal and the SINR_improvement is calculated as a measure of fECG denoising performance ^[31]:

The synthetic data that are generated and used in this paper have the dimensionality of 8 × 10000 (8 channel and 10000 time indices and thus the size of the tensor is 8 × 10000 × 2).

4.1.2.   Real dataset

In addition to the synthetic signals, the real dataset Abdominal and Direct Fetal Electrocardiogram Database (ADFED) is used to evaluate the generalization of the proposed method. ADFED consists of five channels (four channels of abdominal ECG and one channel of fetal scalp ECG) with 1 kHz sampling rate and length of 10 seconds ^[32].

4.2.   Evaluation of the proposed method

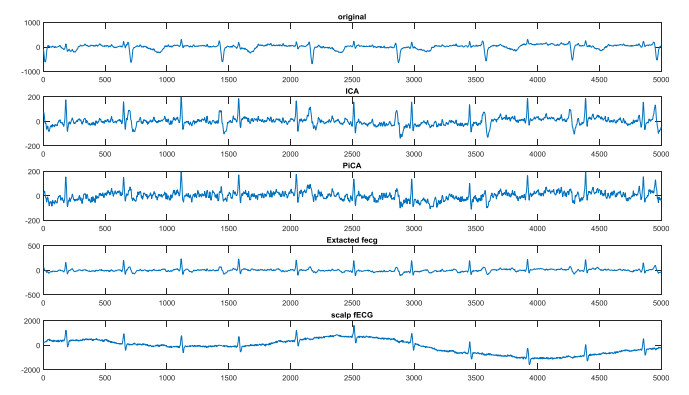
As for real data, the clean fECG is unknown. Therefore, the SINR and the performance of the proposed method can not be calculated quantitatively. Therefore, the proposed approach is evaluated on simulated data with different noise levels. To attain this goal, 10,000 samples of eight lead synthetic ECG mixtures with SINRinput = {-5, -10, -15, -20, -25} and 1000 Hz sampling rate are generated 10 times per SINR. The performance of the proposed method is compared with some related source separation methods such as ICA (using the JADE algorithm) ^[33], πCA ^[29] and πTucker ^[21]. In πCA and ICA methods, first, the components of the mother and fetus are extracted. Then, the fetal subspace is reconstructed using the fetal components. Regarding the πTucker method, the fetal sources are extracted from the observation tensor by using πCA or ICA. Then, the mode 2 factor matrix including the fetal sources is updated, iteratively. Finally, the main tensor is reconstructed again via the updated mode 2 factor matrix.

In the proposed method, we need to have an estimation of the fetal and maternal signals as initial sources. Therefore, the observation tensor has to be matricized to extract initial sources using source separation methods. For automatic detection of mECG and fECG sources, the correlation criterion is applied between the R-peaks of these initial sources and the R-peaks of maternal/fetal signals derived from the maternal/fetal R-peak detection algorithm (section 3.2). Finally, the determined fetal and maternal sources are placed in the B₁ and B₂ factor matrices as the initial estimation of the tensor decomposition. The sources that do not pass the correlation criterion are considered as noise and are placed in the factor matrix B₃.

Here, BTD decomposes the observations tensor into three tensors. According to the proposed method, the factor matrices B₁, B₂ and B₃ are updated using the gradient descent algorithm, alternatively. However, the matrix B₃ could be calculated by solving $\frac{\partial J_{t}}{\partial \bf{B}_{3}} = 0$, considering that no constraint is imposed on it. Eventually, the first, second and third blocks are reconstructed via updated factor matrices. The first slices of the first block and the second block represent fECG and mECG subspaces, respectively. Moreover, to obtain parameters λ_f, λ_m and γ, the data are divided into two parts. A portion of data is utilized to obtain the parameters experimentally, while the remaining part is employed for the algorithm validation. In this algorithm, λ_f, λ_m and γ are chosen to be N², (100N)² and 10^-6, respectively.

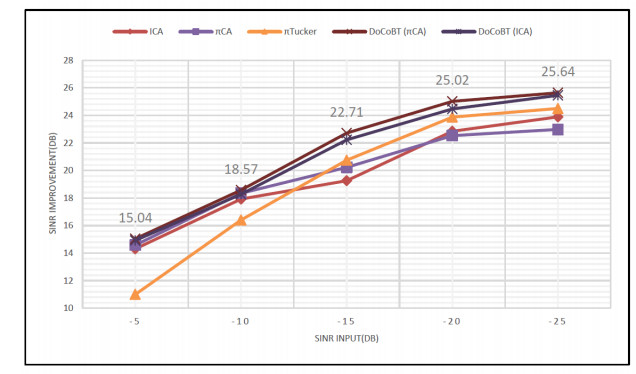
The quantitative results of the evaluation of the proposed methods in comparison with the other mentioned methods are summarized in Table 1 and a visual outline of SINR improvement of all methods can be observed in Figure 8. DoCoBT represents the proposed method. DoCoBT (ICA) corresponds to the case, where the initial sources of the factor matrices are the components of the ICA decomposition and the second slice of the input tensor is the fECG subspace estimated by employing ICA. In DoCoBT (πCA), the second slice of the tensor and the initial sources are estimated through the πCA algorithm.

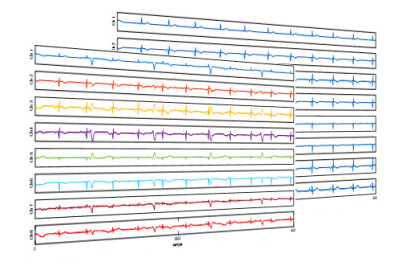
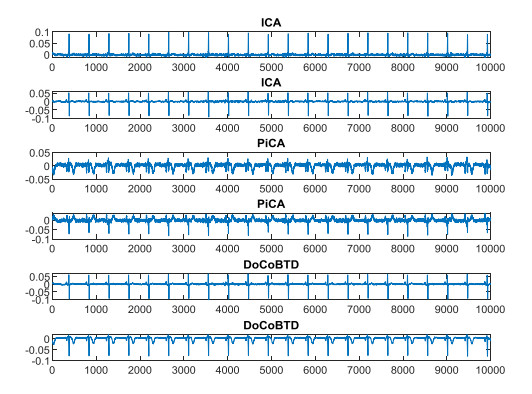
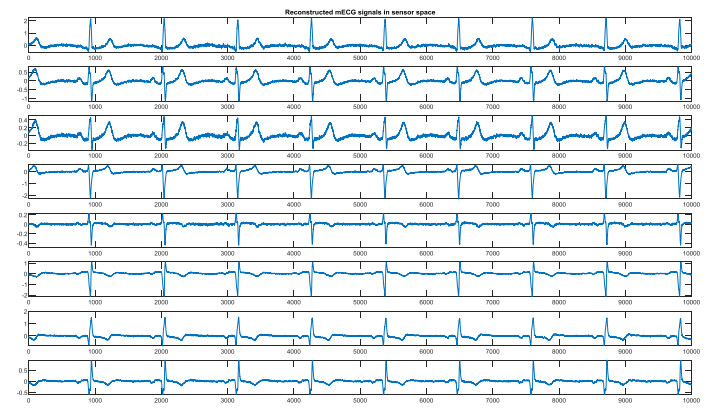
As could be seen, the proposed method performs better than ICA, πCA, and πTucker methods for a large range of SINR_in values. It can also be concluded that using the results of other methods (ICA and πCA) will improve the accuracy of fECG extraction. In fact, one of the advantages of tensor decomposition is that it uses additional information alongside the main observations to obtain more accurate results. The most important conclusion is that the simultaneous usage of maternal and fetal periodicity constraints can result in the extraction of fECG with higher SINR values. The extracted fECG sources using the mentioned methods are shown in Figure 9. In order to demonstrate the performance of the proposed method for subspaces reconstruction, several channels of reconstructed subspaces are illustrated in Figures 10 and 11. In this paper, the real data are used to evaluate the generalization of the methods. The reconstructed fetal components in sensor space are represented in Figure 12. The ability of the proposed method in fetal subspaces reconstruction is obvious in Figures 10 and 12.

5.   Conclusion

In this study, we proposed a constrained tensor decomposition method based on BT tensor decomposition to extract fECG from maternal abdominal recordings. First, the observation tensor is constructed using abdominal recordings and the fECG subspace (obtained from an existing approach, such as ICA). Then, the observation tensor is decomposed into three tensors by using the BT decomposition constrained with two constraints related to the period of the fetus and mother's ECG. In this method, the estimated fetal and maternal sources are placed in the factor matrices as the initial values of the tensor decomposition and updated in an alternative algorithm. Experimental results show that decomposition of the main tensor to three tensors and simultaneous usage of maternal and fetal quasi-periodicity constraints lead to an increase in SINR improvement in noisy conditions compared to ICA and πCA methods. In addition, the limitations of the proposed method are: (1) Slow convergence of the gradient descent algorithm, and (2) the requirement for choosing (tuning) the values of the regularization parameters λ_f and λ_m.

In order to achieve superior results, a post-processing step such as Kalman filtering can be considered to denoise the sources of the factor matrices. Also, the use of other tensor decompositions such as CP and rewriting their cost functions based on periodicity constraints could be considered as another future work.

Conflict of interest

The authors declare no conflict of interest.