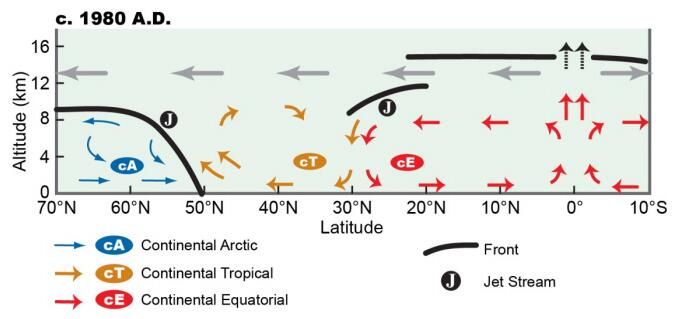
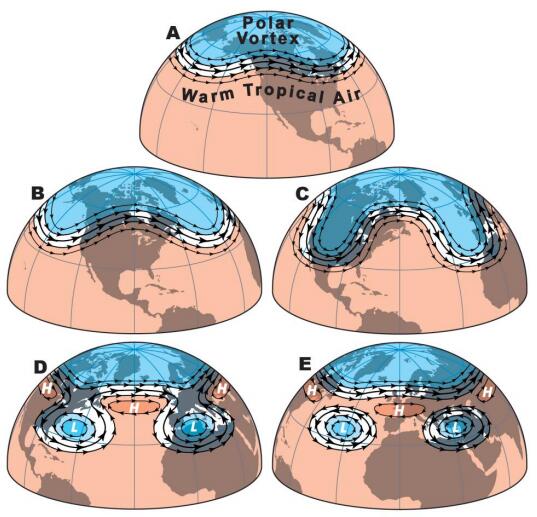
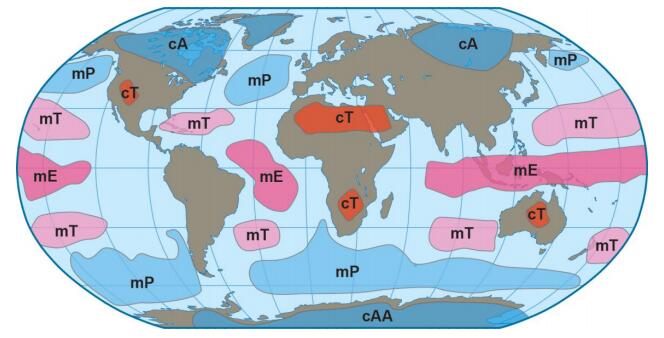
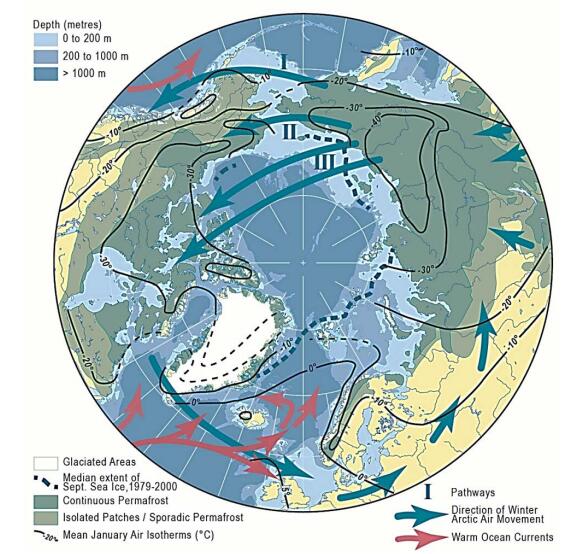
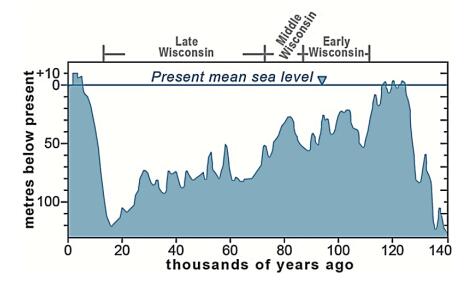
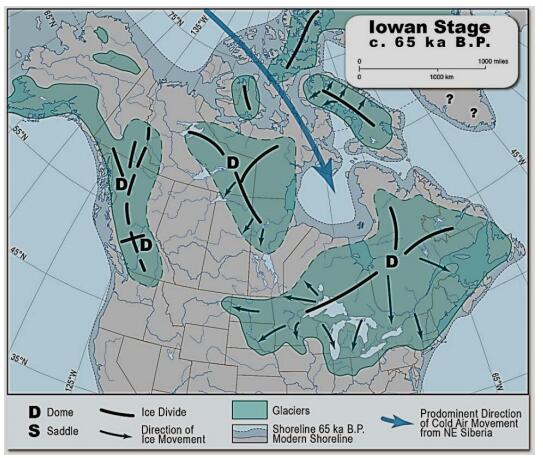
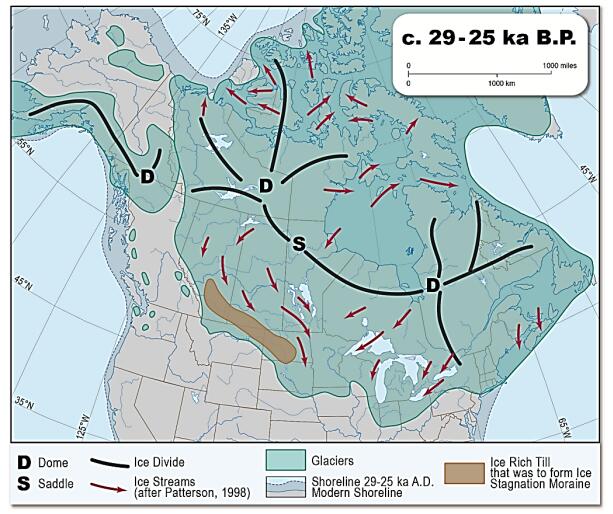
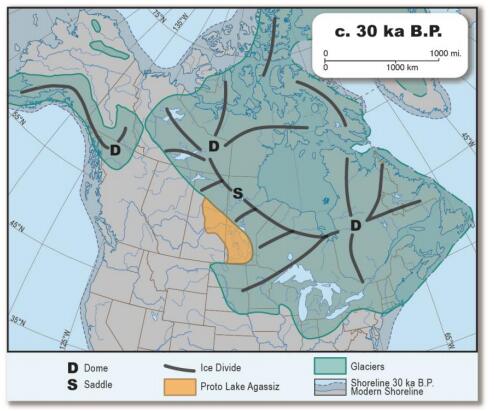
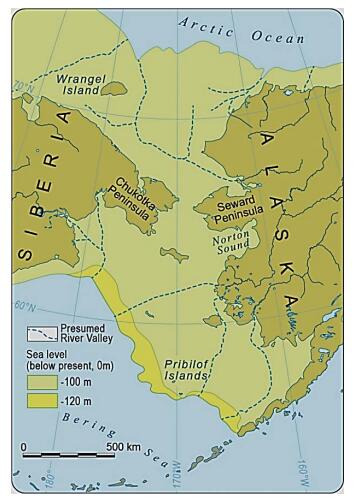
The Arctic air mass is the cold, dry body of air slowly moving eastwards around the North Pole in the northern hemisphere. Its southern boundary consists of four planetary waves known as the Rossby waves that mark the interface with subtropical air bringing heat polewards. The Arctic air mass is constantly being modified by the addition of heat and moisture over the oceans, as well as by winter cooling over the land masses due to limited incoming solar radiation and constant reradiation of heat into the atmosphere. The coldest air in winter is located over northeastern Siberia and moves east, cooling Canada. Warm ocean currents add large quantities of heat to the air mass moving over them, but without this addition of heat, the Arctic air mass becomes significantly colder. Research in Tibet and Northeast Asia on depression of sea level shows that during the Late Wisconsin cold event (65–10 ka B.P.), vast quantities of sea water were sequestered on land primarily as ice sheets, exposing the sea bed in the Bering Strait from 50–10 ka B.P. together with the bottom of the South China Sea between 30–20 ka B.P.. The East China Monsoon failed to reach Tibet and much of Northeast China, resulting in severe cooling of northeast Siberia and northern Tibet. This, in turn, caused severe cooling in eastern Canada together with the development of a vast, predominantly cold-based ice sheet. As the sea levels started to rise (about 19 ka B.P.), the East China Monsoon slowly redeveloped and a gradual warming took place on both continents. However, along the west side of the North American Cordillera, the Late Wisconsin glaciation only began in 29 ka B.P. but continued along the west coast until about 10 ka B.P. This paper explores the relationship of the Late Wisconsin history on the two continents, together with the mechanisms causing the landforms and climatic differences. Finally, the probable effects of these climatic changes on the early peopling of North America are discussed.
1.
Introduction
Vector-borne disease involves a vector (an organism) that transmits infectious pathogens from the infected host to the uninfected host. For example, the malaria parasites are transmitted through the bite of infected female mosquitoes, spreading the disease from mosquitoes to humans and back to mosquitoes [2]. West Nile virus (WNv) is another vector-borne disease caused by Flavivirus and transmitted primarily by mosquitoes (Culex species) to vertebrate hosts, such as humans, birds and horses [3]. Those vector-borne diseases have caused a significant threat to public health as well as wildlife worldwide.
Mathematical models give insights to predict the spread of vector-borne diseases, and to test control strategies. Impulsive (delayed) differential systems are widely used in population biology and epidemiology to study the various factors: birth pulses [4,5], effectiveness of vaccination [6,7,8,9,10], and elimination of vector insects [11,12], see also [13,14] for stochastic effects. To investigate the control strategies against vector-borne diseases, Gourley et al. [11] used two time-delayed models with impulses to evaluate the effectiveness of age-structured culling strategies. Yang et al. [10] studied the effect of impulsive controls in multiple patch models with age-structure. Xu and Xiao [9] considered the impacts of periodic impulsive culling of mosquitoes for control of WNv transmission. Based on [9], the incubation period of mosquitoes was furthered incorporated in [15].
To describe the disease transmission between vector and host as well as the strategy of periodically culling the vector, we use a set of impulsive delayed differential equations to incorporate the extrinsic incubation period (EIP) of vector and host. By the theory recently developed in [1], the basic reproduction ratio R0 of the model is first established. The global dynamics of the model are further investigated in terms of R0. The uniform persistence theory based on dynamical systems is used extensively in population biology and epidemiology models, see for instance [16,17,18,19] and references therein. However, it seems like this dynamical system approach is rarely adapted to time-delayed impulsive systems to study the threshold dynamics. There are two possible issues: first, it is not an easy task to find an appropriate phase space for time-delayed impulsive systems so that the evolution operators are well-defined, which was recently solved by [1] for a large class of time-delayed impulsive systems; second, the solutions of the time-delayed impulsive systems may not be continuous in t, and hence, such systems might not generate continuous periodic semiflows (see [20]), which brings trouble for direct application of the uniform persistence theory in [21] to investigate the sharp permanence of infectious compartments when R0>1. Meanwhile, the analytic method developed in [1,6,7] for the uniform persistence of a time-delayed impulsive system is quite useful for a form like Susceptible-Exposed-Infected-Removed (SEIR), but it would not be easy to apply to the vector-borne model (including multiple infected compartments). We refer to [9,15] for attempts in this direction. Combing the ideas in [1] and [21], we establish the sharp persistence of infectious compartments, by using the uniform persistence theory of discrete-time semiflows on some appropriate phase space. It is worth pointing out that our current approach would be easily applied to the models where the period of model coefficients is the same as that of fixed impulsive moments.
The rest of this paper is organized as follows: In Section 2, we formulate a time-delayed impulsive differential model including several factors: EIP and the strategy of periodically culling the vector, EIP and vertical transmission of host. In Section 3, we first introduce the basic reproduction number R0 for the model and then study the threshold dynamics in terms of R0. In Section 4, we use numerical simulations to test the differences with and without culling, and further explore the impacts of parameters such as time delays and vertical transmission rate on R0. A brief discussion then concludes the paper.
2.
Model formulation
Inspired by the WNv infection process in [9,15,18], we consider an impulsive delay differential equation model to describe the periodic culling of the vector with two differnt EIPs. Let Sv(t), Iv(t), Sh(t), Eh(t) and Ih(t) be the the total numbers of the susceptible adult vector, infected adult vector, susceptible host, exposed host and infected host at time t, respectively. The total number of the adult vector is given by Nh(t)=Sh(t)+Eh(t)+Ih(t). Let Λv and Λh be the recruitment rate of the vector and (susceptible) host, respectively, μv and μh be the natural death rate of vector and host, and dh be the disease-induced death rate of the host. Similar to [7], we suppose that the birth rate of the vector equals its natural death rate. Vertical transmission of the virus in the host population is incorporated by a fraction rvt∈(0,1). For the virus transmission, we assume that the susceptible host becomes infectious given contact with the infected vector, and the susceptible vector can receive the infection by biting a virus-carrying host. By similar arguments to those in [2,17,19], we simply assume that the numbers of newly occurred infectious host and newly occurred infected vector per unit time at time t are given by
respectively, where β is the average biting rate of the vector, b and c are the transmission probabilities of the virus from vector to host and from host to vector, respectively. However, the newly infected vector and infected host need to survive the EIP to become infectious. We denote the finite constants τ1 and τ2 to represent the length of the EIP in the vector and host, respectively. The probability that the vector and host survive the EIP is e−μvτ1 and e−μhτ2, then of those vectors and hosts infected τ1 and τ2 unit times ago, only the proportions
are infectious at time t. Throughout this paper, we suppose that culling occurs at certain particular times, and denote T to be the period of culling. We also assume that spraying reduces both the susceptible and infected vector, p∈[0,+∞) is the culling intensity of those killed, where p=0 means that there is no culling.
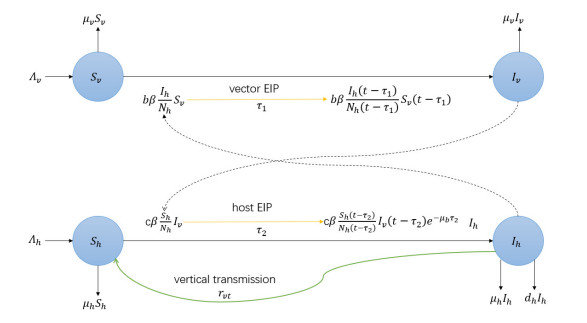
The transmission of cross-infection between vector and host is shown in Figure 1. Consequently, our model takes the form:
All the parameters in model (2.1) are positive. In view of the biological meaning of τ2, we impose the following compatibility condition:
To investigate the long time behavior of system (2.1) from the point view of dynamical systems, we first introduce a few notations related to the phase space (see also [1,22]). Given two constants a<b, let
where ϕ(t+)=lims→t+ϕ(s) and ϕ(t−)=lims→t−ϕ(s). Then for any r>0, PC([−r,0],Rm) is a Banach space with the norm ‖⋅‖r given by ‖ϕ‖r=sup−r≤θ≤0|ϕ(θ)|. Set ˆτ=max{τ1,τ2}>0, ˜J=[−ˆτ,0)∩{tn=nT:n∈Z}(possibly empty) and J=[−ˆτ,0)∖˜J. Denote
and PC+J:={ϕ∈PCJ:ϕ(t)≥0,∀t∈[−ˆτ,0]}. It then follows that PCJ is a Banach space endowed with the norm ‖⋅‖ˆτ, and PC+J is a closed cone of PCJ, which induces a partial ordering on PCJ. Clearly, PCJ⊂PC([−ˆτ,0],R). For any u=(u1,u2,...,u5)∈PC([−ˆτ,η),R5) with η>0, define ut∈PC([−ˆτ,0],R5) by
Define
and
for any ϵ∈(0,Λhμh+dh). Now we are ready to state the well-posed result on the solutions of system (2.1).
Theorem 2.1. For any ϕ∈Dϵ, system (2.1) exists a unique non-negative solution u(t,ϕ) on [0,+∞) with the initial value u0=ϕ, unT∈Dϵ for any n∈N. Moreover, ut+T(ϕ)=ut(uT(ϕ)) for all t≥0 and Φ:=uT admits a global attractor in Dϵ.
Proof. For convenience, we denote
For any t≥0,t≠nT,n∈N,ϕ∈Dϵ, define
where
It is easy to check that f(t,ϕ) satisfies Lipschitz condition for ϕ on any compact subset of R+×X. It follows from [22, Theorems 3.1 and 3.3] that system (2.1) admits a unique solution u(t,ϕ) satisfying ∑5i=3ui(t,ϕ)>ϵ on the maximal existence interval [0,tϕ) with u0=ϕ∈Dϵ and tϕ∈(0,∞).
Next we prove the solution of system (2.1) is non-negative on [0,tϕ). Given ϕ∈Dϵ and t∈[0,T), we see that fi(t,ϕ):=fi(ϕ)≥0 provided i∈{1,2,3,5} and ϕi(0)=0. It follows from [23, Theorem 5.2.1] and its proof that for ui(t,ϕ)≥0,i∈{1,2,3,5}, ∀t∈[0,T)∩[0,tϕ). If T<tϕ, then by the formulas of system (2.1) at the impulsive points, we have ui(t,ϕ)≥0,i∈{1,2,3,5},t∈[0,T]. It then follows from the method of steps that ui(t,ϕ)≥0,i∈{1,2,3,5},t∈[0,tϕ). Meanwhile, by the uniqueness of solutions of system (2.1) and the compatibility condition (2.2), we obtain that
Therefore, u4(t,ϕ)≥0 for t∈[0,tϕ).
Notice that the total host population (Nh(t):=∑5i=3ui(t)) satisfies
which implies Nh(t) is an upper solution of
Denote x(t;Nh(0)) as the unique solution of (2.6) with x(0)=Nh(0), then Nh(t)≥x(t;Nh(0)) for any t∈[0,tϕ). This further yields that Nh(t)≥x(t;Nh(0))≥ϵ for any t∈[0,tϕ) provided Nh(0)≥ϵ with ϵ∈(0,Λhμh+dh). Furthermore,
which implies that if ϵ≤∑5i=3ϕi(0)≤Λhmin{μh,dh}, then ϵ≤∑5i=3ui(t)≤Λhmin{μh,dh} for any t∈[0,tϕ).
Since ϵ≤Nh(t) and u5(t)≤Nh(t) for any t∈[0,tϕ), by comparison, we have
which yields that,
Therefore, the solutions of system (2.1) with initial data in Dϵ exist globally on [0,∞) and are ultimately bounded. By similar argument to that in [1, Lemma 4] (see also [24, Page 192]), we infer that for each n>ˆτT, unT is compact. It then follows from [21, Theorem 1.1.3] that UT:Dϵ→Dϵ admits a global attractor. Moreover, since if ut(ϕ) is a solution of (2.1), then ut+T(ϕ) is also a solution (2.1). By the uniqueness of the solution, we then have ut+T(ϕ)=ut(uT(ϕ)).
3.
Threshold dynamics in terms of R0
In this section, we first introduce the basic reproduction number R0 for system (2.1) and then investigate its threshold dynamics in terms of R0.
3.1. Basic reproduction number
The basic reproduction number R0 is defined as the expected number of secondary infections produced by a typical infectious individual in a completely susceptible population. We will use the theory developed in [1] to give the definition of R0. In order to obtain the disease-free periodic solution of system (2.1), we recall a lemma (see [6, Lemma 1] for detail).
Lemma 3.1. Consider the following impulsive differential equation:
where a,b>0, θ∈(0,1). Then system (3.1) admits a unique positive periodic solution ˆue(t):=ab+(u∗−ab)e−b(t−nT), nT<t<(n+1)T, which is globally asymptotically stable. Here u∗=a(1−θ)(1−e−bT)b(1−(1−θ)e−bT).
Letting Iv=Ih=0 in system (2.1), we then get the following disease-free system:
By Lemma 3.1, system (3.2) exists a unique positive T-periodic solution ˆu(t):=(ˆSv(t),ˆSh), with ˆSh=Λhμh and
which is globally asymptotically stable.
Let E=PC([−ˆτ,0],R2), E+={ϕ∈E:ϕ(t)≥0,t∈[−ˆτ,0]}, and
with the norm ‖v‖XT=supt∈[0,T]|v(t)|. It then follows that XT is a Banach space. Linearizing system (2.1) at its disease-free periodic solution E0(t)=(ˆSv(t),0,ˆSh(t),0,0), we obtain the following linear system for the infectious compartments:
Define F(t):E→R2, where
Set Y(t,s),t≥s as the Cauchy matrix [24, Section 1.2] of
that is,
where each tk denotes the impulsive point on [s,t) and V=(μv00μh+dh). It is easy to check that F(t) and Y(t,s) satisfy the following properties: (a) for each t∈R, F(t) is a positive operator; (b) the matrix −V is cooperative and r(Y(T,0))<1, where r(Y(T,0) is the spectral radius of Y(T,0).
Consequently, the linear impulse periodic differential system (3.5) could be rewritten as:
where P= diag (11+p,1).
After the above settings, we can apply the theory and method in [1] to define basic the reproduction number for system (2.1). Let v(t) be the initial distribution of infected individuals with period T. For t≥s, then F(t−s)vt−s is the distribution of newly infected individuals at time t−s. It is produced by infected individuals introduced during the time interval [t−s−ˆτ,t−s], which means it is the distribution of newly infected at time t−s and still infected at time t. Define the linear operator L on XT:
We define the basic reproduction number as
where r(L) is the spectral radius of the linear operator L. Denote
For any ϕ∈EJ, let w(t,ϕ)=(w1(t,ϕ),w2(t,ϕ)) be the unique solution of (3.4) with the initial value w0=ϕ, and
Let Q(t):EJ→E=PC([−ˆτ,0],R2) be the solution map of (3.4), then
In view of the definition of PCJ, we infer that Q:=Q(T) is the operator from EJ to EJ (in other words, they have the same number of discontinuous points), and set r(Q) to be the spectral radius of Q on EJ. By [1, Theorem 1], we have the following observation:
Lemma 3.2. R0−1 has the same sign as r(Q)−1.
Let
where PCτi is understood as PCJ with ˆτ replaced by τi, and then (Z,Z+) is an ordered Banach space. For any ψ∈Z+, system (3.4) admits a unique non-negative solution z(t,ψ) with the intial value z0=ψ. For all t≥0, we have zt(ψ)=(z1t(ψ),Z2t(ψ)), for all θi∈[−τi,0], and then Zit(ψ)(θi)=zi(t+θi,ψ), i=1,2. For any given t≥0, let ˆQ(t) be the solution map of system (3.4) on Z, that is,
We remark that z1t∈PC([−τ2,0],R) and z2t∈PCτ1 for all t≥0 as z2(t,ψ) is continuous for all t≥0 even if ψ is piecewise continuous. Therefore, ˆQ(T) is a map from Z to Z. Next, we will illustrate that ˆQ(t) is eventually strongly positive on Z+.
Lemma 3.3. ˆQ(t)φ≫0 for any t>3ˆτ provided φ=(φ1,φ2)∈Z+∖{0}.
Proof. For convenience, denote
By the similar argument to that in Theorem 2.1, we obtain that zi(t)≥0 for any t≥0, i=1,2.
In the case that φ1>0. We argue that there exists ˆt∈[0,ˆτ] such that z2(ˆt)>0. Assume, by contradiction, that z2(t)=0 for all t∈[0,ˆτ], that is, z′2(t)=0 for all t∈[0,ˆτ]. Then we deduce from the second equation of system (3.4) that:
This yields φ1(t)≡0 for any t∈[−τ2,0], which is a contradiction. Moreover, from the second equation of system (3.4) and z1(t)≥0 for all t≥−τ2, we obtain
Then by the integral form of the first equation of system (3.4), we have
where
Since ˆt∈[0,ˆτ], it follows that z1(t)>0 for all t>2ˆτ. The result as follows.
In the case that φ2>0. We have
provided t>ˆτ. Then by the integral form of the second equation of system (3.4), we have
whenever t≥2ˆτ. Therefore, ˆQ(t)φ≫0 for t>3ˆτ.
Denote r(ˆQ) as the spectral radius of ˆQ:=ˆQ(T). One might perform the same argument as in [16, Lemma 3.8] to obtain r(Q)=r(ˆQ). Moreover, we have the following observation:
Lemma 3.4. Let μ=lnr(Q)T. Then there exists a positive T-periodic function ˜v(t)=(˜v1(t),˜v2(t)) such that eμtˆv(t) is a solution of system (3.4) with the feasible domain either Z+ or E+J for any t≥0.
Proof. Resembling the arguments in [1, Lemma 4], we infer that for each t>ˆτ, Q(t) and ˆQ(t) are compact on EJ and Z, respectively.
In the case that the feasible domain is Z+, fix an integer n0>0 such that n0T>3ˆτ. It follows that ˆQn0=ˆQ(n0T) is compact and strongly positively on Z. By [25, Lemma 3.1], we obtain that there is a strongly positive eigenvector φ∗=(φ∗1,φ∗2) such that ˆQ(φ∗)=r(ˆQ)φ∗. Let v(t,φ∗) be the solution of system (3.4) with the initial value
Since φ∗≫0, it is easy to see that vt(φ∗)≫0 for any t≥0. Let ˆv(t)=e−μtv(t,φ∗). Then ˆv(t)≫0 satisfies
For θ2∈[−τ1,0] and θ1∈[−τ2,0], we have
This implies ˆvi(θi)=ˆvi(T+θi), i=1,2. Therefore, ˆv(t) is a T-periodic solution satisfying ˜vi(θi)=e−μθiφ∗i(θi), i=1,2.
In the case that the feasible domain is E+J, since eμtˆv(t) given in the above is a function for t∈R. We denote ˆϕ=(^ϕ1,^ϕ2) as:
By the uniqueness of solutions, we have that w(t,ˆφ):=eμtˆv(t) satisfies (3.4) for all t≥0 with the initial value w0=ˆϕ∈E+J.
3.2. Threshold dynamics
We are now in a position to prove a threshold-type result of system (2.1) in terms of R0.
Theorem 3.5. If R0<1 and μh≥dh, then the disease-free periodic solution E0(t)=(ˆSv(t),0, ˆSh(t),0,0) is globally attractive for system (2.1) with respect to Dϵ.
Proof. By the first and sixth equations of system (2.1), we have
Consider the following auxiliary system
According to Lemma 3.1 and the comparison theorem on impulsive differential equations, we have Sv(t,a)≤x(t,a) with the same initial condition Sv(0)=x(0)=a>0, ∀t≥0 and |x(t)−ˆSv(t)|→0 as t→∞ with ˆSv(t) given in (3.3). Then for any δ∈(0,Λhμh), there exists ˆt1>0 such that
When μh≥dh, in view of system (2.1), we have
It then follows that for the above δ, there exists ˆt2>ˆt1 such that
Thus, we have
We consider the following impulsive differential equations with parameter δ:
From Lemma 3.2, we know that R0<1 if and only if r(Q)<1. Let Qδ be the Poincaré map of system (3.9). Observe that limδ→0+r(Qδ)=r(Q)<1 (as r(Qδ) is non-decreasing and upper semi-continuous in δ≥0 but close to 0 (see [26,27] for example), we can fix a small positive number δ such that r(Qδ)<1. By Lemma 3.4, there is a positive T-periodic function ˆvδ(t)=(ˆvδ1(t),ˆvδ2(t)) such that eμδtˆvδ(t) is a positive solution of system (3.9), where μδ=lnr(Qδ)T<0. Choose a positive constant Kδ such that:
Applying the comparison principle for cooperative impulsive delay differential systems [28, Lemma 2.2], we obtain that
Letting t→∞ in (3.10), we have (Iv(t),Ih(t))→(0,0). It then follows from the fourth equation or (2.4) that Eh(t)→0 as t→∞. In view of the theories of asymptotically periodic semiflows and internally chain transitive sets [21], we further deduce from the third equation of system (2.1) that
Then for any given δ1∈(0,δ), there exists ˆt3>ˆt2+ˆτ such that
and hence,
For this inequality, we consider the following impulsive differential equation:
By Lemma 3.1, system (3.11) admits a globally stable T-periodic solution, denoted as ˆSδ1v(t), which depends continuously on δ1. It follows that for the above δ, there exists a ˆt4>ˆt3 such that
This, together with (3.8), yields for any δ1∈(0,δ)
Letting δ1→0+, we obtain for any small δ>0, that there holds
which implies that limt→∞(Sv(t)−ˆSv(t))=0.
The result follows. In the remainder of this section, we investigate the uniform persistence of system (2.1).
Theorem 3.6. Assume that (Sv(t,ϕ),Iv(t,ϕ),Sh(t,ϕ),Eh(t,ϕ),Ih(t,ϕ)) is the unique solution of system (2.1) through ϕ∈X0:={(ϕ1,ϕ2,ϕ3,ϕ4,ϕ5)∈Dϵ:ϕ2(0)>0,ϕ5(0)>0}. If R0>1, then there exists ρ∗>0 such that lim inft→∞Ii(t,ϕ)≥ρ∗,i=v,h.
Proof. Let ∂X0:={ϕ∈Dϵ:ϕ2(0)=0 or ϕ5(0)=0}. For any ϕ∈X0, it is easy to check that
that is, Φn(X0)⊂X0 for any n∈N with Φ:=uT given in Theorem 2.1 having a global attractor in Dϵ. Define
let ω(ψ) be the omega limit set of the forward orbit Γ={Φnψ:n∈N}, and
Claim 1: For any ψ∈M∂, ω(ψ)=M, which is locally stable in M∂.
For any given ψ∈M∂, it follows from the definition of M∂ that for each n∈N, there holds Iv(nT,ψ)=0 or Ih(nT,ψ)=0. Consequently, we infer that either Iv(t,ψ)≡0 or Ih(t,ψ)≡0 for any t≥0 (as if there exists t0≥0 such that Ii0(t0,ψ)≠0 for some i0∈{v,h}, then Ii0(t,ψ)>0 for all t≥t0).
In the case that Iv(t,ψ)≡0 for each t≥0, it follows from the second equation of system (2.1) that Ih(t−τ1)Sv(t−τ1)=0 for any t≥0. By the first and sixth equations of (2.1), we have
This implies there exists ˉt1>0, such that Sv(t)>0 for all t>ˉt1+τ1, and hence, Ih(t)=0 and Eh(t)=0 for all t≥0. Since disease-free system (3.2) admits a globally stable T periodic solution (ˆS(⋅),ˆSh), we obtain that ω(ψ)=M.
In the case that Ih(t,ψ)≡0 for each t≥0, it follows from the fifth equation of system (2.1) that Sh(t−τ2)Iv(t−τ2)=0 for any t≥0. By the third equation of (2.1), we have S′h(t)≥Λh−(μv+cβ)Sh(t),t>0. This implies there exists ˉt2>0, such that Sh(t)>0 for all t>ˉt2+τ2, and hence, Iv(t)=0 and Eh(t)=0 for all t≥0. For the same reason, we obtain that ω(ψ)=M. Therefore, Claim 1 is valid.
For σ∈(0,min{mint∈(0,T]ˆSv(t),ˆSh}), let Qσ(t) be the solution map of the following system and Qσ=Qσ(T) be the associated Poincaré map
For σ close to 0+, by the comparison principle, it follows that the spectral radius r(Qσ) is non-increasing in σ, which implies limσ→0+r(Qσ) exists and limσ→0+r(Qσ)≤r(Q). Note that r(Qσ) is upper semi-continuous in σ≥0 (see [26,27]), which further yields lim supσ→0+r(Qσ)≥r(Q), and hence, limσ→0+r(Qσ)=r(Q)>1. Thus, we can fix a sufficiently small number σ>0 such that r(Qσ0)>1. By Lemma 3.4, there exists a positive T-periodic function ˆvσ=(ˆvσ1,ˆvσ2) such that eμσtˆvσ(t) is a positive solution of system (3.14), where μσ=lnr(Qσ)T>0.
By the continuous dependence of the solution (see [20]) on the initial value, we have for the above chosen σ>0, and there exists σ∗∈(0,σ) such that ‖ut(ϕ)−ut(M)‖<σ for any t∈[0,T] provided ‖ϕ−M‖<σ∗. Next we prove the following claim:
Claim 2: For all ϕ∈X0, there holds lim supn→∞‖Φnϕ−M‖≥σ∗. Assume, by contradiction, that lim supn→∞‖Φnˆϕ−M‖<σ∗ for some ˆϕ∈X0. Then there exists n1≥1 such that ‖Φnˆϕ−M‖<σ∗ for any n≥n1. For any t≥n1T, letting t=nT+t′ with n=[tT] and t′∈[0,T), by Theorem 2.1, we have
It then follows that for any t>n1T−ˆτ, 0<Ii(t)<σ,i=v,h, Sv(t)>ˆSv(t)−σ, ˆSh−σ<Sh(t)≤Nh(t)<ˆSh+3σ. And hence, Sv(t−τ1)Nh(t−τ1)≥ˆSv(t−τ1)−σˆSh+3σ>0 and Sh(t−τ2)Nh(t−τ2)≥ˆSh−σˆSh+3σ>0 for any t>n1T. By the comparison principle for cooperative systems, it follows that Iv(t,ˆϕ) and Ih(t,ˆϕ) in system (2.1) satisfy
Recall that Keμσtˆvσ(t) is a positive solution of (3.14) for any K>0. Choose Kσ>0 such that
Then the comparison theorem for cooperative impulsive delay differential systems implies that
Since μσ>0, we get Iv(t,ˆϕ),Ih(t,ˆϕ)→∞ as t→∞, which leads to a contradiction.
The above claims indicate that M cannot form a cycle for Φ in Dϵ and Ws(M)∩X0=∅, where Ws(M) is the stable set of M for Φ. Now we define a continuous distance function p:Dϵ→R+ by p(ϕ)=min{ϕ2(0),ϕ5(0)}. In view of Claim 1, we have Ws(M)∩p−1(0,∞)=∅. Now by [21, Lemma 1.2.1 and Theorem 1.3.2] and Theorem 2.1, it then follows that Φ is uniformly persistent with respect to (X0,∂X0,p), that is, there exists ρ1>0 such that
Consequently, there exists n2≥1, such that
Now for any t≥n2T, letting t=nT+ˉt with n=[tT] and ˉt∈[0,T), we obtain from the equation of Iv that
Therefore,
Similarly, we see from Ih(t)≥−(μh+dh)Ih(t),t≥nT that
Now set ρ∗=min{ρ1e−μvT2(1+p),ρ1e−(μh+dh)T2}>0, we see that lim inft→∞Ii(t)≥ρ∗,i=v,h.
4.
Numerical simulations
In this section, we perform illustrative numerical simulations to verify theoretical results and explore the influences of key model parameters on the disease transmission. Note that the following simulations were based on the WNv disease transmission process studied in [9,15], where vector and host are mosquito and bird, respectively, and some of parameters were chosen only for the test of parameter sensitivity on the basic reproduction number.
Below, we take day as the time unit. Following the work in [9], we choose the baseline parameters as Λv=100,Λh=2.1,μv=0.05,μh=0.001,β=0.16,c=0.6,dh=0.005. Since the EIP of vector (mosquito) is about 8–12 days, and the EIP of the host (bird) is about 3–5 days, we set τ1=8,τ2=3 unless stated otherwise.
Similar to [15], choose T=10,p=0.6 while R0=1.1490. Figure 2(a) shows that the number of infected vectors tends to the periodical oscillation when culling occurs, whereas it tends to a equilibrium without culling. In addition, we see from Figure 2(a) that culling significantly reduces the amount of infections of the vector compared to the case of no culling. Choose T=10,p=2 while R0=0.7142. As shown in the Figure 3(b), the number of infected hosts that are not culled will continue to increase, and after the action of culling, the number of infected hosts will decrease, and the disease will eventually die out.
Next, we use PRCCs (partial rank correlation coefficients) to obtain the sensitivity analysis of R0. We take Λv,Λh,μv,μh,β,b,c,p,dh and rvt as the input variables and the value of R0 as the output variable. Figure 4 illustrates that parameters Λh,μv,μh,p and dh are negatively correlated with R0 and the others are positively correlated. We also see that R0 is more sensitive to μh,β,b,c and p. Thus, the corresponding control measures should be taken for these sensitive parameters. For instance, to reduce mosquito-bird contact and further control the disease spread, we could burn repellent plants in the bird habitat or at their water sources.
In Figure 5, we investigate the joint effects of β,p on R0. It shows that when the biting rate β is large, it requires very strong culling effect. In Figure 6 we also choose different rvt=0.01,r=0.05,r=0.1, while β=0.05, and get R0 increasing in rvt (compare (a)–(c)). Both Figures 5 and 6 indicate that when all parameters are equal, R0 is decreasing in p. All the results are consistent with the conclusion in sensitivity analysis.
Finally, we examine the impact of the EIP on R0. We let τ1 vary from 0 to 10 and τ2 vary from 0 to 5. Figure 7 describes the dependence of R0 on τ1 and τ2 for three different frequencies of culling (i.e. 1T). As we see from this figure, R0 is decreasing with respect to τ1 as well as τ2 and it increases as T increases for fixed τ2 and τ1. This suggests that culling during the EIP and prolonging the EIP would be beneficial for disease control, while infrequent culling might be counterproductive.
5.
Discussion and conclusions
In this paper, we have formulated an impulsive vector-borne disease model with time delays to investigate the joint effects of the EIP and impulsive intervention. The basic reproduction number R0 is first derived by the theory in [1], which serves as a threshold value to determine the extinction and uniform persistence of the disease. Unlike most existing works [1,6,9,15], we utilize the dynamical system approach to show the sharp uniform persistence as R0>1. As is well known, the uniform persistence theory often gives rise to the existence of a positive periodic solution (see [21, Theorem 1.3.10]). As a complement, we could also show the existence of a positive periodic solution in [1,9,15] via our strategy. However, we emphasize that since our feasible domain Dϵ in (2.3) is non-convex, we could not directly utilize it to verify the existence of the positive periodic solution, and we will leave the general existence and its stability for further investigation.
In addition, there are several possible extensions of this work. For example, EIP is often sensitive to temperature, which would lead to study of the time-varying delay (especially time-periodic delays as in [16]), whose periods might be different from the fixed impulsive moments, and so it requires a more careful and delicate deviation of the theory in [1,21]. At the moment, we are working on a time-periodic impulsive model with constant delays, where the impulsive moments are different from the real-time periods. In a different work, one could elaborate our model by incorporating the stochastic effects, and perform the stability analysis of the model system using some recent results in [29,30,31].
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
We are grateful to anonymous reviewers for their careful reading and valuable suggestions which led to an improvement of our original manuscript. This research was supported by the NSF of China (Nos. 12001205 and 12371169).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: