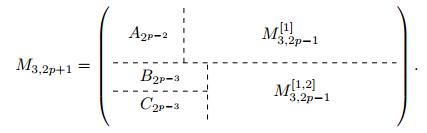1. Introduction

Blood pressure is an important source of diagnostic information that can be used to detect and characterize cardiovascular diseases. Research has shown that studying the propagation of arterial pressure wave in the cardiovascular system leads to clinically useful information [12, 25, 13, 8, 14]. For example, the distensibility of an artery can be found from the speed of the pressure wave propagation in the vessel. Moreover, when a wave encounters an irregularity in the vessel, a transmitted and a reflected wave are generated from both sides of the irregularity [3, 22]. This is particularly important because reflected waves travel backward directly to the heart. These backward waves can apply an additional load on the muscle that is often seen as a risk factor for developing heart disease [11]. Research has shown that with age, due to the stiffening of the vessels and the presence of stenoses or aneurysms, reflected waves are more and more frequent [22]. Other studies were carried out to characterize the reflection coefficients of irregularities such as stenoses [21] and to look at the effect of these irregularities on arterial pressure waves [2, 15].

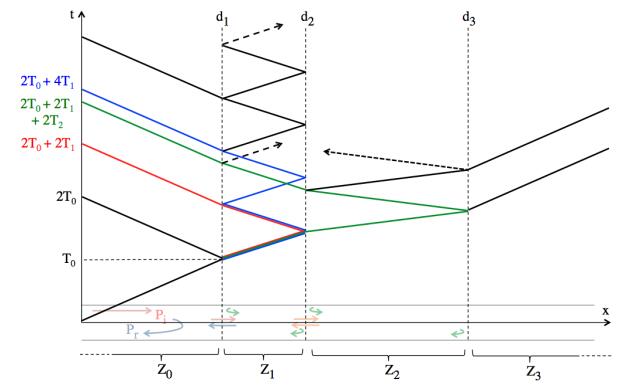
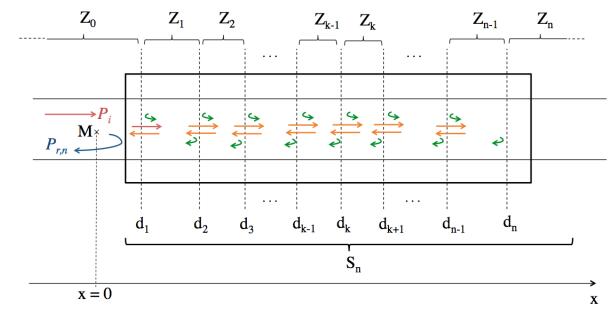
In this research, we model arterial irregularities as local discontinuities in a geometric or mechanical property of the artery. The results apply to any local change in the area of the vessel, such as stenoses, aneurysms or bifurcations, and also apply to changes in other properties, such as the result of local stiffening with age due to plaques or remodelling of the arterial wall. Our model of arterial irregularities consists in an idealized system $S_n$, represented on Figure 1, which models a section of an artery, with $n$ irregularities, modelled by discontinuities $d_k$, where $(k, n) \in \mathbb N^2$ and $1\leq k \leq n$. The scope of this research is to study the effect of successive arterial irregularities modeled by system $S_n$ on an incoming cardiac pulse wave $P_i$. To do so, we investigate on the resulting reflected pressure wave $P_{r, n}$ returning at the entrance of system $S_n$ after the passing of the incoming cardiac pulse wave $P_i$. Thus, we introduce a measurement point, represented by point M at $x = 0$ on Figure 1, at which level we will numerically study the evolution of blood pressure.

As represented on Figure 1, two successive discontinuities $d_k$ and $d_k+1$ delimit a zone $Z_k$ in which the mechanical and geometric properties of the vessel are homogenous. Therefore, waves propagate in $Z_k$ without any perturbation, until they reach either discontinuity $d_{k+1}$, the right delimitation of $Z_k$, for forward propagating waves, or discontinuity $d_{k}$, the left delimitation of $Z_k$, for backward propagating waves. When reaching a discontinuity, waves split into two components : a reflected pressure wave that is reflected within $Z_k$, represented by curled arrows on Figure 1, and a transmitted pressure wave that is transmitted in $Z_{k-1}$ for backward traveling waves, or in $Z_{k+1}$ for forward traveling waves, represented by straight arrows in Figure 1. Finally, $P_i$ is the initially incoming wave that will be interfering with system $S_n$ and that will be used as our input signal in this research. $P_{r, n}$ is the overall reflected pressure wave, that will return at the entrance of $S_n$ after the passing of $P_i$ in system $S_n$, which amplitude will be numerically estimated at the measurement point M in $x = 0$. Using the previous notation, $S_0$ represents a homogenous vessel, $S_1$ represents a single change, such as bifurcation and $S_2$ could be used to model a stenosis or an aneurysm, where there is a section with different properties between two identical sections.

Hemodynamic studies, conducted with in vivo laboratory experiments [9, 1] have been used to test theoretical models, but nowadays, computers and simulations are more frequently used. Indeed, simulations allow us to access specific values such as the wall shear stress or the pressure distribution, which are difficult to extract from in vivo experiments [24, 20, 10, 19, 16]. Moreover, as invasive cardiovascular treatments are problematic, using simulations is particularly helpful to understand these diseases and to predict potential risks of medical complications [18]. Thus, a theoretical model that uses an iterative algorithm is developed in this paper, in order to study the effect of successive arterial irregularities on cardiac pulse waves. The iterative algorithm enables us to simulate the resulting reflected pressure wave at the entrance of $S_n$, at the measurement point M, at $x = 0$ on Figure 1, after the passing of the incident cardiac pulse wave denoted $P_i$. Finally, it is important to study the resulting reflected pressure wave returning at the entrance of $S_n$ denoted $P_{r, n}$ as it is the backward reflected pressure wave traveling upstream directly to the heart. This backward wave can apply excessive pressure on the heart and is often seen as a risk factor for developing cardiovascular diseases. Moreover, knowing the waveform of $P_{r, n}$ could be useful for diagnostic purposes or for following treatment results.

---

2. Modelling cardiac pulse wave

---

2.1. Governing equations

We make the classical assumptions that the blood flow is incompressible, one-dimensional, inviscid, and we neglect gravity. Using these assumptions, the conservation of momentum is given by the Euler equation:

$\rho \left (\frac{\partial {U}}{\partial t}+U\frac{\partial {U}}{\partial x}\right) = -\frac{\partial {P}}{\partial x},$

(2.1)

where $U$ is the axial $x$-component of the blood velocity, $P$ the blood pressure and $\rho$ its density. By applying the mass conservation equation on a differentiable element of the blood vessel:

$\frac{\partial {A}}{\partial t} = -\frac{\partial {(AU)}}{\partial x},$

(2.2)

where $A(x, t)$ is the local cross-sectional area of the differentiable element of the blood vessel, which is the cross-sectional area of the vessel at the considered $x$ absciss at time $t$. Finally, the classical tube law assumption [4, 5, 17, 14] expresses the local area as a function of pressure and position as:

$\left\{ \begin{array}{l} A(x, t) = A(P(x, t), x) \\ \frac{\partial {A}}{\partial P}>0 \end{array} \right.$

(2.3)

and is motivated by many empirical evidences [6, 7, 23]. Using the tube law (2.3), we can rewrite (2.2) in terms of $P$ and $U$ as:

$\frac{\partial {P}}{\partial t}+U\frac{\partial {P}}{\partial x}+\frac{A}{A_{P}}\frac{\partial {U}}{\partial x} = -\frac{UA_{x}}{A_{P}},$

(2.4)

where:

$A_{x} = \frac{\partial {A}}{\partial x}\bigg|_{P} \text{ and } A_{P} = \frac{\partial {A}}{\partial P}\bigg|_{x}.$

(2.5)

Expressing (2.1) and (2.2) in canonical matrix form:

$\frac{\partial}{\partial t}\begin{pmatrix} P\\ U \end{pmatrix} +\begin{pmatrix}U&\frac{A}{A_{P}}\\ \frac{1}{\rho} & U\end{pmatrix}\frac{\partial}{\partial x}\begin{pmatrix}P\\ U\end{pmatrix} = \begin{pmatrix}-\frac{UA_{x}}{A_{P}}\\ 0\end{pmatrix}.$

(2.6)

The eigenvalues of the matrix are $U \pm c$, where $c = \sqrt{1/\rho D}$ is the wave speed: the speed at which disturbances would propagate upstream and downstream in the absence of flow ($U = 0$). $D = A_P/A$ is the distensibility of the vessel that characterizes the vessel's capability of being distended or stretched. Since the eigenvalues are real, the system is hyperbolic and can be solved using the method of characteristics. Finally, from 1-D wave theory, we know that, when a wave encounters a discontinuity in a property of the medium in which it is propagating, it is reflected and transmitted on both sides of this discontinuity. In order to characterize the reflected and transmitted wave, we will use the reflection and transmission coefficients defined by:

$\gamma = \frac{P_{r}}{P_{i}} ~~\text{ and } ~~ \lambda = \frac{P_{t}}{P_{i}},$

(2.7)

where $P_{i}$ is the amplitude of the incident pressure wave, $P_{r}$ the amplitude of the reflected pressure wave and $P_{t}$ the mplitude of the transmitted pressure wave. These reflection and transmission coefficients are linked by the relation $\gamma+\lambda = 1$ [21]. This relation allows us to study the reflected pressure only as a function of reflection coefficient $\gamma$ in the result section.

In this paper, we model two successive irregularities by two discontinuities $d_k$ and $d_{k+1}$ which delimit an homogeneous zone denoted $Z_{k}$ as represented in Figure 1. A zone $Z_k$ is fully characterized by its length $L_k = d_k-d_{k-1}$ and by its constant distensibility $D_k$. By convention, zone 0, $Z_0$ is the semi-infinite zone at the left of the first discontinuity $d_1$ of system $S_n$ and zone n, $Z_n$ is the semi-infinite zone at the right of the last discontinuity $d_n$ of the system. The reflection and transmission coefficients at a discontinuity, defined above, depend on the direction of travel of the incident wave. In the following, a forward traveling wave in $Z_{k}$ will interact with the discontinuity $d_{k+1}$ to generate a backward reflected wave in $Z_{k}$ with the reflection coefficient $\gamma_{kk+1}$ and a forward transmitted wave in $Z_{k+1}$ with the transmission coefficient $\lambda_{kk+1}$. Similarly, a backward wave in $Z_{k}$ will interact with the discontinuity $d_{k}$ generating a forward reflected wave in $Z_{k}$ with the reflection coefficient $\gamma_{kk-1}$ and a backward transmitted wave in $Z_{k-1}$ with the transmission coefficient $\lambda_{kk-1}$. The time for a wave to propagate downstream through $Z_{k}$, from $d_k$ to $d_{k+1}$ is denoted $T_{k}^{+}$, and upstream through $Z_{k}$ from $d_{k+1}$ to $d_k$ is denoted by $T_{k}^{-}$ with :

$T_{k}^{+} = \frac{L_k}{c_k+U} = \frac{|d_{k}-d_{k-1}|}{\sqrt{1/\rho D_k}+U} ~~\text{ and } ~~T_{k}^{-} = \frac{L_k}{c_k-U} = \frac{|d_{k}-d_{k-1}|}{\sqrt{1/\rho D_k}-U}.$

(2.8)

Moreover, as the blood flow velocity is negligible compared to the celerity of pressure waves, we have $U / c_k \ll 1$, therefore :

$T_{k}^{\pm} = \frac{L_k}{c_k\pm U} = \frac{L_k}{c_k \left(1\pm \frac{U}{c_k}\right)} = \frac{L_k}{c_k\left(1\pm \mathcal{O}\left (\frac{U}{c_k}\right)\right)}.$

(2.9)

Under a zeroth-order approximation we can define a unique propagation time $T_{k}$ for backward and forward traveling waves that is :

$T_{k} = \frac{L_k}{c_k} = \frac{|d_{k}-d_{k-1}|}{\sqrt{1/\rho D_k}}.$

(2.10)

Finally, All the properties for each zone $Z_k$ are represented in this one quantity and, in the following, $T_k$ will be used as our model input prescribed in the simulations when modelling different pathological scenarios in the results section. By convention, $T_0$ is the time for the wave to travel from measurement point M (at $x = 0$ in $Z_0$) to the first discontinuity $d_1$ of the system.

---

2.2. Theoretical framework

Assume $n \in \mathbb N$ and $S_{n}$ is a system modelling the section of a vessel with $n$ arterial discontinuities, and $f$ is a continuous function on $[0, T]$ where $T \in \mathbb R_+$ modelling a realistic cardiac pulse wave. We want to know the resulting reflected pressure wave at the entrance of system $S_n$ after the passing of a cardiac pulse wave. This resulting reflected pressure wave at the entrance of $S_n$ is called the response of system $S_n$ and is denoted $P_{r, n}$. In order to study the response of the $S_n$, we model the effect of the system as a functional denoted $F_n$ that will be applied to the continuous function $f(t)$ modelling the incoming cardiac pulse wave on $S_n$, that is $P_{r, n} = F_n\left[f\right]$.

First we study the response of $S_n$ when the incident wave is a single wavefront modelled by the Heaviside function. Since the governing system (2.5) is hyperbolic, wavefronts will be reflected and transmitted within the system and thus the resulting pressure at the entrance of the system is a superposition of shifted Heaviside functions with different amplitudes. In mathematical terms we write:

$F_n\left[H\right]\left(t\right) = \sum\limits_{p = 1}^\infty I_pH\left(t-t_p\right),$

(2.11)

for all $n \in \mathbb N^*$ and $t \in \mathbb R_+$ and where $I_p$ is the amplitude and $t_p$ is the delay time of wave $w_p$.

In the case in which the incident wave is a continuous function $f$ defined on $\left[0, T\right]$, we approximate $f$ with $f_m$, where $f_m$ is a superposition of Heaviside functions, for which $\lim\limits_{m \to \infty}||f-f_m||_{\infty} = 0$ which we define mathematically by:

$\forall t \in \left[0, T\right] \ f_m \left(t\right) = \sum\limits_{k = 1}^{m} \alpha_k H\left(t-t'_k\right),$

(2.12)

where $m\in \mathbb N$ and $m > 1$, $t'_{k} = \left (k-1\right ) \frac{T}{m-1}, t'_{m} = T$, $\alpha_{k} = f\left (k\frac{T}{m-1}\right)-f\left (\left (k-1\right )\frac{T}{m-1}\right ),$ and $\alpha_{m} = f\left (T\right )$. As we mentioned, $f_m$ converges uniformly towards $f$ when $m$ goes to infinity. Before each simulation, a convergence study is done in order to control the convergence of $f_m$ towards $f$. In the results section we choose a value of $m = 10000$ for all simulations to ensure an appropriate convergence of the Heaviside approximation of the incident wave. The effect of the control parameter $m$ on the computational solutions is discussed in the appendices.

From equation (2.8), by using the linearity and the continuity of the functional $F_n$ and by using the expression of $F_n\left[H\right]$ from equation (2.7), we find:

$F_{n}\left[f\right] = F_n \left [\lim\limits_{m \to \infty}\sum\limits_{k = 1}^{m} \alpha_k H \left(t-t'_k\right) \right] = \lim\limits_{m \to \infty}\sum\limits_{k = 1}^{m} \sum\limits_{p = 1}^\infty \alpha_kI_pH\left(t-t'_k-t_p\right).$

(2.13)

Thus we focus on finding the unknowns $I_p$ and $t_p$. In order to solve this problem we wrote an iterative algorithm that returns $I_p$ and $t_p$ for $p \in \left[\!\left[{ 1, N } \right]\!\right]$, where $N\in \mathbb N$ is the number of iteration for which we consider the iterations have converged. The iterative algorithm that returns the unkowns $I_p$ and $t_p$ is explained in the two following subsections. Before each simulation, a second convergence study is done in order to control the convergence of the iterative algorithm, and in order to choose the sufficient number of iterations for the algorithm to converge. To do so, we introduce a second control parameter $\epsilon$ that controls the difference between two iterations. We denote by $F_{n, N}[f]$ the result returned at the $N^{th}$ iteration and $\Delta_{r}(F_N)$ the relative difference between $F_{n, N}[f]$ and $F_{n, N-1}[f]$. Mathematically the final number of iteration $N$ for which the iterative algorithm has converged is such that:

$\Delta_{r}(F_N) = \left \|\frac{F_{n, N}\left[f\right] - F_{n, N-1}\left[f\right]}{\color{black}{F_{n, N-1}\left[f\right]}}\right \|_\infty = \left \|\frac{ \lim\limits_{m \to \infty}\sum\limits_{k = 1}^{m} \alpha_kI_NH\left(t-t'_k-t_N\right)}{\lim\limits_{m \to \infty}\sum\limits_{k = 1}^{m} \sum\limits_{p = 1}^{N-1} \alpha_kI_pH\left(t-t'_k-t_p\right)}\right \|_\infty < \epsilon$

(2.14)

In the result section, we apply this method to physiological scenarios and choose $\epsilon~ = ~0.1$ for each simulation to control the convergence of the algorithm. A senstitivity analysis regarding $\epsilon$ is detailed in the appendices.

---

2.3. History of the waves

In this section, we consider wavefronts propagating in system $S_{n}$ and returning to the entrance, which are the waves that are transmitted from $Z_1$ to $Z_0$. The history of a particular wave can be written in different but equivalent ways: the sequence of zones traversed, the sequence of discontinuities encountered or, most conveniently for our purposes, the sequence of reflections/transmissions that the wave has undergone. Indeed, a wavefront propagating in the system is fully characterized by its list of reflection and transmission coefficients of all the reflection and transmission it went through at each discontinuity $d_k$ within the system. For wave $w_p$, its reflection/transmission coefficient list is denoted as $\widetilde{w_p}$ in the following, often called "the history of wave $w_p$". We illustrate $S_{3}$, the system with three discontinuities, in Figure 2.

In the $(x, t)$-diagram plotted in Figure 2, vertical dashed lines represent the borders of the different homogenous zones, delimited by the discontinuities of the system, while diagonal lines represent the different paths of the waves traveling within the system. The slope of the diagonal lines is constant within a homogenous zone, and is equal to the speed of propagation of a wave through this zone.

We consider returning wavefronts in the $(x, t)$-diagram of Figure 2 and write down their respective reflection/transmission coefficient list as examples. The returning wavefront $w_1$ at time $t = 2T_0$ has only been reflected on $Z_1$ coming from $Z_0$. Its list is $\widetilde{w_1} = (\gamma_{01})$. The returning wavefront $w_2$ at time $t = 2T_0+2T_1$ has been transmitted from $Z_0$ to $Z_1$ through $d_1$, reflected at $Z_2$ while in $Z_1$ and finally transmitted back to $Z_0$ from $Z_1$ through $d_1$. Its list is $\widetilde{w_2} = (\lambda_{01}, \gamma_{12}, \lambda_{10})$. The returning wavefront $w_3$ at time $t = 2T_0+4T_1$ has the same history as the previous wavefront, except it is reflected two more times in $Z_1$: at $Z_0$ the first time and at $Z_2$ the second time. Thus, its list is $\widetilde{w_3} = (\lambda_{01}, \gamma_{12}, \gamma_{10}, \gamma_{12}, \lambda_{10})$. Using the same notation, the returning wavefront $w_4$ at time $t = 2T_0+2T_1+2T_2$ has the list $\widetilde{w_4} = (\lambda_{01}, \lambda_{12}, \gamma_{23}, \lambda_{21}, \lambda_{10})$, and so on.

If we know the history of a wavefront returning at the measurement point M at $x = 0$ then we know the time of arrival and amplitude of the wave. Indeed, for instance, according to the definition of the reflection and transmission coefficients (2.6), if we consider the wavefront $w_1$ that is directly reflected on discontinuity $d_1$ between $Z_1$ and $Z_2$, it returns to the measurement point with the amplitude $\gamma_{01}$ and it took $2T_0$ to return as it traveled back and forth into $Z_0$. Similarly, wavefronts that are transmitted through $d_1$ from $Z_0$ to $Z_1$ has their amplitude firstly multiplied by $\lambda_{01}$, and if we consider the wavefront $w_2$ that is then reflected on $d_2$ between $Z_1$ and $Z_2$, and then transmitted back through $d_1$ from $Z_1$ to $Z_0$, its amplitude is therefore multiplied by the reflection coefficient between $Z_1$ and $Z_2$ which is $\gamma_{12}$ and then by the transmission coefficient from $Z_1$ and $Z_0$ which is $\lambda_{10}$. Thus, the amplitude of the returning wavefront $w_2$ is given by the product $I_2 = \lambda_{01} \cdot \gamma_{12} \cdot \lambda_{10}$, and its time of return is the summation of the different back and forth traveling times through $Z_0$ and $Z_1$ that is $t_2 = T_0+T_1+T_1+T_0 = 2T_0+2T_1$. Therefore, the history of the wavefronts enables us to find $t_p$ and $I_p$ for any wavefront $w_p$. Indeed, according to the definition of the reflection and transmission coefficients, if we know the lists $\widetilde{w_p}$ of reflection/transmission coefficients of any returning wavefront $w_p$, then we know its amplitude as it is given by:

$\forall p \in \left[\!\left[{ 1, N } \right]\!\right],~~~~ I_p = \prod\limits_{\left (i, j, k, l\right ) \atop {\lambda_{ij}\in {\widetilde{w_p}}\atop {\gamma_{kl}\in {\widetilde{w_p}}}}} \lambda_{ij} \cdot \gamma_{kl},$

(2.15)

Moreover, the time for a wavefront to return is, by definition, and as we saw in the previous examples, the summation of the different back and forth traveling times the wave goes through in the system before returning. Therefore, this can be mathematically defined as:

$\forall p\in \left[\!\left[1, N \right]\!\right], \quad {{t}_{p}}=\sum\limits_{\begin{matrix} (i, j) \\ \begin{matrix} {{\lambda }_{ij}}\in \text{ }{\widetilde {{w_p}}} \\ {{\gamma }_{ij}}\in \text{ }{\widetilde {{w_p}}} \\ \end{matrix} \\ \end{matrix}}{{{T}_{i}}},$

(2.16)

where $N$ is the number of iterations.

In this research, we developed an iterative algorithm returning all the lists $\widetilde{w_p}$ which enables us to compute $I_{p}$ and $t_{p}$ for any wave $w_p$ and thus determine $P_{r, n}$. The method is explained in the following section. Then, this algorithm will be applied to different physiological scenarri that are presented with the computational solutions in the results section.

---

3. Method

---

3.1. Explaining the algorithm for 3 discontinuities, $n=3$

The algorithms for determining the lists $\widetilde{w_p}$ for $S_1$ and $S_2$ are too simple to indicate how to develop an algorithm for systems with more discontinuities. The study of a system with 3 discontinuities, $S_3$, however is not trivial and does provide us with a method that can be generalized to larger systems. Thus, the study of system $S_{3}$ with three discontinuities $(n = 3)$ is important because we will see how from the study of this system we can easily have the response for any other systems with any number of discontinuities. An illustration of $S_3$ is given in Figure 2. We study the first reflection/transmission coefficient lists of the wavefronts that are returning the entrance of system $S_{3}$. We stored the lists by their lengths ($i.e$: the number of elements in the list, which is the number of reflection and transmission coefficients) into matrices. The matrices are denoted $M_{n, l}$ where $n$ is the number of discontinuities of system $S_n$ and $l$ the length of the coefficients lists of the matrix (thus the number of columns of the matrix). We first noticed that the length of a list, $l$, can only be an odd number for the wavefront to return at the entrance of the system. We were able to write down manually the first five matrices of the returning wavefronts:

$\begin{align*} M_{3, 1} = \begin{pmatrix}\gamma_{01}\end{pmatrix}, \end{align*}$

$\begin{align*} M_{3, 3} = \begin{pmatrix}\lambda_{01}&\gamma_{12}&\lambda_{10} \end{pmatrix}, \end{align*}$

$\begin{align*} M_{3, 5} = \begin{pmatrix} \lambda_{01}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\lambda_{10} \\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\lambda_{10} \end{pmatrix}, \end{align*}$

$\begin{align*} M_{3, 7} = \begin{pmatrix} \lambda_{01}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\lambda_{10}\\ \lambda_{01}&\gamma_{12}&\gamma_{10}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\lambda_{10}\\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\gamma_{10}&\gamma_{12}&\lambda_{10}\\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\gamma_{21}&\gamma_{23}&\lambda_{21}&\lambda_{10} \end{pmatrix}, \end{align*}$

and,

$\begin{align*} M_{3, 9} = \begin{pmatrix} \lambda_{01}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\lambda_{10}\\ \lambda_{01}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\gamma_{10}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\lambda_{10}\\ \lambda_{01}&\gamma_{12}&\gamma_{10}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\gamma_{10}&\gamma_{12}&\lambda_{10}\\ \lambda_{01}&\gamma_{12}&\gamma_{10}&\lambda_{12}&\gamma_{23}&\gamma_{21}&\gamma_{23}&\lambda_{21}&\lambda_{10}\\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\gamma_{10}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\lambda_{10}\\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\gamma_{10}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\lambda_{10}\\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\gamma_{21}&\gamma_{23}&\lambda_{21}&\gamma_{10}&\gamma_{12}&\lambda_{10}\\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\gamma_{21}&\gamma_{23}&\gamma_{21}&\gamma_{23}&\lambda_{21}&\lambda_{10} \end{pmatrix}. \end{align*}$

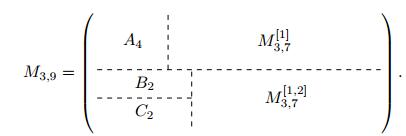
We build larger matrices iteratively using submatrices from previous matrices. We consider the matrix $A_n \in \mathcal{M}_{n,3}$ with n identical rows equal to $(\lambda_{01},\gamma_{12},\gamma_{10})$, the matrix $B_n \in \mathcal{M}_{n,4}$ with n identical rows equal to $(\lambda_{01},\lambda_{12},\gamma_{23},\lambda_{21})$ and the matrix $C_n \in \mathcal{M}_{n,4}$ with n identical rows equal to $(\lambda_{01},\lambda_{12},\gamma_{23},\gamma_{21})$. We now define the matrices $M_{3,7}^{[1]}$ which is equal to $M_{3,7}$ with its first column removed and $M_{3,7}^{[1,2]}$ which is equal to $M_{3,7}$ with its first and second columns removed. Thus, we can express $M_{3,9}$ as:

Furthermore, we show by induction that for any $p>3$:

Thus we develop an iterative algorithm that is able to generate automatically all the matrices, thus all the reflection/transmission coefficient lists of the returning wavefronts, stored in the matrices. From these coefficient lists, we can easily get the values of the unknowns $I_{p}$ and $t_{p}$ using equation (2.10) and equation (2.11). By doing so, the problem is solved for system $S_3$ with three discontinuities. Moreover, both system $S_1$ with one discontinuity and $S_2$ with two discontinuities are also solved. Indeed, $S_1$ (resp. $S_2$) is only a particular cases of $S_3$ for which the reflection and transmission coefficients $\gamma_{12}, \ \gamma_{23}$ and $\lambda_{12}, \ \lambda_{23}$ (resp. $\gamma_{23}$ and $\lambda_{23}$) are equal to 0.

---

3.2. Extending the algorithm from 3 discontinuities to 4 discontinuities, $n=3$ to $n=4$

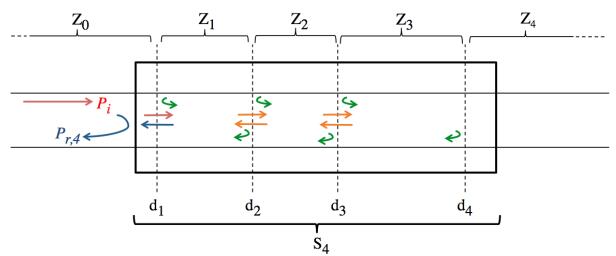
Reflection/transmission coefficients lists for $S_3$ also represent returning waves in $S_4$. Any additions to the lists in $S_4$ compared to the one with $S_3$ occur because the wavefront reached $d_4$. With the presence of the discontinuity $d_4$ in $S_4$, wavefronts can now be transmitted through $d_3$ and still be returning at the entrance of $S_4$ if reflected on $d_4$. System $S_4$ is illustrated in Figure 3.

When a wavefront is transmitted through $d_3$ in zone $Z_3$, a returning wavefront will be transmitted back to $Z_2$ after an odd number of reflections in $Z_3$. Finally, a returning wavefront for $S_4$ cannot be transmitted through $d_4$ as there are no more discontinuities after $d_4$ to be reflected on.

This idea was transplanted into the algorithm. For a wavefront to be propagating in $Z_2$ in the positive $x$-direction, its last reflection and transmission were either the reflection from in $Z_2$ on $d_2$ or the transmission from $Z_1$ to $Z_2$ through $d_2$. This means that the last term of its wave history is either $\gamma_{21}$ or $\lambda_{12}$. In order to generate all the new coefficient lists of the returning wavefronts for $S_4$ from the previously generated matrices for $S_3$ we simply have to add to any lists containing $\gamma_{21}$ or $\lambda_{12}$ in the matrices of $S_3$ the following sequence of coefficients due to:

● The transmission from $Z_2$ to $Z_3$ through $d_3$: $\lambda_{23}$.

● The odd number of reflection in $Z_3$ on $d_3$ and $d_4$: $(...\gamma_{34}, \gamma_{32}, ..., \gamma_{34}, \gamma_{32}, ..., \gamma_{34}, \gamma_{32}, \gamma_{34}, ...)$.

● The final transmission from $Z_3$ to $Z_2$ through $d_3$: $\lambda_{32}$.

We finally have analogous matrices from the one obtained in the previous study of $S_3$ with additional lines, written in bold in the following, due to the presence of the new discontinuity $d_4$:

$\begin{align*} M_{4, 1} = \begin{pmatrix}\gamma_{01}\end{pmatrix}, \end{align*}$

$\begin{align*} M_{4, 3} = \begin{pmatrix}\lambda_{01}&\gamma_{12}&\lambda_{10} \end{pmatrix}, \end{align*}$

$\begin{align*} M_{4, 5} = \begin{pmatrix} \lambda_{01}&\gamma_{12}&\gamma_{10}&\gamma_{12}&\lambda_{10} \\ \lambda_{01}&\lambda_{12}&\gamma_{23}&\lambda_{21}&\lambda_{10} \end{pmatrix}, \end{align*}$

$\begin{align*} M_{4,7}=\begin{pmatrix} \lambda_{01} & \gamma_{12} & \gamma_{10} & \gamma_{12} & \gamma_{10} & \gamma_{12} & \lambda_{10}\\ \lambda_{01} & \gamma_{12} & \gamma_{10} & \lambda_{12} & \gamma_{23} & \lambda_{21} & \lambda_{10}\\ \lambda_{01} & \lambda_{12} & \gamma_{23} & \lambda_{21} & \gamma_{10} & \gamma_{12} & \lambda_{10}\\ \lambda_{01} & \lambda_{12} & \gamma_{23} & \gamma_{21} & \gamma_{23} & \lambda_{21} & \lambda_{10}\\ \mathbf{\lambda_{01}} &\mathbf{ \lambda_{12}} &\mathbf{ \lambda_{23}} &\mathbf{ \gamma_{34}} & \mathbf{\lambda_{32}} &\mathbf{ \lambda_{21}} &\mathbf{ \lambda_{10}} \end{pmatrix}, \end{align*}$

and,

$\begin{align*} M_{4,9}=\begin{pmatrix} \lambda_{01} & \gamma_{12} & \gamma_{10} & \gamma_{12} & \gamma_{10} & \gamma_{12} & \gamma_{10} & \gamma_{12} & \lambda_{10}\\ \lambda_{01} & \gamma_{12} & \gamma_{10} & \gamma_{12} & \gamma_{10} & \lambda_{12} & \gamma_{23} & \lambda_{21} & \lambda_{10}\\ \lambda_{01} & \gamma_{12} & \gamma_{10} & \lambda_{12} & \gamma_{23} & \lambda_{21} & \gamma_{10} & \gamma_{12} & \lambda_{10}\\ \lambda_{01} & \gamma_{12} & \gamma_{10} & \lambda_{12} & \gamma_{23} & \gamma_{21} & \gamma_{23} & \lambda_{21} & \lambda_{10}\\ \lambda_{01} & \lambda_{12} & \gamma_{23} & \lambda_{21} & \gamma_{10} & \gamma_{12} & \gamma_{10} & \gamma_{12} & \lambda_{10}\\ \lambda_{01} & \lambda_{12} & \gamma_{23} & \lambda_{21} & \gamma_{10} & \lambda_{12} & \gamma_{23} & \lambda_{21} & \lambda_{10}\\ \lambda_{01} & \lambda_{12} & \gamma_{23} & \gamma_{21} & \gamma_{23} & \lambda_{21} & \gamma_{10} & \gamma_{12} & \lambda_{10}\\ \lambda_{01} & \lambda_{12} & \gamma_{23} & \gamma_{21} & \gamma_{23} & \gamma_{21} & \gamma_{23} & \lambda_{21} & \lambda_{10}\\ \mathbf{\lambda_{01}} & \mathbf{\gamma_{12}} &\mathbf{ \gamma_{10}} &\mathbf{ \lambda_{12}} & \mathbf{\lambda_{23}} & \mathbf{\gamma_{34}} & \mathbf{\lambda_{32}} &\mathbf{ \lambda_{21}} & \mathbf{\lambda_{10}}\\ \mathbf{\lambda_{01}} & \mathbf{\lambda_{12}} & \mathbf{\lambda_{23}} & \mathbf{\gamma_{34}} & \mathbf{\lambda_{32}} &\mathbf{ \lambda_{21}}&\mathbf{ \gamma_{10}} &\mathbf{ \gamma_{12}} &\mathbf{ \lambda_{10}}\\ \mathbf{\lambda_{01}} & \mathbf{\lambda_{12}} & \mathbf{\lambda_{23}} & \mathbf{\gamma_{34}} &\mathbf{ \lambda_{32}} & \mathbf{\gamma_{21}} & \mathbf{\gamma_{23}} & \mathbf{\lambda_{21}} & \mathbf{\lambda_{10}}\\ \mathbf{\lambda_{01}} & \mathbf{\lambda_{12}} & \mathbf{\gamma_{23}} & \mathbf{\gamma_{21}} &\mathbf{ \lambda_{23}} &\mathbf{ \gamma_{34}} &\mathbf{ \lambda_{32}} & \mathbf{\lambda_{21}} & \mathbf{\lambda_{10}}\\ \mathbf{\lambda_{01}} & \mathbf{\lambda_{12}} & \mathbf{\lambda_{23}} & \mathbf{\gamma_{34}} & \mathbf{\gamma_{32}} & \mathbf{\gamma_{34}} & \mathbf{\lambda_{32}} &\mathbf{ \lambda_{21}} &\mathbf{ \lambda_{10}} \end{pmatrix}. \end{align*}$

---

4. Results for a half-sinusoidal model of a cardiac pulse wave

In the following section, we are going to look at the reflected pressure versus time $P_{r, n}\left(t\right)$ at the entrance of systems with different numbers of discontinuities, when the incident pressure wave is modeled by a half-sinusoidal wave : $P_i\left(t\right) = \sin\left(\pi t/0.1\right)$. We will consider cases of 1, 2, 3 and 4 discontinuities in the system. Each study is directly linked to common physiological scenarios. The results are given by simulations obtained with the previously explained algorithm and after a convergence study done on the two control parameters. We chose in the following simulations $m = 10000$ and $\epsilon = 0.1$ as explained in the theoretical framework. Detailed sensitivity studies regarding the values of the control parameters $m$ and $\epsilon$ are given in the appendices for cases with $n = 2$, $n = 3$ and $n = 4$.

---

4.1. Results for one discontinuity (n =1): Application to a bifurcation or an abrupt change in stiffness

Applying the algorithm to system $S_1$ can be useful to model a bifurcation or an abrupt change in the vessel's stiffness as both can be modelled with a system with only one discontinuity. We looked at the results for different values of reflection coefficients and saw that the results obtained from the algorithm matched with the trivial analytical solution $P_{r, 1}\left(t\right) = ~\gamma_{01}P_i\left(t\right) = ~\gamma_{01}\sin\left(\pi t/0.1\right)$. This comparison allowed us test and valid the algorithm on this example.

---

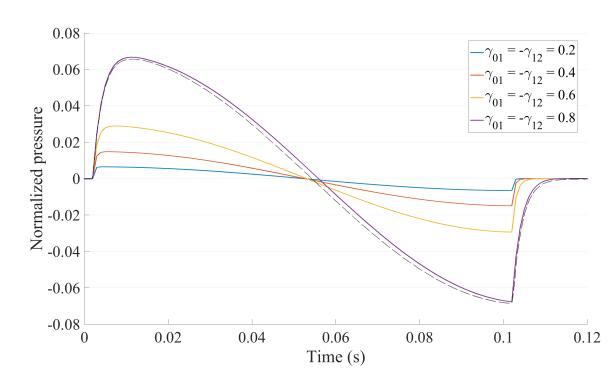
4.2. Results for two discontinuities (n = 2): Application to an isolated stenosis or an isolated aneurysm

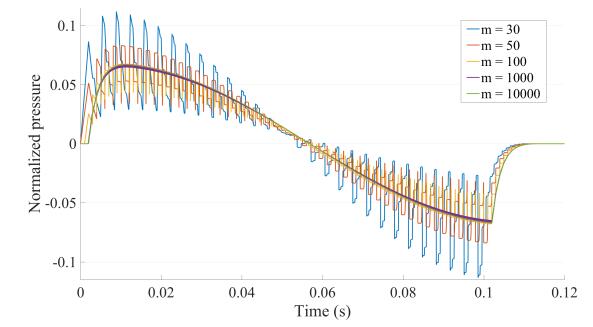
In this section we apply the algorithm to system $S_2$, the system with two irregularities. This is particularly useful to model isolated stenoses or isolated aneurysms. Indeed, these pathologies can be modelled by two successive changes in the vessel's area as the flow undergoes a narrowing which induces a discontinuity in the local area. On Figure 4 are gathered the results of the simulations modelling the reflected pressure at the entrance of an isolated stenosis for different severities by changing the values of the reflection coefficients $\gamma_{01}$ and $\gamma_{12}$. In this particular example, we were able to derive an analytical solution of the reflected pressure (see appendix 6.1). We compared the analytical solution with the results returned by the algorithm by plotting the analytical solution in dashed line on Figure 4 for $\gamma_{01} = \gamma_{12} = 0.8$. We see that the analytical (dashed lines) and the computational responses match, which validates once more the algorithm. The fact that the analytical and the computational solutions are not identical is due to the degree of convergence of the iterations controlled by the parameter $\epsilon$. As $\epsilon \longrightarrow 0$, the computational solution uniformly converges towards the analytical solution as we can see on Figure 12 in the appendices, but computation times increase rapidly. Fixing the value of $\epsilon$ was done by choosing the right balance between computation times and the exactness of the computational solutions. In our simulations, we fixed $\epsilon = 0.1$ because computations are executed fast enough to investigate on different scenarios and we are satisfied of the precision of the computational solutions returned by the algorithm. In these simulations we chose as input parameters : $T_0 = 1$ ms and $T_1 = 0.5$ ms, which corresponds to a $5$ mm long stenosis.

---

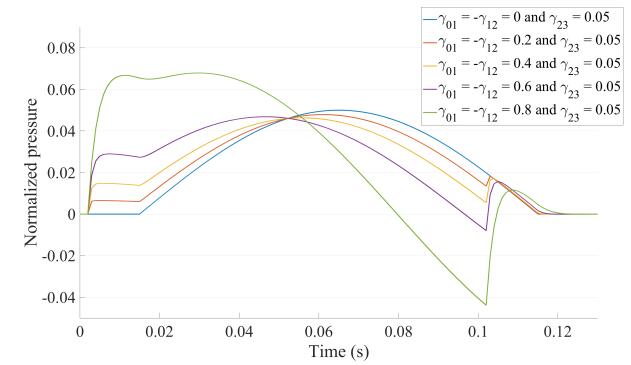
4.3. Results for three discontinuities ($n=3$): Application to a stenosis followed by a bifurcation

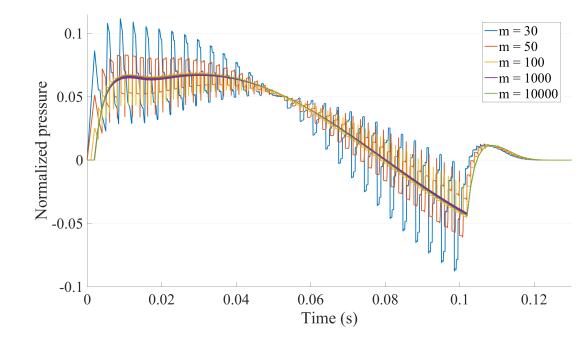
For a number of discontinuities strictly greater than 2 ($n>2$), there are no general analytical solution. This justifies our need to develop the iterative algorithm. Applying the algorithm on system $S_3$ can be helpful to study the influence of a bifurcation downstream a stenosis. As bifurcations have commonly low reflection coefficients we fix at 0.05 the value of the bifurcation's reflection coefficient. On Figure 5 are gathered the simulated reflected pressure waveforms at the entrance of system $S_3$ modelling stenoses with different degrees of severity followed by a bifurcation. In these simulations we chose as input parameters: $T_0 = 1$ ms, $T_1 = 0.5$ ms and $T_2 = 6$ ms which corresponds to a $5~$mm long stenosis followed by a bifurcation 6 cm downtream.We notice that the amplitude of the reflected pressure waveform for all scenarios is around $0.05$ except for the case $\gamma_{01} = 0.8$. This means that for $0\leq\gamma_{01} \leq 0.6$, the amplitude of the incident pressure wave is multiplied by the value of the bifurcation's reflection coefficient. Moreover, we observe a local minima in pressure near $t = 100$ ms for all scenarios, except for the case $\gamma_{01} = 0$ which is the case equivalent to no upstream stenosis. This let us think that this peak is due to the presence of the upstream stenosis as we can also see on Figure 4 the waveform for an isolated stenosis reaching its minimal values near $t = 100$ ms.

---

4.4. Results for four discontinuities (n = 4)

---

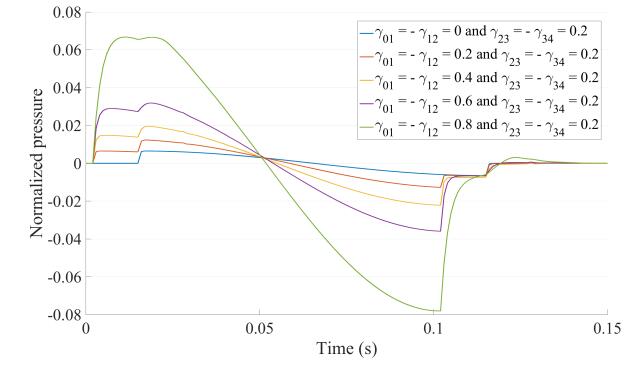
4.4.1. Application to two stenoses in series

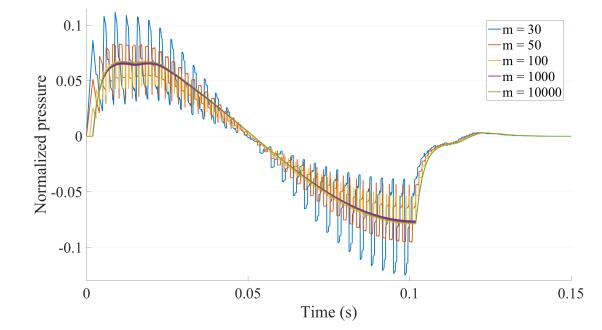
Modelling the reflected pressure waveform upstream two stenoses in series is particularly useful because in some cases, one stenosis can hide a second downstream stenosis. This can easily be modelled using $S_4$, the system with four discontinues because two stenoses in series can be seen as four successive discontinuities in the vessel's area. We fix the reflection coefficients corresponding to the dowstream stenosis and vary the coefficients of the first stenosis to investigate different scenarios. Results are gathered on Figure 6. For these simulations, we chose as input parameters: $T_0 = 1$ ms, $T_1 = 0.5$ ms, $T_2 = 6$ ms and $T_3 = 0.5$ ms which corresponds to a first 5 mm long stenosis spaced 6 cm away from a second 5 mm stenosis downstream. The main difference with the case of one isolated stenosis is the presence of local extrema observed on the returning pressure waveform. A local minimum is observed at time $t = 16$ ms that matches with the time for a single wavefront to reach the downstream stenosis and to return back to where the pressure is recorded. We suppose that this local minimum is due to the presence of the downstream stenosis as it was not observed in the case of an isolated stenosis. Observing such local extrema in the reflected pressure waveform could be helpful to detect stenoses in series and could have important clinical implications explained in the discussion section.

---

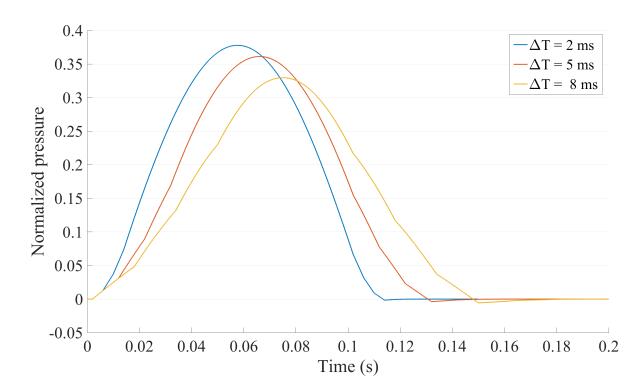
4.4.2. Application to smooth changes in vessel's stiffness

Modelling an abrupt change in stiffness was done with $n = 1$ discontinuity using $S_1$. However, one could expect, in some cases, the changes in stiffness along an artery to occur relatively smoothly. A smooth transition can be modelled by discretizing the progressive change in the arterial property with several local discontinuities in the arterial stiffness. This number of discontinuities depends on how one discretizes this progressive change. The more discontinuities you consider, the better will be the discretization. In our case, we model a smooth change in stiffness by discretizing this progressive change with four localized discontinuities in stiffness that are characterized by their relative reflection coefficients. To do so, we consider system $S_4$ with four discontinuities that all have the same relative reflection coefficients $\gamma$ and for which the propagation times of the pressure wave to travel between two successive discontinuities are the same and are equal to a parameter denoted $\Delta T$ on Figure 7. $\Delta T$ is directly related to the gradient of stiffness of the artery and can physically describe how smooth is the change in the vessel's property. The more $\Delta T$ is important, the more the discontinuities are spaced and thus, the less the gradient in stiffness of the artery is important as the different reflection coefficients are fixed and equal to $\gamma$. On Figure 7 are gathered results of simulations for which we consider the four reflection coefficients fixed and equal to $\gamma = 0.1$ and where we study the effect of $\Delta T$ on the reflected pressure waveform. In our case we observe that the more $\Delta T$ is important, the less the amplitude of the reflected wave is important. This means that the amplitude of the reflected pressure wave decreases with the stiffness gradient as we could physically expect. Interpretations of this result are gathered in the discussion section.

---

5. Discussion and conclusion

This research presents a method that allows clinicians to have qualitative predictions of the resulting reflected pressure waveform upstream a series of successive arterial irregularities. The iterative algorithm developed in this paper is used to model different clinical scenarios and simulate the effect of arterial irregularities, such as stenoses or arterial stiffening, on the pressure waveform. The results we obtained for a single stenosis with the algorithm were compared with the analytical solution developed in the appendix. This comparison allowed us to test the robustness of the algorithm and validate the method we use in this research. The algorithm is applied on more complicated physiological cases than isolated stenoses, such as a stenosis followed by a bifurcation. In that case, the global amplitude of the pressure is multiplied by the reflection coefficient of the downstream bifurcation. Usually, the reflection coefficients of bifurcations are relatively small, around 0.05. Measuring normalized reflected pressure wave with small amplitudes could indicate clinicians the presence of a bifurcation near the measurement point.

We also applied our method to two stenoses in series, which could prevent a stenosis hiding a second downstream stenosis during diagnosis, meaning that only the first stenosis is treated and potentially necessitating a second operation. If clinicians were able to detect directly both stenosis, only one operation would be needed, limiting the risks and the time of the medical procedure. Our model shows that when two stenoses are in series, the reflected pressure looks similar to the case of isolated stenoses but visible local pressure extrema indicate the presence of the second downstream stenosis. From such information, clinicians could directly look for two stenoses instead of one. However, in practice, noise could easily make the local extrema difficult to measure as their amplitude are relatively small compared to the global amplitude of the reflected pressure wave. This would suppose a measuring device able to detect small pressure variations in the blood flow while filtering undesirable noise. At this point, no experimental work has been done. Yet, from the theoretical results of this research, we understand that an experimental study would need precise measuring tools and techniques in order to detect the impact of such arterial irregularities on the pressure waveform.

Finally we investigate on a progressive change in the vessel's properties. We apply the algorithm on smooth changes in stiffness of the vessel's wall. Results show that the less the gradient stiffness is important, the weaker will be the reflected wave. The limit case of infinitely smooth changes in the vessel's properties being the case of a regular uniform vessel in which no reflected wave is generated. The same method of discretizing progressive changes in the vessel's stiffness can be used to model smooth changes in the vessel's area in order to study more realistic stenoses' and aneurysms' geometries which are commonly modeled by an abrupt change in the vessel's area. However, the main limitation with this discretizing technique is that to have a good approximation of a progressive change in vessels' properties, one need to consider many discontinuities which quickly leads to long computation times.

---

6. Appendices

---

6.1. Analytical solution of the returning pressure wave for an isolated stenosis or an isolated aneurysm

In the following we consider a system with two discontinuities $S_2$ modelling an isolated stenosis or an isolated aneurysm for which $\gamma_{01} = \gamma_{12}$. To ease up the notation we take $\gamma_{01} = \gamma_{12} = \gamma$. We look for the response of $S_{2}$ when the incoming pressure wave traveling initially forward through $Z_0$ is modelled by the Heaviside function $H$. At time $t = T_0$, it reaches the first discontinuity $d_1$ of $S_2$, where a reflected wave is generated with amplitude $\gamma$ which travels backward to the measurement point M (Figure 1). The reflected wave reaches the measurement point at time $t = 2T_0.$ Thus :

$\forall t \in [0, 2T_0 [~~~~P_{r, 2} \left( t \right) = 1.$

(6.17)

When the incoming wave reached $d_1$ at $t = T_0$ a transmitted wave was also generated, traveling forward through $Z_1$ with amplitude $1 + \gamma$. When this transmitted wave reaches $d_2$ at time $t = T_0+ T_1$ a reflected wave is generated, traveling backward through $Z_1$ with an amplitude of $(1 + \gamma)(-\gamma)$ which reaches $d_1$ at time $T_0+2T_1$. At this time a transmitted wave is generated and travels through $Z_0$ with the amplitude $(1-\gamma^2)(-\gamma)$ and reaches the measurement point at time $t = 2T_0+ 2T_1$. Thus we can write:

$\forall t \in [2T_0, 2T_0+ 2T_1[~~~~P_{r, 2} \left( t \right) = 1+ \gamma.$

(6.18)

This reflection process within $Z_1$ goes on infinitely and new waves are transmitted to the measurement points every $2T_1$. Thus we can write:

$\forall t \in [2T_0+ 2T_1, 2T_0+ 4T_1[~~~~P_{r, 2} \left( t \right) = 1+ \gamma + (1-\gamma^2)(-\gamma)$

(6.19)

and more generally :

$\forall n \in \mathbb N^* \forall t \in [2T_0+ 2nT_1, 2T_0+ 2(n+1)T_1[~~~~P_{r, 2} \left( t \right) = 1+ \gamma + (1-\gamma^2)\sum\limits_{k = 1}^{n}(-\gamma)^{2k-1}.$

(6.20)

By induction we get the general formula for $P_{r, 2}(t)$ when the incoming wave is modelled by the Heaviside function $H$:

$\forall t \in \mathbb R_+^{*} ~~~~ P_{r, 2}(t) = H(t)+\gamma H(t-2T_0)+(1-\gamma^2) \sum\limits_{k = 1}^{\infty}\left (-\gamma \right) ^{2k-1}H\left(t-\left(2T_0+2kT_1\right) \right ).$

(6.21)

Knowing the response of $S_2$ for an incoming wave modelled by the Heaviside function, one can know the response of $S_2$ for any continuous function as explained in section 2.2. From this analytical method we are able to control and validate the results returned by the algorithm for n = 2 (Figure 4).

---

6.2. Analysis on the speed of convergence for two discontinuities ($n=2$) as a function of the reflection coefficient $\gamma$

We know from equation (6.5) the analytical solution of the reflected pressure for $n = 2$, that can be used, for example, to model an isolated stenosis. The first term $H(t)$ represents the input wave that is modelled by the Heaviside side function for the single wavefront analysis developed above. The second term $\gamma H(t-2T_0)$ comes from the reflection of the input wave before entering in the stenosis. The third and last term $(1-\gamma^2) \sum_{k = 1}^{\infty}\left (-\gamma \right) ^{2k-1}H\left(t-\left(2T_0+2kT_1\right) \right )$ describes the multiple reflections and transmissions occurring within the stenosis. In order to study the asymptotic behavior of $P_{r, 2}$ and its speed of convergence, we will study the sequence defined by the last term:

$\forall N \in \mathbb N^* ~~~~u_N = (1-\gamma^2) \sum\limits_{k = 1}^{N}\left (-\gamma \right) ^{2k-1}.$

(6.22)

The sequence is a geometric series with a common ration of $\gamma$. As we saw in the previous part, $\gamma$ represents the reflection coefficient between $Z_0$ and $Z_1$, thus, $\gamma \in \left [0, 1 \right[$ (the case in which $\gamma = 1$ being the trivial case when the stenosis is fully blocked). The fact that $0 \leq\gamma<1$ indicates that the series converges, as expected. Moreover, as $\gamma \ne 1$, we can rewrite this geometric series as:

$\forall N \in \mathbb N^* ~~~~u_N =-\gamma \left (1- \gamma ^2 \right ) \frac{1-\left ( \gamma^2 \right ) ^{N}}{1-\gamma^2} =- \gamma \left (1 - \gamma ^{2N} \right ).$

(6.23)

In order to study the speed of convergence we consider the following sequence :

$\forall N \in \mathbb N^*~~~~ \Delta u_N = u_N - u_{N-1} = \frac{ \left (\gamma ^2 - 1 \right ) }{ \gamma}\gamma ^{2N}.$

(6.24)

For $\alpha = \frac{ \left (\gamma^2 - 1 \right )}{\gamma}$ we have that :

$\forall N \in \mathbb N^*~~~~ \Delta u_N = \alpha \cdot \gamma ^{2N} = \alpha \cdot e^{2N ln\left (\gamma \right )} = \alpha \cdot e^{- \frac{N}{\tau}}$

(6.25)

where,

$\tau = - \frac{1}{ln \left ( \gamma ^2 \right )}$

(6.26)

is the characteristic number of iterations for convergence that characterizes the speed of convergence. This relation between $\tau$ and $\gamma$ gives us the speed of convergence as a function of $\gamma$ for two discontinuities (n = 2).

---

6.3. Numerical sensitivity analysis of the control parameters $m$

The effect of parameter $m$ on the computational solution is clearly visible. As $m$ increases, the computational solution converges towards the analytical solution as expected. On the following Figures, we plotted the same results obtained in Section 4.2, 4.3 and 4.3 but for different values of $m$. We see that the algorithm converges but a low discretization using Heaviside functions ($m<1000$) leads to a noisy computational solution. For that matter, we chose in our previous simulations of the results section $m = 10000$.

---

6.4. Numerical sensitivity analysis of the control parameter $\epsilon$

---

6.4.1. Numerical sensitivity analysis of the control parameter $\epsilon$ for two discontinuities $n=2$

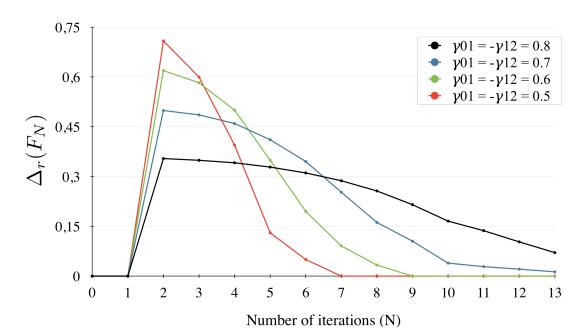
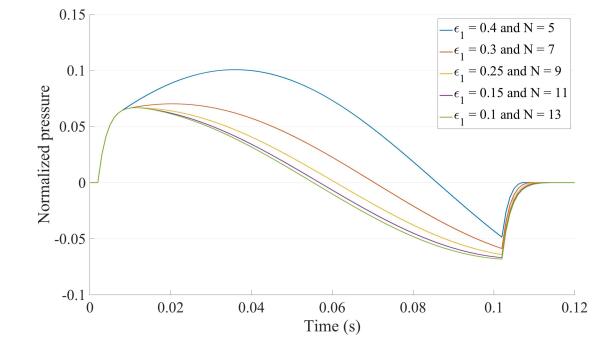
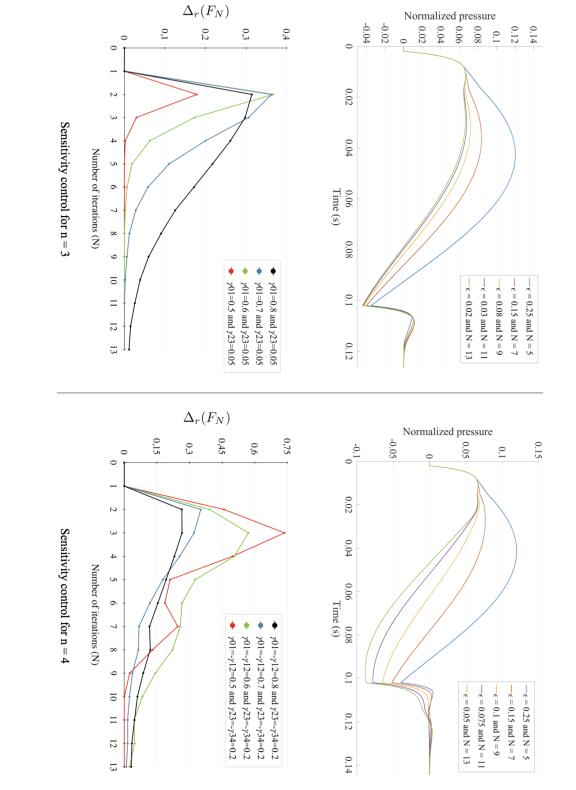
In the case with two discontinuities ($n = 2$), the dynamics of the algorithm convergence can be studied by looking at the evolution of the relative difference between $F_{2, N}\left[f_m\right]$ and $F_{2, N-1}\left[f_m\right]$, which was previously introduced and denoted $\Delta_r(F_N)$, as a function of the number of iterations $N$. This evolution is plotted on Figure 11 on which we can see that the algorithm converges after a certain amount of iterations.We also see that the sufficient number of iterations for having $\Delta_r(F_N) < \epsilon$ for a given $\epsilon$, depends on the value of the reflection coefficient $\gamma_{01}$. As the reflection coefficient increases, the time for the algorithm to converge is more and more important. Therefore, for the simulations in the results section, we chose the optimal number of iterations for which $\Delta_r(F_N) < \epsilon$ in the case where $\gamma = 0.8$. Indeed, as $\gamma = 0.8$ is the highest value of the reflection coefficient that we study, its leads to the longest time of convergence and therefore the highest number of iterations. As we chose a control parameter $\epsilon = 0.1$, the simulations were run with the optimal number of iterations which is $N = 12$ in order to optimize computational time and still have a relevant computational solution close to the analytical one. On Figure 12 is plotted the computational solution for different value of the control parameter $\epsilon$. We see that as $\epsilon \rightarrow 0$, the computational solution uniformly converges to the analytical solution, represented in dashed lines in Figure 12, as expected.

---

6.4.2. Numerical sensitivity analysis of the control parameter $\epsilon$ for more than two discontinuities $n>2$

Similarly, numerical sensitivity studies were done for $n = 3$ and $n = 4$ and results are gathered in Figure 13.

---