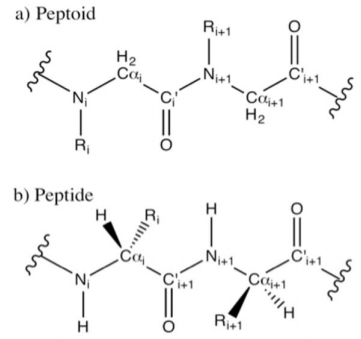
Peptoids, or poly-N-substituted glycines, are synthetic polymers composed of a protein backbone with side chains attached to the nitrogen atoms rather than the α-carbons. Peptoids are biomimetic and protease resistant and have been explored for a variety of applications including pharmaceuticals and coatings. They are also foldamer-type materials that can adopt diverse structures based on the sequences of their side chains. Design of new peptoid sequences may lead to the creation of many interesting materials. Given the large number of possible peptoid side chains, computer models predicting peptoid structure-side chain relationships are desirable. In this paper, we provide a survey of computational efforts to understand and predict peptoid structures. We describe simulations at several levels of theory, along with their assumptions and results. We also discuss some challenges for future peptoid computational research.
1.
Introduction
Several mathematical models in the field of viral dynamics simply regard the host of an infection as a well-mixed compartment [1,2,3] and aim to theoretically determine the threshold, from an overall perspective for determining whether an infection is extinct or persistent. Under the assumption of spatial homogeneity, various functions of different tissues and organs may be overlooked. Given the complexity of the human body, it is essential to regard the host body as composed of multiple compartments and to explore the effect of connection between compartments on the infection [4,5,6].
Viral propagation in human immunodeficiency virus (HIV) infection occurs mainly in lymphoid tissues [5,7], which are composed of primary and secondary lymphoid organs. The primary lymphoid organs include the thymus and bone marrow, which are where lymphocytes are generated; the lymph nodes and the spleen constitute the secondary lymphoid organs, which maintain mature naive lymphocytes and initiate adaptive immune response [8]. Between these tissues, connections are constructed through afferent or efferent lymphatics (or both) [9,10,11], by which cluster or differentiation 4 (CD4)-positive or CD8-positive T lymphocytes and other cells can migrate to execute their functions. This gives rise to the need to explore how the connection of various tissues influences the viral dynamics and curative effect of treatment.
To analyze the spatiotemporal patterns of viral progression, the authors in [12] proposed a reaction-diffusion model by fitting the data to a radially symmetric propagation and numerically identified the initial propagation of the infection front followed by a state of stagnation due to an antiviral response. Infected CD4 T cells can actively migrate over different lymph nodes [13]. Accordingly, another scenario for studying the spatial heterogeneity of viral dynamics is using multi-compartment models to describe the occurrence of infection in various organs. In [14], a heterogeneous environment with various parameters for several grids was constructed, wherein the virus randomly spreading between the grids was modeled as local diffusion. The main result showed that the local dispersion of a virus can reduce the amplitude of viral oscillation. In a recent study [5], the spread of HIV infection throughout the lymphoid tissue was considered from a perspective of network structure. That study numerically determined that HIV infection may persist even under drug administration because a portion of lymphoid tissues fails to receive a sufficient amount of the dose. These studies clarify that considering the spatial heterogeneity is essential in studying viral dynamics.
Most within-host virus models assume transmission solely through virus-to-cell infection, although it is now appreciated that there are multiple infection routes resulting in heterogenous kinetics. The cell-to-cell transmission process of HIV infection has been explored in a compartment such as the lymph nodes and the brain, because CD4+ T lymphocytes are densely agammaegated and frequently interact in lymphoid tissues, and the virus can disseminate through direct transmission from infected cells to uninfected cells through the HIV virological synapse [15,16]. Among the studies that have considered the delayed intracellular reaction but without distinction on infection age, HIV infection was explored in [1] by applying ordinary and delayed differential models, and sustained oscillations of infection were revealed for certain culture parameters. In [17], the infection-age-dependent infectivity of individuals was considered and the dynamics of HIV transmission were studied in a population group. The age-dependent production rate of viral particles and death rate of productively infected cells were considered in [18], in which an in vivo age-structured model of HIV infection was constructed. In order to explore distinct intracellular and extracellular infection kinetics, it is necessary to extend previous virus models by incorporating both age-since-infection and a multi-compartment environment.
Global convergence in viral dynamics models is crucial for predicting the evolution of viral infection, and age-structure of infected cells tends to complicate matters. Our single-compartment model considered in this paper is related to that in [19], wherein a susceptible-infective (SI) epidemic model was incorporated with infection-age and an incidence function derived from the law of mass action. In that study, the system was addressed using an integrated semigroup to determine the persistence of disease; the results demonstrated global convergence to either disease-free or endemic equilibrium through the application of Lyapunov functionals. Notably, the probability of disease transmission was found to depend on the age of infection [19]. Another difficulty in the field arises because of the multigroup structure of the models. In the recent study [20], the authors investigated a multigroup (susceptible-infective-recovered) SIR model with age structure and elaborated on the convergence dynamics when the morality and removal rate were age-independent; because of the constant total host population, the model involved a constant boundary condition. Furthermore, in [21], an aged model in a network environment was considered, and both the age-dependent transmission rate and degree of the network connectivity were found to affect the spread of disease; on the basis of the constant total population, the authors demonstrated that global convergence to the endemic equilibrium occurs when it exists. In [22], a two-group model was adopted to investigate the globally asymptotic behavior of a SI epidemic model incorporating the age of infection. The Lyapunov functional employed in that study was skillfully constructed for the two-group structure. The age-dependent infectivity of infected cells renders it impossible to rewrite the viral infection model as the classic (without aged-structure) SIS or SIR epidemiological models or variant predator-prey models, and it increases the difficulty of exploring the global convergence dynamics, especially in deriving convergence to the endemic equilibrium state.
In this paper, we construct and analyze a virus model consisting of multiple compartments with distinct cell infection-age structured infectivity kernels describing infection spread through various organs. In section 2, we detail the model formulation, along with establishing boundedness and compactness of the generated semiflow. In sections 3 and 4, we derive the basic reproduction number, and show that it is a global threshold determining the viral persistence or extinction. Section 5 concerns extending analysis to non-strongly connected networks through a sequence of threshold values controlling the infection pattern in the whole system. Finally in Section 6, we numerically investigate the viral dynamics for different connection topologies, along with examples of distinct cell infectivity kernels based on data for cell-free and cell-to-cell infection modes.
2.
Model formulation and preliminaries
An infected host with n compartments is described by
for k∈N0:={1,2,⋯,n}, with the boundary condition
and the initial condition
where L1+((0,+∞),R) is the nonnegative cone of L1((0,+∞),R). In the kth compartment, at time t, Tk(t) denotes the concentration of healthy cells, and ik(t,a) is that of infected cells with age a since infection. The parameters λk and dk respectively represent the production and death rates of healthy cells, and αk accounts for the rate of both virus-to-cell and cell-to-cell transmission. Here, we neglect the virus compartment due to its fast kinetics. The function pk(a) accounts for the net infectivity of infected cells from both infection routes, variant in the infection age, and δk(a) represents the death rate of infected cells. All these parameters describe the viral environment in the kth compartment. They may be different from compartment to compartment because of individual function. For instance, the infectivity kernel pk(a) may change according to primary transmission mode (cell-to-cell versus viral), or infection induced death rate, δk(a), may be different in distinct compartments based on predominant target cell type (e.g. T-cell in blood vs. macrophage in brain). The parameter mjk, j≠k, denotes the migration rate of the cells from the kth compartment to the jth compartment. Assuming no loss in the process of migration, it satisfies that ∑nj=1mjk=0 and then mkk=−∑nj≠k,j=1mjk. As mentioned in Section 1, the migration may be asymmetric between any two compartments. In addition, there is no isolated compartments to be considered, however this assumption is relaxed later in Section 5.
Here, we assume that the migration matrix M=(mkj)n×n is irreducible and, for k∈N0,
(A1) λk,dk,αk>0;
(A2) δk(⋅)∈C([0,+∞),R+), dk≤δk(a)≤δk,max<∞, for a≥0;
(A3) pk(⋅)∈C([0,+∞),R+), 0<pk(a)≤pk,max<∞, a∈I0, for some finite interval I0⊂[0,+∞), and pk(a)=0 for a∉I0.
Denoting T(t)=(T1(t),⋯,Tn(t))τ and i(t,a)=(i1(t,a),⋯,in(t,a))τ, where (⋅)τ means the transpose of a vector, the system (2.1) is equivalent to the vector form:
with the boundary condition
and the initial condition T(0)=T0>0,i(0,⋅)=i0(⋅)∈L1+((0,+∞),Rn), where Λ=(λ1,⋯,λn)τ, D=diag(d1,⋯,dn), Γ=diag(α1,⋯,αn), diag(T(t))=diag(T1(t),⋯,Tn(t)), ˜D(a)=diag(δ1(a),⋯,δn(a)), P(a)=diag(p1(a),⋯,pn(a)) and
Following the approach proposed in [23], we reformulate (2.4) as a semilinear Cauchy problem. To this end, we first consider the extended state spaces
and equip the space X with the norm
for u=(u1,⋯,un,v1,⋯,vn,w1(⋅),⋯,wn(⋅))τ∈X. Define the linear operator A:Dom(A)⊂X→X, Dom(A)=Rn×{0Rn}×W1,1((0,+∞),Rn), by
where W1,1 is a Sobolev space, and the operator F:X0→X by
By denoting u(t)=(T(t),0Rn,i(t))τ, we regard system (2.4) as the abstract Cauchy problem:
and assert, by [23,Theorems 2 and 3], that there exists a unique solution semiflow Ψ(t):X0+→X0 related to system (2.7).
Next, by employing the boundary condition and the initial condition, we write (2.4) into the Volterra-type equation,
where Q(t)=i(t,0) and satisfies
Denote
First, we show a priority about the matrix Ω(a0,a).
Lemma 2.1. For fixed a0≥0, there exists a constant γ>0 such that
for all k,j∈N0 and a≥a0, where d_=mink∈N0{dk/2}>0.
Proof. Denote ˜d=maxk∈N0{δk,max}+maxk∈N0{−mkk} and I as the n×n identity matrix. Then, for a≥a0, the matrix −∫aa0˜D(s)ds+˜d(a−a0)I+(a−a0)M is nonnegative and
In addition,
where the last inequality holds since the fact that the quasi-positive matrices A=(akj)≤B=(bkj) with 0≤akj=bkj for all k≠j implies exp(A)≤exp(B). Since the matrix −d_I+M is strictly diagonally dominant and each diagonal entry is negative, all its eigenvalues, say μj, j=1,2,⋯,m, m≤n, have negative real parts [24,Theorem 6.1.10]. We write −d_I+M in its Jordan canonical form, J, with −d_I+M=PJP−1, J=diag(J1,⋯,Jm) and each Jj is a standard Jordan block related to the eigenvalue μj. Obviously,
Since the real part of μj is negative,
as a−a0→+∞. Thus, there exists a positive constant γ such that exp((a−a0)(−d_I+M))≤γI for all a≥a0, where I is the matrix with a value of 1 for all entries, and the assertion is true.
Denote
and equip the space Y with the norm
Then the semiflow generated by (2.1) is point dissipative, as demonstrated in the following lemma.
Lemma 2.2. The solution semiflow generated by (2.1) is point dissipative. Explicitly, the subset of phase space
is positively invariant and attracts all nonnegative solutions, where dmin=mink∈N0{dk}.
Proof. It is easy to show that all solutions of (2.1) are nonnegative. Denote the total infected cells by I(t)=∫∞0i(t,a)da and the total cells by N(t)=T(t)+I(t). Integrating the i-equation in (2.4) with respect to a leads to
Obviously,
and then
By a comparison principle, we derive that
Since each solution of (2.1) remains nonnegative, as previously mentioned, the assertion holds true.
Deriving the uniform persistence and global properties of the solution dynamics is essential in studying viral infection and it is necessary to show that the semiflow Φ(t) generated by (2.1) is asymptotically smooth. Denote
By integrating along the characteristic lines and incorporating the boundary condition and the initial condition of the model, we write equation (2.1) in the following equivalent Volterra integral equation,
Few studies have investigated asymptotically smooth semiflows in a system incorporating both the age structure and the migration of a population. Here, we show the property in the semiflow Φ(t) by using Lemma 1 and a result reported in [25,Lemma 3.2.3].
Lemma 2.3. The semiflow Φ(t) generated by (2.10) ((2.1)) is asymptotically smooth.
Proof. It is easy to check that each function ˜Pk(⋅) is bounded, say with the bound ˉPk, and Lipschitz continuous on R+, say with the Lipschitz constant lk (see [26]). Define Φ(t)=Λ1(t)+Λ2(t), where
for x∈Y. From (2.10) and Lemma 2.1,
Define Δ(r,t)=nrγe−d_t. Then Δ(r,t)→0 as t→+∞ and ‖Λ1(t)x‖≤Δ(r,t) for ‖x‖≤r.
Let B⊂Y be a bounded subset such that Φ(t)B⊂B. Choose r0>0 such that ‖x‖≤r0 for all x∈B. Note, from Lemma 2.2, that ∪(T0,i0(⋅))∈B{T(t)} is bounded in Rn and then is precompact in Rn. Hence, in order to show that Λ2(t)B is precompact, it suffices to verify that the set ˜Λ2(t)B is precompact for
From [27], it is sufficient to verify the following conditions:
(ⅰ) limh→0∑k∈N0∫∞0{|ik(t,a)−ik(t,a+h)|}da=0 uniformly for i(t,a)∈˜Λ2(t)B.
(ⅱ) limh→+∞∑k∈N0∫∞h{|ik(t,a)|}da=0 uniformly for i(t,a)∈˜Λ2(t)B.
From (2.11), ∑k∈N0∫∞h{|ik(t,a)|}da=0 for h≥t, and then the criterion (ⅱ) holds for the set ˜Λ2(t)B. To show the criterion (ⅰ), we directly calculate for k∈N0 and h≤t
Note that
and
According to the assumption (A2), there exists a positive constant h0 such that Ωkj(0,a+h)Ωkj(0,a)<2 for |h|<h0 since that Ωkj(0,a) is continuous in a. Hence,
Solve the equation (2.10) to obtain, for j∈N0,
Accordingly, we have that
From (2.15), (2.16) and the Lipschitz constant, lk, of ˜Pk, it holds that
By (2.12)-(2.14) and (2.17), it concludes that the criterion (ⅱ) holds for the set ˜Λ2(t)B, and then ˜Λ2(t)B is compact. From [25,Lemma 3.2.3], the assertion is true.
From Lemma 2.2, the semiflow Φ(t) is point dissipative and then there exists a positively invariant absorbing set under the semiflow Φ(t), and then Φ(t) maps any bounded subset of Y+ to a precompact set in Y+ and is then compact for any t>0. From Lemma 2.3, the semiflow is asymptotically smooth. Combining these properties and the result on the existence of global attractors in [25,Theorem 3.4.6] (or see [28,Theorem 2.6]), the following lemma is implied.
Lemma 2.4. The solution semiflow Φ(t) generated by system (2.1) in Y+ admits a compact global attractor A⊂Y+.
3.
Basic reproduction number
First, we demonstrate the existence of infection-free equilibrium by examining the convergence dynamics of the no-infection model.
Lemma 3.1. ([29,Sec. 2]) Consider the no-infection model
There exists a positive equilibrium (ˉT1,⋯,ˉTn) that is globally asymptotically stable with respect to Rn+.
Hence, the model (2.1) admits an infection-free equilibrium ˉE=(ˉT,0Rn)τ=(ˉT1,⋯,ˉTn,0,⋯,0)τ. The linearization of (2.4) at the equilibrium ˉE is the system
To determine the basic reproduction number of (2.1), we consider the decoupled i-equation in (3.2):
Define the operators ˆA:L+→L+ by
and
Let ˜Φ=A+B and ˜Φ0 be the restriction of ˜Φ in Y0; that is, Dom(˜Φ0)={(0,f)τ:˜Φf∈Y0}. It is easy to see that (0,f)τ∈Dom(˜Φ0) if it holds that f(0)=∫∞0P(a)f(a)da. From the argument in [30,Sec. 6], the basic reproduction number of system (2.1) is
where ρ(⋅) denotes the spectral radius of an operator (also for that of a matrix). In fact, for (−A−1)(x,g)τ=(0,f)τ, it holds that
and then
Note that the operator −BA−1 has the same spectral radius on Y and Rn×{0L}. Hence,
By the result in [30] (Theorems 3.16, 3.17), R0 plays the threshold value to determine local stability of the infection-free equilibrium, as stated in the following theorem.
Theorem 3.1. The infection-free equilibrium ˉE is locally asymptotically stable (unstable) in (2.1) if R0<1 (R0>1).
Now, as a concrete example we consider a two-compartment system, n=2, with δk(⋅)=δ(⋅) for k=1,2. Then Θ=Θ2, where
Through a direct calculation, we derive that
where
Since the matrix Θ2 is nonnegative and irreducible, ρ(Θ2) is real and positive [24]. Denote ρ(Θ2)=eξ for ξ∈R. Then
To explore the effect of the migration rate on the dynamics of (2.1), we choose pk(a)=e−pa, δk(a)=δ, mk=m, k=1,2, for positive p, δ and nonnegative m. Then (3.6) is equivalent to
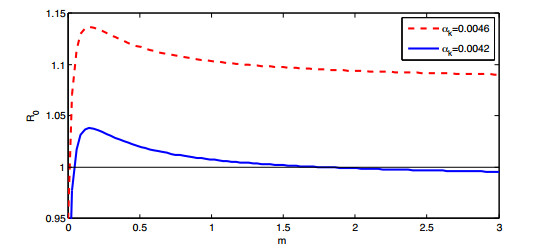
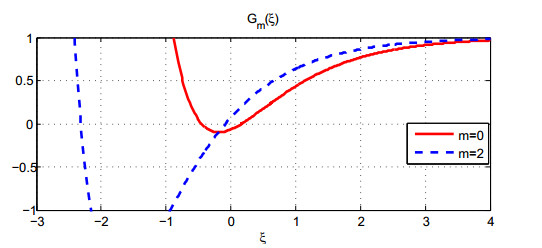
Referring to [31,32,33], we choose λ1=λ2=1, d1=d2=1, α1=0.00065, α2=0.00035, p=0.15, δ=0.4 and adjust m to determine the root of the function Gm. Figure 1 shows that (3.7) admits a positive root, which indicates that ρ(Θ2)>1, when m=0, and there is no nonnegative root to (3.7), which indicates that ρ(Θ2)<1, when m=2. Hence, different values of migration rate m may affect the extinction or persistence of virus in (2.1). Explicitly, in this case, strong circulation facilitates clearing the virus. In Section 6, we shall discuss the effect of the migration rate on the viral dynamics in more cases.
4.
Threshold dynamics
4.1. Extinction of virus
When the reproduction number R0<1, we will demonstrate that the virus becomes extinct. First, the following lemma claims that infection can not occur under non-viable initial infection.
Lemma 4.1. Consider the virus equation in an environment with a constant vector of healthy cells, T0,
with i0(⋅)∈L+ and ∫∞0P(a)i0(a)da=0. Then i(t,⋅)=0(⋅) for all t≥0.
Proof. The well know result in [34] of linear age-structured models reveals that
where ˜Q satisfies
The initial condition, with ∫∞0P(a)i0(a)da=0, leads to
Since ˜Q(0)=0, we have that ˜Q(t)=0 for all t≥0, and then i(t,⋅)=0(⋅) for all t≥0.
With both the multi-compartmental structure and infection-age, it is a challenge to demonstrate the global dynamics in (2.1) by constructing a Lyapunov function [20]. However, the following theorem shows that the virus goes to extinction in system (2.1) when the basic reproduction number is less than or equal to unity.
Theorem 4.1. When R0≤1, the infection-free equilibrium ˉE is globally asymptotically stable in (2.1).
Proof. We first show the assertion for the case with R0<1. By the standard comparison theorem, the solution of (2.1) satisfies that
where ˜Tk(t) is the solution to (3.1). From the assumption R0<1, there exists a sufficiently small ε>0 such that ρ(Θε)<1, where
From Lemma 3.1 and (4.2), there is a t1>0 such that Tk(t)≤ˉTk+ε, k∈N0, for t≥t1. Since the matrix Θε is nonnegative and irreducible, ρ(Θε) is a positive eigenvalue which corresponds to a positive eigenvector, say v=(v1,⋯,vn), with vτΘε=ρ(Θε)vτ. Define
We calculate the derivative of W(t) along the solution of (2.4) and derive, for t≥t1,
and the equality holds if and only if ∫∞0P(a)i(t,a)da=0 for t≥t1. We claim that the largest positively invariant subset M0 of {dW(t)dt=0} is {(T,0(⋅))|T∈Rn}. For ˜X(t)=(˜T(t),˜i(t,a))∈M0, a solution of (2.4), there is a ˜t1>0 such that ∫∞0P(a)˜i(t,a)da=0 for t≥˜t1. Denote ˜q0(⋅)=˜i(˜t1,⋅) and consider the time-rescaled solution ˜Y(t)=˜X(t+˜t1), but remain the symbol ˜Y(t)=(˜T(t),˜i(t,a)). Then
where ˆi(t,a) satisfies (4.1) with T0=ˉT+εI and ˆi0(⋅)=˜q0(⋅). Note that ∫∞0P(a)˜q0(⋅)da=0. From Lemma 4.1, ˆi(t,⋅)=0(⋅) for all t≥0. From (4.3), M0 is in fact the set{(T,0(⋅))|T∈Rn}. In addition, by using the theory of asymptotically autonomous systems [35,Theorem 2.3] and [36], we show that ˉE is globally asymptotically stable in system (2.1), when R0<1.
When R0=1, we show it by contradiction. Suppose there is a k0∈N0 such that lim supt→+∞∫∞0ik0(t,a)da>0, then by Lemma 4.1 we have
From T-equation in (2.1),
We claim that lim supt→+∞Tk0<ˉTk0. Denoting ˜P(t)=diag(˜P1(t),⋯,˜Pn(t)), we rewrite the T-equation in system (2.1) into the vector form
From the variation of constant formula, the solution to (4.4) satisfies
From Lemma 3.1, we have limt→+∞(e−t(D−M)T(0)+∫t0e−(t−s)(D−M)Λds)=ˉT. We next estimate the third term in (4.5). Since the assumption ϵ0>0, there exist sequences of positive numbers {t(k0)l} and {τl} with liml→∞t(k0)l=+∞ such that ˜Pk0(t)≥ϵ02 for t∈[t(k0)l−τl,t(k0)l+τl].
We claim that ˜P′k0(t) is a bounded function. From the assumption (A3), it holds true whenever ∫∞0∂ik0(t,a)∂tda is a bounded function of t. In fact, (2.1) and (2.2) imply that
It shows that ∫∞0∂ik0(t,a)∂tda is a bounded function of t due to the assumptions (A2) and (A3) and Lemma 2.2. Hence ˜P′k0(t) is a bounded function and then the sequence {τl} can be chosen such that liml→∞τl>0. It is easy to show that T(t) has a positive lower bound. In addition, since the matrix e−(D−M) is positive and irreducible, the k0-th component of ∫t0e−(t−s)(D−M)Γ˜P(s)T(s)ds has a positive lower bound. Therefore, there exist ε1>0 and t1>0 such that Tk0(t)<ˉTk0−ε1 for t>t1.
From the monotonicity of the spectral of nonnegative matrices ([37,Corollary (1.5) in Ch2]), and the assumption R0=1, we have ρ(Θε1)<1, where
In addition, since the spectral of a matrix is continuous on each component, there exists a sufficiently small ε2>0 such that ρ(Θε1,ε2)<1, where
By using the method in case of R0<1, we can show that ik(t,⋅)→0(⋅) as t→+∞ for each k∈N0. This contradicts to the assumption on ik0(t,⋅). Therefore, we conclude that ˉE is globally asymptotically stable in system (2.1), when R0=1.
4.2. Uniform persistence
In this subsection, we study the uniform persistence for the model (2.4) when R0>1, by using the persistence theory developed in [38] (or see [19]). Recall that the semiflow Ψ(t) is generated by the Cauchy problem (2.7) which is equivalent to (2.4). Define
Lemma 4.2. The subsets U and ∂U are positively invariant under the semiflow Ψ(t). Furthermore, limt→+∞Ψ(t)u=ˉu=(ˉT,0Rn,0L)τ for each u∈∂U.
Proof. First, we show the positive invariance of the set U. Let u0=(T0,0,i0(⋅))τ∈U. Denote
and define
Since u0∈U, Υ(0)>0. Through a direct calculation, we have
where δmax=max1≤k≤n{δk,max}. Hence, we obtain that
for t≥0, and then Ψ(t)U⊂U.
Next, in order to show the positive invariance of the set ∂U, we consider u0∈∂U. It is clear from Lemma 2.2 that T(t)≤ˆT for some ˆT>0. Then the comparison theorem implies that
where ˆi(t,a) is the solution of the following system
Since ∫∞0i0(a)da=0 and the assumption (A3), it holds that ∫∞0P(a)ˆi(0,a)da=0. From Lemma 4.1, we obtain that ˆi(t,a)=0(⋅) for all t≥0. The comparison in (4.6) implies that i(t,a)=0(⋅) for all t≥0 and then ∂U is positively invariant under the semifolw Ψ(t). In addition, from Lemma 3.1, it is clear that for the solution remaining in ∂U we have T(t)→ˉT. Hence, limt→+∞Ψ(t)u=ˉu for each u∈∂U.
Next, we demonstrate uniform persistence of system (2.7).
Theorem 4.2. When R0>1, the semiflow Ψ(t) generated by (2.7) is uniformly persistent with respect to (U,∂U); that is, there exists a constant ς>0 such that for each u∈U,
where d(⋅,⋅) is the distance associated to the norm in (2.6). Furthermore, there exists a compact subset A0⊂U which is a global attractor for {Ψ(t)}t≥0 in U.
Proof. In the following, we will prove that Ws({ˉu})∩U=∅,whereWs({ˉu})={u∈X0+|limt→+∞Ψ(t)u=ˉu}. Recall from Lemma 4.2 that the infection-free equilibrium ˉu is GAS in ∂U. It is sufficient to show that there exists σ>0 satisfying for each u∈{v∈U|‖v−ˉu‖≤σ} there exists ˜t0≥0 such that ‖Ψ(˜t0)u−ˉu‖>σ. Suppose by contradiction that for each integer m≥0 there is a um∈{v∈U|‖v−ˉu‖≤1m+1} such that ‖Ψ(t)um−ˉu‖≤1m+1 for t≥0. Denote Ψ(t)um=(Tm(t),0Rn,im(t,a))τ=(Tm1(t),⋯,Tmn(t),0Rn,im1(t,a),⋯,imn(t))τ then |Tmj(t)−ˉTj|≤1m+1,j∈N0, for all t≥0. Consider
with Tm0=(Tm10,⋯,Tmn0)τ≥0, im0(⋅)=(im10(⋅),⋯,imn0(⋅))τ≥0(⋅) and ∑k∈N0∫∞0imk0(a)da>0. From the comparison theorem,
for t≥0, where ˜im(t,⋅) is the solution of the following system
or equivalently
for t≥0, x(0)∈¯ˆD(ˆA), the closure of ˆD(ˆA)={0Rn}×(W1,1)n, where x(t)=(0Rn,˜im(t,⋅))τ and the operators ˆA,ˆLm are defined as
Since R0>1, there is a m0>0 large enough such that, for m≥m0,
The dominant eigenvalue λ∗m of system (4.9) satisfies the characteristic equation Δm(λ)=0, where
Note that Rm0>1 implies the existence of λ∗m>0 such that Δm(λ∗m)=0. Denote the solution semiflow of (4.9) by {ˆΨm(t)}t≥0 and let ˆΠm(ˆx):ˆX→ˆX, ˆX:=Rn×L, be the projection of given ˆx∈ˆX on the eigenspace associated to the dominant eigenvalue λ∗m. By the result in [19,Section 2.3], we see an explicit expression for the following projection
for ˆx0=(0Rn,im0(⋅),)τ and
By using (4.11) and directly calculating (λI−ˆA)−1, (I−ˆLm(λI−ˆA)−1)−1 respectively, we obtain that
if and only if
and
Since Δm(λ∗m)=0, we have
By using Reλ∗m>0, (4.10), (4.11) and (4.12), it deduces that limt→+∞‖˜im(t)‖=+∞. The comparison (4.8) implies limt→+∞‖vm(t)‖=+∞, which is a contradiction to the boundedness of the solution. Hence, Ws({ˉu})∩U=∅. Accordingly, we derive from [38,Theorem 4.1,Theorem 4.2] that the semiflow {Ψ(t)}t≥0 is uniform persistence with respect to (U,∂U). In addition, the result in [28,Theorem 3.7] implies that there exists a compact global attractor A0⊂U for {Ψ(t)}t≥0 in U.
Remark 1. According to Theorem 4.2, the uniform persistence of (2.4) indicates that there exists a constant ζ>0 such that for each solution in (2.4) satisfies
We further note that there exists a constant ζ0>0 such that
for each k∈N0. Otherwise, there is a k0∈N0 such that limt→∞∫∞0ik0(t,a)da=0, which contradicts to the ik0-equation in (2.1) and the fact (4.13).
5.
Non-strongly connected within-host structure
The dichotomy of viral persistence or extinction within a host is based on the assumption of irreducible migration matrix. However, the migration matrix may be reducible due to functions of afferent or efferent lymphatics. In this case, the theory of direct graphs developed in [39] provides a method to describe directional connections between all within-host compartments (see also [40]). By building n vertices and assigning a directed edge from vertex j to vertex k when a flow from the j-th compartment to k-th compartment is available, we can associate the matrix M with a direct graph. Then the graph of M reflects the connection structure within a host, and the matrix M is irreducible if and only if for any pair of two compartments there is a path from one compartment to the other. In such a case, we say that the viral environment assumes a strongly connected within-host structure, whereas the case with a reducible matrix M is referred to non-strongly connected structure.
When the within-host structure in non-strongly connected, that is, the matrix M is reducible, one can use a permutation operator to reach a triangular block form, still denoted by matrix M,
where p≤n and each Mll, 1≤l≤p, is a rl×rl irreducible square matrix. We denote P0={1,2,⋯,p} and write N0=∪l∈P0N(l)0, where N(l)0={Σl−1s=1rs+1,Σl−1s=1rs+2,⋯,Σls=1rs}. By this way, we divide the whole within-host environment into p parts of which each part consists of strongly connected compartments. We indicate, by block-l, the part consisting of k-th compartment for k∈N(l)0. Explicitly, given l∈P0 with rl≥2, the compartments in block-l are strongly connected, whereas rl=1 means that the block-l consists of a single compartment. For later convenience, we denote N(l)0={ξl,⋯,ξl}, that is, ξl=Σl−1s=1rs+1 and ξl=Σls=1rs. Notably, under the form of (5.1), there is a connection from the block-l1 into the block-l2 only for 1≤l1<l2≤p. Denote P_(l)0={˜l|1≤˜l<l,Ml˜l≠0} for 1<l≤p and ˉP(l)0={˜l|l<˜l≤p,M˜ll≠0} for 1≤l<p. P_(l)0 is the set of indexes of blocks where each one is connected to block-l through a directional pathway, whereas ˉP(l)0 is that of blocks where each one is connected by a directional pathway from block-l.
Now, for l∈P0, we say that the block-l is infection free if
for all solutions, and is infected if the infected population is uniformly persistent, that is, from Remark 1, there exists a constant ζ0>0 such that
We set the order of the blocks according to (5.1) and employ mathematical induction to analyze the virus dynamics in (2.1). We first introductorily define a sequence of basic reproduction numbers. In the system with only block-1, the basic reproduction number can be formulated as in (3.5) via replacing the matrix M by M11. However, when there are more than one block, it is necessary to reformulate the threshold value to determine the viral dynamics. Explicitly, for k∈N(1)0, we have
Denote X(t)=(T1(t),⋯,Tξ1(t))τ, y(t,a)=(i1(t,a),⋯,iξ1(t,a))τ, L(1)=(λ1,⋯,λξ1)τ, D(1)=diag(d1,⋯,dξ1), G(1)=diag(α1,⋯,αξ1), diag(X(t))=diag(T1(t),⋯,Tξ1(t)), ˜D(1)(a)=diag(δ1(a),⋯,δξ1(a)), P(1)(a)=diag(p1(a),⋯,pξ1(a)) and
with
We rewrite (5.2) into
with
In order to determine the threshold value to conclude viral persistence or extinction in (5.2), we denote
and ˉT(1) satisfies L(1)−D(1)ˉT(1)+M(1)ˉT(1)=0. Note that R(1)0 is not the basic reproductive number for isolated block-1 except that ˉP(1)0=∅.
Next, we start the process to determine the viral dynamics from the first block and the following is a straightforward result from Theorem 4.1 and Theorem 4.2.
Proposition 5.1. The first block is infection free when R(1)0≤1, whereas it is infected when R(1)0>1.
For given l∈P0, we suppose that from block-1 to block-(l−1) are all determined to be infected or infection free. In an infection free block, it satisfies limt→Tk(t)=ˉTk for constants ˉTk>0 derived as in Lemma 3.1 and the virus goes extinction. Next, we check on the connection from these l−1 blocks to the block-l. Explicitly, we say that the block-l is susceptible from an infected block if there exists ˜l∈{1,2,⋯,l−1} such that the block-˜l is infected and Ml˜l≠0.
Here, we denote by an index to determine whether the block-l is susceptible from an infected block. First, we denote
Then there is a (no) connection from the block-˜l to the block-l when S(Ml˜l)=1 (S(Ml˜l)=0). We further denote
Then the block-l is susceptible from an infected ˜l block with ˜l<l if χ(l)=1, whereas it is not susceptible from any infected block-˜l with ˜l<l if χ(l)=0.
Suppose that the block-l is not susceptible from any infected block-˜l with ˜l<l, i.e. χ(l)=0. Then the subsystem with k∈N(l)0 has the limit system
Denote X(t)=(Tξl(t),⋯,Tξl(t))τ, y(t,a)=(iξl(t,a),⋯,iξl(t,a))τ, L(l)=(ˉλξl,⋯,ˉλξl)τ,
D(l)=diag(dξl,⋯,dξl), G(l)=diag(αξl,⋯,αξl), diag(X(t))=diag(Tξl(t),⋯,Tξl(t)), ˜D(l)(a)=diag(δξl(a),⋯,δξl(a)), P(l)(a)=diag(pξl(a),⋯,pξl(a)) and
with
We rewrite (5.6) into
with
In order to determine the threshold value to conclude viral persistence or extinction in (5.8), we denote
and ˉT(l) satisfies L(l)−D(l)ˉT(l)+M(l)ˉT(l)=0. Note that R(l)0 is not the basic reproductive number for isolated block-l except that P_(l)0∪ˉP(l)0=∅.
Accordingly, the virus dynamics in the block-l can be determined as the following.
Theorem 5.2. For 1<l≤p, if χ(l)=1, that is, the block-l is susceptible from an infected block-˜l with ˜l<l, then the block-l is infected; if χ(l)=0, that is, the block-l is not susceptible from any infected block-˜l with ˜l<l, then the block-l is infection free when R(l)0≤1, whereas it is infected when R(l)0>1.
Proof. Consider the block-l with X(l)=1. It holds that, for k∈N(l)0,
Also note that there exists t0 and ˇTk such that Tk(t)≥ˇTk for all k∈N(l)0 for t≥t0. Hence, we consider an auxiliary system
with ˜ik(t,0)=αkˇTk∫∞0pk(a)˜ik(t,a)da and ˜ik(0,a)=ik0(a). By a comparison theory, it reveals that ik(t,a)≥˜ik(t,a) for a≥0 and t≥t0. Denote ˜Ik(t)=∫∞0˜ik(t,a)da for k∈N(l)0, then it satisfies that
where ˜ζk:=∑j∈∪l−1˜l=1N(˜l)0mkjζ(˜l)0 and ζ(˜l)0 is the lower bound in (4.14). Note that the assumption X(l)=1 implies ˜ζk>0. We further consider the auxiliary system
Since the matrix Mll is irreducible, there exists a positive equilibrium which is globally asymptotically stable as in Lemma 3.1. Thus we reveal that
for some positive constants ˇζk. In addition, since ik(t,a)≥˜ik(t,a) for a≥0 and t≥t0, we see that ∫∞0ik(t,a)da≥∫∞0˜ik(t,a)da and then
which concludes that the virus population uniformly persists in block-l.
Next, we suppose that the block-l is not susceptible from any infected block-˜l with ˜l<l, that is X(l)=0. Then in the block-l we obtain a limit system as in (5.4) for k∈N(l)0. Therefore, the value of R(l)0 will determine the viral dynamics and it completes the proof.
Remark 2. Note that, for k∈N(l)0, the value of ˉλk in (5.7) may depend on the connection from block-˜l with ˜l<l. From Theorem 5.2, we see that even if the block-l is not susceptible from any infected block-˜l with ˜l<l, the involved viral dynamics may be affected by the connection from an infection free block.
6.
Effects of connection structure and distinct compartments
Considering each compartment with or without afferent and efferent lymphatics, there are several different connection structures to build the whole system. In this section, we investigate the viral extinction and persistence in the model (2.1) in cases of strongly and non-strongly connected structures, along with compartments containing distinct infection characteristics.
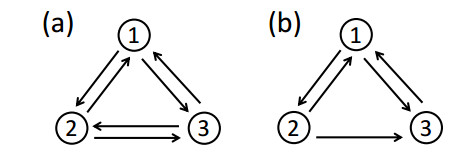
6.1. A strongly connected circular chain
Deep lymph nodes of the head and neck are arranged in a vertical chain along the internal jugular vein and a circular chain consisting of occipital nodes, submental nodes, submandibular nodes, buccal or facial nodes and parotid nodes [41]. Hence, it is necessary to consider the group as a circular chain and to study the influence of removing one connection between lymphoid tissues on the viral infection. In this subsection, we consider three-compartment models with two types of connection matrices; one with a complete connection and the other without the path from compartment 3 to compartment 2, see Figure 2. To explore the effect of the connection topology on the viral infection, we assume identical compartments, λk=λ, dk=d, αk=α, pk(⋅)=p(⋅), and δk(⋅)=δ(⋅), k=1,2,3, and an identical migration rate, mkj=m for k≠j. In the case with the complete connection, it yields that
A direct calculation gives
where ϕ(a)=exp(−∫a0δ(s)ds). Denoting Q1(m,a)=13+23e−3ma and Q2(m,a)=13−13e−3ma, we derive that
Note that R0>1 if and only if there exists a positive constant ξ such that det(I−e−ξΘ)=0, which is equivalent to that the determinant
where
Equation (6.1) holds if and only if
Hence, there exists a positive ξ satisfying det(I−e−ξΘ)=0 if and only if
that is
Thus, the migration of cells between three nodes has no influence on the viral dynamics.
However, in the case without the path from compartment 3 to compartment 2,
where the infection-free equilibrium (ˉT1,0,ˉT2,0,ˉT3,0) is obtained as in Lemma 3.1. A direct calculation reveals that
and then
where
In this circular chain, we choose parameters d=0.09, λ=10, p(a)=e−0.15a, δ=0.4 [42] and change the value of α to see possible effect of migration rate, m, on the viral persistence. When α=0.0046, there is a m∗>0 such that R0<1 for 0≤m<m∗ and R0>1 for m>m∗. Hence sufficiently slow migration of cells will drives the virus to extinction, whereas faster migration of cells will lead to viral persistence, which is different from the non-influence of migration in the completely connected circular chain. Moreover, when α=0.0042, there exist positive constants m∗∗<m∗∗∗ such that R0<1 for 0≤m<m∗∗ or m>m∗∗∗ and R0>1 for m∗∗<m<m∗∗∗. It means that the influence of migration on the viral dynamics is complicated, from eradicating virus in the whole system with sufficiently small migration rate to initiating viral infection by medium value of migration rate, and eradicating virus again with sufficiently large migration rate.
6.2. Two non-strongly connected blocks
Consider a host consisting of four compartments as in Figure 4, where the 1st and 2nd compartments (involved in block-1) are strongly connected and also for the 3rd and 4th compartments (involved in block-2). The only connection between the two blocks is from the 2nd compartment to the 3rd compartment, that is, the block-2 may be susceptible from the block-1 when the latter one is infected. Denote m=m32. Hence, R(1)0=ρ(Θ(1)), where
D(1)=diag(d1,d2), G(1)=diag(α1,α2), ˜D(1)(a)=diag(δ1(a),δ2(a)), P(1)(a)=diag(p1(a),p2(a)),
and ˉT(1)=(ˉT(1)1,ˉT(1)2)τ=(D(1)−M(1))−1L(1). By direct calculation, it yields that
The inner integral in Θ(1) is a positive matrix because of the irreducibility of matrix M(1), and then Θ(1) is positive for all m≥0. We see how the value of m affects that of R(1)0 in the following. All proofs in this subsection will be postponed to Appendix.
Proposition 6.1. The value of R(1)0 is decreasing in m.
On the other hand, R(2)0=ρ(Θ(2)), where
D(2)=diag(d3,d4), G(2)=diag(α3,α4), ˜D(2)(a)=diag(δ3(a),δ4(a)), P(2)(a)=diag(p3(a),p4(a)),
and ˉT(2)=(ˉT(2)1,ˉT(2)2)τ=(D(2)−M(2))−1L(2). Accordingly, we can also see how the value of m affects that of R(2)0.
Proposition 6.2. The value of R(2)0 is increasing in m.
Biologically, a unidirectional connection between two blocks benefits the one with exportation in viral eradication but damages the other one with importation.
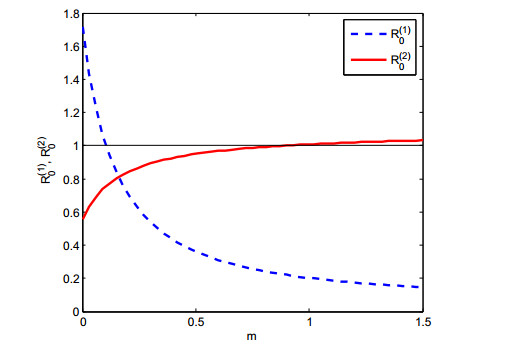
In these two non-strongly connected blocks, we fix the viral environment in each block, including migration rates within the blocks, and change the migration rate between two blocks to explore its influence on the viral dynamics. Explicitly, we choose parameters relevant to block-1 by α1=α2=0.0085, d1=d2=0.09, λ1=λ2=10, m21=m12=1, δ=0.4, p(a)=e−0.15a and those relevant to block-2 by α3=α4=0.00275, d3=d4=0.09, λ3=λ4=10, m43=m34=1, δ=0.4, p(a)=e−0.15a. As depicted in Figure 5, the value of R(1)0 is decreasing in the migration rate, m, whereas the value of R(2)0 is increasing in m. There exist positive constants m∗<m∗∗ with R(1)0(m∗)=1 and R(2)0(m∗∗)=1. Hence, according to Theorem 5.1, we observe the change of viral dynamics from viral persistence in the whole system with small value of m (0≤m<m∗) to virus extinction in the whole system with medium value of m (m∗≤m≤m∗∗), and to virus persistence only in the block-2 when the value of m is sufficiently large (m>m∗∗).
6.3. Distinct gamma distributed infectivity kernels with delay
Recent studies show that for HIV the viral production and cell infection kernels are gamma distributed [43,44] after an intracellular delay for integration of viral genome. The predominant infected cell type or infection mode may determine the shape characteristics of the kernels. In particular, cell-to-cell transmission results in faster infection kinetics [44], and certain tissue compartments may have cells arranged closer together facilitating this infection model [45]. In order to model, compartments with distinct infection kinetics, we consider infected cell death rates δk(a) and infectivity kernels pk(a) of the following piecewise form:
where τk is the intracellular delay, νk is the cell death rate after integration of viral genome, and gk(s) is the gamma-distributed (gk∼ Gamma(κk,θk)) infectivity kernel, for compartment k∈N(l)0. Note that the mean of the gamma distribution gk(κk,θk) is μk=κk/θk, representing the mean time of (secondary) cell infection for an infected cell in the absence of death. In the special case that each compartment has identical delays τk=τ and gamma p.d.f.s, gk=g(κ,θ), with shape parameter κ=n as a positive integer, then the linear chain trick can yield the following equivalent system of delay differential equations:
where Ym(t):=∫∞0θmam−1(m−1)!e−θai(t,a+τ)da,m=1,…n, ˜D=diag(νk), and T(t−τ)∘Yn(t−τ) refers to entry-wise product of the vectors. Note that previous examples fall under this scenario with n=1 and τ=0. Thus for the previous results on how migration rate affects R0 in Figure 3 and Figure 5, we can verify extinction versus persistence by transforming to the ODE to obtain numerical solutions. For the general case of patches with distinct intracellular delays and/or gamma distribution parameters in (6.4), however the system will be infinite-dimensional as our original PDE model (2.1) and we utilize a finite-difference method for example simulations below.
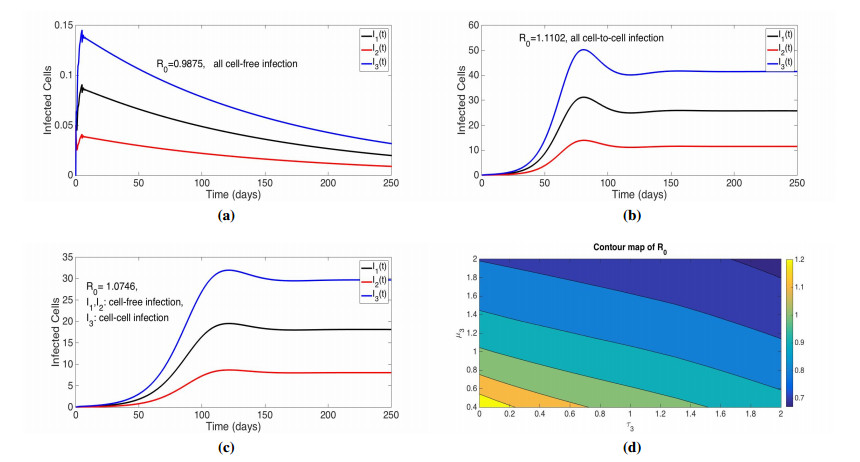
We explore the dynamics in this general setting by considering parameters representative of the study [44], where distinct modes of infection produce different infectivity kernels. Here we consider the case of three compartments connected in a circular chain lacking path from compartment-3 to compartment-2, as in Figure 2(b), with infectivity kernels as (6.4). In Figure 6, we display time-dependent solutions for 3 distinct scenarios; all compartments utilize cell-free infection, all compartments utilize cell-to-cell infection, and finally a mix where the first two compartments display cell-free while compartment-3 utilizes cell-to-cell infection. We also investigate how varying intracellular delay, τ3, and gamma distribution mean, μ3, of compartment-3 affect the overall R0. The fixed parameters utilized are d=0.09, λ=100, ν=0.4, α=0.0011, mij=m=1, and in Figure 6(a)-(c), intracellular delay τ=2/3 and gamma distribution mean μ1,μ2,μ3 either equal to 4/5 (cell-free infection) or 1/2 (cell-to-cell infection) with shape parameter κ fixed at 4. Shorter values of τk and μk result in larger R0, along with faster infection dynamics and larger number of infected cells. Thus, compartments which facilitate cell-to-cell infection may be important for allowing the virus to persist and establish reservoirs, which has been found in studies of HIV under drug treatment [46] or during initial bottleneck of host infection [16].
7.
Conclusion and discussion
The assumption of well-mixed viral environment may ignore diversity of viral dynamics, for example, the existence of viral sanctuary sites and variant viral clearances, and then underestimate the infection within a host. We propose a multi-compartment model incorporating age-since-infection to imitate the migration of cells through afferent and efferent vessels between diverse organs. A threshold, depending on the rate of cell migration, the structure of organic connection and infection kinetics, was found to determine the extinction or persistence of infection. Accordingly, in this paper, we theoretically discussed the effect of the connection structure on the extinction or persistence of infection. Comparing systems with complete connection (with bi-directional connection between any two compartments of the system) and only lacking one connection, we see the influence of the migration rate in latter case. In both strongly connected systems, the influence may non-monotonously depend on the migration rate. As for a non-strongly connected system, we constructed a sequence of threshold values to conclude the infection pattern within a host and revealed that increasing the migration rate from a strongly connected block to another strongly connected block does not always help to eradicate virus in the whole system. Furthermore our inclusion of cell infection-age allows for organ-specific infectivity kinetics based on predominance of cell-free versus cell-to-cell transmission or target cell type. In particular, we demonstrated that individual compartments dominated by cell-to-cell infection may precipitate viral persistence in a strongly connected system with distinct gamma-distributed infectivity kernels representative of experimental studies. These findings complement and extend research on models consisting of a well-mixed compartment.
In this study, the global convergence to the infection-free equilibrium was demonstrated in the case when the basic reproduction number is less than or equal to unity. On the other hand, the global convergence to the unique infection state is a challenging problem. In [20] for studying a multi-group SIR epidemic model with an age structure, an analogous problem was partially solved by using the method of Lyapunov functional and graph theory. However, the convergence dynamics to an infection state in this study remains as an unsolved problem since the model incorporates both the age structure and the migration behavior of cells. Moreover, the connection topology between a group significantly affects the evolution dynamics, and hence attracts researchers to contribute toward either theoretical analysis or application-oriented studies. A portion of a host body can be imitated by a strongly connected structure in which the viral dynamics holds clearance or uniformly persists in the complete part. However, biological evidences show that a functional system within a host, for example, the lymphatic system or the blood circulation system, consists of several such portions which are not strongly connected. Motivated by the study in [40] for infectious diseases via transportation networks, we systematically constructed a sequence of threshold values to find out the infection pattern in the whole system.
We explicitly explored the effect of connection topology or cell infection-age kinetics on the viral dynamics in two basic structures: (a) a strongly connected circular chain with or without a certain directional connection, and (b) a system with one pair of two-compartment blocks connected via a unidirectional pathway. In the first example, either with or without the indicated directional connection, it remains the type of strongly connected. Nevertheless, in the latter case, it may show multiple switches between viral eradication and viral infection in the whole system when increasing the identical migration rate of cells. The second example was devoted to study the connection topology between two strongly-connected blocks. In particular, we explored the effect of the unidirectional migration between two compartments, each is located in a strongly-connected block. An explicit formula shows that increasing the migration rate between two blocks may first change the viral persistence only in the first block to viral eradication in the whole system, and then, for even larger migration rate, trigger the infection in only the flow-in block. Biologically, this unidirectional connection between two blocks benefits the one with exportation in viral eradication but damages the other one with importation. Although these example structures may be limited in number of compartments, they reveal the necessity in distinguishing the connection topology within a host. Finally, we investigated how incorporating intracellular delays and distinct gamma distributed infectivity kernels based on cell-free and cell-to-cell infection data [44] can affect viral dynamics in the strongly connected circular chain. We find that the faster kinetics associated with cell-to-cell infection promote viral persistence and spread, even when only a single compartment in the chain has this transmission mode.
Variable time-dependent drug efficacy is another issue that requires consideration. For drug treatments, such as those administrated through targeted therapy, the treatment focuses on the targeted organ (the target compartment), and the drug efficacy is constant in each compartment. However, under several traditional therapies, drugs may spread throughout the entire body of a host via the circulatory system, in which the drug efficacy would no longer be constant in each compartment. Therefore, it is necessary to formulate the drug circulation among neighboring compartments along afferent and efferent vessels. These considerations will be explored in our next research.
Acknowledgments
C. J. Browne was partially supported by a U.S. National Science Foundation grant (DMS-1815095); C.-Y. Cheng was partially supported by the Ministry of Science and Technology of Taiwan, R.O.C. (MOST 108-2115-M-153-003).
Conflict of interest
All authors declare no conflicts of interest in this paper.
Appendix
To show the dependence of R(1)0 and R(2)0 on the value of m, we begin first from a property of the following exponential matrix S0(β).
Lemma A.1.
Given c,d>0, the value of each component of the matrix
is decreasing in β, for β>0.
Proof. The following matrix can be written into with its diagonal form
where
with
Note that ψ1(β)>0, (ψ1(β))2−(ψ2(β))2=4cd>0, and then ψ1(β)−ψ2(β)>0 and ψ1(β)+ψ2(β)>0. In addition, direct calculations give
Hence, from (7.1), we have
where
By direct calculations and using (7.2), it yields that
Define
It is easy to show that k(x)>0 for all x>0 and h(x, y) < 0 for all x>0. Finally, the fact \psi_1(\beta)>0 implies S'_{ij}(\beta) < 0 for i, j = 1, 2, and it completes the assertion.
Based on this property, we see the dependence of \mathcal{R}_0^{(1)} on m.
Proof of Proposition 6.1:
Proof. Since the spectral of a positive matrix positively depends on each component, it suffices to show that, for a fixed a>0, the value of each component of the matrix
is decreasing in m. For given a>0, if \int^a_0\delta_2(s)da\geq \int^a_0\delta_1(s)da, we rewrite S(m) into
where
Note that \beta(m)>0 and \beta'(m)>0 for all m>0. From Lemma A.1, the value of each component of the matrix \exp(-\int^a_0(\mathcal{\tilde{D}}^{(1)}(s)-\mathcal{M}^{(1)})ds) is decreasing in m. A similar argument can be proceeded by exchanging \delta_1(\cdot) and \delta_2(\cdot) in (7.3) when \int^a_0\delta_1(s)da\geq \int^a_0\delta_2(s)da. In addition, since the spectral of a positive matrix positively depends on each component, the value of \mathcal{R}_0^{(1)} is decreasing in m.
Proof of Proposition 6.2:
Proof. In \Theta^{(2)}, \bar{T}^{(2)} is the only term tdepending on the value of m and, since the inner integral is a positive matrix, the spectral of \Theta^{(2)} depends increasingly on \bar{T}^{(2)}_2. It is easy to see that the spectral bound of the matrix -(\mathcal{D}^{(2)} - \mathcal{M}^{(2)}) is negative and then by the Perron-Frobenious Theorem, the matrix (\mathcal{D}^{(2)} - \mathcal{M}^{(2)})^{-1} is positive. Hence, the value of \bar{T}^{(2)}_2 positively depends on the value of F(m): = m\bar{T}^{(1)}_2(m). Moreover, since
we conclude that the value of \mathcal{R}_0^{(2)} is increasing in m.









 DownLoad:
DownLoad: