Microstructures and anti-phase boundaries in long-range lattice systems

1.   Introduction

In this paper we study the behavior of boundary-value minimum problems related to one-dimensional long-range lattice energies, which in the greatest generality can be stated as the asymptotic behavior as $n\to+\infty$ of solutions $u^n = \{u^n_i\}_i$ of the minimization of functionals of the form

on $n+1$-tuples $u = \{u_i\}_i$ of parameters with $u_i\in\mathbb R$, subjected to boundary conditions $u_0 = 0$ and $u_n = n\ell$. In this generality, the problem is very complex and leads to a variety of different issues with competing short and long-range oscillations and concentration effect, except for the trivial case when all $\psi_k$ are convex, for which the minimizer is essentially unique and coincides with the linear function $u_i = i\ell$, except for boundary effects, which are asymptotically negligible upon some technical assumptions on $\psi_k$. Nevertheless, an averaged description of minimizers is possible in the spirit of $\Gamma$-convergence. To this end, we regard the energies $E_n$ as defined on functions $u\colon[0, 1]\to\mathbb R$, with domain the piecewise-affine functions defined, for some $(n+1)$-tuple $\{u_i\}_i$, as the interpolation of the points $\{(i/n, u_i)\}_{i = 0, \dots, n}$. The $\Gamma$-convergence of such energies can then be studied with respect to the $L^1$-convergence. Upon some growth hypotheses on $\psi_k$ that ensure that limits of sequences $u_n$ with energy of order $n$ belong to some $W^{1, p}(0, 1)$, the $\Gamma$-limit of $\frac1n E_n$ can be written as

for a convex function $\psi_{\rm hom}$ resulting from a nonlinear homogenization process (see ^[5] and ^[2] for the higher-dimensional case).

The $\Gamma$-convergence above only ensures that the (interpolations of the) minimizers of boundary-value problems for $E_n$ converge to the corresponding minimizer, or to one of the minimizers, of the analogous continuum boundary-value problem related to $F$, but brings no further information on their behavior, which may depend on $\ell$. Note that if $\psi_{\rm hom}$ is strictly convex at $\ell$ then the unique minimizer is the linear function $u(x) = \ell x$, while at non-strictly convex points discrete solutions may converge to a particular choice among minimizers.

A particular class of energies for which an analysis of $\psi_{\rm hom}$ leading to a description of the convergence of discrete minimizers has been possible is the one studied in ^[7], where the non-convexity is confined to nearest-neighbour interactions governed by $\psi = \psi_1$, and the long-range potentials are quadratic; that is, $\psi_k(z) = a_k z^2$, with $a_k$ non negative, and the energies can be written as

In that case, the properties of minimizers can be linked to properties of the sequence $a_k$. In particular, in ^[7] the case of double-well $\psi$ is studied, for which a prototype is

in which case it is possible to describe the patterns of the minimizers by tracing whether the value $z_i = u_i- u_{i-1}$ lies in one "well" (i.e., $z_i\le0$) or the other one (i.e., $z_i\ge0$). As such patterns of minimizers are concerned, we recall the following interesting characterization of minimizers of energies (1.3) subjected to Dirichlet boundary conditions $u_0 = 0$ and $u_n = \ell n$ in the case when $a_k = 0$ for all $k\ge 2$ except for one value $k = M$: either

(a) minimizers $u_i$ are such that $z_i = u_i- u_{i-1}$ tend (for $n$ large) to be $M$-periodic with average $\ell$, and take only two values: one, for $m$ indices in the period, in one well and the second one, for $M-m$ indices in the period, in the second well, or

(b) $z_i$ defined as above tends (for $n$ large) to be a mixture of two periodic functions as in (a) with some $\ell'$ and $\ell''$ in the place of $\ell$ and for two consecutive values $m$ and $m+1$ between $0$ and $M$.

This characterization extends a formula known before when only $a_2\neq 0$ (see ^[5]), in which case we have the only three possibilities that either the parameters $z_i$ tends to take a constant value in the first or in the second well, or that we have a $2$-periodic pattern mixing values in both wells.

The appearance of microstructure is a recurring feature of non-convex variational systems. Such microstructures may be driven by a scale-free relaxation phenomenon described by convexification or quasi-convexification of the original energy densities (see, e.g., the books by Buttazzo ^[10] or Dacorogna ^[11]), or present more regular patterns at a specific scale due to competing long-range and short-range effects (as in the seminal paper by S. Müller ^[14]; see also ^[1]). Minimizers of $E_n$ are similar to the latter, with oscillations both driven by short- and long-range microscopic interactions and by mesoscopic non-convexity.

Simple examples of variational problems exhibiting microscopic oscillations are lattice systems defined on "spin functions", i.e., functions taking only a finite number of values, the traditional choice being $-1$ and $1$. If the energies are "frustrated", that is, the system presents interaction potentials that cannot be all separately minimized at the same time by a single function, then minimization may produce periodically modulated phases (see [3, Chapter 7]). Often, the determination of the period and shape of such minimizers is a nontrivial matter as in the case of infinite-range antiferromagnetic systems studied by Giuliani et al. ^[13], and has interesting continuum counterparts (see, e.g., ^[12]).

In the case of double-well problems, the location of the parameter in one or the other well relaxes the strict constraint that the parameter takes two values, that is, the constraint $z\in\{-1, 1\}$ is replaced by a potential $\psi(z)$ where $\psi$ is a strictly positive continuous function minimized in $\{-1, 1\}$. To distinguish between them, we will call the first type of parameters "hard spins" and the second ones "soft spins". For the prototypical double-well potential $\psi$ in Eq (1.4), it is clear that the two "wells" coincide with $z$ negative and $z$ positive. If also long-range interactions are taken into account, minimization for soft spins may produce patterns analogous to those for frustrated hard spins. Furthermore, the "soft" approach allows us to include more easily boundary-value problems as above.

In this paper we carry on a fine analysis of the energies $E_n$ in (1.3) by examining not only minimizers, but also parameters $u_i$ whose energy in Eq (1.3) differs from the minimum by a finite quantity bounded as $n$ tends to $+\infty$. This is done by using a development by $\Gamma$-convergence ([4, Section 1.10] and ^[6]), and it is performed for double-well $\psi$ and $a_k\neq 0$ only for $k = M$, so that the descriptions (a) and (b) above provide the value of minima. The meaningful definition of convergence for functions $u$ depends on whether we are in case (a) or (b) above. For simplicity of illustration, consider that the boundary datum $\ell$ is such that case (a) holds for some $m$. Then, given a sequence $u^n_i$ with bounded energy, the sequence is compact in the following sense: there are a finite number of indices $i^n_j$, which we may suppose to converge after scaling, that is, $i^n_j/n\to x_j$, such that in the intervals in the complement of such indices, each function coincides with an $M$-periodic minimizer $\overline u_i$ as in (a), up to an arbitrary small error. Hence, up to subsequences, each such sequence determines a continuum limit ${\mathbf u}$ whose derivative $\mathbf{u}'$ takes values in the finite set ${\mathbf M}_m$ of $M$-periodic minimizers as in (a). A similar argument holds in case (b), for which we can conclude that the continuum limit ${\mathbf u}$ has derivative with values in ${\mathbf M}_m\cup{\mathbf M}_{m+1}$. Once such a piecewise-affine limit is defined, we will prove that the $\Gamma$-limit has the form

where $S({\mathbf u}')$ denotes the discontinuity set of ${\mathbf u'}$ in $(0, 1)$. This shows that minimization may give rise to microscopic patterns ${\mathbf M}_m$, and microscopic incompatibility may give rise to interfaces between elements of ${\mathbf M}_m$ (antiphase boundaries) and/or interfaces between elements of ${\mathbf M}_m$ and ${\mathbf M}_{m+1}$ (macroscopic interfaces). In order to avoid boundary effects, the analysis will be carried out under some periodicity assumptions.

It is interesting to note that even though the values of the slopes of microscopic minimizers in ${\mathbf M}_m$ depend on the average slope or boundary datum, $\ell$, the set ${\mathbf M}_m$ has a 'universal' form, and its elements are in correspondence with $M$-tuples with $m$ values equal to $1$ and $(m-1)$-values equal to $0$ (a prototypical version of this is in the case $m = 2$; see ^[8]). A final remark is that the presence of $M$-th-neighbor interaction is often compared to that of a singular perturbation with a term containing the $M$-th derivative for continuum double-well problems. However, while in the continuum case the resulting phase-transition energy is essentially independent of $M$ (see ^[9,15]), in the discrete case our result shows an increasing complexity of minimizers as $M$ increases.

2.   Statement of the result

We will fix $M\in\mathbb N$ with $M\ge 2$ and functions $\psi_1, \psi_M\colon\mathbb R\to[0, +\infty)$ satisfying the coerciveness condition

We want to study the overall behavior of functionals with competing nearest-neighbor and M-th-neighbor interactions driven by the potential $\psi_1$ and $\psi_M$, respectively, of the form

defined on discrete functions indexed on $\mathbb Z$. In our assumptions the potential $\psi_1$ will be a double-well energy density which favors oscillations through non-convexity, while $\psi_M$ is a convex potential favoring long-range ordering.

2.1.   Analysis at the bulk scaling

We preliminary analyze a scaled version, whose analysis will suggest a renormalization argument. We use a standard scaling procedure that allows us to use an analytic approach by $\Gamma$-convergence, introducing a reference interval $[0, 1]$ and the small parameter $\varepsilon_n = \frac{1}n$ with $n\in \mathbb N$. The energies above, when we take into account the interaction involved on $n+1$ sites, now parameterized by $\varepsilon_ni$ with $i\in\{0, \ldots, n\}$, take the form

In this notation, $u_i = u(\varepsilon_n i)$. Note that in the last sum we also take into account the values of $u_i$ for $i\in\{n, \ldots, n +M-1 \}$. In the sequel, in order not to have boundary effects, we will define $u_i$ for all values of $i$ using some periodic conditions.

After this parameterization, we can identify such discrete functions with the piecewise-affine interpolation on $[0, 1]$ of the sites $(i \varepsilon_n, u_i)$. We define the space of such functions

and the scaled functionals

if $u \in \mathcal{A}_n(0, 1)$, while $E_{n, M}(u) = + \infty$ if otherwise $u \in L^1(0, 1) \setminus \mathcal{A}_n(0, 1)$. Since

condition (2.1) ensures that functionals $E_{n, M}$ are equicoercive in $W^{1, 1}(0, 1)$, namely, that if $u^n$ is bounded in $L^1(0, 1)$ and $E_{n, M}(u^n)\le C < +\infty$, then, up to subsequences, $u^n$ converges weakly in $W^{1, 1}(0, 1)$ and strongly in $L^1(0, 1)$. The $\Gamma$-limit of $E_{n, M}$ with respect to this convergence is described in the following result, where we also consider periodic conditions. To that end, we fix $\ell\in\mathbb R$ and define

whose discrete counterpart is

Theorem 2.1. The functionals $E_{n, M}$ $\Gamma$-converge, with respect to the $L^1$-topology, to the functional defined on $W^{1, 1}(0, 1)$ by

where $\psi_0$ is given by:

Furthermore, the convergence is compatible with the addition of periodic condition; that is, with fixed $\ell \in\mathbb R$, the functionals defined by

$\Gamma$-converge to

The proof of this result can be found in ^[7] (see also ^[5] for the case $M = 2$).

2.2.   Microscopic analysis

The main point of the analysis at the bulk scaling is the definition of $\psi_0$, which will allow us to renormalize energies (2.2) by subtracting the affine term $r_\ell$ given by the tangent to $\psi^{**}_0$ at $\ell$ and rewriting the sum as

This will be formalized as the computation of a higher-order $\Gamma$-limit starting from $E_{n, M}$. We will consider periodic boundary conditions. We also make the simplifying assumption that $n$ is a multiple of $M$, the general case requiring a more complex notation being stated explicitly in Section 3.2, taking into account possible mismatch at the boundary due to incommensurability. In this case, after noting that $\min E^\ell_M = \psi_0^{**}(\ell)$, and letting $m = m_\ell$ denote the slope of the straight line tangent to $\psi^{**}_0$ at $\ell$, we can consider the energies

where we have used that $\sum_{i = {0}}^{ {n-1}} (u_{i+M}-u_i) = M\ell$ thanks to the $n$-periodicity of $u_i -\ell \varepsilon_n i$.

Until now we have made no assumptions on $\psi_1$ and $\psi_M$. We study a particular case in which $\psi_M$ is a strictly convex function and $\psi_1$ is a double-well potential of the form

where $W_1$ and $W_2$ are two smooth convex functions. Note that this is not a very restrictive hypothesis since in the determination of the $\Gamma$-limit, only the values of $W_1$ and $W_2$ close to the bottom of the wells will be taken into account, so that more general $\psi_1$ of the double-well type can be taken into account. We also make the assumption that $W_1$ and $W_2$ satisfy

for some $c > 0$. This structure provides a useful representation of $\psi_0$. Indeed, we can distinguish two sets $A_1 = \{x\in \mathbb{R} \, |\, \psi_1(x) = W_1(x)\}$ and $A_2 = \{x \in \mathbb{R} \, |\, \psi_1(x) = W_2(x)\}$. Then, we can rewrite the minimum problem in $\psi_0$ as follows:

where the last equality follows from the Jensen inequality. Then, we can define $\overline{\psi}_j(z) = \psi_M(z) + \frac{1}{M}f_j(z)$, where $f_j(z)$ is the value of the inner minimum problem of above. In this way, $\psi_0$ can be represented as follows:

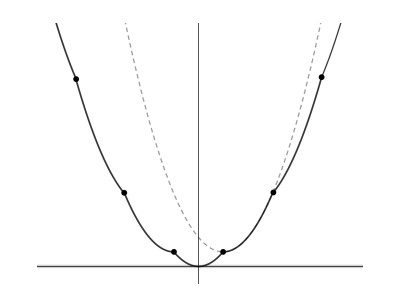
See Figure 1 for a typical form of $\psi_0$.

Remark 2.2. A nontrivial result in ^[7] (see Theorem 4.1 therein) shows that when $\psi_M$ is a parabola, $\psi_0^{**}$ will alternate nondegenerate intervals $[z^l_j, z^r_j]$ in which $\psi_0^{**}(z) = \psi_0(z) = \overline{\psi}_j(z)$ and intervals $[z^r_{j-1}, z^l_j]$, for $j\geq 1$, in which $\psi_0^{**}(z) = r_j(z)$ is a straight line. In this notation, $z^l_0 = -\infty$ and $z^r_M = + \infty$. We will denote $K_j = (z^l_j, z^r_j)$ and $J_j = [z^r_{j-1}, z^l_j]$. We note that the result holds for any strictly convex $\psi_M$ with the same proof. Referring to (2.8), this description gives that if $\ell\in K_j$, then

while if $\ell\in J_j$, then $r_\ell$ is the affine function through $(z^r_{j-1}, \overline{\psi}_{j-1}(z^r_{j-1}))$ and $(z^l_{j}, \overline{\psi}_{j}(z^l_{j}))$.

Note that if we consider

then these values are still positive since $\mathcal{E}^i_n(u) \geq \psi_0^{**}\left(\frac{u_{i+M}-u_i}{M \varepsilon_n}\right) - r_\ell\left(\frac{u_{i+M}-u_i}{M \varepsilon_n}\right)\geq 0$.

Before stating the convergence result, we need some definitions.

Definition 1. We define $\mathbf{M}^\alpha\subset \mathbb{R}^M$ as the set of minimizers for the problem

We will then set

Remark 2.3. $\mathbf{M}^\alpha$ and, consequently also $\mathbf{M}_{\alpha}$, are closed under permutation, that is, if $z = (z_1, \dots, z_M) \in \mathbf{M}^\alpha$, then for any permutation $\sigma$, $(z_{\sigma(1)}, \dots, z_{\sigma(M)})$ also belongs to $\mathbf{M}^\alpha$.

Remark 2.4. When $\psi_M$ is a parabola, we can use the structure of $K_j$ and $J_j$ from Remark 2.2 to simplify the Definition 1 as follows:

Since $\psi_1(z) = \min \{W_1(z), W_2(z)\}$ then, similarly to the way we found (2.9), we can define the minimum problems

such that $\min P = \min\{\min P_j, \; j = 0, \dots, M\}$. By strict convexity, the problem $(P_j)$ admits a unique minimizer $(z_1^j, z_2^j)$, corresponding to $\binom{M}{j}$ minimizers for $(P)$, i.e., the number of possible $M$-tuple such that $j$ entries are $z_1^j$ and $M-j$ are $z_2^j$. Furthermore, for $\alpha \in [z_j^l, z_j^r]$, we have $\min P = \min P_j$, and as a result the set ${\mathbf M}^\alpha$ can be written as

In order to study the limit behavior of $E_{n, M}^1$, we need a notion of convergence of discrete $u^n$ to a vectorial function.

Definition 2. Given $u\in \mathcal{A}_{n, \ell}^\#(0, {1})$, we consider the subintervals

and for $i \in \mathbb{Z}$ we define the set $A_i = \bigcup_{k = 1}^MI_{iM+k}$, which is the union of $M$ such consecutive intervals. For $k\in\{1, \dots, M\}$, we define $u_k$ the $k$-th M-interpolation of $u$ as the piecewise-affine function obtained extending the slope $z^{Mi+k}$, where

to the whole $A_i$, that is, $u_k$ is defined by

Definition 3. We say that a sequence of discrete functions $(u^n)_n$ converges to $\overline{\mathbf{u}} = (\overline{u}_1, \dots, \overline{u}_M)$ in a functional topology (for instance, $L^1(0, 1)$ or $L^{\infty}(0, 1)$) if for each $k$ the $k$-th $M-$interpolation $u_k^n$ converges to $\overline{u}_k$ in that topology.

Theorem 2.5 (Equi-coerciveness of the energies). If a sequence $(u^n)_{n\in \mathbb{N}}$ satisfies $\sup_n E^1_{n, M}(u^n) < + \infty$, then, up to addition of a constant and extraction of a subsequence, the sequence converges uniformly to some $M$-tuple of piecewise-affine functions $\mathbf{\overline{u}} = (\overline{u}_1, \dots, \overline{u}_M)$ with $\overline{\mathbf{u}}'(t)\in \mathbf{M}_{\ell}$ for almost every $t$. Moreover, there exists a finite set $S\subset (0, 1)$ such that $u^n$ converges in $W^{1, \infty}_{\rm loc}((0, 1) \setminus S)$ to $\mathbf{\overline{u}}$ and the jump set $S(\overline{\mathbf{u}}')$ is contained in $S$.

This compactness theorem justifies the use of the convergence in Definition 3 for the $\Gamma$-limit of $E^1_{n, M}$. In order to describe it, we define the following interfacial energy.

Definition 4. Let $\ell \in \mathbb{R}$ and $\mathbf{z} = (z_1, z_2, \dots z_M), \mathbf{z'} = (z'_1, z'_2, \dots z'_M) \in \mathbf{M}_\ell$. The transition energy between $\mathbf{z}$ and $\mathbf{z'}$ is defined by

where $r_\ell$ is the tangent line to $\psi_0^{**}$ at $\ell$ computed at the point $x$ and, for any $\mathbf{z} \in \mathbb{R}^M$, $u_\mathbf{z}$ is the piecewise affine function $\mathbb{R}\longrightarrow \mathbb{R}$ defined as follows:

With this definition, we can state the $\Gamma$-convergence result as follows.

Theorem 2.6 (first-order $\Gamma$-limit with periodic boundary conditions). Assume that $\psi_M$ is a nondegenerate convex parabola, $\psi_1$ is of class $C^1(U)$, where $U\subset \mathbb{R}$ open is such that ${\mathbf M}_{\ell} \subset U^M$, and $\psi_0^{**}$ is differentiable in $\ell$. We define the domain

Then, $E^{1}_{n, M}$ $\Gamma$-converges, with respect to the $L^{\infty}$ topology, to

with domain $D_\ell^\#$.

3.   Proof of the results

In this section, for a greater generality, we consider $L > 0$ and functions parameterized on $[0, L]$ instead of $[0, 1]$. In this case, $\varepsilon_n = \frac{L}n$, and we extend all the notation introduced in the case $L = 1$. With fixed $\ell\in\mathbb R$, the energies we consider are directly written in the form

defined on $\mathcal{A}^\#_{n, {\ell}} (0, L)$. Note that $E^1_{n, M}(u) = \sum_{i = {0}}^{ {n-1}}\mathcal{E}^i_n(u)$, with $\mathcal{E}^i_n$ be given by (2.10).

3.1.   Compactness

We can state the compactness result as in Theorem 2.5 independently of the boundary condition as follows.

Proposition 3.1. Let $\mathcal{E}^i_n$ be given by (2.10). If

then $u^n$ satisfies the claim of Theorem 2.5 with the interval $[0, L]$ in the place of the interval $[0, 1]$.

Proof. Let $\eta > 0$, then we define the set

and, as a consequence of the bound on the sum, we get that

Therefore, if $i\notin I_n(\eta)$, by adding and subtracting $\psi_0\left(\frac{u^n_{i+M}-u^n_i}{M \varepsilon_n}\right)$ to $\mathcal{E}^i_n(u^n)$, we obtain the two inequalities

Note that, if $z$ and $(z_1, \dots, z_M)$ satisfy

a) $\psi_M\left(z\right) + \frac{1}{M}\left(\sum_{k = 0}^{M-1}\psi_1\left(z_k\right)\right) - \psi_0\left(z\right)\leq \eta, \quad \text{for }\sum_{k = 0}^{M-1} z_k = M z$

b) $\psi_0\left(z\right) - r_{{\ell}} \left(z\right)\leq \eta$

then $(z_1, \dots, z_M)$ is close to a minimizing $M$-tuple for the min in the definition of $\psi_0$, while $\psi_0(z)$ is close to $r_{{\ell}}(z)$, the tangent line of $\psi_0^{**}$ in $\ell$. This means that if $\psi_0(\ell) = \psi_0^{**}(\ell)$, then $z$ is close to $\ell$, while if $\ell$ is in some $J_j$, then $z$ is close to either $z^r_{j-1}$ or $z^l_{{j}}$. Hence, for $\eta$ small enough, we can find $\varepsilon > 0$ so that if (a) and (b) are satisfied, then

This entails that for each $i\notin I_n(\eta)$ there exists a unique $\mathbf{z}^n_i = (z^n_{i, 1}, \dots, z^n_{i, M})\in \mathbf{M}_\ell$ such that

for all $k\in\{1, \dots, M\}$. We note that if as well $i+1 \notin I_n(\eta)$, then the unique ${\mathbf z}^n_{i+1}$ must be a cyclic permutation of ${\mathbf z}^n_i$, specifically,

Since $I_n(\eta)$ is a finite set, we can identify $N_n$ pairs of indices $0 = j_0 \leq i_1 < j_1 < i_2 < j_2 < \dots < i_{N_n} < j_{N_n} \leq i_{N_n+1} = n$ such that $I_n(\eta) = \{0, \dots n-1\} \setminus \cup_{k = 1}^{N_n} \{i_k, \dots, j_k\}$, and for all indices $h$ between $i_k$ and $j_k$, we have

where $[h-i_k]$ is the reminder of $h-i_k$ mod $M$.

Since $C \geq E^1_{n, M}(u^n) \geq \eta (N_n-1)$, we must have that $N_n$ is bounded with respect to $n$. Then, we can assume, up to extracting subsequences, that $N_n$ is constantly equal to $N$. Similarly, since $\mathbf{M}_\ell$ is a finite set, we can assume $\mathbf{z}_{i_k}^n = \mathbf{z}_k$. With fixed $k\in\{ 2, \dots, N\}$, for each $n$, we chose an index $\tilde{i}_k \in \{j_{k-1}+1, \dots, i_{k}-1\}$ and defined the sequence $\{\tilde{x}^n_k\}$ such that $\tilde{x}^n_k = \tilde{i}_k \varepsilon_n$, then, up to subsequences, we can assume $x^n_k \rightarrow x_k$. However, $\left|{i_k- j_{k-1}}\right|$ must be bounded independently of $n$ and $k$, since

Then, for any $i \in \{j_{k-1}+1, \dots, i_{k}-1\}$, $\left|{\tilde{x}^n_k - i \varepsilon_n}\right|\leq \frac{C}{\eta} \varepsilon_n$. Therefore, the whole $\{j_{k-1}+1, \dots, i_{k}-1\} \varepsilon_n$ is converging to $x_k$.

Finally, we can define the sets $S = \bigcup_{k = 1}^N \{x_k\}$ and, for a fixed small $\delta$, $S_\delta = \bigcup_{k = 1}^N (x_k-\delta, x_k + \delta)$. By (3.2), we have that for $n$ large enough, the $s$-th $M$-interpolation satisfies

where $\mathbf{Z}(t) = \left(Z_1(t), \dots, Z_M(t)\right)$ is a piecewise-constant function such that $\mathbf{Z}(t) = \mathbf{z}_k$ for $t \in (x_{k-1}, x_k)$.

Note that from the equi-coerciveness of $E_{n, M}$ and hence also of $E^1_{n, M}$, we obtain that $u_{n, s}$ is a pre-compact sequence in $H^1(0, L)$, so we can suppose that they converge uniformly. However, from (3.3), the subsequence is such that $(u_{s}^n)'$ is converging to $Z_s$. In conclusion, by applying a diagonal argument, we have proved that, up to subsequences, $u^n$ converges in $W^{1, \infty}_{\rm loc}((0, L)\setminus S)$ (in the sense of Definition 3) to a function $\mathbf{u}$ such that $\mathbf{u}'(t) = Z(t) \in \mathbf{M}_\ell$ and the jump set $S(\mathbf{u}') \subseteq S$. □

Note that in this proof we have not used the periodicity condition. If it is taken into account that we have to note that $S(\mathbf{u}')$ can also contain the point $0$.

3.2.   Computation of the Gamma-limit

We now compute the $\Gamma$-limit subjected to periodic boundary conditions, without the simplifying assumption that $n$ is a multiple of $M$ used for presentation purposes in the previous section. We will show that the limit exists and can be characterized if more in general $n = q$ modulo $M$. The energy will have the same form as in the case $q = 0$, but the characterization of the domain of the $\Gamma$-limit will depend on $q$, since $M-$interpolations do not necessarily inherit the periodicity condition of $u$. Note in particular that the limit as $n\to+\infty$ does not exist.

For $n\in\mathbb N$, we let $q \in \{0, \dots, M-1\}$ denote its class modulus $M$ ($n\equiv q$ mod $M$), then given $u$ a piecewise-affine function in $W^{1, 1}_{\#, \ell}(0, L)$, for any index $Mi+q$ with $q \in \{0, 1, \dots, M-1\}$, its $M$-interpolations $u_k$ will satisfy:

Since $n = Mr+ q$, we write

which is linked to the $q+k$ interpolation (mod $M$) shifted of $\left\lfloor \frac{n+k}{M}\right\rfloor$. Thus, we have

Proposition 3.2. Consider $n(r) = Mr + q$ for a fixed $q \in\{ 0, \dots, M-1\}$. Consider a sequence $(u^{n(r)})_{r\in \mathbb{N}}$ such that ${\sup_{n(r)} E^1_{n(r), M}(u^{n(r)})} \leq C < + \infty$. Then, there exists a finite set $S \subset (0, L]$ for which $u^{n(r)}$ (up to subsequences) converges in $W^{1, \infty}_{\rm loc}(\mathbb{R} \setminus (S+ {L} \mathbb{Z}))$ to a $\mathbf{u} = (u_1, \dots, u_M)$ as in Theorem 2.5, such that for any $k = 1, \dots, M$ we have

for almost every $t {\, \notin \, } S(\mathbf{u}')$.

Proof. The convergence is given by Proposition 3.1. What remains to prove is the periodicity property. Suppose at first $q+k\leq M$. Fix $t \notin S(\mathbf{u}')$ and suppose $t+L \notin S(\mathbf{u}')$, then there exists a $\delta > 0$ such that $I_\delta(t) = [t-\delta, t+\delta]\subset \mathbb{R}\setminus S(\mathbf{u}')$ and $I_\delta(t+L)\subset \mathbb{R}\setminus S(\mathbf{u}')$. To facilitate the reading, in the following computations we take $n = n(r)$. For every $k$ fixed, $\left (u^n_k \right)'$ converges uniformly on $I_\delta(t)$ and $\left (u^n_{k+q} \right)'$ on $I_\delta(t+L)$. Since $Mr \varepsilon_n = L\left(1 - \frac{q}{n}\right)$, we can rewrite (3.4) as

Taking the limit in ${r}$, the left-hand side is converging to $u'_k(t)$, while for the righthand side we can notice that, since $\mathbf{u}'$ is piecewise constant, $u'_{k+q}(t+L) = u_{k+q}'\Big(t+L-\frac{Lq}{n}\Big)$ for every ${n = n(r)}$ large enough, so that

The case $q+k > M$ follows similarly. □

Remark 3.3. Note that at the limit we have the boundary conditions $u_k'(0^+) = u_{q+k}'(L^+)$, where $q+k$ is intended modulus $M$. This holds also if $0\in S(\mathbf{u}')$.

Proposition 3.4. Given $(u^n)_{n\in \mathbb{N}}$ such that $\sup_n E^1_{n, M}(u^n) = : C < + \infty$. Consider $0 = x_0 < x_1 < \dots < x_N = L$ and $\alpha_1, \dots, \alpha_N \in \mathbb{R}$ such that $\mathbf{M}^{\alpha_j} \subseteq {\mathbf M}_{\ell/L}$ and, by Theorem 2.5, $u^n$ converges to $\mathbf{u}$ satisfying

Then, $\frac{\ell}{L} = \sum_{j = 1}^N \alpha_j(x_j-x_{j-1})$.

Proof. Suppose $L = 1$. By the boundary conditions, we have

Now, with fixed $\delta > 0$, we define $I_\delta^j = (x_j-\delta, x_j+\delta)\cap[0, 1]$, for $j = 0, \dots, N$, and we call $S_\delta = \cup _{j = 0}^N I_\delta^j$. From Proposition 3.1, the interpolation derivative $(u^n_k)'(t)$ converges to $z_k^{\alpha_j}$ on $[x_{j-1}+\delta, x_j-\delta]$, then for an index $i$ such that $[Mi \varepsilon_n, M(i+1) \varepsilon_n]\subset [x_{j-1}+\delta, x_j-\delta]$,

Let $k^-_{j, n}$ be the smallest index multiple of $M$ such that $Mk^+_{j, n} \varepsilon_{n} \geq x_j+\delta$ and similarly let $k^+_{j, n}$ be the largest such that $Mk^-_{j, n} \varepsilon_n \leq x_j-\delta$, so that $\lim_n \varepsilon_n Mk^-_{j, n} = x_j-\delta$ and $\lim_n \varepsilon_n Mk^+_{j, n} = x_j+\delta$. We also define $k^-_{0, n} = 0$ and $k^+_{N, n} = \lfloor \frac{n}{M}\rfloor$. Then,

which tends to $0$ as $n$ tends to infinity. On the other hand, since $\sup_n E^1_{n, M}(u^n) = C$, there exists a constant $C_1$ independent from $n$ such that for every index $i$ we have

where we used the definition of $\mathcal{E}_n^i$ in Eq (2.10). Thus, from the superlinear growth of $\psi_1$, we must have that there exists an $R > 0$ such that $\left|{\frac{u^n_{i+1}-u^n_i}{ \varepsilon_n}}\right| \leq R$. Then, we can conclude

Sending $n$ to $+\infty$, we have

Finally, for arbitrariness of $\delta > 0$, we must have $\ell = \sum_{j = 1}^N \alpha_j (x_j-x_{j-1})$. □

Remark 3.5. Let $\Phi = \Phi ^{(\ell)}$ be as in Definition 4. We note that the minimum is well-defined because of Weierstrass' Theorem. Moreover, the infimum in $N \in \mathbb{N}$ in (2.11) can be replaced with the limit as $N \rightarrow + \infty$ because of the decreasing monotonicity. The terms inside the sums are $0$ for $i\geq N$ or $i\leq -N-M$ when $\mathbf{z}, \mathbf{z}' \in M_{\ell}$. The function $\Phi \colon \mathbf{M}_\ell\times \mathbf{M}_\ell \rightarrow [0, \infty]$ is a sub-additive function. In particular the functional defined by the righthand side of (2.13) is lower-semicontinuous.

Remark 3.6. Given $\xi \in \mathbb{R}$, we can consider

The two formulas are equal because the sums which are involved are invariant under vertical translations of $u$.

Now note that $\Phi (\mathbf{z}, \mathbf{z}', \xi) = \Phi (\mathbf{z}, \mathbf{z}')$ for every $\xi \in \mathbb{R}$, under the assumption that $\psi_M, \psi_1$ are $C^1(U)$ functions, where $U\subset \mathbb{R}$ open is such that ${\mathbf M}_\ell \subset U^M$. Indeed, if $(u^N)_N$ is a minimizing sequence in the definition of $\Phi (\mathbf{z}, \mathbf{z}', \xi)$, then we can consider the following new sequence:

Observe that for varying $N \in \mathbb{N}$, all $\tilde{u}^{2N}$'s are competitors in the definition of $\Phi (\mathbf z, \mathbf z')$. Let $\mathbf{z} \in \mathbf{M}^\alpha$ and $\mathbf{z}' \in \mathbf{M}^{\alpha'}$ with $\alpha, \alpha' \in \mathbb{R}$ such that $\mathbf{M}^{\alpha} \subseteq {\mathbf M}_{\ell}$ and $\mathbf{M}^{\alpha'} \subseteq {\mathbf M}_{\ell}$. We compute the difference between the involved sums for $\tilde{u}^{2N}$ and the ones for $u_N$ by

Now observe that the $C^1$ function $f(\eta) = \psi_M \left (\alpha' - \eta \right) + \dfrac{1}{M} \sum_{k = 0}^{M-1} \psi_1 \left (z_k' - \eta \right) - r _\ell(\alpha' - \eta)$ is always non-negative and it is equal to $0$ if $\eta = 0$, so that $\eta = 0$ is a minimum point for $f$. Hence, by Fermat's Theorem $f'(0) = 0$, and so

In particular, we proved that $\Phi(\mathbf{z}, \mathbf{z'}) \leq \Phi(\mathbf{z}, \mathbf{z'}, \xi)$. Arguing in the same way, one can show the reverse inequality.

Remark 3.7. A last useful remark is that $\Phi(\mathbf{z}, \mathbf{z}')$ is stable under cyclic permutations of the entries of $\mathbf{z}$ and $\mathbf{z}'$. More precisely, if we define for $q = 1, \dots, M-1$ the cyclic permutation $\sigma_q : \mathbf{M}_{\ell} \rightarrow \mathbf{M}_{\ell}$ given by

then $\Phi(\sigma_q(\mathbf{z}), \sigma_q(\mathbf{z}')) = \Phi (\mathbf{z}, \mathbf{z}')$. Indeed, if $u$ is a competitor for the minimum problem in $\Phi(\mathbf{z}, \mathbf{z}')$, then the translation $(T_qu)_i = u_{i-q}$ preserves the value of the objective function in the definition of $\Phi$ and it satisfies

Thus, $T_qu$ is a competitor for the minimum problem in $\Phi(\sigma_q(\mathbf{z}), \sigma_q(\mathbf{z}'))$. Clearly we can argue in the same way with the inverse translation, proving the claim.

Theorem 3.8 (first-order $\Gamma$-limit with periodic boundary conditions). Assume that $\psi_M$ is a nondegenerate strictly convex function, $\psi_1$ is of class $C^1(U)$, where $U\subset \mathbb{R}$ open is such that ${\mathbf M}_{\ell/L} \subset U^M$, and $\psi_0^{**}$ is differentiable in $\frac{\ell}{L}$. Constraining $n \equiv q\; \mathit{\text{mod}}M$, we define the domain

Then $E^1_{n, M}$ $\Gamma$-converges, with respect to $L^{\infty}$ topology, to

with the domain dom$(E_q^1) = D^\#_q$.

Proof. We first consider the case in which $L = 1$ and $n \equiv 0$ mod $M$.

Lower bound. Let $u^n \rightarrow u$ in $L^{\infty}(0, 1)$ be such that $E^{1, \ell}_{n, M}(u^n) \leq C < +\infty$ for every $n \in \mathbb{N}$. Then, by Proposition 3.2, there exists a finite set $S: = \{ x_1, \dots x_N \} \subset (0, 1]$, with $0 < x_1 < \dots x_{N-1} < x_N\leq 1$, and there exist $\mathbf{z}_1, \dots, \mathbf{z}_N \in \mathbf M_{\ell}$ such that $u^n$ (up to subsequences) converges in $W^{1, \infty}_{\rm loc}(\mathbb{R} \setminus (S+ \mathbb{Z}))$ to a $M$-tuple $\mathbf{u} \in D^\#_0$ such that $\mathbf{u}'(t) = \mathbf{z}_j \in \mathbf{M}^{\alpha_j}$ for $t\in (x_{j-1}+k, x_j+k)$ and for all $k \in \mathbb{Z}$ for $j\in\{1, \dots, N\}$, with $x_0 = x_N-1$. For $j \in \{1, ..., N \}$, let $(k_n^j)_n$ be a sequence of natural numbers divisible by $M$ such that

Moreover, let $(h^j_n)_n$ be a sequence in $M \mathbb{N}$ such that

Now, we can write

where $r = r_\ell$, and we have used the notation $h_n^{N+1} = h^1_n + n$. By periodicity we can choose the endpoints $h_n^1$ and $h_n^1+n$ without changing the sum. In order to recover $\Phi$, we define

Since $\mathbf{z}_j\in\mathbf{M}^{\alpha_j}$, we note that for $i\geq h^{j+1}_n-k^j_n$, we have

and similarly for $i\leq h^{j}_n-k^j_n-M$. For $h^j_n-k^j_n\leq i\leq h^{j+1}_n-k^j_n -M$ instead, we have

Then, defining $\xi^n_j = u_{\mathbf{z}_{j+1}}(h^{j+1}_n-k^j_n) - u_{\mathbf{z}_{j+1}}(h^j_n-k^j_n) -\frac{u^n_{h^{j+1}_n} - u^n_{h^j_n}}{ \varepsilon_n}$, we can rewrite

The error $\omega_n$ comes from the difference in behavior between $\tilde{u}^n_i$ and $u^n_{i+k^j_n}$ when $h^{j+1}_n-k^j_n -M < i < h^{j+1}_n-k^j_n$ or $h^{j}_n-k^j_n -M < i < h^{j}_n-k^j_n$. More precisely, for $h^{j+1}_n-k^j_n -M < i < h^{j+1}_n-k^j_n$, $\omega_n$ involves terms of the kind

and similar terms where $\psi_M$ is switched with $\psi_1$ or $-r$. Instead, for the indices $h^{j}_n-k^j_n -M < i < h^{j}_n-k^j_n$, there are terms of the following type:

To show that $\lim_n \omega_n = 0$, it is sufficient to show that

Indeed, by the definition of $\tilde{u}^n$ in (3.12), also $\tilde{u}^n$ satisfies analogous limits. Therefore, the differences of the kind (3.13) are negligible by the continuity of $\psi_M$, $\psi_1$, and $r$. On the other hand, the terms of the form (3.14) will tend to

as a consequence of the fact that ${\mathbf z}_j \in {\mathbf M}^{\alpha_j}$. Let $i_M$ denote the residual class of $i$ with respect to $M$. Then, by the definition of $u_{\mathbf{z}_{j+1}}$ as in Eq (2.12), we have

On the other hand, since there exists a compact around the midpoint of $(x_j, x_{j+1})$, which contains $\varepsilon_n(h^{j+1}_n-M, h^{j+1}_n+M)$ for all $n$, we can use the locally uniform convergence of $\mathbf{u}_n'$ to $\mathbf{u}'$ to gain

The case $i\in (h^{j}_n - k^j_n -M, h^{j}_n - k^j_n +M)$ is analogous. This proves the claim and, consequently, that $\lim_n \omega_n = 0$. In particular, putting everything together, we conclude

In the case $q\neq 0$, the only thing that changes is that we can not define $h^{N+1}_n = h^1_n + n$, because in this way it will not be divisible by $M$ thus, we take $h^{N+1}_n$ the highest index multiple of $M$ below $h^1_n+n$. Consequently, in the decomposition (3.11), there will appear $q$ residual terms of the kind:

but since $i \varepsilon_n$ is close to $1+\frac{x_1+x_0}{2}$, that is, far from any critical point $x_j$, by continuity we have that they tend to $0$.

Upper bound. Let $\mathbf{u}$ be such that $E^1_0(\mathbf{u}) < \infty$ and suppose, without loss of generality, that $\mathbf{u}(0) = 0$, then by definition there exist $N \in \mathbb{N}$, $\mathbf{z}_1, \dots \mathbf{z}_N \in \mathbf{M}_{\ell}$ and we can write $S({\mathbf u}')\cap (0, 1] = \{ x_1, \dots x_N \}$, with $0 < x_1 < \dots x_{N-1} < x_N\leq 1$, $\mathbf{u}'(t) = \mathbf{z}_j \in \mathbf{M}^{\alpha_j}$ for $t\in (x_{j-1}+k, x_j+k)$ and for all $k \in \mathbb{Z}$, with $x_0 = x_N-1$. Up to translations, which do not change the energy, we can always suppose that $1\notin S(\mathbf{u}')$, that is, $x_N < 1$. Moreover, we have that

We first consider the case $q = 0$. With fixed $\varepsilon > 0$, there exists $\tilde{N} = \tilde{N}(\varepsilon) \in \mathbb{N}$ multiple of $M$ and $N$ discrete functions $v^j$ such that

and

for every $j \in\{ 1, \ldots N\}$. Consider now the sequence of functions $(u^n)_n$ defined as follows

where $k^n_j : = \min \{ k \in \mathbb{N} : k \geq x_j n$, and $k$ is multiple of $M \}$ and

We note that $u^n_n - u^n_0 = \sum_{j = 1}^N \alpha_j (k_j^n-k^n_{j-1}) \varepsilon_n$, which in general is different from $\ell$; therefore, in order to adjust the periodicity conditions, we apply a linear correction term $\tilde{u}^n_i = u^n_i + \delta_n \frac{i}{n}$, where $\delta_n = \ell - \sum_{j = 1}^N \alpha_j (k_j^n-k^n_{j-1}) \varepsilon_n$. Since now the the boundary condition is satisfied, we can extend $\tilde{u}^n$ to $\mathbb{R}$ such that $\tilde{u}^n(t) - \ell t$ is $1$-periodic. From Proposition 3.4 and the fact that $|n x_j - k^n_j| \leq M$, we have

Since $\mathbf{u}^n$ is converging uniformly to $\mathbf{u}$ and $\delta_nx \rightarrow 0$ uniformly in $x\in [0, 1]$, we have that $\tilde{u}^n \rightarrow \mathbf{u} \quad \text{in } L^\infty([0, 1])$ (in the notion of 3). As for the convergence of the energy, if we let

then, by Eq (3.15) we have

where $R_n^j = \sum_{i = -\tilde{N}-M+1}^{\tilde{N}-1} \mathcal{E}^n_i (\varepsilon_n v^j)- \mathcal{E}^n_{i + k^n_{j-1}}(\tilde{u}^n)$. However, this $R_n^j$ involves only a finite number of indices, independently from $n$; thus, since $\frac{\tilde{u}^n_{i+M}-\tilde{u}^n_i}{M \varepsilon_n} = \frac{v^j_{i+M}-v^j_i}{M} + \delta_n$ and $\frac{\tilde{u}^n_{i+1}-\tilde{u}^n_i}{ \varepsilon_n} = v^j_{i+1}-v^j_i + \delta_n$, by continuity of $\psi_1, \psi_M$, and $r_\ell$ we have

Instead, for $i = k^n_{j-1}-\tilde{N}, \dots, k^n_j -\tilde{N} -M$, we have $v^j_{i-k^n_{j-1}} = u_{\mathbf{z}_j}(i-k^n_{j-1})$ and then

Note that we lost the dependence on $i$, so by (3.17) we have

By Fermat's Theorem we can conclude that $\lim_n \frac{f_j(\delta_n)}{\delta_n} = f'(0) = 0$; in conclusion

and the claim is proved by the arbitrariness of $\varepsilon$.

When $q\neq 0$, the proof proceeds similarly, but we have to pay attention to the boundary mismatch in the cycle of slopes in $\tilde{u}$. This can be fixed by taking into account that, by Remark 3.7, we can write the energy as

where $\sigma_q$ is defined as in Eq (3.8). Then, we can find some $\tilde{N}$ multiple of $M$ and some $v_j$ as in Eq (3.15) with the condition

Hence, we define $k^n_j : = \min \{ k \in \mathbb{N} : k \geq x_j n$ and $k\equiv q$ mod $M \}$ and we choose $u^n$ as in Eq (3.16). In this way, the interpolations $\mathbf{u}^n$ are still converging uniformly to $\mathbf{u}$ because

Since $n-k_N^n$ is divisible by $M$ and $\frac{u^n_n-u^n_{n-1}}{ \varepsilon_n} = \sigma_q(\mathbf{z_1})_M$, we can extend $u^n$ by periodicity on the whole $\mathbb{R}$ defining a recovery sequence. □

Author contributions

The authors have equally contributed to the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Andrea Braides is an editorial board member for Networks and Heterogeneous Media and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.

The research reported in the present contribution was carried out as part of the projects "A Fluid-Structure Interaction tool for the protection of Clean Energy Production sites (FSI-CEP)" funded by the MUR Progetti di Ricerca di Rilevante Interesse Nazionale (PRIN) Bando 2022 PNRR–grant P20227CSJ5, and "Variational methods for stationary and evolution problems with singularities and interfaces" PRIN 2022J4FYNJ. AB is a member of GNAMPA of INdAM.

Conflict of interest

The authors declare there is no conflict of interest.