Most relevant genetic factors in ovarian cancer development

1.   Introduction

A rumor refers to unsubstantiated information, which has the potential to rapidly and extensively disseminate through various communication channels ^[1]. In the past, rumors were disseminated through oral communication as well as various forms of print media, radio broadcasts, and other mediums. Contemporary social networks can function as an appropriate platform for the rumor propagation, while also satisfying individuals' informational needs ^[2]. For example, individuals' excessive salt consumption can be attributed to the panic of the Fukushima nuclear accident-related rumor. There have been numerous rumors that emerged a range of adverse impacts on the world since the outbreak of COVID-19 ^[3]. The security of individuals and their belongings is significantly compromised due to these rumors. Therefore, it is imperative to grasp the rules of communicating with scientists and create effective methods to intervene, defend, and prevent rumors from spreading.

Since rumor spreading is the analogy to the disease's transmission among individuals, many scholars employ similar rumor models. Early studies on rumor propagation focused a tiny community through individual interaction. According to rumor propagation, the crowd can be classified into three categories: ignorant, spreader, and stifler. In 1964, Daley and Kendall proposed the classic DK rumor-spreading model, which is the first cabin model in rumor propagation ^[4]. Furthermore, in 1973, Maki and Thompson proposed the MT model as an extension of the DK model ^[5]. According to the MT model, once interpersonal communication occurs, the former will no longer propagate. According to several scholars, the complexity of rumor propagation processes cannot be adequately captured by DK and MK models across various network settings, especially in the context of large-scale social networks. Zanette proposed a conceptual framework to simulate the dynamics of rumor propagation in small-world networks ^[6]. By integrating the MK model and the SIR model, Moreno et al. developed a novel rumor propagation model, demonstrating that network topologies can significantly influence the spread of rumors on scale-free networks ^[7]. To gain a deeper comprehension of rumor propagation, an increasing number of factors are being taken into account through the development of more rational models; for instance, hesitating mechanisms ^[8], inhibiting mechanisms, and attitude adjustment ^[9], etc. The innovations of these scholars, to a certain extent, promote rumor propagation to advance research under a variety of changing factors.

Nowadays, given the multiple channels of rumor propagation, individuals can quickly obtain information on social media platforms, thereby complicating the regulation of rumor propagation. Due to the significant damage caused by rumors, several control measures aimed at minimizing losses have been proposed by scholars; for instance, optimal control strategies ^[10], time-dependent controller ^[11], event-triggered control ^[12], and so on. In reality, when rumors prevail on social media platforms, the media coverage disseminates information to debunk these rumors and intervene in individuals' behavior, thereby mitigating social panic and upholding social harmony. Cheng et al. incorporated a nonlinear factor into the contact rate by integrating optimal control and time delay ^[13]. Huo et al. introduced a nonlinear function to effectively capture the impact of misinformation and media reports on the spread of rumors ^[14]. Pan et al. investigated a novel rumor model that integrated media coverage and rumor refuters ^[15]. Further on, Guo et al. proposed two models considering media coverage and a refutation mechanism, respectively ^[16,17]. Numerous mathematical models are available to describe how media coverage affects rumor propagation. Therefore, our proposed model must account for the impact of media coverage on the dissemination of rumors among individuals. Evidently, the aforementioned models have predominantly explored the propagation mechanism of rumors in an integer order.

However, the dynamic behavior of rumors is influenced by historical information. Fractional calculus, as an extension of integral calculus, provides innovative approaches for characterizing the memory effects, which is a generalization of integral calculus. Fractional order Caputo derivatives, extensively employed in various fields such as science, biology, engineering, computer science, chaos theory, and others, have witnessed significant advancements in recent decades ^{[18,19,20,21,22,23,24,25]}. The literature offers a wide range of models described by fractional derivatives, such as the SIR or SIRS model ^[26,27], the SEI model ^[28], the SEIR model ^[29,30,31], the SIQR model ^[32] and the SEIQRS model ^[33]. Rumor diffusion is similar to virus propagation and can be effectively modeled using fractional calculus. Singh proposed the dynamics of a rumor propagation in a social network, utilizing the Atangana-Baleanu derivative ^[34]. Ye et al. investigated a fractional-order reaction-diffusion rumor model in two linguistic contexts ^[35]. The impact of memory was investigated, and the findings clearly demonstrate that fractional calculus can be employed to more accurately characterize the process of rumor propagation.

Revisiting the findings of the previous study, we establish an Ignorants-Spreaders-Calmness-Removers-Media Reports (ISCRM) rumor propagation model with media reports under the Caputo sense by incorporating the memory effect. The subsequent sections of this manuscript are organized as follows: In Section 2, we provide a concise overview of fundamental definitions pertaining to fractional calculus. In Section 3, we propose an enhanced fractional-order ISCRM rumor model. In Section 4, the local and global asymptotic stability of the equilibria is investigated. In Section 5, the optimal control problem is addressed. In Section 6, numerical simulation is examined. In Section 7, the paper culminates with the presentation of our findings.

2.   Preliminaries for the Caputo sense

Various definitions exist regarding fractional derivatives, with the Caputo sense being provided as follows ^[36].

Definition 2.1. For Riemann-Liouville fractional integration with respect to order $\alpha$, the function $f\left(t \right)$ is presented as

where $\alpha \in {R^ + }$, ${t_0}$ represents the initial time, and $\Gamma \left(\cdot \right)$, which is established by $\Gamma \left(z \right) = \int_{{t_0}}^\infty {{t^{z - 1}}{e^{ - t}}dt},$ represents the Gamma function.

Definition 2.2. Define $l - 1 < \alpha \leqslant l, {\text{ }}l \in N$. The Riemann-Liouville fractional derivative with respect to order $\alpha$ is presented as ^[36]

Remark 2.1. The combination of Definitions 2.1 and 2.2 yields ${}_{{t_0}}^{RL}D_t^\alpha \left({{}_{{t_0}}I_t^\alpha f\left(t \right)} \right) = f\left(t \right),$ giving the Riemann-Liouville fractional integrations and derivatives with respect to order $\alpha$.

Definition 2.3. The Caputo fractional derivative with respect to order $\alpha$ is presented as follows:

where $l$ denotes the smallest integer number such that $\alpha < l$.

Remark 2.2. The equivalence between the definitions of Riemann-Liouville fractional integration and Caputo fractional integration are the same. Therefore, from Definitions 2.1 and 2.3, we obtain

giving the Caputo fractional integrations and derivatives with respect to order $\alpha$.

In the subsequent sections of this paper, the notation ${D^\alpha }$ represents the Riemann-Liouville fractional derivative.

Lemma 2.1. Provide a definition for a function $f\left(t \right)$ and a nonzero interval $t \in \left({0, T} \right)$, the condition $\left| {f\left(t \right)} \right| \geqslant {F_1}$, where ${F_1} > 0$, is a constant. Next, a positive constant is given $L = \frac{{{F_1}{T^\alpha }}}{{\Gamma \left({1 + \alpha } \right)}}.$ Thus, the inequality ${}_0I_{{t_1}}^\alpha \left| {f\left(t \right)} \right| \geqslant L$ is held for $t \in \left({0, {t_1}} \right), {\text{ }}{t_1} \geqslant T.$

Proof. The equality is evidently apparent:

By referring to Eq (2.1), which defines fractional integration, the value of ${}_0I_{{t_1}}^\alpha \left| {f\left(t \right)} \right|$ can be determined. Due to the condition $\left| {f\left(t \right)} \right| \geqslant {F_1}$, for at least one nonzero interval $t \in \left({0, T} \right)$, it acquires

Therefore, the inequality ${}_0I_{{t_1}}^\alpha \left| {f\left(t \right)} \right| \geqslant \frac{{{F_1}{T^\alpha }}}{{\Gamma \left({1 + \alpha } \right)}}$ holds for $f\left(t \right)$.

Definition 2.4. Let $F\left(\tau \right)$ be the Laplace transform of the function $f\left(t \right)$. Then, the Caputo fractional derivative Laplace transform is provided as ^[37]

Definition 2.5. The expressions for the Mittag-Leffler functions in both one-parameter and two-parameter forms are provided as ^[36]

where $z, \alpha, \beta \in C.$

Theorem 2.1. ^[36] Consider the autonomous linear fractional-order equation ${D^\alpha }x = Ax, {\text{ }}x\left(0 \right) = {x_0},$ where $0 < \alpha < 1, {\text{ }}x \in {R^n}$ and $A \in {R^{n \times n}}.$ The asymptotic stability of this system implies that

In this scenario, each component of the state's decays toward $0$ as ${t^{ - \alpha }}$.

Theorem 2.2. ^[38] Let $x = 0$ denote an equilibrium point for the equilibrium of the non-autonomous fractional-order equation

where $f\left({x, t} \right)$ satisfies the Lipschitz constant $l > 0$ and $\alpha \in \left({0, 1} \right).$ Provided that it constitutes a Lyapunov function $V\left({t, x\left(t \right)} \right)$ and class-$K$ functions ${\alpha _1}$, ${\alpha _2}$ and ${\alpha _3}$ satisfying the condition

where $\beta \in \left({0, 1} \right)$, the equilibrium point of Eq (2.10) is asymptotic stable.

3.   Rumor propagation model under the Caputo sense

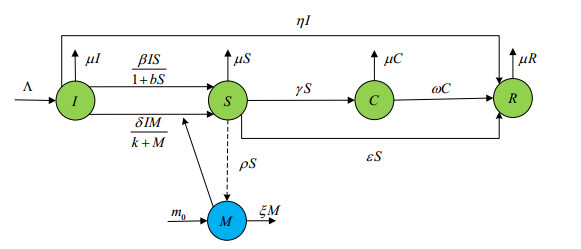
The proposed framework in this section is an Ignorants-Spreaders-Calmness-Removers-Media Reports (ISCRM). All of the crowd are divided into four groups: Ignorants are those who are unfamiliar with the rumors but are willing to believe them, denoted by $I\left(t \right)$; Spreaders are those who acquire the rumors and spread them, denoted by $S\left(t \right)$; Calmness are those who calm down before they refrain from disseminating rumors ^[39], denoted by $C\left(t \right)$; Removers are those who are aware of the rumors and either refute them or have become disinterested in rumor, denoted by $R\left(t \right)$. Since rumor propagation varies over time, media reports will undergo changes over time. We employ a quantization method to measure the impact of media reports, denoted by $M\left(t \right).$

The rules for rumor propagation are as follows:

(ⅰ) When an ignorant contacts a spreader, it will be affected and become a spreader with the exposure rate of $\beta /\left({1 + bS} \right)$, which reflects the reduced amount of contact rate due to the scale of the rumor propagation. $\beta$ denotes the rumor contact rate and $b$ is the measure of inhibition.

(ⅱ) $\delta /\left({k + M} \right)$ represents the influence of the media reports, where $\delta > 1$ and $k \geqslant 0$. $\delta /k$ means the highest availability of media influence effect. $\delta$ represents the rate of contact between the ignorant and the media reports and $k$ is the effect of media reports. $\gamma$ represents calm down rate of the spreader. $\varepsilon$ and $\omega$ represent the forgetting rates.

(ⅲ) We define that the immigrate rate is $\Lambda$ and the emigrate rate is $\mu$ in our study. Furthermore, $\eta$ represents the influence of rumors under the rumor control measures. ${m_0}$ represents the initial value of the media reports. $\rho$ represents the influence of rumor propagation on media reports. The parameters of the model are assumed to be constant and positive.

The mathematical dynamics of rumor propagation under the Caputo sense is derived based on the propagation rules in Figure 1 as follows:

where the initial conditions are denoted by $\left({I\left(0 \right), S\left(0 \right), C\left(0 \right), R\left(0 \right), M\left(0 \right)} \right)$$= \left({{I_0}, {S_0}, {C_0}, {R_0}, {M_0}} \right)$.

In this model, the non-negative initial conditions of Eq (3.1) are obtained as

Theorem 3.1. The solution of the Caputo sense Eq (3.1) subject to the conditions (3.2) is non-negative within the closed set

Proof. For Caputo fractional derivatives (3.1), one obtains

Based on the Laplace transform, it can be demonstrated that $I, S, C, R, M \geqslant 0, {\text{ }}t \in \left[{{t_0}, T} \right).$ Additionally, the total population is determined as $N\left(t \right) = I\left(t \right) + S\left(t \right) + C\left(t \right) + R\left(t \right)$. Thus, adding the first four equations of Eq (3.1), we obtain

By employing the Laplace transform, we obtain $N\left(t \right) \leqslant N\left(0 \right){E_\alpha }\left({ - \mu {t^\alpha }} \right)$$+ \frac{\Lambda }{\mu }\left({1 - {E_\alpha }\left({ - \mu {t^\alpha }} \right)} \right).$ ${E_\alpha }\left({ - \mu {t^\alpha }} \right)$ is the Mittag-Leffler function of parameter $\alpha$. Since $0 \leqslant {E_\alpha }\left({ - \mu {t^\alpha }} \right) \leqslant 1$, we obtain $N\left(t \right) \leqslant \frac{\Lambda }{\mu } + N\left(0 \right).$ Subsequently, by applying the fifth equation of Eq (3.1), we obtain ${D^\alpha }M\left(t \right) \leqslant {m_0} + \frac{{\rho \Lambda }}{\mu } - \xi M\left(t \right),$ and then, $0 \leqslant M\left(t \right) \leqslant \frac{{{m_0}}}{\xi } + \frac{{\rho \Lambda }}{{\mu \xi }} - M\left(0 \right),$ where $M\left(0 \right)$ denotes the initial value of the message of media reports. Thus, $\mathop {\sup }\limits_{t \to \infty } M\left(t \right) \leqslant \frac{{{m_0}}}{\xi } + \frac{\Lambda }{{\mu \xi }}$. This implies that $N\left(t \right)$ is bounded, thus $I\left(t \right), S\left(t \right), C\left(t \right), R\left(t \right)$ and $M\left(t \right)$ are bounded in

So, all solutions of Eq (3.1) are non-negative. Now, we will show that equation has a unique solution.

Theorem 3.2. For any given initial condition $X\left(0 \right) = \left({{I_0}, {H_0}, {S_0}, {R_0}, {M_0}} \right), {\text{ }}\forall t \geqslant 0$, Eq (3.1) has a unique solution $X\left(t \right) \in \Omega$.

Proof. The approach employed in ^[40] is adopted to validate the existence and uniqueness.

Let $H\left(X \right) = \left({{H_1}\left(X \right), {H_2}\left(X \right), {H_3}\left(X \right), {H_4}\left(X \right), {H_5}\left(X \right)} \right)$ as follows:

Furthermore, for any given $X, {X_1} \in \Omega$, a function can be constructed as follows:

where

Therefore, $H\left(X \right)$ satisfies the Lipschitz condition with any initial condition $X\left(0 \right) = \left({{I_0}, {H_0}, {S_0}, {R_0}, {M_0}} \right), {\text{ }}\forall t \geqslant 0$. Equations (3.1) always have a unique solution.

4.   Analysis of the model

In order to explore the rumor-free and rumor-permanence equilibrium points of the fractional order Eq (3.1), we solve the following equations:

By denoting the aforementioned Eq (3.1) with ${S_0} = 0$, the rumor-free equilibrium point can be calculated as: ${E_0} = \left({\frac{\Lambda }{{\eta + \mu }}, 0, 0, 0, \frac{{{m_0}}}{\xi } + \frac{{\rho \Lambda }}{{\xi \left({\eta + \mu } \right)}}} \right).$ By employing the next generation approach ^[41], the basic reproduction number ${R_0}$ is calculated. If $Q = {\left({S, C, M} \right)^T}$, the original equation can be reformulated as

where

The Jacobian matrices of $\mathcal{F}\left(x \right)$ and $\mathcal{V}\left(x \right)$ at the rumor-free equilibrium ${E_0}$, respectively, are

The next-generation matrix for Eq (3.1) is presented as follows:

Subsequently, the basic reproduction number of Eq (3.1) is determined:

The following theorem is utilized to analyze the local and global stability of the two equilibrium points.

Theorem 4.1. Equation (3.1) exhibit local stability of the rumor-free equilibrium ${E_0}$ if ${R_0} < 1$, and if ${R_0} > 1$ it is unstable.

Proof. The stability of the equilibrium point is investigated by examining the Jacobian matrix of Eq (3.1).

The characteristic polynomial of $J\left({{E_0}} \right)$ is derived as follows:

If all roots of $Det\left({\lambda I - J\left({{E_0}} \right)} \right)$ possess negative real parts, the rumor-free equilibrium ${E_0}$ can be considered asymptotically stable.

When $Det\left({\lambda I - J\left({{E_0}} \right)} \right) = 0$, we obtain

and

It is obvious that ${\lambda _1}, {\text{ }}{\lambda _2}$ and ${\lambda _3}$ are negatives roots and thus, the real component of each of Eq (4.2) roots plays a crucial role.

According to Eq (4.1), it defines

Evidently, we obtain

When ${R_0} < 1$, we acquire

Thus, ${b_2} > 0$ is deducted from Eq (4.2) by adding $\frac{{\rho \delta {I_0}}}{k}$ to Eq (4.4), and we obtain

From Eq (4.5), we obtain

By adding the parameter $\xi$ to Eq (4.6), we obtain

Therefore, ${b_1} > 0$ is deduced based on Eq (4.7). After evaluation of different coefficients of Eq (4.2), ${b_0} > 0, {\text{ }}{b_1} > 0, {\text{ }}{b_2} > 0$ and ${b_1}{b_2} > 0$ are obtained. According to the Routh-Hurwitz conditions ^[42], all eigenvalues of $J\left({{E_0}} \right)$ have negative real part. The condition $\left| {\arg \left({{\lambda _i}} \right)} \right| \geqslant \frac{{\alpha \pi }}{2}$ is satisfied and the rumor-free equilibrium ${E_0}$ is locally asymptotically stable if ${R_0} < 1$, and unstable if ${R_0} > 1$.

Theorem 4.2. The rumor-free equilibrium ${E_0}$ of Eq (3.1) is globally asymptotically stable if ${R_0} < 1$.

Proof. Let $V\left({I, S, C, R, M} \right)$, with positive constants ${c_1}$ and ${c_2}$, serve as a Lyapunov function

By differentiating the Lyapunov function with respect to time, we obtain

where ${c_1} \geqslant 0, {\text{ }}{c_2} \geqslant 0.$ Substituting ${D^\alpha }I\left(t \right), {D^\alpha }S\left(t \right), {D^\alpha }C\left(t \right), {D^\alpha }R\left(t \right)$, and ${D^\alpha }M\left(t \right)$ in Eq (3.1) into Eq (4.8) yields

From Eq (4.9), we obtain

Equating the coefficient ${d_1}$ to zero, we obtain

At the rumor-free equilibrium ${E_0}$, $I \leqslant {I^0}$ and $M \leqslant {M^0} = 0$, we obtain $\frac{{{c_1}\delta {I_0}}}{k} = {c_2}\xi$. By considering ${c_1} = \xi, {\text{ }}{c_2} = \frac{{\delta {I_0}}}{k},$ and substituting ${c_1}$ and ${c_2}$ into Eq (4.9), the obtained result is as follows:

If ${R_0} \leqslant 1$, then ${D^\alpha }V\left(t \right) \leqslant 0$. Specially, ${D^\alpha }V\left(t \right) = 0$ if and only if $S\left(t \right) = 0$. Therefore, the largest compact invariant set in $\left\{ {V\left({I, S, C, R, M} \right) \in \Omega :{D^\alpha }V\left(t \right) \leqslant 0} \right\}$ is the singleton set $\left\{ {{E_0}} \right\}$. According to LaSalle's invariance principle ^[43], ${E_0}$ is globally asymptotically stable in $\Omega$ if ${R_0} \leqslant 0$.

Theorem 4.3. If ${R_0} > 1$ and ${l_1}{l_2} - {l_3} > 0, {\text{ }}{l_1}{l_2}{l_3} - l_1^2{l_3} - l_3^2 > 0$, Eq (3.1) exhibits local stability of rumor-permanence equilibrium ${E^*}$.

Proof. Equation (3.1) at the rumor-permanence equilibrium ${E^*}$ can be further simplified as follows:

The Jacobian matrix evaluated at the rumor-permanence equilibrium ${E^*}$ persistence is presented in ^[16] as

where

The corresponding characteristic equation can be derived as

where

For ${R_0} > 1$, $J_{ii}^*{\text{ }}\left({i = 1, 2, 3, 4} \right), J_{12}^*$ and $J_{14}^*$ are all negative, while $J_{21}^*, J_{24}^*, J_{32}^*$ and $J_{42}^*$ are positive. Subsequently, we obtain

Obviously, it is ${\Delta _1} > 0$. If ${l_1}{l_2} - {l_3} > 0, {\text{ }}{l_1}{l_2}{l_3} - l_1^2{l_3} - l_3^2 > 0$, then ${\Delta _2} > 0, {\text{ }}{\Delta _3} > 0$. According to the Routh-Hurwitz criterion ^[42], it can be inferred that all eigenvalues of the eigenequation in Eq (4.10) possess negative real parts.

Therefore, the rumor-permanence equilibrium ${E^*}$ is proven to be locally asymptotically stable and Theorem 4.3 is proven.

5.   Fractional optimal control problem

The objective of our study is to identify the optimal control method and approach in order to minimize the overall cost associated with rumor spreading. The feasible intervention method aims to minimize the dissemination of rumors by individuals. The primary objective of fractional optimal control is to mitigate the relative density of individuals who spread rumors. Furthermore, the consideration of cost control measures is imperative in light of the current circumstances. Therefore, the optimal control strategy for Eq (5.1) is proposed, and its investigation can be facilitated through the application of Pontryagin's maximum principle ^[44].

Equation (3.1), incorporating the control mechanism, is thus formulated as

where the control strengths to the rumor propagation are represented by ${u_1}\left(t \right), {\text{ }}{u_2}\left(t \right)$ and ${u_3}\left(t \right)$ through education or government management. The objective function of the optimal control is formulated as

where ${A_1}$ and ${A_2}$ are the non-negative weights related to $S\left(t \right)$ and $C\left(t \right)$ in Eq (5.2). ${K_1}, {\text{ }}{K_2},$ and ${K_3}$ are relative to cost of the measures.

To determine the optimal interventions proposed in Eq (5.1),

where $u_1^{\max } < 1, {\text{ }}u_2^{\max } < 1,$ and $u_3^{\max } < 1$ are the upper bounds of ${u_1}\left(t \right), {\text{ }}{u_2}\left(t \right),$ and ${u_3}\left(t \right)$, respectively. Optimal controls $u_1^*, u_2^*,$ and $u_3^*$ satisfy $J\left({u_1^*, u_2^*, u_2^*} \right)$ $= \min \left\{ {J\left({{u_1}\left(t \right), {u_2}\left(t \right), {u_3}\left(t \right)} \right):} \right.$$\left. {\left({{u_1}\left(t \right), {u_2}\left(t \right), {u_3}\left(t \right)} \right) \in U} \right\}$.

We derive the optimal controls for minimizing the rumor propagation at minimal cost. Consequently, the following Lagrangian function is obtained:

where ${\lambda _1}, {\lambda _2}, {\lambda _3}, {\lambda _4}, {\lambda _5}$ are adjoint variable functions.

Theorem 5.1. There exists an optimal control with the solution $\left({I, S, C, R, M} \right)$ corresponding to the state equation in Eq (5.1) and the adjoint variables ${\lambda _1}, {\lambda _2}, {\lambda _3}, {\lambda _4}, {\lambda _5}$, we obtain

with boundary conditions ${\lambda _1}\left(t \right) = {\lambda _2}\left(t \right) = {\lambda _3}\left(t \right) = {\lambda _4}\left(t \right) = {\lambda _5}\left(t \right) = 0.$ According to the adjoint variables $I\left(t \right), S\left(t \right), C\left(t \right), R\left(t \right)$ and $M\left(t \right)$, we differentiate the Hamiltonian ${\rm H}$ in Eq (5.2) with respect to each variable.

Proof. From the adjoint variables $I\left(t \right), S\left(t \right), C\left(t \right), R\left(t \right)$ and $M\left(t \right)$, we differentiate the Hamiltonian ${\rm H}$ in Eq (5.2) with respect to each variable:

Moreover, the optimal control of the control variables set ${u_1}, {u_2}, {u_3}$ is attained by partial differential equation as follows:

For $u_1^*, {\text{ }}\frac{{\partial {\rm H}\left({I, S, C, R, M} \right)}}{{\partial {u_1}}} = 0,$

For $u_2^*, \frac{{\partial {\rm H}\left({I, S, C, R, M} \right)}}{{\partial {u_2}}} = 0,$

For $u_3^*, \frac{{\partial {\rm H}\left({I, S, C, R, M} \right)}}{{\partial {u_3}}} = 0,$

Therefore,

The uniqueness of the optimal control has been established based on the boundedness and adjoint variables. The standard control with a bound is obtained as follows:

6.   Sensitivity analysis and numerical simulation

6.1.   Sensitivity analysis

The sensitivity of the parameters in the rumor propagation model is investigated in this section. The following conditions are satisfied:

In conclusion, $\beta$, $\rho$, and $\delta$ are sensitive, and $\eta$, analogous to $\gamma$ and $\varepsilon$ are not sensitive. Sensitivity analysis shows that it is possible to reduce the rumor contact rate $\beta$ and parameters $\rho$ and $\delta$, thus lowering the value of ${R_0}$.

6.2.   Fractional Euler method

In this section, we present the fractional Euler method ^[45], which is employed in solving fractional-order differential equations and obtaining a discretized equation, as described below:

for $p = 1, 2, \ldots, N$ where ${c_{j, p}} = {\left({p - j} \right)^\alpha } - {\left({p - 1 - j} \right)^\alpha }$. The fractional Euler method is employed for the subsequent numerical solutions of the fractional-order differential equations.

6.3.   Several numerical simulations

In this section, we conduct numerical simulations to validate the findings presented in the preceding sections. The initial values are considered as $I\left(0 \right) = 10500, {\text{ }}S\left(0 \right) = 1500, C\left(0 \right) = 750,$${\text{ }}R\left(0 \right) = 750,$ and $M\left(0 \right) = 1500$. Additionally, the parametric values are listed in Table 1. Obviously, the basic reproduction number is ${{\text{R}}_0}{\text{ = 0}}{\text{.4}} < 1$. Figure 2 provides graphs of the evolution of (a) Ignorants, (b) Spreaders, (c) Calmness, (d) Removers, and (e) Media Reports in the rumor-free case for Eq (3.1), employing various values of the differentiation parameter $\alpha = 0.6, 0.7, 0.8, 0.9, 1.$ With the decrease of the order $\alpha$, the convergence rate of the rumor propagation curve slows down and eventually tends to stabilize, which shows the memory effect. From the perspective of public opinion dissemination, it implies that such rumors tend to persist for an extended duration. Moreover, it demonstrates an anomalous propagation pattern at a lower order $\alpha$, characterized by an exponentially rapid growth in the initial phase as depicted in Figure 3(b). Meanwhile, the subsequent phase exhibits a deceleration. When the order is $\alpha = 1$, the fractional-order differential equation turns into an integer-order one.

The initial values are also set to $I\left(0 \right) = 10500, {\text{ }}S\left(0 \right) = 1500, {\text{ }}C\left(0 \right) = 750, {\text{ }}R\left(0 \right) = 750,$ and $M\left(0 \right) = 1500$. Furthermore, the parametric values are provided in Table 2. The calculation result of the basic reproduction number is ${{\text{R}}_0}{\text{ = 1}}{\text{.32}} > 1$. The results corresponding to the simulation of the rumors case are presented in Figure 3 using various values of the differentiation parameter $\alpha = 0.6, 0.7, 0.8, 0.9, 1.$ The convergence rates of rumor propagation vary depending on the order value $\alpha$. The impact of the fractional order is observed through numerical simulation in Figure 3, from which it is demonstrated that reducing the value $\alpha$ can enhance the stability range of model (3.1). The larger the order $\alpha$, the more rapidly the curve approaches stability in the rumor-permanence case. Therefore, it is imperative to consistently and promptly disseminate scientific knowledge while actively debunking rumors in order to effectively suppress rumor propagation.

To illustrate the effectiveness of the media reports, for the basic reproduction number ${R_0} > 1, {\text{ }}\alpha {\text{ = }}0.95$ is established with the parametric values in Table 2. The media reports have an impact on Eq (3.1) governing fractional-order $\alpha {\text{ = }}0.95$ as illustrated in Figure 4. The peak of the Spreaders group decreases as the value of $k$ increases, as shown in Figure 4(b). The statement suggests that there is a positive correlation between the level of media reports and the influence on rumor propagation. Therefore, employing appropriate media strategies can effectively suppress the rumor propagation.

To demonstrate the effectiveness of the fractional optimal control strategy, for the basic reproduction number ${R_0} > 1, {\text{ }}\alpha {\text{ = }}0.95$ is established with the parametric values in Table 2. Figure 5 shows the populations of $I\left(t \right), S\left(t \right), C\left(t \right), R\left(t \right),$ and $M\left(t \right)$, with or without control mechanism. Compared with Eq (5.1), with or without control strategy, the populations of the Ignorants and the Spreaders are significantly influenced. This implies that implementing an effective control mechanism can significantly restrict the rumor diffusion.

7.   Conclusions and discussion

A Caputo sense-based ISCRM rumor propagation model incorporating media reports is proposed. The existence of positive solutions is rigorously established in this study, and the equilibrium solutions are determined for both the rumor-free equilibrium and rumor-permanence equilibrium, along with their local properties. The rumor-free equilibrium ${E_0}$ is locally and globally asymptotically stable if ${R_0} < 1$. The instability of the unique rumor-permanence equilibrium ${E^*}$ exists when ${R_0} > 1$, and for ${l_1}{l_2} - {l_3} > 0, {\text{ }}{l_1}{l_2}{l_3} - l_1^2{l_3} - l_3^2 > 0$, it is locally asymptotically stable. The analytical research was validated by conducting numerical simulations, encompassing a range of fractional orders and initial compartment sizes. In the case of ${R_0} < 1$, stability is rapidly achieved at lower fractional orders, whereas in the case of ${R_0} > 1$, the attainment of stability is rapidly achieved at higher orders. The significance of fractional analysis has been underscored by the achievement of significantly improved and more realistic outcomes. Additionally, a comprehensive analysis of the impact of media reports and an optimal control strategy is presented. The effectiveness of rumor diffusion prevention can be significantly enhanced through the implementation of a control strategy and media reports, thereby mitigating the risk associated with rumor propagation. In future research, the investigation of time delay effects ^[46] and stochastic factors ^[47,48] could be expanded within the framework of complex networks in Caputo sense systems.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.