In plants, different stimuli, both internal and external, activate production of reactive oxygen species (ROS). Photosynthesis is considered as high rate redox-metabolic process with rapid transients including light/photon capture, electron fluxes, and redox potentials that can generate ROS; thus, regulatory systems are required to minimize ROS production. Despite their potential for causing harmful oxidations, it is now accepted that redox homeostasis mechanisms that maintain the intracellular reducing environment make it possible to use ROS as powerful signaling molecules within and between cells. Redox and ROS information from the chloroplasts is a fine-tuning mechanism both inside the chloroplast and as retrograde signal to the cytosol and nucleus to control processes such as gene expression/transcription and translation. Wide repertoires of downstream target genes expression (activation/repression) is regulated by transcription factors. In many cases, transcription factors function through various mechanisms that affect their subcellular localization and or activity. Some post-translational modifications (PTMs) known to regulate the functional state of transcription factors are phosphorylation, acetylation, and SUMOylation, ubiquitylation and disulfide formation. Recently, oxPTMs, targeted in redox proteomics, can provide the bases to study redox regulation of low abundant nuclear proteins. This review summarizes the recent advances on how cellular redox status can regulate transcription factor activity, the implications of this regulation for plant growth and development, and by which plants respond to environmental/abiotic stresses.
1.
Introduction
Throughout this work, Cp×n denotes the set involving p×n matrices with complex entries, and, for A∈Cp×n, rank(A) is its rank, A∗ is its conjugate-transpose matrix, N(A) is its null space, and R(A) is its range. The index ind(A) of A∈Cp×p is the smallest nonnegative integer k for which the equality rank(Ak)=rank(Ak+1) is satisfied. The symbol I denotes the identity matrix of adequate size. Standard notations PS and PS,T denote, respectively, the orthogonal projector onto a subspace S and a projector onto S along T when Cp is equal to the direct sum of the subspaces S and T.
Several definitions and properties of generalized inverses which are upgraded in this research are given. The Moore-Penrose inverse of A∈Cp×n is uniquely determined A†=X∈Cn×p as the solution to well-known Penrose equations [1]:
If X satisfies only equation XAX=X, it is an outer inverse of A. The outer inverse of A which is uniquely determined by the null space S and the range T is labeled with A(2)T,S=X∈Cn×p and satisfies
where s≤r=rank(A) is the dimension of the subspace T⊆Cn, and p−s is the dimension of the subspace S⊆Cp.
The following notation will be used:
The notion of the Drazin inverse was extended to rectangular matrices in [2]. For selected (A,W)∈Cp,n;k, the W-weighted Drazin inverse AD,W=X∈Cp×n of A is uniquely determined by the matrix equations
Especially, if p=n and W=I, AD,I:=AD reduces to the Drazin inverse of A. Further, for ind(A)=1, AD:=A# becomes the group inverse of A. Recall that [2]
The notion of the core-EP inverse, proposed in [3] for a square matrix, was generalized to a rectangular matrix in [4]. If (A,W)∈Cp,n;k, the W-weighted core-EP inverse of A is the unique solution  =X∈Cp×n to
=X∈Cp×n to
In a special case p=n and W=I, 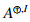 becomes the core-EP inverse
becomes the core-EP inverse 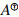 of A. According to original definitions in [5] and [6,7,8], it is important to note
of A. According to original definitions in [5] and [6,7,8], it is important to note
and
Some useful characterizations and representations of the core-EP inverse are presented in [3,9,10,11,12,13,14]. In the case ind(A)=1, 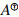 reduces to the core inverse
reduces to the core inverse 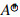 =A#AA† of A [15].
=A#AA† of A [15].
The weak group inverse (WGI) was presented for a square matrix in [16] as an extension of the group inverse. The WGI is extended in [17] to a rectangular matrix and in [18] to Hilbert space operators. For (A,W)∈Cp,n;k, the W-weighted WGI (W-WGI) of A is the unique solution Aⓦ,W=X∈Cp×n of the system [17,18]
and it is expressed by [17,18]
When p=n and W=I, Aⓦ,I:=Aⓦ reduces to the WGI of A
Remark that, for 1=ind(A), Aⓦ=A#. Useful results about WGI were given in [17,18,19,20,21,22,23].
The concept of the m-weak group inverse (m-WGI) was introduced in [24] as an extension of the WGI. Exactly, if m∈N, the m-WGI of A∈Cn×n is the unique matrix Aⓦm=X∈Cn×n such that [25]
Recall that
Clearly, Aⓦ1=Aⓦ, and particularly Aⓦ2=(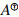 )3A2 becomes the generalized group (GG) inverse of A, established in [26]. It is interesting that, if ind(A)≤m, Aⓦm=AD. Various properties of m-WGI were presented in [24,25,27,28].
)3A2 becomes the generalized group (GG) inverse of A, established in [26]. It is interesting that, if ind(A)≤m, Aⓦm=AD. Various properties of m-WGI were presented in [24,25,27,28].
Recent research about m-WGI as well as the fact that m-WGI is an important extension of the WGI, GG, Drazin inverse, and group inverse motivated us to further investigate this topic. The current popular trend in the research of generalized inverses consists in defining new generalized inverses that are based on suitable combinations of existing generalized inverses as well as in their application in solving appropriate systems of linear equations. Considering the system (1.1) for defining m-WGI, our first aim is to solve a system of matrix equations which is an extension of the system (1.1) from the square matrix case to an arbitrary case. Since the m-WGI is restricted to square matrices, our main goal is to extend this notion to W-m-WGI inverses on rectangular matrices. To solve a certain system of matrix equations on rectangular complex matrices, we extend the notions of m-WGI, W-WGI, and the W-weighted Drazin inverse by introducing a wider class of generalized inverses, termed as the W-weighted m-WGI (W-m-WGI) for a rectangular matrix. Particularly, an extension of the GG inverse on rectangular matrices is obtained. It is important to mention that we recover significant results for the W-weighted Drazin inverse in a particular case. A class of systems of linear equations is found that can be efficiently solved applying W-m-WGI. This results is an extension of known results about the W-weighted Drazin solution and the Drazin solution of exact linear systems.
The global structure of the work is based on sections with the following content. Several characterizations for the W-m-WGI are proved in Section 2 without and with projectors. We develop important expressions for the W-m-WGI based on core–EP, Drazin, and Moore-Penorse inverses of proper matrices. As a consequence, we introduce the weighted version of GG inverse and give its properties. Limit and integral formulae for computing the W-m-WGI are part of Section 3. Section 4 investigates applications of the W-m-WGI in solving specific matrix equations. Numerical experiments are presented in Section 5.
2.
The W-weighted m-WGI
We introduce the W-weighted m-WGI on rectangular matrices as a class of generalized inverses that includes notions of the m-WGI and the W-weighted WGI.
Theorem 2.1. If (A,W)∈Cp,n;k and m∈N, then X=( W)m+1(AW)m−1A is the unique solution to the matrix system
W)m+1(AW)m−1A is the unique solution to the matrix system
Proof. Using the identity AW W
W =
= , the subsequent transformations are obtained for X:=(
, the subsequent transformations are obtained for X:=( W)m+1(AW)m−1A:
W)m+1(AW)m−1A:
which further leads to
Hence, X=( W)m+1(AW)m−1A is a solution to (2.1).
W)m+1(AW)m−1A is a solution to (2.1).
An arbitrary solution X to the system (2.1) satisfies
which leads to the conclusion that X=( W)m+1(AW)m−1A is the unique solution to (2.1). □
W)m+1(AW)m−1A is the unique solution to (2.1). □
Definition 2.1. Under such conditions (A,W)∈Cp,n;k and m∈N, the W-weighted m-WGI (shortly W-m-WGI) inverse of A is defined by the expression
Several special appearance forms of the W-m-WGI show its importance and are listed as follows:
− when p=n and W=I, the I-m-WGI coincides with the m-WGI Aⓦm=(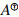 )m+1Am;
)m+1Am;
− if m=1, then ( W)2A=Aⓦ,W, that is, the W-1-WGI reduces to the W-WGI;
W)2A=Aⓦ,W, that is, the W-1-WGI reduces to the W-WGI;
− for m=2, the W-2-WGI is introduced as Aⓦ2,W=( W)3AWA and presents an extension of the GG inverse;
W)3AWA and presents an extension of the GG inverse;
− in the case k≤m, it follows Aⓦm,W=AD,W (see Lemma 2.1).
Some computationally useful representations of the W-m-WGI are developed in subsequent statements.
Lemma 2.1. If (A,W)∈Cp,n;k, m∈N and l≥k, then
Furthermore, for m≥k, it follows that Aⓦm,W=AD,W.
Proof. First, by induction on m, notice that 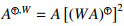 gives
gives
Further, based on
and
we obtain
In the case m≥k, it follows that
□
Remark 2.1. Note that Aⓦm,W=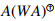 (WA)ⓦm implies the interesting identity WAⓦm,W=PR((WA)l)(WA)ⓦm for l≥k. This last identity is an extension of the classical property of the W-weighted Drazin inverse WAD,W=(WA)D. About the dual property AD,WW=(AW)D, if the equality
(WA)ⓦm implies the interesting identity WAⓦm,W=PR((WA)l)(WA)ⓦm for l≥k. This last identity is an extension of the classical property of the W-weighted Drazin inverse WAD,W=(WA)D. About the dual property AD,WW=(AW)D, if the equality 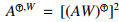 A is satisfied (which is not true in general; for details see [5]), we can verify that Aⓦm,W=
A is satisfied (which is not true in general; for details see [5]), we can verify that Aⓦm,W=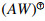 (AW)ⓦmA and so Aⓦm,WW=
(AW)ⓦmA and so Aⓦm,WW=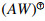 (AW)ⓦmAW.
(AW)ⓦmAW.
Representations for the W-2-WGI and W-weighted Drazin inverse are obtained as consequences of Lemma 2.1 when m=2 or m=l≥k, respectively.
Corollary 2.1. If (A,W)∈Cp,n;k and l≥k, then
and
Notice that Corollary 2.1 recovers the known expressions for the W-weighted Drazin inverse [29,30].
In Lemma 2.2, we show that the W-m-WGI Aⓦm,W is an outer inverse of WAW and find its range and null spaces.
Lemma 2.2. If (A,W)∈Cp,n;k and m∈N, the following representations are valid:
(i) Aⓦm,W=(WAW)(2)R((AW)k),N([(WA)k]∗(WA)m);
(ii) WAWAⓦm,W=PR((WA)k),N([(WA)k]∗(WA)m);
(iii) Aⓦm,WWAW=PR((AW)k),N([(WA)k]∗(WA)m+1W).
Proof. (ⅰ) Based on Lemma 2.1 it follows that Aⓦm,W=A(WA)k[(WA)k+m+2]†(WA)m, which yields R(Aⓦm,W)⊆R((AW)k) and
Another application of Lemma 2.1 yields
and so R((AW)k)⊆R(Aⓦm,W). Thus, R(Aⓦm,W)=R((AW)k). Also,
(ⅱ) By the part (ⅰ), WAWAⓦm,W is a projector, and
The equalities WAWAⓦm,W=(WA)k+2[(WA)k+m+2]†(WA)m and
imply R(WAWAⓦm,W)=R((WA)k).
(ⅲ) It is clear, by (ⅰ), that R(Aⓦm,WWAW)=R(Aⓦm,W)=R((AW)k). The identity N(Aⓦm,WWAW)=N([(WA)k]∗(WA)m+1W) is verified in a similar manner as in (ⅰ). □
Remark 2.2. For A∈Cm×n, B∈Cq×t, C∈Cs×p, M∈Cp×m, and N∈Cn×q, by [31,32], the (M,N)-weighted (B,C)-inverse of A is represented by A(2,M,N)(B,C)=(MAN)(2)R(B),N(C). By Lemma 2.2, Aⓦm,W=(WAW)(2)R((AW)k),N([(WA)k]∗(WA)m), and thus Aⓦm,W is the (W,W)-weighted ((AW)k),[(WA)k]∗(WA)m)-inverse of A. Since the (B,C)-inverse of A is given as A(2)(B,C)=A(2)R(B),N(C) [33], it follows that Aⓦm,W=(WAW)(2)R((AW)k),N([(WA)k]∗(WA)m) is the ((AW)k,[(WA)k]∗(WA)m)-inverse of WAW.
Lemma 2.2 and the Urquhart formula [1] give the next representations for Aⓦm,W.
Corollary 2.2. If (A,W)∈Cp,n;k and m∈N, the W-m-WGI of A is represented as
If m=2 or m=k in Lemma 2.2 and Corollary 2.2, we obtain the next properties related to the W-2-WGI and W-weighted Drazin inverse.
Corollary 2.3. If (A,W)∈Cp,n;k, the following statements hold:
(i) Aⓦ2,W=(WAW)(2)R((AW)k),N([(WA)k]∗(WA)2)=(AW)k([(WA)k]∗(WA)k+3W)†[(WA)k]∗(WA)2;
(ii) WAWAⓦ2,W=PR((WA)k),N([(WA)k]∗(WA)2);
(iii) Aⓦ2,WWAW=PR((AW)k),N([(WA)k]∗(WA)3W);
(iv) AD,W=(WAW)(2)R((AW)k),N((WA)k)=(AW)k([(WA)k]∗(WA)2k+1W)†[(WA)k]∗(WA)k;
(v) WAWAD,W=PR((WA)k),N((WA)k);
(vi) AD,WWAW=PR((AW)k),N((AW)k).
Some necessary and sufficient conditions for a rectangular matrix to be the W-m-WGI are considered.
Theorem 2.2. If (A,W)∈Cp,n;k, X∈Cp×n, and m∈N, the subsequent statements are equivalent:
(i) X=Aⓦm,W;
(ii) AWX=( W)m(AW)m−1A and R(X)=R((AW)k);
W)m(AW)m−1A and R(X)=R((AW)k);
(iii) AWX=( W)m(AW)m−1A and R(X)⊆R((AW)k);
W)m(AW)m−1A and R(X)⊆R((AW)k);
(iv) AWXWX=X, X(WA)k+1W=(AW)k and [(WA)k]∗(WA)m+1WX=[(WA)k]∗(WA)m;
(v) XWAWX=X, R(X)=R((AW)k) and [(WA)k]∗(WA)m+1WX=[(WA)k]∗(WA)m;
(vi) XWAWX=X, AWX=( W)m(AW)m−1A and XWA=(
W)m(AW)m−1A and XWA=( W)m+1(AW)mA;
W)m+1(AW)mA;
(vii) XWAWX=X, WAWX=W( W)m(AW)m−1A and XWAW=(
W)m(AW)m−1A and XWAW=( W)m+1(AW)m+1;
W)m+1(AW)m+1;
(viii) XWAWX=X, AWXWA=( W)m(AW)mA, AWX=(
W)m(AW)mA, AWX=( W)m(AW)m−1A and XWA=(
W)m(AW)m−1A and XWA=( W)m+1(AW)mA;
W)m+1(AW)mA;
(ix) XWAWX=X, WAWXWAW=W( W)m(AW)m+1, WAWX=W(
W)m(AW)m+1, WAWX=W( W)m(AW)m−1A and XWAW=(
W)m(AW)m−1A and XWAW=( W)m+1(AW)m+1;
W)m+1(AW)m+1;
(x) X= WAWX and AWX=(
WAWX and AWX=( W)m(AW)m−1A (or WAWX=W(
W)m(AW)m−1A (or WAWX=W( W)m(AW)m−1A);
W)m(AW)m−1A);
(xi) X=AW WX and
WX and  WX=(
WX=( W)m+1(AW)m−1A;
W)m+1(AW)m−1A;
(xii) X=AD,WWAWX and AWX=( W)m(AW)m−1A (or WAWX=W(
W)m(AW)m−1A (or WAWX=W( W)m(AW)m−1A);
W)m(AW)m−1A);
(xiii) X=( W)m+1(AW)m+1X and AWX=(
W)m+1(AW)m+1X and AWX=( W)m(AW)m−1A (or WAWX=W(
W)m(AW)m−1A (or WAWX=W( W)m(AW)m−1A);
W)m(AW)m−1A);
(xiv) X=XW( W)m(AW)m−1A and XWA=(
W)m(AW)m−1A and XWA=( W)m+1(AW)mA (or XWAW=(
W)m+1(AW)mA (or XWAW=( W)m+1(AW)m+1).
W)m+1(AW)m+1).
Proof. (ⅰ) ⇒ (ⅱ): It follows from Theorem 2.1 and Lemma 2.2.
(ⅱ) ⇒ (ⅲ): This implication is obvious.
(ⅲ) ⇒ (ⅰ): Because R(X)⊆R((AW)k), we have
for some U∈Cp×n. Notice that, by AWX=( W)m(AW)m−1A,
W)m(AW)m−1A,
An application of Theorem 2.1 leads to the conclusion X=Aⓦm,W.
(ⅰ) ⇒ (ⅳ): For X=Aⓦm,W, Theorem 2.1 implies AWXWX=X. The equality (2.2) gives X(WA)k+1W=(AW)k. Using Lemma 2.1, we get X=A(WA)k[(WA)k+m+2]†(WA)m, which implies
(ⅳ) ⇒ (ⅴ): Notice, by X(WA)k+1W=(AW)k and
for arbitrary r∈N, that R(X)=R((AW)k). Hence, X=(AW)kU, for some U∈Cp×n, and
(ⅴ) ⇒ (ⅰ): The assumptions R(X)=R((AW)k) and XWAWX=X give (AW)k=XV=XWAW(XV)=XW(AW)k+1, for some V∈Cn×p. Since X=(AW)kU, for some U∈Cp×n, we get
The assumption [(WA)k]∗(WA)m+1WX=[(WA)k]∗(WA)m yields
Because (2.3) holds, we obtain
Theorem 2.1 gives X=Aⓦm,W.
(ⅰ) ⇒ (ⅵ) ⇒ (ⅶ): These implications are clear.
(ⅶ) ⇒ (ⅰ): Using XWAWX=X, WAWX=W( W)m(AW)m−1A and XWAW=(
W)m(AW)m−1A and XWAW=( W)m+1(AW)m+1, we get
W)m+1(AW)m+1, we get
(ⅵ) ⇔ (ⅷ) and (ⅶ) ⇔ (ⅸ): These equivalences are evident.
(ⅰ) ⇒ (ⅹ): From X=( W)m+1(AW)m−1A, we observe
W)m+1(AW)m−1A, we observe
(ⅹ) ⇒ (ⅰ): Applying X= WAWX and AWX=(
WAWX and AWX=( W)m(AW)m−1A, we obtain X=
W)m(AW)m−1A, we obtain X= W(AWX)=
W(AWX)= W(
W( W)m(AW)m−1A=(
W)m(AW)m−1A=( W)m+1(AW)m−1A.
W)m+1(AW)m−1A.
(v) ⇔ (xiv): This equivalence follows as (ⅰ) ⇔ (ⅶ). □
We also characterize the W-m-WGI in the following two ways.
Theorem 2.3. If (A,W)∈Cp,n;k and m∈N, then
(i) Aⓦm,W is the unique solution to
(ii) Aⓦm,W is the unique solution to
Proof. (ⅰ) By Lemma 2.2, X=Aⓦm,W is a solution to (2.4). If the system (2.4) has two solutions X and X1, notice
and R(X−X1)⊆R((AW)k). Therefore,
i.e., X=X1 is the unique solution of the system of Eqs (2.4).
(ⅱ) Lemmas 2.1 and 2.2 imply validity of (2.5) for X=Aⓦm,W=A(WA)k[(WA)k+m+2]†(WA)m.
The assumption that two solutions X and X1 satisfy (2.5) leads to the conclusion
that is, X=X1. □
Corresponding characterizations of the W-2-WGI and W-weighted Drazin inverse are derived as particular cases m=2 and m=k of Theorem 2.3, respectively.
Corollary 2.4. The following statements are valid for (A,W)∈Cp,n;k:
(i) Aⓦ2,W is the unique solution to
(ii) Aⓦ2,W is the unique solution to
(iii) AD,W is the unique solution to
(iv) AD,W is the unique solution to
3.
Further results on W-m-WGI
Some formulae for the W-m-WGI are given in this section.
We present a relation between a nonsingular bordered matrix and the W-m-WGI. Precisely, by Theorem 3.1, when the inverse of a proper bordered matrix is known, then the corresponding position of that inverse gives the W-m-WGI.
Theorem 3.1. Let (A,W)∈Cp,n;k and m∈N. Assume that full-column rank matrices G and H∗ fulfill
Then,
is nonsingular, and
Proof. Lemma 2.2 gives Aⓦm,W=(WAW)(2)R((AW)k),N([(WA)k]∗(WA)m). Since
we have (I−GG†)(I−WAWAⓦm,W)=0, that is, GG†(I−WAWAⓦm,W)=(I−WAWAⓦm,W). From R(Aⓦm,W)=R((AW)k)=N(H), we get HAⓦm,W=0. Set Y for the right hand side of (3.1). Then,
and similarly YN=I. So, N is nonsingular with N−1=Y.
□
We investigate limit and integral expressions for W-m-WGI motivated by limit and integral formulae of known generalized inverses [34,35,36,37].
Theorem 3.2. If (A,W)∈Cp,n;k, m∈N, and l≥k, then
Proof. Lemma 2.1 gives Aⓦm,W=A(WA)l[(WA)l+m+2]†(WA)m. According to the limit representation for the Moore-Penrose inverse given in [36], we derive
which implies the rest. □
Since W-m-WGI belongs to outer inverses, the limit representation of the outer inverse proposed in [35] implies the limit representation of the W-m-WGI.
Theorem 3.3. Let (A,W)∈Cp,n;k and m∈N. Suppose that H1∈Cp×ss, R(H1)=R((AW)k), H2∈Cs×ns, and n−s is the dimension of the subspace N(H2)=N([(WA)k]∗(WA)m) in Cn. Then,
Proof. Since Aⓦm,W=(WAW)(2)R((AW)k),N([(WA)k]∗(WA)m), by [35, Theorem 7], it follows that
□
Some integral formulae are established for the W-m-WGI.
Theorem 3.4. If (A,W)∈Cp,n;k, m∈N, and l≥k, then
Proof. According to [34],
The proof is completed utilizing Aⓦm,W=A(WA)l[(WA)l+m+2]†(WA)m. □
Theorem 3.5. Let (A,W)∈Cp,n;k and m∈N. If H∈Cp×n, R(H)=R((AW)k), and N(H)=N([(WA)k]∗(WA)m), then
Proof. Applying [37, Theorem 2.2], it follows that
which completes the proof. □
4.
Applications of the W-m-WGI
The W-m-WGI is applicable in studying solvability of some matrix and vector equations.
In the case that A∈Cm×n, x∈Cn, and b∈Cm, to find approximation solution to inconsistent system of linear equations Ax=b, a classical approach is to ask for, so called, generalized solutions, defined as solutions to GAx=Gb with respect to an appropriate matrix G∈Cn×m [38]. It is important to mention that the system GAx=Gb is consistent in the case rank(GA)=rank(G). Such approach has been exploited extensively. One particular choice is G=A∗, which leads to widely used least-squares solutions obtained as solutions to the normal equation A∗Ax=A∗b. Another important choice is m=n, G=Ak, and k=ind(A), which leads to the so called Drazin normal equation Ak+1x=Akb and usage of the Drazin inverse solution ADb.
Starting from the known equation WAWx=b, we use G=[(WA)k]∗(WA)m to obtain the following equation (4.1).
Theorem 4.1. If m∈N and (A,W)∈Cp,n;k, the general solution to
is of the form
for arbitrary vector u∈Cn.
Proof. Let x be represented as in (4.2). Theorem 2.2 gives
So, x is a solution to (4.1) by
If Eq (4.1) has a solution x, based on
one concludes
which yields
Hence, x possesses the pattern (4.2). □
Choosing m=2 or m≥k in Theorem 4.1, we obtain the next result.
Corollary 4.1. Let b∈Cn and (A,W)∈Cp,n;k.
(i) The general solution to
possesses the form
for arbitrary u∈Cn.
(ii) If m≥k, the general solution to
(or equivalently [(WA)k]∗(WA)m+1Wx=[(WA)k]∗(WA)mb)
possesses the form
for arbitrary u∈Cn.
We study assumptions which ensure the uniqueness of the solution to Eq (4.1).
Theorem 4.2. If m∈N and (A,W)∈Cp,n;k, x=Aⓦm,Wb is the unique solution to (4.1) in the space R((AW)k).
Proof. Theorem 4.1 implies that (4.1) has a solution x=Aⓦm,Wb∈R(Aⓦm,W)=R((AW)k).
For two solutions x,x1∈R((AW)k) to (4.1), by Lemma 2.2, we obtain
Hence, the Eq (4.1) has uniquely determined solution x=Aⓦm,Wb in R((AW)k). □
Theorem 4.2 gives the next particular results.
Corollary 4.2. Let b∈Cn and (A,W)∈Cp,n;k.
(i) x=Aⓦ2,Wb is the unique solution in R((AW)k) to (4.3).
(ii) x=AD,Wb is the unique solution in R((AW)k) to (4.4).
Recall that, by [39], for W∈Cn×p∖{0}, A∈Cp×n, ind(AW)=k1, ind(WA)=k2, and b∈R((WA)k2), x=AD,Wb is the uniquely determined solution to
Specifically, if A∈Cn×n, W=I, ind(A)=k, and b∈R(Ak), x=ADb is the unique solution to [40]
For 1=ind(A) and b∈R(A), x=A#b is the uniquely determined solution to Ax=b. Notice that Theorem 4.2 and Corollary 4.2 recover the above mentioned results from [39] and [40].
5.
Numerical examples
The identity (resp., zero) ℓ×ℓ matrix will be denoted by Iℓ (resp., 0ℓ). Denote by Dpℓ, p≥1, the ℓ×ℓ matrix with its pth leading diagonal parallel filled by the entries of the vector 1={1,…,1}∈Cℓ−p and 0 in all other positions.
We perform numerical tests on the class of test matrices of index ℓ, given by
Example 5.1. The test matrix A in this example is derived using ℓ=4 and C=2,C1=3,C2=1 from the test set (5.1), and W is derived using ℓ=4 and C=1,C1=3/2,C2=4 from the test set (5.1). Our intention is to perform numerical experiments on integer matrices using exact computation. Appropriate matrices are
The matrices WA and AW fulfill k=ind(WA)=ind(AW)=2.
(a) In the first part of this example, we calculate the Drazin inverse, the core-EP inverse, and W-m-WGI class of inverses based on their definitions. The Drazin inverse of WA is computed using
and the core-EP inverse of WA is equal to
The W-weighted Drazin inverse of A is equal to
and the W-weighted core-EP inverse of A is equal to
The W-WGI (or W-1-WGI) inverse of A is given by
the W-2-WGI inverse of A is equal to
and for each m≥k the W-m-WGI inverse of A satisfies
Additionally, Aⓦm=AD is checked for each m≥ind(A).
(b) Representations involved in Lemma 2.1 are verified using
(c) In this part of the example, our goal is to verify results of Theorem 2.2.
(c1) The statements involved in Theorem 2.2(ⅳ) are verified as follows.
- In the case m=1 verification is confirmed by
- In the case m=2 results are confirmed by
- Representations in the case m≥3 are confirmed by
(c2) The statements involved in Theorem 2.2(ⅵ) are verified using verification of part (ⅳ) and the following computation.
- In the case m=1
- In the case m≥2 results are confirmed by
Example 5.2. Consider A and W from Example 5.1 and the vector b=(22011201)T with intention to verify Theorem 4.1.
In the case m=1 of (4.1), the general solution to [(WA)2]∗(WA)2Wx=[(WA)2]∗WAb is equal to
where u=(u1u2u3u4u5u6u7u8)T is a vector of unknown variables. Symbolic calculation gives
Obtained vector x1 is verified using [(WA)2]∗(WA)2Wx1=[(WA)2]∗WAb=(404062060901594292).
In the case m≥2 of (4.1), the general solution to [(WA)2]∗(WA)m+1Wx=[(WA)2]∗(WA)mb is equal to
Symbolic calculus produces
Correctness of the vector xm is verified using
6.
Concluding remarks
In this research, we present an extension of the m-weak group inverse (or m-WGI) on the set of rectangular matrices, called the W-weighted m-WGI (or W-m-WGI). The W-m-WGI class presents a new, wider class of generalized inverses since this class involves the m-WGI, W-weighted weak group, and W-weighted Drazin inverse as special cases. Various characterizations and representations of W-m-WGI are developed. Usability of the W-m-WGI class in solving some constrained and unconstrained matrix equations and linear systems is considered. Some new properties of the weighted generalized group inverse and some known properties of the W-weighted Drazin inverse are obtained as corollaries. The given numerical examples confirm the obtained results.
There is increasing interest in the investigation of the WGI and its generalizations, and so for further research in the near future, it may be interesting to consider its generalizations to Hilbert space operators or tensors, iterative methods for approximation of W-m-WGI, or recurrent neural network (RNN) models for computing W-m-WGI.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
Dijana Mosić and Predrag Stanimirović are supported by the Ministry of Education, Science and Technological Development, Republic of Serbia, grant no. 451-03-65/2024-03/200124.
Predrag Stanimirović acknowledges support from the Science Fund of the Republic of Serbia, (No. 7750185, Quantitative Automata Models: Fundamental Problems and Applications - QUAM).
This work is supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2022-1121).
Conflict of interest
P. S. Stanimirović is an editorial board member for Electronic Research Archive and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.










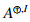 becomes the core-EP inverse
becomes the core-EP inverse 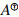 of
of 

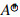











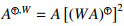 gives
gives


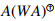


















 DownLoad:
DownLoad: