Dynamics of Bacterial white spot disease spreads in Litopenaeus Vannamei with time-varying delay

1.   Introduction

The dynamical relationship between biological populations has played an important role in ecology since Berryman ^[1] found the dynamical connection between predators and their prey in 1992, which will develop to be one of vital field. Moreover, a number of scholars have paid much attention to the dynamical behavior in the context of predator-prey models. It is evident that these dynamical behaviors encompass various aspects such as stability, periodic oscillations, bifurcation, persistence and chaos ^{[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]}. Understanding these dynamics is essential for comprehending the intricate interactions and patterns exhibited by predator and prey populations in ecological systems.

Furthermore, ecological epidemiology has emerged as a relatively new branch within ecological theory. The predator-prey model, initially proposed by Lotka and Volterra, served as a foundation for this field. In subsequent years, Holmes and Bethel reviewed numerous examples demonstrating how infectious diseases can alter the dynamics of predator-prey interactions. It was then realized that infectious diseases play a significant role in influencing population dynamics ^[27]. This realization inspired Anderson and May ^[28] to embark on mathematical and biological studies to explore the impact of diseases on ecosystems. Their work shed light on the intricate relationship between infectious diseases and ecological systems, providing insights from both mathematical and biological perspectives. As a result, the predator-prey model incorporating infectious diseases has gained increasing attention. In 2002, Venturino ^[29] introduced a scenario where the disease spreads only among predators and proposed two types of infectious disease models in ecological systems, shedding light on the mechanisms of disease transmission within these populations. In recent years, numerous researchers have made substantial contributions to studying the consequences of diseases on predator-prey systems ^{[29,30,31,32,33,34]}. Their research has deepened our understanding of how infectious diseases can impact population dynamics, community structure and ecosystem stability within predator-prey systems.

Inspired by the work in ^[29], Guo et al. ^[33] further considered prey-predator model incorporating disease transmission and Holling II functional response:

Note that, only healthy predators are capable of hunting. Where $X$ represents the density of prey population, $S$ represents the density of susceptible predators, $I$ represents the density of infected predators. All coefficients are positive. $r$ means the intrinsic growth rate of prey, $K$ stands for the maximum capacity of prey, $a$ refers to the predation coefficient, $e$ means the conversion coefficient of prey population to susceptible predators population. $d_{1}$ indicates the mortality rate of susceptible predators, $d_{2}$ indicates the mortality rate of infected predators. and $d_{1} < d_{2}$. Furthermore, Guo et al. presented the abundant conditions for the local asymptotic stability of the equilibriums of the system (1.1) and analyzed the global asymptotic stability of the positive equilibrium in reference ^[33].

In fact, for any actual system (chemical control system, spacecraft, network system, ecosystem, etc.), the influence of environmental factors such as climate, temperature and the maturity time of certain prey populations is not fixed, and the incubation period of a disease is different. As we all know, the delay sometimes is a constant, sometimes is time-varying, or sometimes is random, which is a common phenomenon in many practical systems. The delay is also a key factor that directly affects and determines the stability and performance of systems. At present, the study on the stability of linear systems with constant time delay has been relatively mature. In recent years, with the delay differential equation model used widely in biology, physics, economics, medicine and many other fields, the study of the delay differential equation has become an important field in the differential equation and dynamical system. Numerous studies show that altering the time delay parameter in a model can lead to various effects and characteristics, including oscillation and bifurcation ^[3,9,35].

Based on the model (1.1), Xu and Zhang ^[36] further took into account the pregnancy delay and then formulated the following predator-prey model:

where $X(t)$ refers to the population number of prey population, $S(t)$ stands for the population number of susceptible predators, and $I(t)$ stands for the population number of the infected predators. All coefficients are positive, and $\tau \geq 0$ indicates the pregnancy period of a predator. Suppose that the predator population $N$ consists of two populations: Susceptible predators $S$ and infected predators $I$. Moreover, the disease can spread only in the predator species through contact, not vertically.

We find that certain delay factors, like in neural network systems, are not necessarily constant. The signal transmission speed within the neural network node system is limited, and the interconnection delay between neurons can change over time, making delays in the node system inevitable. Similarly, in ecosystems, the maturity time of certain prey populations is not fixed due to the influence of environmental factors such as climate and temperature, and the incubation period of diseases can vary. Therefore, incorporating variable delays into the model can enhance its practicality, allowing for a more accurate description of population behavior characteristics and aiding in the protection of species and ecosystems.

On the other hand, we also observed an interesting phenomenon that many diseases are not transmitted vertically ^[37]. For example, the relationship between the prey algae and the predator Litopenaeus Vannamei. Bacterial white spot disease (BWSD) is not inherited but spreads among Litopenaeus Vannamei through contact ^[38,39,40]. Furthermore, Litopenaeus vannamei is becoming an important part of China's aquaculture industry, which effectively developed the coastal wasteland area, and made outstanding contribution to the development of agricultural economy ^[41]. However, with the expansion of breeding scale, disease problems have become increasingly evident, hindering industry development. The incidence rate of BWSD in Litopenaeus Vannamei is high, and the infection spreads rapidly, leading to a high mortality rate. Moreover, there is an incubation period for the onset of white spot disease, which is a severe ailment that has attracted the attention of several scholars^[42,43,44]. Even with effective treatment, prevention remains the primary focus. Any outbreak of disease can be disastrous and result in significant losses. In 1992, an extensive outbreak of BWSD resulted in significant industry losses. Against this backdrop, Gao et al. ^[45] established a model that considers Litopenaeus Vannamei's infection with Bacterial white spot disease.

So far, a large number of scholars have studied ecological infectious diseases with delay. Although some scholars have done some research in terms of time-varying delay systems, for example, Ding and Long et al. ^[46,47] studied Nicholson's blowflies system where mature delay and feedback delay are time-varying, and Gao et al. ^[48] studied the neural network system where transmission time between neurons is time-varying; they paid less attention on the model of ecological infectious diseases with time-varying delay. In order to better prevent and control the spread of Bacterial white spot disease, we establish a model to study dynamics where Bacterial white spot disease is transmitted in Litopenaeus Vannamei with time-varying delay, which is enlightened from a Lotka-Volterra predator-prey model with time-varying delay in reference ^[49] and inspired by the following Nicholson's blowflies model ^[46], where mature delay and feedback delay are time-varying.

where $x_i$ represents the population of Nicholson's blowflies in the patch $i$ at time $t$, and the meaning of the other parameters can be referred to in reference ^[46].

In general, delays in ecological models introduce additional complexity and can lead to fluctuations among populations. As a result, delay differential equations exhibit more intricate dynamical behavior compared to ordinary differential equations. Recognizing this, numerous scholars have focused their research on studying ecological models that incorporate one or multiple types of delay ^[50,51,52]. By investigating the effects of these delays on population dynamics, these studies contribute to our understanding of the factors that influence ecological systems and provide valuable insights into the mechanisms driving population fluctuations and ecological patterns.

On the basis of model (1.2), we mostly consider the following facts.

1) Because the infection rate of BWSD is effected during spreading by the quantity of susceptible Litopenaeus Vannamei, we use the Holling II functional response function $\frac{\beta S(t)I(t)}{1+\alpha I(t)}$ instead of the linear infection rate function $\beta S(t)I(t)$.

2) Holling II functional response function is considered between Litopenaeus Vannamei and algae.

3) The incubation period from BWSD to symptoms is a time-varying delay.

As a result, we establish the following differential model with time-varying delay:

where $X(t)$ represents the population number of algae, $S(t)$ refers to the population number of susceptible Litopenaeus Vannamei, and $I(t)$ refers to the population number of infected Litopenaeus Vannamei. $a_{11}$ represents the competition coefficient of algae, $a_{21}$ means the energy conversion efficiency of Litopenaeus Vannamei, $a_{12}$ represents the predation coefficient, $\beta$ represents infection rate BWSD, $\tau(t)$ stands for the incubation period of disease to spread. Model (1.4) satisfies the following initial condition:

where $(\phi_{1}(\vartheta), \phi_{2}(\vartheta), \phi_{3}(\vartheta))\in([-\tau, 0), R_+^3), R_+^3 = \{(X(t), S(t), I(t)):X(t) > 0, S(t) > 0, I(t) > 0\}$.

Generally speaking, this article mostly makes the following contributions:

1) Using some differential inequality methods, we make intensive research on the positivity, existence and persistence of the equilibriums for the system (1.4).

2) We have derived sufficient conditions for the globally asymptotic stability of the system (1.4) at the positive equilibrium and the certain conditions for the local asymptotic stability of the non-trivial equilibriums for the system (1.4) using the differential equation theory under some assumptions.

3) In order to account for that the previous theoretical results are reliability and validity, we choose some different time delay to carry out some numerical simulation to verify it.

The four remaining sections of the article are structured as follows. In Section 2, a number of required preliminary knowledge is given. In Section 3, the global asymptotic stability of the positive equilibrium for the system (1.4) is offered by constructing a proper Lyapunov function. Moreover, in Section 4, numerical simulations means that our previous theoretical results are right. Last, a general discussion is represented in Section 5.

2.   Preliminary results

We first give one definition and two lemmas to prove our main results.

Definition 2.1 (^[53]). System (1.4) has permanence provided that there exist positive constants $\widetilde{M_1}$, $\widetilde{M_2}$, $\widetilde{M_3}, \widetilde{l_1}$, $\widetilde{l_2}$, and $\widetilde{l_3}$ such that for any positive solution $(X(t), S(t), I(t))$ of system (1.4) satisfying

Lemma 2.1. (^[54]).(i) If $a > 0$, $b > 0$ and $\dot{x} \geq x(b-ax)$, when $t\geq0$ and $x(0) > 0$, we have

(ii) If $a > 0$, $b > 0$ and $\dot{x} \leq x(b-ax)$, when $t\geq0$ and $x(0) > 0$, we have

Lemma 2.2. (^[54]).(i) If $a > 0$, $b > 0$ and $\dot{x} \geq b-ax$, when $t\geq0$ and $x(0) > 0$, we have

(ii) If $a > 0$, $b > 0$ and $\dot{x} \leq b-ax$, when $t\geq0$ and $x(0) > 0$, we have

Theorem 2.1. If there are positive constants $M_i, l_i \ (i = 1, 2, 3)$ defined by (2.4), (2.6), (2.8), (2.10), (2.13) and (2.16) respectively and they are independent of the solution of the system (1.4) such that for each positive solution $(X(t), S(t), I(t))$ of system (1.4) with the initial condition (1.5), then system (1.4) is permanent. That is

Proof. It is not difficult to obtain that model (1.4) with initial values $(X(0), S(0), I(0))$ has the positive solution $(X(t), S(t), I(t))$ passing through $(X(0), S(0), I(0))$.

Based on the first equation of model (1.4), we get

It is direct from Lemma 2.1 that

From the definition of the limit, for any positive constant $\varepsilon_1 > 0$, there is a $T_1 > 0$ from (2.4), such that for $\forall \ t > T_1$, we can derive

It follows from the second equation of system (1.4), we can obtain

From the Lemma 2.1, we get

Consequently, according to (2.6), for any positive constant $\varepsilon_2 > 0$, there is a $T_2 > 0$, such that for each $t > T_2$,

Then, according to the third equation of model (1.4), for $t\geq T_1+\tau$, we gain

Similarly, we get

Thus, for any positive constant $\varepsilon_3 > 0$, there exists a $T_3 > 0$ from (2.8), such that for $\forall \ t > T_3$, we get

For another thing, according to the first equation of model (1.4), when $t\geq T_1+\tau$, we obtain

From Lemma 2.2, we can derive that

Combined with (2.4), we get

Based on the second equation of system (1.4), we have

From Lemma 2.2, we obtain

Combined with (2.6), we get

According to the third equation of system (1.4), we obtain

From Lemma 2.2, it is fairly easy to get that

Combined with (2.8), we get

which together with (2.11) and (2.14), reveal that system (1.4) is permanent from Definition 2.1. Therefore the proof is finished.

Corollary 2.1. There exist positive constants $l_i^*$ and $M_i^* \ (i = 1, 2, 3)$ according to Theorem 2.1, such that for all $t > t_0$,

Lemma 2.3. The solutions of system (1.4) have positiveness on interval $[t_0, +\infty)$.

Proof. Set the maximal right-interval of existence be the interval $[t_0, \varpi(\varphi))$ for $I(t_0)$, $I(t_0)\leq \ \parallel \varphi\parallel$, $C_+ = C([-\tau, 0], [0, +\infty))$.

Based on the first equation of system (1.4), we can easily obtain

Integrating simultaneously two sides of Eq (2.19) from $0$ to $t$, we get

Thus, $X(t) > 0,$ for $\forall t\geq t_0.$

In the same way, we can gain

and then $S(t) > 0$, for $\forall t\geq t_0.$

Based on the Theorem 5.2.1 in reference ^[55], from the third equation of system (1.4), for all $t\in[t_0, \varpi(\varphi))$, we have $I(t_0)\in C_+$. Consequently,

Next, we need to demonstrate that $\varpi(\varphi) = +\infty$. For $t\in[t_0, \varpi(\varphi))$, on the basis of Corollary 2.1, set

Then

Combined with the definition of $\Pi_1(t)$, it reveals

By applying the Gronwall-Bellman inequality to the inequality (2.23), we gain

which reveals that $\varpi(\varphi) = +\infty$ according to the works of reference ^[56]. So the solutions of system (1.4) have positiveness on $[t_0, +\infty)$.

3.   The stability of equilibriums

We investigate the local stability of the equilibriums of system (1.4) when $\tau(t) = 0$ in Subsection 3.1, and construct a proper Lyapunov function to achieve the sufficient conditions for the global asymptotic stability of system (1.4) around the positive equilibrium when delay is time-varying in Subsection 3.2.

3.1.   The local stability

It is easy to see that $E_0 = (0, 0, 0)$ is a trivial equilibrium of system (1.4). We can get the following non-trivial equilibriums:

For $E_2(\widetilde{X}, \widetilde{S}, 0)$, we know that $\widetilde{X}$ satisfies

where

Set $t = \widetilde{X}+\frac{a_1}{3a_0}$, then the Eq (3.1) is equal to

where

Then, we can get the positive solution

Consequently,

If (H1): $t_1-\frac{a_1}{3a_0} > 0, 3a_0a_{22}t_1-a_1a_{21} > 0, 3a_0a_2-a_1^2 > 0$ and $3a_0mt_1-a_1m+3a_0 > 0$ is satisfied, then $\widetilde{X}$ and $\widetilde{S}$ are positive.

$E_* = (X_*, S_*, I_*)$ satisfies

where

If (H2): $rm-a_{11} > 0$ and $\sqrt{(d_2 \alpha+a_{33})^2-4a_{33}(d_2-\beta S_*)} > d_2 \alpha+a_{33}$ is satisfied, then $E_*$ is the interior equilibrium.

Next, we will be devoted to exploring the local stability of $E_0, E_1, E_2$ and $E_*$ when $\tau(t) = 0$ respectively.

The characteristic equation of model (1.4) at $E_0(0, 0, 0)$ is

The trivial equilibrium $E_0(0, 0, 0)$ is always unstable because the Eq (3.3) has the only one positive root $\lambda = r$.

The characteristic equation of model (1.4) at $E_1 = (\frac{r}{a_{11}}, 0, 0)$ is

The Eq (3.4) has two negative solutions $\lambda_1 = -r$, and $\lambda_2 = -d_2$. Hence, if $a_{21}r > d_1(a_{11}+mr)$, the non-trivial equilibrium $E_1 = (\frac{r}{a_{11}}, 0, 0)$ is unstable. If $a_{21}r < d_1(a_{11}+mr)$, the non-trivial equilibrium $E_1 = (\frac{r}{a_{11}}, 0, 0)$ is stable.

Next, we can obtain that the characteristic equation at $E_2(\widetilde{X}, \widetilde{S}, 0)$ of model (1.4) is

where

According to Routh-Huruitz theorem, when (H3): $c_1 > 0, c_1c_2 > c_3$ is satisfied, then the non-trivial equilibrium $E_2(\widetilde{X}, \widetilde{S}, 0)$ is locally asymptotically stable.

The characteristic equation of the system (1.4) at $E_* = (X_*, S_*, I_*)$ is

where

According to Routh-Huruitz theorem, when (H4): $g_1 > 0$, $g_1g_2 > g_3$ is satisfied, then $E_* = (X_*, S_*, I_*)$ is locally asymptotically stability.

As a result, we can get following theorem.

Theorem 3.1. When $a_{21}r < d_1(a_{11}+mr)$, the equilibrium $E_1(\frac{r}{a_{11}}, 0, 0)$ is stable. If (H3) is satisfied, then the equilibrium $E_2(\widetilde{X}, \widetilde{S}, 0)$ is locally asymptotically stable. If (H4) is satisfied, then the unique positive equilibrium $E_*(X_*, S_*, I_*)$ is locally asymptotically stable. The trivial equilibrium $E_0 = (0, 0, 0)$ is always unstable.

3.2.   The global asymptotical stability

We have known that model (1.4) has one unique positive solution according to Lemma 2.3, denote it $(X^*(t), S^*(t), I^*(t))$.

Definition 3.1. For any other arbitrary solution $(X(t), S(t), I(t))$ of system (1.4) is positive and bounded, which satisfies the equality as follows, then a bounded positive solution $(X^*(t), S^*(t), I^*(t))$ of system (1.4) is globally asymptotically stable,

Definition 3.2. Set $\widetilde{f}$ be a nonnegative function defined on $[\tilde{h}, +\infty)$, and $\tilde{h}$ is a real number, moreover $\widetilde{f}$ is integrable and uniformly continuous on interval $[\tilde{h}, +\infty)$, then $\lim_{t\rightarrow +\infty}\widetilde{f}(t) = 0$.

Theorem 3.2. Suppose that (H1), (H2) and the following assumptions are true:

(H5) $\lim_{t\rightarrow +\infty}inf A_i > 0$,

where the expression of $A_i (i = 1, 2, 3)$ can be found in (3.12),

(H6) $I(t)$ is continuous at $[t_0, +\infty)$, i.e., for $\forall\frac{\varepsilon_0}{2} > 0, \exists \ \delta = \tau$, when $|t_1-t_2| < \delta$, we have

(H7) $S(t)$ is continuous at $[t_0, +\infty)$, i.e., for $\forall \frac{\varepsilon}{2} > 0, \exists \ \delta = \tau$, when $|t_1-t_2| < \delta$, we have

Then the model (1.4) has a unique positive and globally asymptotically stable solution $(X^*(t), S^*(t), I^*(t))$.

Proof. Based on the results of Theorem 2.1, there are positive constants $l_i, M_i(i = 1, 2, 3)$, for $t > T$ and a $T = \text{max}\{T_1, T_2, T_3\} > 0$ such that

Define

Computing the upper-right derivative of $V(t)$ at the positive solution $(X^*(t), S^*(t), I^*(t))$ of the system (1.4), and for $t > T$, we can obtain

According to Corollary 2.1, it is not difficult to get

and

From (H6), we get

Combined with (3.9)–(3.12), we obtain the upper-right derivative of $V(t)$:

where

Integrating simultaneously two sides of the Eq (3.13) on $[T^*, t]$ and setting $\varepsilon\rightarrow0, \varepsilon_0\rightarrow0$, which yields

By (H5), there exist constants $\alpha_i\ (i = 1, 2, 3)$ and there is a $T^* > T$ such that

It is evident to get

From Theorem 2.1, $X^*(t), S^*(t), I^*(t)$ are bounded for $t\geq T^*$, so $\big|X^*(t)-X(t)\big|, \big|S^*(t)-S(t)\big|,$ and $\big|I^*(t)-I(t)\big|$ are uniformly continuous on $[T^*, +\infty)$ from Definition 3.2. From Barbalat's Lemma ^[57], we have

From the Theorems 7.4 and 8.2 in reference ^[58], we get that the positive solution $(X^*(t), S^*(t), I^*(t))$ is uniformly asymptotically stable. So, the demonstration of Theorem 3.2 is completed.

4.   Numerical simulations

In this part, we use MATLAB software to give some numerical simulations to verify the theoretical results.

Suppose that $r = 1.5, a_{11} = 0.8$, $a_{12} = 1.5, m = 1$, $a_{21} = 1.25, d_1 = 0.16$, $\beta = 0.95, \alpha = 0.001$, $a_{22} = 0.2, d_2 = 0.2, a_{33} = 0.15.$ Thus, the model (1.4) is

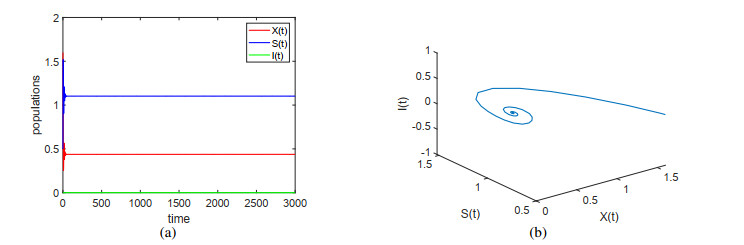
Through calculation, it is easy to achieve that the system (4.1) satisfies the conditions (H1)–(H4) and the conditions of Theorem 3.1, and it is evident to gain the non-trivial equilibriums $E_1 = (1.8750, 0, 0)$, $E_2 = (0.43747, 1.10208, 0)$, the unique positive equilibrium $E_* = (1.66097, 0.30375, 0.58929)$. By numerical simulations, the non-trivial equilibrium $E_2$ and the positive equilibrium of the system (4.1) when $\tau(t) = 0$ are locally asymptotically stable according to Theorem 3.1 (see Figures 1 and 2).

In addition, Figure 1 indicates that the population of Litopenaeus Vannamei is stable and develop sustainably without Bacterial white spot disease. Figure 2 reveals that even if Litopenaeus Vannamei are infected with Bacterial white spot disease, as long as there is no incubation period for Bacterial white spot disease, the disease is controllable and the population of Litopenaeus Vannamei can develop sustainably.

Now, we choose

and

It is evident to see the system (4.1) is permanent from Figure 3, which indicates the conclusions in the Theorem 2.1 is true. Meanwhile, we observe that the positive equilibrium of the system (4.1) is periodic oscillation when $\tau(t) = |\sin(t)|+5$ from Figure 3, and the positive equilibrium is stable when $\tau(t) = \frac{|\sin(1+t^2)|}{1+t^2}$ from Figure 4.

Based on the discussion and numerical simulations, it is evident that time-varying delay is a critical factor that directly influences the performance and asymptotic stability of system (4.1). When the value of $\tau(t)$ is zero or sufficiently small, the system (4.1) is stable. This provides an opportunity to take action to control a widespread outbreak of Bacterial white spot disease. However, a larger time-varying delay can destabilize the system, leading to chaotic oscillations. Thus, early prevention and diagnosis are crucial steps in effectively preventing the spread of Bacterial white spot disease and reducing associated losses. By identifying the factors that impact the stability and behavior of ecological systems, we can develop effective control strategies that mitigate the impact of diseases and other disturbances on predator-prey dynamics.

Moreover, Figure 5 indicates that for system (4.1), the unique positive equilibrium is globally asymptotically stable, confirming the conclusions reached in the Theorem 3.2.

5.   Conclusions

In this paper, we have discussed the dynamics of Bacterial white spot disease spreads in Litopenaeus Vannamei where the incubation time delay of a disease to spread is time-varying. By making use of the theory of functional differential equation and the principle of differential inequality, we have obtained some delay-dependent criteria to declare the persistence and global asymptotical stability for system (1.4) at its unique positive equilibrium. The results we obtained substantiate that it is possible to control the Bacterial white spot disease spreads in Litopenaeus Vannamei in time, which can promote sustainable development of Litopenaeus Vannamei. Some numerical simulations agree with the theoretical results, which is an improvement and supplement of some existing ones. In addition, the method in this paper can be extended to study other dynamical problems of time-varying delay systems.

We also establish the permanence and asymptotic stability of system (1.4), and our numerical simulations suggest that our theoretical results which can be extended to other systems as well. According to the above simulations, we make the following observations. First, sufficiently small delays will lead to the asymptotic stability of the positive equilibrium. Second, large delays or time-varying delays can result in complex behaviors, as reported in previous studies ^[3,10,18]. It is evident that the conclusions drawn from the works cited above cannot fully elucidate the dynamics of systems that involve time-varying delays.

Indeed, the investigation of Hopf bifurcation and its properties has received significant attention in the case of constant delay. However, it is intriguing to explore the existence and properties of Hopf bifurcation, as well as methods to control or mitigate oscillations, in the presence of time-varying delays. Furthermore, when multiple time-varying delays are involved, it raises questions about the dynamic behavior of the system. These aspects serve as potential directions for our future research. By delving into these areas, we aim to advance our understanding of the system's dynamics and potentially contribute to the development of strategies for effective control and reduction of oscillations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the National Natural Science Foundation of China(Grant Nos. 12161054, 11661050 and 11861044), the National Natural Science Foundation of Gansu Province (Grant No. 20JR10RA156), the Doctoral Foundation of Lanzhou University of Technology and the HongLiu First-Class Disciplines Development Program of Lanzhou University of Technology.

Conflict of interest

All authors declare that there are no conflicts of interest in this article.