Impact of general incidence function on three-strain SEIAR model

1.   Introduction

The mathematical model is formulated to protect the environment and ease living beings' lives. Although humans have evolved to fight any circumstance, a state like an outbreak or pandemic still gets critically on our nerves. The biological reasons responsible for the spread of infection must be noted to decrease the hosts' mortality. The wheel of an infection period considers every aspect of the biological, social and physical environment. The genetic core is also a factor to be considered. The SIR (susceptible, infectious and recovered) compartmental model with a homogeneous host population was first studied by McKendrick and Kermack in 1927 ^[1]. Further, the McKendrick model was improved by adding an exposed compartment for the individuals during an incubation period. An incubation period is when the carrier does not show the symptoms of the infection. We have focused on the SEIAR model with two infectious compartments, including symptomatic and asymptomatic classes ^[2,3,4]. Symptomatic is the class of carriers comprising people showing symptoms within or after the incubation period. On the other hand, the asymptomatic class never shows any symptoms.

Strain is biologically defined as a phenotypically/genotypically distinctive group of isolates that depends on the typing scheme due to the emergence of strains and host immune changes ^[5,6]. Malaria, tuberculosis, dengue, influenza, Coronavirus and others have different variants. These variants are like plant branches that are somewhat different but have the same base properties. Variants may act differently in terms of resistance, rate of spread and vaccines. Biological data assures that the host's genetic changes and their response to infectious diseases could cause the genome sequencing of the infection. The multi-strain model ^{[7,8,9,10,11]} considers more than one variant of the infection, considering strains can coexist or compete with each other for their existence ^[4,12]. Here, we are considering three variants of the concerned, alpha, beta and delta, of the Coronavirus for the validation of our mathematical model ^[13,14,15].

Inter-agency assemblies like the Centers for Disease Control and Prevention (CDC) and the World Health Organization (WHO) focus on the quick classification of emergent mutations of viruses to observe the possible effect of viruses. To estimate the danger posed by variants of infectious diseases on the earth and recommend appropriate measures, experts estimate and measure the existing data to calculate the severity of the disease and capability of a blowout in hosts. The variants are categorized as variants being monitored (VBM), variant of interest (VOI), variant of concern (VOC) and variant of high consequence (VOHC) ^[16,17]. VBM comprise those variants whose statistics are directly connected to a severe infection or have amplified spread but are detected to have no long severity. These variants may have a low spread rate at this time. A VOI is a variant whose mutation has caused significant variation widely in the susceptible class. A VOI grows into a VOC if the spread rate increases and causes a devastating effect of the disease, while a VOHC is a stage when WHO informs other organizations about the infection's spread. A lineage is a cluster of related viruses with a common predecessor ^[18].

The incidence rate is the frequency of new infections of any disease considering susceptible populations arising in a certain period. The importance of the incidence rate and different kinds of nonlinear incidence functions ^{[19,20,21,22,23]} is formulated to explain and discuss the transmission rate of the infection amongst the host ^[24,25]. The global dynamics of the mathematical model for the bilinear ^{[26,27,28,29]}, saturated ^[28,29,31], Beddington DeAngelis ^[32,33], fractional, non-monotonic ^[27] and Crowley Martin incidence function ^[34] was studied through SIR and SEIR models. Some mathematical models are studied with homogeneous mixture incidence function, while others consider heterogeneous mixture incidence function. O. Khyar and K. Allali formulated the SEIR model with two strains considering non-monotone and general incidence rates ^{[27,35,36,37,38]}. The main objective of the three-strain model with the generalized incidence function is to cover the class of all mentioned incidence rates and study the effect of incidence rate function (The choice of incidence rate plays an important role in the mathematical model) ^[39,40].

2.   Model formulation

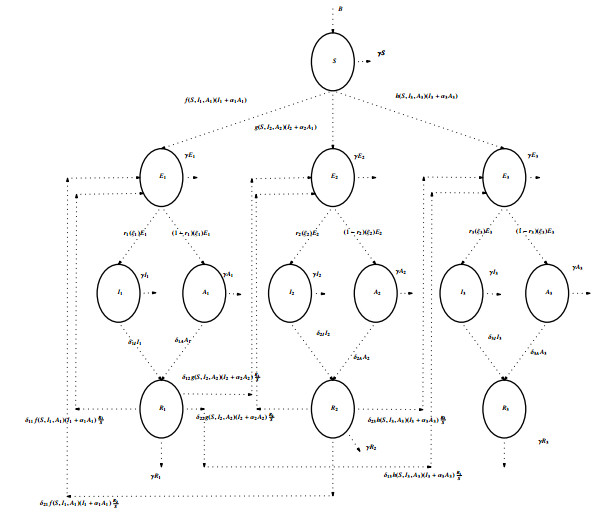
The model includes the vital dynamics where $B$ is the recruitment rate, and $1/\gamma$ is the average life expectancy of the population. The basic model contains five variables, $S_i$ (susceptible), $\; E_i$ (expected), $\; I_i$ (infected), $\; A_i$ (asymptotic) and $\; R_i$ (recovered), where $i = 1, \; 2$ and $3$ according to strain 1, strain 2 and strain 3, respectively. $\alpha_1, \; \alpha_2$ and $\alpha_3$ are the ratios of disease transmission rate by asymptomatic class of strain 1, strain 2 and strain 3, respectively. $\xi_1, \; \xi_2$ and $\xi_3$ are the reciprocals of the latent/incubation periods for strain 1, strain 2 and strain 3, respectively. $\delta_{11}, \; \delta_{21}, \; \delta_{12}, \; \delta_{22}, \; \delta_{13}, \; \delta_{23}$ are multiplicative factors for $\delta_{ij}$, where $i$ represents the rate of infection of individual $R_i$ in recovery class by strain $j$. $r_1, \; r_2$ and $r_3$ are the rates at which exposed individuals become symptomatic with strain 1, strain 2 and strain 3, respectively. $\delta_{1I}, \; \delta_{2I}, \; \delta_{3I}, \; \delta_{1A}, \; \delta_{2A}, \; \delta_{3A}$ are the recovery rates of infectious and asymptomatic classes in accordance with the strains as mentioned in the subscripts of $\delta$. $f(S, I_1, A_1), \; g(S, I_2, A_2),$ and $h(S, I_3, A_3)$ are generalized incidence functions which are assumed to be continuously differentiable in the interior of $\mathbb{R}_{+}^{3}$ and satisfy the properties (2.1, 2.2 and 2.3). It is assumed in the mathematical model that at $t = 0$ there was no infection in the host population. After the emergence of an infection, the first virus of concern is the first strain when $t\leq t_1$. At time $t_1$, the new virus of concern, the second strain, emerges, for $t_1 < t \leq t_2$. At time $t_2$, the third virus of concern is said to emerge. The emerging strain re-infection is not considered. ^[41]

3.   Model analysis

3.1.   Positivity and boundedness of solution

According to the assumptions, the compartmental model (2.4) has all its associated parameters and variables non-negative. The model to fulfill its purpose, must satisfy the well-posedness, for which the existence, positivity and boundedness of the solution with the seed conditions, defined in the Theorem (1), are necessary.

Theorem 1. Let the seed conditions $S_0 = (S(0), \; E_1(0), \; I_1(0), \; A_1(0),$ $R_1(0),$ $\; E_2(0), \; I_2(0), \; A_2(0), \; R_2(0), \; E_3(0), \; I_3(0),$ $\; A_3(0), \; R_3(0))$ be non-negative. Then, the solution $\overline{S} = \{ (S(t), \; E_1(t), \; I_1(t), \; A_1(t), \; R_1(t), \; E_2(t), \; I_2(t),$ $A_2(t), \; R_2(t), \; E_3(t), \; I_3(t), \; A_3(t), \; R_3(t))\}$ of the system of equations of model (2.4) exists, is non-negative and is bounded.

That is, $\overline{\Pi} = \Biggl\{\overline{S}\in \mathbb{R}_+^{13}, \; 0 \leq N(t) \leq \max\Big\{N(0)+\frac{B}{\gamma}\Big\}\Biggr\}$ is the positively invariant feasible region.

Proof. The existence of the unique local solution of the mathematical model (2.4) can be stated by the fundamental theory of ordinary differential equations. To show the non-negativity of the solution, we must prove that any solution initiating from the non-negative region/orthant of $\mathbb{R}_+^{13} = \{\overline{S} \in \mathbb{R}^{13}: S_0\geq 0\}$ resides in it globally.

Let us define

Claim that $\overline{T} = +\infty$. Let us assume that $\overline{T}$ is finite, so with the solution's property of being continuous, $S(\overline{T}) = 0$ or $E_1(\overline{T}) = 0$ or $I_1(\overline{T}) = 0$ or $A_1(\overline{T}) = 0$ or $R_1(\overline{T}) = 0$ or $E_2(\overline{T}) = 0$ or $I_2(\overline{T}) = 0$ or $A_2(\overline{T}) = 0$ or $R_2(\overline{T}) = 0$ or $E_3(\overline{T}) = 0$ or $I_3(\overline{T}) = 0$ or $A_3(\overline{T}) = 0$ or $R_3(\overline{T}) = 0$.

Let us assume $S(\overline{T}) = 0$ before any other variables become zero. Hence,

From the leading equation of mathematical model (2.4) and Eq (2.1), we have

This contradicts the above Eq (3.2). Now, assuming $E_1(\overline{T})$ as zero, before any other variables become zero. Hence,

From the second equation of mathematical model (2.4) and Eq (2.2), we have

This contradicts the above Eq (3.4). Similarly, we can find for $I_1, \; A_1, \; R_1,$ $E_2, \; I_2, \; A_2, \; R_2, \; I_3, \; A_3, \; R_3.$ Hence, $\overline{T}$ could not have a finite value. Thus, the positivity of the solution of model (2.4) is confirmed.

For boundedness of the solution, consider the total population $N(t)$ that is equal to the sum of all the compartments of the mathematical model. The time derivative of the total population found with the help of system of Eq (2.4) is

Therefore,

For time $0\leq t < \infty,$ we find that $N(t)\leq \frac{B}{\gamma}+N(0).$ This states the boundedness of $N(t)$, which confirms the boundedness of $\overline{S}.$ Hence, the local solution of the mathematical model (2.4) is established to have uniqueness, non-negativity and boundedness property globally. □

3.2.   Steady states and basic reproduction number

This subsection studies the basic reproduction number. The basic reproduction denoted as $\mathfrak{R}_0$ is the number measuring the secondary infections caused due to one susceptible host in the entire period of infection ^[42]. It plays a crucial role to decide the risk behind any disease to bloom out. We determine the basic reproduction number by the next generation matrix $\mathfrak{F}\mathfrak{V}^{-1}$ where $\mathfrak{F}$ is the Jacobian matrix of the new infections at time $t_2$, with the co-existence of all the three strains together. The matrix $\mathfrak{V}$ is the Jacobian matrix of infection transfer to other classes that is non-singular at time $t_2$. The spectral radius of the next generation matrix results in the basic reproduction number. The three-strain epidemic model has three eigenvalues of the next generation matrix $\mathfrak{R}_{01}$, $\mathfrak{R}_{0 2}$ and $\mathfrak{R}_{0 3}.$ The basic reproduction number $\mathfrak{R}_0$ here is the maximum of the three for the co-existence of all the three strains at time $t_2$ at an endemic equilibrium point $(\tilde{S}, \tilde{E_1}, \tilde{I_1}, \tilde{A_1}, \tilde{R_1}, \tilde{E_2}, \tilde{I_2}, \tilde{A_2}, \tilde{R_2}, \tilde{E_3}, \tilde{I_3}, \tilde{A_3}, \tilde{R_3})$.

Here,

We know that $\rho\left(\mathfrak{F}\mathfrak{V}^{-1}\right) = \mathfrak{R}_0 = {\max }\{\mathfrak{R}_{01}, \mathfrak{R}_{02}, \mathfrak{R}_{03}\},$ with $\rho$ as spectral radius and $\mathfrak{R}_{01}, \mathfrak{R}_{02}, \mathfrak{R}_{03}$ values as in Eq (3.8). Here, the $\mathfrak{R}_0$ represents the emergence of the third strain in the environment.

The basic reproduction number at the $\mathcal{DFE} = \mathbb{E}_0$ is denoted as $\mathfrak{R}(\mathbb{E}_0) = {\max } \{\mathfrak{R}_{01}(\mathbb{E}_0), \mathfrak{R}_{02}(\mathbb{E}_0), \mathfrak{R}_{03}(\mathbb{E}_0)\}$. It describes the spread of infections by an individual at the initial stage.

Theorem 2. The mathematical model (2.4) has disease free equilibrium $\mathbb{E}_0$ and seven endemic equilibrium points $\epsilon_{s1}, \; \epsilon_{s2}, \; \epsilon_{s3}, \; \epsilon_{s12}, \; \epsilon_{s23},$ $\epsilon_{s13},$ $\epsilon_{s123}.$ These endemic equilibrium points exists in accordance with some conditions. ^[27,43]

(i) The $\epsilon_{s1}$ is the first strain equilibrium which exists when $\mathfrak{R}_{01} > 1.$

(ii) The $\epsilon_{s2}$ is the second strain equilibrium which exists when $\mathfrak{R}_{02} > 1.$

(iii) The $\epsilon_{s3}$ is the third strain equilibrium which exists when $\mathfrak{R}_{03} > 1.$

(iv) The $\epsilon_{s12}$ is the endemic equilibrium which exists when $\mathfrak{R}_{01} > 1$ and $\mathfrak{R}_{02} > 1.$

(v) The $\epsilon_{s23}$ is the endemic equilibrium which exists when $\mathfrak{R}_{02} > 1$ and $\mathfrak{R}_{03} > 1.$

(vi) The $\epsilon_{s13}$ is the endemic equilibrium which exists when $\mathfrak{R}_{01} > 1$ and $\mathfrak{R}_{03} > 1.$

(vii) The $\epsilon_{s123}$ is the endemic equilibrium which exists when $\mathfrak{R}_{01} > 1, \; \mathfrak{R}_{02} > 1$ and $\mathfrak{R}_{03} > 1.$

Proof. For calculating the steady states of the mathematical model (2.4), we equate $\frac{dS}{dt}, \; \frac{dE_1}{dt}, \; \frac{dI_1}{dt}, \; \frac{dA_1}{dt}, \; \frac{dR_1}{dt}, \; \frac{dE_2}{dt}, \; \frac{dI_2}{dt}, \; \frac{dA_2}{dt}, \; \frac{dR_2}{dt}, \; \frac{dE_3}{dt}, \; \frac{dI_3}{dt}, \; \frac{dA_3}{dt}$ and $\frac{dR_3}{dt}$ to zero. The disease free equilibrium is the stage when it is considered that there is zero infection in the environment, also assumed as $t = 0$ stage. The case when there is no infection is $I_1 = 0$, $A_1 = 0$, $I_2 = 0$, $A_2 = 0$, $I_3 = 0$ and $A_3 = 0.$ Hence, the equilibrium point is named as the disease free equilibrium, denoted as $\mathbb{E}_0 = \left(\frac{B}{\gamma}, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0\right).$

(ⅰ) The case when there is an infection due to first strain, that is, $I_1 \neq 0$, $A_1 \neq 0$, $I_2 = 0$, $A_2 = 0$, $I_3 = 0$ and $A_3 = 0.$ Here, the endemic equilibrium is $\epsilon_{s1} = \left(S_{s1}, E_{s1, 1}, I_{s1, 1}, A_{s1, 1}, R_{s1, 1}, 0, 0, 0, 0, 0, 0, 0, 0 \right)$. Here, $S_{s1} = \frac{B}{\gamma} - \frac{f(S_{s1}, I_{s1, 1}, A_{s1, 1}\;) (I_{s1, 1}\; + \alpha_1 A_{s1, 1}\;)}{\gamma}$, $E_{s1, 1} = \frac{(B-\gamma S_{s1})(S_{s1}+ \delta_{11}R_{s1, 1})}{S_{s1}\;m_1}$, $I_{s1, 1} = \frac{r_1\xi_1}{m_2} E_{s1, 1}$, $A_{s1, 1} = \frac{(1-r_1)\xi_1}{m_3}E_{s1, 1}$, $R_{s1, 1} = \frac{(\delta_{1I}I_{s1, 1} + \delta_{2 A}A_{s1, 1}\;)S_{s1}}{\delta_{11} (B-\gamma S_{s1}) +\gamma S_{s1}}.$

(ⅱ) The case when there is an infection due to second strain, that is, $I_1 = 0$, $A_1 = 0$, $I_2\neq 0$, $A_2\neq 0$, $I_3 = 0$ and $A_3 = 0.$ Here, the endemic equilibrium is $\epsilon_{s2} = \left(S_{s1}, 0, 0, 0, 0, E_{s2, 2}, I_{s2, 2}, A_{s2, 2}, R_{s2, 2}, 0, 0, 0, 0 \right)$. Here, $S_{s2} = \frac{B}{\gamma} - \frac{g(S_{s2}, I_{s2, 2}, A_{s2, 2}\;) (I_{s2, 2} + \alpha_2 A_{s2, 2}\;)}{\gamma}$, $E_{s2, 2} = \frac{(B-\gamma S_{s2})(S_{s2}+ \delta_{22}R_{s2, 2}\;)}{S_{s2}m_4}$, $I_{s2, 2} = \frac{r_2\xi_2}{m_5} E_{s2, 2}$, $A_{s2, 2} = \frac{(1-r_2)\xi_2}{m_6}E_{s2, 2}$, $R_{s2, 2} = \frac{(\delta_{2I} I_{s2, 2} + \delta_{2 A}A_{s2, 2}\;)S_{s2}}{\delta_{22} (B-\gamma S_{s2}) +\gamma S_{s2}}.$

(ⅲ) The case when there is an infection due to third strain in the environment, that is, $I_1 = 0$, $A_1 = 0$, $I_2 = 0$, $A_2 = 0$, $I_3 \neq 0$ and $A_3 \neq 0.$ Here, the endemic equilibrium is $\epsilon_{s3} = \left(S_{s3}, 0, 0, 0, 0, 0, 0, 0, 0, E_{s3, 3}, I_{s3, 3}, A_{s3, 3}, R_{s3, 3} \right)$. Here, $S_{s3} = \frac{B}{\gamma} - \frac{h(S_{s3}, I_{s3, 3}, A_{s3, 3}) (I_{s3, 3} + \alpha_3 A_{s3, 3}\;)}{\gamma}$, $E_{s3, 3} = \frac{(B-\gamma S_{s3})}{m_4}$, $I_{s3, 3} = \frac{r_3\xi_3}{m_8} E_{s3, 3}$, $A_{s3, 3} = \frac{(1-r_3)\xi_3}{m_9}E_{s3, 3}$, $R_{s3, 3} = \frac{(\delta_{3I} I_{s3, 3} + \delta_{3 A}A_{s3, 3}\;)S_{s3}}{\gamma}.$

(ⅳ) The case when there is an infection due to the first and second strain surviving in the environment that is, $I_1 \neq 0$, $A_1 \neq 0$, $I_2 \neq 0$, $A_2 \neq 0$, $I_3 = 0$ and $A_3 = 0.$ Here, the endemic equilibrium is $\epsilon_{s12} = (S_{s12}, \; E_{s12, 1}, \; I_{s12, 1},$ $A_{s12, 1}, \; R_{s12, 1}, \; E_{s12, 2}, \; I_{s12, 2}, \; A_{s12, 2}, \; R_{s12, 2}, \; 0, \; 0, \; 0, \; 0).$ Here, $S_{s12} = \frac{B}{\gamma}-\frac{f(S_{s12}, I_{s12, 1}, A_{s12, 1}\;) (I_{s12, 1} \;+\; \alpha_1 A_{s12, 1}\;)}{\gamma} - \frac{g(S_{s12}, \;I_{s12, 2}, \;A_{s12, 2}\;) (I_{s12, 2} \;+\; \alpha_2 A_{s12, 2}\;)}{\gamma}$, $E_{s12, 1} = \frac{f(S_{s12}\;, I_{s12, 1}\;, A_{s12, 1}\;)(S_{s12}\;+\; \delta_{11}R_{s12, 1}\;+\;\delta_{21}R_{s12, 2}\;)(I_{s12, 1} \;+\; \alpha_1 A_{s12, 1}\;)}{S_{s12}\;m_1 }$, $I_{s12, 1} = \frac{r_1\xi_1}{m_2} E_{s12, 1}$, $A_{s12, 1} = \frac{(1-r_1)\xi_1}{m_3}E_{s12, 1}$, $R_{s12, 1} = \frac{(\delta_{1I}\;I_{s12, 1} \;+\; \delta_{2 A}\;A_{s12, 1}\;)S_{s12}}{\delta_{11}\;f(S_{s12}, I_{s12, 1}\;, A_{s12, 1}\;)(I_{s12, 1} \;+\; \alpha_1 A_{s12, 1}\;)\;+\;\delta_{12}g(S_{s12}, I_{s12, 2}, A_{s12, 2}\;)(I_{s12, 2} \;+\; \alpha_2 A_{s12, 2}\;) \;+\;\gamma S_{s1}},$ $E_{s12, 2} = \frac{g(S_{s12}\;, I_{s12, 2}\;, A_{s12, 2}\;)(S_{s12}\;+\; \delta_{12}R_{s12, 1}\;+\;\delta_{22}R_{s12, 2}\;)(I_{s12, 2} \;+\; \alpha_2 A_{s12, 2}\;)}{S_{s12}\;m_4}$, $I_{s12, 2} = \frac{r_2\xi_2}{m_5} E_{s12, 2}$, $A_{s12, 2} = \frac{(1-r_2)\xi_2}{m_6}E_{s12, 2}$, $R_{s12, 2} = \frac{(\delta_{2I} I_{s12, 2} \;+\; \delta_{2 A}A_{s12, 2}\;)S_{s2}}{\delta_{21}f(S_{s12}, I_{s12, 1}, A_{s12, 1}\;)(I_{s12, 1} \;+\; \alpha_1 A_{s12, 1}\;)\;+\;\delta_{22}\;g(S_{s12}\;,I_{s12, 2}\; ,A_{s12, 2}\;)(I_{s12, 2} \;+\; \alpha_2 A_{s12, 2}\;)\;+\;\gamma S_{s12}}.$

(ⅴ) The case when there is an infection due to first and second strain surviving in the environment, that is, $I_1 = 0$, $A_1 = 0$, $I_2 \neq 0$, $A_2\neq 0$, $I_3 \neq 0$ and $A_3 \neq 0.$ Here, the endemic equilibrium is $\epsilon_{s23} = (S_{s23}, \; 0, \; 0, \; 0, \; 0, E_{s23, 2}, I_{s23, 2}, \;A_{s23, 2}, R_{s23, 2}, E_{s23, 3}, I_{s23, 3}, \;A_{s23, 3}, R_{s23, 3}\;).$ Here, $S_{s23} = \frac{B}{\gamma}-\frac{g(S_{s23}, I_{s23, 2}, \;A_{s23, 2}\;) (I_{s23, 2} \;+ \alpha_2 A_{s23, 2}\;)}{\gamma} - \frac{h(S_{s23},\; I_{s23, 3}, \;A_{s23, 3}\;) (I_{s23, 3} \;+ \alpha_3 A_{s23, 3}\;)}{\gamma}$, $E_{s23, 2} = \frac{g(S_{s23}, I_{s23, 2}, \;A_{s23, 2}\;)(S_{s23}\;+ \delta_{22}\;R_{s23, 2}\;)(I_{s23, 2} \;+ \alpha_2 A_{s23, 2}\;)}{S_{s23}\;m_4}$, $I_{s23, 2} = \frac{r_2\xi_2}{m_5} E_{s23, 2}$, $A_{s23, 2} = \frac{(1-r_2)\xi_2}{m_6}\;E_{s23, 2}$, $R_{s23, 2} = \frac{(\delta_{2I} \;I_{s23, 2} \;+ \delta_{2 A}A_{s23, 2}\;)S_{s23}}{\delta_{22}\;g(S_{s23}\;, I_{s23, 2}\;, A_{s23, 2}\;)(I_{s23, 2} \;+ \alpha_2 A_{s23, 2}\;)\;+\;\delta_{23}\;h(S_{s23}\;, I_{s23, 1}\;, A_{s23, 1}\;)(I_{s23, 3} \;+ \alpha_3 A_{s23, 3}\;)\;+\;\gamma S_{s23}},$ $E_{s23, 3} = \frac{h(S_{s23}\;, I_{s23, 3}\;, A_{s23, 3}\;)(S_{s23}\;+ \delta_{23}\;R_{s23, 2}\;)(I_{s23, 3} \;+ \alpha_3 A_{s23, 3}\;)}{S_{s23}\;m_7}$, $I_{s23, 3} = \frac{r_3\xi_3}{m_8} E_{s23, 3}$, $A_{s23, 1} = \frac{(1-r_3)\xi_3}{m_9}E_{s23, 3}$, $R_{s23, 3} = \frac{\delta_{3I}I_{s23, 3} \;+ \delta_{3 A}A_{s23, 3}}{ \gamma }.$

(ⅵ) The case when there is an infection due to first and second strain surviving in the environment, that is, $I_1 \neq0$, $A_1\neq0$, $I_2 = 0$, $A_2 = 0$, $I_3 \neq 0$ and $A_3 \neq 0.$ Here, the endemic equilibrium is $\epsilon_{s13} = (S_{s13}, \; E_{s13, 1}, \; I_{s13, 1},$ $A_{s13, 1}, \; R_{s13, 1}, \; 0, \; 0, \; 0, \; 0, \; E_{s13, 3}, \; I_{s13, 3}, \; A_{s13, 3}, \; R_{s13, 3}).$ Here, $S_{s13} = \frac{B}{\gamma}-\frac{f(S_{s13}, I_{s13, 1}\;, A_{s13, 1}\;) (I_{s13, 1} \;+ \alpha_1\; A_{s13, 1}\;)}{\gamma} - \frac{h(S_{s13}\;, I_{s13, 3}\;, A_{s13, 3}\;) (I_{s13, 3} \;+ \alpha_3 A_{s13, 3}\;)}{\gamma}$, $E_{s13, 1} = \frac{f(S_{s13}, I_{s13, 1}\;, A_{s13, 1}\;)(S_{s13}\;+ \delta_{11}R_{s13, 1}\;)}{S_{s13}\;m_1}$, $I_{s13, 1} = \frac{r_1\xi_1}{m_2} E_{s13, 1}$, $A_{s13, 1} = \frac{(1-r_1)\xi_1}\;{m_3}E_{s13, 1}$, $R_{s13, 1} = \frac{(\delta_{1I}\;I_{s13, 1} \;+ \delta_{2 A}\;A_{s13, 1}\;)S_{s13}}\;{\delta_{11}\;f(S_{s13}\;, I_{s13, 1}\;, A_{s13, 1}\;)(I_{s13, 1} \;+ \alpha_1 \;A_{s13, 1}\;)\;+ \delta_{13}\;h(S_{s13}, I_{s13, 3}\;, A_{s13, 3}\;)(I_{s13, 3} \;+ \alpha_3 A_{s13, 3}\;) \;+ \gamma S_{s13}},$ $E_{s13, 3} = \frac{h(S_{s13}\;, I_{s13, 3}\;, A_{s13, 3}\;)(S_{s13}\;+ \delta_{13}\;R_{s13, 2}\;)}{S_{s13}\;m_7}$, $I_{s13, 3} = \frac{r_3\xi_3}\;{m_8} E_{s13, 3}$, $A_{s13, 1} = \frac{(1-r_3)\xi_3}\;{m_9}E_{s13, 3}$, $R_{s13, 3} = \frac{\delta_{3I}I_{s13, 3} \;+ \delta_{3 A}A_{s13, 3}}{ \gamma }.$

(ⅶ) The case when there is infection due to first, second and third strain in the environment, that is, $I_1 \neq0$, $A_1\neq0$, $I_2 \neq 0$, $A_2\neq 0$, $I_3 \neq 0$ and $A_3 \neq 0.$ Here, the endemic equilibrium is $\epsilon_{s123} = (\tilde{S}, \tilde{E_1}, \tilde{I_1}, \tilde{A_1}, \tilde{R_1}, \tilde{E_2}, \tilde{I_2}, \tilde{A_2}, \tilde{R_2}, \tilde{E_3}, \tilde{I_3}, \tilde{A_3}, \tilde{R_3}).$ Here, $\tilde{S} = \frac{B}{\gamma}-\frac{f(\tilde{S}, \tilde{I_1}, \tilde{A_1}) (\tilde{I_1} + \alpha_1 \tilde{A_1})}{\gamma} - \frac{g(\tilde{S}, \tilde{I_2}, \tilde{A_2}) (\tilde{I_2} + \alpha_2 \tilde{A_2})}{\gamma}- \frac{h(\tilde{S}, \tilde{I_3}, \tilde{A_3}) (\tilde{I_3} + \alpha_3 \tilde{A_3})}{\gamma}$, $\tilde{E_1} = \frac{f(\tilde{S}, \tilde{I_1}, \tilde{A_1})(\tilde{S}+ \delta_{11}\tilde{R_1}+\delta_{21}\tilde{R_2})\;(\tilde{I_1} + \alpha_1 \tilde{A_1})}{\tilde{S}m_1}$, $\tilde{I_1} = \frac{r_1\xi_1}{m_2} \tilde{E_1}$, $\tilde{A_1} = \frac{(1-r_1)\xi_1}{m_3}\tilde{E_1}$, $\tilde{R_1} = \frac{(\delta_{1I}\tilde{I_1} + \delta_{1 A}\tilde{A_1})\tilde{S}}{\delta_{11}f(\tilde{S}, \tilde{I_1}, \tilde{A_1})\;(\tilde{I_1} + \alpha_1 \tilde{A_1})+\delta_{12}g(\tilde{S}, \tilde{I_2}, \tilde{A_2})\;(\tilde{I_2} + \alpha_2 \tilde{A_2})+\delta_{13}h(\tilde{S}, \tilde{I_3}, \tilde{A_3})\;(\tilde{I_3} + \alpha_3 \tilde{A_3}) +\gamma \tilde{S}},$ $\tilde{E_2} = \frac{g(\tilde{S}, \tilde{I_2}, \tilde{A_2})(\tilde{S}+ \delta_{12}\tilde{R_1}+\delta_{22}\tilde{R_2})\;(\tilde{I_2} + \alpha_2 \tilde{A_2})}{\tilde{S}m_4}$, $\tilde{I_2} = \frac{r_2\xi_2}{m_5} \tilde{E_2}$, $\tilde{A_2} = \frac{(1-r_2)\xi_2}{m_6}\tilde{E_2}$, $\tilde{R_2} = \frac{(\delta_{2I} \tilde{I_2} + \delta_{2 A}\tilde{A_2})\tilde{S}}{\delta_{21}f(\tilde{S}, \tilde{I_1}, \tilde{A_1})\;(\tilde{I_1} + \alpha_1 \tilde{A_1})+\delta_{22}g(\tilde{S}, \tilde{I_2}, \tilde{A_2})\;(\tilde{I_2} + \alpha_2 \tilde{A_2})+\delta_{23}h(\tilde{S}, \tilde{I_3}, \tilde{A_3})\;(\tilde{I_3} + \alpha_3 \tilde{A_3})+\gamma \tilde{S}},$ $\tilde{E_3} = \frac{h(\tilde{S}, \tilde{I_3}, \tilde{A_3})(\tilde{S}+\delta_{13}\tilde{R_1}+ \delta_{23}\tilde{R_2})\;(\tilde{I_3} + \alpha_3 \tilde{A_3})}{\tilde{S}m_7}$, $\tilde{I_3} = \frac{r_3\xi_3}{m_8} \tilde{E_3}$, $\tilde{A_3} = \frac{(1-r_3)\xi_3}{m_9}\tilde{E_3}$, $\tilde{R_3} = \frac{\delta_{3I}\tilde{I_3} + \delta_{3 A}\tilde{A_3}}{ \gamma }.$ □

3.3.   Local stability at a disease free equilibrium

This subsection discusses the local stability of disease free equilibrium ($\mathcal{DFE}$). The Jacobian matrix of order thirteen of the system (2.4) is in Eq (3.10).

The appendix section contains all the non zero terms of the matrix $A$. It is hard to determine the further dynamics with the matrix $A$ due to the course of constraints.

Theorem 3. The disease free equilibrium ($\mathcal{DFE}$) of the mathematical model (2.4) is locally asymptotic stable if the basic reproduction $\mathfrak{R}(\mathbb{E}_0)$ is less than one and unstable for greater than one.

Proof. The Jacobian $J_{\mathcal{DFE}}$ of the mathematical model (2.4) at the initial stage when $t = 0$, the infection is not spread (disease free equilibrium) is,

The above matrix $J_{\mathcal{DFE}}$ has the characteristic polynomial as,

Here, $F = f(\frac{B}{\gamma}, 0, 0), G = g(\frac{B}{\gamma}, 0, 0), H = h(\frac{B}{\gamma}, 0, 0)$. From the characteristic polynomial, four eigenvalues of Eq (3.11) are real and negative, and the other nine are the zeros of Eq (3.12).

Here, $A_0 = 1, \; A_1 = m_1+m_2+m_3, \; A_2 = m_1 m_2 \left(1-\mathfrak{R}_{01}^I\right)+m_1 m_3 \left(1-\mathfrak{R}_{01}^A\right)+m_2 m_3,$$\; A_3 = m_1 m_2 m_3 \left(1-\mathfrak{R}_{01}\right), \; B_0 = 1, \; B_1 = m_4+m_5+m_6, \;$$B_2 = m_4 m_6 \left(1-\mathfrak{R}_{02}^A\right)+m_4 m_5 \left(1-\mathfrak{R}_{02}^I\right)+m_5 m_6, \;$$B_3 = m_4 m_5 m_6 \left(1-\mathfrak{R}_{02}\right), \; C_0 = 1, \; C_1 = m_7 + m_8 +m_9, \;$$C_2 = m_7 m_9 \left(1-\mathfrak{R}_{03}^A\right)+m_7 m_8 \left(1-\mathfrak{R}_{03}^I\right)+m_8 m_9,$ and $C_3 = m_7 m_8 m_9 \left(1-\mathfrak{R}_{03}\right).$

By the Liénard Chipart criterion, a polynomial has all its zeros with negative real part if $A_0 > 0, \; A_1 > 0, \; A_2 > 0, \; A_3 > 0, \; B_0 > 0, \; B_1 > 0, \; B_2 > 0, \; B_3 > 0, \; C_0 > 0, \; C_1 > 0,$$\; C_2 > 0, \; C_3 > 0, \; A_1A_2-A_0A_3 > 0, \; B_1B_2-B_0B_3 > 0,$ and $C_1C_2-C_0C_3 > 0.$ It is clear that the conditions hold if $\mathfrak{R}_{01} < 1, \; \mathfrak{R}_{02} < 1$ and $\mathfrak{R}_{02} < 1$.

As $A_1 A_2-A_0 A_3 = (m_1^2 (m_3 (1-\mathfrak{R}_{01}^A)+m_2 (1-\mathfrak{R}_{01}^I))$ $+m_1 (m_3 m_2 (-\mathfrak{R}_{01}^A-\mathfrak{R}_{01}^I+\mathfrak{R}_{01}+2)+m_3^2 (1-\mathfrak{R}_{01}^A)+m_2^2 (1-\mathfrak{R}_{01}^I))+ m_2 m_3$ $(m_2+m_3)),$ $B_1B_2-B_0B_3 = (m_4^2 (m_6 (1-\mathfrak{R}_{02}^A)+m_5 (1-\mathfrak{R}_{02}^I))$$+ m_4 (m_6 m_5 (-\mathfrak{R}_{02}^A-\mathfrak{R}_{02}^I+\mathfrak{R}_{02}+2)+m_6^2 (1-\mathfrak{R}_{02}^A)+m_5^2 (1-\mathfrak{R}_{02}^A))$$+m_5 m_6 (m_5+m_6))$, and $C_1C_2-C_0C_3 = (m_7^2 (m_9 (1-\mathfrak{R}_{03}^A) +m_8 (1-\mathfrak{R}_{03}^I))+$$m_7 (m_9 m_8 (-\mathfrak{R}_{03}^A-\mathfrak{R}_{03}^I+\mathfrak{R}_{03}+2)+m_9^2 (1-\mathfrak{R}_{03}^A) +m_8^2 (1-\mathfrak{R}_{03}^I))+m_8 m_9 (m_8+m_9))$.

Evidently all the thirteen eigenvalues of the Jacobian at disease free equilibrium have real part negative if and only if $\mathfrak{R}_{01} < 1, \; \mathfrak{R}_{02} < 1$ and $\mathfrak{R}_{02} < 1$. This indicates asymptotic local stability of mathematical model (2.4) with the basic reproduction number less than one and instability otherwise. □

4.   Numerical simulation

This section studies importance and the effect of each compartment with different incidence rates (transfer of the infection). Considering the three incidence functions $f(S, I_1, A_1), \; g(S, I_2, A_2)$ and $h(S, I_3, A_3)$ have an impact that cannot be neglected and further clarifies the need to choose the perfect incidence rate in the mathematical model.

Bilinear incidence rate $\beta*\text{Susceptible}$ is used when the susceptible compartment has direct linear impact on the transmission, and all other compartments play a negligible effect. Beddington DeAngelis function $\frac{\beta*\text{Susceptible}}{1+\zeta_1*\text{Susceptible}+\zeta_2*\text{Infected}+\zeta_3*\text{Asymptomatic}}$ shows the nonlinear impact of the infected, asymptomatic and susceptible class on the transmission of the disease. Non-monotone function $\frac{\beta*\text{Susceptible}}{1+\zeta_1*\text{Infected}^2}$ or $\frac{\beta*\text{Susceptible}}{1+\zeta_1*\text{Asymptomatic}^2}$, Crowley Martin function $(\beta*\text{Susceptible})/(1+\zeta_1*\text{Susceptible}+\zeta_2*\text{Infected}+$$\zeta_3*\text{Asymptomatic} +\zeta_1\zeta_2*\text{Infected}*\text{Susceptible}$$+\zeta_1*\zeta_3*\text{Susceptible}*\text{Asymptomatic}+\zeta_2*\zeta_3*\text{Infected}*\text{Asymptomatic})$, saturated function $\frac{\beta*\text{Susceptible}}{1+\zeta_1*\text{Susceptible}}$ or $\frac{\beta*\text{Susceptible}}{1+\zeta_2*\text{Infected}}$ or $\frac{\beta*\text{Susceptible}}{1+\zeta_3*\text{Asymptomatic}}$ and specific nonlinear function $(\beta*\text{Susceptible})/(1+\zeta_1*\text{Susceptible}+\zeta_2*\text{Infected}$$+\zeta_3*\text{Asymptomatic} +\zeta_4*\text{Infected}*\text{Susceptible}+$$\zeta_5*\text{Susceptible}*\text{Asymptomatic}+\zeta_6*\text{Infected}*\text{Asymptomatic})$ all describe the non-linear relationship of the susceptible, infected and asymptomatic compartments in one or another way. The definition of the parameter used in these incidence rates also makes them different in one or another way.

Figure 2 is the result of the simulation with initial values of the variables as $\{81000, 7000,112,100, 10, 6000,203,105, 60, 5200,100,100, 10\}$ with hypothetical values of parameters as $\alpha_1 = 0.79, \; \alpha_2 = 0.85, \; \alpha_3 = 0.78, \; \gamma = 2, \; \delta_{11} = 0.57, \; \delta_{12} = 0.39, \;$$\delta_{22} = 0.3, \; \delta_{13} = 0.4, \; \delta_{21} = 0.59, \; \delta_{23} = 0.459, \; \delta_{1I} = 0.52, \; \delta_{1A} = 0.848, \;$$\delta_{2I} = 0.94, \; \delta_{2A} = 0.68, \; \delta_{3I} = 0.88, \; \delta_{3A} = 0.548, \; r_1 = 0.7, \; r_2 = 0.67, \; r_3 = 0.7, \;$$\xi_1 = 0.45, \; \xi_2 = 0.29, \; \xi_3 = 0.27, \; B = 2*N(0)$, and the parameters included for different choices of incidence rates ($f(S, I_1, A_1), g(S, I_2, A_2)$ and $h(S, I_3, A_3)$) vary.

Figure 2(a) has parametric values as $\beta_1 = 0.88, \; \beta_2 = 0.8\;$ and $\beta_3 = 0.9$ whose graphical plot shows how there is sudden decrease in the susceptible class $S(t)$ and rise in the exposed class $E_3(t)$. The decrease in the exposed class of strain 1 and strain 2 is also observed while the infected class of the third strain rises. Figure 2(b) has the parametric values $\beta_1 = 0.8, \; \beta_2 = 0.76, \; \beta_3 = 0.88, \; \zeta_1 = 0.012, \; \zeta_2 = 0.152, \; \zeta_3 = 0.035, \; \zeta_4 = 0.012, \;$$\zeta_5 = 0.11, \; \zeta_6 = 0.032, \; \zeta_7 = 0.014, \; \zeta_8 = 0.022, \; \zeta_9 = 0.112$. The decline in the number of individuals in the susceptible class and the wave in number of individuals in the exposed class are easily noticed at the time span of one of all strains. There is a rise in the number of infected and asymptomatic class individuals as well. Figure 2(c) has the parametric values $\beta_1 = 0.87, \; \beta_2 = 0.79, \; \beta_3 = 0.85, \; \zeta_1 = 0.018, \; \zeta_2 = 0.07, \; \zeta_3 = 0.0128$. The line plot shows a sudden decrease in the susceptible class at time $0.1$, and at this period exposed classes of all the strain rises, and a little jump in infected class of respected strains are observed. Figure 2(d) has the parametric values $\beta_1 = 0.77, \; \beta_2 = 0.9, \; \beta_3 = 0.75, \; \zeta_1 = 0.012, \; \zeta_2 = 0.02, \; \zeta_3 = 0.01$ with the graphical plot similar to Figure 2(c) but large variation in the number of susceptible and exposed class individuals. Figure 2(e) has the parametric values $\beta_1 = 0.77, \; \beta_2 = 0.9, \; \beta_3 = 0.75, \; \zeta_1 = 0.03, \; \zeta_2 = 0.04, \; \zeta_3 = 0.135, \; \zeta_4 = 0.028$ with the line plot observed to have a rapid decrease in the susceptible class at time $0.1$, and at this period exposed classes of strain 1 rises. Also there is a jump in infected class and asymptomatic infected class of strain 1. Figure 2(f) has the parametric values $\beta_1 = 0.77, \; \beta_2 = 0.8, \; \beta_3 = 0.85, \; \zeta_1 = 0.016, \;$$\zeta_2 = 0.37, \; \zeta_3 = 0.02, \; \zeta_4 = 0.015, \; \zeta_5 = 0.024, \; \zeta_6 = 0.01388, \;$$\zeta_7 = 0.027, \; \zeta_8 = 0.0262, \; \zeta_9 = 0.0125, \; \zeta_{10} = 0.012$, and the plot has an increase in the susceptible class individuals and a fall in the exposed classes of all the strains for the same, and a negligible increase in the infected individuals is also observed. Figure 2(g) has the parametric values $\beta_1 = 0.787, \; \beta_2 = 0.8, \; \beta_3 = 0.87, \; \zeta_1 = 0.04, \; \zeta_2 = 0.03, \; \zeta_3 = 0.06261$, and it is similar to Figure 2(f). Here, the plot indicates the certain increase in the susceptible class individuals from time $0.2$ to $0.6$ and decrement in the exposed classes of all the strains for the same. An increase in the infected individuals is also observed. Figure 2(h) has the parametric values $\beta_1 = 0.7, \; \beta_2 = 0.85, \; \beta_3 = 0.75, \; \zeta_1 = 0.033, \; \zeta_2 = 0.025, \; \zeta_3 = 0.016.$ The two-dimensional line plot shows a sudden decrease in the susceptible class at time almost near to zero, and at this period exposed classes of all the strain rise and a little jump in the number of individuals in the other classes of respected strains is marked. Figure 2(i) has the parametric values $\beta_1 = 0.88, \; \beta_2 = 0.9, \; \beta_3 = 0.92, \; \zeta_1 = 0.02, \; \zeta_2 = 0.25, \; \zeta_3 = 0.014$ with the line plot observed to have a large decrease in the susceptible class at one third time of $0.2$, and at this period exposed classes of all the strains rises. Huge variation in the exposed classes of the strains is noticed in the time span of zero to two. Also there is a jump in infected class and asymptomatic infected class of all strains. Figure 2(j) has the parametric values $\beta_1 = 0.8, \; \beta_2 = 0.9, \; \beta_3 = 0.88, \; \zeta_1 = 0.0327, \;$$\zeta_2 = 0.014, \; \zeta_3 = 0.035, \; \zeta_4 = 0.018, \; \zeta_5 = 0.016, \;$$\zeta_6 = 0.014, \; \zeta_7 = 0.01, \; \zeta_8 = 0.0145, \; \zeta_9 = 0.019, \;$$\zeta_{10} = 0.014, \; \zeta_{11} = 0.0217, \; \zeta_{12} = 0.019, \; \zeta_{13} = 0.0038, \; \zeta_{14} = 0.014, \; \zeta_{15} = 0.0156, \;$$\zeta_{16} = 0.0245, \; \zeta_{17} = 0.0128, \; \zeta_{18} = 0.017$ and is very largely similar to Figure 2(f), and the same dynamics are observed.

Figure 3 interprets the impact of the incidence rates according to the cases in Table 1 on the total number of infected individuals remarkably. Case (a), case (d), case (i), case (e) and case (h) shows the high rise in the number of infected classes. Meanwhile, case (g) and case (j) have a small rise. Case (c) and case (f) show an increase in the number of total infected individuals at the time of $0.25$ and then decrease. Case (b) also increases the total number of infected individuals slowly from a time-span of zero to one. The importance of choosing an incidence rate could lead the mathematical model to interpret different scenarios clearly.

5.   Results and discussion

Predictions made with the mathematical models help to control the forthcoming dangerous situations and handle them smartly. An epidemiological model (2.4) has been formulated to understand the transmission behavior of the multi-strain model with respect to the choice of incidence rate function numerically. An evaluation of the following mathematical and epidemiological results of the proposed model has been discussed in the paper:

$(i)$ The solutions of the system of thirteen differential Eq (2.4) is non-negative and bounded for all times $t > 0$, when initial data is non-negative (Theorem (1)). Thus, the formulated mathematical model (2.4) is mathematically and epidemiologically well-posed in Section 2.

$(ii)$ The three-strain epidemic model has the basic reproduction number $\mathfrak{R}_0$, the maximum of the three $\mathfrak{R}_{01}$, $\mathfrak{R}_{0 2}$ and $\mathfrak{R}_{0 3}.$ $\mathfrak{R}_0$ in Section 3.2. The reproduction number $\mathfrak{R}_0$ defines the number of new infections at the time of emerging of a new strain. The three-strain model has a disease-free equilibrium ($\mathcal{DFE}$) with local-asymptotic stability whenever the associated basic reproduction number $\mathfrak{R}_0$ $(\mathbb{E}_0)$ is lesser than a unit (Theorem 3). Biologically, if the reproduction number is less than a unit, an infectious host will get exposed to less than a host in the tenure of his infection, leading to contraction in the number of cases of the infection.

$(iii)$ The proposed model has eight endemic equilibrium according to the strain influence and its impact in Section 3.2. The existence of the strains and their nature of co-existence and competence leads to the scenarios discussed in the Theorem (3).

$(iv)$ The effect of incidence rate choice leads to different effects on the number of infected persons. Each incidence rate type has equal importance and definition defined in Section 4. Biologically in the transmission of the infection different compartments plays role differently that is described through incidence rate in the differential equation modeling. In both epidemic and virus dynamics models, this general incidence function can represent a wide range of potential incidence functions. The general incidence at which people transition from the class of susceptible individuals to the class of infective individuals has been the focus of such epidemiological models. These common incidences have primarily been modeled using functional responses of the bilinear and Holling types ^[21,29]. Such tactics may involve treatments, vaccines, isolation and educational campaigns for epidemic diseases ^[44,45]. Mathematical models are now crucial tools for understanding how infectious diseases spread and are managed. Incidence function decides the effect of the variables and parameters on the virus spread; hence, it is important to consider the type of function needed according to the flowchart of the infection.

6.   Conclusions

Incidence rates play a crucial role in the epidemiological model formulation. The rapid appearance of any disease can be governed totally by the incidence rate equal to the affected host population in the tenure. Choosing correct incidence rate during the mathematical model formulation could give accurate predictions. Every infectious disease mutates following the host and environment, which shows the importance of multi-strain mathematical models. A variant of an infectious disease can form an epidemic or pandemic during the period.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors have no words of conflict.

Appendix

Entries of the Jacobian matrix of order thirteen associated with the system (2.4) are