Monotonicity properties arising in a simple model of Wolbachia invasion for wild mosquito populations

1.   Introduction

Hyperspectral Image (HSI) is the simultaneous imaging of target areas in dozens to hundreds of continuous spectral bands ^[1,2,3,4]. It effectively integrates the spatial and spectral information in the imaging scene, with strong target detection ability and better material identification ability ^[5,6,7,8]. It is widely used in agriculture and forestry, geological exploration, marine exploration, Environmental monitoring and other fields ^[9,10,11,12]. However, HSI is characterized by high data dimension, large information redundancy and high correlation between bands, which brings great difficulties to its processing and classification ^{[13,14,15,16,17,18,19,20,21,22,23]}. Therefore, how to reduce the redundant information of the data, extract the features of the hyperspectral images effectively, and realize the accurate classification of the hyperspectral images are the hot and difficult issues in the current hyperspectral image processing and classification research.

Sample labeling of hyperspectral images often requires expert knowledge and experience, so the cost of sample labeling is high ^[24,25,26]. When the labeled samples are limited, semi-supervised learning can explore the useful information of the unlabeled samples to participate in the model training and reduce the labeling cost ^[27,28]. In the field of machine learning, semi-supervised learning acquires knowledge and experience from a small number of labeled samples. The usable information is mined from a large number of unlabeled samples, which can improve the classification accuracy ^[29,30,31]. Therefore, a large number of scholars have studied the semi-supervised learning for remote sensing images. Camps-Valls et al. ^[32] proposed a graph-based hyperspectral image classification method, and constructed the graph structure through the graph method. The data context information based on the composite kernel is integrated, and the Nystrom method is used to speed up classification. Yang et al. ^[33] proposed a semi-supervised band selection technique for hyperspectral image classification. A metric learning method has been used to measure the features of hyperspectral images, and a semi-supervised learning method has been used to select a subset of valid bands from the original bands. Tan et al. ^[34] proposed a hyperspectral image classification method based on segmentation integration and semi-supervised support vector machine. The spatial information of the tag samples is extracted by using a segmentation algorithm to filter the samples, and classified based on semi-supervised learning. Samiappan et al. ^[35] combined active learning and co-training to perform semi-supervised classification of hyperspectral images. The initial classification model is trained according to the labeled samples, and the heuristic active learning is performed on the unlabeled samples. Combined with the original data, the labeled samples are divided into views, and the unlabeled samples with high heuristic values are selected to join the training samples. Zhang et al. ^[36] used a semi-supervised classification method based on hierarchical segmentation and active learning to extract spatial information from hyperspectral images, the training set is updated iteratively by using the information of a large number of unlabeled samples to complete the hyperspectral image classification. In addition, some other methods are also proposed in recent years ^{[37,38,39,40,41,42,43,44,45]}.

In hyperspectral images, each pixel corresponds to a spectral curve that reflects its inherent physical, chemical and optical properties. The main basis of hyperspectral image classification is to use the feature information of different pixels to label the pixels belonging to different landmarks and obtain the corresponding classification maps ^[46,47]. Therefore, a large number of scholars have studied hyperspectral image classification. Melgani et al. ^[48] proposed a hyperspectral image classification method based on support vector machines (SVM). The kernel function is introduced to solve the nonlinear separable problem and avoid the curse of dimensionality. Ratle et al. ^[49] introduced neural networks into hyperspectral image classification. In the training phase, the loss function is optimized to avoid local optimization. Chen et al. ^[50] constructed a hyperspectral image classification model based on sparse representation, and compared the classification results of common machine learning methods. In order to improve the shortcomings of sparse representation in dealing with nonlinear problems, Chen et al. ^[51] proposed a kernel sparse representation technique. In addition, Cui et al. ^[52] proposed a multiscale sparse representation algorithm for robust hyperspectral image classification. Automatic and adaptive weight allocation schemes based on spectral angle ratio are incorporated into the multi-classifier framework to fuse sparse representation information at all scales. Tang et al. ^[53] proposed two sparse representation algorithms based on manifolds to solve the instability problem of sparse algorithms. The regularization and local invariance techniques are used, and two manifold-based regularization items are merged into the ${l}_{1}$-based objective function. Wang et al. ^[54] applied the neighborhood-cutting technique to sparse representation, and combined the joint spatial and spectral sparse representation classification method. Wang and Celik ^[55] improved the classification accuracy of hyperspectral images by combining context information in the sparse coefficient domain. Hu et al. ^[56] proposed two weighted kernel joint sparse representation methods, which determine the calculation weight by calculating the kernel similarity between adjacent pixels. Xue et al. ^[57] presented two novel sparse graph regularization methods, SGR and SGR with total variation. Yang et al. ^[58] studied the effect of the p-norm distance metric on the minimum distance technique, and proposed a supervised-learning p-norm distance metric to optimize the value of p. Zhang et al. ^[59] proposed a multi-scale dense network for HSI classification that made full use of different scale information in the network structure and combined scale information throughout the network. Liu et al. ^[60] proposed a class-wise adversarial adaptation method in conjunction with the class-wise probability MMD as the class-wise distribution adaptation network. Wang et al. ^[61] proposed the graph-based semi-supervised learning with weighted features for HSI classification. In addition, some new other methods are also proposed by a lot of researchers ^{[62,63,64,65,66,67,68,69,70,71]}.

To sum up, hyperspectral images contain rich spectral and spatial information of earth surface features, which increases the processing and analysis difficulties. In addition, the training samples of actual hyperspectral images are small and there is a sample labeling problem. The local binary pattern, sparse representation and mixed logistic regression model are used in this paper. A new hyperspectral image feature extraction method based on local binary pattern is proposed to obtain texture features of hyperspectral images and enrich hyperspectral image sample information. A sample selection strategy based on active learning is designed to determine the unlabeled samples. Based on these, a new sample labeling method based on neighborhood information and priority classifier discrimination is deeply studied to expand the training samples. And a novel classification method based on texture features and semi-supervised learning is studied to improve the classification accuracy of remote sensing images.

The main contributions of this paper are described as follows.

(ⅰ) A novel a classification method of hyperspectral remote sensing images based on texture features and semi-supervised learning is proposed by using local binary pattern, sparse representation, hybrid logistic regression.

(ⅱ) The local binary pattern is used to effectively extract the features of spatial texture information of remote sensing images and enrich the feature information of samples.

(ⅲ) A multiple logistic regression model is used to optimally select unlabeled samples, which are labeled by using neighbourhood information and priority classifier discrimination to achieve pseudo-labeling of unlabeled samples.

(ⅳ) A novel classification method of hyperspectral remote sensing images based on semi-supervised learning is proposed to effectively achieve accurate classification of hyperspectral images.

2.   Basic methods

In here, the local binary pattern (LBP) and sparse expression are introduced in order to clearly describe the basic theories of these methods.

2.1.   Local binary pattern (LBP)

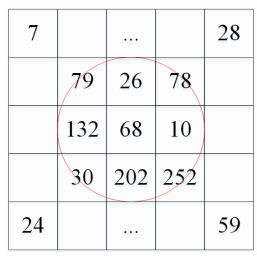
LBP is a feature extraction method, which can extract spatial texture information of images. Texture, which is widely used in image processing and image analysis, represents the slow change or periodic change of the surface structure of the object ^[72]. LBP is also widely used in feature extraction of hyperspectral images due to the simple structure and easy calculation. Give the center pixel ${g}_{c}({x}_{c}, {y}_{c})$ and the neighborhood pixel ${g}_{p}$, which are described as follow.

where, ${g_p}(p = 0, 1, ..., P - 1)$ represents the coordinate values of P pixels uniformly distributed on the circular domain with ${g_c}$ as the centre and R as the radius. The quantized texture feature form of one region is shown in Figure 1.

2.2.   Sparse expression

Sparse representation means that the signal can be approximately represented by using linear combination of the atoms in the dictionary. Now, $X = [{X_1}, {X_2}, ..., {X_c}] \in {R^D}$ is given as the HSI pixel and $D$ is the number of image bands. In here, ${X_i} = [{x_{i1}}, {x_{i2}}, ..., {x_{i{N_c}}}] \in {R^D}$, ${N_c}$ represents the number of samples in the class $i$.

For samples in the class $i$, it can be approximated as follow.

where, ${X_i}$ represents a sparse sub-dictionary of the samples in the class $i$. ${\alpha _i}$ represents the sparse vector of test samples $y$, which contains only a few non-zero values.

In order to obtain the sparsest vector ${\alpha _i}$, the following formula is solved.

where, ${\left\| {{\text{ }}{\text{. }}} \right\|_0}$ is a ${l_0}$ norm, which represents the number of non-zero atoms in the vector, also known as sparsity. A is a sparse dictionary. It is a NP-hard problem to solve the Eq (5) directly. Under some conditions, the minimization solving problem (${l_0}$) is approximated by the minimization solving problem (${l_1}$), which can be relaxed.

Furthermore, the solution can be converted to the following expression.

where, $\varepsilon$ represents the refactoring error. Orthogonal matching pursuit (OMP) algorithm is used to solve the expression (7). After the sparsity coefficient is calculated, the reconstruction residual for each class of the test samples $y$ can be calculated.

where, there is $i \in \{ 1, 2, ..., C\}$.

Finally, the reconstruction residuals of all dictionaries are compared. The minimum residual is the classification y.

3.   A sample labelling method based on neighborhood information and priority classifier discrimination

In hyperspectral remote sensing image classification, the attribute characteristics of each ground feature are subordinated to a specific distribution. If the number of training samples does not reach the amount that depicts the distribution of the ground feature, it will affect the subsequent classification results. In practical applications, there are difficulties, such as fewer labeled samples, difficulty in manual labeling, and time-consuming and labor-intensive problems and so on. Therefore, a new sample labeling method based on neighborhood information and priority classifier discrimination is proposed to obtain the learned pseudo labeled samples in order to expand the labeled samples and improve the classification accuracy of model.

3.1.   A sample selection method based on multiple logistic regression

Before the samples are labeled, sample selection is required. This is because if all unlabeled samples are labeled directly, all unlabeled samples need to be labeled, which will cost a lot of computation time. Moreover, due to the small number of initial labeled samples and the limited available information, it is difficult to label some samples with a certain accuracy. The mislabeled samples obviously affect the classification accuracy of model. The main objective of the sample selection strategy is to select the unlabeled samples with the largest amount of information. These unlabeled samples can construct a valuable training set after labeling, which can effectively promote the improvement of classification results. Therefore, a sample selection method based on multiple logistic regression is proposed to realize the selection of samples.

The classified probability matrix $p\left({y}_{i}^{k}|{x}_{i}\right)$ of each sample by using multiple logistic regression model has a large amount of information that can be mined. The multiple logistic regression classifier is modeled by discriminant Bayesian decision model. According to the generalized linear model, it can be obtained as follow.

The specific expression of multiple logistic regression is described as follow.

where, $g\left(x\right) = [{g}_{1}\left(x\right), {g}_{2}\left(x\right), \dots, {g}_{f}\left(x\right){]}^{T}$ is the feature vectors of the input, and $\eta = [{\eta }_{1}^{T}, {\eta }_{2}^{T}, \dots {\eta }_{k}^{T}]$ represents the regression parameter vector of the classifier. It is worth noting that the feature vector is often represented by introducing the kernel, which is not only used to improve the indivisibility, but also obtain the better classifier by training samples. Generally, the kernel function is radial basis function (RBF), which is described as follow.

After the feature vector is determined, the regression parameter $\eta$ of model is only determined, and the probability matrix $p\left({y}_{i}^{k}|{x}_{i}\right)$ of each unlabeled sample belonging to each class is determined. The sample amount of information is determined by the Breaking Ties (BT) and the Least Confidence (LC). In this paper, the BT is selected to determine the amount of information.

The BT shows the similarity between the two classifications by comparing the difference between the maximum category probability and the sub-maximum category probability. The difference is smaller, the similarity between the two types of samples is greater. The uncertainty is greater, the amount of information is greater. ${S}_{i}$ is the similarity between classifications, which is described as follow.

The ${S}_{i}$ is finally sorted in ascending order. $p\left({y}_{i}^{k}|{x}_{i}\right)$ is the obtained probability matrix of each sample by multiple logistic regression classifier. $maxp\left({y}_{i}^{k}|{x}_{i}\right)$ represents the largest value in the obtained probability matrix, $secondmax\left(p\left({y}_{i}^{k}|{x}_{i}\right)\right)$ represents the second largest value in the obtained probability matrix. $k$ is the number of regression parameters.

3.2.   A sample labeling method based on neighborhood information and priority classifier discrimination

The features of hyperspectral remote sensing images have some correlation. The ground objects are closer, the correlation is stronger. In the research of sample labeling, spatial neighborhood information based on training samples is widely used. However, due to the unknown central pixel and the lack of sufficient information, the neighborhood information of unlabeled samples is relatively less in the research of sample labeling. Generally, each pixel label on hyperspectral image must be consistent with one pixel label in its neighborhood. This property can be used to label the unlabeled samples. The label information of training samples around the unlabeled samples can be used to discriminate the unlabeled samples. The labeling discrimination method based on neighborhood information centers on the sample to be labeled. The unlabeled samples are labeled with a block diagram. All the occurrences of sample labels are recorded and denoted as the neighborhood information. The labeled samples are used to train the classifier and classify the unlabeled samples. Determine whether the predicted sample label by the classifier appears in the neighborhood information of the unlabeled samples. If it appears, the predicted label by the classifier is the sample label. Otherwise, the samples are put into the unlabeled samples. One of the most important problems is whether the unlabeled samples which satisfy the neighborhood information can be reliably labeled by the classifier. At present, some studies use multiple classifiers to discriminate together and achieve good classification effect. However, how to determine the determination of labels, when the predicted labels by multiple classifiers are inconsistent, but all appear in the neighborhood information of unlabeled samples.

Therefore, a sample labeling method based on neighborhood information and priority classifier discrimination is proposed in this paper. For unlabeled samples with the neighborhood information, the classifier with the highest priority is used for prediction. If the obtained prediction marker appears in the neighborhood information, its marker is determined. Otherwise, the classifier with the lowest priority is used for prediction. Determine whether the label can be determined until the sample labeling is ended. The sample labeling process based on neighborhood information and priority classifier discrimination is shown in Figure 2.

The sample labeling method is an iterative process. Although it cannot ensure enough training samples around all unlabeled samples at the initial stage of sample labeling, it can ensure that some unlabeled samples are sufficient. The unlabeled samples are labeled and extended to the training set. With each iteration, the training set grows. Those unlabeled samples whose neighborhood training samples are not sufficient may reach the label condition at a certain labeling. The sample labeling method with replacement ensures the sample labeling accuracy to a certain extent, and improves the performance of classifier.

4.   Hyperspectral image classification method based on texture features and semi-supervised learning

4.1.   The idea of hyperspectral image classification

Hyperspectral remote sensing images consist of pairs of continuous spectral bands, which contain rich spectral and spatial information of earth surface features. Some objects that cannot be identified by conventional remote sensing means can be identified in hyperspectral images. However, the abundant data information increases the processing and analysis difficulties, and there are some problems of fewer labeled samples, difficulty in manual labeling and time-consuming and so on. In order to improve the classification accuracy of hyperspectral remote sensing images, a new classification method of hyperspectral remote sensing images based on texture features and semi-supervised learning is proposed in this paper. Firstly, aiming at the problems of high correlation between bands, information redundancy, high dimension and complex processing, LBP is employed to deal with the hyperspectral images. The texture features of hyperspectral images are effectively extracted to enrich the feature information. To solve the problem of limited label samples, a new sample labeling method based on neighborhood information and priority classifier discrimination is proposed in here. Secondly, a sample selection strategy is designed to find some samples from a large number of unlabeled samples. Finally, the sparse representation and mixed logistic regression are applied to achieve a new classification method to effectively achieve accurate classification of hyperspectral images.

4.2.   The model of hyperspectral image classification

The model of hyperspectral image classification method based on texture features and semi-supervised learning is shown in Figure 3.

The detailed implementation steps of hyperspectral image classification method based on texture features and semi-supervised learning are described as follows.

Step 1. Normalize the hyperspectral images. Principal component analysis is used to perform dimensionality reduction.

Step 2. Calculate the texture for each principal component by using LBP. The histogram statistics are performed according to the symmetric rotation invariant equivalence mode. D-dimensional feature data for each layer is used to obtain feature information for each pixel and retain pixel coordinates.

Step 3. The original hyperspectral images are performed by linear discriminant analysis to obtain a projection matrix.

Step 4. The hyperspectral images are mapped into low dimensional images for suitable Euclidean distance analysis by using a projection matrix.

Step 5. Training sample sets and test sample sets are randomly selected from each type of sample according to a certain proportion of low-dimensional images.

Step 6. Calculate the Euclidean distance from all training samples by using ${L_k} = {\left\| {{y_i} - {A_k}} \right\|_2}$ to maintain K training coordinates that are close to the Euclidean distance of each test sample as the sparse dictionary for the test samples.

Step 7. The extracted feature information is loaded into the test samples and corresponding sparse dictionary according to the corresponding coordinates to obtain the test sample set and sparse dictionary.

Step 8. The sparse representation is solved. Orthogonal matching pursuit (OMP) has been used to calculate the sparse coefficient, and the classifications of the test samples is obtained.

5.   Case analysis

5.1.   Experimental data

1) Indian Pines data

The images of Indian pines in northwest Indiana were collected by AVIRIS sensor. The images consist of 145 × 145 pixels and 224 spectral reflection bands with a wavelength range of 0.4~2.5 nm, including 16 types of feature elements. The false color map and real ground object distribution are shown in Figure 4.

2) Salinas Scene data

The AVIRIS spectrometer collects images of the Salinas Valley in California, USA, with a size of 512 × 217 pixels and a total of 224 bands. After the bands covering the water absorption area are removed, 204 bands are used, including 16 types of ground feature elements. The false color map and the real ground object distribution are shown in Figure 5.

3) Pavia University data

Images of the Italian University of Pavia campus taken by the Rosis Spectrometer. It is 610 × 340 pixels in size and has a total of 115 wavebands. The 103 wavebands after the wavebands covering the water-absorbing region contain a total of 9 types of features are removed. The false color map and the real ground object distribution are shown in Figure 6.

In the experiment, 10% of each type of ground object of the three kinds of data is randomly selected as the training samples, and the rest is the test samples.

5.2.   Evaluation criteria

Confusion Matrix (CM) is usually used in the classification and evaluation of hyperspectral images. A confusion matrix is generally defined as follow.

where, n denotes the number of objects in the category, ${p}_{ij}$ represents the number of samples belonging to the class i that are assigned to the class j. The total amount of data in each row denotes the true number of objects in the category. The total amount of data in each column represents the total number of samples.

Based on the confusion matrix, three classification indexes can be obtained, which are Overall Accuracy (OA), Average Accuracy (AA) and Kappa coefficient.

where, N represents the total number of samples in the classification. ${p}_{ii}$ represents the number of correctly classified samples of the class i. OA represents the probability that the classified result corresponds to its true label for each random sample.

where, ${N}_{i}$ represents the total number of samples for the first category in the class i. $C{A}_{i}$ represents the probability that category i is correctly classified.

The Kappa coefficient comprehensively considers the number of correctly classified objects and the error of misclassified objects on the confusion matrix.

5.3.   Parameter determination and analysis

5.3.1.   Parameter settings

In the experiment, a large number of alternative values are tested, and some classical values are selected from literatures, these parameter values are experimentally modified until the most reasonable parameter values are determined. These selected parameter values have obtained the optimal solution, so that they can accurately and efficiently verify the effectiveness.

5.3.2.   Sample selection methods

The quality of sample selection directly affects the efficiency of the experiment, and also affects the performance of classifier. In order to select the best samples, the experimental results of Information Entropy (IE), Min Error (ME), Breaking Ties (BT) and Least Confidence (LC) on three kinds of hyperspectral images are compared. The experiment is 10 initial samples for each class, and all remaining samples are test samples. Two hundred unlabeled samples are selected by four sample selection methods in each iteration. The label samples are used to expand the training samples, train the classifier and classify the test samples. The quality of the selection samples is determined according to the classification results after each iteration is executed. The classification accuracy of different sample selection methods on different data sets is shown in Table 1.

From Table 1, it can be seen that the classification accuracies of ME, BT and LC are greatly improved on the three data sets with the increase of the number of iterations. The results of the BT method are significantly better than those of the other methods. The accuracy can be improved in the first few iterations, which indicate that the BT method can select samples with greater classification improvement. Therefore, the BT method is chosen as the sample selection method in this paper.

5.3.3.   Determination of sample size

In the labeling process, the samples are not completely labeled correctly. The more samples are screened, the more samples may be misclassified. This will make the training set noisier and affects the generalization ability of the classifier. If the number of samples is too small, the number of labeled samples will not improve the classification accuracy of the classifier or will reduce the classification efficiency. The results of classification accuracy under different sample sizes are shown in Table 2.

It can be seen from Table 2 that the sample selection screening quantity in different data sets presents different rules. Indian Pines datasets have the highest classification accuracy after 10 iterations are finished. Pavia University datasets have the highest classification accuracy after 8–10 iterations are finished. Salinas Scene datasets have the highest classification accuracy after 2–4 iterations are finished. The sample screening quantity with the highest accuracy is regarded as the experiment parameter, which are 1600 for Indian Pines, 1400 for Pavia University and 600 for Salinas Scene.

5.3.4.   Determination of block window size

The size of the block window determines the neighborhood information of the samples, which directly affect the accuracy of the pseudo-tagging method. Due to the different size of data, the optimal block window size is also determined by a large number of experiments. The classification accuracy under different block window sizes is shown in Table 3.

As can be seen from Table 3, there have different changes in classification accuracy for different datasets. Compared with the other two data sets, the size of Indian Pines is the smallest, so its experimental block window side length values are from 3 to 10. With the increase of the number of iterations, the classification accuracy showed a trend of gradual increase, and the optimal accuracy is obtained when the side length is 7. When the side length of the block window for Pavia and Salinas datasets is too small, the classification accuracy will not improve with the increase of iterations. This indicates that the neighborhood information cannot distinguish the category at this time.

With the increase of the side length of the block window, the number of iterations to achieve the optimal classification accuracy is advanced, but the optimal accuracy decreases. The block window size is larger, the more noise information will be introduced, and it will affect the sample labeling accuracy. Therefore, the block window size of the Indian Pines dataset is 7 × 7, and the block window sizes of the Pavia and Salinas datasets are 25 × 25 and 20 × 20, respectively.

5.3.5.   Determination of priority classifier

In fact, the determination of pseudo-tags of samples mainly depends on the determination of classifiers. K-Nearest Neighbor (KNN), Sparse Representation-Based Classifier (SRC), Neighbor Rough Set (NRS) and mixed logistic regression (MLR) are employed to determine the pseudo-tags. The experimental results of single classifier and different combination classifiers on different datasets are shown in Tables 4–6.

As can be seen in Table 4, with the increase of iterations, the classification accuracy of each category samples increased gradually. Compared with the results of the single classifier, the SRC has the largest number of samples after 10 iterations are finished, but the classification effect is not the best value. The classifier with the best classification effect is NRS. The number of samples and classification accuracy of the combination classifiers are mostly better than that of single classifier. The experiment results are different for combination classifiers with different priority. The classifier with NRS can achieve more than 90% classification effect after 10 iterations are finished. The number of combinations with MLR is more than 6600 after 10 iterations are finished, and the best combination is MLR + NRS after 10 iterations are finished.

As can be seen in Table 5, compared with the experimental results by single classifier, the number of labeled samples with SRC is the largest value after 10 iterations are finished, which is higher than the other three methods. However, the MLR obtained best classification results. After 10 iterations are finished, the number of labeled samples of two classifiers is more than that of the single classifier. KNN, SRC and NRS are considered as the first priority classifiers, the classification results of the sample set after 10 iterations are not as good as those of MLR. The combination of MLR as the first priority classifier has better classification effect than single MLR after 10 iterations are finished.

For Salinas Scene data, the number of labeled samples by MLR after 10 iterations is the smallest result, but the classification accuracy of the labeled samples is the highest result. After 10 iterations are finished, the number of iterations of the two classifiers is also higher than that of the single classifier. However, from the perspective of the performance of labeled samples in classification, MLR+SRC has higher classification accuracy than MLR, which indicates that the addition of classifiers improves the classification accuracy.

From three experiment results, it can be seen that the method with the largest number of labeled samples does not necessarily achieve the best classification results. The labeled samples are needed to improve the classification accuracy of the classifier, so the obtained labeled samples after 10 iterations are taken as the evaluation criteria. The Indian Pines dataset uses a combination of classifiers MLR + NRS. The Pavia University and Salinas Scene data sets use MLR + SRC.

5.4.   Experimental results and analysis

Based on the analysis, the settings of the related parameters are shown in Table 7.

Firstly, the LBP is used to extract the features of spatial texture information of hyperspectral remote sensing images. Secondly, the sample labeling method based on neighborhood information and priority classifier discrimination is used to obtain the learned pseudo-labeled samples. The SRC classifier is trained with the labeled samples, and the test samples are predicted. The obtained classification results are compared with those of the SRC classifier on the training data, and the classification results of training models with different training dataset are shown in Table 8.

It can be seen from Table 8, for Indian Pines dataset, the classification results of AA, OA and KAPPA are 84.7%, 94.42% and 0.914, respectively. For Pavia University dataset, the classification results of AA, OA and KAPPA are 81.87%, 88.53% and 0.848, respectively. For Salinas Scene dataset, the classification results of AA, OA and KAPPA are 87.76%, 92.64% and 0.918, respectively. Therefore, the proposed classification method obtains higher classification accuracy.

The classification visualizations of the proposed classification method for the initial samples and labeled samples are shown in Figures 7 and 8.

By comparing with the results of the experiments, it can find that the classification results of the trained classifier with expanded samples on the three datasets are better than those of the trained classifier with initial samples. Moreover, from the classification visualization, it can also see that the obtained classification results by the classifier and the labeled samples is smoother and has fewer discrete points, which indicates that the generalization ability of the classifier is improved by labeling the samples.

6.   Conclusions

For the processing and analysis difficulties of hyperspectral images, a new sample labeling method based on neighborhood information and priority classifier discrimination is developed to implement a new classification method of hyperspectral remote sensing images based on texture features and semi-supervised learning by introducing LBP, sparse representation and mixed logistic regression. The LBP is employed to extract the texture features of the hyperspectral remote sensing images. The multivariate logistic regression model is used to select the unlabeled samples with the largest amount of information, and the unlabeled samples with neighborhood information and priority classifier tags are selected to obtain the pseudo-labeled samples after learning. The problem of limited labeled samples of hyperspectral images is solved. The Indian Pines dataset, Salinas scene dataset and Pavia University dataset are selected in here. The experiment results show that the block window of Indian Pines dataset is 7 × 7, and the block windows of Pavia University and Salinas scene are 25 × 25 and 20 × 20, respectively. The combination of MLR and SRC can obtain better classification results. The obtained classification results are smoother and have fewer discrete points, which indicate that the generalization ability of the classifier is improved by labeling the samples. For Indian Pines dataset, the classification results of AA, OA and KAPPA are 84.7%, 94.42% and 0.914, respectively. For Pavia University dataset, the classification results of AA, OA and KAPPA are 81.87%, 88.53% and 0.848, respectively. For Salinas Scene dataset, the classification results of AA, OA and KAPPA are 87.76%, 92.64% and 0.918, respectively. Therefore, the proposed classification method obtains higher classification accuracy by comparing with the other methods.

However, the proposed classification method has the more computing time, so the next step should be more in-depth research to reduce the time complexity.

Acknowledgments

This research was funded by the Sichuan Science and Technology Program, grant number 2021YFS0407, 2022YFS0593, 2023YFG0028; the Sichuan Provincial Transfer Payment Program, Chian under Grant R21ZYZF0006; the A Ba Achievements Transformation Program under Grant R21CGZH0001, R22CGZH0006, R22CGZH0007; the Chengdu Science and technology planning project, grant number 2021-YF05-00933-SN, the Research Foundation for Civil Aviation University of China grant number 2020KYQD123.

Conflict of interests

The authors declare no conflict of interest.