Adaptive group testing in a compartmental model of COVID-19^*

1.   Introduction

The emergence of COVID-19 has motivated a number of real-time modeling studies to assess its potential for global spread (see e.g., ^[1,2,3]). Later, healthcare systems in many countries were facing difficult situations in terms of appropriate response. Various types of interventions have been introduced to suppress or mitigate the outbreaks, including mass testing of the population. The World Health Organization recommends reverse transcription polymerase chain reaction (RT-PCR) to confirm the presence of the virus, by detecting the RNA of the coronavirus ^[4]. The test is performed on respiratory samples obtained from a nasopharyngeal swab, throat swabs, deep airway material collected via suction catheter, sputum or saliva ^[5,6]. Other molecular tests include isothermal nucleic acid amplification tests and CRISPR gene editing technology ^[7,8]. Antigen tests are based on the identification of antigen proteins from the viral surface, the application of these tests are usually faster, however, their sensitivity is usually lower. For this type of test, samples are collected by nasal or nasopharyngeal swab or from saliva ^[9].

The main advantage of testing is that it enables to recognize presymptomatic and asymptomatic infected, who have a very important role in disease dynamics. Testing also helps in various ways: breaking the chain of transmission, enabling the isolation of infectious individuals, potential contact tracing of their contacts potentially infected, and estimating the proportion of asymptomatic carriers and their role in transmission. Testing also helps to find clusters of transmission and to have a more precise estimate on transmission rates and death rates. With the application of these results, testing provides a guide to make decisions on social distancing policy and other measures including the allocation of medical resources.

The method of widespread testing – combined with contact tracing and isolation – is the focus of various studies ^[10,11,12] and was successfully implemented in various countries in southeastern Asia ^[13,14], but the availability of diagnostic tests remained a global problem and in several countries testing (and confinement) is limited to people with severe symptoms, thus leaving those with mild symptoms and asymptotic carriers undetected who continue to make contact with others. To cope with the difficulty caused by shortage of testing kits, pooling approaches have been suggested, in which biological specimens from multiple subjects are diluted into a testing pool and tested via a single test. This technique, first applied for screening recruits at the United States Army for syphilis ^[15], is often used as a part of surveillance measures to significantly decrease the number of required tests to intervene and give a positive response. A follow-up provides a more precise result and prevents the unnecessary confinement of healthy people, however, at the same time, it also necessitates additional tests and more complex logistics.

Using a pooling approach for the standard RT-qPCR test, it was found that a single positive sample can be detected even in a pool of up to 32, or even 64 samples ^[16]. We study two possible ways of pooling, with or without follow-up: in the first case, all people whose sample was in the positively tested pool will be isolated, while in the second case, additional tests are evaluated so that only those who are really infected will be isolated. In the first case, many people are unnecessarily removed from society, while in the second case, more test kits are needed.

The method of pooling can reduce the number of tests needed, but it requires adequate logistics of organizing sample collection and transportation.

Since the outbreak of the current COVID-19 pandemic, mass testings have been performed in several occasions. In May 2020, the entire population of Wuhan was tested. In October 2020, following the emergence of a new cluster of COVID-19 leading to 13 new infections, the whole population of the Chinese city Qingdao was tested, using pooling with pool sizes varying from 3 to 10 people. Samples in a positively tested pool were tested again individually ^[17].

On 31 October and 1 November 2020, two thirds of Slovakia's population were tested ^[18]. A week later, further 2 million people were tested in the worst-hit regions. This attempt resulted in identifying 57,500 new infections countrywide.

In 2020, the UK government was planning a program of mass testing called Operation Moonshot ^[19], but the project was cancelled.

The Austrian government facilitated access to free tests to every citizen from 1 March 2021 ^[20]. The City of Vienna initiated the programme "Alles gurgelt" ("Everyone gargles") for citizens of Vienna in February 2021 ^[21] offering every Viennese up to four free "gargalisation" PCR tests per week, performed at home in a very easy way. Tested people may then take their test kit to various supermarkets or gas stations. 200,000 samples can be checked a day, meaning 1.4 million samples per week, but this number could rise to 2 million per week.

In this paper we investigate the feasibility of this approach in terms of detecting and isolating COVID-19 cases. We establish and study an $\mathit{SLPIR}$-type delay differential equation model with pooling approach, with and without follow-up and quarantine. In Section 2, we consider our model comparing regular and Dorfman pooling. In Section 3, we develop a method to optimize the pool size for Dorfman pooling depending on disease prevalence, considering a scenario where testing capacity is limited to a certain number of tests per day. In Section 4, we perform numerical experiments to assess strategies employing the optimized pooling. We establish an adaptive strategy where a varying pool size is applied depending on actual prevalence. The paper is closed by a discussion.

2.   Transmission models with pooling

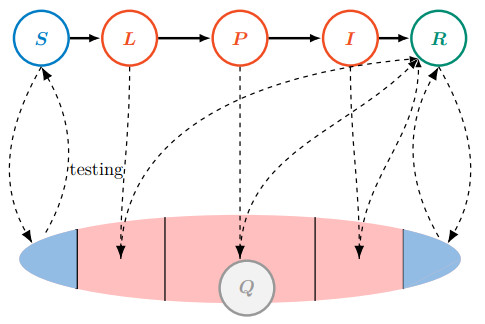
In this section, we develop a compartmental model to describe mass testing along with the application of various pooling methods and confinement of those tested positively. The population is divided into five classes: susceptibles, latent, presymptomatic, infected and removed, denoted by $S$, $L$, $P$, $I$ and $R$, respectively. Susceptibles are those who can be infected by coronavirus, latent are those who have been infected, but do not show symptoms, and neither can transmit the disease. Presymptomatic individuals still do not show symptoms but they can infect others as well. Latent individuals move to the infected class after a latency period, while following recovery, people from the infected class proceed to the removed compartment. In this model, we ignore any disease-induced death and demography. This $\mathit{SLPIR}$ model is further developed by considering the effects of mass testing in our equations, i.e., we include terms for removing individuals whose test evaluated positively (from any of the five classes). In the following, compartment $Q(t)$ will stand for the temporarily confined at time $t$, and we assume an active quarantine, in which the population compensates the loss of links rewiring the ineffective connections towards nonquarantining nodes ^[29]. After an isolation of $\tau$ days, the quarantined individuals move back into the $S$ or $R$ class, depending on the status of a given individual. We introduce the notation $N(t) = S(t)+L(t)+P(t)+I(t)+R(t)$ for the total active population, i.e., for those who are not in confinement. We note that, as we mentioned before, the total population $S(t)+L(t)+P(t)+I(t)+R(t)+Q(t) = \Pi$ is constant.

Removal of positively tested individuals and putting back those who have passed $\tau$ days in confinement are both considered in various ways in the equations, modeling different methods applied in mass testing. Namely, we consider two different pooling methods.

2.1.   Regular pooling

In the case of regular pooling, we select $k$ individuals and perform a single RT-PCR test on their combined (pooled) samples. Even if the test comes back as positive, no additional tests are performed to identify the infected individuals, instead of that, everybody in the pool will be confined. We apply the notation $p$ for the sensitivity of the test, i.e., the probability that a test gives a correct positive result when the sample contains viral particles. In general, the sensitivity of the tests may depend on several factors, for example the brand of the test, whether the tested individual was symptomatic or asymptomatic, the number of days elapsed since exposure, in the case of pooling the size and the composition of the pool. For simplicity, here we assume an average sensitivity value $p = 0.9$, which is in line with ^[16,27], and use this value throughout the paper. We denote by $1-\rho$ the specificity of the test, i.e., $\rho$ is the probability of the test giving a false positive result in case of a non-infected person being tested. In the following, $\sigma$ stands for the number of people tested each day. With this approach, we determine the number of individuals removed from each compartment on a given day. We note that the sensitivity and specificity of testing a pool of several samples might differ from those of an individual test as it might depend on the number of positive samples included in the pool. However, for the sake of simplicity, we will ignore this difference in this paper.

The number of individuals isolated from the $L$, $P$ or $I$ compartments is given by the number of individuals from these compartments being tested multiplied by the sensitivity, i.e., $\sigma \cdot \tfrac{L(t)}{N(t)} \cdot p, \, \sigma \cdot \tfrac{P(t)}{N(t)} \cdot p$ and $\sigma \cdot \tfrac{I(t)}{N(t)} \cdot p,$ respectively.

The number of individuals isolated from the $S$ or $R$ compartments can be obtained by the following. Assume someone is in a positive pool. Considering the other $k-1$ individuals in the same pool,

1. either there is an individual who is in compartment $L$, $P$ or $I$ and the pool is true positive,

2. or everyone else is from the $S$ or $R$ compartment as well, and the pool is false positive.

Therefore we obtain that the expected number of individuals being isolated from the $S$ or $R$ compartment can be obtained as

where

where $\pi(t) = \tfrac{L(t)+P(t)+I(t)}{N(t)}$ stands for the disease prevalence. The delay differential equation system describing the dynamics (we start to test individuals at $t = 0$) can be written as

where

is the Heaviside step function. The parameter $\beta$ is used for disease transmission rate, $\alpha_{_L}^{-1}$ denotes the average length of the latent period, $\alpha_{_P}^{-1}$ stands for the average time from becoming infectious until symptoms onset, while $\gamma$ denotes recovery rate.

The above mentioned compartment $Q(t)$ is aggregated as

Let us note that the quarantine compartment does not appear in any of the equations of (2.1), hence, it can be studied independently from the equation of $Q(t)$.

System (2.1) is an $\mathit{SLPIR}$-type disease model assuming exponentially distributed latent, presymptomatic and infectious period. The basic reproduction number of the model without mass testing (i.e., for $\sigma = 0$), considering infectiousness for compartments $P$ and $I$ is given by

We assume that infected individuals are removed from compartments $L$, $P$ and $I$ with rate $p \sigma$ and put back to the compartments $\tau$ days later. We catch the latter event in the system using terms with time-delay. Therefore, introducing the notation $\hat\sigma = \frac{\sigma}{\Pi}$ for the fraction of the population tested each day, and tracking the progress of a single infected individual through the infected compartments, we get the control reproduction number as

The parameters and their values used in our simulations are shown in Table 1. The model is parame-trized by values from various studies in the literature ^{[24,25,26,27,28]}.

2.1.1.   Numerical results for regular pooling

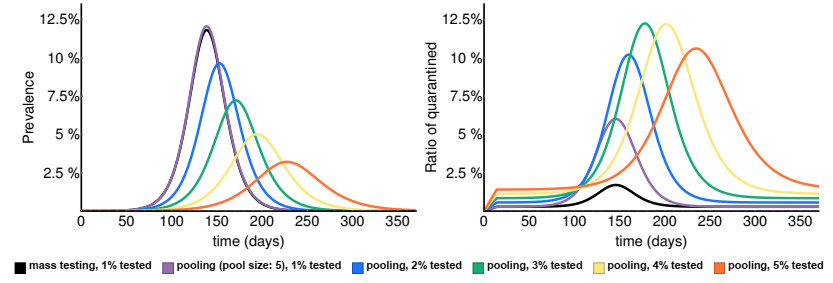
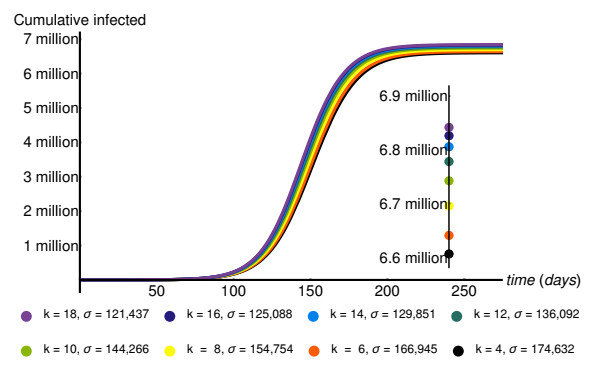
In this subsection, we present the effect of regular pooling on the epidemic curves of the infected and quarantined. Below we compare six different scenarios: a simple mass testing method with 1% of the population tested daily, and five cases of regular pooling with pool sizes of 5, and 1–5% of the population being tested daily.

Figure 1 shows a comparison of these scenarios, suggesting that with the same amount of tests performed, pooling can be much more effective for mitigating the epidemic. However, regular pooling with a large pool size will increase the number of quarantined people to such an extent which is impossible to be realized in real life.

2.2.   Dorfman pooling

In the case of Dorfman pooling, we select $k$ individuals and perform a single RT-PCR test on their combined (pooled) samples. If the pooled test yields a positive result, then each sample is retested separately and we only remove those individuals who were retested as positive; otherwise, everyone is declared negative. We note that there are other, more intricate methods for arranging the pools ^[30].

We determine the number of individuals removed from each compartment on a given day. If this person is from compartment $L$, $P$ or $I$, then we obtain the expected number of individuals being isolated from these compartments by multiplying the number of latent, presymptomatic or infected people being tested with two probabilities: that of the pool comes back as positive and that of the individual test gives a correct positive result.

This product gives us $\sigma \frac{L(t)}{N(t)} \cdot p^2, \, \sigma \frac{P(t)}{N(t)} \cdot p^2, \,$ and $\sigma \frac{I(t)}{N(t)} \cdot p^2,$ respectively.

The number of individuals isolated from the $S$ or $R$ compartments can be obtained by the following. Assume that a non-infected is in a positive pool. Considering the other $k-1$ individuals in the same pool,

1. either there is an individual who is in compartment $L$, $P$ or $I$, the pool is true positive and the individual test is a false positive;

2. or everyone else is from the $S$ or $R$ compartment as well, the pool is false positive and the individual test is false positive result as well.

Therefore we obtain that the expected number of individuals being isolated from the $S$ or $R$ compartment can be obtained as

where

The system describing the dynamics can be written as

with the equation for the quarantine compartment $Q(t)$ obtained as

The control reproduction number of the model with pooling using follow-up can be calculated as

2.3.   Comparison of regular and Dorfman pooling

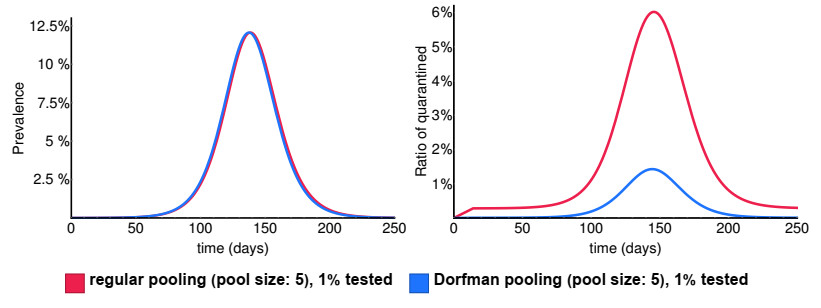
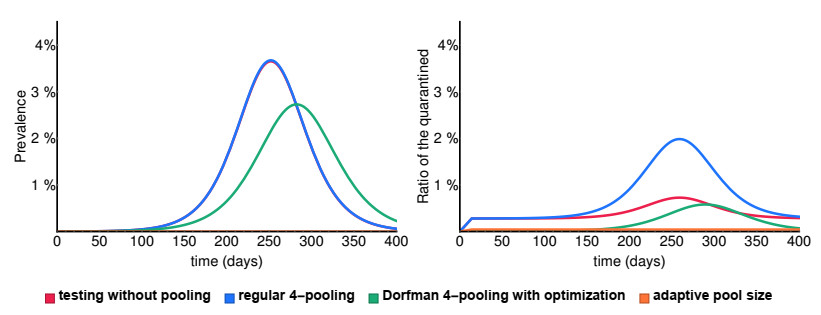
In this subsection, we compare the effect on the epidemic curves of the infected and quarantined applying regular and Dorfman pooling.

Figure 3 shows a comparison of these scenarios, suggesting that with Dorfman pooling, the number of infected slightly increases. An explanation to this is that individuals from the infectious compartments need to give an additional true-positive test in order to get confined. The most important effect of the followup measure shows on the number of quarantined. This is caused by the fact that the number of individuals getting quarantined from non-infected compartments decreases substantially.

Using Dorfman pooling has another important advantage. Considering a situation after the outbreak diminishes, susceptible or removed individuals will get confined because of the false-positive tests. With regular pooling, one false-positive test is enough to become isolated, that is,

while, with Dorfman pooling,

We have to consider, though, that in (2.2), considering Dorfman pooling, if we test the same number of individuals, we require significantly more tests because of those we use for the individual tests. In Section 3, we investigate this issue rigorously.

3.   Optimization of Dorfman pooling

As we mentioned, Dorfman pooling is more feasible in terms of the number of isolated people, but on the other hand, it requires higher testing capacity. It is straightforward that as the prevalence increases, the probability of a positive pool increases as well, therefore we need more tests and fewer people can be removed from the epidemic chain. Note that, in general, testing capacities are limited, usually there is a certain number of tests which can be evaluated in a day. In the following, let us denote the number of tests available for one day by $\mathcal{T}$. We consider a feasible range of prevalence $\pi$ varying during the course of the outbreak as $0 \leq \pi \leq 0.1$.

Thus, we can derive

Which yields

We would like to emphasize that the prevalence is changing according to the disease dynamics, therefore, $\sigma$ is changing in time as well.

3.1.   Finding $\mathcal{T}$ for a fixed pool size

Now we can determine the maximal number of tests which could be necessary for obtaining the blue curve on Figure 2. Using the parameters from Table 1 for $p$ and $\rho$, with basic calculus we can obtain that the maximum of the denominator in (3.1) is obtained at $\pi = 0.1$ indeed, and it is

However, we only need $100,000/5 = 20,000$ tests per day for obtaining the red (regular pooling) curve.

3.2.   Optimizing the pool size depending on prevalence

An important question regarding pooling is to determine the optimal pool size. A large pool size enables to test several samples at the same time, however, a large sample size can lead to inaccuracies and also increases the probability of the presence of a positive sample. This, in turn implies that all samples in that pool have to be tested again. Hence, if prevalence is high, then large pool sizes might make nullify the benefits of pooling. On the other hand, if prevalence is low, larger pool sizes seem to be the better choice as there is a larger probability of samples being negative.

To complete all the necessary follow-up tests, we need to allocate a fraction of available tests. Next we determine the minimal quantity required for this purpose, which are sufficient for any possible prevalence.

We would like to determine the worst case scenario, namely, the minimal value of $\sigma(t)$ with our restrictions. We can always confine that many individuals, regardless of the prevalence.

In other words, we are looking for the maximum of the denominator in (3.1).

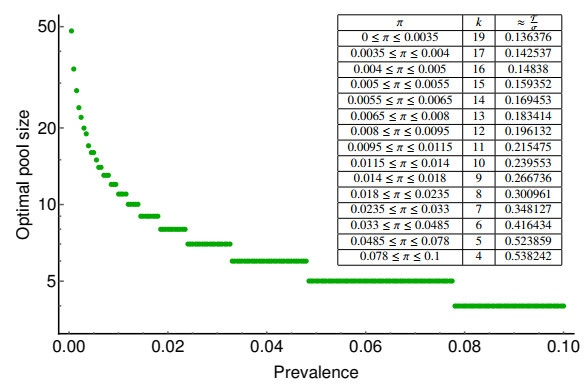
To determine the optimal pool size $k$ in order to maximize the denominator in (3.1), we differentiate

w.r.t. $k$ to obtain the extreme value rounded up to the nearest integer, depending on $\pi$. We also give the ratio $\frac{\mathcal{T}}{\sigma}$, namely, the number of tests needed to use for one individual during the testing process. We summarize these results in Figure 4; the optimal pool size $k$ which maximizes $\sigma$ for a given interval of prevalence $\pi$ and the corresponding value of $\frac{\mathcal{T}}{\sigma}$.

4.   Strategies employing optimized Dorfman pooling

In this section, we present some numerical results employing optimized strategies with Dorfman pooling.

4.1.   Fixed pool size during the pandemic

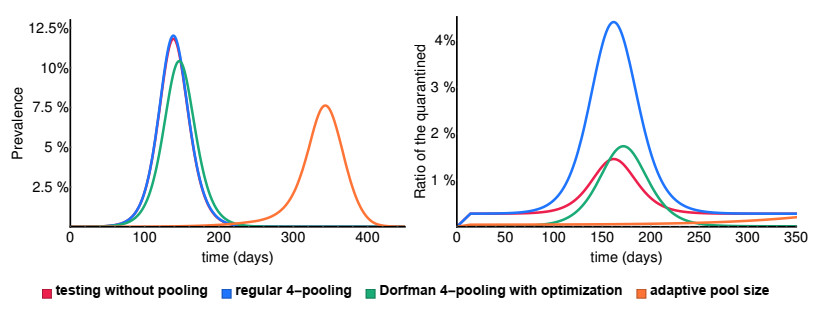
First, we consider different, fixed pool size values $k$ which we apply in (2.2) regardless of the prevalence, and a corresponding optimized $\sigma$ according to (3.1). In the following, the daily testing capacity $\mathcal{T}$ is fixed to $100,000$ which is feasible as it is 1% of the total population $\Pi$. According to the result in Section 3.1, for the optimized strategy we take $\pi = 0.1$. Figure 5 shows a comparison for these scenarios for different $k$ values. We can see that choosing pool size $k = 4$ is the best strategy, and considering $\Pi = 10,000,000$, $\approx2\%$ of the total population can avoid the infection simply by choosing another, more appropriate pool size.

4.2.   Adaptive strategy: variable pool size

In this section, we consider a changing pool size $k(\pi(t))$ dependent on the disease prevalence (see Section 3.2). In Figures 6 and 7, we compare all testing methods we discussed earlier: mass testing without pooling, regular pooling, Dorfman pooling with optimized $\sigma$ for every prevalence $0 \leq \pi(t) \leq 0.1$ and adaptive, changing pool size $k(\pi(t))$ and $\sigma(\pi(t))$. We can see that choosing a large pool size and a corresponding $\sigma$ at the start of the testing allows a widespread testing opportunity in the population. This intervention is enough to prevent an outbreak (see Figure 6) or in the case of a bigger reproduction rate it is capable to shift the peak and flatten the curve for a foreseeable time period.

5.   Conclusions

The COVID-19 epidemic, started late 2019, has soon become a pandemic, affecting almost all countries of the world. Governments have been evaluating several different strategies to lessen the spread and the economic effect of the epidemic.

In this paper, we aim to analyse the possible application of mass testing in mitigating the epidemic. Using a system of delay differential equations, we have established a compartmental model including a temporary isolation of those tested positively (correctly or falsely) during a mass testing. We consider mass testing with pooling (i.e., mixing several samples and testing the mixed sample with a diagnostic test), with or without follow-up. The latter means that all individuals whose sample were included in positively tested pools are tested once again, this time individually. Our results show that although it may effectively reduce the number of infected, pooling without follow-up increases the number of quarantined people to such an extent that it makes a real-life application of this method impossible.

On the other hand, though requiring more tests, pooling with follow-up is shown to be an efficient tool. At the same time, using some kind of pooling method, we can avoid placing healthy people in quarantine unnecessarily. We have shown that choosing an optimal (fixed) pooling size, disease burden can be reduced significantly. Furthermore, if pool size is continuously adapted during the epidemic to the actual prevalence, one may achieve a remarkable reduction in the number of infections with a significant shift in the time of the epidemic peak even in the case of a severe outbreak. In the case of a milder epidemic with a lower reproduction number, applying such an intervention may even completely prevent an outbreak.

There are many layers of complexities of the COVID-19 pandemic that we have not considered in our model. Here we have focused solely on the benefits of pooling, and its optimization. As future work we propose to study the combination of pooling and more involved testing strategies, such as risk oriented testing, where risk can be assessed by symptoms, contacts, activity, or exposure.

Acknowledgments

This work was completed in the National Laboratory for Health Security, Hungary. Authors were supported by National Research, Development and Innovation Fund of Hungary grants FK 124016, PD 128363, KKP 129877, respectively, and TKP2021-NVA-09.

Conflict of interest

The authors declare there is no conflict of interest.