Constrained hybrid control for parametric uncertainty systems via step-function method

1.   Introduction

Impulsive control can not only greatly save control costs but also efficiently transmit information in many applications ^[1,2,3]. Hybrid control systems including impulsive signals are ubiquitous in many actual systems, such as robotic control systems, neural control systems and insect population control systems, since the impulsive effect widely exists in the real world ^[4,5,6]. Over the years, Lyapunov-like function methods have been widely used in the stability analysis of control systems with impulsive signals ^{[7,8,9,10,11,12]}. Generally speaking, the traditional Lyapunov-like function methods require that there are constraints on the upper and lower bounds of the impulse interval, and the Lyapunov-like function is continuous and monotonic with time in each impulsive interval, which usually leads to the conservative stability conditions ^[13]. In order to overcome the above shortcomings, the authors in ^[14] established a new method, the step-function method, for the stability analysis of bouncing ball systems, in 2012. Motivated by ^[14], the authors in ^[13] formulated a new stability analysis framework based on step-functions for general impulsive systems, in 2022. The step-function is an extension of Lyapunov-like stability theory, which can relax some restrictions of the existing Lyapunov-like function methods. Also, it can be used to analyze the stability with Zeno behavior, which is not easily addressed by traditional Lyapunov-like function methods.

Due to measurement error of parameters, model construction and installation error, the parameters of nonlinear systems might not be accurately measured ^[15,16,17]. Generally speaking, the parameters of the systems will change in a certain interval ^[18,19]. The parametric uncertainty in nonlinear systems has received wide attention because it can be used to describe many practical engineering problems. The sliding-mode control problems for linear uncertain systems with impulse effects via switching gains were studied in ^[20]. Paper ^[21] investigated the controller design techniques for robust sampled-data dynamic output-feedback for nonlinear systems in the Takagi-Sugeno fuzzy form with parametric uncertainties and $L_2/L_\infty$ disturbances.

Still, most parametric uncertainty systems assume that the actuator can execute unlimited control signals, i.e., they do not consider the actuator saturation phenomenon in the whole control process. In actual engineering systems, physical actuators cannot execute infinite signals ^[22,23]; or, considering the safety of the system, it is necessary to limit the effective control signals generated by the actuators. Then, it is very important to consider the saturation phenomenon when designing the control system. There have been many results about continuous or discrete control systems with actuator saturation. Paper ^[24] investigated the problem of robust exponential stabilization of dynamic systems with time-varying delays, external disturbances and control saturation. The discrete time-varying systems with state-delayed and saturating actuators were studied in ^[25]. The hybrid impulsive and sampled-data control framework problems for a class of nonlinear dynamical systems with input constraints were addressed in ^[4]. However, due to the difficulties of designing control gains with parametric uncertainty and the discontinuity caused by the impulsive effect, parametric uncertainty hybrid control systems including impulsive control signals, subject to input constrains via Lyapunov-like stability theory, are rarely reported in the existing results, let alone those adopting step-function methods.

Moreover, most of the existing results assume all the control signals are valid and correct. However, in the real environment, the transmission of a signal may be interrupted for a certain period of time, or there might be signal input errors due to the interference of an external signal or some influence of the transmission medium. How to formulate a constrained hybrid control system considering parametric uncertainty and signal interruption or signal error is a problem of practical significance.

In summary, the applied research on the step-function method has just started, and there is still some work to be done. To the best of our knowledge, there is not research on the stabilization of nonlinear systems under actuator saturation via the step-function method. Then, our results in this paper will enrich the existing research. Motivated by the above analyses, considering parametric uncertainty, signal interruption, signal error and actuator saturation, we study the stability of hybrid control nonlinear systems via the step-function method. Moreover, we investigate the design of the control gains and the auxiliary control gains for easily finding the suitable control signals, the auxiliary signals and the estimation of the attraction domain.

The main contributions of the results in this paper are listed as follows:

a) Considering parametric uncertainty, signal interruption, signal error and actuator saturation, we establish a novel class of parametric uncertainty hybrid control system models including the impulsive control signals, subject to saturated inputs, which can reflect the signal transmission process more realistically.

b) An improved polytopic representation approach which is less conservative than the traditional polytopic representation approach is introduced to deal with the hybrid saturated inputs. The comparative experiments reflect the superiority of the improved polytopic representation approach.

c) The step-function method is first used for the stability analysis of nonlinear systems subject to saturated inputs.

d) In order to easily find the suitable control signals, the auxiliary signals and the estimation of the attraction domain, we investigate the design of the control gains and the auxiliary control gains.

Notations: $R^n$ and $R^+$ denote the $n$-dimensional real column vector space and the non-negative real numbers, respectively. $I$ denotes the identity matrix of appropriate dimensions. For a vector (matrix) $M$, $M_{(l)}$ refers to the $l$-th component (line) of $M$. $G \in R^{n \times n} > 0$ means a symmetric positive-definite matrix. $|| \cdot ||$ denotes the Euclidean norm. For a positive integer $n$, $\mathcal{I}[1, n]$ refers to the integers between $1$ and $n$. $co\{\mathcal{F}\}$ means the convex hull of a set $\mathcal{F}$. For matrix $F \in R^{n \times n}$, $\mathrm{He}(F)$ refers to $\mathrm{He}(F) = F+F^T$. Set $\mathcal{E}_0 = \{x(t) \in R^n: x^T(t)Gx(t) \le 1\}$ with $G \in R^{n \times n} > 0$. For $M \in R^{n\times n}$, set $\mathcal{L}(M) = \{x(t) \in R^n: ||Mx(t)||_\infty \le 1 \}$, with $||Mx(t)||_\infty = \max\limits_{l}|M_{(l)}x(t)|$, for $\forall$ $l\in \mathcal{I}[1, n]$.

2.   Problem formulation

We formulate the following nonlinear uncertain system (2.1) with hybrid saturated control input and assume the solutions of system (2.1) are left continuous at $t = t_s$.

where $x(t) \in R^n$ is the state vector, and $x_0$ is the initial state. For the time sequence, there is $0 = t_0 < \theta_0 < t_1 < \theta_1 \cdots < t_{s-1} < \theta_{s-1} < t_{s} < \theta_s \cdots < t_\infty$, and $\lim_{s\rightarrow \infty} t_s = t_ \infty$. Note that $t_\infty$ could be an infinity, and it could also be a finite number. $A(t)$ and $B(t)\; \in R^{n\times n}$ are time-varying matrices. $C$, $D$, $E_s$ and $J_s \; \in R^{n\times n}$ are constant matrices. $h(\cdot):R^n \to R^n$ is a continuous nonlinear function with $h(0) = 0$. There is a diagonal matrix $H\in R^{n\times n}$, $H > 0$, such that $||h(x(t))||^2 \le x(t)^THx(t)$ for $\forall\; x(t)\in R^{n}$. $\mathrm{Sat}(Dx(t)) = (\mathrm{Sat}(D_{(1)}x(t)), \mathrm{Sat}(D_{(2)}x(t))\cdots\mathrm{Sat}(D_{(n)}x(t)))^T$, and $\mathrm{Sat}(J_sx(t)) = (\mathrm{Sat}(J_{s(1)}x(t)), \mathrm{Sat}(J_{s(2)}x(t))\cdots\mathrm{Sat}(J_{s(n)} x(t)))^T \; \in R^n.$ For $l \in \mathcal{I}[1, n]$, $\mathrm{Sat}(D_{(l)}x(t))$ and $\mathrm{Sat}(J_{s(l)}x(t))$ are the saturation functions, with

and

$A(t)$ and $B(t)$ are of the following forms: $A(t) = A+\Delta A(t)$ and $B(t) = B+\Delta B(t)$. $A \in R^{n \times n}$ and $B \in R^{n \times n}$ are known constant matrices. $\Delta A(t)$ and $\Delta B(t)$ are unknown matrices which are of the following forms: $\Delta A(t) = \tilde{C}\tilde{J}(t)\tilde{F}$ and $\Delta B(t) = \hat{C}\hat{J}(t)\hat{F}$, where $\tilde{C}$, $\hat{C}$, $\tilde{F}$ and $\hat{F} \; \in R^{n \times n}$ are known constant matrices. $\tilde{J}(t)$ and $\hat{J}(t)$, which represent time-varying parametric uncertainties, satisfy $\tilde{J}^T(t)\tilde{J}(t) \le I$ and $\hat{J}^T(t)\hat{J}(t) \le I$.

Remark 1. In system (2.1), when $t\in (\theta_{s-1}, t_s]$, there is not any control signal, since the transmission of a continuous control signal may be interrupted for a certain period of time due to the interference of an external signal or some influence of the transmission medium.

Remark 2. In the whole time series, there are not additional upper and lower bound constrains of the time interval between $t_{s-1}$ and $\theta_{s-1}$, or between $\theta_{s-1}$ and $t_{s}$. Then, system (2.1) can approximate two extreme cases: When $t\in (t_{s-1}, t_s]$, there are only continuous control signals or are not any control signals. Note that, Zeno behavior might also occur.

Remark 3. The control gain can be different at each impulse instant, and this model (2.1) dose not require that all impulses be stabilizing impulses or can occur as the impulse perturbation.

Definition 1. ^[26] Define the following functions:

a) $\epsilon \in \mathcal{K}$, if $\epsilon \in C([0, a), [0, \infty))$ is strictly increasing, and $\epsilon(0) = 0$.

b) $\epsilon \in \mathcal{KL}$, if $\epsilon: [0, a)\times [0, \infty) \to [0, \infty)$ is continuous, and for every fixed $\Im$, $\epsilon(\beta, \Im) \in \mathcal{K}$. For every fixed $\beta$, $\epsilon(\beta, \Im)$ is decreasing, and moreover, $\epsilon(\beta, \Im) \to 0$ as $\Im \to \infty$.

Definition 2. ^[13,14] The origin of system (2.1) is referred to as Uniformly Attractively Stable if there is a $\mathcal{KL}$ function $\gamma$ such that every solution $x(t, t_0, x_0)$ starting from the admissible initial set $\mathcal{S}$ satisfies $||x(t, t_0, x_0)|| \le \gamma(||x_0||, t-t_0)$ for almost all $t\ge t_0$. $\mathcal{S}$ is a set which contains the open region of the origin. If $\mathcal{S} = R^n$, it can be said to be Globally Uniformly Attractively Stable.

Lemma 1. ^[27] Given a scalar $\delta > 0$ and any real matrices $\mathcal{A}_1, \mathcal{A}_2, \mathcal{A}_3$ of appropriate dimensions, such that $0 < \mathcal{A}_3 = \mathcal{A}_3^T$, the following inequality then holds:

Lemma 2. ^[28,29] For given matrices $\mathcal{D}$, $\mathcal{J}$ and $\mathcal{F}$ with $\mathcal{J}^T\mathcal{J} \le I$ and scalar $\delta > 0$, the following inequality holds:

Lemma 3. ^[30,31] Let $J, M_q \in R^{n \times n}$ with $q\in \mathcal{I}[1, 2^n]$. Assume that $x(t) \in \mathcal{L}(M_q)$ for $\forall$$q\in \mathcal{I}[1, 2^n]$. Then, $\mathrm{Sat}(Jx(t)) \in co\{\mathscr{E}_q Jx(t)+\mathscr{E}_q^-M_qx(t): q\in \mathcal{I}[1, 2^n]\},$ where $\mathscr{E} \in R^{n \times n}$ is the set of diagonal matrices with diagonal elements that are either $1$ or $0$, and $\mathscr{E}_q$ is the $q$-th element in set $\mathscr{E}$. Also, $\mathscr{E}_q^- = I-\mathscr{E}_q$.

From (2.1)–(2.3) and Lemma 3, if there exist some constant matrices $\tilde{M}_q$ and $M_{sq} \in R^{n \times n}$, assume that $|\tilde{M}_{q(l)}x(t)| \le 1$ and $|M_{sq(l)}x(t_s)| \le 1$ for $\forall \; q \in \mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$ and $s = 1, 2, \cdots$. Then, $\mathrm{Sat}(Dx(t)) \in co\{\mathscr{E}_qDx(t)+\mathscr{E}_q^-\tilde{M}_qx(t): q \in \mathcal{I}[1, 2^n]\}$, and $\mathrm{Sat}(J_{s}x(t_{s})) \in co\{\mathscr{E}_qJ_s x(t_{s})+\mathscr{E}_q^-M_{sq}x(t_{s}): q\in \mathcal{I}[1, 2^n]\}.$

Remark 4. Some auxiliary matrices $\tilde{M}_q$ and $M_{sq}$ are introduced to deal with the actuator saturation problem of the continuous control signals and the impulsive signals, respectively. While most of the existing saturated control methods use the traditional polytopic representation approach to deal with the actuator saturation problem, the improved polytopic representation approach, which is less conservative than the traditional polytopic representation approach, is used in our method. In the improved polytopic representation approach, at each impulse instant or the continuous control interval, $2^n$ auxiliary matrices are introduced to deal with the constrained control input problem instead of just one auxiliary matrix being introduced.

Lemma 4. ^[13,14] Let $x(t, t_0, x_0)$ be the solution of system (2.1) starting from the admissible initial set $\mathcal{S}$. Assume that there are an integer $j\ge 1$ and a positive definite function $\mathcal{V}$: $R^n\to R^+$, $R^+ = [0, +\infty)$, such that the step-function

with $\ell = 2, 3, \cdots$, satisfies the following:

a) $Se(t_j) \le \epsilon(\mathcal{V}(x_0))$, in which $\epsilon$ is a class $\mathcal{K}$ function.

b) $Se(t)$ decreases with time $t$, and $\lim \limits_{t \to t_\infty} Se(t) = 0$.

Then, the origin of system (2.1) is Uniformly Attractively Stable, and if $t_\infty = \infty$, the origin of system (2.1) is Asymptotically Stable.

3.   Main results

The sufficient conditions which can guarantee the stability of this control system (2.1) for every initial state in the estimation of the attraction domain via the step-function method are given in this section.

Theorem 1. Given an integer $j \ge 1$, assume that there exist some scalars $\beta_s > 0$, $\tau > 0$, $\delta_1 > 0$, $\delta_2 > 0$, $\alpha$, $h$ and some $n \times n$ matrices $G > 0$, $\tilde{M}_q$, $M_{sq}$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, the following conditions hold:

$\Gamma_q =$

Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, the origin of the nonlinear uncertain system (2.1) is Uniformly Attractively Stable, and if $t_\infty = \infty$, the origin of system (2.1) is Asymptotically Stable. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

Proof. The step-function $Se(t)$, (2.4), and the following function $\mathcal{V}(t)$ are constructed:

When $s = 1$, $t \in [t_0, \theta_0]$, the trajectory of system (2.1) starts from $\mathcal{E}_{0}$. Due to the satisfaction of inequality (3.1), it is easy to find that $x_0 \in \mathcal{E}_{0}\subseteq \mathcal{E}_{\mathcal{Q}} \subset \mathcal{L}(\tilde{M}_q)$ with $\mathcal{E}_{\mathcal{Q}} = \{x(t) \in R^n: x^T(t)Gx(t) \le \mathcal{Q}\}$. Then, Lemma 3 can be applied. Differentiating $\mathcal{V}(x(t))$ with respect to $t$ along system (2.1), one has

According to Lemma 1, there is

Then, one obtains

Let

and

Obviously, there is $\Xi_q(t) = \tilde{\Xi}_q+\hat{\Xi}(t)$. Moreover, according to Lemma 2, one obtains that

with

Because $\tilde{\Xi}_q+\acute{\Xi} = \Gamma_q$ and according to the satisfaction of condition (3.3), $\Xi_q(t) \le 0$ will be feasible. Thus, when $t \in [t_0, \theta_0]$, one obtains

and

When $t \in (\theta_0, t_1]$, according to (3.10), one has

Let

and

There is also $\aleph(t) = \tilde{\aleph}+\hat{\Xi}(t)$. Similar to (3.12), $\hat{\Xi}(t)\le \grave{\Xi}$, and $\tilde{\aleph}+\grave{\Xi} = \tilde{\Gamma}$, with

From the satisfaction of condition (3.4), $\aleph(t) \le 0$ will also be feasible. Thus, when $t \in (\theta_0, t_1]$, one obtains

and

It is easy to find that

According to (3.2), there is $x({t_1}) \in \mathcal{E}_{\mathcal{Q}} \subset \mathcal{L}(M_{1q})$. Then, Lemma 3 can be applied. When $t = t_1$, due to the satisfaction of (3.5), it follows that

According to mathematical deduction, when $s = j-1$, $t\in(t_{j-2}, \theta_{j-2}]$, we suppose that

Then, we have

When $t\in(\theta_{j-2}, t_{j-1}]$,

and

According to (3.2), there is also $x(t_{j-1}) \in \mathcal{E}_{\mathcal{Q}} \subset \mathcal{L}(M_{(j-1)q})$. Then, Lemma 3 can be applied. When $t = t_{j-1}$, similar to (3.14), one obtains

When $s = j$, $t\in(t_{j-1}, \theta_{j-1}]$ from (3.1), there is $x(t^+_{j-1}) \in \mathcal{E}_{\mathcal{Q}} \subset \mathcal{L}(\tilde{M}_{q})$. Then, Lemma 3 can be applied. Similar to (3.9)-(3.13), when $t\in (t_{j-1}, \theta_{j-1}]$, one has

When $t\in (\theta_{j-1}, t_j]$, one obtains

Obviously, it is easy to find that when $t\in (t_{j-1}, t_j]$,

Then, according to (3.6), we have, when $t\in [t_0, t_j]$,

Thus, when $t\in [t_0, t_j]$,

Then, the condition a) in Lemma 4 is satisfied. Similarly, from (3.7), when $t\in (t_{j(\ell-1)}, t_{j\ell}]$,

Thus, when $t\in (t_{j(\ell-1)}, t_{j\ell}]$,

and

Then, we have

Since $\tau < 1$,

Then, there is

Thus, the condition b) in Lemma 4 is also satisfied.

According to Lemma 4, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, the origin of system (2.1) is Uniformly Attractively Stable, and if $t_\infty = \infty$, the origin of system (2.1) is Asymptotically Stable. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

Remark 5. When $j = 1$, the step-function (2.4) is a one-span step-function, and when $j > 1$, the step-function (2.4) is a multi-span step-function.

Remark 6. In Theorem 1, there is no constraint on scalar $\alpha$ and scalar $h$, since the control signals are not necessarily efficient, and the system itself may be stable or unstable. For impulsive control signals, there is also no additional constraint on scalar $\beta_s$. For example, we do not need to limit the value of $\beta_s$ to be between $0$ and $1$ or be greater than $1$. Because control signal error or control signal failure is allowed in our theoretical research, our results are less conservative than many existing results.

Remark 7. Every trajectory starting from $\mathcal{E}_{0}$ will not go out of $\mathcal{E}_{\mathcal{Q}}$. Because $\mathcal{E}_{\mathcal{Q}}\subset \mathcal{L}({\tilde{M}_q})$, and $\mathcal{E}_{\mathcal{Q}}\subset \mathcal{L}({M_{sq}})$, for $t\ge t_0$ and $t \to t_\infty$, there are always $x(t)\in \mathcal{L}({\tilde{M}_q})$ and $x(t)\in \mathcal{L}({M_{sq}})$. Also, the trajectory will eventually converge to the origin.

If the traditional polytopic representation approach is used to deal with the actuator saturation, one can obtain Corollary 1.

Corollary 1. Given an integer $j \ge 1$, assume that there exist some scalars $\beta_s > 0$, $\tau > 0$, $\delta_1 > 0$, $\delta_2 > 0$, $\alpha$, $h$ and some $n \times n$ matrices $G > 0$, $\tilde{M}$, $M_{s}$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, (3.4), (3.6), (3.7) and the following conditions hold:

$\Gamma_q =$

Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, the origin of system (2.1) is Uniformly Attractively Stable, and if $t_\infty = \infty$, the origin of system (2.1) is Asymptotically Stable. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

Proof. Similar to the proof of Theorem 1, it is easy to get Corollary 1.

4.   Design of the control gains and the auxiliary control gains

In order to make the conditions in Theorem 1 and Corollary 1 easily solved by some software, we will try to transform these associated inequalities and try to find the design of the control gains and the auxiliary control gains, which can ensure the stabilization of (2.1).

Theorem 2. Given an integer $j \ge 1$, $\beta_s > 0$, $\tau > 0$, $\alpha$ and $h$, assume that there exist some scalars $\delta_1 > 0$, $\delta_2 > 0$ and some $n \times n$ matrices $\mathscr{G} > 0$, $\mathscr{\tilde{M}}_q$, $\mathscr{M}_{sq}$, $\mathscr{D}$ and $\mathscr{J}_s$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, (3.6), (3.7) and the following conditions hold:

Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, with the design of the control gains $D = \mathscr{D}\mathscr{G}^{-1}$ and $J_s = \mathscr{J}_s\mathscr{G}^{-1}$ and the auxiliary control gains $\tilde{M}_q = \mathscr{\tilde{M}}_q\mathscr{G}^{-1}$ and $M_{sq} = \mathscr{M}_{sq}\mathscr{G}^{-1}$, the origin of system (2.1) is Uniformly Attractively Stable, and if $t_\infty = \infty$, the origin of system (2.1) is Asymptotically Stable. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

Proof. Let us pre- and post-multiply (3.1)–(3.5) by $diag(\mathscr{G}, I)$ with $\mathscr{G} = G^{-1}$. According to the Schur complement and letting $D\mathscr{G} = \mathscr{D}$, $\tilde{M}_q\mathscr{G} = \mathscr{\tilde{M}}_q$, $J_s\mathscr{G} = \mathscr{J}_s$ and $M_{sq}\mathscr{G} = \mathscr{M}_{sq}$, in which $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$ and $s = 1, 2, \cdots$, one obtains conditions (4.1)–(4.5).

Similar to Theorem 2, it is easy to get Corollary 2.

Corollary 2. Given an integer $j \ge 1$, $\beta_s > 0$, $\tau > 0$, $\alpha$ and $h$, assume that there exist some scalars $\delta_1 > 0$, $\delta_2 > 0$ and some $n \times n$ matrices $\mathscr{G} > 0$, $\mathscr{\tilde{M}}$, $\mathscr{M}_{s}$, $\mathscr{D}$ and $\mathscr{J}_s$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, (3.6), (3.7), (4.4) and the following conditions hold:

Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, with the design of the control gains $D = \mathscr{D}\mathscr{G}^{-1}$ and $J_s = \mathscr{J}_s\mathscr{G}^{-1}$ and the auxiliary control gains $\tilde{M} = \mathscr{\tilde{M}}\mathscr{G}^{-1}$ and $M_{s} = \mathscr{M}_{s}\mathscr{G}^{-1}$, the origin of system (2.1) is Uniformly Attractively Stable, and if $t_\infty = \infty$, the origin of system (2.1) is Asymptotically Stable. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

Proof. Similar to (4.1)–(4.3) and (4.5), pre- and post-multiply (3.15)–(3.18) by $diag(\mathscr{G}, I)$ with $\mathscr{G} = G^{-1}$. Letting $D\mathscr{G} = \mathscr{D}$, $\tilde{M}\mathscr{G} = \mathscr{\tilde{M}}$, $J_s\mathscr{G} = \mathscr{J}_s$ and $M_{s}\mathscr{G} = \mathscr{M}_{s}$, in which $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$ and $s = 1, 2, \cdots$, one obtains (4.6)–(4.9).

5.   Application to the fixed time impulse problems of uncertain systems subject to actuator saturation with or without Zeno behavior

Theorem 2 and Corollary 2 are appropriate to deal with fixed time impulse problems of uncertain systems subject to actuator saturation with or without Zeno behavior.

5.1.   System (2.1) with upper and lower bounds on the impulse interval via two-span step-function

Corollary 3. Given some scalars $\beta_s > 0$, $max(\alpha, h) > 0$ and $\tau > 0$, when $j = 2$, $\tilde{T}\le t_{s+1}-t_{s} \le T$ with positive constants $\tilde{T}$ and $T$, assume that there exist some scalars $\delta_1 > 0$, $\delta_2 > 0$ and some $n \times n$ matrices $\mathscr{G} > 0$, $\mathscr{\tilde{M}}_q$, $\mathscr{M}_{sq}$, $\mathscr{D}$ and $\mathscr{J}_s$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, (4.1)-(4.5) and the following condition hold:

Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, with the design of the control gains $D = \mathscr{D}\mathscr{G}^{-1}$ and $J_s = \mathscr{J}_s\mathscr{G}^{-1}$, the design of the auxiliary control gains $\tilde{M}_q = \mathscr{\tilde{M}}_q\mathscr{G}^{-1}$ and $M_{sq} = \mathscr{M}_{sq}\mathscr{G}^{-1}$ and $\mathcal{Q} = \max\{\exp(\max(\alpha, h)T), \beta_{1}\exp(2\max(\alpha, h)T)\}$, the origin of the nonlinear uncertain system (2.1) is Asymptotically Stable. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

Corollary 4. Given some scalars $\beta_s > 0$, $max(\alpha, h) > 0$ and $\tau > 0$, when $j = 2$, $\tilde{T}\le t_{s+1}-t_{s} \le T$ with positive constants $\tilde{T}$ and $T$, assume that there exist some scalars $\delta_1 > 0$, $\delta_2 > 0$ and some $n \times n$ matrices $\mathscr{G} > 0$, $\mathscr{\tilde{M}}$, $\mathscr{M}_{s}$, $\mathscr{D}$ and $\mathscr{J}_s$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, (4.4), (4.6)-(4.9) and (5.1) hold. Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, with the design of the control gains $D = \mathscr{D}\mathscr{G}^{-1}$ and $J_s = \mathscr{J}_s\mathscr{G}^{-1}$, the design of the auxiliary control gains $\tilde{M} = \mathscr{\tilde{M}}\mathscr{G}^{-1}$ and $M_{s} = \mathscr{M}_{s}\mathscr{G}^{-1}$ and $\mathcal{Q} = \max\{\exp(\max(\alpha, h)T), \; \beta_{1}\exp(2\max(\alpha, h)T)\}$, the origin of the nonlinear uncertain system (2.1) is Asymptotically Stable. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

5.2.   System (2.1) with Zeno behavior via one-span step-function

Inspired by ^[13], if we set $t_s = \wp-\frac{1}{s}$ with $\wp > 1$ and $s = 1, 2, \cdots$, there will be Zeno behavior. Then, one has Corollary 5, 6.

Corollary 5. Given an integer $j = 1$ and given some scalars $\beta_s > 0$, $max(\alpha, h) > 0$ and $\tau > 0$, assume that there exist some scalars $\delta_1 > 0$, $\delta_2 > 0$ and some $n \times n$ matrices $\mathscr{G} > 0$, $\mathscr{\tilde{M}}_q$, $\mathscr{M}_{sq}$, $\mathscr{D}$ and $\mathscr{J}_s$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, (4.1)-(4.5) and the following condition hold:

Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, with the design of the control gains $D = \mathscr{D}\mathscr{G}^{-1}$ and $J_s = \mathscr{J}_s\mathscr{G}^{-1}$, the design of the auxiliary control gains $\tilde{M}_q = \mathscr{\tilde{M}}_q\mathscr{G}^{-1}$ and $M_{sq} = \mathscr{M}_{sq}\mathscr{G}^{-1}$ and $Q = \exp(\max(\alpha, h)(\wp-1))$, the origin of system (2.1) is Uniformly Attractively Stable with Zeno behavior. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

Corollary 6. Given an integer $j = 1$ and given some scalars $\beta_s > 0$, $max(\alpha, h) > 0$ and $\tau > 0$, assume that there exist some scalars $\delta_1 > 0$, $\delta_2 > 0$ and some $n \times n$ matrices $\mathscr{G} > 0$, $\mathscr{\tilde{M}}$, $\mathscr{M}_{s}$, $\mathscr{D}$ and $\mathscr{J}_s$ such that for any $q\in\mathcal{I}[1, 2^n]$, $l \in \mathcal{I}[1, n]$, $s = 1, 2, \cdots$ and $\ell = 2, 3, \cdots$, (4.4), (4.6)-(4.9) and (5.2) hold. Then, for any initial condition $x(t_0)\in \mathcal{E}_{0}$, with the design of the control gains $D = \mathscr{D}\mathscr{G}^{-1}$ and $J_s = \mathscr{J}_s\mathscr{G}^{-1}$, the design of the auxiliary control gains $\tilde{M} = \mathscr{\tilde{M}}\mathscr{G}^{-1}$ and $M_{s} = \mathscr{M}_{s}\mathscr{G}^{-1}$ and $Q = \exp(\max(\alpha, h)(\wp-1))$, the origin of system (2.1) is Uniformly Attractively Stable with Zeno behavior. $\mathcal{E}_{0}$ can be regarded as the estimation of the attraction domain.

6.   Simulation results

Let us consider the following two-dimensional dynamic neural network system:

with $x(t) = (x_1(t), x_2(t))^T$, $h(x(t)) = (\frac{|x_1(t)+1|-|x_1(t)-1|}{2}, \frac{|x_2(t)+1|-|x_2(t)-1|}{2})^T$,

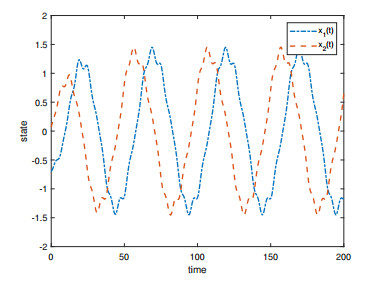
$\tilde{C} = diag(0.1, 0.1)$, $\tilde{F} = diag(-0.2, -0.2)$, $\hat{C} = diag(0.5, 0.5)$, $\hat{F} = diag(-0.2, -0.2)$, $\tilde{J}(t) = diag(\exp(-t), \exp(-t))$, and $\hat{J}(t) = diag(sin(t), sin(t))$. We can also find $H = diag(1, 1)$. When $x_0 = (-0.6912, 0.06667)^T$, the result of the time response of (6.1) is shown in Figure 1.

One continuous control signal and two kinds of impulsive signals with different control gains are inputted into system (6.1).

Case 1. The stabilization of system (6.1) without Zeno behavior via two-span step-function

Let $j = 2$ (the two-span step-function is introduced here), $\alpha = 0.4$, $h = 0.6$, $0.5\le t_{s+1}-t_{s} \le 0.6$, $\beta_1 = 0.4$, $\beta_2 = 1.1$, $\tau = 0.99$,

If we assume $\mathscr{M}_{s1} = \mathscr{M}_{s2} = \mathscr{M}_{s3} = \mathscr{M}_{s4}$, $\mathscr{\tilde{M}}_1 = \mathscr{\tilde{M}}_3$, $\mathscr{\tilde{M}}_2 = \mathscr{\tilde{M}}_4$, $\mathscr{M}_{1q} = \mathscr{M}_{3q} = \mathscr{M}_{5q} = \cdots$, $\mathscr{M}_{2q} = \mathscr{M}_{4q} = \mathscr{M}_{6q} = \cdots$, $\mathscr{J}_1 = \mathscr{J}_3 = \mathscr{J}_5 = \cdots$, and $\mathscr{J}_2 = \mathscr{J}_4 = \mathscr{J}_6 = \cdots$, according to Corollary 3, we can easily find the following results by Matlab.

$\delta_1 = 0.5420$, $\delta_2 = 0.3375$, and $\mathcal{Q} = 1.4333$. Then, we have

According to the design of the control gains and the auxiliary control gains in Corollary 3, one obtains

and

Thus, the estimation of the attraction domain $\mathcal{E}_{0}$ and the other domain $\mathcal{E}_{\mathcal{Q}}$ can be listed as

and

The control gains $D$, $J_1$ and $J_2$ are used to realize the stabilization of system (6.1), and the results and the control signal saturation functions are shown in Figures 2 and 3 with $p = 1, 2.$

On the other hand, $\mathcal{V}(t)$ and $\mathcal{S}e(t)$ are depicted in Figure 4

The estimation of the attraction domain $\mathcal{E}_{0}$ and the other domain $\mathcal{E}_{\mathcal{Q}}$ are depicted in Figure 5. The smaller ellipsoid is $\mathcal{E}_{0}$, which can be taken as the estimation of the attraction domain. The bigger ellipsoid is $\mathcal{E}_{\mathcal{Q}}$. The regions bounded by the green, blue, yellow and black dotted lines are $\mathcal{L}({\tilde{M}_1})$, $\mathcal{L}({\tilde{M}_2})$, $\mathcal{L}({{M}_{1q}})$ and $\mathcal{L}({{M}_{2q}})$, respectively.

If we assume $\mathscr{M}_{1q} = \mathscr{M}_{3q} = \mathscr{M}_{5q} = \cdots$, $\mathscr{M}_{2q} = \mathscr{M}_{4q} = \mathscr{M}_{6q} = \cdots$, $\mathscr{J}_1 = \mathscr{J}_3 = \mathscr{J}_5 = \cdots$, and $\mathscr{J}_2 = \mathscr{J}_4 = \mathscr{J}_6 = \cdots$, according to Corollary 3, we can easily find the following estimation of the attraction domain $\mathcal{\tilde{E}}_{0}$ by Matlab.

Under the same assumptions, if we use the traditional polytopic representation approach, according to Corollary 4 and fixing the other parameters, we can find a different estimation of the attraction domain $\mathcal{\hat{E}}_{0}$.

$\mathcal{\tilde{E}}_{0}$ and $\mathcal{\hat{E}}_{0}$ are shown in Figure 6. Obviously, in this situation, $\mathcal{\tilde{E}}_{0}$, using the improved polytopic representation approach, is bigger than $\mathcal{\hat{E}}_{0}$, using the traditional polytopic representation approach.

Case 2. The stabilization of system (6.1) with Zeno behavior via one-span step-function

We assume $t_s = 1.4-\frac{1}{s}$ with $s = 1, 2, \cdots$, and then there will be Zeno behavior. Here, we simulate the stabilization of (6.1) with actuator saturation and Zeno behavior.

If we fix other parameters, let $j = 1$ (one-span step-function is introduced here), $\alpha = 0.5$, $\beta_1 = 0.5$, and $\beta_2 = 0.7$. Using the traditional polytopic representation approach, we assume $\mathscr{M}_{1q} = \mathscr{M}_{3q} = \mathscr{M}_{5q} = \cdots$, $\mathscr{M}_{2q} = \mathscr{M}_{4q} = \mathscr{M}_{6q} = \cdots$, $\mathscr{J}_1 = \mathscr{J}_3 = \mathscr{J}_5 = \cdots$ and $\mathscr{J}_2 = \mathscr{J}_4 = \mathscr{J}_6 = \cdots$. According to Corollary 6, we can easily find the following results by Matlab.

and $\mathcal{Q} = 1.2712$. Then, we have

According to the design of the control gains and the auxiliary control gains in Corollary 6, one obtains

and

Thus, the estimation of the attraction domain $\mathcal{E}_{0}$ and the other domain $\mathcal{E}_{\mathcal{Q}}$ can be listed as

and

When $x_0 = (0.7295, -0.02667)^T$, the control gains $D$, $J_1$ and $J_2$ are used to realize the stabilization of system (6.1), and the results are shown in Figures 7 and 8.

7.   Conclusions

The step-function is an extension of Lyapunov-like stability theory, which can relax some restrictions of the existing Lyapunov-like function methods. Also, it can be used to analyze the stability of a nonlinear system with Zeno behavior, which is not easily addressed by traditional Lyapunov-like function methods. Then, in this paper, considering signal interruption or signal error, we formulated a novel class of parametric uncertainty hybrid control system models including the impulsive control signals under saturated inputs. Based on the step-function method, an improved polytopic representation approach and Schur complement, the problem of stability of parametric uncertainty systems under actuator saturation was investigated by us. In order to easily find the suitable control signals, the auxiliary signals and the estimation of the attraction domain, we investigated the design of the control gains and the auxiliary control gains. Our main results were applied to the fixed time impulse problems of uncertain systems with or without Zeno behavior. Simulation results for the uncertain neural network systems were presented to show the feasibility and effectiveness of our stabilization methods using the step-function. The results in this paper can better reflect the signal transmission process in the real environment, and the conditions here are less conservative than those with traditional Lyapunov-like function methods or with the traditional polytopic representation approach, so it will enrich the existing research. The stabilization of time-delay nonlinear systems with saturated impulsive inputs via the step-function method is another interesting topic, which is worthy of our future research.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (Grant No. 61873213) and the Natural Science Foundation Project of Chongqing, China (Grant No. cstc2021jcyj-msxmX0051).

Conflict of interest

The authors declare there is no conflict of interest.