1.
Introduction
A new viral infection, COVID-19 (Coronavirus Disease 2019) emerged in early 2020 and attracted widespread attention. The virus spread around the world at a very high speed and many studies have been carried out examining different epidemic patterns of COVID-19 based on official data [1,2,3]. There are many routes through which COVID-19 can spread, and it is possible that the virus may mutate at any time [4]. That is why the epidemic is difficult to control and was designated as a global pandemic by the World Health Organization (WHO). According to statistics from the WHO, more than 482 million people have been diagnosed with COVID-19, and more than 6 million people have died due to this disease as of March 30, 2022. The situation remains severe even now. Therefore, many scholars are looking for ways to contain the epidemic.
Many epidemic models of COVID-19 have been developed [5,6,7,8,9]. Studying the effects of factors such as incubation periods and vaccines on the spread of COVID-19 by analyzing the dynamic property of the system has been an important area of research. Abdy et al. [10] constructed a COVID-19 SIR Model with fuzzy parameters, taking into account vaccination, treatment, compliance with health protocols, viral load, and other factors. Their simulation results showed that differences in coronavirus loads would also cause differences in the transmission of COVID-19. Likewise, the factors of vaccination and compliance with health protocols had the same effect in slowing or stopping the transmission of COVID-19 in Indonesia. In the work of Wang et al. [11], a SVEIR epidemic model with media impact, age-dependent vaccination and latency was proposed, where the efficacy of vaccines depended on the time since vaccination.
Clearly, vaccines play a vital role in controlling infectious diseases. For COVID-19, a specific vaccine, which significantly reduces the risk of COVID-19 infection, has already been developed and has attracted much attention. In reference [12], Olorunsaiye et al. found that the global differences in the rates of immunization with the COVID-19 vaccine resulted in different levels of COVID-19 immunity in different countries. Based on the study of Anderson et al. [13] and the epidemic data available so far, we found that only a small number of people in Western developed countries have been immunized after paying a heavy toll of death due to COVID-19 infection, and they have had to use mass vaccination to achieve herd immunity. Therefore, it is necessary to study the effects of vaccines in models of COVID-19. Zhai et al. [14] studied vaccination control in an epidemic model with time delay and applied it to COVID-19.
These studies all point to the importance of vaccination against COVID-19. The development of COVID-19 also highlights the need to increase public awareness of disease prevention and promote proper understanding of vaccination. Vaccination rates are related to public opinion [15,16]. In reference [15], Yang et al. show that communication channels are one of the basic factors affecting the level of COVID-19 vaccination awareness in society. Agaba et al. [16] studied vaccination in a time-delay epidemic model with consciousness. Their model accounted for the contribution of global information campaigns to overall awareness, direct contact between uninformed and informed individuals, and reported cases of infection.
Many studies have shown that media coverage is an effective way to raise awareness of the epidemic and increase people's willingness to be vaccinated. In the study of Kiss et al. [17] in 2010, a model was developed to study whether some people became consciously susceptible and others became unconsciously susceptible after recovering from the disease. They showed that if the dissemination of information is fast enough, infection will be eradicated. When this is not possible, information transmission has an important effect on reducing the prevalence of the infection. In reference [18], Kar et al. established a SEIR model, analyzed the existence and stability of the disease-free equilibrium point of the model, and found that the system had the phenomenon of backward bifurcation, which considered the two important control measures of treatment and media coverage. Obviously, media coverage can affect the psychology of people and, thus, control the spread of infectious diseases.
According to the characteristics of the COVID-19 epidemic, time delay plays an important role in the epidemic models studied. Liu et al. [19] developed a differential equation with time delay to assess the impact of the incubation period on the epidemiological dynamics of COVID-19 before an infected person was able to transmit the infection to others. In reference [20,21,22,23], it showed that the model with the time delay could better describe the epidemic trend of infectious diseases. In some cases, the original stable equilibrium became unstable and destroyed the stability of endemic disease equilibrium.
COVID-19 is an infectious disease that is not completely controlled and, therefore, has great research significance. Considering the effectiveness of vaccines, studying the impact of media coverage on people's willingness to get vaccinated against COVID-19 is key for analyzing the role of media in controlling the spread of COVID-19. Therefore, the main objectives of this paper include constructing a COVID-19 vaccination willingness model in the context of media coverage and analyzing the stability of the model and the existence and stability of Hopf bifurcation.
The rest of the content is arranged as follows. In Section 2, we establish a model based on the characteristics of media coverage and COVID-19 transmission. In Section 3, we analyse the existence and stability of equilibria and the existence of Hopf bifurcation for models with time delay. In Section 4, we derive the normal form of the Hopf bifurcation of the above model and analyse the stability of the periodic solution of the bifurcation. In Section 5, we present numerical simulations to verify the correctness of our analysis. Finally, the conclusion is drawn in Section 6.
2.
Mathematical modeling
Media coverage has an impact on epidemic prevention and control. In reference [24], Misra et al. studied the time delay of media broadcasting and established the following model:
where X, Y, and Xm denote the numbers of susceptible, infected and conscious people, respectively, and M denotes the number of people affected by media coverage. A=X+Xm+Y is the number of total population individuals. τ is the time delay of the media coverage effect. Misra et al. [24] analyzed the Hopf bifurcation of their model and concluded that although awareness programs cannot eradicate infection, they help in controlling the prevalence of disease.
People who are susceptible to COVID-19 can become infected, and vaccination is one of the effective ways to reduce the likelihood of the susceptible population becoming infected. We will improve the system (2.1) based on the work of Misra et al. [24] and assume that the country has sufficient vaccine resources. We study the influence of media coverage on vaccination and COVID-19 epidemic control.
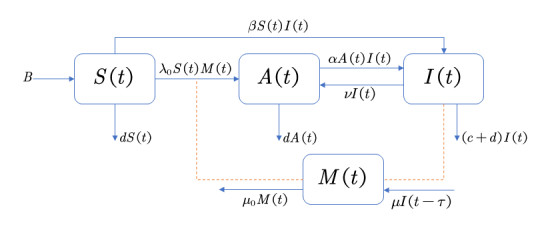
We divide the people into three groups. One group includes susceptible people who do not have antibodies in their bodies (S); that is, they have not received the vaccine. Another group includes people who have antibodies (A). The third group includes infected people (I). Most people from A obtain antibodies through vaccination (S→A). We assume these people are influenced by media because they need to be informed about vaccines through media coverage. The remaining people in A were infected and developed antibodies after recovering since the vaccine is an inactivated virus [25] (I→A). Both S and A are likely to suffer from COVID-19 after contact with infected people and become infected people I. First, this is because current vaccines reduce the infection rate but do not impart complete immunity. Second, recovered people can be reinfected [26] (see Figure 1).
As shown in Figure 1, we present a differential equation model with a time delay, and the relationships among the four populations are obtained. The solid line represents the flow relationship among the non-antibody population S, the antibody population A and the infected population I. The dotted line indicates that cabin (M) does not participate in the population flow, but it is affected by cabin I and affects the conversion rate from S to A. In this model, it is clear that people with antibodies are less likely to be infected, that is, the proportion of A converting to I is less than that of S, which means α<β. Some infected people die of the disease, while others are cured after treatment and have antibodies. We define the cure rate as ν. After τ days since the epidemic was reported by the media, people realized the seriousness of the epidemic. We assume the people who don't exhibit vaccination willingness at the beginning, but accept the idea of vaccination after being influenced by the media are (M). Media broadcast has an attenuation rate μ0. The number of people who follow the media will influence the vaccination rate with an influence coefficient λ0. This is consistent with the fact that the greater the number of people who pay attention to the news and think it is necessary to get vaccinated is, the higher the vaccination rate, converting S to A. Thus, we construct the following model:
where B, β, d, λ0, α, ν, c, μ, μ0 are positive parameters; S, A, I, M are variables; and τ is the time delay for people to change their willingness to vaccinate. It is influenced by media coverage of the epidemic. The specific descriptions are given in Table 1.
3.
Stability analysis of equilibria and the existence of Hopf bifurcation
In this section, the system (2.2) is considered. Clearly, the system (2.2) has two equilibria:
where S∗=BβI∗+d+ξI∗, A∗=Bd−BβI∗+d+ξI∗−c+ddI∗, M∗=μμ0I∗,
I∗=−[(c+d)αd−(αB−(ν+c+d)d)(β+ξ)]2(c+d)α(β+ξ)+√[(c+d)αd−(αB−(ν+c+d)d)(β+ξ)]2−4(c+d)α(β+ξ)[(ν+c+d)d2−Bdβ]2(c+d)α(β+ξ), with ξ=λ0μμ0.
It is straightforward to find that the basic regeneration number of the system (2.2) is
When R0<1, there is only one semitrivial equilibrium P1=(Bd,0,0,0). Transferring the equilibrium P1 to the origin and linearizing the surrounding system (2.2), we obtain the characteristic equation of the linearized system as follows:
The characteristic equation Eq (3.2) of equilibrium P1 is independent of τ. Equation (3.2) has four roots: λ1=λ2=−d, λ3=βBd−ν−c−d,λ4=−μ0. Thus the equilibrium P1 is locally asymptotically stable for any τ≥0 due to d>0,μ0>0,R0<1.
When R0=1, there is also only one semitrivial equilibrium P1=(Bd,0,0,0). The Eq (3.2) has a root: λ=0. Therefore, the equilibrium P1 undergoes a fixed point bifurcation.
When R0>1, the equilibrium P1 is unstable, and the other equilibrium P2 = (S∗,A∗,I∗,M∗) for the system (2.2) exists and is positive.
Similarly, transferring the equilibrium P2=(S∗,A∗,I∗,M∗) to the origin and linearizing the system (2.2) around it, we obtain the characteristic equation of the linearized system as follows:
where
When τ=0, Eq (3.3) becomes
We consider the following assumption obtained by the Routh-Hurwitz criterion:
(H1) C1>0, C1D1−A1−E1>0, C1[D1(A1+E1)−C1(B1+F1)]−(A1+E1)2>0, B1+F1>0. Under the assumption (H1), all the roots of Eq (3.4) have negative real parts, and the equilibrium P2=(S∗,A∗,I∗,M∗) is locally asymptotically stable when τ=0.
When τ>0, we try to discuss the existence of Hopf bifurcation. We assume that λ=iω(ω>0) is a pure imaginary root of Eq (3.3). Substituting it into Eq (3.3) and separating the real and imaginary parts, we obtain:
Eq (3.5) derives the following:
Adding the square of the two equations in Eq (3.5), letting z=ω2, we obtain
where c3=C21−2D1, c2=2F1−2C1E1+D21, c1=E21−2D1F1−A21, c0=F21−B21.
We hypothesize that Eq (3.7) has k(k=1,2,3,4) positive roots and denote them as z1<z2<z3<z4. Substituting ωk=√zk(k=1,2,3,4) into Eq (3.6), we obtain the expression of τ:
where
Lemma 3.1. If R0>1 and (H1) holds, when τ=τ(j)k(k=1,2,3,4;j=0,1,2,⋯), then Eq (3.3) has a pair of pure imaginary roots ±iωk, and all the other roots of Eq (3.3) have nonzero real parts.
Furthermore, let λ(τ)=α(τ)+iω(τ) be the root of Eq (3.3) satisfying α(τ(j)k)=0, ω(τ(j)k)=ωk(k=1,2,3,4;j=0,1,2,⋯).
Lemma 3.2. If R0>1 and (H1) holds, and zk=ω2k, h′(zk)≠0, where h′(z) is the derivative of h(z) with respect to z. Then, we have the following transversality condition:
Re(dτdλ)|τ=τ(j)k=Re(dλdτ)−1|τ=τ(j)k=h′(zk)A21zk+B21≠0, k=1,2,3,4,j=0,1,2,⋯.
Theorem 3.1. Considering system (2.2), we draw the following conclusions.
(1) If R0<1 holds, there is only one semitrivial equilibrium P1 for the system (2.2), and it is locally asymptotically stable for any τ≥0.
(2) If R0=1 holds, the only semitrivial equilibrium P1 undergoes a fixed point bifurcation.
(3) If R0>1 holds, the equilibrium P1 is unstable, and the other equilibrium P2 = (S∗,A∗,I∗,M∗) for the system (2.2) exists and is positive.When (H1) holds as well, the equilibrium P2 of the system (2.2) undergoes Hopf bifurcation at τ=τ(j)k(k=1,2,3,4;j=0,1,2,⋯), where τ(j)k is given by Eq (3.8), and
(a) If h(z) has one positive root z1, then when τ∈[0,τ(0)1), the equilibrium P2 is locally asymptotically stable and unstable when τ>τ(0)1.
(b) If h(z) has two positive roots z1 and z2, we suppose z1<z2; then, h′(z1)<0,h′(z2)>0; note that τ(0)1>τ(0)2. Then, ∃ m∈N makes 0<τ(0)2<τ(0)1<τ(1)2<τ(1)1<⋯<τ(m−1)1<τ(m)2<τ(m+1)2. When τ∈[0,τ(0)2)∪m⋃l=1(τ(l−1)1,τ(l)2), the equilibrium P2 of the system (2.2) is locally asymptotically stable, and when τ∈m−1⋃l=0(τ(l)2,τ(l)1)∪(τ(m)2,+∞), the equilibrium P2 is unstable.
(c) If h(z) has three or four positive roots, the phenomenon of stability switching similar to the case of (b) will occur.
4.
Normal form of Hopf bifurcation
In this section, we derive the normal form of Hopf bifurcation for the system (2.2) by using the multiple time scales method. To reflect the actual situation, we focus on the delay in people formulating ideas about COVID-19 vaccination and study the impact of the delay on epidemic control. Therefore, we consider the time-delay τ as a bifurcation parameter. Let τ=τc+ετε, where τc is the critical value of Hopf bifurcation given in Eq (3.8), τε is the disturbance parameter, and ε is the dimensionless scale parameter. When τ=τc, the characteristic Eq (3.3) has eigenvalue λ=iω(k)(k=1,2,3,4), at which system (2.2) undergoes a Hopf bifurcation at equilibrium P2=(S∗,A∗,I∗,M∗).
System (2.2) can be written as ˙X(t)=A2X(t)+B2X(t−τ)+F[X(t),X(t−τ)], we let t→t/τ, then the system (2.2) turns to
where X(t)=(S,A,I,M)T, X(t−1)=(S(t−1),A(t−1),I(t−1),M(t−1))T,
We suppose h is the eigenvector of the linear operator corresponding to the eigenvalue iω(k)τ of Eq (4.1) for equilibrium P2, and h∗ is the normalized eigenvector of the adjoint operator of the linear operator corresponding to the eigenvalue −iω(k)τ and satisfies ⟨h∗,h⟩=¯h∗Th=1. By simple calculation, we obtain:
where d=1¯h1¯h∗1+h2¯h∗2+h3¯h∗3+h4¯h∗4.
We suppose the solution of Eq (4.1) is as follows:
where X(T0,T1,T2,⋯)=[S(T0,T1,T2,⋯),A(T0,T1,T2,⋯),I(T0,T1,T2,⋯),M(T0,T1,T2,⋯)]T,Xk(T0,T1,T2,⋯)=[Sk(T0,T1,T2,⋯),Ak(T0,T1,T2,⋯),Ik(T0,T1,T2,⋯),Mk(T0,T1,T2,⋯)]T.
The derivative with respect to t is transformed:
where Di=∂∂Ti, i=0,1,2,⋯.
Note that
Then, we obtain
Using a Taylor series expansion of X(t−1), we obtain that
where Xi1=Xi(T0−1,T1,T2,⋅⋅⋅), i=1,2,3,⋅⋅⋅.
As we stated, τ is the bifurcation parameter, and τ=τc+ετε. Substituting Eqs (4.3)–(4.5) into Eq (4.1) and balancing the coefficients before ε on both sides of the equation, the following expression is obtained:
Thus, Eq (4.6) has the following solution form:
The expression of the coefficient before ε2 is as follows:
Substituting Eq (4.7) into the right-hand side of Eq (4.8), and the coefficient vector of eiω(k)τcT0 is denoted by m1. According to the solvability condition ⟨h∗,m1⟩=0, the expression of ∂G∂T1 is obtained as follows:
where Nk=iω(k)1+μh3¯h∗4e−iω(k)τcd,k=1,2,3,4.
Since τε is a disturbance parameter, we only consider its effect on the linear part. It has little effect on the high order, so it can be ignored. Therefore, we ignore the part containing τε in the higher order. We suppose the solutions of Eq (4.8) are given as follows:
where
with h1,h2,h3,h4 are given in Eq (4.2) and
The expression of the coefficient before ε3 is:
Substitute Eqs (4.6), (4.10) and (4.11) into the right-hand side of Eq (4.12), and the coefficient vector of eiω(k)τcT0 is denoted by m2. According to the solvability condition ⟨h∗,m2⟩=0, the expression of ∂G∂T2 can be obtained as follows:
where
with hk given in Eq (4.2), gk,lk given in Eq (4.11), and Nk given in Eq (4.9).
Let G→G/ε; then, the deduced third-order normal form of Hopf bifurcation of system (2.2) is:
where Nk is given in Eq (4.9), and Mk is given in Eq (4.13).
Substituting G=reiθ into Eq (4.14), the following normal form of Hopf bifurcation in polar coordinates is obtained:
According to the normal form of Hopf bifurcation in polar coordinates, we only need to consider the first equation in system (4.15). Thus, the following theorem holds:
Theorem 4.1. For the system (4.15), when Re(Nk)τεRe(MkNk)τc<0, there is a semitrivial fixed point r=√−Re(Nk)τεRe(MkNk)τc, and system (2.2) has periodic solution.
(1) If Re(Nk)τε<0, then the periodic solution reduced on the center manifold is unstable.
(2) If Re(Nk)τε>0, then the periodic solution reduced on the center manifold is stable.
5.
Numerical simulations
In this section, we carry out numerical simulations to verify our theoretical analysis. Then, we study two important parameters, that is, the media influence rate μ and attenuation rate of media μ0, and simulate the impact of these two parameters on the time required for people to be willing to vaccinate. Finally, we explore the influence of timely media coverage and the propaganda efforts of media coverage on the epidemic, and we propose reasonable suggestions for effectively controlling the COVID-19 epidemic.
5.1. Determination of parameter values
Based on official statistics (https://github.com/CSSEGISandData/COVID-19; https://voice.baidu.com/act/newpneumonia/newpneumonia/?from=osari_pc_3#tab 4), we obtain data on national case fatality rates and cure rates for different countries. To ensure that the data can relect the average, we retain representative data and eliminate outliers. Finally, we screen the death rates due to disease for 29 countries and cure rates for 30 countries. According to the data, we generate bar charts, which are presented in Figures 2 and 3.
Figure 2 shows the national case fatality rates of these countries are mostly in the range of 0.001 to 0.002,so we calculate the mean value 0.0016 and choose it as the value of c. Cure rates v are almost at the same level through the red dotted line in Figure 3,so we calculate the average rate for 30 countries and set 0.861 as the value of v. To find the value of the natural mortality rate d,we select population data from the National Bureau of Statistics (http://www.stats.gov.cn/enGliSH/) over the last 20 years and obtain a relatively stable natural mortality rate d=0.00707.
Based on the above consideration and values, we take two groups of parameters as follows:
(1) B=28,β=0.00021,d=0.00707,λ0=0.00073,μ=100,μ0=0.25, v=0.861,c=0.0016,α=0.000051;
(2) B=28,β=0.00816,d=0.00707,λ0=0.00051,μ=100,μ0=0.25, v=0.861,c=0.0016,α=0.00011.
5.2. The numerical simulations
First, we show the simulation results under the first group of parameters (1):
It is easy to find that the basic regeneration number of the system (2.2) R0=βBd(ν+c+d)<1, so there is only one semitrivial equilibrium P1=(S∗1,A∗1,I∗1,M∗1)=(3960.39,0,0,0) of system (2.2) according to expression (3.1). The equilibrium P1 is locally asymptotically stable for any τ≥0 by Theorem 3.1. This means that P1 is a disease-free equilibrium.
For the initial values [4000, 10, 10, 10], we choose τ=0 and τ=5 for the simulations. Clearly, the equilibrium P1 is locally asymptotically stable, as shown in Figure 4.
When τ=0, the solution is shown in Figure 4(a). Although there are fluctuations in 0–500 days, it tends to be stable after the 500th day. There will be no infected people, and the COVID-19 epidemic will be eliminated completely. This means that in this case, people pay attention to media reports regarding the epidemic and the epidemic will not develop, which verifies our theoretical analysis.
When τ=5, people's willingness to be vaccinated will change after 5 days of media coverage. It represents the situation in which people are unable to pay timely attention to news reported by the media and they do not want to get vaccinated immediately. As we can see in Figure 4(b), compared with τ=0, it takes a bit longer for equilibrium P1 to stabilize. However, eventually, there will be no infected people, and the disease will still disappear in this case.
Remark 1: According to the numerical simulations of parameters (1), we find that for any τ≥0, the equilibrium P1 of the system (2.2) is locally asymptotically stable, and the COVID-19 epidemic is completely eliminated. The smaller τ is, the faster the equilibrium stabilizes. This suggests that the influence of media on people's willingness to vaccinate does not change the stability of the disease-free equilibrium, and no matter how long it takes people to accept the idea of vaccination after viewing media coverage, the disease will eventually disappear. However, the less time it takes for people to change their vaccination intentions after viewing media coverage, the more it helps to contain the epidemic. This corresponds to the actual situation.
For the group of parameters (2):
we find that R0>1 and (H1) hold. Then, we calculate the equilibria P1=(S∗1,A∗1,I∗1,M∗1)=(3960.39,0,0,0) and P2=(S∗2,A∗2,I∗2,M∗2)=(53.96,3903.48,2.41,965.06) by expression (3.1). Due to Theorem 3.1, the equilibrium P1 is unstable for any τ≥0, and P2 is locally asymptotically stable when τ=0. Substituting parameters (2) into Eq (3.6), we obtain τ(0)1=1.4448,sin(ω1τ)=0.3680,cos(ω1τ)=0.9298 by MATLAB. We know that P2 is locally asymptotically stable for any 0<τ<τ(0)1=1.4448 and unstable for any τ>τ(0)1=1.4448. Then, we calculate the normal form of Hopf bifurcation and obtain Re(Nk)>0,Re(MkNk)<0 from Eq (4.15). The periodic solution is stable when τε>0 according to Theorem 4.1.
When τ=0, it means that as soon as the media report the situation of the epidemic, it will receive widespread attention from the public, and many people will change their willingness to vaccinate. We choose the initial values [100, 3000, 10, 1000], and the equilibrium is locally asymptotically stable, as shown in Figure 5.
As seen in Figure 5, although there are fluctuations of S,I,M in 0–100 days, it tends to be stable after the 100th day. In contrast, A tends to stabilize more slowly. This suggests that although the epidemic has almost stabilized and the number of infected people has stopped rising, people still want to protect themselves by getting vaccinated. Therefore, the number of people with antibodies continues to rise until a long time after the epidemic has stabilized. The number of people with antibodies is significantly greater than that of people who do not have antibodies, as shown in Figure 5. This means that in this case, the efficiency with which people consistently monitor the epidemic situation is meaningful, but this situation is under perfect conditions. Considering that it takes a certain amount of time for people to pay attention to media coverage, this situation is basically impossible.
When τ=1∈(0,τ(0)1) with τ(0)1=1.4448, which means that people respond to media reports of the epidemic one day later, we still choose the initial values [100, 3000, 10, 1000], and the solution of numerical simulations is shown in Figure 6.
In Figure 6, we find that equilibrium P2 is also locally asymptotically stable. The fluctuation in the first 400 days is obvious, but it gradually stabilizes after the 400th day, and the disease can also be controlled. Although its regional stability speed is significantly less than when τ=0, it will still reach stability in a short time. That is, if people respond to the epidemic and become willing to vaccinate within 1 day after receiving media reports, the rate of vaccination will increase to effectively control the epidemic.
Through the analysis of Hopf bifurcation, we obtain that when τ>τ(0)1=1.4448, which means that people respond to media reports of the epidemic after τ days later, the equilibrium P2 is unstable. Since Re(Nk)>0,Re(MkNk)<0,τε>0, system (2.2) has a forward periodic solution, and the bifurcating periodic solutions near τ(0)1 are locally asymptotically stable. We still choose the initial values [100, 3000, 10, 1000], and the solution of the numerical simulations when τ=2 is shown in Figure 7.
In Figure 7, we find that the bifurcating periodic solution is stable, which verifies our theoretical analysis. In fact, with the development of the epidemic, more people will be vaccinated, so the number of A tends to increase. On the other hand, people without antibodies and infected people will be largely affected whether the epidemic is severe or not, so periodic solutions of S and I fluctuate with the change in epidemic.
To study the situation in which people do not pay attention to the media and change their willingness to vaccinate in time, we carry out the numerical simulations when τ=10 with the same initial values [100, 3000, 10, 1000] in Figure 8.
Figure 8 shows that when τ=10, the periodic solution of the system (2.2) is stable as well. However, compared with the situation of τ=2, the periodic solutions exhibite larger fluctuations and longer periods. In fact, the longer it takes people to change their willingness after media reports, the longer the epidemic is temporarily contained and the worse the situation is, which is consistent with our simulation results.
Remark 2: According to the numerical simulations of parameters (2), we can obtain the following: when 0<τ<τ(0)1=1.4448, the equilibrium P2 of the system (2.2) is locally asymptotically stable, and the shorter the time that people spend changing their willingness, the better the epidemic can be controlled. However, if τ>τ(0)1=1.4448, the equilibrium P2 will be unstable. This means that under this group of parameters, if people do not respond to the epidemic situation within 1.5 days after the media report, the impact and timeliness of the media will be diminished. Therefore, the epidemic will be difficult to control. However, for any τ in the small neighborhood of τ>τ(0)1=1.4448, the system (2.2) has a stable periodic solution, indicating that the timeliness and influence of media reports are not the main factors for the development of the epidemic. Under the circumstance that the governments of various countries take measures such as isolation treatment for the epidemic, there will not be a large-scale outbreak. However, we still hope to avoid this situation to effectively control the epidemic and prevent recurrence.
Then, we simulate the change in time that people required to respond to media under different media influence intensities μ and attenuation rates of media μ0 (see Figure 9). The media's influence intensity μ here means that if the number of cases in a region exceeds a certain threshold, the media coverage may result in a larger number of susceptibles becoming conscious. We find that when μ∈[40,1000],μ0∈[0.065,0.8] and other parameters remain unchanged, the stability of the Hopf bifurcation is similar to the situation under the group of parameters (2). Moreover, we choose μ changes within [40,600] and μ0=0.05,0.15,0.25,0.35 specifically (see Figure 10).
According to Figures 9 and 10, we can clearly see the following:
(1) τ(0)1 decreases as μ increases when the other parameters are fixed. This is consistent with the fact that when the media influence μ increases, it indicates that the epidemic is very serious, or the government attaches importance to the epidemic, so the media propaganda is increased. This requires people to respond to media coverage in a shorter time and develop a desire to be vaccinated to increase vaccination rates and achieve herd immunity to control the spread of the disease.
(2) τ(0)1 decreases when μ0 decreases from 0.35 to 0.05 and the other parameters are fixed. In fact, people are most alert when they first receive media reports about the severity of the epidemic and think it is necessary to be vaccinated. However, there is an attenuation rate of media μ0, and the attenuation rate will be smaller if most people still believe that vaccination is needed to control the epidemic after they have calmed down. This means that the epidemic is serious, so the time needed for people to respond to the epidemic is shorter, which means that τ(0)1 is smaller.
5.3. Analysis of simulations
Based on the above numerical simulations, we draw the following conclusions.
(i) For the first group of parameters (1), we find that for any τ≥0, the equilibrium P1 of the system (2.2) is locally asymptotically stable, and the COVID-19 epidemic will be completely eliminated. For the second group of parameters (2), the disease-free equilibrium P1 is unstable, and although the epidemic may stabilize, it will not disappear. Therefore, we compare the two groups of parameters and find that the first group had low rates of infection and a high rate of vaccination. This suggests that if we can strengthen self-protection, such as wearing masks and other precautions to reduce the risk of infection, develop our vaccine, make it effective enough, and vaccinate the majority of people, then the COVID-19 epidemic will disappear completely. This corresponds to reality.
(ii) Through the simulations of parameters (2), we find that people's willingness to vaccinate will be improved and the epidemic will be effectively controlled if people respond to the epidemic situation and change their vaccination willingness within τ(0)1 days after the media reported. The shorter the time that people spend changing their mind, the better the epidemic can be controlled. While the impact and timeliness of the media is diminished, people's willingness to be vaccinated will be even harder to change, and the epidemic will be difficult to control if the time people respond to media reports is larger than the critical time delay.
(iii) When the media influence intensity μ increases or the attenuation rate of media μ0 decreases, this shows that the epidemic is very serious, and the government and the media attach great importance to it. Therefore, people need to react to media coverage in a shorter time. Therefore, to keep the epidemic under control, the media needs to step up their propaganda efforts according to the changes in the epidemic and make sure that people can respond within τ(0)1.
(iv) Considering the limitations of the actual epidemic situation and the numerical simulations we have performed, we can better apply the model to real life.
Case 1: Since the vaccine is so new, it is unknown whether it will cause side effects many years later, so people may have doubts about the efficacy and safety of the COVID-19 vaccine. This means that people may be hesitant to get vaccinated. In this case, people may be initially motivated to be vaccinated by the media but become reluctant to be vaccinated after a while. This means that the impact factor of vaccination rate λ0 decreases. According to the analysis of (i), when λ0 decreases, the disease-free equilibrium will be unstable, and the epidemic will always exist, although it may become stable. This shows that vaccine hesitancy can have a negative effect on controlling the epidemic. Therefore, to effectively control the epidemic, people need to understand the COVID-19 vaccine. We recommend that the government use the media to disseminate more reports on the protective effects of vaccines and the importance of vaccination in the current situation and put forward policies that benefit the vaccinated population to guide people to dispel their fears about vaccines and actively get vaccinated against COVID-19.
Case 2: There is false information in media reports about the epidemic in this case. This causes the media attenuation rate μ0 to increase. That's because people are less willing to get vaccinated when they learn the epidemic is not as serious as reported. Therefore, the time needed for people to respond to the epidemic is longer, which is consistent with our analysis in (iii). However, we advise the media to ensure the accuracy of information so that people have a more accurate understanding of the epidemic situation, avoiding too little attention or too much attention, causing panic.
Case 3: The government can take preventive measures in a timely manner. For example, when an infected person is identified, he or she is isolated immediately, or the government requires people to reduce social activities, wear masks when going out and other precautions. This means that in this case, the infection rates α and β will decrease. Then, the disease-free equilibrium may be stable, which means that these measures have a positive impact on epidemic control based on analysis (i). Thus, we consider it necessary for the government to take timely measures and advise people to strictly abide by relevant government measures and regulations.
6.
Conclusions
In this paper, considering vaccination and the characteristics of the COVID-19 epidemic, we have constructed a new SAIM model with a time delay for people to change their vaccination willingness, which is influenced by news reported in the media. We have studied the stability of the equilibria and the existence of Hopf bifurcation. Then, we have analyzed the stability and bifurcating direction of the Hopf bifurcating periodic solution by calculating the normal form with the multiple time scales method.
Based on the observed data, we have carried out numerical simulations. First, the change in the epidemic situation has been simulated through two groups of parameters to verify the theoretical analysis results. We have found that when media coverage is more effective and the vaccination rate will increase as people respond to the epidemic within the critical time τ after the media report, the epidemic will be effectively controlled. The shorter the time it takes for people to change their vaccination willingness, the better the epidemic can be controlled. Next, we have simulated the impact of media coverage and conclude that if media propaganda is increased and the attenuation rate decreases, that is, the epidemic is serious, this requires people to respond to media coverage in a shorter time and develop a desire to be vaccinated to increase vaccination rates and gain herd immunity to control the spread of the disease. In our analysis, we consider the limitations of the actual epidemic situation to better apply our model to the real-world conditions.
We also highlight the influence of the media based on our model; that is, to keep the epidemic under control and prevent a sustained outbreak, the media needs to step up or down their propaganda efforts according to the changes in the epidemic and ensure that people can respond within a critical time.
Acknowledgments
The authors wish to express their special gratitude to the editor and the reviewers for the helpful comments given for this paper. This study was funded by Heilongjiang Provincial Natural Science Foundation of China (Grant No. LH2019A001) and College Students Innovations Special Project funded by Northeast Forestry University of China (No. 202110225003).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad:












