New classifications of monotonicity investigation for discrete operators with Mittag-Leffler kernel

1.   Introduction

Sustained oscillations in the number of infections have been observed for some infectious diseases. A classic example is the highly regular biennial pattern in measles case numbers in England and Wales from 1950 to 1967 (depicted in Fine and Clarkson, 1982 ^[1]), which is driven by a combination of births and seasonality of transmission related to the opening of school terms.

Mathematically, sustained oscillations can be demonstrated by relatively simple models. Such models focus on a key mechanism such as seasonality in transmission (Aron and Schwartz, 1984 ^[2]), births and vaccinations (Earn et al., 2000 ^[3]), pathogen evolution through time scale separation of within and between season dynamics (Andreasen, 2003 ^[4]) or in combination with seasonality forcing (Dushoff et al., 2004 ^[5]), changes in human social behavior (d'Onofrio and Manfredi, 2009 ^[6]), importations of infectious individuals (Silva and Monteiro, 2014 ^[7]), heterogeneity in transmission due to chronological age (Kuniya and Inaba, 2023 ^[8] in this special issue) and change in behavior of healthy individuals due to social pressure (Baccili and Monteiro, 2023 ^[9]). These mechanisms can drive a surge in infections through three main methods: (i) replenishment of susceptible individuals, (ii) replenishment of infectious individuals and (iii) variation of the transmission parameter. Sustained oscillations are possible in these models for certain choices of parameter values.

We argue that waning immunity is also a mechanism that can, by itself, produce sustained oscillations in infection numbers. For diseases with waning immunity, previous infection or vaccination only confers a temporary period of full protection against reinfection. The duration of protection ranges from a few weeks or months for the Omicron variant of SARS-CoV-2 (Burkholz et al., 2023 ^[10] and Bobrovitz et al., 2023 ^[11]), to possibly a few years for pertussis (Wendelboe et al., 2005 ^[12]). As fully immune individuals wane, more individuals become susceptible to infection and more infections occur. Eventually, fewer susceptibles remain and the number of infections falls. When new individuals lose full immunity, replenishment of susceptibles occurs and the cycle repeats.

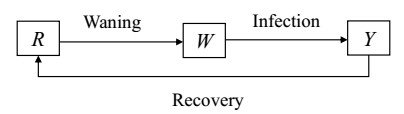
Here, we present a discrete-time waning immunity model (SIRWY model) that features the aforementioned loss of full immunity as a general population waning distribution, where the proportion of fully immune individuals who wane can be specified on a daily basis. In this Susceptible-Infectious-Immune-Waned-Infectious (SIRWY) model, S and I represent susceptible and infectious individuals without prior immunity, R represents fully immune individuals and W and Y represent waned (susceptible) and infectious individuals with prior immunity.

A special case of SIRWY is the Susceptible-Infectious-Recovered-Susceptible (SIRS) model with geometric distributions for waning and recovery. This is the discrete-time counterpart to the continuous-time classic SIRS model with exponential distributions (Hethcote, 1976 ^[13]):

In these equations, $\omega$ is the waning rate, $\beta$ is the transmission rate per infectious individual and $\gamma$ is the recovery rate. For all parameter values, the number of infections either tends to zero or the endemic equilibrium via exponential decay or damped oscillations (see Hethcote, 1976 ^[13] or a different proof in §6 of this paper). A variation of the classic SIRS is the SIR₁...R_nS model with Erlang distribution (sum of exponentials), in which individuals wait in the additional immune sub-compartments before becoming susceptible. It has been shown that sustained oscillations are possible for the SIR₁...R_nS model when $n\ge3$ (Hethcote et al., 1981 ^[14]). In this paper, we show that the discrete-time version of SIRS with geometric distributions can generate undamped oscillations, and the oscillatory regime disappears when discrete-time tends to continuous-time.

A different special case of SIRWY is one with homogeneous waning and recovery distributions. This model has fixed waning and recovery times, in which individuals spend exactly the same number of days fully immune and are infectious for exactly same number of days if infected. Due to this fixed delay in terms of time spent in the immune compartment, surges in susceptibles occur at fixed intervals. We show that sustained oscillations can be produced, similar to continuous-time models with delays (Hethcote et al., 1981 ^[14], Diekmann and Montijn, 1982 ^[15] and Kyrychko and Blyuss, 2005 ^[16]).

Besides having a general waning distribution, the full SIRWY model features another effect of waning immunity, the loss of partial immunity, which also contributes to oscillatory dynamics. After losing full immunity, individuals still have partial immunity that reduces their susceptibility to reinfection and potentially also their infectiousness if infected. However, partial immunity wanes over time and individuals become more susceptible and infectious. The accumulation of susceptibility and infectiousness in the population leads to a surge in infections. Similar to the loss of full immunity, this results in a cyclical pattern in infection numbers.

While waning immunity is a mechanism that can generate oscillations, it does not always do so as it depends on the choice of waning immunity effects (losses of full and partial immunity) and how exactly these effects are represented in the model (discrete/continuous time, population waning distribution, changes in susceptibility and infectiousness over time). As a general model which also encompasses different simpler sub-models, SIRWY allows an appropriate model to be chosen based on what is currently known about the infectiousness of the disease and the effects of waning immunity in the population, before scaling up to the full model when needed. Furthermore, for model implementation, discrete-time SIRWY is a system of difference equations, which makes numerical simulations easier to perform as compared with integro-differential equations in continuous-time.

The rest of this paper is structured as follows. We start by presenting the Susceptible-Infectious-Immune-Waned-Infectious (SIRWY) model in §2, before presenting a stability analysis about the disease-free and endemic equilibria in §3. We then proceed to recover two sub-models of the SIRWY model, one with fixed waning and recovery times in §4 and another with geometric distributions for waning and recovery in §5. For these sub-models, we perform bifurcation analysis, on top of the stability analyses about the disease-free and endemic equilibria. We then study the continuous-time exponential SIRS model (equation 1.1) in §6, before making the connection between this model and its discrete-time counterpart in §7 to show that the oscillatory regime disappears in continuous-time.

2.   The RWY model

Since our goal is to understand how waning immunity shapes the long term dynamics of a disease, we consider a population comprising individuals with some degree of immunity because all individuals would have been infected at least once in the long run. Furthermore, as the focus is on waning immunity, other mechanisms that replenish susceptibles such as births are not included (similar to how the evolutionary model is constructed in Pease, 1987 ^[17]). Since we are also not considering pathogen evolution, this means that all properties of the disease related to infection, recovery and waning of immunity are unchanged over extended periods. Let $R_{t}$, $W_{t}$ and $Y_{t}$ denote the proportions of the population who are in the fully immune, waned and infectious compartments respectively on day $t$. Here, we always discuss in terms of proportions of population in each compartment rather than exact numbers. For completeness, we give the full Susceptible-Infectious-Immune-Waned-Infectious (SIRWY) model in Appendix 12 but our focus is on the Immune-Waned-Infectious (RWY) model (Figure 1) for the rest of the paper.

Each compartment in the model (R, W and Y) is further divided into sub-compartments based on time since most recent recovery $\tau$ (first introduced by Kermack and McKendrick, 1932 ^[18]) with respect to day $t$. For example, $R_{t, \tau}$ denotes the proportion of population in the immune R compartment on day $t$ and day $\tau$ since recovery. In this notation, we can deduce the day of recovery by subtracting the second subscript from the first subscript (day $t-\tau$ for $R_{t, \tau}$).

The use of time since recovery $\tau$ allows us to track the total number of days an individual spends in the R, W and Y compartments. Time since recovery $\tau$ starts from day $0$ when the individual first joins the R compartment and increases with the day as the individual progresses through the waned W and infectious Y compartments. The value of $\tau$ then resets to $0$ when the individual rejoins the R compartment (see Figure 2 for an example). This formulation tracks a full RWY cycle (R$\rightarrow$W$\rightarrow$Y$\rightarrow$R$\rightarrow \cdots$), not just the time spent in each compartment (Inaba, 2001 ^[19]).

We cover the entire immune spectrum as we have the fully immune R compartment and the waned W and infectious Y compartments with partial immunity based on each day $\tau$ since recovery. We do not have the fully susceptible S in the RWY model but it is present in the full SIRWY model. The R compartment represents full immunity against infection, unlike that in Kermack and McKendrick (1932) ^[18], where R individuals are partially susceptible to infection. Partial immunity provides a reduction in susceptibility $\alpha_{\tau}$ of waned W individuals and a reduction in infectiousness $\chi_{\tau}$ of infectious Y individuals. Since the susceptibility of waned individuals depends on the time since recovery $\tau$, there is no need to use the method of stages to partition susceptibles into a fixed number of sub-compartments S₁, S₂, ..., S_$n$ with $n$ different susceptibilities.

The RWY model, along with a summary of terms in Table 1, is described by the following system of difference equations,

and the conservation of individuals means that

Each compartment (R, W and Y) can be defined in terms of their corresponding sub-compartments (see Table 2).

In the RWY model (equation 2.1), the newly infected $y$ is used instead of the infectious $Y$ because the infectious $Y_t = \sum_{\theta = 0}^{\overline{\theta}}\phi_\theta y_{t-\theta}$ can be expressed in terms of newly infected $y$ at time $t$ and earlier times, with $\phi_{\theta}$ representing the fraction of $y_{t-\theta}$ still infectious on day $\theta$ since infection (as similarly defined by Kermack and McKendrick, 1927 ^[20]). Here, $\phi_{0} = 1$ because all infecteds would have just joined the infectious compartment the same day they became infected, which is day $0$ since infection. By defining the maximum allowable infectious period to be $\overline{\theta}+1$ days, the fraction still infectious $\phi_{\theta} = 0$ for $\theta\ge\overline{\theta}+1$ and the infectious $Y_{t}$ is expressed in terms of newly infecteds $y_{t-\overline{\theta}}$ to $y_{t}$.

The force of infection $F_{t}$ has contributions from the fraction $\phi_{\theta}$ of newly infecteds $y_{t-\theta, \tau}$ who are still infectious on day $\theta$ since infection. On day $t$, each of these individuals contributes a baseline infectiousness $\xi_{\theta}$ based on the time since infection $\theta$, which is then reduced by a factor of $\chi_{\tau}$. Here, the $\tau$ in both $\chi_{\tau}$ and $y_{t-\theta, \tau}$ refers to the number of days since recovery with respect to the day of infection $t-\theta$ and not with respect to day $t$. As the maximum infectious period is $\overline{\theta}+1$ days, infectiousness $\xi_{\theta} = 0$ for $\theta\ge\overline{\theta}+1$.

Individuals who recover on day $t+1$ join the newly recovered $R_{t+1, 0}$ immune compartment. Using the fraction still infectious $\phi_{\theta}$, we define the population recovery distribution $\phi_{\theta}-\phi_{\theta+1}$, which gives the proportion of newly infected $y_{t-\theta}$ who recover on day $\theta +1$ since infection.

We define the immune $R_{t}$ in a similar way as the infectious $Y_{t}$. Here, $R_{t} = \sum_{\tau = 0}^{\overline{\tau}}\zeta_{\tau}R_{t-\tau, 0}$, where $\zeta_{\tau}$ represents the fraction of newly recovered $R_{t-\tau, 0}$ still immune on day $\tau$ since recovery. Again, $\zeta_{0}$ is equals to $1$ because all individuals would have just joined the immune compartment the day they recover. By defining the maximum allowable immune period to be $\overline{\tau}+1$ days, the fraction still immune $\zeta_{\tau} = 0$ for $\tau\ge\overline{\tau}+1$ and the immune $R_{t}$ only consists of newly recovereds $R_{t-\overline{\tau}, 0}$ to $R_{t, 0}$. Since individuals can only remain in the immune compartment for $\overline{\tau}+1$ days and the immune compartment is the first compartment individuals join after recovery, we can express $R_{t} = \sum_{\tau = 0}^{\overline{\tau}}R_{t, \tau}$ in terms of its sub-compartments $R_{t, \tau}$, with the final term being $R_{t, \overline{\tau}}$ as $R_{t, \tau} = 0$ for $\tau\ge\overline{\tau}+1$. Using the fraction still immune $\zeta_{\tau}$, we define the population waning distribution $\zeta_{\tau-1}-\zeta_{\tau}$, which gives the proportion of newly recovered $R_{t-(\tau-1), 0}$ who wane on day $\tau$ since recovery.

The waned $W_{t}$ and newly infected $y_{t}$ can also be expressed in terms of their sub-compartments. For the waned on day $t$, $W_{t, \tau}$ starts from $W_{t, 1}$ rather than $W_{t, 0}$ because individuals are assumed to spend at least one day in the immune compartment before moving to the waned compartment. By the same reasoning, $y_{t, \tau}$ starts from $y_{t, 2}$ because individuals are assumed to spend at least another day in the waned compartment. By defining a maximum value of $\tau = \tilde{\tau}$, we have $W_{t} = \sum_{\tau = 1}^{\tilde{\tau}}W_{t, \tau}$ and $y_{t} = \sum_{\tau = 2}^{\tilde{\tau}}y_{t, \tau}$, where the final terms $W_{t, \tilde{\tau}}$ and $y_{t, \tilde{\tau}}$ comprise all waned and newly infecteds individuals respectively with $\tau\ge\tilde{\tau}$. We may also define the infectious $Y_{t} = \sum_{\tau = 2}^{\tilde{\tau}}Y_{t, \tau}$, in terms of its sub-compartments $Y_{t, \tau}$, where $Y_{t, \tilde{\tau}}$ comprises all infectious individuals with $\tau\ge\tilde{\tau}$.

The waning of partial immunity is a decrease in protection, which is equivalent to decreases in the value of the reduction in susceptibility $\alpha_{\tau}$ and potentially also the reduction in infectiousness $\chi_{\tau}$ as $\tau$ increases. As we are using a maximum value of $\tau = \tilde{\tau}$, the reduction in susceptibility $\alpha_{\tau}$ reaches a constant value $\alpha_{\tilde{\tau}}$ for $\tau\ge\tilde{\tau}$ and the reduction in infectiousness $\chi_{\tau}$ a constant value $\chi_{\tilde{\tau}}$ for $\tau\ge\tilde{\tau}$. Together with the population waning distribution $\zeta_{\tau-1}-\zeta_{\tau}$, these three features specify how the losses of full and partial immunity are modeled in the RWY model.

We conclude this section by remarking that we have intentionally made a linear approximation on how the newly infected $y_{t}$ depends on the force of infection $F_{t}$ (Hernandez-Ceron et al., 2013 ^[21], Diekmann et al., 2021 ^[22]). The full description is the following:

This form, however, cannot be utilized easily as $F_{t}$ is also a function of newly infected $y_{t}$ at earlier times. As long as the force of infection $F_{t}$ is not too large, we can work with the linearized equation (2.1) to perform stability analysis. Equation 2.1 also allows for efficient numerical simulations to be performed via matrix-vector multiplications.

3.   Stability analysis

In this section, we derive the model equations (equation 2.1) at steady state. Letting time tend to infinity and using $*$ to denote the steady state, the immune $R$ equations become

after substituting $\sum_{\theta = 0}^{\overline{\theta}}(\phi_{\theta}-\phi_{\theta+1}) = 1$. Adding the equations in (3.1), the proportion of recovered individuals in the population at steady state is

where we have used $\zeta_{0} = 1$. Performing a similar analysis on the waned equations, we get:

where we have substituted $R_{*, 0} = y_{*}$. The waned equations can also expressed in terms of $y_{*}$ and its components:

Note that in the above analysis, we do not have an expression for $W_{*, \tilde{\tau}}$ yet. The steady state equations for the force of infection and newly infectious are:

Since $Y_t = \sum_{\theta = 0}^{\overline{\theta}}\phi_\theta y_{t-\theta}$, the infectious proportion of population at steady state is

The steady state equations above will be used to derive the disease-free and endemic equilibria in the sub-sections that follow.

3.1.   Disease-free equilibrium

We derive the disease-free equilibrium by setting the newly infected proportion of the population $y_{*, \tau}$ to be zero for all $\tau$ in the steady state equations 3.1, 3.4 and 3.5. By the conservation of individuals (equation 2.2), we find that in the disease-free equilibrium, all individuals end up in the waned $W_{*, \tilde{\tau}}$ compartment, with

We now proceed to set up a vector system of the model for linear stability analysis about the disease-free equilibrium. Let $x_{t+1} = g(x_{t})$, where $x_{t}$ is a vector that is formed by the newly infected $y_{t-\overline{\tau}-\overline{\theta}}$ to $y_{t}$ and the waned $W_{t}$. Here, $g$ is a function to be specified using the model equations (2.1 and 2.2).

Linearizing about the disease-free equilibrium and performing elementary column operations on $J-\lambda I$ (where $J$ is the Jacobian for the model equations evaluated at the disease-free equilibrium), we obtain the following characteristic equation:

Theorems related to the zeroes of polynomial are discussed in Appendix B. Using Theorem B.6 and Lemma B.7, we find that the disease-free equilibrium is asymptotically stable if and only if $\mathcal{R}_{0} < 1$, where the modified basic reproductive ratio is defined as $\mathcal{R}_{0} = (1-\alpha_{\tilde{\tau}})(1-\chi_{\tilde{\tau}})\sum_{k = 0}^{\overline{\theta}}\xi_{k}\phi_{k}$. Note that $\mathcal{R}_{0} < 1$ is the explicit threshold for all solutions to tend towards the disease-free equilibrium. Here, $\mathcal{R}_{0}$ is a modified basic reproductive ratio because $\alpha_{\tilde{\tau}}$ and $\chi_{\tilde{\tau}}$ are not necessary zero, in particular, waned $W$ individuals at $\tau = \tilde{\tau}$ may still be less susceptible to infection than susceptible $S$ individuals.

There are two key observations. First, $\mathcal{R}_{0}$ depends on the reductions in infectiousness $\chi_{\tau}$ and susceptibility $\alpha_{\tau}$ only when $\tau = \tilde{\tau}$ and not earlier values of $\tau$. This is because earlier values of $\tau$ are transient and hence not present in the steady disease-free equilibrium. The only value of $\tau$ that has a lasting effect is when $\tau$ takes the maximum value of $\tilde{\tau}$ because $\tau$ remains at this value thereafter even as the day increases. Second, $\mathcal{R}_{0}$ is independent of population recovery distribution $\phi_{\theta}-\phi_{\theta+1}$ and population waning distribution $\zeta_{\tau-1}-\zeta_{\tau}$ (see equation 2.1). Again, this is because recovery takes place for a maximum allowable period of $\overline{\theta}+1$ days (infectious period) and waning for a maximum allowable period of $\overline{\tau}+1$ days (immune period), which are transient periods that do not continue until $\tau = \tilde{\tau}$.

3.2.   Endemic equilibrium

For the endemic equilibrium, an explicit form is difficult to obtain because the steady state equations (3.1, 3.4 and 3.5) are non-linear in $y_{*, \tau}$. We can make progress in the special case where the reduction in susceptibility and infectiousness are independent of $\tau$, namely, $\alpha_{\tau} = \alpha$ and $\chi_{\tau} = \chi$ respectively. Then, the force of infection and the newly infected (equation 3.5) can be simplified to:

where we have substituted $\mathcal{R}_{0} = (1-\chi)(1-\alpha)\sum_{\theta = 0}^{\overline{\theta}}\xi_{\theta}\phi_\theta$ defined earlier. Summing up the $y_{*, \tau}$ equations, we get $W_{*} = \frac{1}{\mathcal{R}_{0}}$. Substituting this equation along with equations 3.2 and 3.6 into $R_{*}+W_{*}+Y_{*} = 1$, we obtain an expression for $y_{*}$:

The term in brackets is the sum of the fraction of newly recovered who remain immune and the fraction of newly infecteds who remain infectious throughout the entire immune and infectious period respectively. Clearly, $y_{*}$ exists (is greater than zero) if and only if $\mathcal{R}_{0}$ is greater than one. Now, $W_{*}$ and $y_{*}$ are completely defined in terms of parameter values. Using $W_{*} = \sum_{\tau = 1}^{\tilde{\tau}}W_{*, \tau}$, equation 3.4 and $W_{*} = \frac{1}{\mathcal{R}_{0}}$, we can express $W_{*, \tilde{\tau}}$ in terms of $y_{*, \tau}$:

This equation, along with equations 3.9 and 3.3, allow us to obtain a closed form for the endemic equilibrium:

In this case, the endemic equilibrium is uniquely defined. Proceeding, we perform stability analysis for the simplest case ($\tilde{\tau} = 3$, $\overline{\tau} = 1$ and $\overline{\theta} = 1$). Here, $\mathcal{R}_{0} = (1-\chi)(1-\alpha)(\xi_{0}\phi_{0}+\xi_{1}\phi_{1})$. Equation 3.10 for $y_{*}$ simplifies to $y_{*} = \frac{\mathcal{R}_{0}-1}{\mathcal{R}_{0}\left(2 + \phi_{1} + \zeta_{1} \right)}$ and the endemic equilibrium (equation 3.12) is

Performing elementary column operations on $J-\lambda I$ (where $J$ is the Jacobian for the model equations evaluated at the endemic equilibrium), we get the following characteristic equation:

where

Here, we have used the short-form $\sigma_{\theta} = \xi_{\theta}\phi_{\theta}$. Using Theorem B.6, we obtain sufficient conditions for the endemic equilibrium to be asymptotically stable. Depending on the sign of $k_{2}$ and $k_{3}$, there are four different cases to consider:

1. For $k_{2} < 0$ and $k_{3} > 0$, i.e., $1+\frac{2+\phi_{1}+\zeta_{1}}{\sigma_{0}+\sigma_{1}}\sigma_{0} < \mathcal{R}_{0} < 1+\frac{2+\phi_{1}+\zeta_{1}}{\sigma_{0}+\sigma_{1}}\sigma_{1}$,

the condition for stability is $\mathcal{R}_{0} < 1+\frac{2\sigma_{0}(2+\phi_{1}+\zeta_{1})}{(\sigma_{0}+\sigma_{1})(\phi_{1}+\zeta_{1})}$.

2. For $k_{2} > 0$ and $k_{3} < 0$, i.e., $1+\frac{2+\phi_{1}+\zeta_{1}}{\sigma_{0}+\sigma_{1}}\sigma_{1} < \mathcal{R}_{0} < 1+\frac{2+\phi_{1}+\zeta_{1}}{\sigma_{0}+\sigma_{1}}\sigma_{0}$,

the condition for stability is $\mathcal{R}_{0} < 1+\frac{2\sigma_{1}(2+\phi_{1}+\zeta_{1})}{(\sigma_{0}+\sigma_{1})(\phi_{1}+\zeta_{1})}$.

3. For $k_{2} > 0$ and $k_{3} > 0$, i.e., $\mathcal{R}_{0} > 1+\frac{2+\phi_{1}+\zeta_{1}}{\sigma_{0}+\sigma_{1}}\max(\sigma_{0}, \sigma_{1})$,

the condition for stability is $\mathcal{R}_{0} < 3$.

4. For $k_{2} < 0$ and $k_{3} < 0$, i.e., $\mathcal{R}_{0} < 1+\frac{2+\phi_{1}+\zeta_{1}}{\sigma_{0}+\sigma_{1}}\min(\sigma_{0}, \sigma_{1})$,

the condition for stability is $\phi_{1}+\zeta_{1} < 2$.

Using Lemma B.7, the necessary conditions for the endemic equilibrium to be asymptotically stable are:

1. $\mathcal{R}_{0} < 1 + \frac{2+\phi_{1}+\zeta_{1}}{\zeta_{1}\phi_{1}}$

2. $\mathcal{R}_{0} < 1 + \frac{2\sigma_{0}(2+\phi_{1}+\zeta_{1})}{(\sigma_{0}+\sigma_{1})(\phi_{1}+\zeta_{1}-2\zeta_{1}\phi_{1})}$ if $\zeta_{1}\phi_{1} < \frac{1}{2}(\phi_{1}+\zeta_{1})$

$\mathcal{R}_{0} > 1 + \frac{2\sigma_{0}(2+\phi_{1}+\zeta_{1})}{(\sigma_{0}+\sigma_{1})(\phi_{1}+\zeta_{1}-2\zeta_{1}\phi_{1})}$ if $\zeta_{1}\phi_{1} > \frac{1}{2}(\phi_{1}+\zeta_{1})$.

Unlike the case for the disease-free equilibrium, the sufficient and necessary conditions here do not together provide equivalence conditions for asymptotic stability. As such, we do not have explicit thresholds for the solutions to be in the endemic equilibrium regime. This is similar to models with varying delays in continuous-time, in which sufficient conditions for the endemic equilibrium regime are obtained (Stech and Williams, 1981 ^[23]) or numerical bifurcation analysis is performed (Blyuss and Kyrychko, 2010 ^[24]).

4.   Sub-model with fixed waning and recovery times

We consider the case where every individual follows exactly the same waning and recovery trajectory. Infected individuals join the immune compartment on day $\overline{\theta}+1$ since infection and recovered individuals join the waned compartment on day $\overline{\tau}+1$ since recovery. Similar to how classic SIRS is formulated, we consider the simplest model by dropping the dependence on time since infection $\theta$ and time since recovery $\tau$, arriving at a constant value of infectiousness $\xi$, reduction in susceptibility $\alpha$ and reduction in infectiousness $\chi$. The RWY model (equation 2.1) becomes:

where $\beta = \xi(1-\chi)(1-\alpha)$. Note that the proportions of the population in the sub-compartments $y_{t+1, \tau}$ and $W_{t+1, \tau}$ are no longer needed to be considered individually as they have been summed up. In addition, from the RWY model (equation 2.1), we get $R_{t+1, 0} = y_{t-\overline{\theta}}$ and $R_{t} = \sum_{\theta = \overline{\theta}+1}^{\overline{\theta}+\overline{\tau}+1} y_{t-\theta}$. Substituting the latter expression and $W_{t} = 1-R_{t}-Y_{t}$ into the last equation of (4.1), we obtain a non-linear scalar equation:

We linearize about the disease-free equilibrium by setting $y_{t} = \epsilon\lambda^{t}$, where $\epsilon$ is small, to get the following characteristic equation:

By Theorem B.6 and Lemma B.7, the disease-free equilibrium is asymptotically stable if and only if $\mathcal{R}_{0} < 1$, where $\mathcal{R}_{0} = \beta(\overline{\theta}+1)$. The endemic equilibrium can be found using equation (4.2) to be $y_{*} = \frac{\mathcal{R}_{0}-1}{\mathcal{R}_{0}(\overline{\theta}+\overline{\tau}+2)}$, which is uniquely defined. Linearizing about the endemic equilibrium, we get the following characteristic equation:

Applying Theorem B.6, the sufficient conditions for asymptotic stability are:

The second condition requires the infectious period to be greater than the immune period for stability. This agrees with what other continuous-time models have found (Diekmann and Montijn, 1982 ^[15], Hethcote et al. (1981) ^[14] and Stech and Williams (1981) ^[23]): a long immune period can lead to instability of the endemic equilibrium. On the other hand, applying Lemma B.7, the necessary conditions for asymptotic stability are given by:

Note that $\overline{\theta}+\overline{\tau}+3$ is the minimum amount of time an individual spends going through the $R$ ($\overline{\tau}+1$ days), $W$ ($1$ day) and $Y$ ($\overline{\theta}+1$ days) compartments before returning to the $R$ compartment.

To obtain explicit thresholds, we consider two special cases. Case 1: If the immune period is one day ($\overline{\tau} = 0$), then using Theorem B.5, the endemic equilibrium is asymptotically stable if and only if equation (4.6) holds. Case 2: If the infectious period is one day ($\overline{\theta} = 0$), then we use the Determinantal Criterion directly (Theorem B.3) for $\overline{\tau} = 1$, $2$ and $3$ to get $1 < \mathcal{R}_{0} < \frac{5}{2}$, $1 < \mathcal{R}_{0} < 5-2\sqrt{2}$ and $1 < \mathcal{R}_{0} < \frac{19-5\sqrt{5}}{4}$ respectively.

We perform bifurcation analysis for these two cases. For case 1 ($\overline{\tau} = 0$), at the critical value $\mathcal{R}_{0} = \overline{\theta}+3$, the endemic equilibrium loses stability. There are two sub-cases.

1. For $\overline{\theta}$ odd, setting $\overline{\theta} = 2n+1$, the characteristic polynomial is $\lambda^{2n+3}+\frac{2n+1}{2n+2}\sum^{2n+2}_{j = 1}\lambda^{j}+1$. We apply Theorem (B.8) with $a = \frac{2n+1}{2n+2}$, and find that all eigenvalues lie on the unit circle. One of the eigenvalues is $-1$ and there are $(n+1)$ complex conjugage pairs. A flip (also known as period doubling) and Neimark-Sacker bifurcation occur concurrently.

2. For $\overline{\theta}$ even, setting $\overline{\theta} = 2n$, the characteristic polynomial is $\lambda^{2n+2}+\frac{2n}{2n+1}\sum^{2n+1}_{j = 1}\lambda^{j}+1$. Again, applying Theorem (B.8) with $a = \frac{2n}{2n+1}$, all eigenvalues lie on the unit circle and there are $(n+1)$ complex conjugate pairs. A Neimark-Sacker bifurcation occurs.

(a) If $\overline{\theta} = 0$, the eigenvalues are $\pm i$, which leads to a $1:4$ (also known as period $4$) resonance, for which the constants $b$ and $d$ in the complex normal form can be computed using equations (C.11) and (C.12) to be $\frac{9}{4}-\frac{9i}{8}$ and $-\frac{9i}{8}$ respectively.

For case 2 ($\overline{\theta} = 0$), for $\overline{\tau} = 1$ to $3$, at the critical value of $\mathcal{R}_{0}$, we have a pair of complex conjugate eigenvalues with modulus 1, leading to a Neimark-Sacker bifurcation. There is no strong resonance for these eigenvalues found. The invariant expression $d$ can be computed using equation (C.9) and they are all negative, which means that a stable closed invariant curve bifurcates from the fixed point for $\mathcal{R}_{0}$ greater than the critical value.

Our analysis above for the RWY sub-model with fixed recovery and waning times implies that there are three dynamic regimes - (i) disease-free equilibrium, (ii) endemic equilibrium and (iii) oscillatory solutions due to flip or Neimark-Sacker bifurcations.

5.   Sub-model with geometric distributions

We now consider geometric distributions for both recovery and waning. At the individual level, on each day, an infectious individual has a probability $\gamma$ of recovering and a recovered individual has a probability $\omega$ of joining the waned compartment. At the population level, the fraction still infectious is $\phi_{\theta} = (1-\gamma)^{\theta}$ and the fraction still immune is $\zeta_{\tau} = (1-\omega)^{\tau}$. The $R$ equations can thus be expressed as:

Note that both the immune period and the infectious period are infinite days long. Furthermore, if we assume that the infectiousness $\xi$, reduction in susceptibility $\alpha$ and reduction in infectiousness $\chi$ are constants, then the RWY model (using equations 2.1, 2.2 and 5.1) becomes:

where the transmission parameter $\beta = \xi(1-\chi)(1-\alpha)$. Using the property of geometric distributions, we note that the mean number of days an individual stays in the infectious and immune compartments is $\frac{1}{\gamma}$ and $\frac{1}{\omega}$ respectively. Such a model with geometric distributions is often described as 'memoryless' because the probabilities that an infectious individual remains infectious and an immune individual remains immune on a particular day do not depend on the number of days they have already spent in the infectious and immune compartments respectively.

Substituting $R_{t} = 1-Y_{t}-W_{t}$ and $W_{t} = \frac{1}{\beta Y_{t}}[Y_{t+1}-(1-\gamma)Y_{t}]$ into the second equation of (5.2), we obtain a scalar nonlinear difference equation:

We linearize about the disease-free equilibrium by letting $Y_{t} = \epsilon\lambda^{t}$, where $\epsilon$ is small, and obtain the characteristic equation $\omega[\lambda-(1-\gamma+\beta)] = 0$. The disease-free equilibrium is asymptotically stable if and only if $\mathcal{R}_{0} < 1$, where $\mathcal{R}_{0} = \frac{\beta}{\gamma}$.

From equation (5.3), the endemic equilibrium can be found to be $Y_{*} = \frac{\omega(\beta-\gamma)}{\beta(\omega+\gamma)}$, which is uniquely defined. Linearizing about the endemic equilibrium, we get the characteristic equation $\lambda^{2} + p_{1}\lambda + p_{0} = 0$, where $p_{1} = -2+\omega+\frac{\omega(\beta-\gamma)}{\omega+\gamma}$ and $p_{0} = 1 - \omega + \omega(\beta-\gamma)(\frac{\omega+\gamma-1}{\omega+\gamma})$. Using the Determinantal Criterion for order 2 (equation B.2), the endemic equilibrium is asymptotically stable if and only if

where

At the critical value $\mathcal{R}_{0}^{*} = 1 + \frac{2(2-\omega)(\gamma + \omega)}{\gamma\omega(2-\gamma-\omega)}$, the eigenvalues are $-1$ and $-\frac{2+(\gamma+\omega)(-3+\omega)}{-2+\gamma+\omega}$. The latter eigenvalue cannot take the value $1$ or $-1$ under the constraints for $\gamma$ and $\omega$. Hence, the Jacobian $J$ has a simple critical eigenvalue $-1$ and a flip bifurcation occurs. The invariant formula $b$ in the normal form of a flip bifurcation (equation C.6) can be calculated using the formula (equation C.7) to be

Under the constraints for $\gamma$ and $\omega$, $b$ is always greater than $0$, which means that a stable period two cycle bifurcates from the fixed point for $\mathcal{R}_{0} > \mathcal{R}_{0}^{*}$.

On the other hand, at the critical value $\mathcal{R}_{0}^{*} = 1+ \frac{\gamma+\omega}{\gamma(\gamma+\omega-1)}$, the eigenvalues are

which have modulus one under the constraints for $\gamma$ and $\omega$. Thus, a Neimark-Sacker bifurcation occurs at the critical value $\mathcal{R}_{0}^{*}$.

Like the RWY sub-model with fixed recovery and waning times, our analysis here for the sub-model with geometric distributions in discrete-time implies that there are three dynamic regimes - (i) the disease-free equilibrium, (ii) the endemic equilibrium and (iii) oscillatory solutions due to flip or Neimark-Sacker bifurcation.

6.   Sub-model with exponential distributions

We take the limit as time step tends to zero for the discrete-time sub-model with geometric distributions (equation 5.2), to get the continuous-time RWY model with exponential distributions:

where $\beta$ is the transmission rate per infectious individual, $\omega$ is the waning rate and $\gamma$ is the recovery rate. We present the following analysis in the same manner as earlier sections of the paper, and refer the reader to Hethcote, 1976 ^[13] for an alternative derivation of these results.

The disease-free equilibrium is given by: $R_{*} = 0$, $W_{*} = 1$ and $Y_{*} = 0$. It is asymptotically stable if and only if $\mathcal{R}_{0} < 1$, where $\mathcal{R}_{0} = \frac{\beta}{\gamma}$.

The endemic equilibrium is given by: $R_{*} = \frac{\gamma(\beta-\gamma)}{\beta(\omega+\gamma)}$, $W_{*} = \frac{\gamma}{\beta}$ and $Y_{*} = \frac{\omega(\beta-\gamma)}{\beta(\omega+\gamma)}$, which is uniquely defined. Note that the expression for the endemic equilibrium in continuous-time is the same as that in discrete-time. The eigenvalues of the Jacobian matrix are

where $\check{\omega} = \omega\left(\frac{\frac{\omega}{\gamma}+\mathcal{R}_{0}}{\frac{\omega}{\gamma}+1}\right)$. The endemic equilibrium is asymptotically stable if and only if both eigenvalues are negative, which occurs if and only if $\mathcal{R}_{0} > 1$. Hence, the RWY sub-model with exponential distributions in continuous-time only has two dynamic regimes: the disease-free equilibrium and the endemic equilibrium. No oscillatory solution is possible.

7.   Bridging between discrete-time and continuous-time sub-models with geometric distributions

In this section, we seek to understand how the dynamic regimes change when we transit from discrete-time to continuous-time. The discrete-time sub-model with geometric distributions with time step $h$ is:

which is almost identical to the discrete-time sub-model with geometric distributions (equation 5.2), except that each of the parameters $\omega$, $\beta$ and $\gamma$ is scaled by $h$. By taking into account this factor $h$ in previous results for the discrete-time model with a time step of one day, we see that as before, $\mathcal{R}_{0} = \frac{\beta}{\gamma}$ and the disease-free equilibrium is asymptotically stable if and only if $\mathcal{R}_{0} < 1$. The endemic equilibrium also remains the same: $R_{*} = \frac{\gamma(\beta-\gamma)}{\beta(\omega+\gamma)}$, $W_{*} = \frac{\gamma}{\beta}$ and $Y_{*} = \frac{\omega(\beta-\gamma)}{\beta(\omega+\gamma)}$. It is asymptotically stable if and only if $1 < \mathcal{R}_{0} < 1 + q_{h}$, where

In the limit as $h$ tends to zero, the top case in equation 7.2 collapses and $q_{h}$ tends to infinity. Hence, the endemic equilibrium is asymptotically stable if and only if $\mathcal{R}_{0} > 1$ and the last regime with flip/Neimark-Sacker bifurcation in discrete-time disappears (see Figure 3). The number of dynamic regimes decreases from three to two and oscillatory solutions are no longer possible.

8.   Discussion

We have intentionally chosen to focus on waning immunity to improve our understanding of the underlying mechanism behind the recent waves of COVID-19 infections in this ongoing pandemic. The emergence of new variants has often been invoked as the reason causing waves of surges in case numbers. However, our work shows that the waning of prior immunity, whether that immunity is from infection or vaccine, is sufficient on its own to drive oscillations. Hence, at least in theory, pathogen evolution may be purely consequential rather the cause of these waves.

In practice, COVID-19 waves are unlikely to be driven by a single mechanism. The effects of phylodynamics (Grenfell et al., 2004 ^[25]) are complex and there is likely a feedback loop between waning immunity dynamics and pathogen evolution. However, we argue that for diseases with evidence of waning immunity, the loss of immunity should be considered to be a candidate for the main mechanism driving oscillatory dynamics. This is particularly true for diseases with a short temporary period of strong protection like COVID-19, where parsimonious waning immunity models can be used to explain the key trends of observed oscillations in case numbers.

From the public health point of view, policy makers may want to know whether surges in case numbers will happen in the long term for endemic diseases with waning immunity. Surges in case numbers are particularly problematic if the disease has severe health outcomes, especially when healthcare capacity is a major constraint. Models can help by distinguishing between two model outcomes for endemic diseases – the endemic equilibrium and sustained oscillations. The former does not lead to long term surges in case numbers but the latter does. If waning immunity plays a role in sustaining oscillations, then understanding the population infection dynamics can help policy makers decide the timing of booster campaigns to reduce the size of future case surges.

Acknowledgements

We thank the three anonymous reviewers for their useful feedback, which helped to improve this manuscript.

Desmond Z. Lai is supported by the Trinity Hall Research Studentship and Cambridge International & Department of Applied Mathematics and Theoretical Physics (DAMTP) Scholarship. Julia R. Gog is supported by the JUNIPER partnership (MRC grant no MR/X018598/1).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare that there is no conflict of interest.

Appendix A.   The SIRWY model

The SIRWY model (see Figure 4) is an extension to the RWY model as it takes into account individuals in the population who do not have prior immunity to the disease. These individuals belong to either the susceptible ($S$) or infectious ($I$) compartment. The proportion of population that is infectious at time $t$ is denoted by $I_t = \sum_{\theta = 0}^{\overline{\theta}}\check{\phi}_\theta i_{t-\theta}$, which is defined in an analogous manner as its counterpart $Y_{t}$ with prior immunity. Table 3 gives a list of the variables, indices and parameters used in SIRWY model, comparing terms with/without prior immunity whenever possible. The SIRWY model is described by the following system of difference equations,

and the conservation of individuals means that

The I, R, W and Y compartments can be defined in terms of their corresponding sub-compartments (see Table 4). Similar to the RWY model, the SIRWY model is specified using the proportion of newly infecteds ($i$ and $y$) rather than the proportion of infectious individuals ($I$ and $Y$).

Appendix B.   Theorems regarding zeroes of polynomial

For a $k^{th}$ order difference equation, we define the following characteristic polynomial:

where $p_{i}$ are real numbers in our case.

Definition B.1 (Inners of a matrix). (Jury, 1971 ^[26], Jury, 1974 ^[27] and Elaydi, 2005 ^[28]) The inners of a matrix $B = (b_{ij})$ are the matrix itself and all the matrices obtained by sequentially removing the first and last rows and the first and last columns. For example, other than the matrix itself, the inners of the following matrices are indicated by boxes:

Definition B.2 (Postive Innerwise). (Jury, 1971 ^[26], Jury, 1974 ^[27] and Elaydi, 2005 ^[28]) A matrix $B$ is positive innerwise if the determinants of all of its inners are positive.

Theorem B.3 (Determinantal Criterion, a special case of Schur-Cohn Criterion). (Jury, 1964 ^[29], Jury, 1971 ^[26], Jury, 1974 ^[27] and Elaydi, 2005 ^[28]) The zeroes of the characteristic polynomial (equation B.1) lie inside the unit disc if and only if the following hold:

(i) $p(1) > 0$

(ii) $(-1)^{k}p(-1) > 0$

(iii) The $(k-1)$ by $(k-1)$ matrices

are positive innerwise.

Corollary B.4. (Eladyi, 2005 ^[28]) The three criteria in the Determinantal Criterion have an explicit form for lower orders.

For $k = 2$,

For $k = 3$,

In the event that equation B.1 is of the following form with only 2 parameters:

we have an explicit form for the necessary and sufficient conditions for asymptotic stability.

Theorem B.5. (Tomášek, 2015 ^[30]) Let $a$ and $b$ be real non-zero constants and $k \ge 2$. The zeroes of the characteristic polynomial (equation B.4) lie inside the unit disc if and only if

(i) $b > a-1$

(ii) $b < 1$

(iii) $b > (1-k)a - 1$.

Theorem B.6 (Sufficient condition for stability). (Eladyi, 2005 ^[28]) The zeroes of the characteristic polynomial (equation B.1) lie inside the unit disc if

Lemma B.7 (Necessary conditions for stability). (Bistritz, 1984 ^[31]) If the zeroes of the characteristic polynomial (equation B.1) lie inside the unit disc, then the following hold:

(i) $|p_{0}| < 1$

(ii) $p(1) > 0$

(iii) $(-1)^{k}p(-1) > 0$.

Theorem B.8. (Botta et al., 2014 ^[32]) The zeroes of the polynomial $p(\lambda) = \lambda^{k}+a(\lambda^{k-1}+\cdots+\lambda) + 1$, $a\in\mathbb{R}$, of degree $k > 1$ lie on the unit circle if and only if

(i) $-\frac{2}{k-1} \le a \le 2$ if $k$ is even

(ii) $-\frac{2}{k-1} \le a \le 2 + \frac{2}{k-1}$ if $k$ is odd.

Appendix C.   Theorems regarding bifurcation analysis

We first start from the following discrete time dynamical system (map) given by

To perform a bifurcation analysis on the fixed point $x^{*}$ at the critical parameter value $\omega^{*}$, we do a coordinate shift, placing the fixed point at the origin. Now, in the new coordinates, after renaming and keeping the same variable $x$, we assume that this system can be written in the form

where $J$ is the Jacobian matrix and $F(x)$ is a smooth function of order $\mathcal{O}(\vert\vert x \vert\vert^{2})$ with the following Taylor expansion

Here, $K(x, y)$ and $L(x, y, z)$ are defined by

and

for $i = 1, \cdots, n$. This presentation and subsequent results in this section are attributed to Kuznetsov, 2004 ^[33].

C.1.   Flip Bifurcation

Here, assume that the Jacobian $J$ has a simple eigenvalue $-1$ on the unit circle. The map (equation C.2), when restricted to the center manifold, can be transformed to the normal form

where $b$ gives the direction of bifurcation of the period-two cycle and can be computed using the following invariant formula:

In this case, $q$ is the real eigenvector satisfying $Jq = -q$ while $p$ is the real adjoint eigenvector satisfying $J^{T}p = -p$. The eigenvectors $p$ and $q$ have been normalized such that $\langle p, q\rangle = 1$. Functions $K(x, y)$ and $L(x, y, z)$ are as defined in equation C.4 and C.5 respectively.

If $b > 0$, then a stable period-two cycle bifurcates from the fixed point for parameter values $\omega$ larger than the critical parameter value $\omega^{*}$. When $b < 0$, then the cycle of period-two is unstable. The case of $b = 0$ means that the bifurcation is more degenerate than the normal form.

C.2.   Neimark-Sacker Bifurcation

C.2.1.   Absence of strong resonances

Assuming that the Jacobian $J$ has a simple pair of eigenvalues on the unit circle $e^{\pm i\theta_{0}}$, where $\theta_{0}\in(0, \pi)$ and these are the only eigenvalues with modulus 1. The absence of strong resonances means that $e^{ik\theta_{0}} \ne 1$ for $k \in\{1, 2, 3, 4\}$. Then, the map (equation C.2) can be restricted to the center manifold and transformed to the complex normal form

where $d =$Re $d_{1}$ gives the direction of the closed invariant curve and can be computed using the following invariant expression

Here, $q$ is the complex eigenvector satisfying $Jq = e^{i\theta_{0}}q$ and $J\overline{q} = e^{-i\theta_{0}}\overline{q}$ while $p$ is the complex adjoint eigenvector satisfying $J^{T}p = e^{-i\theta_{0}}p$ and $J^{T}\overline{p} = e^{i\theta_{0}}\overline{p}$. The scalar product $\langle p, q\rangle = \overline{p}^{T}q$ is the standard one in $\mathbb{C}^{n}$; $p$ and $q$ have been normalized such that $\langle p, q\rangle = 1$. Functions $K(x, y)$ and $L(x, y, z)$ are as defined in equation C.4 and C.5 respectively.

If $d < 0$, then a stable closed invariant curve bifurcates from the fixed point for parameter values $\omega$ larger than the critical parameter value $\omega^{*}$. When $d > 0$, then the closed invariant curve is unstable. The case of $d = 0$ means that the bifurcation is more degenerate than the normal form.

C.2.2.   1:4 resonance

In this case, Jacobian $J$ has eigenvalues $e^{\pm i\frac{\pi}{2}} = \pm i$ and the map (equation C.2) can be transformed to the following complex normal form

where

and

As before, the terms $K$, $L$, $p$ and $q$ are as defined in the previous section where there is an absence of strong resonances.