1.
Introduction and model formulation
The addiction to heroin, smoking, alcohol and other substances remain a major social problem in many regions in world. For example, in the latest report of WHO [1] estimates that in 2016 there were some 3 million deaths caused by the harmful use of alcohol. The social pressure due the current COVID-19 pandemic had fuel different types of addictions [2] including alcohol addiction.
The mathematical modeling of the substances addiction use the epidemiological aspect of this problem, as the addiction is contagious and spreads from one person to another, like infectious diseases. In fact, there are many mathematical models that studies addiction problems as example heroin addiction [3,4,5], smoking addiction [6], alcohol addiction [7,8], Cocaine [9].
Our goal in this work is to formulate a mathematical model that describes the spread of alcohol addiction, where our starting point will be from the model investigated by Mulone et al. in [10] that contains a model with three population classes formulated by ordinary differential equations, which is structured as:
with S(t),H(t),R(t) are respectively the density of the susceptible individuals, alcohol drinkers, recovered individuals at time t. Λ is the density of persons entering into the S-class in a given time interval, μ is the death coefficient. The rate β represents the probability (per unit time) for being a drinkers, and the bilinear incidence term stands for susceptible turning to drinker through peer influence and pressure of the drinkers. δ stands for the fraction of alcohol users (per unit time) who enters into treatment. ε stands for the fraction of the persons in treatment (per unit time) that relapse into alcohol consumption again. The authors obtained a global threshold in terms of the basic reproduction number R0, where the for R0<1 the addiction of alcohol consumption will extinct from the population, and persist in the case R0>1. Further, there are numerous other approximations that investigate the spread of the addiction of this substance as by a delayed system [7], by an age structured model [8]. Our objective in this research is to use different approach that takes into consideration the effect of recovering duration before the repulse into alcohol addiction again. Moreover, due to social pressure and problems a susceptible person can enters into addicted class without influence of the addicted person (alcohol user in this case). Taking in consideration the above mentioned points into the system (1.1), we propose the following delayed system:
η is the mortality rate due to over consumption of alcohol. d represents the recovered density that been successfully established the full treatment procedure. α is the responsible rate for the susceptible addiction due to the social pressure and problems. The term ∫τ0k(σ)e−(μ+d)σδH(t−σ)dσ=∫tt−τk(t−σ)e−(μ+d)(t−σ)δH(σ)dσ is the repulse density of recovered into alcohol consumers. The term δH(t−σ) represents the density of individuals that been entered into the treatment stage at the time t−σ and e−(μ+d)(t−σ) is the surviving probability between the periods t−σ and t, the kernel k(σ) stands for the probability of returning into the alcohol use again after recovering that last σ unit of time, τ is the maximal duration spent in recovered stage before becoming a full recovered person and after this duration isn't possible repulse into the alcohol use. Further, the kernel function verifies ∫τ0k(σ)dσ=1. We consider also the following initial conditions:
with ϕ=(ϕ1,ϕ2,ϕ3)∈C([−τ,0],R3+), we presume also that ϕ2≢0. This system can be applied to model different addiction epidemics as heroin addiction [3,4], smoking addiction [6], cocaine addiction [9]. To mention that the distributed delay is a subject of interest of many recent research activities as example [11,12,13,14,15], which shows its importance in modeling numerous natural behavior. Our main contribution through this research is to study the global dynamics of the model (1.2). In [3,4], the authors proposed a model that studies the spread of the heroin addiction in a population, where it can be considered as particular case of the model (1.2) (means α=0), where it is obtained that the model has threshold dynamics in terms of the basic reproduction number R0, where for R0<1 the disease free equilibrium is globally asymptotically stable, and for R0>1 the unique positive equilibrium is globally asymptotically stable. Indeed, we will show that the our system (1.2) has no notion of the basic reproduction number, and there is no threshold dynamics and the unique positive equilibrium is always globally stable independent of the value of the kernel function k and any positive value of α and the delay τ. To mention that the non existence of basic reproduction number is proved for epidemiological models in the case of the presence of immigration [16]. Through this paper we develop another case which eliminates the notion of the basic reproduction number (or the threshold dynamics) that can be hold in addiction epidemic models. For this purpose we organize the paper in the following structure:
In the next section, we will provide some preliminaries regarding the positivity of solution, also the existence and uniqueness of the positive equilibrium. Next, we will show that the unique equilibrium is locally stable independent of the kernel function k(σ). This result is expanded in section 4, where using a Lyapunov function we will prove that this equilibrium is globally stable.
2.
Preliminaries and existence and uniqueness of positive equilibrium
Theorem 2.1. The quadrant is positively invariant to the semi flow of the system (1.2). For all ε>0 we set:
There exist ε>0 such that Ωε is non-empty and attracts all the solutions of (1.2) initiating in the positive quadrant.
Proof. First, using the continuity of the solutions, for any initial conditions S0,H0:[−τ,0]→(0,∞), there exists T such that S(t)>0, H(t)>0 for any t∈(0,T). Now, we calculate
we get:
hence N(t)≤min{Λμ,N(θ)},θ∈(−τ,0), which means that S(t),H(t),R(t) remains bounded. By assuming that supθ∈[−τ,0]|N(θ)|∈Ω0 we deduce that the solution exists for all t≥0 and remains in Ω0.
In Ω0, if S=0, then dSdt=Λ. Since the vector field is continuous and Ω0 is compact, there exists ε0>0 such that dSdt>0 for S≤ε0. Hence, S will increase to be larger than ε0, and will remain above this level. therefore, we presume that S>ε0 for all t≥0. Then, we can get dHdt≥βε0H+αε0. Hence, there exists ε1>0 such that H will increase to be larger than ε1, and will remain above that level. Similarly we can obtain bounds ε2 for R.
We let ε=min{ε0,ε1,ε2}. Then Ωε is positively invariant and attracts all the solution initiating in the positive quadrant.
Clearly, the two first equations of the model (1.2) are independent of R. Hence, R can be completely determined by H(t), thus the following system can be separated from the model (1.2):
Regarding the existence and the uniqueness of the positive equilibrium we set the following lemma:
Lemma 2.2. The system (2.1) has always a unique positive equilibrium, for any value of the kernel k(σ).
Proof. The positive equilibrium is the solution of the following system:
with ˜k=∫τ0k(σ)e−(μ+d)σdσ. From the first equation of (2.2) we have:
by summing the two equations of the system (2.2) along with the previous equality, we get:
which is equivalent to
Clearly, (2.3) has a unique positive root which is:
Hence the system (2.2) has always a unique positive solution. The proof is completed.
3.
Local stability of the positive equilibrium
Theorem 3.1. The positive equilibrium is locally asymptotically stable for any delay kernel k(σ) and any value of the delay τ.
Proof. The local stability can be deduce by analyzing the roots of the following characteristic equation
which can be expressed as:
with
Clearly, fτ(0)=β2S∗H∗>0, hence λ=0 is not a solution of fτ(λ)=0. Now, we set τ=0, then f0(λ) is written as:
clearly, f0(λ)=0 has two roots with negative real part. It is well known that delay can generate instability of a stable equilibrium, hence, we seek for the roots of the form iy,y>0. Thus, fτ(λ)=0 can be expressed as:
Separating the real and the imaginary parts, we get:
The multiplication of the first equation by ΛS∗ and the second on by y, and the sum of the obtained two yields:
Since δ∫τ0k(σ)e−(μ+d)σcos(yσ)dσ≤δ∫τ0k(σ)e−(μ+k)σdσ=δ˜k, the equation (3.1) cannot have root of the form λ=iy. Then, the unique positive equilibrium is always locally asymptotically stable for any delay kernel k(σ). The proof is completed.
4.
Global stability
In this section, we employ a Lyapunov function to obtain the global stability of the unique positive equilibrium. The obtained results are resumed in the following theorem:
Theorem 4.1. The unique positive equilibrium of the system (2.1) is globally asymptotically stable, regardless the delay kernel k(σ) and the time delay τ.
Proof. We consider the following Lyapunov function:
with
where g is Volterra function g(w)=w−1−lnw,w∈R+, which has a global minimum at w=1, and g(w)>0 for all w∈R+. Note that V(t) is nonnegative defined and has a global minimum at the positive equilibrium (S∗,H∗). The time derivative of the function V(t) is given in the following form:
Using Λ=βS∗H∗+(μ+α)S∗ we get
Using the equilibrium propriety, that is (μ+δη)H∗=βS∗H∗+αS∗+˜kH∗, we obtain:
Now calculating dV2dt
Note that
hence, we obtain
Now, we calculate dVdt, we get:
Using the fact that H(t)[βS∗−(μ+δ+μ)+δ˜k]=−αS∗H(t)H∗, we get
By a simple calculation we have
and
and
It follows that V(t) has non-positive derivative dV(t)dt. We let Γ be the largest invariant subset of {(S(t),H(t))|dV(t)dt=0}. Now, let us determine the set Γ. Note that dV(t)dt=0, leads to S(t)=S∗, and H(t)=H(t−σ). Hence, at each point in Γ, we get S(t)=S∗, therefore, dV(t)dt=0 in Γ, from the first equation of (2.1), we get 0=Λ−βS∗H(t)−(μ+α)S∗ for all t, yields, H(t)=H∗, for all t. Then, Γ={E∗}. Using Theorem 1.2 and the LaSalle invariance principle [10], every solution of (2.1) goes to E∗, hence it is globally asymptotically stable, which completes the proof.
Remark 4.2. By analyzing the system (2.1) we deduce that S(t), H(t) goes to S∗, H∗, as t tends to infinity, respectively. By replacing this result into the third equation of the system (1.2), we get R(t) goes to R∗=δH∗(1−˜k)μ+d. Therefore the positive fixed point of (1.2) is global asymptotically stable.
5.
Numerical results and discussion
In this section, we will check our theoretical results numerically. The detailed discussion is provided through the following aspects:
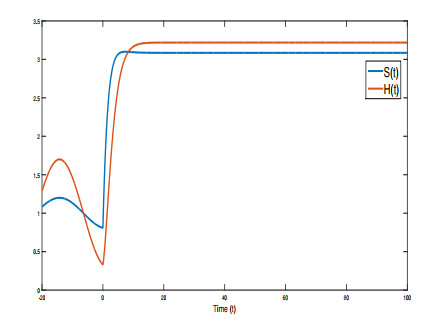
Figure 1 In this figure, we investigated the global stability of the unique positive equilibrium for the values Λ=2, μ=0.1, β=0.015, η=0.4, d=0.2, δ=0.1, α=0.5, τ=20 and the initial conditions S(t)=1+0.2cos(0.2t), U1(t)=1+0.7cos(0.2t) for t∈[−τ,0]. This result guarantees the results obtained through section 4 for the chosen initial conditions.
Figure 2 In this case, we investigate the impact of the new alcohol users without on the asymptotic behavior of the solution of the system (2.1) for the values Λ=2, μ=0.1, β=0.015, η=0.4, d=0.2, δ=0.1, τ=20 and the initial conditions S(t)=1+0.2cos(0.2t), H(t)=1+0.7cos(0.2t) for t∈[−τ,0]. Here, we established the global stability of the unique equilibrium for any positive value of α>0 with the same initial condition. Moreover, we determined the influence of a on the value of the unique positive equilibrium, where it is obtained that α affects positively the density equilibrium of the alcohol users, and negatively the density equilibrium of the susceptible individuals.
Figure 3 This simulation seek to illustrate the effect of the maximal duration of the remission of alcohol consumption on the asymptotic behavior of the solution of (2.1) for the set of parameters Λ=2, μ=0.1, β=0.015, η=0.4, d=0.2, δ=0.1, α=0.05, and different values of the delay τ. Here, we studied the influence of the delay on the behavior of the solution, where we obtained that the delay has no influence on the stability of the unique positive equilibrium, differently from numerous researches, where it can generate a Hopf bifurcation [17,18,19]. Here, the delay has an influence on the density equilibrium of both populations but not on the behavior of solution.
Figure 4 The sensitivity of the unique endemic equilibrium with respect to alpha for the following set of parameters: Λ=2, μ=0.1, β=0.015, η=0.4, d=0.2, δ=0.1, τ=0.1. Here, we studied the sensitivity of the unique positive equilibrium with respect to the rate α, where it is obtained that the social pressure coefficient α has a positive influence of the alcohol users density equilibrium, and negative impact on the susceptible density equilibrium.
6.
Conclusion
This paper dealt with an alcoholism model and distributed delays. The main objective is investigate the effect of the social pressure that leads to addiction without the influence of the alcohol users. which is reflected in our model by the rate α. For α=0, there is a threshold dynamics in terms of the basic reproduction number R0 which it was obtained in [3,4] which is obtained as:
In this case there is a sharp threshold properties of the model. i.e. the addiction free equilibrium (Λμ,0) is globally stable for R0<1, and the positive equilibrium (S∗,H∗)=(ΛμR0,μ(R0−1)β) is globally stable for R0>1
Our finding showed that for α≠0, the model (1.2) has no threshold dynamics. More precisely, the system (1.2) has a unique positive equilibrium which is globally asymptotically stable for any value of α>0 and any value of the kernel k(σ). This means the social pressures will lead to the persistence alcohol addiction. This study can be applied to other addiction epidemic models as smoking, heroin, cocaine, social media.
Acknowledgements
The authors would like to thank the anonymous reviewers for their valuable comments.}
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad:






