A framework for efficient brain tumor classification using MRI images

1.   Introduction

The COVID-19 has been the most serious outbreak worldwide since 2000, and it is currently in the prevention and control phase. The novel coronavirus is in lineage B of the genus $\beta$-coronavirus of the coronavirus family, in which severe acute respiratory syndrome-related coronavirus (SARS-CoV) and Middle East respiratory syndrome-related coronavirus (MERS-CoV) are also included. These pathogens are enveloped positive-sense RNA viruses that are widespread in mammals, including humans, and they can destroy the respiratory systems of humans and cause severe acute respiratory syndrome ^[1,2,3]. Despite global vaccination efforts, the epidemic situation is still critical for two main reasons. One reason is that the COVID-19 vaccination proportion remains low in some countries, such as low-income countries in Africa ^[4], leading to a lack of global immune barriers. Another issue that cannot be ignored is that the antibodies produced in the body do not fully defeat variable strains, and the effectiveness of antibodies decreases as the virus mutates ^[5]. According to data published by the Israeli Ministry of Health, the protective effect of the Pfizer COVID-19 vaccine decreases after 6 months of vaccination. Based on available statistics, it has been confirmed that some people who have been vaccinated against COVID-19 have been diagnosed, and this number is increasing. Therefore, there has been a global consensus to implement the booster vaccinations. By receiving the booster vaccine, a strong immune response can be rapidly produced in the body, and the level of neutralizing antibodies can significantly increase, thereby improving the overall immunity level and achieving outbreak control.

In 1927, Kermack and McKendrick first used dynamic research methods to study the spread of infectious diseases ^[6]. Since then, an increasing number of researchers have engaged in mathematical modeling of infectious diseases considering their transmission mechanisms and control measures ^[7,8,9,10]. Vaccination and even booster shots were added to the model to study the dynamic behaviors of the corresponding infectious diseases ^[11,12,13]. In particular, since the outbreak of COVID-19, researchers worldwide have been very concerned, and corresponding infectious disease models have been developed to simulate epidemic trends to provide policy recommendations ^{[14,15,16,17,18,19]}. The models are not limited to ordinary differential equations (ODEs), and the use of partial differential equations (PDEs) is also a good way to study such problems ^[20,21,22].

During the early stage of the outbreak, the treatment process was difficult because people had never been exposed to this disease. Although we have better research on treatments and have continued to learn about the disease, studies have shown that COVID-19 drugs have side effects on our bodies ^[23,24]. Therefore, vaccination is considered an effective strategy to prevent COVID-19 and control the outbreak. Thus, as vaccines gradually enter clinical trials and continue to spread worldwide, an increasing number of scholars have added vaccination to their models^[25,26]. Given the current situation, most people have been vaccinated, but the mutations may lead to the failure of original antibodies. To maintain sustained immunity, it is feasible and meaningful to vaccinate with booster shots ^[27].

Adding the necessary "time delay" to the model tends to make it more realistic. Sometimes, the model is sufficient to describe facts and phenomena accurately even with only one time delay ^{[28,29,30,31]}. However, sometimes, one time delay is not enough to describe complex phenomena fully, and double time delays or even multiple time delays are necessary ^{[32,33,34,35,36,37,38]}. When we add the effect of booster vaccination to the epidemic model, there are two periods of time that we cannot ignore: the time of antibody failure and the time of booster vaccination. Therefore, we introduce two time delays into the model to describe the problem better.

For differential equation models, stability and Hopf bifurcation analysis have always been popular research topics. Mahata et al. ^[39] studied a fractional-order dynamical system of Susceptible-Exposed-Infected-Recovered-Vaccinated ($SEIRV$) in the infectious population. The stability of all equilibria was analyzed with respect to the delay parameter, and threshold values of delay were found, beyond which the system exhibited Hopf bifurcation and the solutions were no longer periodic. Zhang et al. ^[40] studied an epidemic model involving nonlinear birth in population and vertical transmission. They discussed the existence of Hopf bifurcation and obtained the stability and direction of Hopf bifurcation by using normal form theory and center manifold theorem. References ^{[41,42,43,45,46,47]} discussed different dynamic properties of Hopf bifurcation in different systems. We hope that we can also analyze the dynamic properties after establishing the model and use the results to make reasonable recommendations for vaccination.

The motivations of our study are as follows. First, although COVID-19 vaccines have shown good protective efficacy and great safety in both clinical trials and real-life applications, there are some cases of infection in people who have been vaccinated, suggesting that vaccine-induced immunity is not permanent. Therefore, booster vaccination is necessary and we need to take this into account in our model. Second, there is a time delay between booster vaccination and initial vaccination, which has a profound impact on the development of the epidemic. Different booster vaccination time will cause different phenomena in the model, which is essential to understand the development of epidemic and to formulate the effective policies. Third, when is the booster vaccination most beneficial for the development of the epidemic when taking into account the economy, national power and medical level? What measures should we take to minimize the impact of the epidemic on human life? Finally, COVID-19 exhibits a constantly and dynamically evolving mutational landscape, with relatively abundant genetic diversity and a high evolutionary capability over time^[48,49,50]. As the virus continues to mutate, what effect will this have on the time of booster vaccination?

Through the study of this paper, we have a more accurate grasp of when to carry out booster vaccination. By simulating the current epidemic state, a reasonable time range for booster vaccination is proposed, which can ensure that the epidemic can reach a stable state instead of getting out of control. This is meaningful to the formulation of epidemic prevention and control policies.

This paper is organized as follows. In Section 2, we establish a delayed differential system with two time delays to study the impact of vaccination on the epidemic and determine the optimal time for the booster vaccination. In Section 3, we analyze the conditions for the existence and stability of equilibria and the existence of Hopf bifurcation. Next, the normal form of Hopf bifurcation is deduced by using the multiple time scales method in Section 4. In Section 5, numerical simulations are carried out to verify the theoretical analysis based on the parameters through statistical analysis. Finally, we draw conclusions about the optimal time range of booster vaccination by combining all aspects and provide some reasonable suggestions in Section 6.

2.   Mathematical modeling

2.1.   Proposing mathematical model

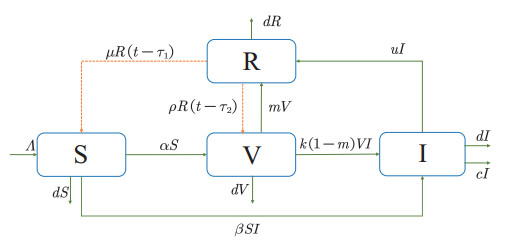
In the traditional model of infectious disease, susceptible people ($S$) can be infected through contact with a source of infection, which converts them into infected people ($I$). With treatment, those infected people can be cured and then become recovered people ($R$) with antibodies. Considering the characteristics of COVID-19, vaccination has become the global trend, and vaccinated people have become a large group that cannot be ignored. Therefore, we need to represent them as a separate compartment denoted as vaccinated people ($V$), which is a more accurate representation of the current outbreak. However, it is important to note that vaccinated people ($V$) are those who have completed the vaccination but have not fully developed antibodies. This group of people is still at risk of being infected. For those who have fully developed antibodies, we classify them as recovered people ($R$) since the process of producing antibodies is similar to the mechanism of cure after infection. This can be understood as recovering from the risk of infection. Combined with the above considerations, we choose the Susceptible-Vaccinated-Infective-Recovered ($SVIR$) model for our study of COVID-19 with booster vaccination.

Similar to the traditional $SIR$ model, susceptible people ($S$) will be transformed into infected people ($I$) when they effectively contact $I$. Infected people ($I$) will be transformed into recovered people ($R$) after healing through treatment. As schematically shown in Figure 1, after vaccination, susceptible people ($S$) can be transformed into vaccinated people ($V$). However, not all vaccinated people are able to complete the immune response and further produce antibodies. For those who are able to produce the immune response ($mV$), we also classify them as recovered people ($R$) since they share the same characteristics as those who are cured after infection. By contrast, those who cannot produce antibodies due to individual variability ($(1-m)V$) are clearly at risk of infection with an infection rate of $k$. Therefore, the term to transfer from $V$ to $I$ is $k(1-m)VI$. In the case of COVID-19, even though antibodies have been produced in the body, this immunity is temporary. After a period of time, recovered people ($R$) are faced with losing immunity, thus returning to susceptible people. We call this "antibody failure". However, if the booster vaccination is given before antibody failure, there is a return to vaccinated people ($V$) and thus a chance to reproduce the immune response.

In our model, we consider antibody failure in two main ways, partly because antibody levels decrease significantly over time and partly because the efficiency of existing antibodies against mutated strains is greatly reduced due to virus mutations. Both of these conditions increase the risk of infection. At the time of booster vaccination, the antibody level decreases compared to before and mutated strains are produced. Therefore, we believe that the current antibodies are much less efficient at the time of booster vaccination. For different mutated strains, booster shots are developed for their specific characteristics. Due to individual differences, it may occur that some people produce antibodies completely with the first vaccination but do not complete the immune response after booster vaccination, increasing the risk of infection. The specific definitions of variables and parameters are given in Table 1, and the rates are all expressed as the average over a year.

Since we want to know when the booster vaccination is necessary and when it is most effective, we let $\tau_2$ represent the time delay between $R$ and $V$ for booster vaccination and simulate different vaccination time by changing the size of $\tau_2$. However, in the case of COVID-19 vaccines, the vaccines are nonpermanent, that is, antibodies produced by the vaccines have a problem of failure. The failure time is not negligible relative to $\tau_2$, so we use $\tau_1$ to express the time for antibody failure. In order to improve herd immunity and control the epidemic better, booster vaccination usually occurs before antibody failure, so we assume $\tau_2 < \tau_1$.

Therefore, the $SVIR$ epidemic model is constructed to explore the optimal booster vaccination time. The equation is presented as follows:

where $\tau_1$ is the time delay of antibody failure, $\tau_2$ is the time delay of booster vaccination and the specific definitions of variables and parameters are given in Table 1.

For convenience of calculation, we let $\gamma\triangleq k(1-m)$ in the following text.

2.2.   Positivity and boundedness of the solutions

The initial condition of system (2.1) is given by $S (\theta) = {\phi _1}(\theta), V(\theta) = {\phi _2}(\theta), I(\theta) = {\phi _3}(\theta), R(\theta) = {\phi _4}(\theta)$, $\theta\in[-\tau, 0]$, $\tau = \max{\{\tau_1, \tau_2\}}$, with $\phi = [\phi _1, \phi _2, \phi _3, \phi _4]\in \mathbb{C}$ such that $\phi _i\ge 0, i = 1, 2, 3, 4$ for $\theta\in[-\tau, 0]$ where $\mathbb{C}$ denotes the Banach space of continuous functions mapping the interval $[-\tau, 0]$ into $\mathbb{R}_{ + 0}^4 = \{(S, V, I, R)|S > 0, V > 0, I > 0, R > 0\}$.

When $t\in[0, \tau]$, the solution of system (2.1) is as follows:

Obviously, $I(t) > 0$. In the current state, the open policy leads to an increase in the number of infected people. The mutation of the virus makes many people choose booster vaccination when they face body failure. Therefore, the numbers of $V$ and $I$ might be higher. Although $R(t)$ is large, $R(t-\tau_1)$ and $R(t-\tau_2)$ will not be large compared to the current values since the time delays are in years as a unit. Therefore, it is reasonable to assume that $mV+uI-\mu R(t-\tau_1)- \rho R(t-\tau_2) > 0$. Thus, $R(t) > 0$ based on the expression of $R(t)$ in Eq (2.2). Furthermore, we can get $R(t-\tau_1) > 0, R(t-\tau_2) > 0$ when $t\in[0, \tau]$. Thus, $S(t) > 0, V(t) > 0$.

Overall, when $t\in[0, \tau]$, all the solutions of system (2.1) are positive after we consider the realistic situation and make some assumptions. Through the similar approach, it can be shown that all solutions of system (2.1) are also positive on $[\tau, 2\tau]$ under some restrictions. This conclusion can be extended to the interval $[n\tau, (n+1)\tau]\; (n\in N)$. Therefore, for any $t > 0$, all solutions of system (2.1) are positive with the restrictions.

Although the positivity of our model is conditional, our analysis of the epidemic shows that the present state satisfies the conditions for the existence of positivity, therefore our model is reasonable and meaningful.

Let $N(t) = S(t)+V(t)+I(t)+R(t)$, and $N(t)$ represents the total number of people at time $t$. Adding four equations of system (2.1), we obtain $N'(t) = \Lambda-dN(t)-cI(t)$. According to the discussion on the positivity of solutions, we can find that $I(t) > 0$. Thus, $N'(t) = \Lambda-dN(t)-cI(t)\leq \Lambda-dN(t)$. Based on the comparison theorem, we can obtain:

Therefore, $\mathop {\lim }\limits_{t \to \infty } \text{sup}\; N(t) \leq \frac{\Lambda }{d }$ and the solutions $S(t)$, $A(t)$, $I(t)$, $R(t)$ of system (2.1) are bounded when $t > 0$.

The boundedness of the solutions of system (2.1) must hold. Its practical significance is that the number of people in each cabin can be stabilized within a specific range regardless of the current epidemic situation, which is optimistic for controlling the epidemic.

Under the positivity and boundedness of solutions discussed above, we mark the feasible region of the system (2.1) as:

3.   Stability of equilibria and existence of Hopf bifurcation

Next, we will analyze system (2.1). It has three equilibria,

with

Then, we show the following assumptions:

where $A, B, p$ are given in Eq (3.1). We can easily find that there is always an equilibrium $E_1$. If equilibrium $E_1$ is stable, there are no infected people in the final stable state, that is, the virus can finally be eliminated, which is called the disease-free equilibrium. Then, equilibrium $E_2$ makes sense under (H1) and equilibrium $E_3$ is meaningful under (H2). If equilibrium $E_2$ or $E_3$ is stable, the final state is always accompanied by some infected people, which means that the virus will always coexist with humans and we have no way to eliminate it. We call it the endemic equilibrium.

Without loss of generality, we assume that the system (2.1) has three equilibria $E_k\; (k = 1, 2, 3)$. Then, we transfer the equilibrium $E_k$ into the original point: $\tilde{S} = S-S_{k}^{*}$, $\tilde{V} = V-V_{k}^{*}$, $\tilde{I} = I-I_{k}^{*}$, $\tilde{R} = R-R_{k}^{*}$ and re-denote $\tilde{S}, \tilde{V}, \tilde{I}, \tilde{R}$ as $S, V, I, R$. We obtain the following model:

For the equilibrium $E_1 = (S_1^*, V_1^*, I_1^*, R_1^*)$, we can obtain the characteristic equation of system (3.2) as follows:

Similar to the equilibrium $E_1$, we can also obtain the characteristic equation at the equilibrium $E_k\; (k = 2, 3)$:

where

3.1.   The case for $\tau_1=0, \tau_2=0$

When $\tau_1 = \tau_2 = 0$, (3.3) becomes:

Clearly, Equation (3.5) has the roots $\lambda_1 = \beta S_1^*+\gamma V_1^*-(d+u+c)$, $\lambda_2 = -d$, and the remaining roots $\lambda_3, \lambda_4$ are given by the following equation:

According to Vieta's theorem, we can obtain $\lambda_3+\lambda_4 = -(m+\alpha+2d+\mu+\rho) < 0$ and $\lambda_3\lambda_4 = (m+d)(\alpha+d)+\mu(m+\alpha+d)+\rho(\alpha+d) > 0$, thus, $\mathrm{Re}(\lambda_3) < 0$ and $\mathrm{Re}(\lambda_4) < 0$. Then, we show the following assumption:

Under (H3), we can find that all the characteristic roots of Eq (3.5) are negative, so the equilibrium $E_1$ is locally asymptotically stable when $\tau_1 = \tau_2 = 0$. If (H3) does not hold, $\lambda_1 = \beta S_1^*+\gamma V_1^*-(d+u+c) > 0$, the equilibrium $E_1$ is unstable when $\tau_1 = \tau_2 = 0$.

For the equilibrium $E_k\; (k = 2, 3)$, Equation (3.4) is transformed to the following form when $\tau_1 = \tau_2 = 0$:

where $a_{1, k} = \varrho_{1, k}+\mu+\rho, \; a_{2, k} = \varrho_{2, k}+\mu\sigma_{1, k}+\rho\varsigma_{1, k}, \; a_{3, k} = \varrho_{3, k}+\mu\sigma_{2, k}+\rho\varsigma_{2, k}, \; a_{4, k} = \varrho_{4, k}+\mu\sigma_{3, k}+\rho\varsigma_{3, k}$ with $\varrho_{1, k}$, $\varrho_{2, k}$, $\varrho_{3, k}$, $\varrho_{4, k}$, $\sigma_{1, k}$, $\sigma_{2, k}$, $\sigma_{3, k}$, $\varsigma_{1, k}$, $\varsigma_{2, k}$, $\varsigma_{3, k}$ given in Eq (3.4). According to Routh-Hurwitz stability criterion, we propose the following hypothesis:

If (H4) is satisfied, all eigenvalues of Eq (3.7) have negative real parts, the equilibrium $E_k\; (k = 2, 3)$ of model (2.1) is locally asymptotically stable when $\tau_1 = \tau_2 = 0$.

Theorem 3.1. For system (2.1) with $\tau_1 = 0, \tau_2 = 0$, the stability results for equilibrium $E_k\; (k = 1, 2, 3)$ are given as follows.

1) Equilibrium $E_1$ always exists. If (H3) holds, equilibrium $E_1$ is locally asymptotically stable. On the contrary, if (H3) does not hold, equilibrium $E_1$ is unstable;

2) When the assumption (H1) or (H2) holds, the equilibrium $E_2$ or $E_3$ is meaningful respectively. Further, if (H4) holds, equilibrium $E_2$ or $E_3$ is locally asymptotically stable. If (H4) does not hold, equilibrium $E_2$ and $E_3$ are unstable.

3.2.   The case for $\tau_1 > 0, \tau_2=0$

For the equilibrium $E_1$, when $\tau_2 = 0, \tau_1 > 0$, the characteristic equation of system (3.3) becomes:

If (H3) holds, $\lambda_1 = \beta S_1^*+\gamma V_1^*-(d+u+c) < 0$, $\lambda_2 = -d < 0$. We only need to consider the remaining part of Eq (3.8):

Substituting $\lambda = \mathrm{i}\omega\; (\omega > 0)$ into Eq (3.9) and separating the real and imaginary parts, we obtain:

Thus,

Adding the square of the two equations in Eq (3.11) and letting $z = \omega^2$, we obtain:

where $\kappa_1 = -2(m+d+\rho)(\alpha+d)+(\alpha+m+2d+\rho)^2-\mu^2, \kappa_0 = (m+d+\rho)^2(\alpha+d)^2-mu^2(m+\alpha+d)^2.$ Therefore, we show the following assumptions:

If (H5) and (H6) do not hold, the equilibrium $E_1$ is always locally asymptotically stable for any $\tau_1 > 0$. If (H5) holds, Equation (3.12) has the unique positive root $z_1$, $h'(z_1) > 0$. Under (H6), Equation (3.12) has two positive roots: $z_2$ and $z_3$. Assuming $z_2 > z_3$, we get $h'(z_2) > 0, \; h'(z_3) < 0$. By substituting $\omega_{11, l} = \sqrt{z_l}\; (l = 1, 2, 3)$ into Eq (3.11), we can obtain:

where $Q_{11, l} = {\sin(\omega\tau_1)}|_{\omega = {\omega _{11, l}}, \tau = \tau _{11, l}^{(j)}}, {P_{11, l}} = \cos(\omega\tau _{1}) |_{\omega = {\omega _{11, l}}, \tau = \tau _{11, l}^{(j)}},$ $\sin(\omega\tau_1)$ and $\cos(\omega\tau _1)$ are given in Eq (3.11).

Then the following transversality condition holds:

For the equilibrium $E_k\; (k = 2, 3)$, Equation (3.4) becomes the following form when $\tau_1 > 0$ and $\tau_2 = 0$.

where $\upsilon_{1, k} = \varrho_{1, k}+\rho, \upsilon_{2, k} = \varrho_{2, k}+\rho\varsigma_{1, k}, \upsilon_{3, k} = \varrho_{3, k}+\rho\varsigma_{2, k}, \upsilon_{4, k} = \varrho_{4, k}+\rho\varsigma_{3, k}$ with $\varrho_{1, k}$, $\varrho_{2, k}$, $\varrho_{3, k}$, $\varrho_{4, k}$, $\sigma_{1, k}$, $\sigma_{2, k}$, $\sigma_{3, k}$, $\varsigma_{1, k}$, $\varsigma_{2, k}$, $\varsigma_{3, k}$ given in Eq (3.4).

Assuming that $\lambda = \mathrm{i}\omega \left(\omega > 0\right)$ is a pure imaginary root of Eq (3.14), we substitute it into Eq (3.14) and separate the real and imaginary parts, and we have:

Thus,

Adding the square of the two equations in Eq (3.16) and letting $z = \omega^2$, we get:

where $\tilde{\kappa}_{1, k} = -2\upsilon_{2, k}+\upsilon_{1, k}^2-\mu^2, \; \tilde{\kappa}_{2, k} = \upsilon_{2, k}^2+2\upsilon_{4, k}-2\upsilon_{1, k}\upsilon_{3, k}-\mu^2\left(\sigma_{1, k}^2-2\sigma_{2, k}\right),$$\tilde{\kappa}_{3, k} = -2\upsilon_{2, k}\upsilon_{4, k}+\upsilon_{3, k}^2-\mu^2\left(-2\sigma_{1, k}\sigma_{3, k}+\sigma_{2, k}^2\right), \; \tilde{\kappa}_{4, k} = \upsilon_{4, k}^2-\mu^2\sigma_{3, k}^2$ with $\sigma_{1, k}, \sigma_{2, k}, \sigma_{3, k}$ given in Eq (3.4) and $\upsilon_{1, k}, \upsilon_{2, k}, \upsilon_{3, k}, \upsilon_{4, k}$ given in Eq (3.14). We hypothesize that Eq (3.17) has $l \left(l = 1, 2, 3, 4\right)$ positive roots marked as $z_1 > z_2 > \dots > z_{l}$, $\left(l = 1, 2, 3, 4\right)$, so $h'(z_l)\neq0$. Substituting $\omega_{1k, l} = \sqrt{z_{l}}$ into Eq (3.16), we can get the expression of $\tau_{1k, l}^{(j)}$:

where $Q_{1k, l} = {\sin(\omega\tau_1)}|_{\omega = {\omega _{1k, l}}, \tau = \tau _{1k, l}^{(j)}}, {P_{1k, l}} = \cos(\omega\tau _{1}) |_{\omega = {\omega _{1k, l}}, \tau = \tau _{1k, l}^{(j)}},$ $\sin(\omega\tau_1)$ and $\cos(\omega\tau _1)$ are given in Eq (3.16).

Thus, we obtain the transversality condition:

Theorem 3.2. For system (2.1) with $\tau_2 = 0, \tau_1 > 0$, the following conclusions hold when the stability conditions of Theorem 3.1 hold.

1) Equilibrium $E_1$

(a) If (H5) and (H6) do not hold, the equilibrium $E_1$ is locally asymptotically stable when $\tau_1 > 0$.

(b) If (H5) holds, $h(z)$ has only one positive root $z_1$, the system (2.1) undergoes Hopf bifurcation at $E_1$ when $\tau_1 = \tau_{11, 1}^{(0)}$, where $\tau_{11, 1}^{(0)}$ is given by Eq (3.13). If $\tau_1 \in [0, \tau_{11, 1}^{(0)})$, the equilibrium $E_1$ is locally asymptotically stable. When $\tau_1 \in [\tau_{11, 1}^{(0)}, +\infty)$, the equilibrium $E_1$ is unstable.

(c) If (H6) holds, $h(z)$ has two positive roots $z_2$ and $z_3$, and system (2.1) undergoes Hopf bifurcation at $E_1$ when $\tau_1 = \tau_{11, 2}^{(0)}, \tau_{11, 3}^{(0)}$, where $\tau_{11, 2}^{(0)}$ and $\tau_{11, 3}^{(0)}$ are given by Eq (3.18). Supposing $z_2 > z_3$, we get $h'(z_2) > 0, h'(z_3) < 0$. Then, $\exists\; m \in N$, which can make $0 < \tau _{11, 2}^{(0)} < \tau _{11, 3}^{(0)} < \tau _{11, 2}^{(1)} < \tau _{11, 3}^{(1)} < \cdots < \tau _{11, 2}^{(m)} < \tau _{11, 2}^{(m+1)}$. When $\tau_1 \in(0, \tau _{11, 2}^{(0)})\cup \bigcup_{i = 1}^{m}{(\tau _{11, 3}^{(i-1)}, \tau _{11, 2}^{(i)})}$, the equilibrium $E_1$ of the model (2.1) is locally asymptotically stable. When $\tau_1 \in \bigcup_{i = 0}^{m-1}{(\tau _{11, 2}^{(i)}, \tau _{11, 3}^{(i)})\cup(\tau_{11, 2}^{(m)}, +\infty)}$, the equilibrium $E_1$ is unstable.

2) Equilibrium $E_k\; (k = 2, 3)$

(a) If $h(z)$ has no positive root, the equilibrium $E_k$ is locally asymptotically stable when $\tau_1 > 0$.

(b) If $h(z)$ only has one positive root $z_1$, the system (2.1) undergoes Hopf bifurcation at $E_k$ when $\tau_1 = \tau_{1k, 1}^{(j)}$ and $h'(z_1) > 0$. We get $\forall\; 0 < \tau_1 < \tau_{1k, 1}^{(0)}$, the equilibrium $E_k$ is asymptotically stable, and when $\tau_1 > \tau_{1k, 1}^{(0)}$, the equilibrium $E_k$ is unstable.

(c) If $h(z)$ has two positive roots $z_1$, $z_2$, the system (2.1) undergoes Hopf bifurcation at $E_k$ when $\tau_1 = \tau_{1k, 1}^{(j)}$ and $\tau_1 = \tau_{1k, 2}^{(j)}$. Assuming $z_2 < z_1$, we can get $h'(z_1) > 0, h'(z_2) < 0$. Thus, assuming $\tau_{1k, 1}^{(0)} < \tau_{1k, 2}^{(0)}$, there exists $m$, which makes $0 < \tau_{1k, 1}^{(0)} < \tau_{1k, 2}^{(0)} < \tau_{1k, 1}^{(1)} < \tau_{1k, 2}^{(1)} < \dots < \tau_{1k, 1}^{(m)} < \tau_{1k, 1}^{(m+1)}$. When $\tau_1\in[0, \tau _{1k, 1}^{(0)}) \cup \bigcup_{i = 1}^m{(\tau _{1k, 2}^{\left(i-1 \right)}, \tau _{1k, 1}^{\left(i \right)})}$, the equilibrium $E_k$ is locally asymptotically stable. When $\tau_1\in\bigcup_{i = 0}^{m-1}{(\tau_{1k, 1}^{(i)}, \tau_{1k, 2}^{(i)})}\cup (\tau_{1k, 1}^{(m)}, +\infty)$, the equilibrium $E_k$ is unstable.

(d) If $h(z)$ has three positive roots $z_1$, $z_2$, $z_3$, the system (2.1) undergoes Hopf bifurcation at $E_k$ when $\tau_1 = \tau_{1k, l}^{(j)} (l = 1, 2, 3)$. We assume $z_3 < z_2 < z_1$, so we have $h'(z_1) > 0, h'(z_2) < 0, h'(z_3) > 0$. Similar to the analysis of (c), the equilibrium $E_k$ switches between stability and instability with increasing $\tau_1$. Finally, the equilibrium $E_k$ is unstable.

(e) If $h(z)$ has four positive roots $z_1$, $z_2$, $z_3$ and $z_4$, the system (2.1) undergoes Hopf bifurcation at $E_k$ when $\tau = \tau_{1k, l}^{(j)} (l = 1, 2, 3, 4)$. Assuming that $z_4 < z_3 < z_2 < z_1$, we can obtain $h'(z_1) > 0, h'(z_2) < 0, h'(z_3) > 0, h'(z_4) < 0$. Similar to the analysis of (c), the equilibrium $E_k$ switches between stability and instability with increasing $\tau_1$. Ultimately, the equilibrium $E_k$ is unstable.

3.3.   The case for $\tau_1 > 0, \tau_2 > 0$

In this subsection, we suppose $\tau_1 = \tau_1^*\in(0, \tau_{1k, 0}), \tau_{1k, 0} = \underset{l, j}{\min}\; \tau_{1k, l}^{(j)}\; (k = 1, 2, 3;l = 1, 2, 3, 4;j = 1, 2, \cdots)$ which means that the antibody failure time is $\tau_1^*$. Then, we choose $\tau_2$ as the bifurcation parameter, which is the booster vaccination time. Similar to the situation of $\tau_1 > 0, \tau_2 = 0$, we have the following conclusions. The calculation details are presented in Appendix A.

Theorem 3.3. For system (2.1) with $\tau_2 > 0, \tau_1 > 0$, when the stability conditions of Theorems 3.1 and 2 hold, the following conclusions hold.

1) For equilibrium $E_1$, under (H7) and (H8), the equilibrium $E_1$ of system (2.1) is locally asymptotically stable when $\tau_2\in[0, \tau_{21, 0})$ for the chosen $\tau_1^*$.

2) For equilibrium $E_k\; (k = 2, 3)$, under (H9) and (H10), the equilibrium $E_2$ or $E_3$ of system (2.1) is locally asymptotically stable when $\tau_2\in[0, \tau_{2k, 0})$ for the chosen $\tau_1^*$.

4.   Normal form and bifurcation analysis

In this section, we derive the normal form of Hopf bifurcation about system (2.1) by using multiple time scales method. When $\tau_1 = \tau_1^*, \tau_2 = \tau_{2k, 0} \; (k = 1, 2, 3)$, we assume that the characteristic equation (3.3) or (3.4) has a pair of pure imaginary roots $\lambda = \pm\mathrm{i}\omega^*$ at which system (2.1) undergoes Hopf bifurcation at equilibrium $E_k = (S_k^*, V_k^*, I_k^*, R_k^*)\; (k = 1, 2, 3)$. For convenience, we let $S^*\triangleq S_k^*$, $V^*\triangleq V_k^*$, $I^*\triangleq I_k^*$, $R^*\triangleq R_k^*$. Since we are more concerned about the effect of booster vaccination time on the epidemic, we select $\tau_2$ as the bifurcation parameter. We can obtain the normal form as follows. The calculation details can be referred to Appendix B.

where $G$ is the coordinate projected on the center manifold and $M, H$ are given in Eqs (B9) and (B14).

Let $G = r\text{e}^{\text{i}\theta}$ and substitute it into Eq (B15), we can obtain the normal form of Hopf bifurcation in polar coordinates:

Then, we have the theorem as follows.

Theorem 4.1. If $\frac{\mathrm{Re}\left(M \right) \tau _{\varepsilon}}{\mathrm{Re}\left(H \right) \tau _c} < 0$ holds, the system (2.1) exists periodic solution around the equilibrium.

1) If $\mathrm{Re}(M){{\tau }_{\varepsilon }} < 0$, the periodic solution of system (2.1) is unstable.

2) If $\mathrm{Re}(M){{\tau }_{\varepsilon }} > 0$, the periodic solution of system (2.1) is stable.

Proof. Although system (4.1) is two-dimensional, we find that the first equation is independent of $\theta$, which represents the argument component in polar coordinates, so we only need to consider the first equation of system (4.1). If $\frac{\mathrm{Re}\left(M \right) \tau _{\varepsilon}}{\mathrm{Re}\left(H \right) \tau _c} < 0$, $\dot{r} = \text{Re}\left(M \right) \tau _{\varepsilon}r+\text{Re}\left(H \right) r^3$ has a nontrivial fixed point $r^* = \sqrt{-\frac{\mathrm{Re}\left(M \right) \tau _{\varepsilon}}{\mathrm{Re}\left(H \right) \tau _c}}$. At this equilibrium $r^*$, the eigenvalue is $\lambda = -2\mathrm{Re}(M)\tau_\epsilon$. According to Lyapunov indirect method, if $\mathrm{Re}(M)\tau_\epsilon < 0$, the equilibrium $r^*$ is unstable. On the contrary, if $\mathrm{Re}(M)\tau_\epsilon > 0$, the equilibrium $r^*$ is stable. Therefore, the periodic solution of system (2.1) is unstable if $\mathrm{Re}(M){{\tau }_{\varepsilon }} < 0$ and is stable if $\mathrm{Re}(M){{\tau }_{\varepsilon }} > 0$.

5.   Numerical simulations

In this section, we first analyze the official data for rationalization and select the parameter values that are realistic. Second, the accuracy of the theoretical analysis is verified by simulating under these parameters. According to the results, we select the most suitable booster vaccination time and provide some reasonable suggestions to control the epidemic.

5.1.   Determination of parameter values

In this section, we use statistical methods to analyze the values of parameters, and on this basis, we select two groups of parameters most consistent with reality.

1) Cure rate: $u$

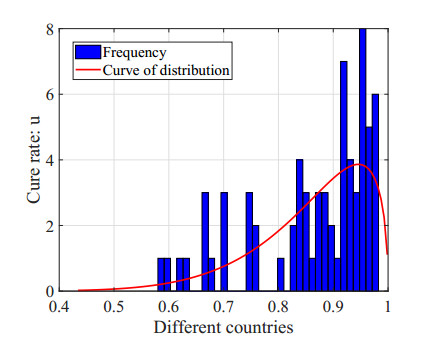
We obtain the average annual cure rates in different countries from the World Health Organization website (https://www.who.int/). By eliminating the missing values and outliers, we get the cure rates for 65 countries and plot the histogram in Figure 2.

We can clearly find that the cure rates of these countries are primarily concentrated in two categories: one is countries with cure rates greater than 0.8, which are mainly concentrated at approximately 0.95. We call it the first echelon. The other group is countries with cure rates between 0.6 and 0.8. We call it the second echelon, typically represented by the United States, with a cure rate of 0.66. Clearly, the higher the cure rate is in a country, the easier it is to control the outbreak. However, since we want to control the epidemic as effectively as possible, we focus on countries in the second echelon, choosing the cure rate $u = 0.7\in(0.6, 0.8)$.

2) Vaccination rates: $\alpha$

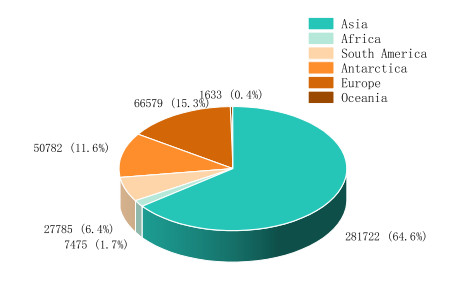
By visiting the official website of Our World in Data (https://ourworldindata.org/covid-vaccinations), we get different vaccination amounts from different countries around the world. Following data collation, the global intercontinental distribution of vaccination was obtained, as shown in Figure 3. According to the law of large numbers, the more experiments there are, the closer the frequency is to the probability, that is, the more accurately and reliably we can approximate the probability with frequency. Based on this, after obtaining the vaccination rates of each continent, we use them as the weights of the vaccination rates of each continent so that the coverage rate is more reliable.

Based on the intercontinental distribution of global vaccination, we can easily see that although 4.4 billion doses have been vaccinated worldwide, the distribution is very uneven. At the intercontinental level, Asia accounts for 65% of global vaccinations with more than 2.8 billion doses, followed by Europe with 15%, North America with 12%, and South America with 6%, while Africa, with nearly 20% of global population, accounts for less than 2% of global vaccinations. Therefore, we need to find a vaccination rate that reflects the global vaccination situation. Our approach is a weighted average of cure rates across continents. Europe and North America are the continents with the highest vaccination rates per 100 people, and Europe has recently surpassed North America with nearly 90 doses per 100 people. South America is at the same level as Asia, with an average of 55 doses per 100 people. Oceania ranks fifth with 32 doses per 100 people, and Africa has only five doses per 100 people, which is much lower than others. Based on the above information, we weight the vaccination rates of each continent and finally obtain the average annual vaccination rate $\alpha = 0.63$.

3) Natural mortality rate: $d$

Since 2019, the outbreak of the COVID-19 epidemic has caused thousands of deaths and a new increase in mortality. However, for the natural mortality rate of the population, we no longer have access to data from official statistics due to the interference of deaths from infection. Here, our approach is to count the official population mortality rates (https://databank.worldbank.org/) before the outbreak and obtain an estimate of the natural mortality rate after the COVID-19 outbreak through fitting. With the 95% confidence interval, we select the following fit results based on the merits of the best fit, which are shown in Table 2. We find that the error sum of squares SSE is small, indicating that the error is small and the fit is great.

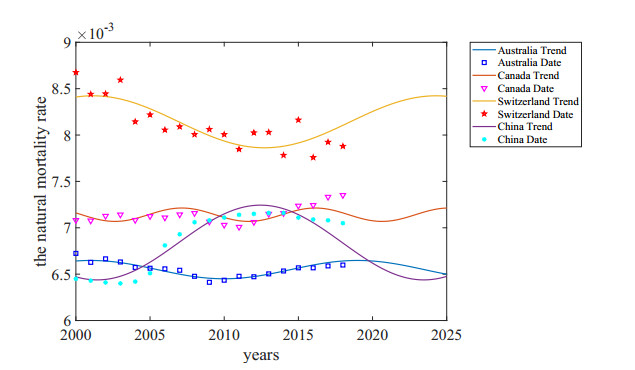
Based on the fitting results, we predict the natural mortality rates of the population after the outbreak, and the results for the next five years are shown in Figure 4.

We find that the natural population mortality rate is distributed between 0.0065 and 0.0085 for the four representative countries in 2019–2025, so we choose $d = 0.00714$ as the natural population mortality rate.

4) COVID-19 mortality rate: $c$

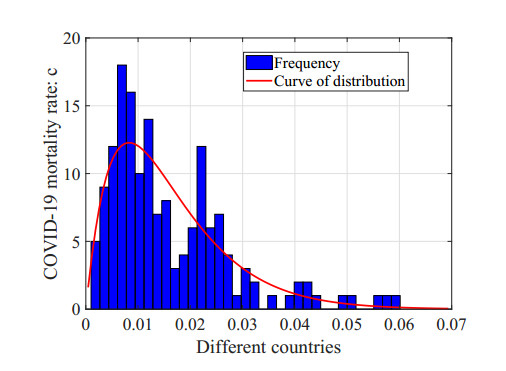
We also obtain the average annual COVID-19 mortality data of different countries from the official website of the World Health Organization (https://www.who.int/). After data processing, we select the rates from 160 countries and draw the corresponding histogram with the beta distribution density curve, as shown in Figure 5. We find that the frequency of the distribution of COVID-19 mortality rates peaks at approximately $c = 0.01$ and $c = 0.02$. To simulate the real situation because of the different medical capacities in different regions and the different characteristics of mutated virus at different time, we finally choose $c = 0.01$ and $c = 0.02$ as the COVID-19 mortality rates.

5) Booster vaccination rates: $\rho$

For the booster vaccination every year on average, we use the analytical estimation method. Since the booster vaccination is for people who already have antibodies, that is, the booster vaccination rate is relative to $R$ and a large portion of $R$ comes from vaccination, the initial vaccination has already screened out those who could not be vaccinated due to individual reasons. Therefore, $R$ has a stronger desire to be vaccinated than $S$, so we believe that the rate of booster vaccination is higher than that of initial vaccination. With the above considerations, we choose the average annual booster vaccination rate $\rho = 0.7$.

6) Infection rate: $\beta$, $\gamma$

Since the global COVID-19 outbreak, countries have paid great attention to the infection and have adopted policies to stop the spread of the epidemic. One of the most important parts is wearing masks in public, which has led to a significant reduction in the infection rate. However, since the epidemic differs in its ability to spread in different countries, the infection rate also varies. Here, we take $\beta$ to be 0.0009 and 0.00015 respectively. In addition, the immune barrier of $V$ has not been fully formed although these individuals are vaccinated. Therefore, there is also a specific transmission rate for them, but this rate is significantly smaller than that of susceptible people. Therefore, we take $\gamma = 0.0002$ and $\gamma = 0.00008$.

Based on the above discussion and estimating the reality of the situation, we take the following two groups of parameters:

(Ⅰ): $\Lambda = 10,$ $\mu = 0.7,$ $\alpha = 0.63,$ $\beta = 0.0009,$ $\gamma = 0.0002,$ $d = 0.00714,$ $\rho = 0.7,$ $u = 0.7,$ $c = 0.02,$ $m = 0.9;$

(Ⅱ): $\Lambda = 80,$ $\mu = 0.8,$ $\alpha = 0.63,$ $\beta = 0.00015,$ $\gamma = 0.00008,$ $d = 0.00714,$ $\rho = 0.7,$ $u = 0.7,$ $c = 0.01,$ $m = 0.9.$

5.2.   Simulations and verification

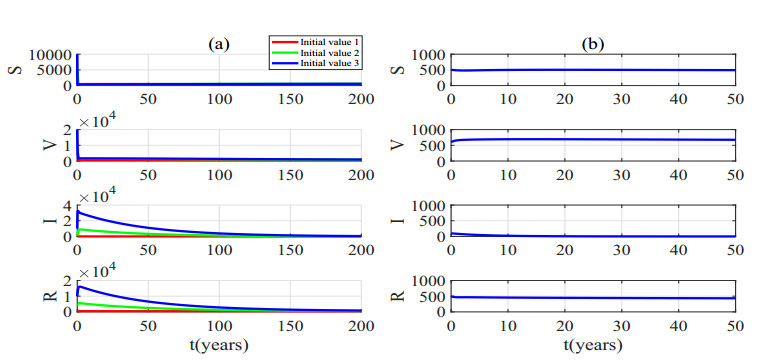
For the group of parameters (Ⅰ): $\Lambda = 10, \; \mu = 0.7, \; \alpha = 0.63, \; \beta = 0.0009, \; \gamma = 0.0002, \; d = 0.00714$, $\rho = 0.7, \; u = 0.7, \; c = 0.02, \; m = 0.9$, we calculate the disease-free equilibrium $E_1 = [431, 591, 0, 378]$. We find that the assumptions (H1) and (H2) are not valid, so equilibria $E_2$ and $E_3$ do not exist. Under the group of parameters, (H3) holds, so $E_1 = [431, 591, 0, 378]$ is locally asymptotically stable when $\tau_1 = \tau_2 = 0$. When $\tau_1 > 0, \tau_2 = 0$, we can obtain (H4) holds and $h(z)$ only has one positive root, $\omega_{11, 1} = 0.2073$, $\sin(\omega_{11, 1}\tau_{11, 1}^{(0)}) = 0.3039$, $\cos(\omega_{11, 1}\tau_{11, 1}^{(0)}) = -0.9527$, $\tau_{11, 0} = \tau_{11, 1}^{(0)} = 13.66$. We choose $\tau_1 = \tau_1^* = 4.5$ and substitute it into Eqs (9.1)$-$(9.4), we have $\omega_{21, 1} = 0.61$, $\sin(\omega_{21, 1}\tau_{21, 1}^{(0)}) = 0.5821$, $\cos(\omega_{11, 1}\tau_{11, 1}^{(0)}) = -0.8131$, $\tau_{21, 0} = \tau_{21, 1}^{(0)} = 1.57$. If ${\bf(H7)}$ and ${\bf(H8)}$ hold, the equilibrium $E_1$ is locally asymptotically stable when $\tau_2\in\left[\left.0, \tau_{21, 0}\right)\right.$.

When $\tau_1 = \tau_2 = 0$, the equilibrium $E_1$ is locally asymptotically stable according to Theorem 3.1. This means that the antibody expires instantaneously, and people maintain the effectiveness of the antibodies through uninterrupted booster shots. First, we choose $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [500, 600, 100, 500]^\mathrm{T}$ for $t\in[-\tau_2, 0]$ as the initial function, which represents the initial state of the epidemic and then draw a time history graph in Figure 6(b). We can see that in this case, the epidemic basically reaches stability in 5 years and is eliminated after 10 years. This result is very optimistic. Next, we select three sets of initial functions 1) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [500, 600, 100, 500]^\mathrm{T}$, 2) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [5000, 6000, 1000, 5000]^\mathrm{T}$, 3) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [10, 000, 20, 000, 10, 000, 10, 000]^\mathrm{T}$ for $t\in[-\tau_2, 0]$, which represent different initial states of the epidemic. We find that when the initial functions are far from equilibrium, the fluctuations are large during the initial years, and the time taken to reach stability is long, as shown in Figure 6(a). However, the epidemic eventually reaches stability regardless of the initial functions, so we conjecture that the equilibrium is not only locally asymptotically stable, but may also be globally stable. This finding suggests that under this set of parameters, even if the epidemic is severe in a given region, the epidemic will eventually reach a manageable level and will be eliminated through uninterrupted booster vaccination. However, as far as reality is concerned, the vaccines we have developed cannot be immediate and uninterrupted, so this situation does not exist.

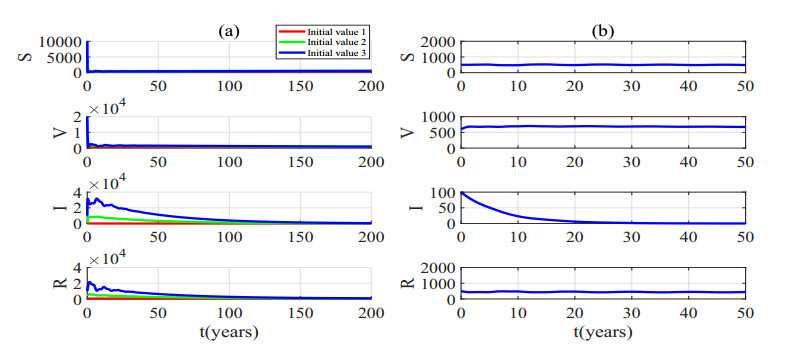
When $\tau_1 = 4.5\in(0, \tau_{11, 0}) = (0, 13.66)$, $\tau_2 = 1\in(0, \tau_{21, 0}) = (0, 1.57)$, the equilibrium $E_1$ is locally asymptotically stable according to Theorem 3.3. $\tau_1 = 4.5$ means the vaccine will fail 4.5 years after individuals acquires antibodies, and $\tau_2 = 1$ means that people begin the booster vaccination after 1 year to cope with the decline in antibodies.

First, we still choose the initial function $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [500,600,100,500]^\mathrm{T}$ for $t\in[-\tau_2, 0]$ and show the variation in the number of people in different compartments over time in Figure 7(b). This figure suggests that receiving the booster vaccinations after one year will lead to a stable epidemic in 10 years and the society will persist in this state consistently. In addition, the number of infected people would eventually approach 0, meaning that the epidemic can eventually be eliminated. That is the most desirable outcome. After that, we choose 1) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [500,600,100,500]^\mathrm{T}$, 2) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [5000,6000,1000,5000]^\mathrm{T}$, 3) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [10,000,20,000,10,000,10,000]^\mathrm{T}$ for $t\in[-\tau_2, 0]$ as three sets of initial functions that are same as $\tau_1 = \tau_2 = 0$, and the results are shown in Figure 7(a). Although the amplitude of fluctuation and the time taken to reach stability increase gradually as the initial function moves away from equilibrium, it will eventually stabilize. Thus, if we carry out booster vaccination after one year, the outbreak will be controlled. However, the time needed to contain the outbreak depends on the current situation. The more severe the epidemic is, the more difficult it will be to control. According to the above results, we guess that the equilibrium $E_1$ is not only locally asymptotically stable but also globally stable under this group of parameters.

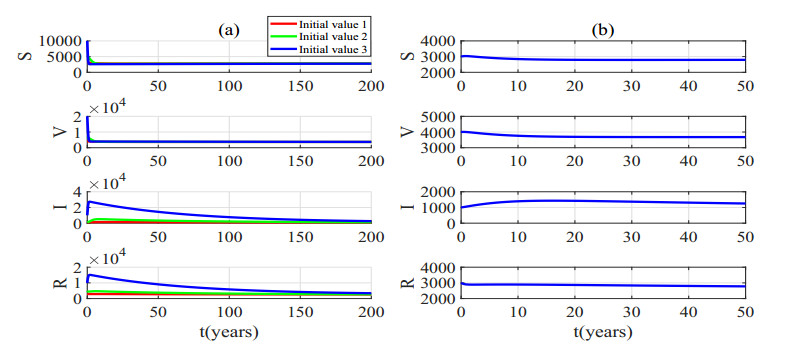
For the group of parameters (Ⅱ): $\Lambda = 90, \; \mu = 0.8, \; \alpha = 0.63, \; \beta = 0.00015, \; \gamma = 0.00008, \; d = 0.00714,$ $\rho = 0.7, \; u = 0.7, \; c = 0.02, \; m = 0.9,$ we find that (H1) holds, so equilibrium $E_2$ makes sense and is [2817, 3683, 875, 2605]. (H2) and (H3) do not hold, equilibrium $E_1$ is unstable and equilibrium $E_3$ is meaningless. Substituting this group of parameters into Eq (3.7), (H4) is satisfied, so equilibrium $E_2$ is locally asymptotically stable when $\tau_1 = \tau_2 = 0$. When $\tau_1 > 0, \tau_2 = 0$, we can get that $h(z)$ has three roots and $z_3 = 0.0004 < z_2 = 0.0206 < z_1 = 0.1458$, $\omega_{12, 1} = 0.38$ $\sin(\omega_{12, 1}\tau_{12, 1}^{(0)}) = 0.4150$, $\cos(\omega_{12, 1}\tau_{12, 1}^{(0)}) = -0.9098$, $\tau_{12, 0} = \tau_{12, 1}^{(0)} = 7.11$. Choosing $\tau_1 = 4$, we obtain that (H9) and (H10) hold and $\omega_{22, 1} = 0.66$, $\sin(\omega_{22, 1}\tau_{22, 1}^{(0)}) = 0.5738$, $\cos(\omega_{22, 1}\tau_{22, 1}^{(0)}) = -0.8190$, $\tau_{22, 0} = \tau_{22, 1}^{(0)} = 0.92$. Substitute the parameters (Ⅱ) into Eqs. (B9) and (B14), we have $\mathrm{Re}(M) > 0, \mathrm{Re}(H) < 0$. We can deduce $\tau_\varepsilon > 0$, $\mathrm{Re}(M_k)\tau_\varepsilon > 0$, the periodic solution is stable based on Theorem 4.1.

When $\tau_1 = \tau_2 = 0$, we choose 1) $[S(t), V(t), I(t), R(t)]^\mathrm{T}$ = $[3000,4000,1000,3000]^\mathrm{T}$, 2) $[S(t), V(t), I(t), R(t)]^\mathrm{T}$ = $[5000,8000,2000,5000]^\mathrm{T}$, 3) $[S(t), V(t), I(t), R(t)]^\mathrm{T}$ = $[10,000,20,000,5000,10,000]^\mathrm{T}$ for $t\in[-\tau_2, 0]$ as the initial functions separately. We draw a plot of the epidemic over time for the three sets of initial functions and a separate time history graph with initial function 1) in Figure 8.

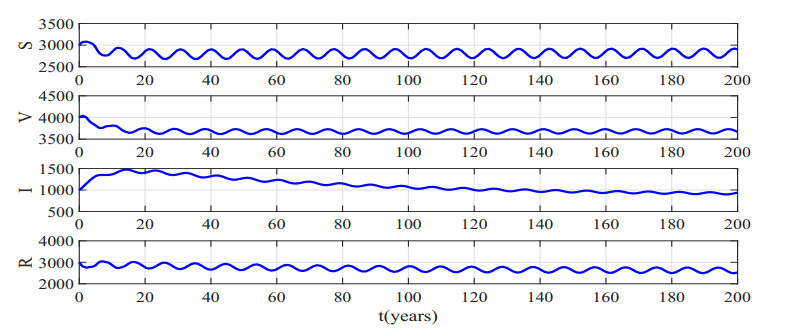
It is easy to observe from Figure 8(b) that the epidemic reaches stability rapidly within 8 years. However, it cannot be eradicated and coexists with humans for a long time. In Figure 8(a), the initial function 3) takes longer to reach the steady state, and the stabilization effect is not as good as that of 1) and 2), but it eventually reaches stability. Therefore, we conjecture that the equilibrium $E_2$ is globally stable. Thus, we can get the following results: it is effective to control the epidemic through uninterrupted booster vaccination, but the time needed to control the epidemic mainly depends on the current state. The more severe the epidemic, the more difficult it will be. This finding shows that booster vaccination is of great significance, but considering that the vaccines developed at present are not instantaneous failures and vaccines cannot be administered in a short period of time, $\tau_1 = \tau_2 = 0$ is basically impossible.

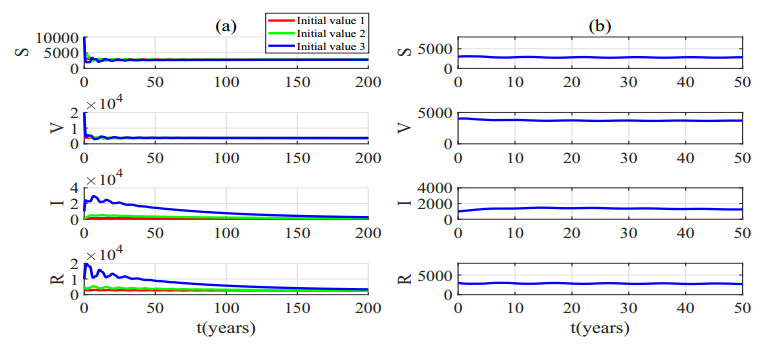
When $\tau_1 = 4\in(0, \tau_{12, 0}) = (0, 7.11), \tau_2 = 0.8\in(0, \tau_{22, 0}) = (0, 0.92)$, the antibody expires after 4 years and we re-inject booster shots after 0.8 years. We also choose the three sets of initial functions: 1) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [500,600,100,500]^\mathrm{T}$, 2) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [5000,6000,1000,5000]^\mathrm{T}$, 3) $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [10,000,20,000,10,000,10,000]^\mathrm{T}$ for $t\in[-\tau_2, 0]$ and make figures respectively similar to the above situation. The results are shown in Figure 9.

With antibody failure after 4 years and booster vaccination after 0.8 years, the system quickly becomes stable when the initial function is chosen near equilibrium according to (b) in Figure 9. From the figure, we also find that although the epidemic cannot be eliminated, it can always stay in a stable state. In Figure 9(a), as the initial function moves away from equilibrium, the epidemic worsens. It fluctuates dramatically in a short period of time and will take decades to stabilize. But no matter what initial function is chosen, the epidemic will eventually be controlled. Therefore, we hypothesize that this stability is global. Even if the current epidemic is not optimistic in some countries, the trend will be better with the booster vaccination in time.

When $\tau_1 = 4, \; \tau_2 = 1.11 > \tau_{22, 0} = 0.92$, which means that the antibody will expire after 3.9 years and booster vaccination will be carried out after 1.11 years, the equilibrium $E_2$ of system (2.1) is unstable. According to Theorem 4.1, system (2.1) has a forward Hopf bifurcation near $\tau_{22, 1}^{(0)} = 0.92$ and the periodic solution is stable. We choose $[S(t), V(t), I(t), R(t)]^\mathrm{T} = [3000,4000,1000,3000]^\mathrm{T}$ for $t\in[-\tau_2, 0]$ as the initial function, and the epidemic situation is shown in Figure 10.

In this case, the epidemic will continue to fluctuate, which is not promising for controlling the epidemic.

Based on the above simulations, we know that the only way to avoid out-of-control epidemic is to carry out booster vaccinations within the critical time. However, when is the best time to vaccinate? Next, we will analyze the optimal time of booster vaccination. First, we take the first set of parameters as the study object given $\tau_2 = 0.1, 0.4, 0.7, 1.0, 1.3$ respectively, and then we draw the images of the infected people ($I$) with time as shown in Figure 11.

In Figure 11(a), we find that the time to eventual stabilization is essentially the same regardless of the booster vaccination time we select, but when we focus on the case near the peak in Figure 11(b), we find that the smaller the booster vaccination time is, the smaller the number of infections will be. This finding reveals that the earlier the booster vaccination is performed, the fewer people will be infected with COVID-19. However, considering human and material resources and financial resources, it is not an easy task to complete community-wide vaccination, so we need to implement booster vaccinationss as soon as possible according to the local reality and within the scope of ensuring the normal operation of the community.

From a medical point of view, it is generally believed that the immune effect weakens after six months of vaccination, so 6 months after the completion of the initial vaccine is the critical period for booster vaccination ^[51,52]. For the optimal strategy of vaccine distribution, researchers solve the optimal scheduling of the mixed vaccination strategy by using different optimization methods ^[53,54,55]. From the point of view of completing one round of vaccination, we need to allow sufficient time for booster vaccination ^[56]. Taking these considerations into account, we can obtain the optimal booster vaccination time.

5.3.   Comments and suggestions

Based on the above simulations and analysis, we have the following results.

1) When the time of antibody expiration is determined, the epidemic will become increasingly not controllable as the time of booster vaccination increases, and when the time of booster vaccination exceeds the critical value, the system (2.1) will be unstable, and the epidemic will be out of control. However, the time of booster vaccination is not as small as possible. In reality, we need to consider the comprehensive capacity of the country to ensure that booster vaccination time is minimized within the capacity.

2) After simulating the changes in epidemic development under three different sets of initial functions, we find that the epidemic will eventually be controlled, so we assume that the stability of equilibrium $E_k\; (k = 1, 2, 3)$ is not only locally asymptotically stable, but may also be globally stable. That is, even if the current epidemic is not optimistic in a certain region, the possible global stability ensures that the epidemic can eventually reach effective control after timely booster vaccination.

3) When the equilibrium $E_1$ satisfies the condition of locally asymptotical stability, the epidemic can eventually be eliminated. If the selected parameters meet the existence and stability of equilibrium $E_2$ or $E_3$, it can reach a stable state. Although the epidemic cannot be eliminated, to some extent, it can be considered to be effectively controlled.

4) Our model is flexible. The current state of the epidemic varies from country to country, and we can simulate the epidemic of different countries by changing the parameters. For example, when a mutant strain is found in a country and has been confirmed to spread widely around the country, we can simulate this situation by increasing the infection rate $\alpha$ and determine the population size by natural population growth $\Lambda$. If the current vaccine is found to be less resistant to the mutant strain, we can simultaneously increase $\gamma$, $\mu$ and determine population size by natural population growth $\Lambda$. After determining the parameters, we can calculate the critical booster vaccination time. When the booster vaccination time is less than the critical value, the system can reach stability, that is, the current outbreak can be controlled. Based on the above analysis, we can develop a policy applicable to this region that allows to control the epidemic as much as possible within the capacity of the region.

Based on the above conclusions, we give the following recommendations.

1) The time of the booster vaccination should be kept within the threshold so that the epidemic can be controlled eventually. However, the overall strength of the area, such as economic development, medical level, etc., also needs to be assessed. For example, in the second group of parameters, $\tau_{22, 0}$ = 0.92. If this is a well-developed country, we would suggest that the booster shot is needed after 0.5–0.92 years. As the epidemic continues to evolve, we are concerned about more than just one booster shot. Our model can apply to more than one booster shot, gradually developing a presence similar to that of the annual influenza vaccination. So we need booster vaccinations every 0.5–0.92 years to ensure the continued effectiveness of the antibodies.

2) Even if the development of the epidemic in a given country is not promising, it should not be taken lightly. Although providing booster vaccination at an appropriate time cannot guarantee that the epidemic will reach control within a short period of time, it has a positive effect on the development of the epidemic. Because the possible global stability ensures that the epidemic will eventually be effectively controlled.

3) It is necessary to detect changes in the epidemic continuously, such as the emergence of new mutant strains and changes in the time of antibody expiration. We can regain a critical booster vaccination time through calculation and then change the booster vaccination strategy in time to cope with the variable COVID-19.

6.   Conclusions

In this paper, we have constructed an $SVIR$ model with two time delays to study the suitable time for booster vaccination. We have considered the existence and stability of equilibria in our model. Then, we have also analyzed the existence and dynamic properties of Hopf bifurcation. In Section 5, we chose two groups of parameters by analyzing the data from official websites. Then, we have carried out numerical simulations to verify the analytical results and provide some reasonable suggestions to control the development of the epidemic.

According to the results of numerical simulations, we found that the epidemic would become increasingly difficult to control as the booster vaccination time $\tau_2$ increased. Considering the factors of all aspects, we suggest that it is suitable to vaccine with the booster shots approximately 6–11 months later for the group of parameters (Ⅱ). We also found that the equilibrium of system (2.1) might be globally stable when $\tau_2$ is within the threshold value. That means, the booster vaccination is effective for outbreak control, so it is crucial to provide booster vaccination in time even if the current epidemic is serious. In addition, considering that the selection of parameters might change due to virus mutation or other factors, we need to continuously monitor the status of the epidemic in real time and adjust the strategy to ensure that the epidemic can be effectively controlled.

Acknowledgments

This study was funded by Fundamental Research Funds for the Central Universities of China (Grant No.2572022DJ06).

Conflict of interest

All the authors declare no conflicts of interest in this paper.

Appendix A

For equilibrium $E_1$, we let $\lambda = \mathrm{i}\omega\; (\omega > 0)$ be a pure imaginary root of Eq (3.3) and substitute it into Eq (3.3). Then separating the real part and imaginary part, we have:

where $b_1 = m+\alpha+2d, b_2 = (m+d)(\alpha+d), c_1 = m+\alpha+d, c_2 = \alpha+d.$ Eq (A1) leads to:

Adding the square of the two equations in Eq (A2), we get:

where $b_1, b_2, c_1, c_2$ are given in Eq (A1). We suppose:

Under (H7), we have $F_1(0) = \mu^2c_1^2-\rho^2c_2^2+2\mu b_2c_1 < 0$, $F_1(\infty) > 0$. Therefore, there is at least one positive root of $F_1(\omega) = 0$. We assume there are $l$ positive roots of $F_1(\omega) = 0$, hence, there is the expression of $\tau_{21, l}^{(j)}, j = 0, 1, 2, \cdots$.

where $Q_{21, l} = {\left. {\sin(\omega\tau_2)} \right|_{\omega = {\omega _{21, l}}, \tau = \tau _{21, l}^{(j)}}}, {P_{21, l}} = \cos(\omega\tau _{2}) {\left. \right|_{\omega = {\omega _{21, l}}, \tau = \tau _{21, l}^{(j)}}},$ $\sin(\omega\tau_2)$ and $\cos(\omega\tau _{2})$ are given in Eq (A2).

Let $\tau_{21, 0} = \min\; \tau_{21, l}^{(j)} = \tau_{21, l}^{(0)}, j = 0, 1, 2, \cdots$. When $\tau_2 = \tau_{21, 0}$, Equation (3.5) has a pair of purely imaginary roots $\pm\mathrm{i}\omega_{21, 0}$. Assume:

Under ${\bf(H8)}$, the equilibrium $E_1$ is locally asymptotically stable when $\tau_2\in\left[\left.0, \tau_{21, 0}\right)\right.$.

For equilibrium $E_k\; (k = 2, 3)$, similar to the above analysis, we let $\lambda = \mathrm{i}\omega(\omega > 0)$ be a pure imaginary root of characteristic equation (3.4) and substitute it into Eq (3.4). Then, separating the real part and imaginary part, we have:

Then, we can obtain:

Adding the square of the two equations in (A6), we have:

Then we give the following assumption:

Under (H9), we can deduce $F_k(0) < 0$ and $F_k(\infty) > 0$. Thus, $F_k(\omega) = 0$ has at least one positive root. We assume that there are $l$ positive roots of $F_k(\omega) = 0$ and denote them as $\omega_{2k, l}$.

where $Q_{2k, l} = {\sin(\omega\tau_2)}|_{\omega = {\omega _{2k, l}}, \tau = \tau _{2k, l}^{(j)}}, {P_{2k, l}} = \cos(\omega\tau _{2}) |_{\omega = {\omega _{2k, l}}, \tau = \tau _{2k, l}^{(j)}},$ $\sin(\omega\tau_2)$ and $\cos(\omega\tau _{2})$ are given in Eq (A6).

Let $\tau_{2k, 0} = \min\; \tau_{2k, l}^{(j)}, j = 0, 1, 2, \cdots, k = 2, 3$. When $\tau_2 = \tau_{2k, 0}$, Equation (3.5) has a pair of purely imaginary roots $\pm\mathrm{i}\omega_{2k, 0}$. Assume

Under ${\bf(H10)}$, the equilibrium $E_k\; (k = 2, 3)$ is locally asymptotically stable if $\tau_2\in\left[\left.0, \tau_{2k, 0}\right)\right.$.

Appendix B

The system (2.1) can be written as follows:

where

Let $h = (h_{ 1}, h_{ 2}, h_{ 3}, h_{ 4})^T$ be the eigenvector of the linear operator corresponding to the eigenvalue $\mathrm{i}\omega^*$, and let $h^* = (h_{ 1}^*, h_{ 2}^*, h_{ 3}^*, h_{ 4}^*)^T$ be the normalized eigenvector of the adjoint operator of the linear operator corresponding to the eigenvalues $-\mathrm{i}\omega^*$ satisfying the inner product $< h^*, h > = 1$. By a simple calculation, we can obtain:

The solution of Eq (B1) $X(t)$ can be written as:

where $X({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots)$$= {{[S({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots), V({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots), I({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots), R({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots)]}^\mathrm{T}}$, ${{X}_{n}}({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots)$$= {{[{{S}_{n}}({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots), {{V}_{n}}({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots), {{I}_{n}}({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots), {{R}_{n}}({{T}_{0}}, {{T}_{1}}, {{T}_{2}}, \cdots)]}^\mathrm{T}}$, $T_i = \epsilon^i t$, $i = 0, 1, 2, \cdots$ and $T_i$ is the scaling transform in the time direction.

$X'(t)$ can be written as:

where $D_i = \frac{\partial}{\partial T_i} (i = 1, 2, 3, \cdots)$ is differential operator.

Since we are more concerned about the influence of booster vaccination time, we take $\tau_2$ as the bifurcation parameter. We let $\tau_2 = \tau_c+\varepsilon\tau_\varepsilon$, where $\tau_c$ is the critical time delay given in Eqs (A4) or (A8), $\tau_\varepsilon$ is the disturbance parameter and $\varepsilon$ is the dimensionless scale parameter. Using Taylor expansion of $X(t-\tau_1^*)$ and $X(t-\tau_2)$ respectively, we have:

where $X_{j, \tau_1^*} = X_j(T_0-\tau_1^*, T_1, T_2, \cdots)$, $X_{j, \tau_c} = X_j(T_0-\tau_c, T_1, T_2, \cdots)$, $j = 1, 2, 3\cdots$. Then we substitute Eqs (B3)–(B5) into Eq (B1). For the $\varepsilon$-order terms, we have:

Since $\pm \mathrm{i}{{\omega }^{*}}$ are the eigenvalues of the linear part of Eq (B1), the solution of Eq (B6) can be expressed in the following form:

where $h$ is given in Eq (B2).

For the $\varepsilon^2$-order terms, we obtain:

Then, we substitute Eq (B7) into the right side of Eq (B8) and mark the coefficient before $\text{e}^{\text{i}\omega^* T_0}$ as vector $m_1$. In accordance with the solvability condition $< h^*, m_1 > = 0$, we can obtain the expression of $\frac{\partial G}{\partial T_1}$:

where $M = \frac{\rho \text{i}\omega^* \left(h_{4}\bar{h}_{4}^{*}-h_{4}\bar{h}_{2}^{*} \right)}{1-\mu \text{e}^{-\mathrm{i}\omega^*\tau _1^*}\left(h_{4}\bar{h}_{4}^{*}-h_{4}\bar{h}_{1}^{*} \right) -\rho \tau _c\text{e}^{-\mathrm{i}\omega^*\tau _c}\left(h_{4}\bar{h}_{4}^{*}-h_{4}\bar{h}_{2}^{*} \right)}$.

We assume that the solution of Eq (B8) will take the following form:

Substituting them into Eq (B8), we can solve the expression of $g_{1}$, $g_{2}$, $g_{3}$, $g_{4}$, $l_{1}$, $l_{2}$, $l_{3}$, $l_{4}$ from the following equations:

where $\epsilon_1 = \alpha +\beta I^*+d, \epsilon_2 = m+d+\gamma I^*, \epsilon_3 = -\beta S^*-\gamma V^*+d+u+c, \epsilon_4 = d+\mu \text{e}^{-\mathrm{i}\omega^*\tau _1^*}+\rho \text{e}^{-\mathrm{i}\omega^*\tau _2}.$ For $\varepsilon^3$-term, we have:

We substitute Eqs (B7), (B9) and (B10) into the right expression of Eq (B13) and note the coefficient of $\text{e}^{\text{i}\omega^*T_0}$ as vector $m_2$. According to solvability condition $< h^*, m_2 > = 0$, we have the expression of $\frac{\partial G}{\partial T_2}$. Since $\tau_\varepsilon^2$ has less impact on the normal form, we can ignore the $\tau_\varepsilon^2G$ term. Thus, we can obtain:

where $H = \frac{\beta \left(h_{1}l_{3}+\bar{h}_{1}g_{3}+h_{3}l_{1}+\bar{h}_{3}g_{1} \right) \left(-\bar{h}_{1}^{*}+\bar{h}_{3}^{*} \right)}{1+\mu \left(h_{4}\bar{h}_{1}^{*}-h_{4}\bar{h}_{4}^{*} \right) \text{e}^{-\mathrm{i}\omega^*\tau _1^*}+\rho \tau _c\text{e}^{-\mathrm{i}\omega^* \tau _c}\left(h_4\bar{h}_{1}^{*}-h_{4}\bar{h}_{4}^{*} \right)} +\frac{\gamma \left(h_{2}l_{3}+\bar{h}_{2}g_{3}+h_{3}l_{2}+\bar{h}_{3}g_{2} \right) \left(-\bar{h}_{2}^{*}+\bar{h}_{3}^{*} \right)}{1+\mu \left(h_{4}\bar{h}_{1}^{*}-h_{4}\bar{h}_{4}^{*} \right) \text{e}^{-\mathrm{i}\omega^*\tau _1^*}+\rho \tau _c\text{e}^{-i\omega^* \tau _c}\left(h_4\bar{h}_{1}^{*}-h_{4}\bar{h}_{4}^{*} \right)}.$

Then, we let $G\rightarrow G/\varepsilon$. Therefore, we obtain the normal form of Hopf bifurcation for system (2.1):

where $M, H$ are given in Eqs (B9) and (B14).