Noise-induced transitions in a non-smooth SIS epidemic model with media alert

1.   Introduction 

These days have witnessed the horrible pandemic of COVID-19. As is known to the public, key characteristic of this killer is its silent spreads. Before we fully understand the virus, it has already established. In general, what do we do once a disease has invaded into a population? To mitigate the spread of a disease and eventually get a full control to the disease, the behavior changes at the population level can bend the infection curve. How to promote a massive behavior change? Two typical governing systems function differently. A central government can force a mandatory behavior change without any court challenge, period. If a mandatory preventive measure cannot be exercised or the administration failed to act following a scientific manner, media and social network are able to propagate the positive message in order to persuade behavior changes. A behavior change at the population level is highly media oriented. In fighting COVID-19 pandemic, WHO Director-General Tedros Adhanom Ghebreyesus ever mentioned "We're not just fighting an epidemic; we're fighting an infodemic." For emerging and re-emerging epidemic diseases, research has shown that positive media coverage is an effective measure to control the diseases ^[1].

Massive media propagation and social network response to an epidemic take off only after an outbreak has been observed, so that the initial infection growth is following the regular epidemic process. The study here focuses on how to mitigate an epidemic through the awareness by media and social network. Media and social network response to an epidemic have to be based upon the number of known infected. That is, the pressure from media and social network impose to the population only until the prevalence reaches certain tipping point. We, therefore, will set up a cutting point for the number of infections, then let the media or the social network play its role in our model. A quick searching across the board of relevant literature, this question has been tackled mainly from the view of deterministic modeling. Scholars have proposed media functions to model the transmission rates ^{[2,3,4,5,6,7]}. For instance, Cui et al. ^[3] analyzed a susceptible-exposed-infected model by using $\beta(1-e^{-mI})$ to characterize the effect of media coverage. Their results showed that weak media effects may not be helpful because the infections oscillate periodically. Misra et al. ^[8] formulated an SIS model to study the impact of awareness programs conducted by a media campaign on the spread of an infectious disease and showed that the spread of an infectious disease can be controlled by using awareness programs but the disease remains endemic due to immigration.

Research work in highlighting the role of media coverage and social media network without tipping point can be read in ^[2,3,5,6,7]. In reality, because of time delay and asymptotic infections, we consider that only when the number of infected individuals reaches a tipping value, the alerts and the pressure from media and social network can take place ^[9,10]. Liu et al. ^[4] set a base line of infection (the tipping point) $I_c$ to launch media alert. They consequently proposed a non-smooth but continuous transmission rate:

where nonnegative constant $p$ denotes the intensity of the media coverage. By assuming that the susceptible individuals follow the logistic growth and newborns directly enter into the susceptible class, they studied the following model:

where $S(t)$ and $I(t)$ are the sizes of susceptible and infectious population at time $t$, respectively. All parameters are positive. $r$ is the intrinsic growth rate of the susceptible population; $a$ is the carrying capacity of the community in the absence of infection; $d$ denotes the natural death rate; $\gamma$ represents the recovery rate of the infected individuals; $\epsilon$ is the disease-induced death rate. Liu et al. ^[4] conducted a rigorous and complete mathematical analysis to model (2).

Deterministic models always give us a good start to catch certain characteristic of a disease transmission. Obviously, these mean-field models are based upon the homogeneous population, uniform individual behavior, and steady environmental settings. In managing to fight an epidemic or pandemic infections, unexpected random factors also play a significant role. A certain false claims, misinformation, conspiracy theories can change the course of epidemic. The rumors such as black people are immune to COVID-19 and coconut oil kills the virus of COVID-19 have misled some communities in battling the virus. Spreading false or misleading information may prevent the timely and effective adoption of appropriate behaviours and of public health recommendations or measures ^[11]. Occasional political bias or unusual unscientific statements can even create a temporal chaos in favor of the disease spread. In the real world, the transmissions of infectious diseases are inevitably affected by these unexpected factors. The variations of physical environmental factors ^[12], such as humidity, temperature, etc. can have a significant impact on the transmission of a disease. A well-known work was the experimental result of Lowen et al. ^[13].

The introduction of environmental noise into deterministic setup could exhibit unexpected behaviors which have no analogue in the deterministic models ^[14]. In the last few decades, researchers have done a lot of work regarding to this aspect ^{[14,15,16,17,18,19,20,21,22,23,24,25]}. In ^[24], a stochastically forced predator-prey model with environmental toxins was proposed to analyze the dynamical behavior of noise-induced transitions from coexistence to prey-only extirpation in the bistable zone. Nonlinear dynamical models can exhibit various new phenomena, such as stochastic resonance ^[26], noise-induced transitions ^[27], noise-induced ordering ^[28], noise-induced chaos ^[29], and noise-induced complexity ^[30]. Studies of the environmental noise effects on systems with multiple attractors have been steady growing ^[31]. Multi-stable systems of deterministic models can exhibit noise-induced state switching between deterministic attractors ^{[32,33,34,35]} when a noise is considered. Using the stochastic sensitivity functions (SSF), Bashkirtseva et al. ^[36] developed a new technique to construct the analytical description of stochastically forced equilibria and cycles of discrete-time models. In the present paper, we will use the SSF technique to explore the noise-induced state switching between two epidemic equilibria and estimate a threshold value of the noise intensity.

We organize this paper as following. In Section 2, we review the main results of deterministic model (2) and propose its stochastic counterpart. The studies of noise-induced transitions between two epidemic equilibria and construction of the confidence ellipses for equilibria will be presented in Section 3. Finally, we conclude our study by a simple discussion in Section 4.

2.   Model formulation and the global existence and uniqueness of the solutions 

We first briefly review the main results of deterministic model (2), then we study the corresponding stochastic counterpart.

2.1.   A summary to the deterministic model 

Notice that model (2) always exists two equilibria: the origin $O(0, 0)$ and the disease-free equilibrium $E_0(a, 0)$. The basic reproductive number is

Here, we highlight the interested results from ^[4], which will be directly used in the subsequent stochastic analysis.

Lemma 2.1. If $R_0 < 1$, $E_0(a, 0)$ is globally asymptotically stable. If $R_0 > 1$ together with certain extra conditions, in addition to saddles $O(0, 0)$ and $E_0(a, 0)$, there exist three endemic equilibria $E_1$, $E_2$ and $E_3$, where $E_1$ and $E_3$ are asymptotically stable and $E_2$ is a saddle. The separatrices (the stable manifolds of the saddle $E_2$) separate the domain of attractions of $E_1$ and $E_3$. Hence, bistable dynamics could be observed in model (2) if $R_0 > 1$.

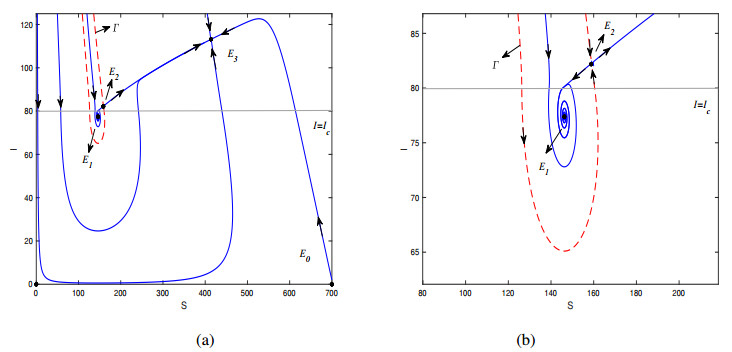
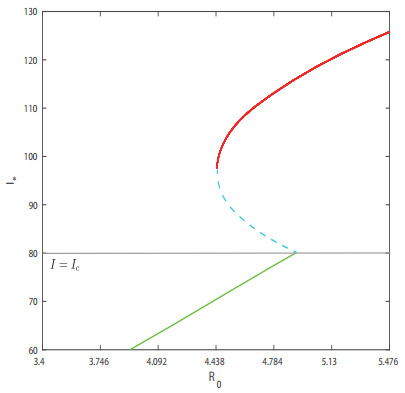
In this paper, we pay more attentions to the epidemiological implications. Model (2) was set to investigate the media effects after the disease has already invaded the population. So the media alert and the pressure from social network have no impact to the initial growth of the disease. That is why the basic reproductive number $R_0$ is independent of the media alert parameters $I_c$ and $p$. The appearance of the bistable dynamics is the straightforward outcome of the introduction of media impact. A bifurcation diagram is shown in Figure 1. It can be seen that model (2) undergoes a backward bifurcation at $R_{0} \approx 4.8705$. There is a window $(4.3515, 4.8705)$ for $R_{0}$ where model (2) can have two stable equilibria $E_{1}$ and $E_{3}$ and a saddle $E_{2}$ (see also Figure 2 (a) where $\beta = 0.0139$). The appearance of the stable endemic state competing with the other stable endemic state is known as the bistability phenomenon. The media is helpful to interfare the infections by forcing (2) to choose smaller endemic $E_{1}$ as the attractor.

2.2.   The stochastic model 

In this paper we intend to explore the stochastic version of model (2). Stochastic factors such as the environmental noise, social noise, random misinformation spread though media and social network and political motivated biased information are not easy to handle with deterministic models. We integrate all these random factors into the deterministic model (2) to look into the following stochastic differential equation:

where $B_{1}$ and $B_{2}$ are standard one-dimensional independent Brownian motions. We use $\sigma_{S}$ and $\sigma_{I}$ to denote the noise intensities. For the simplicity of discussion in this research, we assume $\sigma_{S} = \sigma_{I} = \sigma$. Because system (4) is piecewise defined, we distinguish the noise intensities by $\sigma = \sigma_{1}$ when $I > I_{c}$ and $\sigma = \sigma_{2}$ when $I \leq I_{c}$.

2.3.   Global existence and uniqueness of solutions 

Since we are more interested in the asymptotic behavior of the model, we first anticipate that all solutions exist for all forward times. Now we prove the existence and uniqueness of the global positive solution of stochastic model (4).

Theorem 2.2. For any given positive initial value $(S(0), I(0)) \in \Re^2_{+}$, model (4) has a unique positive solution $(S(t), I(t))$ for $t \geq 0$. Moreover, the solution will remain in $\Re^2_{+}$ with probability one, namely, $(S(t), I(t)) \in \Re^2_{+}$ for all $t \geq 0$ almost surely (a.s.).

Proof. Without loss of generality, we assume that $I(0) > I_{c}$. Let us introduce the stopping time sequence $\{\tau_{i}\}, i = 1, 2, \cdots$ as follows:

and

for $n = 1, 2, \cdots$. Thus when $t \in [\tau_{2n}, \tau_{2n+1})$, model (4) becomes

and when $t \in [\tau_{2n+1}, \tau_{2n+2})$, model (4) becomes

where $n = 0, 1, 2, \cdots$ and $\tau_{0} = 0$. Notice that (5) and (6) both have a unique global positive solution for any initial value $(S(0), I(0)) \in \Re^2_{+}$. This implies model (4) has a unique local positive solution $(S(t), I(t))$ on $[0, \tau_{e})$, where $\tau_{e}$ is the explosion time. In order to prove the solution is global, we only need to prove $\tau_{e} = \infty$, a.s.

Let $k_0 > 0$ be sufficiently large such that $S(0)$ and $I(0)$ both lie within the interval $\left[\frac{1}{k_0}, k_0\right]$. For all integer $k > k_0$, we define the stopping time

Clearly, $\tilde{\tau}_{k}$ is an increasing function as $k \to \infty$. Let $\tilde{\tau}_{\infty} = \lim_{k \rightarrow \infty} \tilde{\tau}_{k}$, whence $\tilde{\tau}_{\infty} \leq \tau_{e}$, a.s. If we can prove $\tilde{\tau}_{\infty} = \infty$, then $\tau_{e} = \infty$, and $(S(t), I(t)) \in \Re^2_{+}$ for all $t \geq 0$, a.s. Hence, we only need to show that $\tilde{\tau}_{\infty} = \infty$, a.s. We prove this by contradiction. If this assertion is false, then there exists a pair of constants $T > 0$ and $\varepsilon \in (0, 1)$ such that $P\{\tilde{\tau}_{\infty} \leq T\} > \varepsilon$, hence there exists $k_{1} > k_{0}$ such that

for all $k \geq k_{1}$. Define a nonnegative $\mathcal{C}^{2}$-function $V:\Re^{2}_{+} \to \Re_{+}$ by

where $m = \frac{d+\epsilon}{\beta}$. Applying Itô's formula, we obtain respectively from (5) and (6) that for $t \in [\tau_{2n}, \tau_{2n+1})$,

where

and that for $t \in [\tau_{2n+1}, \tau_{2n+2})$,

where

where $M_1$ and $M_2$ are two positive numbers. Therefore, we have that for $t \in [\tau_{2n}, \tau_{2n+1})$,

and that for $t \in [\tau_{2n+1}, \tau_{2n+2})$,

Without loss of generality, we assume that $(\tilde{\tau}_{k} \land T) \in [\tau_{2m}, \tau_{2m+1})$ for some $n = m$ (same logic follows when $(\tilde{\tau}_{k} \land T) \in [\tau_{2m+1}, \tau_{2m+2})$). This together with (8) and (9) yields

Taking the expectations on both sides of the above inequality leads to

where $M = \max\{M_{1}, M_{2}\}$. Thus

Let $\Omega_{k} = \{\omega \in \Omega: \tilde{\tau}_{k} = \tilde{\tau}_{k}(\omega) \leq T \}$ for $k \geq k_{1}$ and, by (7), $P\{\Omega_{k}\} \geq \varepsilon$. Note that for every $\omega \in \Omega_{k}$, we have either $S(\tilde{\tau}_{k}, \omega)$ or $I(\tilde{\tau}_{k}, \omega)$ equals either $k$ or $\frac{1}{k}$. Hence $V(S(\tilde{\tau}_{k}, \omega), I(\tilde{\tau}_{k}, \omega))$ is no less than either

where "$a\land b$" means "the smaller one of $a$ and $b$". It then follows from (10) that

where $I_{\Omega_{k}}$ is the indicator function of $\Omega_{k}$. Letting $k \rightarrow \infty$ we have

a contradiction. So we must have $\tau_{\infty} = \infty$, a.s. This completes the proof.

In the following, we study the phenomenon of noise-induced transitions between two stochastic attractors for stochastic model (4).

3.   Analysis of noise-induced transitions 

In this section, the phenomenon of noise-induced transitions between two endemic equilibria is studied by constructing confidence ellipses with the technique of stochastic sensitivity functions (SSF).

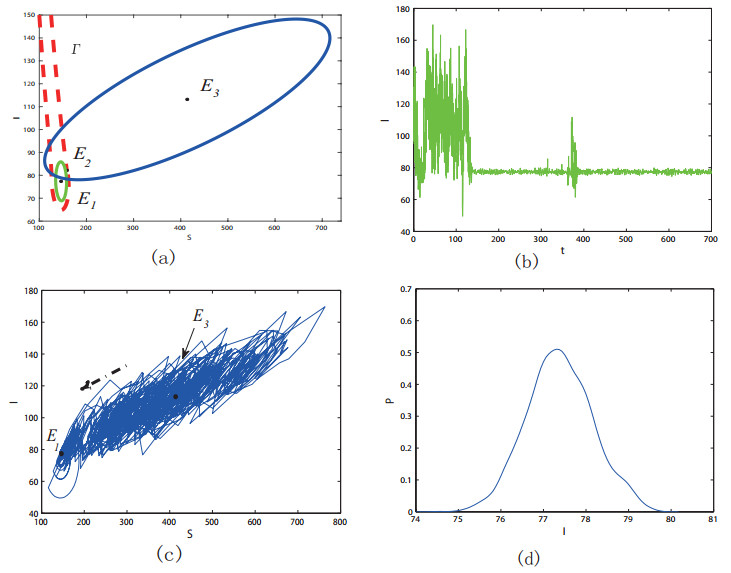
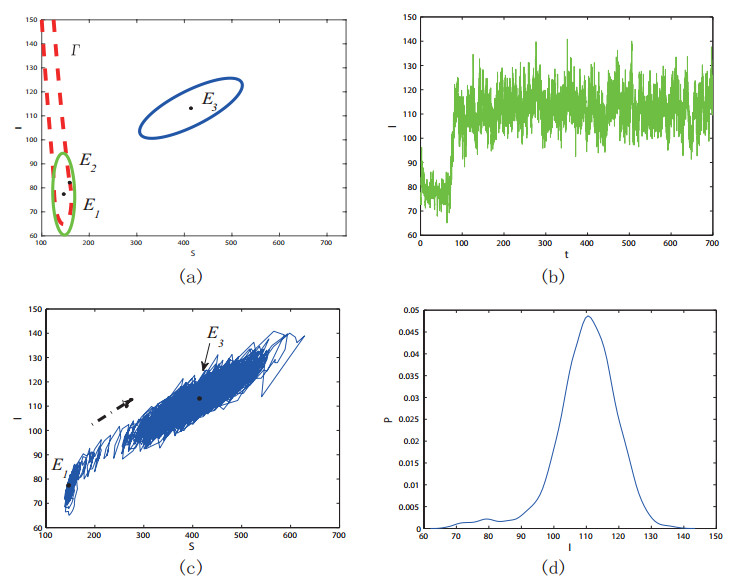
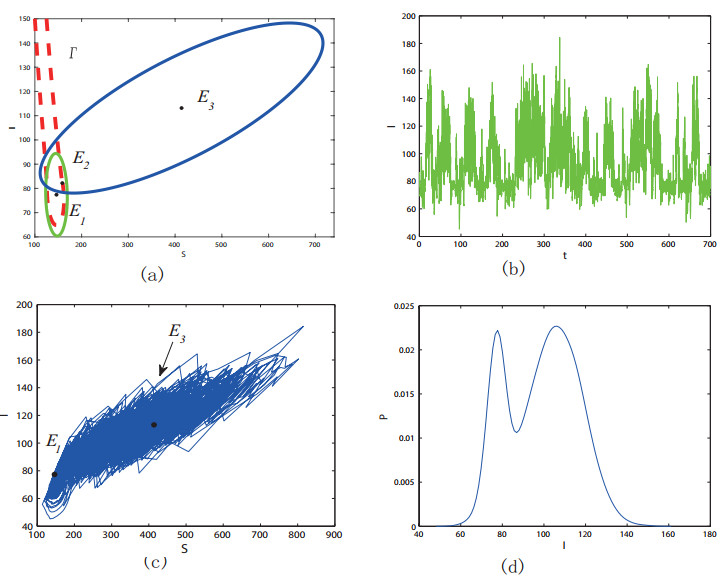
We take the parameter values in Table 1 and set $I_c = 80$. The three endemic equilibria for model (2) are $E_1 = (146.2542, 77.3821)$, $E_2 = (159.3644, 82.3223)$, $E_3 = (413.8380,113.1525)$. In Figure 2, phase plane of the deterministic model with parameters in Table 1 is shown, where the red-dotted curve $\Gamma$ (the stable manifold of $E_2$) is the separatrix of two basins of attraction and the gray one ($I = I_{c}$) is the separatrix of two subsystems. As one can see, for the deterministic model, the trajectories with initial value inside of $\Gamma$ tend to $E_1$, and the trajectories with initial value outside of $\Gamma$ approach $E_3$.

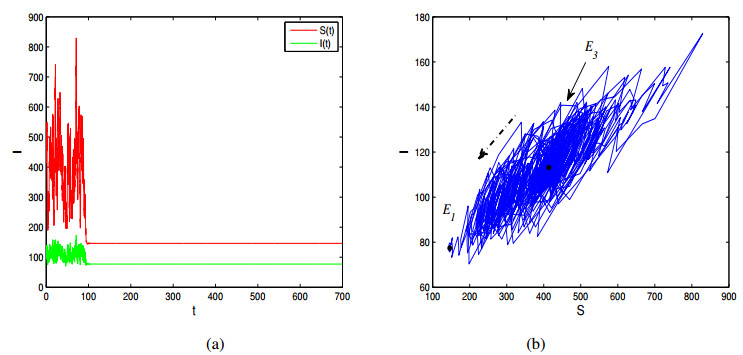
For the stochastic model, we take endemic equilibria $E_3$ as an example. It is worth noting that endemic equilibria $E_3$ is located above the threshold $I_c$. When the noise intensity is small, here, we take $\sigma_1 = 0.1$, the stochastic trajectories with initial value near $E_3$ will hover around it (see Figure 3). However, as the noise intensity increases ($\sigma_{1} = 0.25$), the steady state switches from high epidemic $E_3$ to low epidemic $E_1$ (see Figure 4). It is also observed that the noise-induced transitions from low epidemic $E_1$ to high epidemic $E_3$.

3.1.   Noise-induced state frequent switching 

In the following, we construct confidence ellipses for stochastic model (4) by applying the stochastic sensitivity function technique (see the Appendix in ^[37]). We then further estimate the critical value of the noise intensity that causes state switching.

For an endemic equilibrium $\bar{E} = (\bar{S}, \bar{I})$ of deterministic model (2), let $F = \left(\begin{array}{cccc} f_{11} & f_{12}\\ f_{21} & f_{22} \\ \end{array}\right)$ be the Jacobian matrix of $(f, g)$ with respect to $(S, I)$ at $\bar{E}$, where

We define $g_{11} = \bar{S}$, $g_{22} = \bar{I}$, and $G = \left(\begin{array}{cccc} g_{11} & 0 \\ 0 & g_{22} \\ \end{array}\right)$. After solving the following system of linear equations for $w_{ij}, i, j = 1, 2,$

we obtain the stochastic sensitivity matrix $W = \left(\begin{array}{cccc} w_{11} & w_{12}\\ w_{21} & w_{22} \\ \end{array}\right).$ Given that a noise intensity $\bar{\sigma}$ and a fiducial probability $P$, then applying the formula A.3 from ^[37] we obtain the confidence ellipse equation for the equilibrium $\bar{E} = (\bar{S}, \bar{I})$

Applying (11) to $E_3 = (413.8380,113.1525)$, the corresponding stochastic sensitivity matrix and its inverse are

The confidence ellipse equation of $E_3$ is

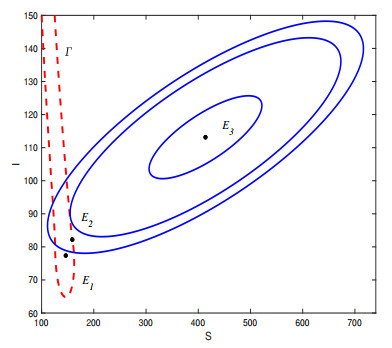
Fixing fiducial probability $P = 0.95$, we next observe how different intensity noise affects the confidence ellipse. When $\sigma_1 = 0.1$, the corresponding stochastic states and confidence ellipses of subsystem (5) are shown in Figure 5. As shown in the figure, the random states of the stochastic model are distributed around the deterministic endemic equilibrium $E_3$, and located inside of the confidence ellipses with probability $0.95$.

We then take two larger noise intensities $\sigma_1 = 0.24$ and $\sigma_1 = 0.28,$ the corresponding confidence ellipses are shown in Figure 6. As the noise intensity increases, the confidence ellipse is growing. It crosses separatrix $\Gamma$ (the stable manifold of $E_2$) and ultimately arrives at the domain of attraction of the low endemic equilibrium $E_{1}$. The noise intensity value that corresponds to the confidence ellipse intercepts with $\Gamma$ can be regarded as the critical noise intensity $\hat{\sigma}_1$. Here $\hat{\sigma}_1 \approx 0.24$. A typical example that the trajectory of stochastic model (4) starting near the endemic equilibrium $E_3$ converges to the other endemic equilibrium $E_1$ is shown in Figure 4 in which $\sigma_1 = 0.25 > \hat{\sigma}_1$.

Next we construct the confidence ellipse for $E_{1}$. The corresponding stochastic sensitivity matrix and its inverse of endemic equilibrium $E_{1}$ are

The corresponding equation of the confidence ellipse for $E_{1}$ is

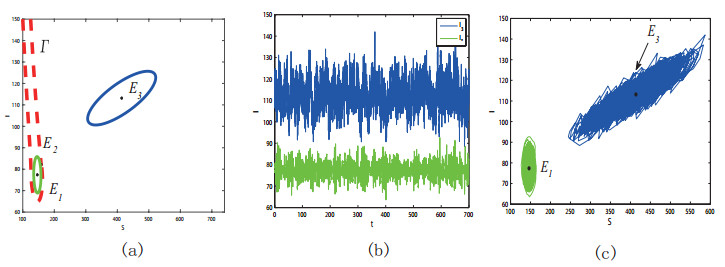
Putting the confidence ellipses for $E_1$ and $E_3$ together can give us a better looking of the whole system. For weaker noise ($\sigma_{1} = 0.1, \sigma_{2} = 0.02$), confidence ellipses of both $E_1$ (green) and $E_3$ (blue) are located inside their own attraction basin. They are distinctly separated by the separatrix $\Gamma$ (in red) (see Figure 7 (a)). The random trajectories starting from inside of the separatrix will fluctuate around the endemic equilibrium $E_1$, and the ones starting from outside of the separatrix will fluctuate around the endemic equilibrium $E_3$. The random trajectories leaving the unforced deterministic attractors concentrate in their small neighborhoods (see Figure 7 (c)). One can see the weaker noise does not affect the dynamics of the stochastic model (4).

We fix $\sigma_{2} = 0.02$ and increase $\sigma_{1}$ to 0.28, then the confidence ellipse (blue) of $E_3$ crosses the separatrix (see Figure 8 (a)). The stochastic trajectories starting within the attraction basin of $E_3$ will cross the separatrix and approach $E_1$ with high probability (see Figure 8 (c)). This is also shown by the time series (see Figure 8 (b)): the number of infected cases ultimately is stabilized around $I_1$ (a smaller value). To better understand this, we numerically obtain the stationary probability density (SPD) of model (4). In Figure 8 (d), we can see that the SPD for stochastic model (4) has a maximum value at $I_{1}$, which implies that the sample trajectory will stay for a longer time in the neighborhood of $I_{1}$. In other words, $I_{1}$ is stable in the meaning of probability (with a bigger probability). This illustrates that the phenomenon of noise-induced transition occurs as the noise intensity $\sigma_{1}$ increases.

We also obtain a symmetric result by fixing $\sigma_{1} = 0.1$ and increasing $\sigma_{2}$ to 0.04 (see Figure 9). In this scenario, the confidence ellipse of $E_{1}$ crosses the separatrix $\Gamma$. That is, the number of infected cases ultimately maybe jump to $I_{3}$ (a bigger value), thus making the infections worse.

Finally, we let both intensities change, increasing $\sigma_{1}$ to 0.28 and $\sigma_{2}$ to 0.04. As expected that the phenomenon of frequent random hopping occur between two attractors $E_1$ and $E_3$ is observed. We can see from Figure 10 (a) that both the two confidence ellipses of $E_{1}$ and $E_3$ cross the separatrix $\Gamma$, and the region that the two confidence ellipses intersect builds a "transition bridge" between basins of attraction. In this overlapped region, noise-induced transitions can occur with greater probability (see Figure 10 (b) and (c)). In addition, we can also see from Figure 10 (d) that the SPD for stochastic model (4) has two maximum value at $I_{1}$ and $I_{3}$. In this case, stochastic force can worse the picture of infection, it can also mitigate an infection.

4.   Discussion 

What do we do "if the horse has left the barn"? We are still optimistic. Never too late to take an action. Scientific oriented media alert and positive energy spread over the social network are able to guide us walking out of the woods. For epidemics associated with emerging and re-emerging infectious diseases, we can bend the infection curve if we are oriented scientifically. We can smartly use the media coverage and social network to help us to fight an epidemic. Using mathematical model we have shown that alerts from media and/or social network play an important role in the battle of fighting the disease spread.

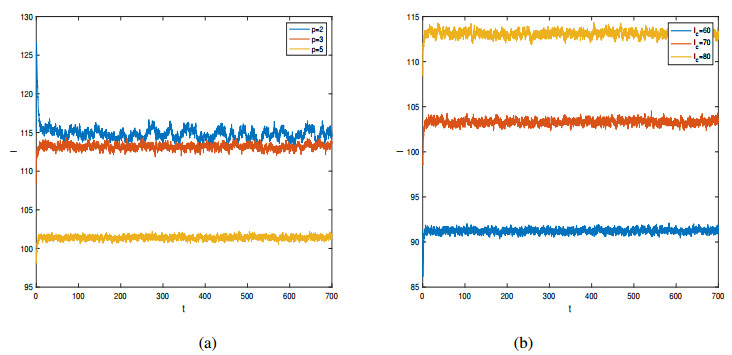
The final size of the epidemic depends on the media and social network coverage parameters $p$ and $I_{c}$. A clear monotonic patten of the final size can be seen shown in Figure 11 (a). Under the same noise intensity (we set $\sigma_{1} = 0.005$), the greater the media and social network coverage, the smaller the final size. The same monotonic patten is observed in Figure 11 (b), the final infection scale decreases when the threshold $I_{c}$ decreases. This suggests that the decision makers should set appropriate threshold $I_{c}$ to minimise the infection scale.

Since the alerts from media social network are triggered only after an initial epidemic, it does reduce the magnitude of the infection. However, one cannot overstate its role in containing an epidemic, mainly because these alerts do not modify the basic reproductive number. It is out of the reach of these alerts to bring the basic reproductive number less than one.

The magnitude of a confidence ellipse is proportional to the intensity of the noise. The bigger the noise, the bigger the corresponding confidence ellipse. Then we are sure that intensifying the noise will raise the likelihood of endemic state shift. However, in terms steady state mobile attributed to the noise, current model cannot distinguish whether it bring the epidemic downward or upward.

Acknowledgments 

We are very grateful to both the editor and the reviewers for their valuable comments and suggestions, which have greatly improved the quality and presentation of our paper. This work was supported by the National Natural Science Foundation of China (11671260; 12071293).

Conflict of interest 

The authors declare there is no conflict of interest.