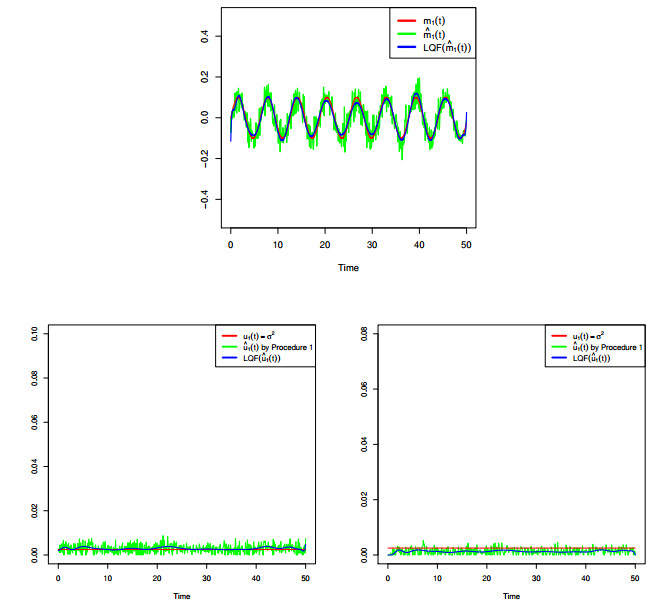
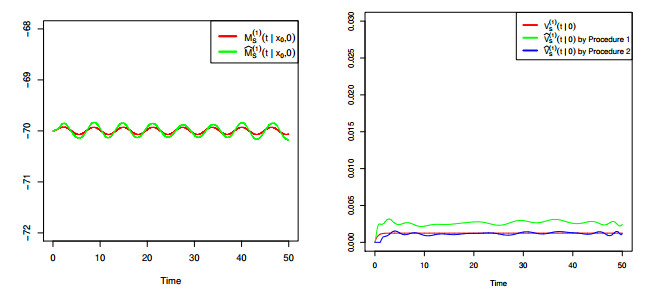
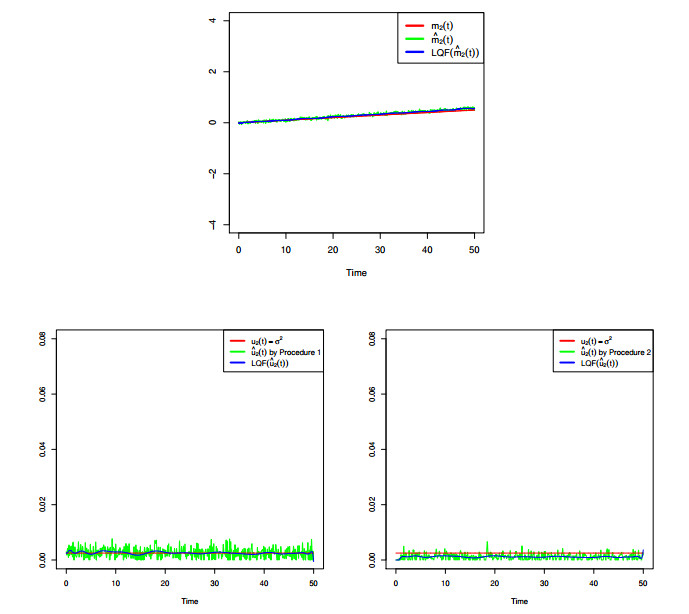
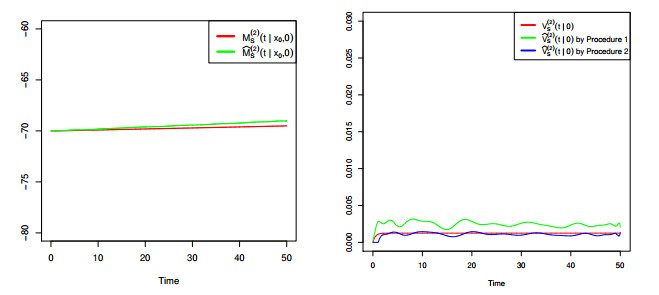
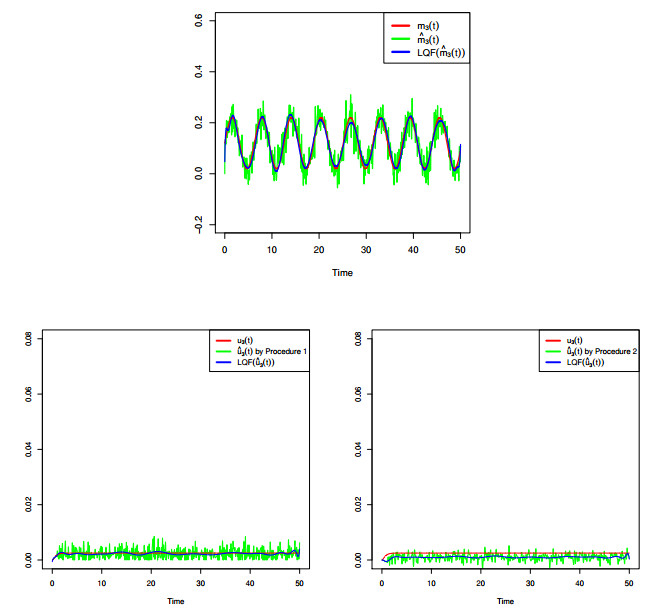
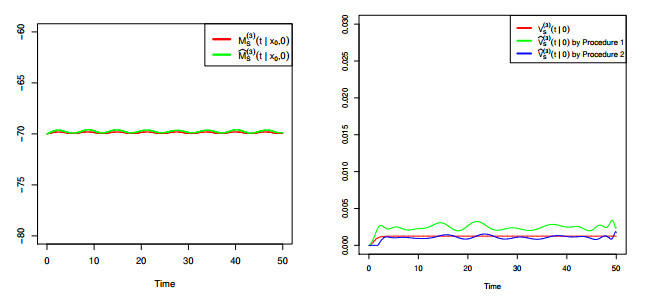
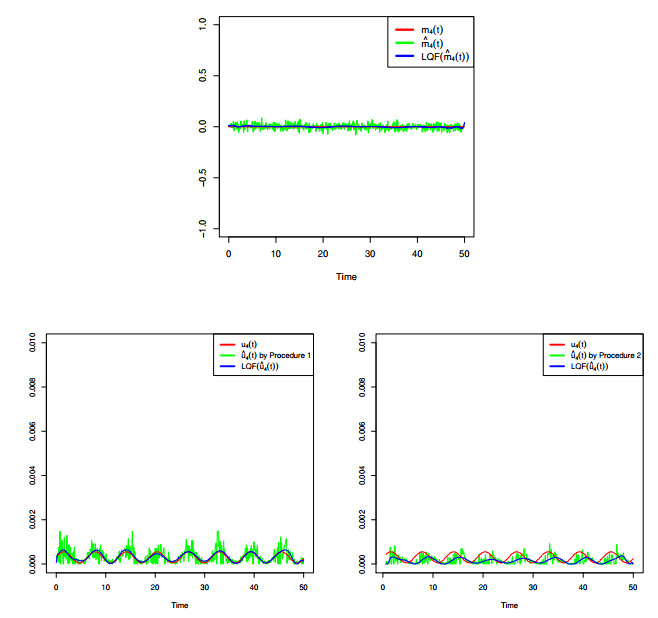
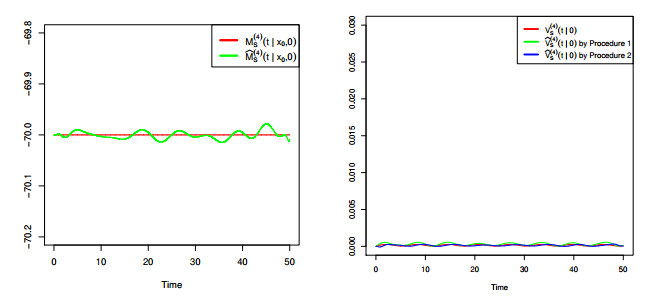
A non-homogeneous Ornstein-Uhlembeck (OU) diffusion process is considered as a model for the membrane potential activity of a single neuron. We assume that, in the absence of stimuli, the neuron activity is described via a time-homogeneous process with linear drift and constant infinitesimal variance. When a sequence of inhibitory and excitatory post-synaptic potentials occurres with generally time-dependent rates, the membrane potential is then modeled by means of a non-homogeneous OU-type process. From a biological point of view it becomes important to understand the behavior of the membrane potential in the presence of such stimuli. This issue means, from a statistical point of view, to make inference on the resulting process modeling the phenomenon. To this aim, we derive some probabilistic properties of a non-homogeneous OU-type process and we provide a statistical procedure to fit the constant parameters and the time-dependent functions involved in the model. The proposed methodology is based on two steps: the first one is able to estimate the constant parameters, while the second one fits the non-homogeneous terms of the process. Related to the second step two methods are considered. Some numerical evaluations based on simulation studies are performed to validate and to compare the proposed procedures.
1.
Introduction
Cassava cultivation is primarily distributed in tropical and subtropical regions, typically within the geographical range of up to 30° parallels [1]. Its starch–rich tuberous root serves as a staple for over 800 million low–income individuals, positioning it as the fifth most significant energy crop following maize, rice, wheat, and potato [2]. Furthermore, cassava cultivation contributes to employment generation, while its trade serves as a crucial source of economic income [3,4]. From an agronomic perspective, farmers favor this starchy crop due to its minimal input requirements, attributed to its wide adaptability to various soil and climate conditions, including drought tolerance and resilience in marginal soils [5]. Hence, cassava is cultivated across approximately 29.95 million hectares, predominantly in the African continent (60.9%), followed by Asia (29.4%) and America (9.6%), with a total production exceeding 319 million tons of fresh roots [6].
The cassava harvest highlights two key aspects: First, a substantial amount of biomass remains in the field, including stems and leaves, with proportions typically around 44% and 6%, respectively [7]; and second, solid (bagasse and peel) and liquid (wastewater) co–products from the starch extraction industry are prevalent and widely utilized [8] due to their application as raw materials for high–value food and non–food industrial processes [2]. Despite lignocellulosic solid co–products being historically utilized for biofertilizer [9], and for heat and power cogeneration within the cassava agroindustry [10], these agricultural residues are undervalued. There exists a significant opportunity to integrate them into the biorefinery and circular bioeconomy model, enabling the efficient utilization of biomass by harnessing its potential for multiple bioenergy benefits and bioproducts, thereby advancing sustainability; a focal point of contemporary green technology [11].
While cassava has been promoted for renewable energies generation, such as first–generation bioethanol, as realized in China [12], it has also been suggested that in Brazil, cassava bagasse could substitute up to 24% of sugarcane ethanol [13]. However, not only cassava bagasse but also stems, rhizomes, leaves, and peel can be utilized for this purpose. Moreover, they can be employed in the production of various other bioenergy sources, including biobutanol, biodiesel, bio–oil, biohydrogen, and biochar [14,15,16,17,18,19]. The utilization of lignocellulosic co–products has gained traction in the energy sector [20] due to rising fossil fuel prices and environmental concerns related to emissions of pollutant gases, biodiversity loss, monocultures, and land–use changes. Consequently, bioconversion could yield not only economic benefits but also social and environmental advantages.
Furthermore, agroindustrial co–products from cassava have been proposed for synthesizing various food and non–food bioproducts, particularly in the health sector [21]. For instance, they could be utilized in the development of prebiotics such as xylooligosaccharides [22], exopolymeric substances [23], and the identification of active components with antioxidant, anti–inflammatory, and immune–enhancing properties [21,24,25]. Additionally, there is potential for producing biomaterials for heavy metal removal, dye absorption in contaminated waters [26,27,28], and even bioplastics production [29,30], while also offering a wide range of biochemicals. Interestingly, considering a cassava biorefinery approach could increase the economic value of co–products, strengthen the value chain, and, most importantly, contribute to sustainable production by addressing environmental and social challenges.
2.
Results
2.1. Origin and distribution
Cassava (Figure 1) is among the 100 species of trees, shrubs, and perennial herbs within the genus Manihot, originating from the Americas [31], with distribution primarily in tropical and subtropical regions worldwide, particularly in developing countries [1]. The southern Brazilian Amazon has been identified as the center of origin of cassava, supported by geographic, molecular, and DNA studies indicating Manihot esculenta ssp. Flabellifolia (Pohl) is the wild progenitor species [32,33,34,35]. Domestication likely occurred in this same area, estimated to have taken place between 6 500 to 5 500 BC [36], as well as in the Cerrado savanna ecoregion [37,38,39], and the region known as Mesoamerica [40,41].
Reportedly, at the time of European contact in the 16th century, cassava constituted part of the diet in the lowlands of the Neotropics [42,43]. During this historical event, Portuguese colonizers transported it across the Atlantic Ocean from Brazil to the Congo in Africa. Two hundred years later, it was cultivated in the west and center of the continent and then spread eastward to Mozambique, Kenya, Madagascar, and Zanzibar [44,45,46]. By the 18th and 19th centuries, the species had become established in the south and southeast regions of Asia [47]. Consequently, it is known by a great variety of names: In English–speaking countries, it is called cassava, caxamote, farinha, guacamote, huacamote, mañoco; in Brazil, it is known as aipim, macaxeira, mandioca, and mandiya; in Africa, it is referred to as maniok; and in China, it can be called mu shu, shu ge, and shu shu [48].
2.2. World production
Cassava is produced in 103 countries (Figure 2), distributed across Africa (60.9%), Asia (29.4%), and the Americas (9.6%). In 2021, a production of 319 million tons of fresh roots was reported, mostly concentrated in Nigeria, the Democratic Republic of Congo, Thailand, Ghana, Brazil, and Indonesia. Although the world average is 13.02 t ha-1, there is wide variation (ranging from 0.99 to 43.07 t ha-1), among which stand out Guyana (43.07 t ha-1), India (37.93 t ha-1), Zambia (35.54 t ha-1), Laos (32.10 t ha-1), Niger (29.02 t ha-1), St. Vincent and the Grenadines (28.30 t ha-1), Cambodia (27.41 t ha-1), and Indonesia (26.6 t ha-1) [6]. An upward trend in production has been observed compared to the initial reports of commercialization in the 1960s until 2021 (Figure 3), which is explained by the increase in planted area, yield, versatility of use in bioproducts, and government policies promoting cultivation and integrated processing [49].
In this regard, there has been an upward trend in production when comparing the initial marketing reports from the 1960s to the year 2022 (Figure 3). This trend can be attributed to the expansion of cultivated areas, improvements in yield, and government policies aimed at promoting cultivation. For example, Nigeria, the leading global producer of cassava, has experienced a 4.3% annual production increase since the 1990s, largely due to government agricultural programs [50,51]. Similarly, countries like Thailand, Cambodia, Vietnam [52], and Laos have expanded cassava cultivation to meet the demand of the Chinese market, which imports 80% of international cassava trade in various forms including fresh, chilled, frozen, chopped, pellets, or starch [2,53]. Vietnam, for instance, witnessed a 238% increase in planted area (from 237 600 ha in 2000 to 547 883 ha in 2017), accompanied by a yield intensification from 8.4 to 18.83 t ha-1 [54]. However, a slowdown in cassava growth in 2016 was possibly due to the reserve use and technological advancements in maize cultivation in China, leading to reduced utilization of cassava for bioethanol production [12], and other derived products like animal feed and processed food. Consequently, this resulted in the abandonment of cassava cultivation in major exporting countries [2]. Moreover, its commercialization declined during the COVID–19 pandemic, as regions dependent on cassava redirected it for household consumption, with the remaining produce directed towards local sales to generate economic resources [55].
2.3. Cassava for human consumption
Cassava is typically harvested between 10 to 12 months after planting (MAP) to be available as food [56]. This timeframe coincides with a higher yield of tuber roots, dry matter, and starch [57], as well as lower fiber content [58]. However, it can be harvested between 8 to 24 MAP [59]. Additionally, in the areas of cultivation, cassava production generates employment [4], and the sale of tubers (Figure 4) serves as an income source [3].
Worldwide, approximately 800 million people rely on cassava to meet their food needs [60], with reported average intakes of up to 19.8 kg per year. Consequently, it is considered the fifth most important energy crop after maize, rice, wheat, and potato [2]. This is due to its richness in carbohydrates, primarily starch, although it also contains vitamins and minerals (Table 1). Despite its low protein content, it contains 2.79% mainly unsaturated fatty acids and is a rich source of potassium. Notably, it contains polyphenols and flavonoids (31.95 and 0.85 g per 100 g-1, respectively), as well as superoxide dismutase and DPPH radical scavenger activity. Additionally, it can inhibit α-glucosidase and α-amylase, with values of 69.02% and 36.30%, respectively, which, coupled with its antioxidant capacity, may positively affect its anti–diabetic activity [61].
However, the presence of anti–nutrients such as nitrates, phytates, tannins, oxalates, saponins [62], and HCN (ranging from 16 to 1212 ppm on a dry basis), which differs by variety and growing region [63], requires various preparation techniques to ensure safety before consumption. According to the Codex Alimentarius, levels of HCN should not exceed 50 and 10 mg kg-1 [64]. Notably, there are biofortified varieties of cassava with yellow pulp (a vitamin A precursor) that could enhance the vitamin and protein intake of consumers due to their nutritional quality [65].
Additionally, cassava leaves play a significant role in human nutrition, particularly in certain regions of the African continent and in Brazil in the Americas, where they are incorporated into various traditional dishes [66,67]. Moreover, the processing and sale of cassava leaves represent a rapidly growing emerging sector [68]. Despite containing cyanogenic glycosides with values ranging from 346 to 7484 ppm on a dry basis [63], the levels can be reduced through techniques such as oven drying, squeezing, boiling, and crushing, resulting in reductions to 55.99%, 50.79%, 32.01%, and 25.15%, respectively, and also decreasing the tannins presence [69]. Compared to the root, the leaves provide a higher protein contribution [70], containing 18 of the 20 amino acids, including all nine essential amino acids [63,71]. Additionally, the leaves are rich in minerals and vitamins, including thiamine, riboflavin, niacin, vitamin A, and vitamin C (Table 1). When processed into flour, the proportions of these nutrients are higher compared to other leafy vegetables, legumes, cereals, eggs, milk, and cheese [72]. Furthermore, cassava leaves contain carotenoids in significant amounts, ranging from 174 to 547 µg per gram on a dry basis [63]. The consumption of these compounds is crucial for nutrition and health [73], making cassava leaves a viable option to address issues of human malnutrition and contribute to food security.
2.4. Cassava cultivation and generation of agricultural co–products
Cassava production varies from complex systems with extensive plantations and mechanized tillage to low–input survival agriculture practices and intercropping [31,74]. Regardless of the system type, there is an imperative to enhance productivity to meet the escalating food demand [75]. Presently, cassava yields, as a carbohydrate source, outperform other roots, tubers, and cereals under tropical conditions due to its drought tolerance and adaptability to marginal soils [76]. This is why cassava cultivation proves more dependable than other species susceptible to such conditions, such as corn [60].
Approximately 1696.28 million hectares of marginal lands worldwide have been identified as potential areas for establishing cassava crops and achieving profitable yields [1]. However, realizing the optimal productivity of the species requires adherence to suitable edaphoclimatic conditions, proper crop management practices [83], and utilization of highly productive varieties developed through biotechnological techniques [84]. It is estimated that yields of between 80 and 100 t ha-1 of tuberous roots could be attained [85,86], highlighting those current yields are only about 10% of its potential productivity.
Following cassava harvesting, stems and leaves are produced, with proportions typically around 44% and 6%, respectively [7], which may vary by genotype and harvesting time [87]. While a portion of the stems is allocated for agronomic seed, the majority is underutilized, akin to the leaves, constituting the initial batch of co–products subject to waste [88]. Consequently, approximately 200 kg of dry matter per ton of harvested tuber is disposed of in situ, facilitating nutrient recycling [74]. However, this biomass could be immediately repurposed; for instance, the stems could serve as a substrate for mushroom cultivation [89], provide thermal energy in households due to its calorific value [90], or be used in the production of briquettes, recognized as environmentally friendly and renewable non–fossil fuels [91]. Therefore, these alternatives represent viable options for adoption by rural dwellers and low–income cassava producers.
2.5. Starch extraction
Given the post–harvest deterioration issues of cassava roots, processing them to extend their shelf life is a common practice [92]. Among the processed products, starch holds the greatest economic impact [93]. The extraction of starch involves several stages (Figure 5), at an industrial scale, typically conducted in facilities equipped with mechanized systems for each step [94,95]. Such facilities utilize equipment that requires mechanical, heat, and electrical energy, averaging about 2 208 MJ per ton of processed root [96], and 0.20 to 0.50 kWh per kilogram of extracted starch [10]. Nevertheless, less advanced manufacturing processes, equipment, and even artisanal methods are prevalent. The resulting product is typically native starch with a moisture content ranging from 10% to 14%, suitable for marketing [97]. Various factors, including agricultural practices [98], variety, environmental conditions [99,100], and the applied technologies in the extraction process [101], influence the yield, quality, and physicochemical properties of the starch.
2.6. Industrial use of starch
Numerous plants store carbohydrates as reserve sources in the form of starch across various plant organs such as roots, tubers, seeds, and grains [102]. The industrial sector derives starch from several crops, including maize, cassava, potato, and wheat, each differing in their field productivity and starch yield (Table 2) [103,104]. Carbohydrates, owing to their physical and chemical properties, are utilized in various high–value food and non–food industrial applications, either in native or modified starch form. These applications span a wide range including paper production, textiles (predominating the food market), pharmaceuticals, cosmetics, adhesives, sweeteners (fructose, glucose, sucrose, and sorbitol), food additives (monosodium glutamate, and maltodextrin), dextrins, dextrose, lactose, animal feed, biofuels, manufacturing of bioplastics and packaging, as well as applications in nanotechnology, regenerative medicine, and 3D printing materials [105,106,107]. Commercial prospects for starch–based products are anticipated to grow annually, driven particularly by the production of bioplastics and packaging [108].
2.7. Generation of industrial co–products from cassava
Similarly, to other industrial crops, cassava–based starch production generates significant amounts of lignocellulosic biomass, including bagasse, peel, and liquid wastewater (Figure 5). Bagasse, accounting for 60% of the total tuberous root, is produced during the filtration stage [109]. To produce one ton of starch, 2.5 tons of this co–product are generated [110]. Peel production ranges between 100 to 300 kg per ton of cassava [9,50], along with more than 17.4 m3 of liquid wastewater. The emission of greenhouse gases is also evident, with values reaching 2.21 kg CO2 eq. per ton of starch [111].
It is highlighted that during the starch extraction process, 75 to 90% of the solid co–products are disposed of in the open air or burned near the processing sites, while liquid wastewater is indiscriminately discharged into drainage or natural water sources [9]. These practices pose potential public health problems [23], damage to riparian flora and fauna caused by turbidity, toxicity, and high chemical oxygen demand has been documented [112]. Thus, the lack of management of co–products poses a threat to water consumption by the population and constitutes an ecocide of aquatic fauna. Urgent solutions are necessary to promote a reduction in the problems associated with the disposal of solid and liquid waste.
2.8. Potential use of agroindustrial co–products
The recurring challenge in the agroindustrial sector is the disposal of co–products, partly due to the inherent characteristics of these materials. Although cassava agroindustry residues contain toxic substances, they also encompass structural non–toxic components (Table 2). Bagasse primarily comprises starch [30], alongside structural elements such as holocellulose (cellulose and hemicellulose) and lignin, whereas the peel is characterized by a higher protein and lipids content (Table 2). As for the liquid waste effluent (Table 3), this is an acid or weakly acid liquid composed of organic elements in suspension, thus, starch can be present at a rate of 9.6 to 37.5 g L-1, fibers, minerals [97], cyanogenic compounds, nitrates, nitrites, sulfates, heavy metals [46,113], as well as macronutrients, such as nitrogen and phosphorus, with amounts ranging from 780 to 1 300 mg L-1, in addition to micronutrients [114].
In this sense, it is possible to obtain similar or higher yields of cassava starch per hectare due to its high yield of fresh roots per hectare and starch percentage compared to other tubers and cereals. This is not to mention its socioeconomic and environmental advantages, which include sugarcane bagasse, the latter being one of the most abundant and widely used agroindustrial co–products worldwide [115]. Although many of the crops currently used for industrial purposes are staple foods in developing countries in the tropics [116], expanding the secondary sector could jeopardize food security. Therefore, it is necessary to explore other non–conventional sources of starch that are not used for food purposes in specific geographical areas.
Hence, it is possible to demonstrate the broad potential of cassava and its co–products due to their complex chemical composition, which makes them low–cost and highly available raw materials for a range of high–value–added applications. This would bring about an increase in their economic value while also representing a sustainable alternative to mitigate environmental problems [110]. This approach is oriented towards a circular economy, biorefinery [7,10], and the fulfillment of current green technology objectives aimed at finding sustainable and ecological solutions at social, economic, and environmental levels [11]. In this regard, one strategy for sustainable management of ALR involves making certain adjustments to settling ponds to decrease organic sediments and turbidity [97], coupled with the cultivation of microalgae such as Chlorella, Spirulina, and wild strains. These aspects could reduce BOD levels (89–99%), the presence of phosphates, nitrates, and cyanide [112,136]. Additionally, treated waters could be circulated in the starch extraction process, reducing freshwater needs by up to 66% [137]. Thus, to optimize resources, mitigate pollution issues, and enhance economic benefits, the implementation of new techniques and facilities within the industrial process is necessary.
2.8.1. Animal feed
Traditionally, cassava root is often utilized for animal feed in the form of chips, pellets, or silage [31,60]. Even whole plant silage is possible [138], and leaves are often offered in fresh or dehydrated form [139,140]; however, solid and liquid co–products from the starch industry can also fulfill this function. In Brazil, in artisanal farina production, peels are donated to livestock farmers for incorporation into animal feed [141]. In Nigeria, 10 to 25% of the peel and bagasse are disposed of as pig feed [142], representing a viable use option. Furthermore, disposing of bagasse in a fermented state economically achieves a higher net present value, lower investment cost and environmental impact, and a shorter payback period compared to other uses, such as the production of edible mushrooms [110]. The potential of wastewater has also been demonstrated for inclusion in the diets of fattening lambs [143].
However, to enhance the nutritional profile and safety, it is necessary to maximize the protein content and consider additional treatments to decrease HCN presence and antinutrients such as tannins and polyphenols [21,81,144]. Additionally, improving digestibility is essential since protein and fiber are the limiting factors for forage use in the tropics [138]. Techniques such as soaking, boiling, sun drying, or microbial fermentation can be useful to ameliorate these limiting factors [145]. Okike et al. [146] proposed a technique to obtain high–quality peel for animal nutrition, reducing sun drying time from 2 to 3 days to just 6 to 8 hours during the dry season through shredding, mechanical dehydration, fermentation, pulverization, and sieving, followed by subsequent solar drying. Additionally, Marin et al. [147] reported that subjecting a mixture of cassava leaves and bagasse (3:7) to solid–state fermentation (SSF) with the fungus Lentinula edodes decreased cyanide content by 64.8% while increasing protein content by 36.19% and lipid content by 2.36 times.
Similarly, de Sousa et al. [148] observed that cultivating Pleurotus ostreatus on cassava peel for 35 days led to increases in protein (from 3.93% to 8.87%), lipid (from 1.49% to 3.52%), and fiber (from 9.96% to 35.18%) content, along with a slight increase in digestibility (5.2%). Boundy–Mills et al. [77] utilized cassava leaves supplemented with glucose as a substrate for yeasts to convert solubilized structural protein into digestible protein. On the other hand, alternatives such as adding soybean meal, fish meal [139], methionine [145], or mixing cassava root with young leaves, sprouts, peep residues, and bagasse [15], or even silaging cassava pulp with fresh leaves [149], can improve the nutrient profile. Furthermore, a saving of 0.23 and 2.24 tons of soybean and corn, respectively, is possible when using a feed based on cassava and sorghum meal as an energy source and soybean and mulberry meal as protein in diets for pigs [150]. Furthermore, Williams et al. [151] found that dietary cassava peels and leaves in a 5:1 ratio do not affect performance in pigs fed corn and soybean.
Finally, methods such as heat and acid precipitation and spontaneous fermentation have been proposed to produce cassava leaf protein concentrate for feed and animal feed. However, although the protein content and amino acid profile are comparable with soybean, the cyanogenic potential needs to be decreased to ensure its use [81]. Thus, if properly managed, cassava co–products can be used as a substitute for corn or other cereals in diets for the livestock sector, which would undoubtedly improve the income of small and medium–scale livestock producers.
2.8.2. Biofertilizer production
In the area surrounding cassava processing sites, the generation of biofertilizers is one of the main uses of solid co–products [9]. The low moisture content, bulk density, high porosity, and good water absorption capacity of biofertilizers made from this raw material are parameters that positively affect plant growth [152,153], especially when combined with synthetic sources of nutrients. Thus, it has been observed that the combined application of 2.5 tons of cassava peel compost with 25 kg of N ha-1 improved dry matter and nutrient content in Amaranthus cruentus L [154]. However, Nguefack et al. [155] reported an increase in nutritional and antioxidant parameters, as well as a yield enhancement of up to 187% compared to synthetic fertilizers. Additionally, the addition of compost and vermicompost from solid co–products increased fertility, structure, and even lowered soil salinity levels [156]. Moreover, the amount of nutrients contained in liquid waste effluents (Table 2) makes it promising for use as a biofertilizer [135]. Thus, the application of 120 m3 per hectare of this wastewater has the capacity to increase the concentration of available phosphorus and exchangeable potassium in the soil, making it an ideal input for adoption by small–scale farmers [157].
In summary, recycling waste not only serves as a disposal mechanism but also aligns with resource management practices, considering that these materials are highly available in processing areas and are practically inexpensive raw materials.
2.8.3. Bioenergy
Lignocellulosic biomass is an alternative renewable energy resource with the potential to replace fossil fuels and GHG emissions. Agroindustrial co–products from cassava cultivation can be combusted for cogeneration of heat and electricity [158] due to their high calorific value since 15.27 to 18.86 MJ kg-1 are generated [159,160].
However, extensive research has focused on the study of stems, rhizomes, leaves, peel, and bagasse for the cogeneration of second–generation biofuels [17,161,162,163,164] such as bioethanol, biobutanol, biodiesel, bio–oil, biochar, and biohydrogen [15,18,123,165], these through biomass disintegration processes, such as biochemical (hydrolysis and fermentation) and thermochemical (direct combustion, gasification, slow pyrolysis, fast pyrolysis, and oxy–combustion) [166,167], although to improve sustainability it is necessary to implement novel strategies such as green technology within biosynthesis processes and circular economy principles [168].
In general, bagasse is considered a co–product with extensive research in bioethanol production [169,170] given its high content of starch, cellulose, hemicellulose, and low concentration of protein and lipids [171]. Moreover, the production yield depends on the chemical composition of the co–product and the process conditions [13,172]. Thus, Huang et al. [173] reported > 0.30 g g-1 and a productivity of ~0.3 g L h-1 of n–butanol in ABE (acetone–butanol–ethanol) fermentation from cassava bagasse.
Economically, it has been shown that it is possible to produce at $0.91 kg-1 or $2.73 gal-1 for 50 000 metric tons of cassava bagasse, compared to $7.41 gal-1 when using dextrose and $5.0 gal-1 if corn starch is used. Biobutanol is an interesting fuel due to its higher–octane rating and lower volatility, which is similar in air–to–fuel ratio to gasoline, compared to ethanol [114]. Thus, cassava bagasse is shown to be an economically attractive feedstock due to its low cost and abundance for biofuel cogeneration.
However, for the peels subjected to enzymatic saccharification, it is also possible to generate bioethanol, with a yield of 0.53 g g-1 [17], a yield that could be maximized using green technology. In this respect, it has been reported that using mild and green chemical pretreatments on lignocellulosic biomass, the latter using green proteins from Amaranthus retroflexus leaves as a biosurfactant in the saccharification process, it is possible to generate an additional 6 400 to 12 400 tons of bioethanol, ten times higher than using soybean seed proteins and chemical surfactants [174], as well as using subcritical hot liquid water and the addition of organic acids (acetic, lactic, and formic), which increases the yield of fermentable sugars [175].
On the other hand, the peel and bagasse are raw materials to produce biogas, a fuel useful to generate heat or achieve electricity cogeneration, representing savings of 4 to 11% in the production costs of the cassava industry [10,176]. Techniques utilizing the principles of green chemistry, such as pretreatment with hot liquid water, can enhance the removal of hemicellulose and starch, increasing methane production rate and yield by 1.6 times and 35%, respectively, compared to untreated bagasse [177]. Moreover, the utilization of pyrolyzed cassava stems and peels combined with cow manure in anaerobic digestion can be implemented in factories to yield multiple benefits, including wastewater treatment, electricity cogeneration, as well as biogas and biofertilizer production [19]. Similarly, it is possible to capture the wastewater effluents in biodigesters [15,167], and cogenerate 357.8 m3 for every 17.6 m3 of wastewater. This approach of circular economy and green technology undoubtedly would enhance the economic and environmental profitability of industrial operations [10].
Now, bagasse, being a waste composed of lignocellulose and carbohydrates, is a perfect substrate for fermentative hydrogen production, in this regard, Chatellard et al. [14] found a yield of < 1 ml H2 g-1 of dry matter for lignocellulosic residues, compared to 240 ml H2 g-1 of dry matter for purified starch, therefore, it is possible to increase the potential of the residues by choosing a good microbial consortium, subjecting the substrates to pretreatments and achieving the optimization of the technical production parameters.
It is also possible to cogenerate bio–oil, which is a precursor of renewable fuels and high–grade petrochemicals, the production of which could minimize dependence on fossil fuels and toxic chemicals [178]. In line with this, Rueangsan et al. [179], extracted bio–oil by fast pyrolysis with a yield of 65 % by weight of dry biomass from stems and rhizomes, the latter being of better quality due to lower oxygen content, higher calorific value and storage stability.
However, other by–products can be derived, such as syngas (CH4, H2, CO, and CO2) [15], and biochar, which, in addition to being directed as a solid biofuel, has the potential as a soil improvement [16], and biosorbent for wastewater dyes [180].
Specifically, although cassava is oriented as a first–generation energy crop with a 2% share, especially in China and Thailand [181], its use is controversial due to the increase in food prices caused by the rising demand for biofuels, a demand that enhances food conversion by planting bioenergy crops [104]. Thus, bioenergy production through its residual biomass is proposed as a promising alternative to minimize land use and safeguard food security [88]. Therefore, it is important to manage co–products from the cassava agroindustry, where biofuel production offers an economically and technologically attractive solution [14] that is capable of significantly reducing energy demand and decreasing greenhouse gas emissions [164], bringing environmental, economic, and social benefits [182], as population growth continues to rise inversely to the production of fossil fuels. It is also necessary for co–products to undergo pretreatment to break down the structure of the structural components and increase extraction efficiency [183]. Thus, co–products constitute an optional source to generate bioenergy in countries that are economically dependent on cassava cultivation [88]; however, barriers such as the lack of technological maturity and the high cost of production hinder significant growth in the energy market [104].
2.8.4. Bioproducts
The co–products generated during cassava processing possess enormous potential for synthesizing bioactive compounds such as carotenoids, phenols, and organic acids (including gallic acid, catechin, rutin, chlorogenic acid, caffeic acid, citric acid, acetic acid, lactic acid, and poly–γ–glutamic acid (γ–PGA)), as well as flavonoids. These secondary metabolites offer specific health benefits, including the prevention of certain chronic non–communicable diseases, along with anti–inflammatory, anticarcinogenic, cardiovascular, and antioxidant properties, among others [21,24,25,184]. Regarding the peel, when subjected to physical, chemical, and biological processes, the lignin structure is modified, releasing the hemicellulosic base, a raw material for obtaining xylooligosaccharides (XOS). XOS serves as a useful prebiotic, promoting beneficial microbial activity in the organism [185]. Additionally, bacterial structures can be isolated from the residue to synthesize exopolymeric substances (EPS), particularly from the genus Bacillus [23].
Furthermore, leaves and stems contain various phytochemicals conferring antioxidant, anti–inflammatory, anthelmintic, and antidiabetic properties, offering an alternative to improving various health conditions [72,186]. This makes them suitable for use in the food industry; however, further safety and bioavailability studies of these active compounds are required [22]. Residual liquid effluents also serve as an optimal substrate for the growth of microorganisms that synthesize highly demanded bioproducts in both food and non–food industrial sectors [135].
Additionally, these co–products can be utilized in synthesizing bioplastics such as the copolymer poly (3–hydroxybutyrate–co–3–hydroxyvalerate) [29]. They can also serve as filler materials in polyurethane foams, reducing polyethylene glycol usage by 24% [30]. Furthermore, due to their morphological, physical, chemical, mechanical, and thermal properties, they can act as reinforcing agents in the polymeric matrix of biocomposites [187]. Thus, these co–products represent inexpensive raw materials that, if utilized in the biopolymer industry, could ensure sustainable and profitable production with positive environmental effects.
2.8.5. Other uses
The peel can remove heavy metals (chromium VI) [26], and can also absorb dyes like methylene blue, making it useful for primary treatments of industrial liquid co–products [27], suggesting its potential in the field of bioremediation. Furthermore, bagasse can be used as an adsorbent material for food dyes, offering a promising application to replace commercial products such as activated carbon. For instance, Santos et al. [28] reported the biosorption of up to 74.4% of the dye tartrazine in effluents from the juice industry using 7.5 g L-1, attributed to its unique characteristics such as an irregular, heterogeneous surface, and the presence of pores. Other alternatives are also depicted in Table 4.
3.
Conclusions
The availability of a considerable volume of co–products from the cassava agroindustry leads to exploring their potential use for the development of bioenergy and bioproducts with high added value, especially in those places where cassava represents a fundamental pillar of the rural economy. Energy generation is one of the most studied aspects, which, if implemented within the factories, these methods could lead to a true circular economy, and with the principles of green technology, they would promote energy security, adequate land use, thus increasing the efficiency of low–value resources, and addressing environmental problems associated with cassava co–products, such as the discharge of liquid effluents into water sources, the production of unpleasant odors, and the emission of greenhouse gases. Finally, the potential high–value products that can be derived from these bio–waste products could bring benefits to the agroindustrial chain.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
We thank the Facultad de Ciencias Biológicas y Agropecuarias, Región Córdoba–Orizaba of the Universidad Veracruzana.
Conflict of interest
All authors declare that there are no competing interests.










 DownLoad:
DownLoad: