Research on multi-load AGV path planning of weaving workshop based on time priority

1.   Introduction

Most of weaving workshops have adopted the mode of loading cloth manually, which lead to require a large amount of physical labor. Due to the poor quality of manual cloth loading, some cloth loading tasks would easily missed, resulting in cloth rolls with different lengths, thus affecting customer satisfaction. Therefore, there is an urgent need to replace people with machines in the cloth loading process and adopt an automatic method of cloth loading.

A multi-load AGV is mainly applied in the weaving workshop to automatically drop off the finished rolled cloth and transport it to the cloth inspection workshop, which can reduce the need for labor and reduce the operation costs ^[1]. Because of the unique layout and production mode, the path planning method of the multi-load AGV in a weaving workshop urgently needs to be discussed.

At present, with respect to the strategy of task allocation in the multi-load AGV's path planning problem, Li Guo Min ^[2] presented an improved harmony search algorithm to solve tasks assigning and sequencing of multiple AGVs. Dong-Hyun Lee ^[3] proposed a resource based task allocation algorithm for multi-robot systems.

In terms of shortest paths, Tian Jian Chen ^[4] presented a dynamic routing method for the shortest path planning and conflict prevention in the AGV system, which scheduled the shortest and conflict-free route by utilizing the Dijkstra algorithm and the Dynamic Time-Window Method. Adam ^[5] presented a modified particle swarm optimization method to search for a minimal time path for a solar-powered unmanned ground vehicle (UGV). Smolic-Rocak ^[6] proposed a routing method using time windows with a vectorial form. The use of time windows makes the algorithm prone to other scheduling and routing problems.

With respect to establishing the path planning model, KG Huo ^[7] regarded the minimum total operational costs as the planning target; the operational restrictions, the length of the time window and the load balance as constraint conditions; and the scheduling policy driven for events as the research method to establish a mixed-integer programming model for the scheduling of the multi-load AGV. Li Guo Min ^[8] established a mathematical model with a new objective function, which incorporates two indicators, that is, the standard deviation of the waiting time of computer numerical control material buffers and the total travel distance of automated guided vehicle. Maryam Mousavi ^[9] studied a multi-objective optimization method, including task scheduling, the minimum number of vehicles and the time costs. Fazlollahtabar ^[10] proposed an approach for finding an optimal path in a flexible jobshop manufacturing system considering two criteria of time and cost. H. Fazlollahtabara ^[11] considered time, costs and AGV capabilities as a triple standard and applied a mathematical programming method to achieve the optimal path selection of AGV transportation on the basis of the BOM.

With respect to the solution of the model, V. K. Chawla ^[12] proposed a combination of particle swarm optimization (PSO) for a global search and the Memetic Algorithm (MA) for a local search, termed the modified memetic particle swarm optimization algorithm (MMPSO), for the scheduling of multi-load AGVs in an FMS. Soovadeep Bakshi ^[13] presented an algorithm for the scheduling of an AGV that traverses desired locations on a manufacturing floor; the algorithm enables the AGV to find an optimal route. Hamed Fazlollahtabar ^[14] proposed a mathematical formulation that was first adapted to a minimum cost flow (MCF) model and then optimized using a modified network simplex algorithm (NSA). Grunow ^[15] took advantage of the effectiveness of vehicles, proposed a scheduling algorithm based on priority to solve the problem for multi-load AGV scheduling, and established an MILP model to verify the effectiveness of the scheduling algorithm. Tong-Jin Park ^[16] proposed an algorithm to calculate the real path and obstacle's length and planned the path using the algorithm.

The implementation of a multi-load AGV in a weaving workshop can be regarded as task assignment and path planning problems in the transportation network. The above literature has substantial reference value for the task assignment strategy, the establishment of a mathematical model and the solution for multi-load AGV path planning, but it is not fully applicable to a weaving workshop. At present, the scheduling problem of weaving workshop is focused on production scheduling, there is a lack of research results on the logistics scheduling of weaving workshop. On the basis of the above documents, this paper studies the problem of multi-load AGV path planning in a weaving workshop; considers the speed differences of AGVs on main streets, roadways and corners to search for the path with the shortest time; presents a method for multi-load AGV path planning based on the shortest time; and proposes the GA-PSO algorithm with a better search performance to solve the path planning model. The result of this research on multi-load AGV is practical and can be applied to the weaving workshops and other industries.

2.   Problem description

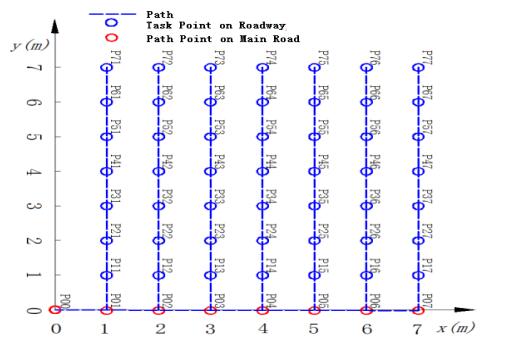
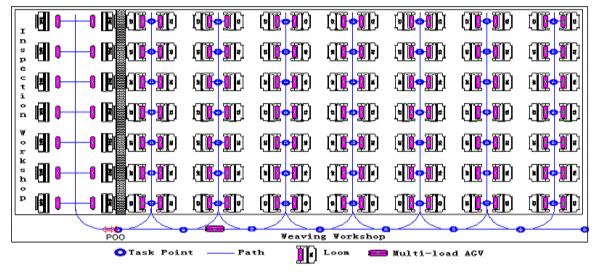
The layout of the weaving workshop and the horizontal transportation path are shown in Figure 1. The loom is arranged in a laneway pattern; the blue line in the Figure indicates the path, and blue circle indicates the task point needed for load cloth. The multi-load AGV (automated guided vehicle) starts from the cloth inspection workshop (arriving at point P00 can be regarded as entering the weaving workshop) and travels along the feasible path to the path node corresponding to the set weaving machine. After loading the cloth automatically, the AGV transfers the cloth roller to the inspection workshop (to point P00 point that can be considered as entering the inspection workshop). After unloading the cloth roller, the AGV returns to the weaving workshop to carry the finished cloth and handles all the loaded cloth.

The path planning method consists of completing all tasks, carrying a full load in each single task (the capacity of each AGV is 4), minimizing the transport costs, and maximizing the production efficiency, which is the goal of path planning. The AGV serves each task point only once in each task batch, and the AGV has a load limitation. Therefore, the problem can be considered as a TSP problem with limited load.

According to the actual layout of the workshop, the following constraints are mainly considered in constructing the transportation network:

(1) Path constraint: the AGV has only one shortest path between the task points in the transportation process;

(2) Task constraint: the AGV shall finish all tasks;

(3) Capacity limitation constraint: The number of cloth rolls on the AGV must not exceed the upper limit (4 rolls).

The key questions are how to schedule the AGV reasonably according to tasks, and which scheduling rules can get the highest benefits. According to the practical situation, this paper considers scheduling the AGV according to the minimum loom waiting and AGV working times, and the model for multi-load AGV path planning is based on the lowest time.

3.   Mathematics model generation

3.1.   Topology diagram of the workshop

To facilitate the description of the problem, in this study, the cloth loading point is 0, the loom is $1, 2, \ldots, 98$, the task point number is $1, 2, \ldots, n$, and the set of task points for cloth loading is $R = \left\{ {1, ...i, ...j, ...n} \right\}$. Figure 2 shows the topological diagram of the weaving workshop.

(1) P00 represents the entrance and exit of the inspection workshop.

(2) The blue nodes (P1, P21, ...and P77) represent the task nodes (decision points). Each node in the path corresponds to the loading task of two looms, such as the AGV running to P22, which can execute the loading tasks of looms 16 and 23.

(3) The red nodes (P01, P02..., and P07) represent the turning nodes of the AGV when it enters the roadway.

3.2.   Model description

(1) The time of the occurrence of the loading tasks are known, and all are different.

(2) Starting from P00, the AGV will arrive at each task node that needs loaded cloth, and each task point will be visited only once. After loading 4 rolls of cloth, the AGV will return to P00 to unload, and then start the next task.

In actual production, if the AGV arrives at the cloth loading point later than the cloth loading time, it will cause the loom to weave fabric beyond the original length. Therefore, how to execute the task with a lower loom waiting time and a lower AGV working time to improve the machine utilization rate is the key problem.

3.3.   Parameters instructions

3.4.   Calculate $\mathop t\nolimits_{ij}$

The shortest path problem model is one of the most basic and core models in the optimal design of networks. The shortest path problem that satisfies all kinds of path weight constraints can be summed up as an NP-hard problem of multi-objective combinatorial optimization. In this paper, since the velocities of the AGVs in the main road, roadways and curves are different, the route with shortest distance between two points is not necessarily the route with the shortest time consumption. In order to make the AGV execute the task as quickly as possible, we need to find the shortest time consumption path between any two task points in the network.

In order to ensure the normal operation of AGVs, it is necessary to set the turning radius. The formula for the minimum outer circle turning radius is as follow:

The AGV wheelbase is $l$, the front suspension is $d$, the inner ring radius is $r$, and the width of the AGV is $b$.

There are many paths between task points in an intelligent weaving workshop. In this paper, we use the Warshall-Floyd ^[17] algorithm to find the shortest path between two task points.

The basic idea of the Warshall-Floyd algorithm is that for any vertex ${v_k} \in V$, the shortest path from vertex ${v_i}$ to vertex ${v_j}$ is passed or not passed by vertex ${v_k}$. Compare the value of the vertex ${d_{ij}}$ to the vertex ${d_{ik}} + {d_{kj}}$. If ${d_{ij}} > {d_{ik}} + {d_{kj}}$, then ${d_{ij}} = {d_{ik}} + {d_{kj}}$, keeping ${d_{ij}}$ as the shortest distance between the vertex ${v_i}$and the vertex ${v_j}$for the current search. Repeat this process, and finally, when all vertices ${v_k}$ are searched, the shortest distance from the vertex ${v_i}$ to the vertex ${v_j}$is obtained.

We construct an undirected weighted graph G = (V, E), where V is a set of vertices that consist of the intersecting points between the curves, the main road and the roadways in the weaving workshop and all the decision points of the layout in the roadway, and E is the side formed by the adjacent vertices that marks the length of each side. According to the following formula, the time that the AGV needs in order to travel on this side is calculated as the weight value of each side of graph G.

where ${S_c}$, ${S_r}$, and ${S_m}$, respectively, represent the curve distance, the roadway distance and the main road distance of the sides in Figure G.

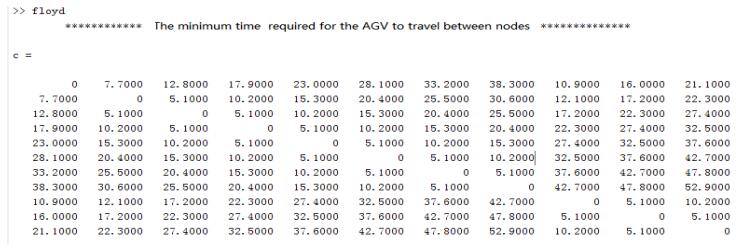
The Warshall-Floyd algorithm is used to calculate the shortest time for the AGV to travel between each two task points ${t_{ij}}$, and the matrix is expressed as follows:

${t_{ij}}$ represents the shortest time between two path points, where a subscript with 0 represents the time between P00 and the weaving task point.

3.5.   Mathematical model

3.5.1.   Task sequencing based on time priority

Each cloth loading task is generated based on the degree of urgency, which is usually determined by one or more characteristic parameters of the task. In the cloth loading task, the time of the task's occurrence, ${T_i}$, and the distance between the task point and P00, ${d_i}$, can reflect the task urgency, and so these 2 parameters are the bases for determining the priority of the task. To facilitate the comparison of the size of the emergency coefficient, we unify the units of the two characteristic parameters according to the relation between time and distance and convert ${d_i}$ to ${t_i}$. Thus, the task urgency coefficient is as follow:

where ${\omega _1}$and ${\omega _2}$ are the weights of the two parameters.

3.5.2.   Mathematical modeling

The set of task points is $R = \left\{ {0, 1, 2...i, j...n} \right\}$, and the 0-1 variable ${x_{ij}}$ indicates the existence of the path between the task point $i$ and the task point $j$. The definition of the variable is as follow:

The objective function of path planning is to calculate:

subject to the following:

where Eq 5 represents the time for the AGV to reach the task point $j$; Eq 6 represents the waiting time of the loom at task point $j$, which is non-negative; and Eqs 7 and 8 indicate that the AGV serves each task point only once.

4.   Proposed algorithm

4.1.   Algorithm process

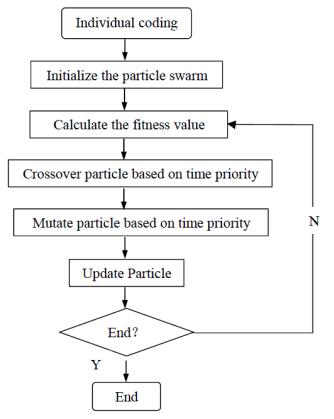
In the traditional GA-PSO algorithm, in order to improve the ability to get the optimal solutions by increasing the population diversity, we can randomly select the location of the cross-mutation of the particle. However, with the increase in population diversity, the convergence speed of the algorithm decelerates. Many scholars have conducted numerous studies ^{[18,19,20,21,22,23,24,25,26]} on how to improve the convergence speed and optimization ability of the algorithm. Moreover, there are some practical problems regarding the path planning of the multi-load AGV in an intelligent weaving workshop. For example, tasks with a higher urgency coefficient will be prioritized with higher probabilities. In a bid to solve this problem, this paper proposed the time-priority GA-PSO algorithm on the premise of preserving the mechanism of the cross-mutation, Introducing the task orderings based on time priority to guide the evolution of particles to a certain extent makes the evolution have a stronger directivity and improves the algorithm's convergence speed.

Step 1: Individual coding based on task ordering

Individual particle coding adopts the method of integer coding based on task ordering. Each particle represents the order in which the cloth loading vehicle performs the loading task. For example, the individual code is [8 7 6 4 3 9 5 1 2 12 11 10], indicating that the cloth loading vehicle executes the task successively with the priority of 8, 7, 6….

Step 2: Calculate the fitness value

The particle is a feasible solution for the planning scheme. The fitness value of the particle is expressed as the objective function's value. Since the cloth loading vehicle must return to the starting and ending point after loading 4 rolls, the actual walking plan of the loading vehicle needs to add the starting and ending points. If the individual code is [8 7 6 4 3 9 5 1 2 12 11 10], the actual walking route of the loading vehicle is [0 8 7 6 4 0 3 9 5 1 0 2 12 11 10 0]. The definition of the variable is as follow:

Step 3: Crossover operation

The crossover method adopts the integer crossover method, and the individual is updated by intersecting it with the extremum of the individual and the extremum of the group. The position of the crossover is selected according to the degree of deviation between the individual and the task sorting, and the two positions in the individual with the largest deviation from the task sorting are selected as the cross positions. New individuals are generated after the intersection and, if there is a duplicate position, replace the repeated task points with the task points not included in the individual.

Experiments show that under this crossover rule, the convergence effect of the first few iterations is obvious, but it is also easier to fall into the local optimum. To avoid the algorithm from prematurely converging, if the position with the highest priority deviation is less than the median of the priority, we randomly select the intersection position. The operation method is as follow:

To ensure that the individual after crossing can keep the strategy of the outstanding individual, the particle is updated only when the new particle's fitness value is better than the old one.

Step 4: Mutation operation

It uses the method of exchanging two positions within an individual. Select the two positions where one has a non-negative value with the maximum priority deviation and the other has a non-positive value with the maximum priority deviation as mutation positions and exchange the two mutation positions. The operation method is as follow:

Similarly, in order to ensure that a mutated individual retains the strategies of an excellent individual, the particle is updated only when the fitness of the new particle is better than the old particle. The algorithm flow chart is as follow:

5.   Experimental results

Taking 12 loading data in a certain period of time as an example, in the algorithm, we set the size of the particle swarm to 300 and the number of iterations to 200.

(1) Construct the adjacency matrix between the nodes according to the layout of the workshop. The turning radius of the AGV is 2.3 m. Considering the different speeds of the AGV in the main roads, the roadway and the curves, assign the weights to each side accordingly. The Floyd algorithm is used to find ${t_{ij}}$, which is the minimum time required for the AGV to travel between nodes. The calculation results are shown in Figure 4.

(2) By calculating the path node and root corresponding to the loading cloth loom and calculating ${T_i}$ according to the loading time, the emergency coefficient of each task can be calculated. The calculation results are shown in Table 1.

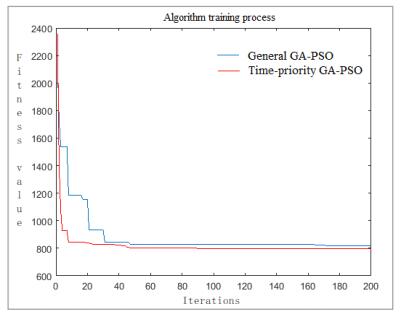
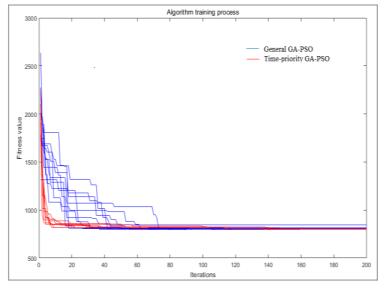
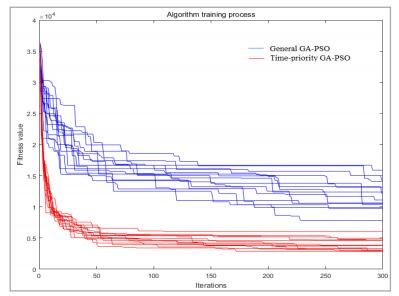
(3) Use the algorithmic logic proposed in this paper to calculate the order of the AGV to perform the loading task. The calculation result is shown in Figure 5. After comparing the GA-PSO algorithm for randomly selecting the crossover mutation position, the convergence effect is shown in Figure 6.The fitness value of the optimal solution after 10 runs of the algorithm is shown in Table 2, the overall operational result of the algorithm is shown in Table 3.

6.   Conclusion

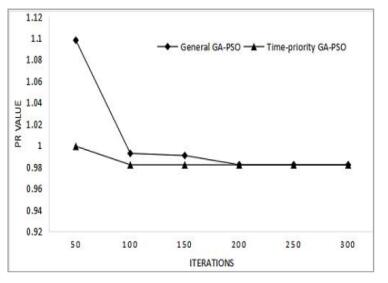
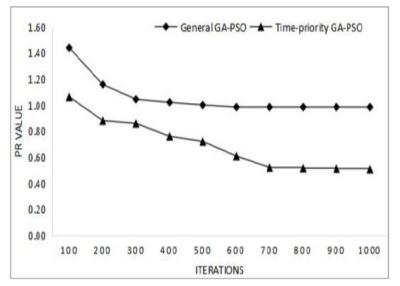
The planning of the multi-load AGV is an NP-hard problem. This paper proposes a task-sorting strategy based on the time priority with consideration of the timing of the task in the weaving workshop. In addition, it applies this strategy to guide the evolutionary direction of the particle in the GA-PSO algorithm to obtain a GA-PSO algorithm with faster convergence and a better search ability. Figure 7 and 8 are comparison of the algorithm results for 12 tasks and 40 tasks, Figure 9 and 10 are comparison of the iterations versus the values of PR for 12 tasks and 40 tasks, The value of PR is the number that the algorithm optimization results under the current iteration divided by the referenced optimal solution, the smaller the value of PR, the algorithm convergence and optimization ability better.The simulation results show that the GA-PSO algorithm proposed in this paper shows better convergence speed and optimization stability when dealing with a small number of tasks. When the number of tasks is large, it can find not only the approximate optimal solution with a faster convergence speed but also the GA-PSO algorithm with a better ability than random selection for cross-variation positioning. The proposed algorithm can be applied to the multi-load AGV path planning problem in a weaving workshop.

In addition, compared with the actual production situation, applying the planning method in this study can reduce the cloth failure rate of the workshop from 15% to 2.5%.

The correctness and feasibility of the multi-load AGV path planning method proposed in this paper is apparent. It ensures that the scheduling is carried out in an orderly manner while improving the utilization rate of the machines. This has important practical significance to reduce the costs of loading cloth, to improve the efficiency of loading cloth and to improve production efficiency.

Acknowledgments

This study was funded by Hubei provincial key laboratory of digital textile equipment, project number DTL2017010.

Conflict of interest

The authors declare no conflict of interest in this paper.