Modeling nutrient and disease dynamics in a plant-pathogen system

1.   Introduction

Industry, agriculture, transportation, and other human activities cause large amounts of nitrogen and phosphorus to enter terrestrial and aquatic systems ^[73,21,70]. In terrestrial plant systems, nutrient inputs can alter plant diversity and yield ^[18,12,37] as well as disease severity (i.e. the extent of symptoms on an individual) and prevalence (i.e. the frequency of infection in the population) ^[50,24,65]. One potential mechanism behind the relationship between nutrient supply and disease dynamics is the link between within-host pathogen populations and disease severity and prevalence ^[17,71]. For instance, high host carbon to phosphorus ratios (C:P) also have been shown to inhibit viral production of Paramecium bursaria Chlorella virus-1 (PBC-1) in the fresh water alga, Chlorella NC64A ^[19]. In a study by Mancio-Silva et al., Plasmodium blood-stage parasites were found to rearrange their transcriptome and adjust their multiplication rate when host dietary calorie alterations were changed ^[49]. Nutrient supply can alter the prevalence and competitive interactions among two viruses coinfecting plants ^[47]. Therefore, understanding how disease dynamics change with nitrogen and phosphorus enrichment is important because of the potential impact on crop yields and community diversity.

The increase in recent studies linking disease ecology and human alterations of nitrogen, carbon and phosphorus cycles have motivated the development of mathematical modeling approaches for studying within-host pathogen dynamics that incorporate nutrient effects ^[7,34]. For instance, mathematical models have suggested that phosphorus levels have implications for controlling cancer cell growth ^[46,31,45]. While within-host pathogen models have been used for decades mainly for assessing various disease severity pathways and the evolution of virulence, researchers have only recently started incorporating nutrient effects into mathematical models of within-host pathogen dynamics ^{[4,20,3,5,6,58]}. The models that have been developed that included nutrients and within-host pathogen dynamics yield useful insights for aquatic and human systems, so they are likely to be useful for terrestrial plant systems too.

1.1.   Background

Barley and cereal yellow dwarf virus (B/CYDV), a group of the Luteoviridae family, is a positive-sense single-stranded RNA virus ^[42]. B/CYDVs infect over 150 grass species and generally causes leaf discoloration, stunted growth and reduced seed production. Cereal yellow dwarf virus RPV is vectored by Rhopalosiphum padi (the "RP" in RPV) ^[23]. The virus is transmitted by feeding aphids in a persistent manner, that is, the virus must be first taken up by the aphid's stylet, then pass through the gut and the salivary glands before the aphid can infect another plant ^[2]. In addition, the virus is circulative, meaning it does not replicate while inside of the aphid ^[2].

After being injected by an infected aphid, RPV enters the phloem cells of its plant host, where it replicates. The virus moves relatively quickly through the plant host, infecting cells throughout the phloem in less than 24 hours ^[15]. The phloem cells in plants are used to transport sucrose throughout the plant ^[61] and help in spreading the virus. Phloem cells within grasses come in two general types: sieve tube elements (the cells that "transport" sucrose) and cells that support the sieve tube elements.

Since RPV infect sieve tube elements and ultimately damage or destroy them, they inhibit the movement of crucial resources and carbohydrates to the roots and leaves. The reduction of nutrients to these plant structures is the proposed mechanism by which RPV reduces the growth of its plant host ^[29].

Previous studies have examined the impact nitrogen and phosphorus have on viral loads and infection prevalence of Barley and Cereal Yellow Dwarf Viruses ^{[13,47,56,63,65,75]}. RPV has been shown to be subdued by higher levels of P ^[47], however there is no evidence that it is limited by N or P ^[11,48,65].

1.2.   Motivation

Several groups have used mathematical models to investigate plant virus dynamics. Spatiotemporal dynamics of plant virus infection was considered by work of Tromas et al. ^[72]. They used a type of "patch" model that considered the fraction of infected cells in each leaf of an infected plant host. They concluded that virus expansion between-cells is restricted, most likely due to the spatial structure of the host environment. Other researchers have employed delayed differential equations to model the time delay in post-transcriptional gene silencing (i.e. a plant defense against viruses) and the maturation time of the growing plant tissue ^[52]. While they did not parameterize the model, they did identify parameter regions associated with recovery and resistant plant phenotypes and possible chronic infections. In addition to modeling post-transcriptional gene silencing, Neofytou et al., introduced a new mathematical model to investigate the role of RNA silencing in a plant infected with two competing viruses ^[51].

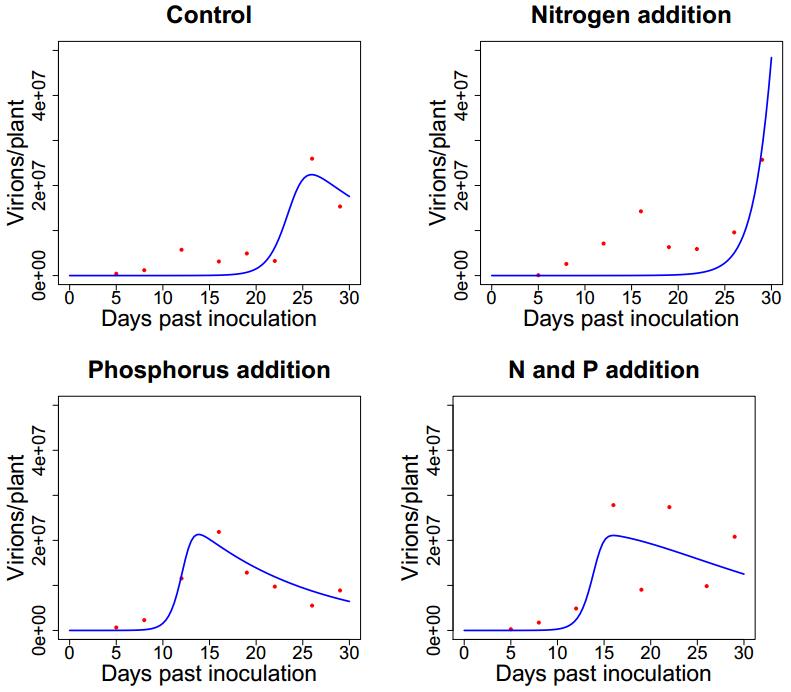
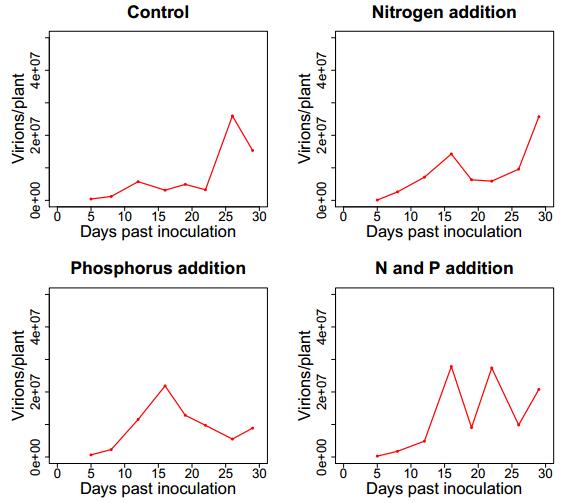
In an experiment by Kendig et al., individuals of Avena sativa (common oats) were inoculated with RPV ^[41]. Plants were randomly assigned to four different nutrient solution treatments to test the effects of nutrient concentration on virus dynamics within the plants. Plants were treated with a control solution (CTRL) that specifically was very low in N and P levels and was chosen because it has been shown to highly limit plant growth ^[64], a nitrogen addition solution (+N), a phosphorus addition solution (+P) and finally a treatment with both nitrogen and phosphorus addition (+NP), see Figure 1.

Figure 1 shows the change in virion population dynamics under different nutrient treatments. In the control treatment, the virion population remain low, until 18 days post inoculation when it grows quickly. Furthermore, the virion population in the control treatment is larger than all other treatments. In the nitrogen addition treatment, the virion population dips after 15 days, but ultimately increases over the 29-day timespan. The phosphorus addition treatment we also see this dip and a slight increase around 25-29 days after inoculation. Lastly, the data suggests that the virus population oscillates during the +NP treatment.

At the very basic level, the models typically used to study virus dynamics usually stem from modeling the susceptible cells, infected cells and free virus particles. Many of these models rely on constant or logistic growth of healthy cells and typically assume that an infected cell produces a fixed number of virus particles over its lifespan. A model that incorporates these concepts may take the simple form of:

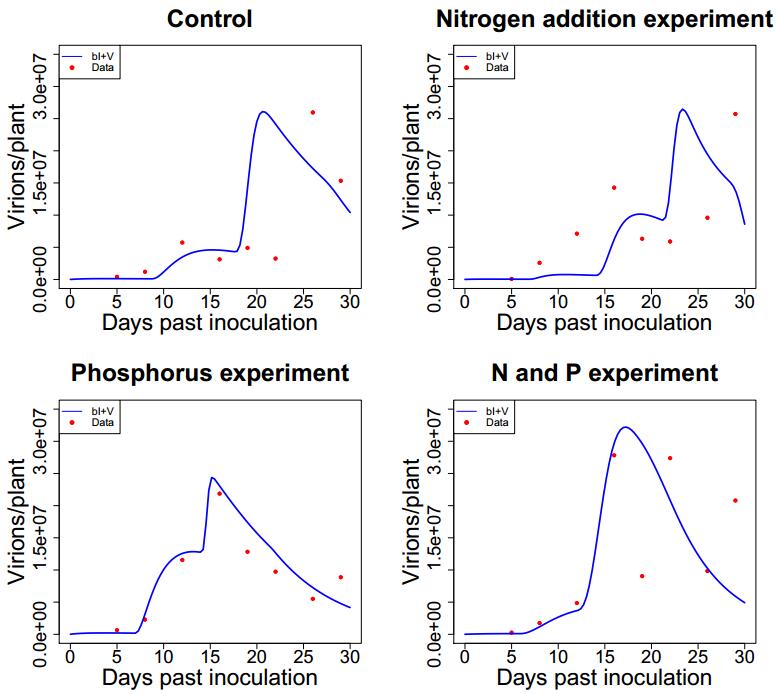
$S$ represents the number of susceptible cells, $I$ represents the number of infected cells and $V$ is the number of free virus particles. Susceptible cells are produced by a logistic growth term and die at constant rate $m$. Infected cells release $b$ virus particles continuously throughout their lifespan and die at rate $\delta$. Smith et al., simplified the logistic term to depend only on $S$. This simplification allowed them to fully analyze the global dynamics of the model ^[67]. Figure 2 illustrates the best fit solution to the data of Kendig et al. We fitted $bI+V$ since this represents the total virion population. This simple model can fit reasonably well to the majority of the cases, but cannot reproduce the early dynamics seen in the CTRL and +N treatments between days 5-20. In addition, the model does not accurately reproduce the dynamics of the +NP treatment between 15-30 days past inoculation.

Like parasites, viruses use resources from their host cells to reproduce. In addition, the regulation of proteins and viral nucleic acids by host cell growth rate have been observed ^[10,35]. Although, the precise mechanisms and relationships between host growth rate and virus replication are not fully understood, multiple studies have been published that observed sensitivity between host growth rate and virus replication rates ^{[14,16,53,54,77]}.

A shortcoming to this model formulation is that production of healthy susceptible cells is described by the logistic term and this growth rate does not rely on any type of nutrient or resource from the environment from which the plant is rooted in. Moreover, the above model and the formulation by Smith et al., do not relate the production of virus particles as a function of those same nutrients that are taken up by their host cell ^[67]. We argue that a more robust and biologically grounded model can be formulated by including nutrient limited growth into the dynamics of healthy cell growth and virus production.

Another way of modeling a more realistic form of virion production implicitly is to include a delay for the time it takes for virions to be manufactured inside the host cell. Specifically, the delay in virion production is caused by nutrient conditions. This would do away with the need to include a dynamically changing nutrient variable in the model while still capturing effects of nutrient limitation that would occur inside the infected cell.

Motivated by the changes in virion population under different nutrient supply rates compared to the control conditions, we (1) derive a within-host pathogen model where growth of the virus population is dependent on the resource nutrient concentration taken up by the plant; and we (2) test the hypothesis that the temporal change in virus titer within plant hosts in response to differing nutrient supply ratios can be explained by a delay in virus reproduction. In this article, we model within-host interactions of RPV from an experiment by Kendig et al ^[41].

2.   Model 1: Nutrient growth model

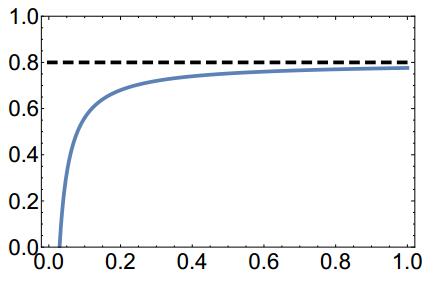
Since virions can only replicate within a host's cell, it is important to accurately describe the amount of nutrient in the host's cells. Nutrient-controlled growth rates can be employed via the Droop cell model ^[25,26,27]. Droop showed that there existed an empirical relationship between algal specific growth rate and the intracellular concentration of vitamin B$_{12}$ inside the chemostat in which algae were being grown. Droop defined the cell quota, $Q$, as the total cell nutrient per unit biomass. He discovered a simple relationship between specific growth rate $(\mu)$ and the cell quota:

where the subsistence quota, $q$, is interpreted as the minimum $Q$ required for life and $\mu_{m}$ is the maximum specific growth rate. Figure 3 is an illustration of Droop's cell quota equation (equation 2.1).

Recently, the Droop equation has been applied to model dynamics of cancer growth ^[31,32,55] and has been used to derive the logistic equation ^[44]. It should be noted that nutrient growth functions for plants have also been developed by Ågren ^[1]. These growth functions, although specifically developed for plants, rely on a minimum function that makes mathematical analysis slightly challenging, but not impossible. For our analysis here, we use the Droop equation for its simplicity. However, it should be noted that Ågren's growth model has been shown to be mathematically equivalent to Droop's, but with slightly different interpretations ^[28].

To generalize to $n$ nutrients, one could use Liebig's law of the minimum: an organism's growth will be limited by the resource that is in lowest supply with respect to the organism's needs:

Let $S$ and $I$ be the number of susceptible and infected cells respectively and $V$ be the number of free virions. Since virus particles that cause cereal yellow dwarf disease are restricted to the phloem of host plants we let $S$ represent a typical phloem cell. Consider the following model derivation with nutrient limited virus and cell growth.

2.1.   Healthy phloem cells and nutrient uptake

We assume that in the absence of infection, the susceptible cells obey nutrient limited growth via the Droop equation ^[25,26,27]. That is, let $N_S$ and $N_f$ be the nutrient in the plant's cells and the free nutrient respectively, then the total amount of nutrient in the (closed) system is $N_t = N_S+N_f$. By free nutrient, we mean nutrient that is inside the plant that is available to the phloem cells, but not actually inside them. Let $Q = Q(t)$ be the plant's cell nutrient quota. With this, we may write down a governing equation for $S$,

where the maximum specific growth rate is $\mu_m$ and we have included a natural death rate, $m$, of the cells.

To formulate a governing equation for $Q$, we let the rate of change of free nutrient, $N_f$, change according to

where the first term approximates the loss of free nutrient by the uptake by cells, and the second term represents the nutrient that is released back into the intra-plant environment when cells die. Since $N_S = QS$ we obtain $N_t = N_f+QS$. Solving for $Q$ and differentiating with respect to $t$ and using the fact that $\frac{dN_f}{dt} = -\alpha S N_f+mSQ$, we obtain

Therefore, we arrive at a simple model for nutrient cell growth in the absence of infection,

Under the assumption that all parameters are positive, Everett showed this model exhibits a unique positive steady state that is globally asymptotically stable ^[30].

2.2.   Infected phloem cells

We assume that infection of healthy phloem cells is governed by mass action and that infected cells die upon production of virus particles. With these assumptions the governing equation for the rate of change of infected phloem cells is

Due to the introduction of infected cells and virus particles, we include the cell quota contained within infected cells and virus particle, $I\left(Q+\theta\right)$ and $\theta$, respectively, in the equation for total nutrient,

Where we have assumed that the infected cell population has their growth mechanism hijacked by the virus and the amount of nutrient contained within a virus particle is equal to $\theta$.

2.3.   Free virions

Our modeling approach as of now has been similar to work by Fuhrman et al., but we now diverge from their work by incorporating nutrient dependent virus growth ^[34].

Virions are relatively homeostatic and must process nutrients within the host to replicate. Furthermore, virions are simple in structure (a genome and protein capsid) and elemental composition. Thus we make the assumption that the cell nutrient inside of a virus particle is constant for all time and is equal to $\theta$.

One way to model the growth function of the virion population is to simply assume that it also behaves like the Droop equation. That is

where $q_v$ is the minimum amount of nutrient needed for virion production. In the case when $Q<q_v$, we assume that there is not enough nutrient for virus production and is therefore $0$, which ultimately amounts to introducing the maximum function. In short, this function relates the growth rate of the virus ($b(Q)$) to the nutrient concentration inside the cells of the host plant ($Q$).

Free virions are produced at a maximum rate, $b_m$, per infected phloem cell per unit of time and are destroyed or cleared by the immune system at rate $d$. Free virions that are not destroyed or cleared are assumed to be absorbed by neighboring susceptible phloem cells.

2.4.   Free nutrient equation

With the added infected cell and virus populations we obtain an updated equation that governs the free nutrient within the system, equation (2.4). As we did before, to find an updated governing equation for $Q$, we let the change of free nutrient change according to

where the first term is the loss of free nutrient due to cell uptake, the second and fourth are from the release of nutrient due to healthy cell death and virus death and the third term represents nutrient that is released when infected cells die, where,

$\hat{Q}$ is interpreted as the remaining nutrient from an infected cell after virus release that has not been taken up by the virus particles ^[34].

2.5.   Full model

The full model with nutrient dependent virus growth is summarized below:

where $b\left(Q\right) = b_m\max\{\left(1-\frac{q_v}{Q}\right), 0\}$. If we assume $b(Q) = b_m$ we obtain the model by Fuhrman et al., who have studied this system fully ^[34].

The assumption that the nutrient is constant allows this model to be reduced to 4 equations. Indeed, to see this conservation law note that total nutrient is $N_t = N_f(t)+S(t)Q(t)+I(t)(Q(t)+\theta)+\theta V(t)$ and therefore,

Canceling like terms, this reduces to

and allows us to reduce the model to a system of 4 equations.

We would like to note that to keep our modeling approach simple, we have decided not to model explicitly the virus population within the infected cell population. We assume that in each infected cell there are $b(Q)$ virus particles and therefore the total virus population is $b(Q)I+V$. In addition, the nutrient model assumes that there is only one nutrient limiting the growth of the plant and virus, and that this nutrient is the same for both.

2.6.   Basic analysis of the nutrient model

Due to the different time scales between nutrient absorption, cell reproduction and virion reproduction, we apply the quasi steady state argument to $Q$ and obtain the following system,

Equations 2.6a-2.6d yield two biologically relevant equilibria: $E_1 = \left(S_1, 0, 0, Q_1\right)$ and $E_2 = \left(S_2, I_2, V_2, Q_2\right)$. We call these the disease free and endemic equilibria respectively. We find that

In the case of the endemic equilibrium, solving for $Q_2$ is mathematically challenging, if not impossible. In the case of the disease free equilibrium, we find that it is mathematically tractable. Below we assume that $\mu_m>m$ and $\alpha N_t\mu_m - \alpha N_t m > \mu_m m$. This ensures that $S_1>0$ and $Q_1>0$.

2.7.   The virus reproduction number

To derive the virus reproduction number, $R_0$, we first observe that at the disease-free steady state, the average number of virions produced per individual per timestep is $\beta \delta b(Q_1)$ and the average lifetime of a virion is $\frac{1}{\delta(d+\beta S_1)}$. Multiplying these together yield the basic reproduction number for the model:

where, $S_1$ is the size of the phloem cell population at steady state. Note that by modeling the production of virus particles as a function of $Q$, we find that $R_0$ depends on $Q = Q_1$, where $Q_1$ is the cell quota at the disease free equilibrium.

proposition 1. The disease free equilibrium of system 2.6, $E_1$, is locally asymptotically stable if and only if $R_0<1$. If $R_0>1$, then $E_1$ is unstable.

Proof. The jacobian matrix at $E_1$ is,

The eigenvalues are $a_{11} = -\frac{S_1q\mu_m\left(N_t\alpha +q\mu_m\right)}{\alpha N_t^2} (<0)$ and the resulting eigenvalues from the $2\times2$ matrix,

We find that the trace and determinant are

Therefore the two eigenvalues of $J$ are negative if and only if $R_0<1$. Furthermore, if $R_0>1$ then $E_1$ is unstable.

3.   Virion production delay model

The second model, which we'll call the delay model, is an adapted version of the model found in ^[8], but standard incidence is used in place of mass action to describe infection of susceptible cells. We develop a mathematical model that incorporates a delay in virus production. This leads naturally to a system of delay differential equations.

As in the previous model, let $S$ and $I$ be the number of susceptible and infected cells respectively and $V$ be the number of virions. Consider the following model derivation with a delayed virus production.

3.1.   Healthy phloem cells

We assume that in the absence of infection, the susceptible cells obey logistic growth with carrying capacity $K$. Furthermore, we assume a maximum per-capita proliferation rate $\mu$ and a constant per-capita death rate $m$:

3.2.   Rate of infection

We employ a standard incidence rate of infection:

where $N(t) = S(t)+I(t)$ and $\beta$ can be interpreted as the maximum rate at which virions infect healthy phloem cells or the probability that a single virion infects a healthy phloem cell.

3.2.1.   Infected phloem cells

We assume the virus is produced with a time delay $\tau$, where we interpret that each infected phloem cell on average produces $b$ viruses in its lifetime with average life expectancy $\frac{1}{\delta}$ after infection of $\tau$ days.

At any time $t$, the density of the infected plant cells, $I(t)$, is obtained by integrating

for $u\geq 0$. Here $\frac{\beta S(t-u)V(t-u)}{S(t-u)+I(t-u)}$, represents the rate of infection at previous times, and $e^{-\delta u}$ represents the probability of a cell surviving the infection from $t-u$ to $t$ with natural mortality rate $\delta$. Finally, we note that for any time, $t$, we do not integrate past $-\tau$, because these virions have already been released and left the $I$ class. With these observations we obtain a governing equation for $I(t)$:

With a change of variables $s = t-u$ we obtain:

and differentiating with respect to $t$ yields

We note that equation 3.2 can also be derived from the Mckendrick-von Foerster age-structured model ^[36].

3.3.   Free virions

Free virions are produced at rate $b$ per infected phloem cell per unit of time and are destroyed or cleared by the (innate) immune system at rate $d$. Free virions that are not destroyed or cleared are absorbed by neighboring phloem cells. With these observations we obtain the governing equation for $V,$

3.4.   Full model

With the above considerations we obtain the following delayed virus production compartmental model,

For simplicity and parameter estimation purposes we rewrite the equation for $S$ as

where $\hat{r} = r-m$ and $\hat{K} = K\frac{\hat{r}}{r}$.

Initial data for the system takes the form of

where

3.5.   The basic reproduction number

To derive $\tilde{R}_0$ we first observe that at the average number of virions produced per infected cell per timestep is $\beta b e^{-\delta \tau}$ and the average lifetime of a virion is $\frac{1}{d+\beta}$. Multiplying these together yield the basic reproduction number for the model:

3.6.   Basic analysis of the delay model

When modeling populations, it is important that the model makes biological sense. In particular, populations should never become negative and also be bounded above by some finite number. We show below that solutions of system (3.3) with nonnegative initial conditions remain nonnegative and bounded (and hence exists for all time) for all $t>0.$

proposition 2. Each component of system (3.3), subject to initial conditions (3.5), remains nonnegative and bounded for all $t>0$.

Proof. Observe that system (3.3) is locally Lipschitz at $t = 0$. Hence the solution of system (3.3), subject to initial conditions (3.5), exists and is unique on $[0, c)$ for some $c>0$. Furthermore, if $S(0) = 0$, then $S(t)\equiv0$ for all $t>0$. Therefore we may assume that $S(0)>0$. In a similar fashion, if $V(0) = 0$, then $V(t)\equiv0$ for all $t>0$. Therefore we may also assume that $V(0)>0$.

To see that $S+I$ is bounded, observe that,

This implies that

and integrating yields

Therefore, if $S(0)+I(0)<\hat{K}$, then $S(t)+I(t)<\hat{K}$ for all $t>0$.

Case 1: By way of contradiction we assume that there exists $t_1\in(0, c)$ such that $S(t_1) = 0$ and $S(t)>0$, $I(t)>0$ and $V(t)>0$ for $t\in(0, t_1)$. Observe that for $t\in[0, t_1]$,

Where $\alpha = \max_{t\in[0, t_1]}\left\{\frac{\beta V}{S+I}\right\}$ and integrating yields,

which is a contradiction when $t = t_1$. Therefore $S(t)>0$ for $t\in[0, c)$.

Case 2: Assume that there exists a $t_1\in(0, c)$ such that $V(t_1) = 0$, $I(t)>0$ and $S(t)>0$, $I(t)>0$ for $t\in(0, t_1)$. Therefore, for $t\in[0, t_1]$,

where $\alpha_1 = \max_{t\in[0, t_1]}\left\{d + \frac{\beta S}{S+I}\right\}$. This implies,

which yields a contradiction for $t = t_1$. Therefore $V(t)>0$ for $t\in[0, c)$.

Case 3: Assume that there exists a $t_1\in(0, c)$ such that $I(t_1) = 0$ and that $S(t)>0$, $I(t)>0$ $V(t)>0$ for $t\in (0, t_1)$. Since $I(t) = \int_{t-\tau}^{t} \frac{\beta S(s) V(s)e^{\delta(s-t)}}{S(s)+I(s)}ds$, we have

a contradiction. Therefore $I(t)>0$ for $t\in[0, c)$.

Finally we prove a rather large bound for the entire system. Consider $W = S+I+\frac{1}{bV}$. Then differentiating yields,

Integrating finally yields

Therefore

where $\alpha_2 = \min\left\{\delta, d, \hat{r}\right\}.$ Thus we may conclude that all state variables are bounded.

The above contradictions together show that components of the solution of system (3.3), subject to initial data (3.5), are nonnegative for all $t\in[0, c)$. This together with the uniform boundedness of $W = S+I+\frac{1}{b}V$ imply that $c = \infty$. This completes the proof of the proposition.

There exists two biologically relevant steady states: $\tilde{E}_0 = \left(\hat{K}, 0, 0\right)$ and $\tilde{E}^* = \left(\tilde{S}^{*}, \tilde{I}^{*}, \tilde{V}^{*}\right)$ where,

and $R^{*} = \frac{e^{\delta \tau}\left(\beta \delta +d\left(\hat{r}+\delta\right)\right)}{d\hat{r}+b\beta\delta}$. $\tilde{E}_0$ represents a healthy plant and is called the disease free steady state. $\tilde{E}^{*}$ is the called the endemic equilibrium and represents chronic infection of the plant by the virus.

Turning our attention to the endemic equilibrium, it's easy to see that it exists exactly when the following conditions hold:

We focus on the stability of the biologically relevant equilibria. With this in mind we compute the characteristic polynomial,

The matrices $P$ and $Q$ are given by,

and

At $\tilde{E}_0$ the characteristic equation is

where the roots are $\lambda_1 = -\hat{r}$, $\lambda_2 = -\delta$ and $\lambda_3$ satisfies $\lambda_3 = b\beta e^{-(\lambda_3+\delta)\tau}-(d+\beta)$. Setting $\lambda_3 = 0$ and rearranging this we obtain,

the basic reproduction number for the standard incidence model. This further confirms our definition of the basic reproduction number since it determines the stability of the disease free steady state.

proposition 3. $\tilde{E}_0$ is asymptotically stable if $\tilde{R_0}<1$.

Proof. For $\tilde{E}_0$ to exists, $\tilde{S}^*>0$ and therefore $\hat{K}>0$. By the above discussion the roots of the characteristic polynomial are given by $\lambda_1 = -\hat{r}$, $\lambda_2 = -\delta$ and $\lambda = b\beta e^{-(\lambda+\delta)\tau}-(d+\beta)$. Hence, the first two roots have negative real part. Thus the stability of the disease free equilibrium depends on the roots of,

We prove that $g(\lambda)$ cannot have a root with nonnegative real part when $\tilde{R_0}<1$. By way of contradiction, assume $\tilde{R_0}<1$, but there does exist a root with nonnegative real part, $\lambda = x+iy$ where $x\geq0$ and $x, y\in\mathbb{R}$. Setting $g(\lambda) = 0$ yields $\lambda = b\beta e^{-\delta}e^{-\lambda\tau}-(d+\beta)$ and substituting $\lambda = x+iy$ we obtain,

Equating real parts yields,

a contradiction. Thus, any root of $g(\lambda)$ must have negative real part.

proposition 4. $\tilde{E}_0$ is unstable if $\tilde{R_0}>1$.

Proof. As in the previous proof, for $\tilde{E}_0$ to exist, $\tilde{S}^*>0$ and therefore $\hat{K}>0$. Furthermore, stability depends on,

Assume $\tilde{R_0}>1$, then $g(0) = d+\beta -b\beta e^{\delta\tau}<0$. Furthermore, for $\lambda\geq0$ we have

Finally, $\lim\limits_{\lambda\rightarrow\infty}g(\lambda) = \infty$. Since $g(\lambda)$ is a continuous function that is negative at $\lambda = 0$ and increases to $+\infty$ as $\lambda\rightarrow+\infty$, it must cross the $\lambda$-axis. This proves the existence of a positive real root. Therefore, the disease free steady state is unstable.

It is notable to mention that there are other ways to prove the stability of the disease free steady state. Indeed, exercise $4.9$ from ^[66] or theorem 3.1 from ^[9] along with theorem 1.4 from ^[43] are other ways to prove the theorems. We decided to include the proofs that we did, because of their simple and intuitive arguments.

4.   Numerical work

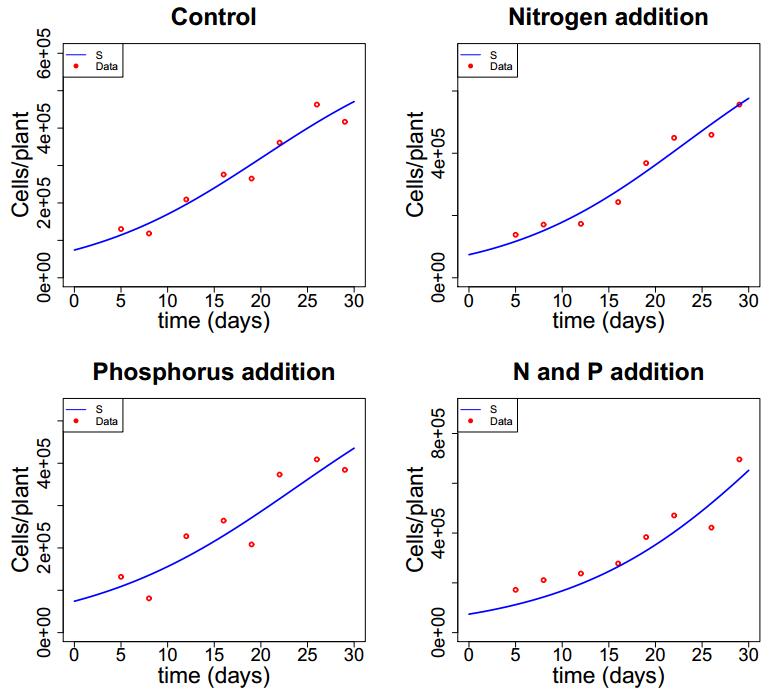
We fit our mathematical models to the virion data from the four different treatments in the experiment carried out by Kendig et al. We use shoot mass from healthy plants that were grown under CTRL, +N, +P and +NP and convert this mass into numbers of healthy cells under the assumption that there are roughly $10^9$ plant cells for 1 gram of plant tissue ^[74]. Initial conditions were set to $S_0 = 74157.7$; $I_0 = 30$; $V_0 = 2000$ for both models and $Q_0 = 0.13$.

4.1.   Nutrient model

Parameter estimations and data fitting were conducted in two rounds. The first round of parameter estimations used healthy plant data and the disease-free model of the nutrient model (equations 2.3a-2.3b). We used nonlinear least squares (implemented with R version 3.3.2 using the FME package ^[57,69]) with susceptible cell data to estimate parameters $\mu$, $m$, $\alpha$, $q$ and initial conditions $S(0)$ and $Q(0)$. These parameter estimations were then fixed when fitting the complete model (system 2.5) in the second round, except for $Q(0)$ which was refitted in the second round. This was done for all four nutrient treatments. Despite differences in nutrient supply rates across the experimental treatments, we used the same value of $N_t$ for all datasets. Therefore, differences in plant and virus growth due to the experimental treatments are reflected in various parameter estimates.

The second round was conducted by fitting $b(Q)I+V$ to virion data to generate parameter estimations for $\beta$, $q_v$, $m$, $d$ $b_m$ and $Q(0)$. $\delta$ was held constant at $1/13$ day$^{-1}$ as estimated in ^[33] for a virus similar to CYDV-RPV. As discussed above, during this second round of parameter estimations, we fixed the previous estimations of $\mu$, $m$, $\alpha$ $q$, $S(0)$. In both rounds, best fit parameters were obtained by minimizing the following error function:

The $i^{th}$ virion observation is given by $\bar{V_i}$ and the analogous value given by our model is $b(Q_i)I_i+V_i$. We use $b(Q_i)I_i+V_i$ because $\bar{V_i}$ represents all virions (inside infected cells and free). $N$ is the number of data points.

Model fittings are presented in Figure 5 and fitted parameters can be found in Table 1. Model fittings are quite similar to what is seen with the typical SIV model, but the nutrient model allows us to investigate how dynamics change with respect to physiological and environmental parameters.

4.1.1.   The reproduction number

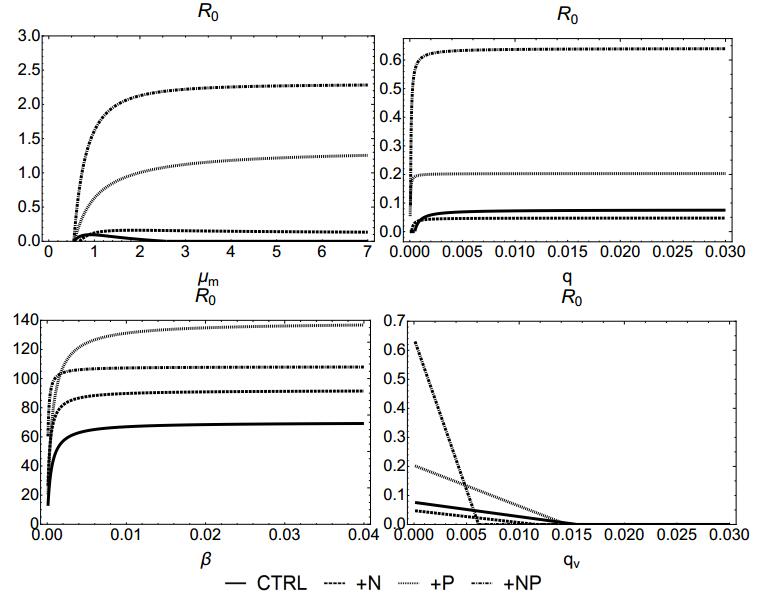
The reproduction number for the nutrient model allows us to gather deeper insight into what mechanisms increase its value. Using the computer software program, 38 version 11.1 ^[38], we numerically explored the reproduction number using the calibrated parameters from Table 1 in Figure 6. The explicit reproduction number is:

Results show that $R_0$ is sensitive to physiological attributes of the host and the virus. Assuming all other parameters are held constant, the reproduction number increases with infection rate, $\beta$. In addition, $R_0$ also increases with the minimal cell quota for the host, $q$. Intuitively, if a higher minimal cell quota is needed to sustain host growth, then this would also increase the amount of resources available to the virus and thus increase its replication rate. In contrast, $R_0$ decreases with respect to the virus's minimal cell quota, $q_v$. This makes good sense, since requiring more resources for minimal growth of the virus would decrease the number of viruses being produced. Lastly, the reproduction number is an increasing function of $\mu_m$ except for the +CTRL treatment. One might expect that increasing growth rate would allow for more susceptible cells to become infected, and hence increase the reproduction number. However, the model also predicts that a high enough growth rate can overcome the infection (+CTRL treatment).

4.2.   Delay model

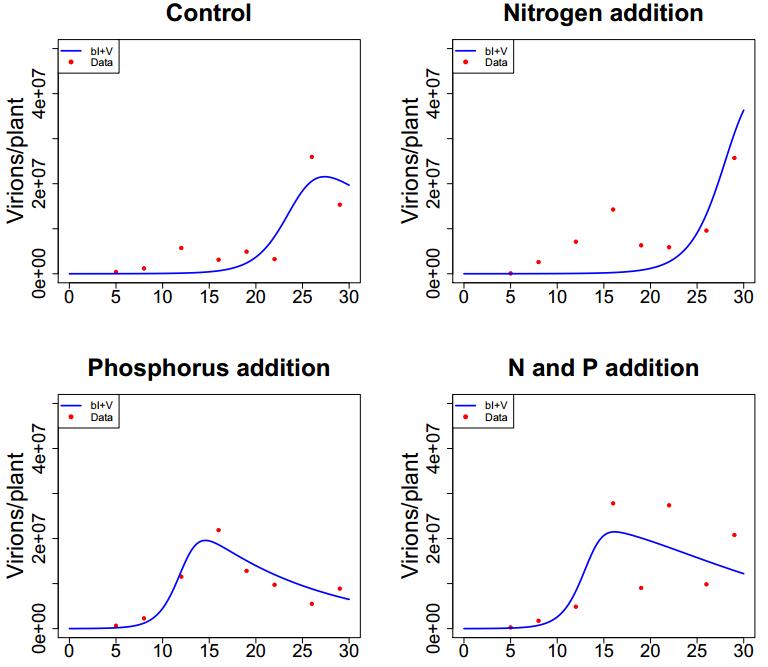
As with the nutrient model, $\hat{r}$, $S(0)$ and $\hat{K}$ were estimated using equation 3.1 and fitting it to healthy plant cell data. These parameters were then used as the initial values when fitting the full model to the virion data. Our decision not to keep $\hat{r}$ and $\hat{K}$ fixed but used as the initial starting values was to allow for stochastic changes that can occur to the plant parameters when the virus is introduced. We did not do this in the nutrient model since the limiting nutrient ($Q(t))$) should change, not $\mu_m$, $q$ $\alpha$ and $m$. For example, when the virus is introduced into the nutrient model, the specific growth rate changes due to the now lower $Q(t)$ (from virion uptake), not the maximum specific growth rate, $\mu_m$. The method of nonlinear least squares was use again with an analogous error function as Equation 4.1. We present model fits to virion data in Figure 7 and fitted parameters in Table 2.

Table 3 and 4 compares the SIV (system 2.5), nutrient (system 2.5) and delay model (system 3.3) using the mean square error and mean absolute percentage error (MAPE). The SIV model outperformed the other two models in the CTRL treatment, but was slightly surpassed in the +P and +NP treatments when comparing the MAPE values.

5.   Discussion

In this article we formulated two mathematical models to investigate the virion dynamics of a plant virus under different nutrient regimens. Both models were motivated and guided by the nature of the data and research with this system. Our first model was motivated by the hypothesis that nutrient conditions inside the infected cells controlled the virion production. With this in mind, we designed a mathematical model that was based off Fuhrman et al., that related virus production to nutrient concentration in its host cells ^[34]. By assuming that virus production can be approximated by the Droop equation (equation 2.1), we were able to capture the general dynamics of the virion data. Although the nutrient model and SIV model returned relatively similar model fiitings, the nutrient model gave us deeper insight into the behavior of the reproduction number. Indeed, the nutrient model captured physiological and environmental aspects of the reproduction number that cannot be captured by the SIV model.

Our second modeling approach was designed to investigate the plausibility that the different nutrient treatments delayed the virion production in response to altered supply ratios within infected cells. Model fits for the control, nitrogen addition and phosphorus addition experiments suggest that delayed virus production in response to changes in elemental supply ratios is a plausible mechanism for explaining the dynamics seen in the virion data. The best fit solutions from our models uncover patterns that otherwise would be hard to detect when viewing the data by itself, see Figure 7. Moreover, this modeling approach results in at least two new questions: what mechanisms are capable of delaying virus production in response to altered nutrient supply and what roles do phosphorus and nitrogen play in these mechanisms?

The delay model suggests that virion production delay is another reasonable mechanism for explaining the results from 3 of 4 experimental treatments (CTRL, +N and +P), see Figure 7 and Table 2. Since virion estimations from the experiment were taken from leaf tissue samples, virus particles that move to the roots to replicate and then return to the leaves ^[33] could explain the bumps in the data. Another mechanism for describing the data could be that the nutrient treatments are changing the host's innate immune system ^[39]. RNA silencing is one such defense a plant has against infectious particles and perhaps this mechanism is eventually overcome by viral silencing suppressors ^[22], allowing the virus population to increase as best seen in the data and model fittings from Figure 7. In the +NP treatment, the delay model yields unsatisfactory results and does not capture the oscillatory nature of the data. However, it is well known that delay models usually are prone to oscillatory dynamics because of their very nature ^[43,66]. Further analysis of the delay model should be directed towards locating parameter regions where oscillatory behavior might manifest. Interestingly, the time delay, $\tau$, decreased as the nitrogen and/or phosphorus supply was elevated. Indeed, environmental nutrient supply has been linked to indirectly manipulating virus growth ^[48] and our modeling exercise may give one such viable way of how nutrients manipulate that growth. Ultimately, since some of the data points were collected after a nutrient addition, it is plausible that the patterns in the data could have resulted from the increased supply of nutrient.

Since the nutrient model is based on nutrient limited growth mechanisms, we should not be surprised that its virus reproduction number is as well. In a study by Smith et al., the reproduction number of an SIV model was explored in the context of resource content and physiological state of infected hosts, but did not explicitly model nutrient dynamics ^[68]. The nutrient model allows for a deeper understanding of what and how environmental and physiological attributes change the reproduction number. To our knowledge, this is the first time a reproduction number has been derived within a nutrient-explicit disease model. Thus, with the increasing interest in the relationship between nutrition and infection, this approach can serve as a framework to further develop this field.

The error metrics from Tables 1 and 2 show slight discrepancies between model fits, but the delay model does have a higher MAPE value for the CTRL treatment (almost double than the other models). Qualitatively, we see vastly different dynamics. The delay equation captures the earlier (approximately 0-15 days past inoculation) virion population levels much better than the other two models. However, the delay model fails to predict the behavior near the end of the experiment during the +N and +NP treatments.

Although we did parameterize the model to the best of our abilities, there is much work to be done. Neither of our modeling approaches explicitly model the virus particles within each infected cell, and instead we assume that there are $b(Q)$ viruses per infected cell. This was done, due to the lack of data and the need for first iteration models. Future model iterations should incorporate both free and intracellular virus particles to capture deeper insight into nutrient and pathogen dynamics. In addition, the nutrient model assumes that both the plant and virus are limited by the same nutrient. In the future, this simplifying assumption can be built upon by incorporating multiple nutrients using Liebig's law of the minimum (equation 2.2). Another future direction would be to consider a specific limiting nutrient supplied. When considering a specific nutrient, parameter values can be more accurately specified and the model more constrained.

Parameter identifiability and sensitivity analysis could guide the direction for future model iterations, experiment design and further investigation of the reproduction number (equation 4.2). Indeed, preliminary investigations using local sensitivity analysis showed that the virus population is not sensitive to $\alpha$ with the associated fitted parameters. Sensitivity analysis could be implemented by various methods such as the Morris and Sobol' methods, Latin hypercube sampling-partial rank correlation coefficient and the sensitivity heat map method ^[76], while parameter identifiability could be implemented by the Differential Algebra Identifiability of Systems (DASIY) and other such methods discussed in ^{[62,40,60,59]}.

Acknowledgments

This paper is dedicated to the memory of our dear friend and colleague, Professor Val H. Smith, who passed away on April 2, 2016. Val is a pioneer of resource ratio theory and ecological stoichiometry. We would also like to thank Eric Seabloom, Melissa Rudeen, Christelle Lacroix, Tashina Picard, Emily Boak, and multiple undergraduate researchers at UMN for their contributions to experimental design and procedures. The research of Yang Kuang is partially supported by NSF grant DMS-1615879.

Conflict of interest

The authors declare there is no conflict of interest.