DAFNet: A dual attention-guided fuzzy network for cardiac MRI segmentation

1.   Introduction

Cardiac and vascular disease (CVD) poses a significant threat to human life with high rates of morbidity and mortality. According to the World Health Organization (WHO) statistics, there are over 500 million global cases of CVD, resulting in approximately 17.9 million deaths annually, making it the leading cause of mortality worldwide ^[1]. Current clinical diagnosis methods for CVD include the ultrasound (US), computed tomography (CT), and magnetic resonance imaging (MRI). The MRI has become a crucial tool for physicians due to its ability to capture characteristics of original 3D cross-sectional medical images without reconstruction ^[2]. However, in clinical practice, the manual identification of cardiac regions on MRI images introduces a risk of high subjective variation and poor reproducibility. Therefore, there is a pressing need for accurate, rapid, and batch cardiac segmentation methods, which hold widespread application and significant research importance for physicians in diagnosing cardiovascular diseases ^[3].

While traditional image processing methods yield satisfactory results for cardiac segmentation in clear images ^[4,5], they exhibit limitations when confronted with the multi-temporal, multi-modal and low-quality images. These shortcomings hinder their performance and fail to assist doctors effectively in achieving accurate diagnostic outcomes. Additionally, these methods require physician involvement, leading to a potential waste of medical resources and inefficiencies in disease diagnosis.

Recent advances in artificial intelligence technology have enabled scholars to apply deep learning to segmentation and detection tasks in medical images. Tran et al. ^[6] were among the pioneers to utilize the fully convolutional network (FCN ^[7]) for medical images segmentation, demonstrating that deep learning methods outperform traditional segmentation methods in terms of accuracy and speed. Khened et al. ^[8] introduced a long-skip and short-cut connection structure, which is efficient. However, medical images are characterized by sparse samples, low information density, and simple semantic content compared to the natural scene images, leading to overfitting problems when solely relying on FCN for cardiac segmentation. This limitation prevents network from obtaining more accurate performance. Ronneberger et al. ^[9] addressed this challenge by introducing a U-shaped structure known as U-Net. However, the simplicity of U-Net structure compromises its performance in extracting object features, as illustrated in Figure 1. Subsequent research has witnessed scholars enhancing and integrating U-Net, striving for performance improvement. Painchaud et al. ^[10] designed a variational self-encoder structure in the post-processing stage to rectify invalid cardiac shapes, achieving higher anatomical validity. Cheng et al. ^[11] developed a feature rectification and fusion module based on orientation fields to address issue of inter-class indistinguishability and intra-class inconsistency. Tong et al. ^[12] proposed a loop feedback architecture to enhance features and improve the features extraction performance of the network. Wang et al. ^[13] proposed a framework that combines semi-supervised learning and self-training to be able to train the network better using fewer samples. Gao et al. ^[14] propose a powerful hybrid Transformer architecture that integrates self-attention into a CNNs. Rahman et al. ^[15] introduce a diffusion model that produces multiple plausible outputs by learning a distribution of group insights.

Figure 1.  The cardiac region segmentation results of U-Net. (a) input images; (b) cardiac regions label by expert; (c) segmentation results of U-Net. Blue, yellow, and red color represent the right ventricular (RV), myocardial (Myo) and left ventricular (LV), respectively.

DownLoad: Full-Size Img PowerPoint

Despite these improvements, the limited deterministic information in the medical images can negatively affect the features extraction performance of neural networks. The integration of attention mechanisms is the key to solving this problem. It can reduce the interference of irrelevant information and enable network to focus on the limited deterministic information. Schlemper et al. ^[16] designed a spatial attention gate on skip connection structure of U-Net, which weighted up-sampling results of the decoder by calculating the spatial attention of output feature maps from encoder, achieving better performance than U-Net. Hu et al. ^[17] proposed a squeeze-and-excitation network (SE-Net), which assigned the attention weight to feature maps in channel dimension, allowing network to ignore the irrelevant information. Woo et al. ^[18] designed a convolutional block attention module (CBAM) by combining channel and spatial attention to improve the segmentation performance. Although, these attention mechanisms can reduce the negative impact of irrelevant information, they also lead to the network disregarding the significance of fuzzy information in medical images. Fuzziness is a condition in which the boundary pixels cannot be segmented accurately due to the weak grayscale variation in medical images. Therefore, the pixels of each tissue boundary may contain fuzzy information. The fuzzy information in cardiac MRI can cause neural networks to extract incorrect features of the left ventricle, right ventricle, and myocardium, leading to poor segmentation results. This shortcoming obstacles the network's ability to sufficiently utilize the large amount of valuable fuzzy information, thus adversely affecting the overall performance of the network.

Therefore, in this study, we proposed a dual attention-guided fuzzy network called the DAFNet, and aimed to improve overall segmentation performance. A fuzzy convolution module (FCM) that combines spatial attention and channel attention is designed. FCM allowes the network to significantly utilize fuzzy information while retaining the advantages of attention mechanisms to obtain more accurate and informative object features. Then, we designe a multi-scale feature refinement structure (MSFR) in the decoder to aggregate segmentation maps on different decoding features. MSFR enables the network to achieve more accurate segmentation results. Moreover, a pixel segmentation prediction structure is designed to further enhance pixel segmentation performance of the network according to the dynamic convolutional theory ^[19]. We also provide a patient cardiac MRI dataset provided by a hospital.

2.   Materials and methods

2.1.   Datasets

We evaluated the segmentation performance of DAFNet using three cardiac MRI datasets. The dataset 1 (ACDC ^[20]) is an open-source and fully labeled dataset, comprising 150 patient scans each featuring a short-axis MRI acquired on a 1.5T Siemens Area and a 3.0T Siemens MR instruments. In data acquisition of dataset 1, only two-chamber scans of cardiac on conventional axial were included. Dataset 2 (M&Ms-1 ^[21]) contains MR data of 375 patients from six clinical centers in Spain, Canada, and Germany, acquired under four scanner vendors (1.5T Siemens, 3.0T Siemens, 1.5T Philips, 1.5T General Electric, and 1.5T Canon). The dataset 3 was collected by the Chongqing Traditional Chinese Medicine Hospital, consisted of 12 patient scans, each including a short-axis MRI acquired on the GE Healthcare SIGNA Architect 3.0T superconducting MR instrument. In data acquisition of dataset 3, two-chamber, three-chamber, and four-chamber scans of cardiac on sagittal, coronary, conventional axial were included. The basic information of cardiac MRI image on the three datasets is shown in Table 1. Since the resolution of these MRI images is not fixed, we uniformly resize them to 212×212 pixels during experiments.

Table 1.  Basic information of cardiac MRI images on the three datasets.

Dataset	Frames	Train	Test	Resolution	Ground Truth
dataset 1	2,979	1,902	1,076	$\leqslant 256 \times 256$ pixels	Background, LV, RV, Myo
dataset 2	3,264	1,643	1,621	$\leqslant 256 \times 256$ pixels	Background, LV, RV, Myo
dataset 3	4,649	0	4,649	$\leqslant 512 \times 512$ pixels	LV end-diastolic inner diameter

---

 | Show Table

DownLoad: CSV

Representative slices of these three cardiac MRI datasets are shown in Figure 2, from which it can be seen that dataset 3 has a higher level of noise and artifacts, and the overall image quality is not as good as that of dataset 1 and dataset 2. In addition, there is a phenomenon of insignificant difference in the grayscale of some of the image pixels between dataset 2 and dataset 3, which is more pronounced in dataset 3. These differences allow us to make a more comprehensive assessment of the overall performance of DAFNet.

Figure 2.  Partial slice visualization of the three datasets.

DownLoad: Full-Size Img PowerPoint

2.2.   DAFNet architecture

We aimed to achieve accurate segmentation of the LV, RV and Myo categories based on MRI. Figure 3 shows that the proposed DAFNet was developed based on the U-Net ^[9] architecture, which consisted of encoder and decoder. Noticeably, we are not limited to U-Net architecture, these proposed modules can be migrated to any network architecture, but as a general rule, we improve and introduce on the U-Net architecture.

Figure 3.  The network architecture of the proposed DAFNet. The operation Up×2 is representing that up-sampling ratio is 2. The Concat operation is representing that the concatenation of two feature maps on the channel dimension, consistent with U-Net. Symbol seg means the segmentation maps.

DownLoad: Full-Size Img PowerPoint

Specifically, encoder consists of two convolutional layers (Conv) with a kernel size of 3×3 and four FCM, and outputs five different scale feature ${F_1}, {F_2}, {F_3}, {F_4}, {F_5}$. FCM comprised of a max-pooling layer (MaxPool), a spatial fuzzy convolutional layer (SFConv), and a channel fuzzy convolutional layer (CFConv). The decoder adopts the designed MSFR structure, takes the output feature maps of the encoder as input, and outputs four multi-scale feature maps ${O_1}, {O_2}, {O_3}, {O_4}$. The segmentation map is acquired through our designed dynamic pixels segmentation convolution (dyConv) structure. During training phase, the training loss of DAFNet was calculated as the sum of the losses of four segmentation maps and the label. In testing phase, the final cardiac segmentation results are obtained by aggregating the four segmentation maps in the MSFR structure.

2.3.   Fuzzy convolutional modules

The attention mechanisms (Attention) computes the attention weight of a feature map in spatial or channel dimension, aiming to enhance the positive influence of deterministic information and to mitigate the negative effects of the irrelevant information on object features extraction ^[18]. This directs CNNs-based methods toward the deterministic information, thereby improving the overall performance. However, medical images not only contain the limited directly usable deterministic information but also include the substantial amount of overlooked yet valuable fuzzy information. The introduction of the attentional mechanism makes networks ignore the fuzzy information because it is provided with a low attentional weight, which hinders the networks' performance. Addressing the challenge posed by the abundance of fuzzy information in cardiac MRI images, we proposed FCM that not only retained the benefits of attention mechanisms but also effectively leveraged fuzzy information to improve the network's performance. The FCM contained two convolutional layer structures: Spatial and channel fuzzy convolutional layer.

The first convolutional layer structure, a spatial fuzzy convolution, is illustrated in Figure 4. This structure enabling the network to learn and infer the fuzzy information from the spatial dimension. The forward inference process of SFConv is outlined as follows

where $i \in [1, 4]$, u is the fuzzification of each pixel in spatial dimension, and 1-u is the determinacy of each pixel. Similarly, the feature map ${F_{i + 1}}$ and ${F_i}$ in the encoder can also be replaced by the feature map ${O_i}$ and ${O_{i + 1}}$ in the decoder.

Figure 4.  Structure of spatial fuzzy convolution. Symbol Eq.2 is the Eq (2).

DownLoad: Full-Size Img PowerPoint

We utilized information entropy theory to compute the fuzzification of each feature. When the probability of a feature belonging to a particular category is higher, the information entropy is smaller, approaching 0, indicating higher deterministic. Conversely, when the probability of a feature belonging to some categories is similar, the information entropy increases, approaching 1, indicating higher fuzzification. Thus, the two branches in Eq (1) can simultaneously retain the deterministic and fuzzy information of the convolutional feature map.

The fuzzification in the spatial dimension is calculated as follows

where ${\mu _i}$ represents the probability that each feature of ${F_i}$ belongs to category j in the spatial dimension, and N is the categories number to be detected.

The second convolutional layer structure, a channel fuzzy convolution, is show in Figure 5. This structure enabling network to learn and infer the fuzzy information from the channel dimension. The forward inference process of CFConv is outlined as follows

where v is the fuzzification of each channel in the channel dimension, and 1-v is the determinacy of each channel. The fuzzification in the channel dimension is calculated as follows

where ${\eta _i}$ represents the probability that each feature of ${F_i}$ belongs to category j in the channel dimension.

Figure 5.  Structure of channel fuzzy convolution.

DownLoad: Full-Size Img PowerPoint

2.4.   Multi-scale feature refinement

In the convolutional neural networks, deep features have high-level semantics and generate strong responses to the detected object. While shallow features contain a large amount of local information and can provide a rich context to accurately identify object contour boundaries. allowing the network to access deep features, high-level semantics can be exploited to accurately extract object features. Allowing the network to access shallow features and rich context can be exploited to further refine the detected object contour boundaries ^[22]. However, the existing networks only focus on deep features and ignore the improvements of shallow features. To address this issue, we designed a MSFR structure in the decoder portion of the DAFNet, as shown in Figure 6a. This structure allowed the network to simultaneously access deep and shallow features, thereby significantly enhancing the performance of the network. The forward inference process of MSFR is outlined as follows

where ${y_{{\rm{seg}}}}$ is the final segmentation result, ${f_{{\rm{seg}} i}}( \cdot )$ is the dyConv structure we design for predicting each segmentation map, ${f_{{\rm{up}}}}\left( \cdot \right)$ is the bilinear interpolation method. The final pixel segmentation map ${y_{{\rm{seg}}}}$ is aggregated from four predicted pixel segmentation maps ${f_{{\rm{seg}} i}}(i \in [1, 4])$ in channel dimension by adding operation. The final mask is obtained by the argmax function on the final pixel segmentation map ${y_{{\rm{seg}}}}$.

Figure 6.  Multi-scale feature refinement structure. Symbols b, C, H, and W in the figure represent the batch size, channels number, height, and width of the input feature map, respectively. GAvgPool and GMaxPool means the global average-pooling and max-pooling layer. GConv k×k (·) represents a group convolutional layer (GConv ^[23]) with a kernel size k×k. The green square is the kernel coefficients matrix of GConv.

DownLoad: Full-Size Img PowerPoint

Since using the Conv as a pixel segmentation convolutional structure will reduce the network performance, we designed a higher-performance dyConv structure based on the dynamic convolution theory. It calculates the attention of the feature map in channel or spatial dimension first, and then dynamically adjusts the convolution kernel and kernel parameters according to the attention. Then, a more accurate decoded feature map is extracted. The dyConv structure is shown in Figure 6b, and its forward inference process is outlined as follows

where mlp(·) is a multi-layer perceptron, and ${W_i}$ is the kernel coefficients matrix of convolutional layer. ${g_1}$ is the calculated attention weight of the kernel coefficient matrix in spatial dimension, and ${g_2}$ is the calculated attention weight of the kernel in channel dimension. h(·) is the forward inference process of the group convolutional layer.

2.5.   Implementation details

We utilized a composite loss function by merging the Dice loss and the cross-entropy loss for the training of DAFNet. The Dice loss is employed to evaluate the level of overlap between the segmented maps and the labeled image. Moreover, the cross-entropy loss is utilized to evaluate the accuracy of pixel-wise classification. The computation of the composite loss is outlined as follows

where ${\mathcal{L}_{{\rm{dice}}}}$ and ${\mathcal{L}_{{\rm{ce}}}}$ represents the computed Dice loss and cross-entropy loss. Symbol $\alpha$ denotes the weight assigned for balancing each loss, which was set at 0.5. ${p_{ijk}}$ and ${g_{jk}}$ is the predicted segmentation maps and corresponding label.

The experiments were carried out on Ubuntu 21.04 system using PyTorch 1.7.1. We incorporated random rotation, diagonal mirroring, and vertical mirroring for image data augmentation during training. Additionally, the input image was resized to 212×212 pixels. The batch size coefficient b was set to 16. Since the LV, RV, Myo and background pixels were segmented from the cardiac MRI in this study, the number of category N that the network needed to predict was set to 4. During the training of DAFNet on dataset 1, the Adam optimizer with a weight decay coefficient of 0.0001 and a cosine annealing decay strategy with a learning rate of 0.001 were employed. The training epoch was set to 30. Since neither dataset contains a validation set, the proposed method is trained without employing validation loss and early stopping. The detailed overview of the proposed DAFNet structure parameter settings is shown in Figure 7.

Figure 7.  The parameter setting of DAFNet. The coefficients c, s and p in the figure is represent the stride size, padding scheme and channels number, respectively.

DownLoad: Full-Size Img PowerPoint

2.6.   Evaluation metric

The Dice similarity coefficient (DSC) and Hausdorff distance (HD) metric are sensitive to the segmentation regions and boundarys. These metrics gauge similarity and distance by evaluating the correspondence between segmentation maps and their corresponding labels. The DSC and HD metrics are outlined as follows

where $P$ represents the set of pixels in segmented map, while ${T_i}$ is the set of pixels in corresponding label image. i signifies the category of LV, RV or Myo. $| \cdot |$ is utilized to obtain the number of elements in the set, $|| \cdot ||$ is utilized for calculating the distance between points in two sets.

The LV diastolic inner diameter typically falls within range of 45−55mm for males and 35−50mm for females. Abnormal increases in LV end-diastolic inner diameter (LVd) can potentially lead to cardiac failure. In clinical practice, the deviation from indicators such as LVd and normal values is commonly used to evaluate the cardiac function. For a more precise evaluation, we used accuracy to quantify the concordance between predicted LVd and the label. The accuracy metric is outlined as follows

where ${P_{{\rm{LVd}}}}$ is the LVd computed from predicted segmentation map, and ${T_{{\rm{LVd}}}}$ represents the LVd measured by experts.

3.   Results

3.1.   Quantitative results of ablation studies

For dataset 1, we recorded the qualitative results of the Attention, FCM, MSFR, and dyConv to verify the effectiveness of these proposed modules, as shown in Table 2. Since dataset 1 provided only the LV, RV, Myo, and background labels, we use the DSC and HD as metrics to evaluate the performance of methods. The results of row 1 show the cardiac segmentation performance of the baseline. Row 2 shows the performance after adding the FCM. Row 3 shows the performance after adding the FCM and MSFR. Row 4 shows the performance of the proposed DAFNet. The p-values in rows 2−5 indicate whether the baseline uses attention, or FCM, the methods of the third row and fourth row, and the method of the fourth row and fifth row, respectively. We found that the FCM, which enables the network to learn and utilize fuzzy information, MSFR, which aggregates multi-scale segmentation results, and dyConv, which improves pixel segmentation accuracy, can improve the segmentation performance of the network, thereby verifying the effectiveness of these proposed modules.

Table 2.  Qualitative results of these proposed modules. The mean DSC represents the average of the DSC values for each category, except the background category. Baseline adopts the U-Net structure declared in Section 2.2. The last column is the significance test on the DSC metric. FLOPs are the number of floating-point computations of the networks.

Baseline	Attention	FCM	MSFR	dyConv	mean DSC(%)	mean HD(mm)	p-values	FLOPs(G)
√					89.23	4.94	−	7.85
√	√				90.86(+1.63)	3.82(−1.12)	0.2698	7.86
√		√			92.28(+3.05)	3.22(−1.72)	0.0010	11.64
√		√	√		93.19(+3.96)	2.73(−2.21)	0.1045	11.64
√		√	√	√	94.42(+4.94)	2.50(−2.44)	0.0340	11.73

---

 | Show Table

DownLoad: CSV

In medical images, the difference in gray-scale values between the different categories contour boundaries pixel are exceedingly subtle, which brings a challenge to cardiac segmentation. Figure 8 visualizes segmentation results after progressively adding the FCM, MSFR, and dyConv to the baseline. The first and last columns are the segmentation results of the baseline and DAFNet respectively. The results demonstrated that the RV segmentation accuracy of the baseline is very low, while DAFNet achieve high segmentation accuracy. Therefore, it is verified that the segmentation performance is greatly improved after integrating these modules.

Figure 8.  Segmentation results of these proposed modules. (a) input image; (b) label; (c) to (f) represent the segmentation results of the row 1 and rows 3−5 in Table 2, respectively.

DownLoad: Full-Size Img PowerPoint

To further validate the effectiveness of FCM, we investigated the impact of different FCM structures on segmentation performance. Table 3 shows the segmentation performance of DAFNet based on different FCM structures. It can be found that both SFConv and CFConv effectively enhance the performance compared to the convolutional layer, and the combination of the last row has the best results. Therefore, this combination is used as the proposed FCM structure in this article.

Table 3.  Qualitative results of different FCM structures. The last column is the significance test on the DSC metric. The p-value of each row is the comparison between the current row and the first row. The last row has a p-value of $3.42 \times {10^{ - 6}}$, but only 4 decimal places are shown for uniform formatting.

Structure	DSC(%)				HD(mm)				p-values
	LV	RV	Myo	mean	LV	RV	Myo	mean
Conv+Conv	89.31	89.45	94.07	90.94	5.61	3.00	2.53	3.71	−
Conv+CFConv	89.76	89.51	94.21	91.16	5.66	3.03	2.47	3.72	0.7831
CFConv+Conv	90.16	89.35	93.77	91.09	5.15	3.04	2.53	3.57	0.8480
CFConv+CFConv	89.38	89.97	93.79	91.05	6.42	3.34	2.84	4.20	0.5628
Conv+SFConv	90.33	89.55	94.00	91.29	5.16	2.79	2.38	3.44	0.7843
SFConv+Conv	90.15	89.29	94.08	91.17	5.27	2.98	2.19	3.48	0.5673
SFConv+SFConv	88.48	89.06	94.06	90.53	5.96	2.93	2.39	3.76	0.3872
CFConv+SFConv	93.95	90.49	94.29	92.91	3.90	2.79	2.36	3.02	0.0173
SFConv+CFConv	95.23	91.53	95.76	94.17	3.20	2.34	1.96	2.50	< 0.0001

---

 | Show Table

DownLoad: CSV

In addition, to further illustrate that the FCM cannot only enable the network to obtain better encoding features, but also enable to obtain better object features in the decoding stage, we conducted relevant experiments. As shown in Table 4, the impact of the FCM on the segmentation performance during the encoding and decoding stages demonstrates that using FCM in both encoding and decoding stages can achieve the best performance improvement.

Table 4.  The performance of DAFNet using or not FCM in the encoder and decoder. The last column is the significance test on the DSC metric. The p-value of each row is the comparison between the current row and the first row.

Encoder	Decoder	DSC(%)				HD(mm)				p-values
		LV	RV	Myo	mean	LV	RV	Myo	mean
		89.31	89.45	94.07	90.94	5.61	3.00	2.53	3.71	−
√		93.87	90.28	94.88	93.01	3.75	2.69	2.20	2.88	0.0021
	√	92.17	88.89	94.13	91.73	6.07	3.73	3.18	4.33	0.2526
√	√	95.23	91.53	95.76	94.17	3.20	2.34	1.96	2.50	0.0128

---

 | Show Table

DownLoad: CSV

Figure 9 depicts the Dice loss and DSC changes of the baseline and DAFNet on dataset 1. The results showed that under the same experiment environment, DAFNet not only accelerates the convergence rate of the Dice loss, but also reduces the final convergence loss. Moreover, DAFNet achieves higher DSC faster than the baseline. The Dice loss and DSC in Figure 9 are the average of five additional experiments, as shown in Table 5.

Figure 9.  The Dice loss and DSC of the baseline and DAFNet on dataset 1.

DownLoad: Full-Size Img PowerPoint

Table 5.  The baseline and DAFNet are trained five times identically on dataset 1, and their Dice loss and DSC are recorded. ${\sigma ^2}$ shows the variance of each row of data.

Method		Numbers	1	2	3	4	5	mean	${\sigma ^2}$
Baseline	Dice loss	Train	0.0574	0.0537	0.0609	0.0549	0.0526	0.0559	8.7960×10-6
		Test	0.0848	0.0834	0.0945	0.0799	0.0834	0.0852	2.4244×10-7
	DSC(%)	Train	93.02	93.61	92.58	93.42	93.73	93.27	0.1777
		Test	89.39	89.66	88.12	90.09	89.68	89.39	0.4520
DAFNet	Dice loss	Train	0.0468	0.0459	0.0457	0.0454	0.0449	0.0457	3.9600×10-7
		Test	0.0505	0.0500	0.0502	0.0481	0.0489	0.0495	8.1200×10-7
	DSC(%)	Train	94.53	94.68	94.68	94.72	94.77	94.68	0.0064
		Test	94.05	94.13	94.09	94.36	94.24	94.17	0.0127

---

 | Show Table

DownLoad: CSV

3.2.   Comparison with state-of-the-art results

Table 6 records the performance of different methods on dataset 1. The proposed DAFNet obtained the best mean DSC and HD results. However, the results in Table 6 show that the right ventricle segmentation performance is not satisfactory. This is due to the complex shape, ill-defined thin edges, large variations among patients, and pathology of the right ventricle ^[24]. The results in lines 16-17 of Table 6 show that DAFNet can further improve the performance of other methods. Figure 10 shows representative segmentation results of different methods on dataset 1, indicating that DAFNet outperformed other methods in terms of the segmentation and obtained contour boundaries in various parts. Under the right ventricle, the results of existing methods are not accurate enough. Under the left ventricle and myocardium, the proposed method obtains better segmentation results, verifying that utilizing fuzzy information can solve the challenge of boundary pixels that cannot be accurately segmented due to fuzziness. The reduction in HD indirectly supported the effectiveness of the proposed network. Compared with other methods, the proposed DAFNet basically obtains the highest DSC metric and the lowest HD metric in the three categories. The DAFNet-Res18 architecture means adding these proposed modules in the ResNet-18 ^[25] architecture instead of the U-Net architecture described in Section 2.2. Table 7 and Figure 11 show the results of different methods on dataset 2.

Table 6.  The segmentation results of different methods on dataset 1. The bold is the best result, and the underline is the second-best result.

Methods	LV				RV				Myo				mean
	DSC(%)		HD(mm)		DSC(%)		HD(mm)		DSC(%)		HD(mm)		DSC(%)	HD(mm)
	ED	ES	ED	ES	ED	ES	ED	ES	ED	ES	ED	ES
Reference [9]	90.38	85.61	6.74	6.93	87.27	86.78	3.88	5.06	95.57	89.80	3.23	3.81	90.94	3.71
Reference [12]	96.60	91.80	7.95	8.18	94.80	89.80	11.67	12.84	90.50	91.50	9.50	9.57	92.50	9.95
Reference [16]	96.13	92.37	3.62	4.37	90.14	90.65	2.48	3.03	97.27	93.36	1.98	2.67	93.32	3.03
Reference [14]	96.31	92.84	3.13	3.97	90.65	90.93	2.76	3.96	96.79	93.23	1.88	2.55	93.46	3.04
Reference [15]	95.59	91.94	3.82	4.33	90.03	90.43	3.04	4.03	96.37	92.67	2.38	3.14	93.36	3.46
Reference [26]	96.70	92.80	6.40	7.60	93.60	88.90	13.30	14.40	89.10	90.40	8.30	9.60	91.92	9.93
Reference [27]	96.10	91.80	7.50	9.60	92.80	87.20	11.90	13.40	87.50	89.40	11.10	10.70	90.80	10.70
Reference [28]	96.30	91.10	6.50	9.20	93.20	88.30	12.70	14.70	89.20	90.10	8.70	10.60	91.37	10.40
Reference [29]	96.70	92.80	5.50	6.90	94.60	90.40	8.80	11.40	89.60	91.90	7.60	7.10	92.67	7.88
DAFNet-Ref. [18]	96.01	92.57	3.31	4.38	90.38	90.43	2.33	3.10	97.17	93.20	1.92	2.58	93.29	2.94
DAFNet-Ref. [19]	96.42	92.66	3.43	4.03	92.04	92.34	2.18	2.89	97.52	94.15	1.87	2.43	94.18	2.81
DAFNet-Res18(Ours)	96.53	92.78	3.01	3.89	92.12	90.89	2.90	2.84	96.89	91.99	2.10	3.62	93.53	3.06
DAFNet-Res34(Ours)	96.41	92.89	2.96	3.77	91.97	91.03	2.99	2.65	97.13	92.78	2.03	3.03	93.70	2.91
DAFNet(Ours)	96.72	93.74	2.78	3.61	91.68	91.38	2.09	2.59	97.53	93.99	1.70	2.22	94.17	2.50

---

 | Show Table

DownLoad: CSV

Figure 10.  The segmentation results of different methods on dataset 1.

DownLoad: Full-Size Img PowerPoint

Table 7.  The segmentation results of different methods on dataset 2.

Method	LV		RV		Myo		mean
	DSC (%)	HD (mm)	DSC (%)	HD (mm)	DSC (%)	HD (mm)	DSC (%)	HD (mm)
Reference [9]	87.69	6.93	81.13	4.57	85.63	3.64	84.82	5.05
Reference [12]	89.21	5.68	83.68	4.28	87.25	3.29	86.71	4.42
Reference [16]	90.94	5.34	85.59	3.79	87.74	3.12	88.09	4.08
Reference [30]	91.25	9.10	85.30	11.70	88.50	12.25	88.35	11.03
Reference [31]	90.90	9.40	84.55	11.85	87.95	12.65	87.80	11.30
Reference [32]	90.50	10.00	84.10	12.45	87.50	12.65	87.37	11.70
DAFNet-Res18	92.34	5.23	84.28	3.24	87.23	3.23	87.95	3.90
DAFNet-Res34	91.23	5.63	84.47	3.68	87.84	2.67	87.85	3.99
DAFNet (Ours)	92.58	4.87	84.17	3.97	88.68	2.54	88.47	3.79

---

 | Show Table

DownLoad: CSV

Figure 11.  The segmentation results of different methods on dataset 2.

DownLoad: Full-Size Img PowerPoint

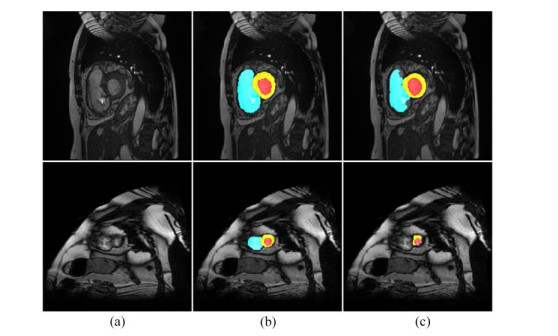
Additionally, in clinical diagnosis, considering the different cardiac image acquisition methods of different instruments, different noise and artifacts will be introduced. Achieving robust segmentation across datasets is therefore critical to assist physicians in diagnosing cardiac disease. For dataset 3, since it provided only the Lvd label, we use the accuracy as a metric. We evaluate their performance using different methods trained on dataset 1 to predict LVd, as shown in Table 8. We found that the LVd obtained by DAFNet are in good agreement with the results manually measured by experts, which further confirms the effectiveness of DAFNet. Figure 12 shows the segmentation results of different methods on dataset 3. Under the left ventricle and myocardium, the other methods appear to under-segment or over-segment, and the proposed method is able to obtain better results by utilizing fuzzy information. Under the right ventricle, only eference ^[12] can barely segment, which is due to the fact that right ventricle segmentation is usually a difficult problem in cardiac MRI segmentation ^[24].

Table 8.  The segmentation results of different methods on dataset 2.

Methods	Patients	1	2	3	4	5	6	7	8	9	10	11	12	mean	${\sigma ^2}$
	${T_{{\rm{LVd}}}}$	44.00	47.00	58.00	42.00	51.00	54.00	68.00	44.00	45.00	47.00	61.00	38.00	—	—
Reference [9]	${P_{{\rm{LVd}}}}$	41.72	43.78	53.33	40.77	54.34	51.81	65.93	46.32	43.65	44.14	59.74	39.84	—	—
	accuracy	94.82	93.15	91.95	97.07	93.45	95.94	96.96	94.73	97.00	93.91	97.93	95.16	95.17	1.77
Reference [12]	${P_{{\rm{LVd}}}}$	42.32	45.37	57.88	41.30	50.80	52.72	66.94	45.22	43.79	45.44	59.26	39.06	—	—
	accuracy	96.18	96.53	99.79	98.33	99.61	97.63	98.44	97.23	97.31	96.68	97.15	97.21	97.67	1.22
Reference [16]	${P_{{\rm{LVd}}}}$	42.30	45.18	56.97	40.85	50.55	53.30	66.66	45.64	43.34	45.13	59.79	39.01	—	—
	accuracy	96.14	96.13	98.22	97.26	99.12	98.70	98.03	96.27	96.31	96.02	98.02	97.34	97.30	1.13
DAFNet-Res18	${P_{{\rm{LVd}}}}$	44.38	48.25	56.88	41.78	51.21	54.79	67.32	45.39	44.13	45.39	61.79	38.67	—	—
	accuracy	99.14	97.34	98.07	99.48	99.59	98.54	99.00	96.84	98.07	96.57	98.70	98.24	98.30	0.94
DAFNet-Res34	${P_{{\rm{LVd}}}}$	45.79	48.17	57.03	41.42	51.43	55.67	68.77	43.75	45.76	46.21	62.68	38.94	—	—
	accuracy	95.93	97.51	98.33	98.62	99.16	96.91	98.87	99.43	98.31	98.32	97.25	97.53	98.01	0.97
DAFNet(Ours)	${P_{{\rm{LVd}}}}$	45.33	48.07	57.94	42.51	50.71	55.26	68.59	42.14	45.88	46.83	61.69	38.26	—	—
	accuracy	96.98	97.72	99.90	98.79	99.43	97.67	99.13	95.78	98.04	99.64	98.87	99.32	98.44	1.18

---

 | Show Table

DownLoad: CSV

Figure 12.  The segmentation results of different methods on dataset 3.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

In deep learning, the segmentation performance improvement can be achieved through four avenues. The excellent pre-processing pipeline ^[33] highlights feature through data augmentation methods. The effective post-processing pipeline ^[34] optimizes the prediction results through clustering algorithms. Excellent neural networks ^[12,16] extract precise features by improving network structure. Superior training skill ^[35] enable the network to fitting object better by fine-tuning. These avenues can complement each other to further enhance the performance.

In this study, we introduced the DAFNet method for cardiac segmentation by improving the networks structure to improve the segmentation performance, which consist of two pivotal components: The FCM and MSFR structure. The FCM excels in extracting more nuanced and informative features during both the encoding and decoding processes, while the MSFR provides different level of feature information during the decoding, thereby optimizing the final segmentation result. Both components synergistically enhance the overall performance and robustness of the network.

In ACDC and M&Ms-1 competition, due to the different instruments collected, there are image quality inconsistencies, artifacts, noise, and other problems between the data, which make it difficult to segment the organization in the image. To address this problem, many researchers have aimed to enhance U-Net to improve segmentation accuracy. Lossau et al. ^[36] propose a fully automatic dynamic pacemaker artifact reduction pipeline, which is built from three CNNs ensembles. Tong et al. ^[12] utilized the staggered attention module to effectively fuse multi-level contextual information, regulating the information transmitted to the decoding stage. Schlemper et al. ^[16] introduced an attention gate structure in the skip-connection of the network, enabling the network to learn crucial information from the original image and suppress unimportant regions. However, their methods involved only the simple insertion of attention mechanisms, limiting the segmentation performance of U-Net. As shown in Figures 10 and 11, despite the slight improvement in accuracy, the segmentation results of the boundaries region are not optimized. Tables 6 and 7 demonstrate that DAFNet outperformed other methods, achieving superior results in HD and DSC metric. In clinical datasets, segmentation of various cardiac tissues is a difficult task due to the older instruments used for acquisition and slightly poorer image quality. The excellent feature extraction structure of the DAFNet greatly contributes to the performance. In Table 8 and Figure 12, although the clinical data did not provide labeled images, the DAFNet outperforms the other methods by comparing it with the LVd in the hospital-collected data with high stability. Even in some of the basal slices, it performs well.

Although the proposed DAFNet can solve the fuzzy information challenge to obtain better results, the method has some limitations. First, in the FCM, the deterministic and fuzzy information is obtained by matrix multiplication, which means that the network computation will be more intensive. Second, DAFNet is a supervised learning method, which means that complete cardiac label need to be provided in order to train network. However, there will be differences in the cardiac images captured by different devices and the labels are costly to produce, which leads to the possibility that the network may be overfitted to a particular dataset during the training process. These factors limit the generalization ability and practical application of the proposed method in real scenarios.

5.   Conclusions

In this study, we proposed a high-performance automatic cardiac segmentation method named DAFNet, which was designed to effectively address the challenges of accurate extracting cardiac feature on different datasets. The proposed fuzzy convolutional module greatly utilizes fuzzy information, which is easily ignored in medical images and deterministic information, is widely valued in attention mechanism, and improves the network's feature extraction performance. Compared with other networks that obtain segmentation results only on the shallowest decoded feature maps, the proposed multi-scale feature refinement structure further improves performance by aggregating segmentation results on different scale decoded feature maps. Extensive experiments for the three cardiac MRI datasets show that DAFNet demonstrate state-of-the-art performance compared to existing CNN-based methods. This achievement establishes robust foundation for applications in cardiac disease diagnosis, treatment planning, and postoperative measurements.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Authors are grateful to the reviewers and editors for their suggestions and comments to improve the manuscript.

Authors also thank the financial support from National Natural Science Foundation of China (No. 11461037), Yunnan Fundamental Research Projects (No. 202101BE070001-050; 202301AU070184), Chongqing Science and Health Joint Medical Research key Project (No. 2024ZDXM001), and Chongqing Natural Science Foundation project (No. cstc2021jcyj-msxm0727), and Xinglin Scholar Research Premotion Project of Chengdu University of Traditional Chinese Medicine (No. YYZX2022136) and Kunming University of Science and Technology Self discipline Talent Introduction Scientific Research Foundation Project (No. KKZ3202307033).

Conflict of interest

The authors declare no conflicts of interest in this paper.

Supplementary: Data availability statement

The ACDC dataset (dataset 1) that supports this research is available at: https://acdc.creatis.insa-lyon.fr/description/databases.html. The M&Ms-1 dataset (dataset 2) that supports this research is available at: https://www.ub.edu/mnms. The hospital clinical datasets (dataset 3) generated and analyzed during this research are not publicly available due to the nature of this research; participants did not agree for their data to be shared publicly.