Bias correction based on AR model in spurious regression

Zhongzhe Ouyang; Ke Liu; Min Lu; Zhongzhe Ouyang; Ke Liu; Min Lu

doi:10.3934/math.2024410

AIMS Mathematics

2024, Volume 9, Issue 4: 8439-8460. doi: 10.3934/math.2024410

Previous Article Next Article

Research article

Bias correction based on AR model in spurious regression

1.
Department of Biostatistics, University of Michigan, MI 48109, USA
2.
School of Economics and Statistics, Guangzhou University, Guangzhou 510006, China
3.
Business School, Hunan Normal University, Changsha 410081, China

Received: 16 January 2024 Revised: 22 February 2024 Accepted: 26 February 2024 Published: 28 February 2024
MSC : 62G05, 62J05, 91B84, 62M10

The regression of mutually independent time series, whether stationary or non-stationary, will result in autocorrelation in the random error term. This leads to the over-rejection of the null hypothesis in the conventional t-test, causing spurious regression. We propose a new method to reduce spurious regression by applying the Cochrane-Orutt feasible generalized least squares method based on a bias-corrected method for a first-order autoregressive model in finite samples. This method eliminates the requirements for a kernel function and bandwidth selection, making it simpler to implement than the traditional heteroskedasticity and autocorrelation consistent method. A series of Monte Carlo simulations indicate that our method can decrease the probability of spurious regression among stationary, non-stationary, or trend-stationary series within a sample size of 10–50. We applied this proposed method to the actual data studied by Yule in 1926, and found that it can significantly minimize spurious regression. Thus, we deduce that there is no significant regressive relationship between the proportion of marriages in the Church of England and the mortality rate in England and Wales.

Keywords:

Citation: Zhongzhe Ouyang, Ke Liu, Min Lu. Bias correction based on AR model in spurious regression[J]. AIMS Mathematics, 2024, 9(4): 8439-8460. doi: 10.3934/math.2024410

Related Papers:

[1]	Jacobo Campo-Robledo, Cristian Castillo-Robayo, Julimar da silva Bichara . Quantile and interquantile regression models for returns to education by economic sector and vulnerable population in Colombia. AIMS Mathematics, 2024, 9(12): 35091-35124. doi: 10.3934/math.20241669
[2]	Ali A. Al-Shomrani . An improvement in maximum likelihood estimation of the Burr XII distribution parameters. AIMS Mathematics, 2022, 7(9): 17444-17460. doi: 10.3934/math.2022961
[3]	Oussama Bouanani, Salim Bouzebda . Limit theorems for local polynomial estimation of regression for functional dependent data. AIMS Mathematics, 2024, 9(9): 23651-23691. doi: 10.3934/math.20241150
[4]	Abdallah Sayah, Nassima Almi . Improved the bias in kernel quantile function estimation. AIMS Mathematics, 2023, 8(1): 1784-1799. doi: 10.3934/math.2023092
[5]	Kittiwat Sirikasemsuk, Sirilak Wongsriya, Kanogkan Leerojanaprapa . Solving the incomplete data problem in Greco-Latin square experimental design by exact-scheme analysis of variance without data imputation. AIMS Mathematics, 2024, 9(12): 33551-33571. doi: 10.3934/math.20241601
[6]	Lijie Zhou, Liucang Wu, Bin Yang . Estimation and diagnostic for single-index partially functional linear regression model with $p$ -order autoregressive skew-normal errors. AIMS Mathematics, 2025, 10(3): 7022-7066. doi: 10.3934/math.2025321
[7]	Jinling Gao, Zengtai Gong . Uncertain logistic regression models. AIMS Mathematics, 2024, 9(5): 10478-10493. doi: 10.3934/math.2024512
[8]	Ruiyuan Chang, Xiuli Wang, Mingqiu Wang . Corrected optimal subsampling for a class of generalized linear measurement error models. AIMS Mathematics, 2025, 10(2): 4412-4440. doi: 10.3934/math.2025203
[9]	Yifei Pan, Siyao Zhu, Jinliang Wang . A note on a ZIKV epidemic model with spatial structure and vector-bias. AIMS Mathematics, 2022, 7(2): 2255-2265. doi: 10.3934/math.2022128
[10]	Hongxin Xue, Lingling Zhang, Haijian Liang, Liqun Kuang, Huiyan Han, Xiaowen Yang, Lei Guo . Influenza trend prediction method combining Baidu index and support vector regression based on an improved particle swarm optimization algorithm. AIMS Mathematics, 2023, 8(11): 25528-25549. doi: 10.3934/math.20231303

Abstract

1. Introduction

The spurious phenomenon can be traced back to Yule ^[1], who found that two independent variables have a significantly correlated relationship. This has received much attention over the last several years. Spurious regression may occur in various fields, particularly within economic and financial research. Our usual approach involves examining the relationships between multiple factors, determining if there is any correlation and then building a regression model. Finally, we propose relevant economic policies based on the derived results. Therefore, when studying these relationships between several variables, it is critical to not only establish whether a genuine correlation exists from a theoretical economic perspective, but also to confirm their statistical significance prior to building a regression model. For example, in studies investigating factors influencing economic growth ^[2,3,4], variables affecting financial conditions ^[5,6,7,8], and the impact of foreign direct investment ^[9], similar consideration for spurious regression is necessary. The same holds true when examining the effects of digital transformation ^[10] or a digital economy ^[11,12,13], and in green innovation research ^{[14,15,16,17]}. In addition, when analyzing how investor sentiment affects the stock market or the environment ^[18,19,20], investigators must figure out whether there is a direct relationship or an indirect impact that is mediated by other factors.

Previous studies have shown that spurious regression can occur between stationary and non-stationary time series ^[21,22]. For example, Kim et al. ^[23] found that when the sample size approaches infinity, the ordinary least square (OLS) estimator of regression coefficient for two series with trends convergence in probability to the ratio of the corresponding trend component, rather than the true correlation coefficient value between two series. If we ignore spurious regression, the conclusion we get from the regression model is wrong. Therefore, how to avoid spurious regression is an urgent problem to be solved.

One widely accepted explanation for spurious regression is as follows. The error term in the regression model displays serial correlation or heteroskedasticity. Ventosa-Santaulària ^[24] attributes spurious regression to the distortion of the test statistic. Liu ^[25] pointed out that using OLS estimation in the regression model for two mutually independent stationary series will lead to the existence of autocorrelation and heteroskedasticity in unknown forms within the random error term. If autocorrelation and heteroskedasticity are ignored, the estimation of the standard error will be biased, causing the t-test to over-reject the null hypothesis and induce spurious regression. Similarly, MaCallum ^[26] found that spurious regression between random walk series and highly autocorrelated series is due to substantial autocorrelation in the random error term. Based on these studies, autocorrelation and heteroskedasticity^* in the error term are responsible for spurious regression and we will prove it in the following section.

^*While the proposed method focuses on eliminating the autocorrelation of the random error term in the regression model to solve the spurious regression problem, the Monte Carlo simulations in the subsequent section demonstrate that this method can handle spurious regression issues in series with heteroskedasticity.

Currently, there are two aspects of literature dedicated to solving the issue of spurious regression. The first involves constructing a robust test statistic by correcting the standard error. Liu ^[27,28] proposed a series of advanced heteroskedasticity and autocorrelation consistent (HAC) methods to correct the standard error of the OLS estimation and further reduce the probability of spurious regression. However, the HAC methods requires choosing a kernel function and bandwidth, and different choices will impact the results. Moreover, HAC methods can only obtain consistent estimates when the sample size approaches infinity. The second aspect aims to reduce spurious regression by directly eliminating the autocorrelation within the random error term of the regression model. Choi et al. ^[29] suggested that, if the random error term is a unit root process, the feasible generalized least squares (FGLS) estimator based on the Cochrane-Orutt transformation (hereinafter referred to as CO-FGLS) is asymptotically equivalent to that in the differenced regression. The Cochrane-Orcutt transformation, i.e., a generalized difference method, is frequently used to handle the autocorrelation problem. They also argued that CO-FGLS estimates remain asymptotically consistent and robust, irrespective of whether the random error term is stationary or non-stationary. Further, Wu ^[30] demonstrated through simulations and theoretical arguments that the CO-FGLS method is capable of solving spurious regression between stationary processes or unit root series. Wu suggested that autocorrelation within the error term could be eliminated by using this method, regardless of the existence of a co-integration relationship between integrated series. Given these facts, the CO-FGLS method, being effective and easy to implement, is therefore the method that we have chosen to reduce spurious regression.

The CO-FGLS method requires the use of a first-order autoregression (AR) model to fit the random error term. However, both the common OLS estimator and maximum likelihood estimator are consistent only with large sample sizes. Besides, when the root of the AR(1) model is near the unit circle^*, the bias of the estimator will be significantly large. For instance, Sørbye et al. ^[31] discovered that the smaller the sample size, the larger the bias between the estimation and the true value. They also found that if the true parameter is close to one, the estimator is biased downward. Kim ^[32] observed that the OLS estimator of the slope coefficient for the AR(1) model exhibiting linear trend is biased downward, while the trend coefficient is biased upward. These finite sample biases can impact the statistical inferences in real-world applications, such as forecasting economic time series. Therefore, given that the sample sizes in practical applications are often finite or small, it is imperative to correct the bias of the parameters in finite samples when using the CO-FGLS method. This adjustment aims to minimize the incidence of spurious regression.

^*If the series is a near unit root process, the autoregressive coefficients exhibit a finite sample bias when fitted using the AR(1) model.

Numerous scholars have proposed bias correction methods for the AR(1) model in finite samples. These methods include restricted maximum likelihood estimation, median-unbiased estimation, and as Kim ^[32] suggested a bootstrap mean bias-corrected estimation method (BootBC) to enhance the precision of forecasting in the AR models exhibiting trends in finite samples. Recently, Sørbye et al. ^[31] devised new estimators by modeling the relationship between the true and initially estimated AR coefficients using weighted orthogonal polynomial regression. They accounted for the sampling distribution of the original estimators, minimized the model, and derived the final estimator^†. Their simulations suggest that this new method performs well. In this paper, we apply a feasible generalized least squares estimation method based on the Cochrane-Orutt transformation by using the bias-corrected method proposed by Sørbye et al. to correct the bias of an AR(1) model in finite samples and consequently reduce the spurious regression (CO-BCE).

^†In Sørbye et al.'s simulation, the initial estimates are obtained by using various estimation methods such as maximum likelihood estimation (MLE), or conditional MLE. The initial estimates obtained by using the different methods can be effectively corrected for the bias, with little variance in the extent of the corrections. In the Monte Carlo simulation of the initial estimates in the later section the MLE method is used.

The main content and contributions of the paper can be summarized as follows. First, our theoretical findings reveal that the autocorrelation components contained in the explanatory variables and the explanatory variables cause the autocorrelation in the random error term, leading to spurious regression. The asymptotic distribution of the t-test statistic is related to the degree of autocorrelation of the series, and the higher the degree of autocorrelation, the higher the probability of spurious regression. Second, we use the CO-FGLS method to solve the spurious regression caused by error correlation and non-stationary unit root processes. In other words, the CO-FGLS method eliminates the possible serial correlation of the error term through the use of Cochrane-Orutt transformation, avoids model error setting, and reduces the spurious regression. Third, considering that real economic variables are usually short time series, the parameter of the AR(1) model is biased in finite samples. We use the CO-FGLS method and then correct the parameter in the AR(1) model by using a bias-corrected method to reduce the spurious regression. This method avoids estimation of the variance of the error term and is easy to implement since the estimation of the long-run variance of error refers to the choice of kernel function and bandwidth. Furthermore, instead of proposing a new test to determine whether there is spurious regression, we only need to use a traditional t-test of slope coefficients; this means that, if the absolute value of the t-value is greater than 1.96, we reject the null hypothesis of no linear relationship between explanatory variables and response variables at a 5% critical value. Fourthly, the proposed method is able to solve the spurious regression problem between mutually independent stationary and non-stationary series. For series with trends, the probability of spurious regression can be reduced by adding a trend term in the regression model and then using the CO-BCE method. A series of simulations show that the CO-BCE method is effective for stationary series, unit root processes, or series with trends. In addition, some economic variables may contain autoregressive conditional heteroskedasticity (ARCH) or generalized autoregressive conditional heteroskedasticity (GARCH) effects, so we also simulated such data and found that the proposed CO-BCE method can also reduce the probability of spurious regression between series with conditional heteroskedasticity. Finally, we applied the CO-BCE method to the proportion of marriages in the Church of England and the mortality rate in England and Wales from 1866 to 1911, as studied by Yule. Our findings confirm no significant regressive relationship between the two variables, indicating that the CO-BCE method can effectively solve the spurious regression problem.

The rest of the paper is organized as follows. The causes of spurious regression are analyzed theoretically in Section 2. Sections 3 and 4 introduce the Cochrane-Orutt FGLS method proposed by Choi et al. ^[29] and the bias-corrected estimation proposed by Sørbye et al. ^[31]. Section 5 investigates the spurious regression that occurred in the time series with trends and the solution. The data with the simulations of the method are presented in Section 6. Section 7 contains some conclusions and future studies.

2. Theoretical analysis of the causes of spurious regression

Autocorrelation or heteroskedasticity^* in the random error terms will lead to bias in their standard errors, and the t-test statistic will over reject the null hypothesis, resulting in spurious regression. Referring to Liu ^[25], he deduced the cause of spurious regression. Consider the following univariate regression model:

^*The reason for the spurious regression is illustrated the perspective of containing autocorrelation in the random error term; containing heteroskedasticity also generates spurious regression, and the method proposed in this paper is also valid for series containing heteroskedasticity.

$\begin{equation} y_t = x_t\beta+u_t, \ t = 1, \cdots, n, \end{equation}$

(2.1)

where $y_t$ is a response variable, $x_t$ is a scalar explanatory variable for simplicity and error term $u_t$ . If $u_t$ exhibits serial correlation or has a unit root process, OLS estimation will lead to spurious regression; $n$ is the length of time series. The OLS estimator of $\beta$ is $\hat{\beta}_{OLS} = (X^{'}X)^{-1}X^{'}Y = \beta+(X^{'}X)^{-1}X^{'}u$ , where $X$ , $Y$ and $u$ are the matrix forms of $x_t$ , $y_t$ and $u_t$ respectively, and $X^{'}$ is the transpose of $X$ . If $u_t$ satisfies the four basic assumptions of using OLS estimation, i.e., the expectation $E(u_t) = 0$ , $u_t$ is not related to $X$ , variance $Var(u_t) = \sigma^2$ for $t = 1, \dots, n$ and covariance $Cov(u_i, u_j) = 0$ for $i, j = 1, \cdots, n, i\neq j$ , then according to the central limit theorem given by

$\begin{equation} \sqrt{n}(\hat{\beta}_{OLS}-\beta)\stackrel{asy}{\longrightarrow}N(0, \sigma^2Q^{-1}), \end{equation}$

(2.2)

where $asy$ is asymptotic, $\hat{\beta}_{OLS}$ follows the above normal distribution when the sample size $n$ tends to infinity, and $Q = \lim_{n\to \infty}\frac{X^{'}X}{n}$ . T-statistics also follow the standard normal distribution when $n\to\infty$ :

$\begin{equation} t_{\hat{\beta}_{OLS}} = \frac{\hat{\beta}_{OLS}-\beta}{S_{\hat{\beta}_{OLS}}}\stackrel{asy}{\longrightarrow}N(0, 1), \end{equation}$

(2.3)

where $S_{\hat{\beta}_{OLS}}$ is the standard error of the regression model and it is important for hypothesis testing. Now, we shall analyze the mechanism of spurious regression. Since economic variables usually contain an autocorrelation component, we assume that the dependent variable $y_t$ and explanatory variable $x_t$ is an independent first-order stationary autoregressive process:

$\begin{equation} \begin{aligned} &y_t = \alpha_yy_{t-1}+u_{yt}, \\ &x_t = \alpha_xx_{t-1}+u_{xt}, \end{aligned} \end{equation}$

(2.4)

where $\alpha_y\in[0, 1)$ , $\alpha_x\in[0, 1)$ , $u_{yt}\sim IID(0, \delta_y^2)$ , $u_{xt}\sim IID(0, \delta_x^2)$ , and $u_{yt}$ and $u_{xt}$ are independent of each other. If we build the regression model given by Eq (2.1) for these AR(1) series $y_t$ and $x_t$ , the regression coefficient $\beta$ should equal 0. Besides, the autocorrelation and heteroskedasticity of $u_t$ in Eq (2.1) has the same structure as $y_t$ ; then, applying the basic assumptions above, which state that the variance is a constant and the covariance is zero are not satisfied. At this point, the estimator of covariance of $\beta$ , i.e., $\Phi = \lim_{n\to +\infty}\frac{1}{n}Q^{-1}X^{'}\Omega XQ^{-1}$ where $\Omega$ is the covariance of the error term:

$\begin{equation} \Omega = \delta_y^2 \begin{bmatrix} 1&\alpha_y&\cdots&\alpha_y^{n-1} \\ \alpha_y&1&\cdots&\alpha_y^{n-2}\\ \vdots&\vdots&\vdots&\vdots\\ \alpha_y^{n-1}&\alpha_y^{n-2}&\cdots&1 \end{bmatrix}, \end{equation}$

(2.5)

and the error term is also a first-order autoregressive process with slope coefficient $\alpha_y$ . After the deduction, the limiting distribution of the t-test statistic is as follows^*:

^*For the detailed process, please refer to Liu ^[25].

$\begin{equation} t_{\hat{\beta}_{OLS}} = \frac{\hat{\beta}_{OLS}-\beta}{S_{\hat{\beta}_{OLS}}}\stackrel{asy}{\longrightarrow}N(0, \frac{1+\alpha_y\alpha_x}{1-\alpha_y\alpha_x}) . \end{equation}$

(2.6)

This is not a standard normal distribution. In real economic applications, the regression coefficient is often larger than 0; thus, the variance of the above t-test statistic is larger than 1. If the probability of the t-test statistic taking extreme values is greater than for the standard normal distribution, then it is more likely that the null hypothesis will be rejected, and finally, spurious regression will occur. To sum up, due to the autocorrelation of the explanatory variables and the explanatory variables, the random error term also has an autocorrelation structure, which causes spurious regression. In addition, according to Eq (2.6), the closer the autoregressive coefficient of the series is to 1, the higher the probability of spurious regression; however, when its autoregressive coefficient is small, spurious regression may not occur, which is confirmed by the Monte Carlo simulation section. Also, when the autoregressive coefficient is 0.9, the probability of pseudoregression is greater than that for the autoregressive coefficient is 0.5.

3. CO-FGLS

The CO-FGLS method proposed by Choi et al. ^[29] and the limiting distribution of the CO-FGLS estimator is proven to be the same as the differencing estimators. CO-FGLS can be used for the serial correlation error term in the regression model since the error term of the model after the Cochrane-Orutt transformation has no autocorrelation. Then, we can use the normal t-statistics test method.

First, obtain the OLS estimator $\hat{\beta}_{\rm OLS}$ of the model given by Eq (2.1); we have the estimator of the error term:

$\begin{equation} \hat{u}_t = y_t- x_t\hat{\beta}_{\rm OLS}. \end{equation}$

(3.1)

In order to apply the CO-FGLS estimator, we fit $\hat{u}_t$ with the AR(1) model:

$\begin{equation} \hat{u}_t = \hat{\phi}u_{t-1}+\hat{e}_t, \end{equation}$

(3.2)

$\hat{\phi}$ is the OLS estimator of the autocorrelation efficient in the AR(1) model. If the random error term is a unit root process, the value of $\hat{\phi}$ is close to 1 and there is a finite sample bias in $\hat{\phi}$ in the case of insufficient sample size. The Cochrane-Orcutt transformation of series in the regression is performed as follows:

$\begin{equation} \tilde{y}_t = y_t-\hat{\phi}y_{t-1}, \ \tilde{x}_t = x_t-\hat{\phi}x_{t-1}, \ \tilde{u}_t = u_t-\hat{\phi}u_{t-1}. \end{equation}$

(3.3)

Then consider the OLS estimation of the model

$\begin{equation} \tilde{y}_t = \tilde{x}_t\beta+error, \end{equation}$

(3.4)

where the 'error' term satisfies the basic assumption of using least squares. We have

$\begin{equation} \hat{\beta}_{\rm CO{-}FGLS} = \left(\sum\limits_{t = 1}^{n} \tilde{x}_t\tilde{x}_t\right)^{-1}\sum\limits_{t = 1}^{n}\tilde{x}_t \tilde{y}_t, \end{equation}$

(3.5)

where $\hat{\beta}_{\rm CO{-}FGLS}$ is a consistent and robust estimator of spurious regression ^[29].

Thus, in this paper, we use CO-FGLS to solve the spurious regression problem in finite samples that is caused by the serial correlation of the error term; we then use the bias-corrected method to correct the bias of parameters in the AR(1) model.

4. Bias-corrected estimation

Economic variables often have short time periods, and the slope coefficient of the AR model for this kind of dataset is biased when the time series are short. Sørbye et al. ^[31] proposed a new method to correct the bias of the estimators, and the simulations show a smaller bias than other estimators.

Suppose that $\hat{\phi}$ is an initial coefficient estimator for $\phi$ of the AR(1) process; see the first-order autocorrelation coefficient in Eq (3.2). The method requires us to construct a bias-corrected estimator $\hat{\phi}_c = \hat{\phi}-E(\hat{\phi}-\phi)$ , with $E(\hat{\phi}_c) = \phi$ for all values $\phi$ . The main idea of the method is to use a weighted orthogonal polynomial regression model to model the relationship between the true values and the estimated values by using the true values as the response variables in the regression model and minimizing this model to obtain the bias-corrected estimators. The method is as follows. First, introduce a monotonic transformation to avoid constraints on the support of $\phi$ :

$\begin{equation} g(\phi) = {\rm logit}(\frac{\phi+1}{2}). \end{equation}$

(4.1)

The transformation has finite support. This is helpful for optimization and means that the inverse transformed bias-corrected estimate will always be within the stationary area of the AR (1) model.

Model the real AR model with an orthogonal polynomial model:

$\begin{equation} \phi = f(\hat{\phi}, \beta) = g^{-1}\left(\sum\limits_{k = 0}^{K}\beta_kh_k(g(\hat{\phi}))\right), \ \hat{\phi}\in(-1, 1), \end{equation}$

(4.2)

where $\beta = \{\beta_k\}_{k = 0}^K$ is defined as a fixed set of regression coefficients and $\{h_k(\cdot)\}_{k = 0}^K$ is a set of orthogonal polynomials of order k. We chose to use the probabilists' Hermite polynomials; see ^[31]. These polynomials are denoted by

$\begin{equation} h_0(x) = 1, \ h_1(x) = x, h_{k+1}(x) = xh_k(x)-kh_{k-1}(x), \ k\geq1. \end{equation}$

(4.3)

Then, to estimate $\beta$ for a given sample size n, the method generates $m = 1000$ time series for a fine grid of $\phi$ values that can be seen as the training set. We note that the suggested estimator is a nonlinear function of $\hat{\phi}$ implying that

$\begin{equation} E(f(\hat{\phi}, \beta))\neq f(E(\hat{\phi}, \beta)). \end{equation}$

(4.4)

So, the optimization can consider the estimated value for each time series rather than the average estimate of the $m$ simulations. Thus, solving the optimization problem to obtain the regression coefficients can proceed as follows:

$\begin{equation} \begin{aligned} \hat{\beta}& = \mathop{\arg\min}\limits_{\beta}\sum\limits_{r = 1}^{l}\frac{1}{s_r^2}\left(\frac{1}{m}\sum\limits_{j = 1}^{m}g^{-1}\left(\sum\limits_{k = 0}^{K}\beta_kh_k(g(\hat{\phi_{rj}}))\right)-\phi_r\right)^2\\ & = \mathop{\arg\min}\limits_{\beta}\sum\limits_{r = 1}^{l}\frac{1}{s_r^2}\left(\frac{1}{m}\sum\limits_{j = 1}^{m}f(\hat{\phi}_{rj}, \beta)-\phi_r\right)^2, \end{aligned} \end{equation}$

(4.5)

where $\hat{\phi}_{rj}$ is the estimator of $\phi_r$ in simulation $j$ . We have chosen $\phi_r\in(-0.95, -0.94, \cdots, 0.95)$ and $l = 191$ . The sample variances $s^2_r$ of the $m$ estimator of $\phi_c$ are used as weights; other details can be seen in ^[31], and the paper also gave a bias correction procedure for the AR(2) model^*. From here, we obtain the estimator $\hat{\beta}$ and the bias-corrected estimator $\hat{\phi}_c = f(\hat{\phi}, \hat{\beta})$ .

^*This work does not need to use the bias-correction method for AR(2), so we chose to not expand the description.

The proposed method involves using this bias correction estimation method to correct the finite sample biases of the autoregressive coefficients $\hat{\phi}$ in Eq (3.2) within the CO-FGLS method, and then plugging the corrected estimate $\hat{\phi}_c$ into Eq (3.3).

5. Spurious regression with trend series

Macro-micro economic variables are often affected by factors such as the market, policy, or a financial crisis, and they exhibit trend characteristics over time. For example, Wang and Hu ^[33] pointed out that since China's economic reform and opening up, the gross domestic product (GDP) series has shown significant stable growth over time, i.e., the deterministic trend^*, which is brought about by the growth of production factors as well as technological advances, etc.; in addition to this, it also contains some random factors, such as natural disasters or financial crises, that may affect the economy, i.e., the stochastic trend, which is presented as a unit root process in the series. Moreover, there have been many studies showing that the GDP series of the vast majority of countries can be represented by unit root processes. Precisely, the GDP series of China contains both deterministic and stochastic trends. There are many other economic variables with this kind of non-stationary data structure, and the spurious regression among the non-stationary series can be solved directly by using the proposed CO-BCE method. However, the limitation of the method is that it cannot handle series with trends. This is because CO-BCE cannot eliminate the trend feature in the series, and the trend component can induce the spurious regression phenomenon since there is an indirect correlation between two mutually independent series. Therefore, we refer to the existing methods to solve the spurious regression between series containing trends.

^*Deterministic trends are typically represented by a linear trend in a model.

Many studies have shown that spurious regression occurs between stationary time series with trends, e.g., Kim et al. ^[23] proved that the regression coefficient between stationary series with trends is related to the proportion of the coefficients of the corresponding trend, and that the t-test statistic is divergent. Hence, some scholars have studied the method of spurious regression between series with trends. Noriega and Ventosa-Santaulària ^[34] and García-Belmonte and Ventosa-Santaulària ^[35] suggest that adding a trend term in the regression model can eliminate the spurious regression caused by a trending mechanism. Wu and You ^[36] also added a trend term to the regression model to avoid spurious regression for series with trends.

Considering its practical implications in real-world economics, the proposed method was designed to resolve spurious regression between trending series. This can be achieved by incorporating a time-trend term into the regression model and consequently applying the CO-BCE technique to this modified model. We can build a regression model with a trend term:

$\begin{equation} y_t = x_t\beta+\alpha t+u_t, \end{equation}$

(5.1)

where $\alpha t$ could capture the deterministic trend of the regressors and $\alpha$ is the parameter of the trend term^†. The rest of the variables are the as same as in Eq (2.1). If $u_t$ is a white noise series, we can use the OLS estimate and the t-statistics is convergent; however, when there is an autocorrelation or a unit root process in $u_t$ , spurious regression occurs by using OLS, and it is necessary to use the method of CO-FGLS to effectively prevent spurious regression; and for the analysis of the economic indicators with a shorter length of the time series, such as the study of China's GDP growth and other related issues, we need to use the GDP series with a non-stationary trend, and the CO-FGLS method has a finite sample bias, so we can effectively use the proposed CO-BCE method for the above model.

^†The model can contain drift, e.g., the explanatory $x_t$ can be a vector whose first element is value one.

6. Simulations

6.1. Monte Carlo

Section 2 theoretically explains that the reason for spurious regression is the existence of autocorrelation in the random error term in the regression model; thus, here, we further verify it via Monte Carlo simulation. Consider the following data generation process: $x_t$ is a first-order AR model with $\alpha_x = 0.9$ , and $y_t$ is also a first-order AR model with $\alpha_y$ . The autocorrelation structure of the random error term is the same as that of the explanatory variables; then, in order to explore the spurious regression that is due to the autocorrelation of the random error term, the cases without and with autocorrelation were set up respectively. The random error terms of their data generation process all followed the standard normal distribution. $y_t$ and $x_t$ are independent of each other, and we built the model as given by Eq (2.1) by using OLS estimation.

We simulated all data generation processes with 1000 iterations, and in each replication, 200 + $n$ observations were generated ( $n$ = 20, 30, 40, and 50), of which the first 200 observations were discarded to eliminate the impact of initial values.

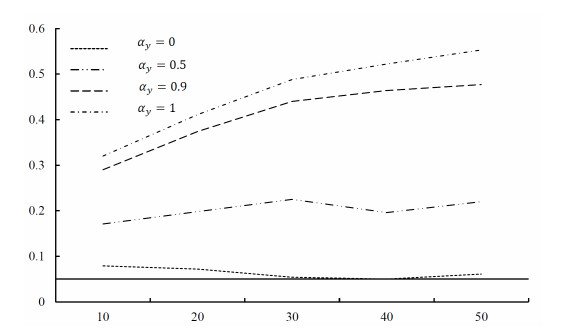
As shown in , the y axis represents the percentage of occurrences in 1000 simulations at a significance level of 0.05, i.e., the proportion of spurious regression. When $\alpha_y = 0$ , $y_t$ is a stationary series following a standard normal distribution; the random error term in the regression model does not contain autocorrelation components; and the probability of spurious regression using the OLS estimation method is very small and close to a given significant level of 0.05, and it can be judged to be a phenomenon of no spurious regression. Alternatively, when $y_t$ is a first-order autocorrelation process, there is spurious regression, and the larger the degree of its autocorrelation, the higher the probability of the appearance of spurious regression, which is consistent with the conclusion demonstrated by the previous theory in Section 2.

Figure 1. The proportion of spurious regression under different levels of autoregressions for random error terms.

*Note: The black solid line in the figure represents a significance level of 0.05.

DownLoad: Full-Size Img PowerPoint

To investigate the finite sample properties of the CO-BCE method in spurious regression, we performed some Monte Carlo simulations and compared the results with those of other three methods: OLS, CO-FGLS ^[29], and BootBC ^[32]. We separated the simulation into three subsections: the first one is the series without a trend, the second one is the series with a trend, and the third one is the series with heteroskedasticity.

6.1.1. Series with no trend

Suppose that we have the following common data generation processes:

$(1)$ DGP1: $z_t = 0.5z_{t-1}+e_t$ ,

$(2)$ DGP2: $z_t = 0.9z_{t-1}+e_t$ ,

$(3)$ DGP3: $z_t = z_{t-1}+e_t$ ,

$(4)$ DGP4: $z_t = \gamma_1z_{t-1}+\gamma_2z_{t-2}+e_{t}$ ,

$(5)$ DGP5: $z_t = z_{t-1}+e_{t}+\eta e_{t-1}$ ,

$(6)$ DGP6: $z_t = \gamma_1z_{t-1}+e_{t}+\eta e_{t-1}$ ,

where $z_t$ stands for $x_t$ or $y_t$ , and $e_t$ follows standard normal distribution. For simplicity, we did not add drift in the regression model; however, we also simulated data processes with drift and found that the drift does not affect the result. $x_t$ and $y_t$ were generated through the use of autocorrelated autoregressive series (DGP1, 2, and 4), a non-stationary Ⅰ(1) process (DGP3), and ARIMA(0, 1, 1) (DGP5) and ARMA(1, 1) (DGP6) data processes. We modeled the regression of Eq (2.1) for the above data generation process. The following tables display the percentage of rejection of the null hypothesis of no linear relationship between $x_t$ and $y_t$ , i.e., the absolute value of the t-value of slope coefficients greater than 1.96.

displays the percentage of rejection for different sample sizes^*, as well as the data generation forms as compared with the other three methods (OLS, CO-FGLS, and BootBC). The results show that the CO-BCE method exhibited the best performance in terms of solving the spurious regression in many situations. It exhibited a low likelihood to obtain the spurious regression between the two stationary and non-stationary independent variables, which means that CO-BCE can also manage the spurious regression between stationary and non-stationary variables. However, when the explanatory variable $x_t$ and interpreted variable $y_t$ are stationary, the performance of the method is not optimal, but it is still good. This is because spurious regression is not likely to occur in two stationary time series when the sample size is small, that is, when the sample size is so small that the characteristics of the time variables are not clear and the correlation of the variables is opaque. When variables $x_t$ and $y_t$ have a strong correlation with the lag, the method CO-BCE performs better. We also simulated the data with drift. The results were the same as the results without drift in . When the sample size becomes large, e.g., $n > 50$ , the probability of the spurious regression will increase, so we just need to use the CO-FGLS method to avoid it^†.

^*When $x_t$ and $y_t$ are other data types, such as when $y_t$ is a second-order autoregressive series and when $x_t$ is a first-order autoregressive series, the method proposed in this paper still has good results. We show only part of the data results to save space.

^†Least squares estimators or other common estimators give very similar results for large sample sizes ^[31].

Table 1. Spurious regression results for the case of a unit root or near unit root process.

	method	20	30	40	50
$x\sim {\rm DGP}1$	OLS	0.208	0.221	0.225	0.213
$y\sim {\rm DGP}2$	CO-FGLS	0.090	0.080	0.077	$\mathbf {0.058}$
	BootBC	$\mathbf {0.084}$	0.072	0.080	0.062
	CO-BCE	${0.085}$	$\mathbf{0.067}$	$\mathbf {0.073}$	${0.059}$
$x\sim {\rm DGP}2$	OLS	0.202	0.218	0.213	0.213
$y\sim {\rm DGP}1$	CO-FGLS	0.151	0.116	0.091	0.081
	BootBC	0.146	0.100	0.074	0.072
	CO-BCE	$\mathbf {0.143}$	$\mathbf{0.097}$	$\mathbf {0.072}$	$\mathbf{0.068}$
$x\sim {\rm DGP}1$	OLS	0.225	0.227	0.255	0.218
$y\sim {\rm DGP}3$	CO-FGLS	0.100	0.073	0.076	0.056
	BootBC	0.098	0.074	0.072	0.056
	CO-BCE	$\mathbf{ 0.082}$	$\mathbf {0.070}$	$\mathbf{0.071}$	$\mathbf{0.055}$
$x\sim {\rm DGP}3$	OLS	0.194	0.242	0.225	0.226
$y\sim {\rm DGP}1$	CO-FGLS	0.139	0.139	0.122	0.081
	BootBC	0.132	0.122	0.100	0.069
	CO-BCE	$\mathbf {0.129}$	$\mathbf{0.119}$	$\mathbf {0.097}$	$\mathbf{0.069}$
$x\sim {\rm DGP}2$	OLS	0.470	0.480	0.521	0.572
$y\sim {\rm DGP}3$	CO-FGLS	0.226	0.165	0.161	0.111
	BootBC	0.178	0.131	0.122	0.089
	CO-BCE	$\mathbf{0.156}$	$\mathbf{0.105}$	$\mathbf{0.109}$	$\mathbf{0.075}$
$x\sim {\rm DGP}3$	OLS	0.452	0.524	0.510	0.557
$y\sim {\rm DGP}2$	CO-FGLS	0.224	0.209	0.165	0.134
	BootBC	0.178	0.161	0.123	0.105
	CO-BCE	$\mathbf{0.158}$	$\mathbf {0.146}$	$\mathbf{0.101}$	$\mathbf{0.097}$
$x\sim {\rm DGP}1$	OLS	0.128	0.118	0.130	0.129
$y\sim {\rm DGP}1$	CO-FGLS	0.106	0.077	0.070	0.071
	BootBC	$\mathbf{0.105}$	0.075	0.068	$\mathbf{0.070}$
	CO-BCE	${0.107}$	$\mathbf {0.073}$	$\mathbf {0.067}$	${0.072}$
$x\sim {\rm DGP}2$	OLS	0.421	0.454	0.437	0.466
$y\sim {\rm DGP}2$	CO-FGLS	0.203	0.164	0.117	0.108
	BootBC	0.167	0.128	0.100	0.086
	CO-BCE	$\mathbf{0.157}$	$\mathbf {0.113}$	$\mathbf {0.088}$	$\mathbf{0.076}$
$x\sim {\rm DGP}3$	OLS	0.534	0.602	0.632	0.687
$y\sim {\rm DGP}3$	CO-FGLS	0.278	0.237	0.226	0.190
	BootBC	0.208	0.183	0.169	0.127
	CO-BCE	$\mathbf{0.178}$	$\mathbf {0.158}$	$\mathbf {0.144}$	$\mathbf{0.103}$
Note: The value in the table denotes the percentage of $\|t\| > 1.96$ .

| Show Table

DownLoad: CSV

presents the probability of the spurious regression under the DGP4 to 6 when $x$ and $y$ have the same structures and we also set various values in the data generating processes. The CO-BCE method can control perfectly the spurious regression problem under several typical cases. However, we can see in the table that the CO-BCE method is not good when $x$ and $y$ both have a weak serial correlation. The first reason is that spurious regression is unlikely to occur between stationary time series in small sample sizes. Second, the error term in the regression model built from two stationary variables may not have serial correlation.

Table 2. Spurious regression results for the case of two similar data generation processes.

	method	20	30	40	50
$x\sim {\rm DGP 4} (0.7, 0.2)$	OLS	0.295	0.336	0.335	0.373
$y\sim {\rm DGP4} (0.65, 0.1)$	CO-FGLS	0.182	0.164	0.120	0.102
	BootBC	0.156	0.139	0.103	0.088
	CO-BCE	$\mathbf {0.148}$	$\mathbf{0.133}$	$\mathbf {0.101}$	$\mathbf{0.087}$
$x\sim {\rm DGP4} (0.65, 0.1)$	OLS	0.291	0.313	0.346	0.356
$y\sim {\rm DGP 4} (0.7, 0.2)$	CO-FGLS	0.152	0.119	0.100	0.086
	BootBC	0.132	0.100	0.086	0.079
	CO-BCE	$\mathbf {0.125}$	$\mathbf{0.096}$	$\mathbf {0.081}$	$\mathbf{0.078}$
$x\sim {\rm DGP5} (0.5)$	OLS	0.573	0.630	0.654	0.698
$y\sim {\rm DGP5} (0.3)$	CO-FGLS	0.293	0.222	0.230	0.181
	BootBC	0.216	0.177	0.163	0.118
	CO-BCE	$\mathbf {0.170}$	$\mathbf{0.146}$	$\mathbf {0.126}$	$\mathbf{0.096}$
$x\sim {\rm DGP5} (0.3)$	OLS	0.564	0.619	0.655	0.692
$y\sim {\rm DGP5} (0.5)$	CO-FGLS	0.242	0.236	0.211	0.170
	BootBC	0.185	0.157	0.146	0.118
	CO-BCE	$\mathbf {0.149}$	$\mathbf{0.123}$	$\mathbf {0.111}$	$\mathbf{0.095}$
$x\sim {\rm DGP6} (0.9, 0.5)$	OLS	0.411	0.436	0.441	0.453
$y\sim {\rm DGP6} (0.8, 0.3)$	CO-FGLS	0.209	0.161	0.133	0.110
	BootBC	0.169	0.132	0.109	0.085
	CO-BCE	$\mathbf {0.139}$	$\mathbf{0.123}$	$\mathbf {0.095}$	$\mathbf{0.082}$
$x\sim {\rm DGP6} (0.8, 0.3)$	OLS	0.406	0.404	0.432	0.427
$y\sim {\rm DGP6} (0.9, 0.5)$	CO-FGLS	0.171	0.119	0.092	0.087
	BootBC	0.132	0.109	0.079	0.071
	CO-BCE	$\mathbf {0.115}$	$\mathbf{0.097}$	$\mathbf {0.065}$	$\mathbf{0.066}$
Note: The value in the table denotes the percentage of $\|t\| > 1.96$ . DGP( $\cdot$ ) represents the value of the parameters in the data generation process, e.g., DGP4 (0.7, 0.2) denotes $\gamma_1=0.7$ and $\gamma=0.2$ , DGP5(0.5) denotes $\eta=0.5$ .

| Show Table

DownLoad: CSV

displays the cases in which the explanatory and response variables have different data structures. When the response variable $y$ has strong autocorrelation, the probability of spurious regression is close to a significance level of 0.05.

Table 3. Spurious regression results for different types of data generation processes.

	method	20	30	40	50
$x\sim {\rm DGP 4} (0.65, 0.1)$	OLS	0.359	0.383	0.416	0.418
$y\sim {\rm DGP 5} (0.3)$	CO-FGLS	0.134	0.081	0.071	0.055
	BootBC	0.104	0.066	0.060	0.046
	CO-BCE	$\mathbf {0.092}$	$\mathbf{0.061}$	$\mathbf {0.053}$	$\mathbf{0.042}$
$x\sim {\rm DGP 5} (0.3)$	OLS	0.339	0.396	0.428	0.424
$y\sim {\rm DGP 4} (0.65, 0.1)$	CO-FGLS	0.203	0.199	0.164	0.173
	BootBC	0.167	0.162	0.132	0.134
	CO-BCE	$\mathbf {0.158}$	$\mathbf{0.145}$	$\mathbf {0.126}$	$\mathbf{0.118}$
$x\sim {\rm DGP 4} (0.65, 0.1)$	OLS	0.289	0.303	0.315	0.327
$y\sim {\rm DGP 6} (0.8, 0.3)$	CO-FGLS	0.124	0.088	0.068	0.063
	BootBC	0.103	0.070	0.061	0.051
	CO-BCE	$\mathbf{0.090}$	$\mathbf{0.064}$	$\mathbf {0.053}$	$\mathbf{0.049}$
$x\sim {\rm DGP 6} (0.8, 0.3)$	OLS	0.292	0.316	0.311	0.323
$y\sim {\rm DGP 4} (0.65, 0.1)$	CO-FGLS	0.165	0.145	0.116	0.087
	BootBC	0.142	0.125	0.096	0.075
	CO-BCE	$\mathbf {0.131}$	$\mathbf{0.119}$	$\mathbf {0.083}$	$\mathbf{0.071}$
$x\sim {\rm DGP 5} (0.5)$	OLS	0.398	0.459	0.493	0.495
$y\sim {\rm DGP 6} (0.8, 0.3)$	CO-FGLS	0.200	0.189	0.145	0.125
	BootBC	0.149	0.154	0.113	0.080
	CO-BCE	$\mathbf {0.121}$	$\mathbf{0.125}$	$\mathbf {0.097}$	$\mathbf{0.074}$
$x\sim {\rm DGP 6} (0.8, 0.3)$	OLS	0.425	0.437	0.480	0.500
$y\sim {\rm DGP 5} (0.5)$	CO-FGLS	0.197	0.120	0.106	0.093
	BootBC	0.150	0.096	0.083	0.084
	CO-BCE	$\mathbf {0.118}$	$\mathbf{0.085}$	$\mathbf {0.082}$	$\mathbf{0.078}$
Note: The value in the table denotes the percentage of $\|t\| > 1.96$ .

| Show Table

DownLoad: CSV

Briefly, for stationary or non-stationary series with no trend, spurious regression will occur to a great extent as a result of applying OLS to finite samples, i.e., reject the null hypothesis that there is a significant relationship between $x_t$ and $y_t$ according to the t-test of the slope coefficients. CO-FGLS can also reduce the spurious regression but the percentages of rejections of the CO-BCE method will be lower and almost reach the significance level of 0.05^*, which means that the probability of spurious regression has been largely reduced. In a word, CO-BCE can efficiently to solve the spurious regression problem.

^*In some situations, the rejection value is smaller than 0.05.

6.1.2. Series with a trend

Economic variables are usually time series with trends. We also simulated the data with the trend as follows:

$\begin{align} &z_t = z_{t-1}+f_zt+e_t, \end{align}$

(6.1a)

$\begin{align} &z_t = 0.9z_{t-1}+f_zt+e_t. \end{align}$

(6.1b)

Let $x_t$ and $y_t$ be $z_t$ ; $f_zt$ is the trend term and $e_t$ is similar to the data generation processes above in Section 6.1.1^†. We chose to solve this spurious regression between these kinds of time series by adding a trend term in the regression model given by (5.1) mentioned in Section 4.

^†This data generation process just considers the unit root and high autocorrelated series with the trend since we just need to use OLS estimation for the error term with no serial correlation or unit root.

Table 4 displays the variables with trends and unit root processes; see Eq (6.1a). Even though CO-FGLS can reduce the probability of spurious regression, CO-BCE is the best among all of the methods. When the explanatory and response variables have the same trending properties, spurious regression will occur as a result of using OLS estimation. And, when the sample size is increased, the effect of CO-BCE is improved; thus, the problem of spurious regression can be largely solved.

Table 4. Spurious regression results for the case of normal distribution for unit root series.

	method	20	30	40	50
$f_x=0$	OLS	0.530	0.647	0.679	0.723
$f_y=0.2$	CO-FGLS	0.122	0.082	0.071	0.069
	BootBC	0.107	0.076	0.067	$\mathbf{0.057}$
	CO-BCE	$\mathbf{0.098}$	$\mathbf {0.070}$	$\mathbf {0.060}$	${0.058}$
$f_x=0.2$	OLS	0.562	0.623	0.715	0.738
$f_y=0$	CO-FGLS	0.128	0.097	0.085	0.080
	BootBC	0.114	0.084	0.074	${0.064}$
	CO-BCE	$\mathbf{0.110}$	$\mathbf {0.077}$	$\mathbf {0.065}$	$\mathbf{0.062}$
$f_x=0$	OLS	0.713	0.791	0.791	0.822
$f_y=0.9$	CO-FGLS	0.098	0.062	0.052	0.054
	BootBC	0.096	0.075	0.063	${0.051}$
	CO-BCE	$\mathbf{0.089}$	$\mathbf {0.063}$	$\mathbf {0.051}$	$\mathbf{0.051}$
$f_x=0.9$	OLS	0.713	0.764	0.806	0.818
$f_y=0$	CO-FGLS	0.109	0.079	0.073	0.066
	BootBC	0.093	0.064	0.063	$\mathbf{0.055}$
	CO-BCE	$\mathbf{0.087}$	$\mathbf {0.063}$	$\mathbf {0.058}$	${0.060}$
$f_x=0.2$	OLS	0.803	0.847	0.897	0.927
$f_y=0.9$	CO-FGLS	0.096	0.073	0.068	0.067
	BootBC	0.095	0.080	0.061	0.058
	CO-BCE	$\mathbf{0.093}$	$\mathbf {0.068}$	$\mathbf {0.051}$	$\mathbf{0.057}$
$f_x=0.9$	OLS	0.780	0.856	0.897	0.928
$f_y=0.2$	CO-FGLS	0.108	0.079	0.084	0.071
	BootBC	0.097	0.074	0.069	$\mathbf{0.059}$
	CO-BCE	$\mathbf{0.087}$	$\mathbf {0.068}$	$\mathbf {0.065}$	${0.062}$
$f_x=0.2$	OLS	0.583	0.708	0.788	0.833
$f_y=0.2$	CO-FGLS	0.110	0.084	0.085	0.076
	BootBC	0.107	0.077	0.072	0.070
	CO-BCE	$\mathbf{0.100}$	$\mathbf {0.071}$	$\mathbf {0.064}$	$\mathbf{0.068}$
$f_x=0.9$	OLS	1.000	1.000	1.000	1.000
$f_y=0.9$	CO-FGLS	0.126	0.096	0.106	0.092
	BootBC	0.111	0.083	0.086	0.079
	CO-BCE	$\mathbf{0.100}$	$\mathbf {0.075}$	$\mathbf {0.076}$	$\mathbf{0.075}$
Note: The value in the table denotes the percentage of $\|t\| > 1.96$ .

| Show Table

DownLoad: CSV

In Table 5, we show the spurious regression results for the variables with strong correlation and trends; see Eq (6.1b). Compared with Table 4, variables with strong correlation in Table 5 have the lower percentage of rejection of all methods, whereas using CO-BCE can cause the rejection rate to almost reach 0.05. Even though CO-FGLS can also solve the spurious regression, CO-BCE has a lower rejection value.

Table 5. Spurious regression results for the case of normal distribution for highly correlated series.

	method	20	30	40	50
$f_x=0$	OLS	0.436	0.543	0.602	0.617
$f_y=0.2$	CO-FGLS	0.111	0.090	0.063	0.056
	BootBC	0.107	0.087	0.056	$\mathbf{0.051}$
	CO-BCE	$\mathbf{0.092}$	$\mathbf {0.083}$	$\mathbf {0.048}$	${0.052}$
$f_x=0.2$	OLS	0.443	0.520	0.561	0.627
$f_y=0$	CO-FGLS	0.111	0.087	0.085	0.069
	BootBC	0.104	0.085	0.070	${0.062}$
	CO-BCE	$\mathbf{0.102}$	$\mathbf {0.082}$	$\mathbf {0.063}$	$\mathbf{0.057}$
$f_x=0$	OLS	0.594	0.656	0.661	0.682
$f_y=0.9$	CO-FGLS	${0.087}$	${0.066}$	$\mathbf{0.046}$	$\mathbf{0.051}$
	BootBC	0.098	0.070	0.048	0.053
	CO-BCE	$\mathbf{0.087}$	$\mathbf {0.066}$	${0.048}$	${0.053}$
$f_x=0.9$	OLS	0.597	0.635	0.621	0.662
$f_y=0$	CO-FGLS	0.101	$\mathbf{0.064}$	0.065	0.058
	BootBC	0.087	0.067	0.052	0.056
	CO-BCE	$\mathbf{0.086}$	${0.071}$	$\mathbf {0.046}$	$\mathbf{0.054}$
$f_x=0.2$	OLS	0.779	0.889	0.955	0.992
$f_y=0.9$	CO-FGLS	0.103	0.069	0.067	0.055
	BootBC	0.097	0.070	0.054	0.054
	CO-BCE	$\mathbf{0.089}$	$\mathbf {0.067}$	$\mathbf {0.050}$	$\mathbf{0.054}$
$f_x=0.9$	OLS	0.773	0.901	0.955	0.988
$f_y=0.2$	CO-FGLS	0.100	$\mathbf{0.067}$	0.077	0.067
	BootBC	0.091	0.072	0.065	0.062
	CO-BCE	$\mathbf{0.084}$	${0.076}$	$\mathbf {0.062}$	$\mathbf{0.059}$
$f_x=0.2$	OLS	0.558	0.763	0.864	0.958
$f_y=0.2$	CO-FGLS	0.109	0.083	0.077	0.070
	BootBC	0.107	0.079	0.071	0.065
	CO-BCE	$\mathbf{0.104}$	$\mathbf {0.079}$	$\mathbf {0.067}$	$\mathbf{0.064}$
$f_x=0.9$	OLS	1.000	1.000	1.000	1.000
$f_y=0.9$	CO-FGLS	0.123	0.092	0.093	0.077
	BootBC	0.105	0.087	0.084	$\mathbf{0.066}$
	CO-BCE	$\mathbf{0.098}$	$\mathbf {0.083}$	$\mathbf {0.075}$	${0.068}$
Note: The value in the table denotes the percentage of $\|t\| > 1.96$ .

| Show Table

DownLoad: CSV

To sum up, we found that the CO-FGLS method is also effective when we compared the series with the trend with the series without a trend, but CO-BCE is better. In Section 4, we mentioned that the reason for adding a linear trend in the regression model is to omit the important explanatory variables when response variables or explanatory variables have trends. Hence, the coefficient of the AR(1) model used in the CO-FGLS method exhibited little bias, so the effect of bias-corrected estimation in CO-BCE is limited. But, CO-BCE is still good and further reduces the percentage of rejection. In general, the CO-BCE method performs better in terms of solving the spurious regression problem.

6.1.3. Series with heteroskedasticity

Some economic variables have ARCH or GARCH effects, such as the time series of stock prices. In order to verify that CO-BCE is also effective for series containing heteroskedasticity, we considered the explanatory variable $y_t$ to exhibit ARCH and GARCH processes respectively:

$\begin{align} &y_t = g+u_{yt}, \end{align}$

(6.2a)

$\begin{align} &x_t = 0.9x_{t-1}+e_t, \end{align}$

(6.2b)

where $g$ follows AR or ARMA processes, $u_{yt}$ is an ARCH or a GARCH process, $x_t$ is an AR(1) process^*, and $x_t$ and $y_t$ is independent of each other.

^*In order to verify whether the method proposed is still valid for the heteroskedasticity present in the random error term, $y_t$ was set to exibit ARCH or GARCH effects and $x_t$ was set as a first-order autoregressive process because the autocorrelation and heteroskedasticity structure in the random error term is consistent with the explanatory variable $y_t$ . In this part of the simulation, the parameters of the ARCH and GARCH processes were used with the default parameter values from the fGarch package in R; see https://cran.r-project.org/web/packages/fGarch/fGarch.pdf.

As shown in Table 6, spurious regression occurred as a result of applying the OLS method to four data generation processes, and the greater its autocorrelation, the greater the probability of spurious regression, i.e., for the third and fourth groups of generated data in the table, the rate of spurious regression that occurs when the autoregressive coefficient is 0.9 is greater than that when the coefficient is 0.5, and the result also supports the conclusions obtained via theoretical analyses of spurious regression in Section 4. The proposed CO-BCE method yielded a lower probability of spurious regression in many data generation processes, and this result was better than that of the other compared estimation methods, so CO-BCE still has good results for series containing heteroskedasticity. Overall, the CO-BCE works well as a method to solve the spurious regression problem in finite samples, and it is robust under a variety of data structures.

Table 6. Spurious regression results for ARCH or GARCH processes.

	method	20	30	40	50
$y_t\sim$ AR(1)-ARCH(2)^†	OLS	0.191	0.202	0.206	0.201
	CO-FGLS	0.132	0.095	0.091	0.090
	BootBC	0.124	0.082	0.076	0.087
	CO-BCE	$\mathbf {0.123}$	$\mathbf{0.081}$	$\mathbf {0.075}$	$\mathbf{0.087}$
$y_t\sim \rm AR([1,5])-GARCH(1, 1)$	OLS	0.184	0.206	0.246	0.244
	CO-FGLS	0.127	0.126	0.112	0.116
	BootBC	0.111	0.108	0.097	0.096
	CO-BCE	$\mathbf {0.110}$	$\mathbf{0.103}$	$\mathbf {0.096}$	$\mathbf{0.096}$
$y_t\sim \rm ARMA(1, 2)-GARCH(1, 1)$	OLS	0.177	0.185	0.185	0.176
$ar=0.5$	CO-FGLS	0.105	0.083	0.068	0.067
	BootBC	0.099	0.071	$\mathbf {0.052}$	0.059
	CO-BCE	$\mathbf {0.099}$	$\mathbf{0.068}$	0.054	$\mathbf{0.056}$
$y_t\sim \rm ARMA(1, 2)-GARCH(1, 1)$	OLS	0.373	0.415	0.442	0.453
$ar=0.9$	CO-FGLS	0.165	0.125	0.119	0.108
	BootBC	0.119	0.096	0.094	0.088
	CO-BCE	$\mathbf {0.107}$	$\mathbf{0.082}$	$\mathbf {0.084}$	$\mathbf{0.084}$
Note: The value in the table denotes the percentage of $\|t\| > 1.96$ , $ar$ is the value of efficient of AR model.

| Show Table

DownLoad: CSV

6.2. A real example

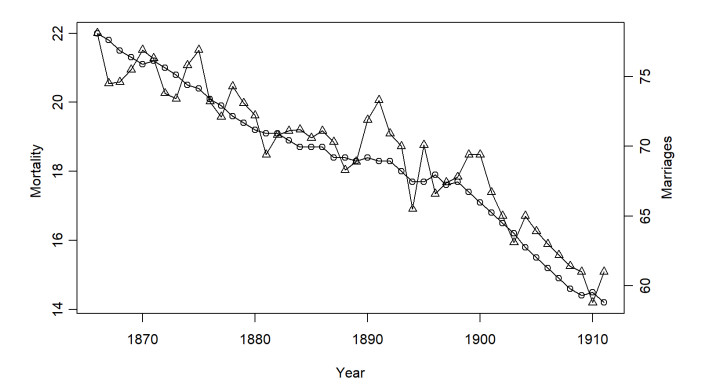
The spurious regression problem was proposed by Yule ^[1]. By using OLS estimation, he found that, from 1866 to 1911, the proportion of the England Church marriages and the mortality rate in England and Wales had a strong correlation. Two time series seem to have similar trends, as can be seen in Figure 2, but they are not correlated with each other according to their actual meaning.

Figure 2. The mortality rate (line with circle in left) and Church rate of England marriages (line with triangle in right) in England and Wales.

DownLoad: Full-Size Img PowerPoint

To test the efficiency of the CO-BCE method as a tool to solve the spurious regression for series with a trend, we used the data from Yule ^[1] and chose $y_t$ to denote the mortality rate (per 1000 persons) of England and Wales^*; $x_t$ denotes the ratio of Church of England marriages to all marriages (per 1000 persons) in England and Wales^†. Then, we employed OLS, CO-FGLS, and CO-BCE methods for the model given by Eq (5.1).

^*https://github.com/renatopp/arff-datasets/blob/master/statlib/numeric/mhsets_roberts-yule1.arff.

^†https://github.com/renatopp/arff-datasets/blob/master/statlib/numeric/mhsets_roberts-yule2.arff.

According to , both time series have obvious trends, so we used the model given by Eq (5.1) with drift. presents the drifts, slope coefficients, and their corresponding t-values. When we used OLS to apply the regression model for this real example without a trend term, spurious regression occurred, i.e., the slope coefficient was 0.4185 and the t-value was larger than 1.96 at the significance level of 0.05, which means that they have a significant linear relationship. The result for CO-FGLS shows that the method can manage the spurious regression problem since the t-value (1.1392) of the slope coefficient was smaller than 1.96 and the estimator of the coefficient was 0.0193. The results of BootBC and CO-BCE were similar. The slope coefficient estimators of BootBC and CO-FGLS was 0.0124 and 0.0132, respectively, and their t-values were further reduced relative to the CO-FGLS to a certain extent. BootBC and CO-BCE were more effective than CO-FGLS in terms of solving the spurious regression problem between two independent variables. We mentioned that the t-value of $\beta$ was 0.8127 and 0.8543 for BootBC and CO-BCE which are both small, and BootBC exhibited a slightly lower t-value than CO-BCE. The possible reason for this result is that the series in the real example contained the random disturbances. The random disturbances may affect the result. In addition, most data generation processes in the simulations, CO-BCE performed better than BootBC. Also, the t-value of $\beta_0$ and $\alpha$ for CO-BCE were lower than for BootBC. Therefore, we think that CO-BCE performs significantly better. In summary, it means that there is no significant linear relationship between church marriages and mortality.

Table 7. Empirical results.

	$\beta_0$	$\beta$	$\alpha$
OLS	$-10.8466^{***}$	$0.4185^{***}$	-
	(-7.61447)	(20.5251)
CO-FGLS	$7.0961^{***}$	0.0193	$-0.0532^{***}$
	(15.4128)	(1.1392)	(-18.057630)
BootBC	$5.7454^{***}$	$0.0124$	$-0.0431^{***}$
	(17.3894)	(0.8127)	(-17.5125)
CO-BCE	$5.9327^{***}$	$0.0132$	$-0.0445^{***}$
	(17.1250)	(0.8543)	(-17.6583)
Note: $\beta_0$ is drift in the regression model, $^{***}$ denotes the significance level of 0.05, and the values in brackets represents the t-value of the corresponding parameter.

| Show Table

DownLoad: CSV

7. Conclusions

In this paper, we applied the Cochrane-Orcutt feasible generalized least squares method based on a bias-corrected method to solve the spurious regression problem caused by the error term with autocorrelation or a unit root process in the regression model for the case of finite samples. We have demonstrated, through the use of theoretical inference, that spurious regression is caused by the autocorrelation component in the random error term. The proposed CO-BCE method is easy to implement and we do not have to estimate the long-run variance of the error term to avoid the choice of kernel function and bandwidth. A series of simulations has shown that CO-BCE is efficient as a tool to solve the spurious regression problem, unlike the other OLS, CO-FGLS, and BootBC methods. In the case of a small sample size, the performance of the CO-BCE methods can reduce the spurious regression as much as possible. Besides, when the response variable is a highly autocorrelated series or unit root, the effect of the CO-BCE method is better. Moreover, the effect of CO-BCE as a tool to reduce spurious regression is good regardless of whether the variable is stationary or non-stationary. We have also taken into account that real economic variables usually exhibit trends over time, and we proposed a time-series model with trends to solve the spurious regression between series exhibiting trends. In addition, common time-series data may contain ARCH or GARCH effects; the series containing heteroskedasticity were simulated, and it was found that CO-BCE is also effective. Finally, we applied CO-BCE to the mortality and Church marriages data from Yule and found that there is no significant relationship between these two variables. The real example illustrates that our method is practical.

Several interesting and valuable issues deserve further study. For example, it will be important to investigate the more general method in the case of the AR(p) process for the error term in the regression model or more complex data structures; see Wang and Hafner ^[37]. Spurious regression also occurs in panel data ^[38]. Besides, spurious regression has recently been further extended to the factor analysis model ^[39]. The form of a trend in a series could be nonlinear or polynomial. Adding a linear trend term in the regression model is not efficient. Some new methods should be proposed to solve this problem. In real application, stock data have different forms of characteristics and can usually be characterized by using GARCH family models ^[40]. Whether other components in the data will cause pseudo regression remains to be investigated.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by the National Social Science Fund of China (Grant No. 23BTJ043).

Conflict of interest

The authors declare no conflicts of interest.

References

[1]	G. U. Yule, Why do we sometimes get nonsense-correlations between time-series, J. Royal Stat. Soc., 89 (1926), 1–63. https://doi.org/10.1017/CBO9781139170116.012 doi: 10.1017/CBO9781139170116.012
[2]	Y. Wen, Y. Xu, Statistical monitoring of economic growth momentum transformation: empirical study of Chinese provinces, AIMS Math., 8 (2023), 24825–24847. https://doi.org/10.3934/math.20231266 doi: 10.3934/math.20231266
[3]	Z. Li, F. Zou, B. Mo, Does mandatory CSR disclosure affect enterprise total factor productivity, Econ. Res., 35 (2022), 4902–4921. https://doi.org/10.1080/1331677X.2021.2019596 doi: 10.1080/1331677X.2021.2019596
[4]	N. Stanojević, K. Zakić, China and deglobalization of the world economy, Natl. Account. Rev., 5 (2023), 67–85. https://doi.org/10.3934/NAR.2023005 doi: 10.3934/NAR.2023005
[5]	Y. Liu, Z. Li, M. Xu, The influential factors of financial cycle spillover: evidence from China, Emerg. Mark. Financ. Tr., 56 (2020), 1336–1350. https://doi.org/10.1080/1540496X.2019.1658076 doi: 10.1080/1540496X.2019.1658076
[6]	Z. Li, J. Zhong, Impact of economic policy uncertainty shocks on China's financial conditions, Financ. Res. Lett., 35 (2020), 101303. https://doi.org/10.1016/j.frl.2019.101303 doi: 10.1016/j.frl.2019.101303
[7]	Z. Li, B. Mo, H. Nie, Time and frequency dynamic connectedness between cryptocurrencies and financial assets in China, Int. Rev. Econ. Financ., 86 (2023), 46–57. https://doi.org/10.1016/j.iref.2023.01.015 doi: 10.1016/j.iref.2023.01.015
[8]	N. T. Giannakopoulos, D. P. Sakas, N. Kanellos, C. Christopoulos, Web analytics and supply chain transportation firms' financial performance, Natl. Account. Rev., 5 (2023), 405–420. https://doi.org/10.3934/NAR.2023023 doi: 10.3934/NAR.2023023
[9]	Z. Li, Z. Huang, H. Dong, The influential factors on outward foreign direct investment: evidence from the "the belt and road", Emerg. Mark. Financ. Tr., 55 (2019), 3211–3226. https://doi.org/10.1080/1540496X.2019.1569512 doi: 10.1080/1540496X.2019.1569512
[10]	M. Hong, J. He, K. Zhang, Z. Guo, Does digital transformation of enterprises help reduce the cost of equity capital, Math. Biosci. Eng., 20 (2023), 6498–6516. https://doi.org/10.3934/mbe.2023280 doi: 10.3934/mbe.2023280
[11]	Z. Li, J. Zhu, J. He, The effects of digital financial inclusion on innovation and entrepreneurship: a network perspective, Electron. Res. Arch., 30 (2022), 4740–4762. https://doi.org/10.3934/era.2022240 doi: 10.3934/era.2022240
[12]	Z. Li, H. Chen, B. Mo, Can digital finance promote urban innovation? Evidence from China, Borsa Istanb. Rev., 23 (2023), 285–296. https://doi.org/10.1016/j.bir.2022.10.006 doi: 10.1016/j.bir.2022.10.006
[13]	Z. Li, C. Yang, Z. Huang, How does the fintech sector react to signals from central bank digital currencies, Financ. Res. Lett., 50 (2022), 103308. https://doi.org/10.1016/j.frl.2022.103308 doi: 10.1016/j.frl.2022.103308
[14]	Y. Liu, L. Chen, H. Luo, Y. Liu, Y. Wen, The impact of intellectual property rights protection on green innovation: a quasi-natural experiment based on the pilot policy of the Chinese intellectual property court, Math. Biosci. Eng., 21 (2024), 2587–2607. https://doi.org/10.3934/mbe.2024114 doi: 10.3934/mbe.2024114
[15]	Y. Wang, J. Liu, X. Yang, M. Shi, R. Ran, The mechanism of green finance's impact on enterprises' sustainable green innovation, Green Financ., 5 (2023), 452–478. https://doi.org/10.3934/GF.2023018 doi: 10.3934/GF.2023018
[16]	J. Duan, T. Liu, X. Yang, H. Yang, Y. Gao, Financial asset allocation and green innovation, Green Financ., 5 (2023), 512–537. https://doi.org/10.3934/GF.2023020 doi: 10.3934/GF.2023020
[17]	Z. Li, Z. Huang, Y. Su, New media environment, environmental regulation and corporate green technology innovation: evidence from China, Energy Economics, 119 (2023), 106545. https://doi.org/10.1016/j.eneco.2023.106545 doi: 10.1016/j.eneco.2023.106545
[18]	S. K. Agyei, A. Bossman, Investor sentiment and the interdependence structure of GIIPS stock market returns: a multiscale approach, Quant. Financ. Econ., 7 (2023), 87–116. https://doi.org/10.3934/QFE.2023005 doi: 10.3934/QFE.2023005
[19]	J. Saleemi, Political-obsessed environment and investor sentiments: pricing liquidity through the microblogging behavioral perspective, Data Sci. Financ. Econ., 3 (2023), 196–207. https://doi.org/10.3934/DSFE.2023012 doi: 10.3934/DSFE.2023012
[20]	T. C. Chiang, Stock returns and inflation expectations: evidence from 20 major countries, Quant. Financ. Econ., 7 (2023), 538–568. https://doi.org/10.3934/QFE.2023027 doi: 10.3934/QFE.2023027
[21]	C. Granger, N. Hyung, Y. Jeon, Spurious regression with stationary series, Appl. Econ., 33 (2001), 899–904. https://doi.org/10.1080/00036840121734 doi: 10.1080/00036840121734
[22]	C. Granger, P. Newbold, Spurious regressions in econometrics, J. Econometrics, 2 (1974), 111–120. https://doi.org/10.1016/0304-4076(74)90034-7 doi: 10.1016/0304-4076(74)90034-7
[23]	T. H. Kim, Y. S. Lee, P. Newbold, Spurious regressions with stationary processes around linear trends, Econ. Lett., 83 (2004), 257–262. https://doi.org/10.1016/j.econlet.2003.10.020 doi: 10.1016/j.econlet.2003.10.020
[24]	D. Ventosa-Santaulária, Spurious regression, J. Probab. Stat., 2009 (2009), 1–27. https://doi.org/10.1155/2009/802975 doi: 10.1155/2009/802975
[25]	H. Liu, The analysis of spurious regressions instationary processes without drifts, J. Quant. Tech. Econ., 27 (2010), 142–154. https://doi.org/10.13653/j.cnki.jqte.2010.11.001 doi: 10.13653/j.cnki.jqte.2010.11.001
[26]	B. T. McCallum, Is the spurious regression problem spurious, Econ. Lett., 107 (2010), 321–323. https://doi.org/10.1016/j.econlet.2010.02.004 doi: 10.1016/j.econlet.2010.02.004
[27]	H. Liu, A study on the properties and correction of HAC method and its application in the spurious regression, J. Quant. Tech. Econ., 32 (2015), 148–161. https://doi.org/10.13653/j.cnki.jqte.2015.11.010 doi: 10.13653/j.cnki.jqte.2015.11.010
[28]	H. Liu, C. Li, Application of bias-correction prewhitening HAC methods in the spurious regression, J. Quant. Tech. Econ., 30 (2013), 109–123. https://doi.org/10.13653/j.cnki.jqte.2013.08.021 doi: 10.13653/j.cnki.jqte.2013.08.021
[29]	C. Y. Choi, L. Hu, M. Ogaki, Robust estimation for structural spurious regressions and a Hausman-type cointegration test, J. Econometrics, 142 (2008), 327–351. https://doi.org/10.1016/j.jeconom.2007.06.003 doi: 10.1016/j.jeconom.2007.06.003
[30]	M. Wu, Fgls method based on finite samples, J. Quant. Tech. Econ., 30 (2013), 148–160. https://doi.org/10.13653/j.cnki.jqte.2013.07.022 doi: 10.13653/j.cnki.jqte.2013.07.022
[31]	S. H. Sørbye, P. G. Nicolau, H. Rue, Finite-sample properties of estimators for first and second order autoregressive processes, Stat. Infer. Stoch. Pro., 25 (2022), 577–598. https://doi.org/10.1007/s11203-021-09262-4 doi: 10.1007/s11203-021-09262-4
[32]	J. H. Kim, Forecasting autoregressive time series with bias-corrected parameter estimators, Int. J. Forecast., 19 (2003), 493–503. https://doi.org/10.1016/S0169-2070(02)00062-6 doi: 10.1016/S0169-2070(02)00062-6
[33]	S. Wang, J. Hu, Trend-cycle decomposition and stochastic impact effect of Chinese GDP, Econ. Res. J., 44 (2009), 65–76.
[34]	A. E. Noriega, D. Ventosa-Santaulária, Spurious regression and trending variables, Oxford Bull. Econ. Stat., 69 (2007), 439–444. https://doi.org/10.1111/j.1468-0084.2007.00481.x doi: 10.1111/j.1468-0084.2007.00481.x
[35]	L. García-Belmonte, D. Ventosa-Santaulária, Spurious regression and lurking variables, Stat. Probab. Lett., 81 (2011), 2004–2010. https://doi.org/10.1016/j.spl.2011.08.015 doi: 10.1016/j.spl.2011.08.015
[36]	M. Wu, P. You, Solution of spurious regression with trending variables, J. Quant. Tech. Econ., 12 (2016), 113–128. https://doi.org/10.13653/j.cnki.jqte.2016.12.007 doi: 10.13653/j.cnki.jqte.2016.12.007
[37]	C. S. H. Wang, C. M. Hafner, A simple solution of the spurious regressionproblem, Stud. Nonlinear Dyn. Econ., 22 (2018), 1–14. https://doi.org/10.1515/snde-2015-0040 doi: 10.1515/snde-2015-0040
[38]	C. Kao, Spurious regression and residual-based testsfor cointegration in panel data, J. Econometrics, 90 (1999), 1–44. https://doi.org/10.1016/S0304-4076(98)00023-2 doi: 10.1016/S0304-4076(98)00023-2
[39]	A. Onatski, C. Wang, Spurious factor analysis, Econometrica, 89 (2021), 591–614. https://doi.org/10.3982/ECTA16703 doi: 10.3982/ECTA16703
[40]	M. Khumalo, H. Mashele, M. Seitshiro, Quantification of the stock market value at risk by using fiaparch, hygarch and figarch models, Data Sci. Financ. Econ., 3 (2023), 380–400. https://doi.org/10.3934/DSFE.2023022 doi: 10.3934/DSFE.2023022

This article has been cited by:

Xinglin Liu, Jing Zhou, Susmita Lahiri (Ganguly),, Analysis of the Kuznets curve relationship between economic development and ecological environment in Aba Prefecture, 2025, 20, 1932-6203, e0319929, 10.1371/journal.pone.0319929

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1329) PDF downloads(61) Cited by(1)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Bias correction based on AR model in spurious regression