An efficient numerical scheme in reproducing kernel space for space fractional partial differential equations

1.   Introduction

Fractional differential equations (FDEs) can describe various practical problems, but due to the non-locality of fractional operators, their numerical methods and theoretical analysis are in the early stage of development, which brings challenges to the acquisition of exact solutions. Therefore, the search for numerical solutions to these equations is difficult and urgent. FDEs have been widely applied in ecology, medicine, physics, hydrology, and other fields ^{[1,2,3,4,5,6]}. For example, space FDEs have been applied in image denoising and enhancement, and have important application value in medical images, transportation, remote sensing images, and other fields ^[7,8,9].

The theoretical study for FDEs has been developed rapidly ^{[10,11,12,13,14,15,16]}. Luchko ^[17] established the unique existence for solutions to time FDEs. Sakamoto and Yamamoto ^[18] proved the unique existence for solutions to space FDEs. Cheng et al. ^[19] studied the uniqueness for inverse problems to FDEs. Li et al. ^[20] established the stability for FDEs with non-instantaneous integral pulses and multi-point boundary conditions.

In terms of numerical methods, references are growing rapidly ^{[21,22,23,24,25]}. Qazza, Saadeh, and Salah ^[26] proposed a direct power series method for FDEs. Hashemi et al. ^[27] applied shifted Chebyshev polynomials to time-fractional diffusion-wave equations. Peykrayegan et al. ^[28] proposed the Jacobi-Gauss collocation approach to approximate fractional singular delay integro-differential problems. Turkyilmazoglu ^[29] applied the adomian decomposition method to FDEs. Shikrani et al. ^[30] used the hybrid B-spline collocation approach to solve the space FDEs. Jiang and Lin ^[31] used the reproducing kernel (RK) approach to approximate fractional advection-dispersion equations.

The following space FDEs ^[30] are considered in this article:

Here, $T > 0$ and $L > 0$ are fixed, $c\left({x, t} \right),$$\vartheta \left(x \right),$$d\left({x, t} \right),$${\theta _1}\left(t \right),$$f\left({x, t} \right)$, and ${\theta _2}\left(t \right)$ are known functions that are smooth enough. The Riemann-Liouville derivative for $2 > \alpha > 1$ is shown in ^[9] by

We aim to establish a numerical scheme for space FDEs by the RK method. In addition, the advantages of this approach are as follows:

1) The high-precision global approximate solution to the equation is obtained.

2) The numerical calculation program is simple.

3) Smaller errors can occur when larger step sizes are used. Therefore, high precision approximate solutions can be obtained in a very short time.

RK functions in Hilbert Spaces and their related theories are widely used in digital image processing, neural network modeling, and numerical simulations ^{[32,33,34,35]}. In practical applications, the RK method is widely applied to solve various integral and differential equations because of its global nature and high precision ^[36,37,38]. Within the last ten years, more scholars have used the RK approach to solve various FDEs ^{[39,40,41,42]}. The literature proves that the RK approach has many advantages and deserves further study.

In this paper, the approximate solution to Eqs (1.1) and (1.2) is given in RK space. Driven by ^[43], a procedure is presented for improving the existing approach, bypassing the Gram-Schmidt orthogonal (GSO) process proposed in ^[31], which has lower accuracy and slower operation speed under the same conditions. Subsequently, enlightened by ^[44], a simpler RK than ^[45] is applied, promoting greater acceleration of the calculation and further improvements in accuracy ^[43,46].

In order to solve Eqs (1.1) and (1.2) in the RK space, the conditions (1.2) need to be homogenized. For convenience, the solution to the new equations is expressed by $u(x, t),$ so,

where $L:\; W\left(D \right) \to \tilde W\left(D \right),$ $W\left(D \right)$ and $\tilde W\left(D \right)$ will be given in the following sections.

2.   RK space $W\left(D \right)$

In this section, RK space $W\left(D \right)$ is constructed from ^[44] as a premier book about numerical approaches of RK spaces, which constructs a much simpler RK than ^[45].

First, the RK spaces ${W_1}\left[{0, T} \right],$ ${W_2}\left[{0, L} \right]$ and ${W_3}\left[{0, L} \right]$ are introduced as follows.

Definition 2.1. ${W_1}\left[{0, T} \right] = \left\{ {\left. \nu \right|} \right.\nu '$ is a real-valued function that is absolutely continuous in $\left[{0, T} \right]$, $\nu \left(0 \right) = 0$, $\left. {\nu '' \in {L^2}\left[{0, T} \right]} \right\}.$ Its inner product in ${W_1}\left[{0, T} \right]$ is defined by

Definition 2.2. ${W_2}\left[{0, L} \right] = \left\{ {\left. \nu \right|} \right.\nu ''$ is a real-valued function that is absolutely continuous in $\left[{0, L} \right]$, $\nu \left(L \right) = 0$, $\nu \left(0 \right) = 0$, $\left. {\nu ''' \in {L^2}\left[{0, L} \right]} \right\}$. Its inner product in ${W_2}\left[{0, L} \right]$ is defined as

Definition 2.3. ${W_3}\left[{0, L} \right] = \left\{ {\left. \nu \right|} \right.\nu$ is a real-valued function that is absolutely continuous in $\left[{0, L} \right]$, $\left. {\nu ' \in {L^2}\left[{0, L} \right]} \right\}$. Its inner product in ${W_3}\left[{0, L} \right]$ is defined as:

The norms are defined by ${\left\| \nu \right\|_{{W_k}}} = \sqrt {{{\left\langle {\nu, \nu } \right\rangle }_{{W_k}}}}$ for $k = 1, 2, 3.$ It is shown that ${W_1}\left[{0, T} \right]$, ${W_2}\left[{0, L} \right]$ and ${W_3}\left[{0, L} \right]$ are all RK spaces, whose RKs

which are given by (9) and (11) in ^[31] and ^[47], respectively.

Definition 2.4. $W\left(D \right) = \left\{ \nu \right.|\frac{{{\partial ^3}\nu }}{{\partial {x^2}\partial t}}$ is a real-valued function that is absolutely continuous in $D$, $\nu \left({x, 0} \right) = 0,$$\nu \left({L, t} \right) = 0,$$\nu \left({0, t} \right) = 0,$$\frac{{{\partial ^5}\nu }}{{\partial {x^3}\partial {t^2}}} \in \left. {{L^2}\left(D \right)} \right\}$. Its norm and inner product in $W\left(D \right)$ are respectively defined as

with reference to ^[38], $W\left(D \right)$ is an RK space, and its RK is

Here, $K1\left({ \cdot, \cdot } \right)$ and $K2\left({ \cdot, \cdot } \right)$ are respectively shown by (2.4) and (2.5).

Similarly, $\tilde W\left(D \right)$ is an RK space, and its RK is

Here, $K3\left({ \cdot, \cdot } \right)$ is given by (2.6).

3.   Numerical method

The series form for the numerical solution of Eqs (1.4) and (1.5) and its implementation in the RK space $W\left(D \right)$ are given in this section.

In (1.4) and (1.5), $L:W\left(D \right) \to \tilde W\left(D \right)$ is a linear bounded operator because $F\left(x, t\right),$$c\left({x, t} \right)$ and $d\left({x, t} \right)$ are smooth enough. A countable dense subset ${\left\{ {\left({{x_l}, {t_l}} \right)} \right\}_{l \in \mathbb{N}}} \subset D$ is chosen. Put ${\varphi _l}(x, t) = \tilde K\left({x, {x_l}, t, {t_l}} \right)$ and ${\phi _l}(x, t) = {L^ * }{\varphi _l}(x, t).$ Here $\tilde K$ is the RK for $\tilde W\left(D \right),$ ${L^ * }$ is the adjoint operator for $L$. Define

Here, $K\left({x, \varsigma, t, \tau } \right)$ is the RK in $W\left(D \right)$, denoted by (2.9).

Theorem 3.1. If $D$ is closed, then ${\varphi }_{l}\in W\left(D\right), l\in \mathbb{N}.$

Proof: By Definition 2.4, it is first shown that $\partial _{{x^3}{t^2}}^5{\phi _l} \in {L^2}\left(D \right)$ and that $\partial _{{x^2}t}^3{\phi _l}$ is absolutely continuous in $D$.

From (2.9) and (3.1),

Then,

In view of the Definitions 2.1 and 2.2 and expressions (2.4) and (2.5) of $K1\left({t, \tau } \right)$ and $K2\left({x, \varsigma } \right)$, there are normal numbers ${N_1}$, ${N_2}$, and ${N_3}$ such that

for $(x, t) \in D$ and $\tau \in [0, T].$ Thus,

where ${N_4}$ is a normal number. Thus, $\partial _{{x^3}{t^2}}^5{\phi _l} \in {L^2}\left(D \right).$ Since $D$ is closed, $\partial _{{x^2}t}^3{\phi _l}$ is absolutely continuous in $D$.

Then, it is proved that ${\phi _l}(x, t)$ satisfies (1.5). Note that $K1\left({t, \tau } \right) \in {W_1}\left[{0, T} \right]$ with respect to $\tau \in [0, T],$$K2\left({x, \varsigma } \right) \in {W_2}\left[{0, L} \right]$ with respect to $\varsigma \in [0, L],$ and $\partial _{{\varsigma ^2}}^2K2\left({L, \varsigma } \right) = 0,$ $\partial _{{\varsigma ^2}}^2K2\left({0, \varsigma } \right) = 0,$ ${\partial _\tau }K1\left({0, \tau } \right) = 0,$ $K2\left({L, \varsigma } \right) = 0,$ $K2\left({0, \varsigma } \right) = 0,$ $K1\left({0, \tau } \right) = 0.$

By (3.2), ${\phi _l}\left({x, 0} \right) = 0$, ${\phi _l}\left({0, t} \right) = 0$, ${\phi _l}\left({L, t} \right) = 0,$ $l \in \mathbb{N}$.

Therefore, ${\varphi }_{l}\in W(D), l\in \mathbb{N}$ by Definition 2.4.

The proof methods for the following theorems are similar to those of ^[43,46].

Theorem 3.2. Assume the uniqueness of Eqs (1.4) and (1.5). Then in $W(D),$ system ${\left\{ {{\phi _l}} \right\}_{l \in \mathbb{N}}}$ is complete.

Proof: By Theorem 3.1, ${\varphi }_{l}\in W(D), l\in \mathbb{N}.$ For each $u \in W(D)$, set ${\left\langle {{\phi _l}, u} \right\rangle _{W(D)}} = 0, \; \; l \in \mathbb{N},$ which means that

In $D,$ $Lu(x, t) = 0$ because ${\left\{ {\left({{x_l}, {t_l}} \right)} \right\}_{l \in \mathbb{N}}}$ is dense. Because of the uniqueness for Eqs (1.4) and (1.5), $u(x, t) \equiv 0.$

The orthonormal system ${\left\{ {{{\bar \phi }_l}} \right\}_{l \in \mathbb{N}}}$ in $W(D)$ can be obtained by the GSO process of ${\left\{ {{\phi _l}} \right\}_{l \in \mathbb{N}}},$

Theorem 3.3. In $W(D),$ the unique solution for Eqs (1.4) and (1.5) is represented by

Proof: In $W(D),$ $u\left({x, t} \right)$ is expanded to a Fourier series by the orthonormal basis ${\bar \phi _l}\left({x, t} \right)$:

Thus, the approximate solution ${u_n}\left({x, t} \right)$ is acquired by

Theorem 3.4. Suppose $u$ is the exact solution to (1.4) and (1.5), ${u_n} = {P_n}u,$ in which ${P_n}$ is the orthogonal projection of $W\left(D \right)$ to $Span{\left\{ {{{\bar \phi }_l}} \right\}_{l \in \mathbb{N}}},$ then

Proof:

From (3.7) and (3.10),

Let ${\overline C _l} = \mathop \sum \limits_{j = 1}^l {\lambda _{lj}}F\left({{x_j}, {t_j}} \right).$ Then,

where ${C_l} = \sum\limits_{k = l}^n {{\lambda _{kl}}} \sum\limits_{j = 1}^k {{\lambda _{kj}}F\left({{x_j}, {t_j}} \right)}.$

According to Theorem 3.4,

where functions $L, \; F$ and ${\phi _l}$ are defined in (1.4) and (3.1), respectively.

In short, the main steps of the approach presented in this article are as follows:

1) From Eq (3.15), ${C_l}, {\text{ }}l = 1, 2, ..., n$ can be obtained.

2) By substituting the above ${C_l}, {\text{ }}l = 1, 2, ..., n$ into Eq (3.14), the numerical solution of Eqs (1.4) and (1.5) can be obtained.

The above calculation steps show that the current numerical algorithm bypasses the GSO procedure used in ^[31] (the GSO step is required only for proof, not for numerical calculations) Therefore, compared with ^[31], this method has higher precision and less computation time ^[43,46]. This approach can solve some model problems efficiently and can obtain the global approximate solution with high precision.

4.   Convergence analysis

${u_n}\left({x, t} \right)$ and $u\left({x, t} \right)$ are respectively approximate and exact solutions to Eqs (1.4) and (1.5). Set ${\left\| u \right\|_C} \triangleq \mathop {\max }\limits_{\left({x, t} \right) \in D} \left| {u\left({x, t} \right)} \right|.$ Similar to ^[43], the coming theorem can be found.

Theorem 4.1. Suppose $u \in W\left(D \right)$. Then,

1) ${\left\| {u - {u_n}} \right\|_{W\left(D \right)}} \to 0,$ $n \to \infty$. Furthermore, ${\left\| {u - {u_n}} \right\|_{W\left(D \right)}}$ decreases monotonously with $n$.

2) ${\left\| {\frac{{{\partial ^{i + k}}u}}{{\partial {x^i}\partial {t^k}}} - \frac{{{\partial ^{i + k}}{u_n}}}{{\partial {x^i}{t^k}}}} \right\|_C} \to 0$, $n \to \infty$; $k = 0, 1$; $i = 0, 1, 2$; $i + k = 0, 1, 2.$

Proof: 1) From (3.8) and (3.10),

Thus,

Furthermore,

Clearly, ${\left\| {u - {u_n}} \right\|_{W(D)}}$ decreases monotonically with $n$.

2) With reference to the properties of RK $K\left({x, \varsigma, t, \tau } \right)$ in ^[44],

According to (2.9), Definitions 2.1 and 2.2, and expressions (2.4) and (2.5) of $K1\left({t, \tau } \right)$ and $K2\left({x, \varsigma } \right)$, there are normal numbers ${C_l}, \; l = 1, 2, \cdots, 5$ such that

To all $(x, t) \in D,$

Hence,

5.   Numerical results

Numerical experiments verify the effectiveness and reliability for the presented approach in this section. All numerical calculations were performed using Mathematica 13.0 software. $D$ is separated into ${m_1} \times {m_2}$ grids with steps $1/{m_1}$ and $1/{m_2}$ in the $x$ and $t$ directions. Here, ${m_1}, {m_2} \in \mathbb{N}.$

Example 5.1. Consider Eqs (1.1) and (1.2) under the following conditions ^[30]:

The exact solution is

According to steps 1) and 2) in Section 3, $50 \times 50$ points that are the same as ^[30] are selected on $D$, the absolute errors of the proposed method and ^[30] are shown in Tables 1–3. As can be seen from the tables, the accuracy for the proposed approach is high, and the results obtained using the proposed approach are better than ^[30].

Subsequently, root-mean-square errors for $u\left({x, t} \right)$ are given in Table 4, which verifies that the proposed method can achieve a smaller error with a larger step size, and the accuracy increases with the decrease of step size.

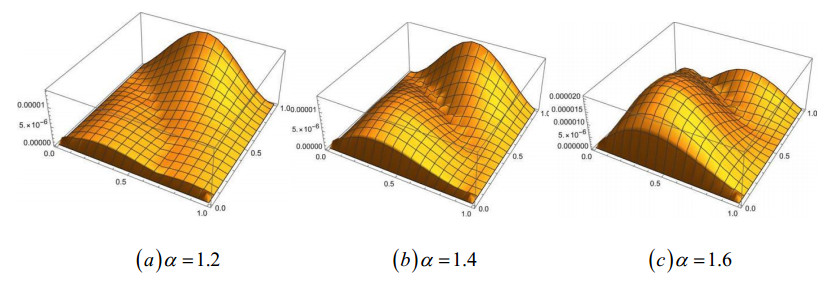
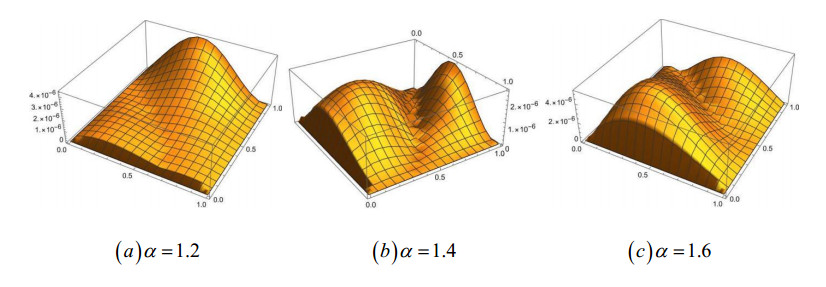
In addition, errors $\left| {u - {u_{20 \times 20}}} \right|, \left| {u - {u_{30 \times 30}}} \right|, \left| {u - {u_{40 \times 40}}} \right|:\alpha = 1.2, \alpha = 1.4, \alpha = 1.6$ are shown in Figures 1–3, respectively, which proves that the presented approach provides high-precision global approximate solutions.

6.   Conclusions and discussion

The approach proposed in this paper is successfully applied to space FDEs. Based on RK space, this method improves the method ^[31,45], avoids the GSO process ^[31], and obtains a simpler RK than ^[45]. This approach can improve accuracy and greatly reduce run time. Numerical results verify that the approach has high computational accuracy, and the error to the approximate solution tends to monotonously decrease. According to ^[46], in which the RK method is extended from one-dimensional to two-dimensional, the proposed approach in this paper is applicable to two-dimensional FDEs, which will be discussed in a later article.

Author contributions

Boyu Liu: conceptualization, formal analysis, software, writing-original draft preparation; Wenyan Wang: conceptualization, methodology, validation, reviewing and editing, funding acquisition. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors thank the anonymous reviewers and the members of the management editorial board for their valuable comments. This study was funded by Fundamental Research Funds for the Central Universities of China (No. 2572023DJ05), Innovative Training Plan Program for College Students funded by Northeast Forestry University (No. 202410225451) and National Nature Science Foundation of China (No. 11401086).

Conflict of interest

All authors declare no conflicts of interest in this paper.