Values and bounds for depth and Stanley depth of some classes of edge ideals

1.   Introduction

Let $S = K[x_1, \dots, x_n]$ be the polynomial ring in $n$ variables over a field $K$. Let $M$ be a finitely generated $\mathbb{Z}^n$-graded $S$-module. The $K$ subspace $aK[W]$ which is generated by all elements of the form $aw$ where $a$ is a homogeneous element in $M$, $w$ is a monomial in $K[W]$ and $W\subseteq\{x_1, x_2, \dots, x_n\}$. $K[W]$, is called a Stanley space of dimension $|W|$ if it is a free $K[W]$-module. A decomposition $\mathcal{D}$ of the $K$-vector space $M$ as a finite direct sum of Stanley spaces $\mathcal{D} \, : \, M = \bigoplus_{j = 1}^r a_j K[W_j],$ is called Stanley decomposition of $M$. Stanley depth of $\mathcal{D}$ is the minimum dimension of all the Stanley spaces. The quantity

is called the Stanley depth of $M$.

Depth of a finitely generated $R$-module $M$, where $R$ is the local Noetherian ring with unique maximal ideal $m: = (x_1, \dots, x_n)$, is the common length of all maximal $M$-sequences in $m$. For introduction to depth and Stanley depth we recommend the readers ^[5,9,15]. Stanley conjectured in ^[17] that for any $\mathbb{Z}^n$-graded $S$-module $M$, $\text{sdepth} (M)\geq \text{depth} (M).$ This conjecture has been studied in various special cases; see ^[6,12,14], this conjecture was later disproved by Duval et al. ^[4] in $2016$, but it is still important to find classes of $\mathbb{Z}^n$-graded modules which satisfy the Stanley inequality. Let $I\subset J\subset S$ be monomial ideals. Herzog et al. ^[10] showed that the invariant Stanley depth of $J/I$ is combinatorial in nature. The most important thing about Stanley depth is that it shares some properties and bounds with homological invariant depth; see ^[1,6,16].

Let $G = (V_{G}, E_{G})$ be a graph with vertex set $V_G$ and edge set ${E}_{G}$. A graph is called simple if it has no loops and multiple edges. Through out this paper all graphs are simple. A graph $G$ is said to be connected if there is a path between any two vertices of $G$. If $V_{G} = \{v_{1}, v_{2}, \dots, v_{n}\}$ and $S = K[x_{1}, x_{2}, \dots, x_{n}]$, then edge ideal $I(G)$ of the graph $G$ is the ideal of $S$ generated by all monomials of the form $x_ix_j$ such that $\{v_i, v_j\} \in E_G$. Let $n\geq2$. A path on $n$ vertices say $\{u_{1}, u_{2}, \dots, u_{u}\}$ is a graph denoted by $P_{n}$ such that $E_{P_n} = \{\{u_{i}, u_{i+1}\}: 1\leq i\leq n-1\}$. Let $n\geq 3$. A cycle on $n$ vertices $\{u_{1}, u_{2}, \dots, u_{n}\}$ is a graph denoted by $C_{n}$ such that $E_{C_n} = \{\{u_{i}, u_{i+1}\}: 1\leq i\leq n-1\} \cup \{u_{1}, u_{n}\}$. A simple and connected graph $\mathcal{T}$ is said to be a tree if there exists a unique path between any two vertices of $\mathcal{T}$. If $u, v\in$ $V_G$ then the distance between $u$ and $v$ is the length of the shortest path between $u$ and $v$. The maximum distance between any two vertices of $G$ is called diameter of $G$, denoted by $d(G)$. The degree of a vertex $u$ in a graph ${G}$ is the number of edges incident on $u$, degree of $u$ is denoted by deg$(u)$. A graph with only one vertex is called a trivial graph. We denote the trivial graph by $T$. Any vertex with degree $1$ is said to be a leaf or pendant vertex of $G$. Internal vertex is a vertex that is not a leaf. A tree with one internal vertex and $k-1$ leaves incident on it is called k-star, we denoted $k-$star by $S_{k}$.

The aim of this paper is to study depth and Stanley depth of the quotient rings of the edge ideals associated with the corona product of firecracker graphs, some classes of caterpillar graphs and some newly defined unicyclic graphs with an arbitrary non-trivial connected graph $G$. We compute formulae for the values of depth that are the functions of depth of the quotient ring of the edge ideal $I(G)$ see Theorem 3.1, Theorem 3.2, Theorem 3.3 and Theorem 3.4. As a consequence we also prove that if the Stanley's inequality holds for the quotient ring of the edge ideal $I(G)$, then it also holds for the quotient rings of the edge ideals associated to the corona product of the graphs we considered with $G$. We also compute values of depth and Stanley depth and verify Stanley's inequality for the quotient ring of the edge ideals associated with some special classes of caterpillar graphs, see Theorem 4.1 and Theorem 4.2.

2.   Definitions and notations

In this section some definitions from Graph Theory are presented. For more details we refer the readers to ^[7,8,18]. We also present some known results from Commutative Algebra that are frequently used in this paper. Note that by abuse of notation, $x_i$ will at times be used to denote both a vertex of a graph $G$ and the corresponding variable of the polynomial ring $S$. For a given graph $G$, $K[V_G]$ will denote the polynomial ring whose variables are the vertices of the graph $G$.

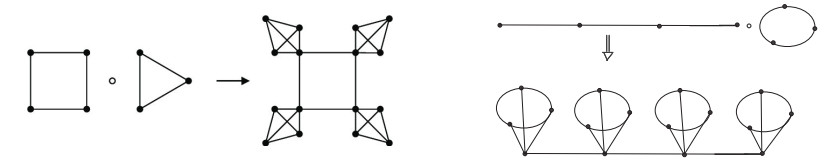
Definition 2.1 (^[7]). Let $G_1$ and $G_2$ be two graphs with order $n$ and $m$ respectively. The corona product of $G_1$ and $G_2$ denoted by $G_1 \circ G_2$, is the graph obtained by taking one copy of $G_1$ and $n$ copies of $G_2$; and then by joining the $i$-th vertex of $G_1$ to every vertex in the $i$-th copy of $G_2$; see Figure 1.

Definition 2.2. Let $z\geq 1$ and $k\geq 2$ be integers and $P_z$ be a path on $z$ vertices ${u_1, u_2, \dots, u_z}$ that is, $E_{P_z} = \{u_iu_{i+1}:1\leq i\leq z-1\}$ (for $z = 1$, $E_{P_z} = \emptyset$). We define a graph on $zk$ vertices by attaching $k-1$ pendant vertices at each $u_i$. We denote this graph by $P_{z, k}$; see Figure 2.

Definition 2.3. Let $z\geq 3$ and $k\geq 2$ be integers and $C_z$ be a cycle on $z$ vertices ${u_1, u_2, \dots, u_z}$ that is, $E_{C_z} = \{u_iu_{i+1}:1\leq i\leq z-1\}\cup \{u_1u_z\}$. We define a graph on $zk$ vertices by attaching $k-1$ pendant vertices at each $u_i$. We denote this graph by $C_{z, k}$; see Figure 2.

Definition 2.4 (^[18]). Firecracker is a graph formed by the concatenation of $\alpha$ number of $k$-stars by linking exactly one leaf from each star. It is denoted by $F_{\alpha, k}$; see Figure 3.

Definition 2.5. The graph obtained by joining the end vertices of the path joining the leaves of the $\alpha$ stars in $F_{\alpha, k}$. We call this graph circular firecracker and is denoted by $CF_{\alpha, k}$; see Figure 3.

Definition 2.6. Let $z\geq3$ be an odd integer and $k_{1}, k_{3}, k_{5}, \dots, k_{z}$ be integers greater than $1$. Let $P_z$ be a path on $z$ vertices ${u_1, u_2, \dots, u_z}$ that is, $E_{P_z} = \{u_iu_{i+1}:1\leq i\leq z-1\}$. Let $a\in\{1, 3, 5, \dots, z \}$, we define a graph by attaching $k_{a}-1$ pendant vertices at each vertex $u_{a}$ of $P_z$. We denote this graph by $\mathcal{P}_z$; see Figure 4.

Definition 2.7. Let $z\geq 2$ and $k\geq 3$ be integers and $P_z$ be a path on $z$ vertices $\{u_1, u_2, \dots, u_z\}$ that is, $E_{P_z} = \{u_iu_{i+1}:1\leq i\leq z-1\}$. We denote by $\mathcal{P}_{z, k}$ the graph obtained by attaching $k+i-2$ pendant vertices at each $u_i$ of $P_z$; see Figure 4.

Here we recall some known results that will be used in this paper.

Lemma 2.8. ([2,Proposition 1.2.9]). (Depth Lemma) If $0 \longrightarrow E_1 \longrightarrow E_2 \longrightarrow E_3 \longrightarrow\ 0$ is a short exact sequence of modules over a local ring $S$, or a Noetherian graded ring with $S_0$ local then

(1) $\mathit{\text{depth}}(E_1) \geq \min \{ \mathit{\text{depth}}(E_2) \, , \, 1+ \mathit{\text{depth}}(E_3) \}$.

(2) $\mathit{\text{depth}}(E_2) \geq \min \{ \mathit{\text{depth}}(E_1) \, , \, \mathit{\text{depth}}(E_3) \}$.

(3) $\mathit{\text{depth}}(E_3) \geq \min \{ \mathit{\text{depth}}(E_1) -1 \, , \, \mathit{\text{depth}}(E_2) \}$.

Lemma 2.9 ([14,Lemma 2.4]). If $0 \rightarrow E_1 \rightarrow E \rightarrow E_2 \rightarrow 0$ is a short exact sequence of $\mathbb{Z}^{n}-$graded $S$-module, then

Proposition 1 ([16,Corollary 1.3]). If $I \subset S$ is a monomial ideal and $u\in S$ is a monomial such that $u\notin I$, then $\mathit{\text{depth}}_S (S/(I :u)) \geq \mathit{\text{depth}}_S (S/I)$.

Proposition 2 ([3,Proposition 2.7]). If $I \subset S$ is a monomial ideal and $u\in S$ is monomial such that $u\notin I$, then $\mathit{\text{sdepth}}_S (S/(I :u)) \geq \mathit{\text{sdepth}}_S (S/I)$.

Lemma 2.10 ([13,Lemma 3.6]). Let $I\subset S$ be a monomial ideal. If $S' = S\otimes_K K[x_{n+1}]\cong S[x_{n+1}]$, then $\mathit{\text{depth}}(S'/ I'S') = \mathit{\text{depth}}(S/I) +1$ and $\mathit{\text{sdepth}}(S'/ I'S') = \mathit{\text{sdepth}} (S /I) +1.$

Lemma 2.11 ([3,Proposition 1.1]). If $I' \subset S' = K[x_1, \dots, x_m]$ and $I^{''} \subset S'' = K[x_{m+1}, \dots, x_n]$ are monomial ideals, with $1 \leq m < n$, then

Lemma 2.12 ([3,Proposition 1.1]). If $I' \subset S' = K[x_1, \dots, x_m]$ and $I^{''} \subset S'' = K[x_{m+1}, \dots, x_n]$ are monomial ideals, with $1 \leq m < n$, then

Proof. Proof follows by [19,Proposition 2.2.20] and [19,Theorem 2.2.21].

Theorem 2.1 ([16,Theorem 3.1]). If $I' \subset S' = K[x_1, \dots, x_m]$ and $I'' \subset S'' = K[x_{m+1}, \dots, x_n]$ are monomial ideals, with $1 \leq m < n$, then

Lemma 2.13. If $I' \subset S' = K[x_1, \dots, x_m]$ and $I'' \subset S'' = K[x_{m+1}, \dots, x_n]$ are monomial ideals, with $1 \leq m < n$, then

Proof. By [19,Proposition 2.2.20], we have $S'/I'\otimes_K S''/I''\cong S/(I'S+I''S)$, by Theorem 2.1 the required result follows.

Let $m\geq2$ be an integer, and consider $\{M_{j}:1\leq j \leq m\}$ and $\{N_{i}:0\leq i \leq m\}$ be sequence of $\mathbb{Z}^{n}-$graded $S-modules$ and consider the chain of short exact sequences of the form

$\vdots$

Then the following lemmas play key role in the proofs of our theorems.

Lemma 2.14. ([11,Lemma 3.1]). If $\mathit{\text{depth}} M_{m} \leq \mathit{\text{depth}} N_{m}$ and $\mathit{\text{depth}} M_{j-1} \leq \mathit{\text{depth}} M_{j}$, for all $2\leq j \leq m$, then $\mathit{\text{depth}} M_{1} = \mathit{\text{depth}} N_{0}$.

Lemma 2.15. $\mathit{\text{sdepth}} N_{0} \geq \min\{ \mathit{\text{sdepth}} M_{j}, \mathit{\text{sdepth}} N_{m}:1\leq j \leq m\}.$

Proof. Proof follows by applying Lemma 2.9 on the above chain of short exact sequences.

Proposition 3 (^[1]). If $I$ is an edge ideal of $n$-star, then $\mathit{\text{depth}}(S/I) = \mathit{\text{sdepth}}(S/I) = 1$, and $\mathit{\text{depth}}(S/I^t), \mathit{\text{sdepth}}(S/I^t) \geq 1$.

Corollary 2.16 ([6,Theorem 3.2]). Let $G$ be a connected graph. If $I = I(G)$ and $d$ is the diameter of $G$, then

Theorem 2.2 ([6,Theorem 4.18]). Let $G$ be a connected graph. If $I = I(G)$ and $d$ is the diameter of $G$, then for $1\leq t \leq 3$ we have

Corollary 2.17. Let $G$ be connected graph. If $I = I(G)$ and $d$ is the diameter of $G$, then we have

3.   Caterpillar and firecrackers graphs and the corona product

In this section we prove our main results related to corona product of graphs. We start this section with some elementary results that are necessary for our main results. Let $T$ be a trivial graph and $G$ any non-trivial and connected graph. The first lemma of this section give depth and Stanley depth of the cyclic modules associated with $T\circ G$. For examples of $T\circ G$; see Figure 5.

Lemma 3.1. Let $T$ be a trivial graph and $G$ be any connected non-trivial graph. If $I = I(T\circ G)$ and $S: = K[V(T\circ G)]$, then $\mathit{\text{depth}}(S/I) = 1$ and $\mathit{\text{sdepth}}(S/I) = 1$.

Proof. By definition of $T\circ G$ the only vertex $x$ of $T$ has an edge with every vertex of $G$. Consider the following short exact sequence

Therefore $S/(I:x) \cong K[x]$, and $\text{depth} (S/(I:x)) = 1$. Now $S/(I, x)\cong S_x/I(G)$, where $S_x: = S/(x)$. We have $\text{depth}(S/(I, x)) = \text{depth}(S_x/I(G))\geq1,$ by Corollary 2.16. Now by using Depth Lemma, we have $\text{depth}(S/I) = 1$. For the Stanley depth since $S/(I:x) \cong K[x]$ we have $\text{sdepth} (S/(I:x)) = 1$. Now $S/(I, x)\cong S_x/I(G)$. We have $\text{sdepth}(S/(I, x)) = \text{sdepth}(S_x/I(G))\geq1$, by using Lemma 2.9 and Proposition 2, we have $\text{sdepth}(S/I) = 1$.

Proposition 4. For $n, k\geq2$, let $G$ be a non-trivial connected graph. If $S: = K[V(S_{k}\circ G)]$, then

where $t = \mathit{\text{depth}} \big(K[V(G)]/I(G)\big)$. Also

where $s = \mathit{\text{sdepth}} \big(K[V(G)]/I(G)\big).$

Proof. First we prove the result for depth. Let $k = 2$. If $e$ be a variable corresponding to a leaf in $S_{2}$. Consider the following short exact sequence

it is easy to see that $S/(I:e)\cong K[V(G)]/I(G){\otimes_K} K[e]$ and

By Lemma 3.1, Lemma 2.10 and [19,Theorem 2.2.21], we have $\text{depth}(S/(I:e)) = 1+t$ and $\text{depth}(S/(I, e)) = 1+t = \text{depth}(S/(I:e)).$ Thus by Depth Lemma we have $\text{depth}(S/I) = 1+t$.

Let $k\geq 3$. We will prove the required result by induction on $k$. Let $e$ be a variable corresponding to a leaf in $S_k$. Consider the following short exact sequence

we have

By Lemmma [19,Theorem 2.2.21], we have

by Lemma 3.1, we get $\text{depth}(S/(I:e)) = k-2+t+1 = k-1+t.$ It can easily be seen that

Thus by [19,Theorem 2.2.21]

applying induction on $k$ we get

Hence by Depth Lemma we have $\text{depth}(S/I) = k-1+t$. This completes the proof for depth.

For Stanley depth the result follows by Lemma 2.13 instead of [19,Theorem 2.2.21] and Lemma 2.9 instead of Depth Lemma.

Corollary 3.2. If Stanley's inequality holds for $K[V(G)]/I(G)$ then it also holds for $S/I(S_k\circ G)$.

Theorem 3.1. Let $z\geq1$ and $k\geq 2$ be integers. If $G$ is a connected graph with $|V(G)|\geq 2$ and $S: = K[V(P_{z, k}\circ G)]$, then

where $t = \mathit{\text{depth}}((K[V(G)])/I(G))$ and

where $s = \mathit{\text{depth}}((K[V(G)])/I(G))$; see Figure 6.

Proof. First we prove the result for depth. We consider the following cases.

$1.$If $z = 1$ and $k\geq 2$ then the result follows from Proposition 4.

$2.$Let $z = 2$. We consider the following subcases:

(a) If $k = 2$ and $e$ is a variable corresponding to a leaf in $P_{2, 2}$. Consider the following short exact sequence

then $S/(I:e)\cong K[V(S_{2}\circ G)]/I(S_{2}\circ G){\otimes_K}K[V(G)]/I(G){\otimes_K} K[e],$

$S/(I, e)\cong K[V(S_{3}\circ G)]/I(S_{3}\circ G){\otimes_K}K[V(G)]/I(G)).$ By [19,Theorem 2.2.21],

By Proposition 4 we have $\text{depth}(S/(I:e)) = t+1+t+1 = 2(1+t)$ and $\text{depth}(S/(I, e)) = 2+t+2 = 2(1+t) = \text{depth}(S/(I:e)).$ Hence by Depth Lemma we have $\text{depth}(S/I) = 2(1+t)$ and we are done in this special case.

(b) Let $k\geq3$. Let $e_{1}, e_{2}, \dots, e_{k-1}$ be leaves attached to $u_2$ in $P_{2, k}$ and $I = I(P_{2, k}\circ G)$. For $0\leq i\leq k-2$, $I_i: = (I_{i}, e_{i+1})$, where $I_0 = I$. Consider the chain of short exact sequences of the form

By [19,Theorem 2.2.21]

hence by Lemma 3.1 and Proposition 4, we get

Also we have

By [19,Theorem 2.2.21] we have

and similarly

by Proposition 3.1, we get

Hence by Lemma 2.14, we have

This completes the proof for $z = 2$.

3. Let $z\geq 3$. We consider the following subcases:

(a) If $k = 2$, We will prove the result by induction on $z$. Let $u_{z}$ be the vertex in the definition of $P_{z, 2}$. Consider the following short exact sequence

we have $S/(I:u_{z})\cong K[V(P_{z-2, 2}\circ G)]/I(P_{z-2, 2}\circ G)\underset{j = 1}{\overset{2}{ \otimes_{K}}}K[V(G)]/I(G)$

${\otimes_K}K[V(T\circ G)]/I(T\circ G){\otimes_K} K[e],$

By induction on $z$, [19,Theorem 2.2.21], and Lemma 3.1, we have

and similarly

Thus by Depth Lemma we have $\text{depth}(S/I) = z(1+t)$ and the result is proved for the case $k = 2$.

(b) Now consider $k\geq3$. Let $e_{1}, e_{2}, \dots, e_{k-1}$ be leaves attached to $u_z$ and $I = I(P_{z, k}\circ G)$. For $0\leq i\leq k-2$, $I_i: = (I_{i}, e_{i+1})$ where $I_0 = I$. Consider the chain of short exact sequences of the form

we have,

By [19,Theorem 2.2.21] we have

Thus by Lemma 3.1, Proposition 4 and induction on $z$ we get,

Also we have

and similarly

By [19,Theorem 2.2.21] and Proposition 4, we get

Hence by Lemma 2.14, we get

This completes the proof.

For Stanley depth the result follows by Lemma 2.13 instead of [19,Theorem 2.2.21] and Lemma 2.15 instead of Lemma 2.14.

Corollary 3.3. If Stanley's inequality holds for $K[V(G)]/I(G)$ then it also holds for $S/I(P_{z, k}\circ G)$.

Theorem 3.2. Let $z\geq3$ and $k\geq 2$ be integers and $G$ be a connected graph with $|V(G)|\geq 2$. Consider $S: = K[V(C_{z, k}\circ G)]$. We have

where $t = \mathit{\text{depth}}((K[V(G)])/I(G))$ and

where $s = \mathit{\text{sdepth}}((K[V(G)])/I(G))$; see Figure 7.

Proof. First we prove the result for depth.

$1.$Let $z = 3$. We consider the following subcases:

(a) Let $k = 2$. Let $u$ be a variable corresponding to a vertex of $C_{3}$ in $C_{3, 2}$. Consider the following short exact sequence

we have

Hence by using Lemma 3.1, [19,Theorem 2.2.21] and Theorem 3.1, we have

Thus by Depth Lemma we have $\text{depth}(S/I) = 3(1+t)$.

(b) Let $k\geq 3$. Let $e_{1}, e_{2}, \dots, e_{k-1}$ be leaves attached to $u_{3}$ in $C_{3, k}$ and $I = I(C_{3, k}\circ G)$. For $0\leq i\leq k-2$, $I_i: = (I_{i}, e_{i+1})$ where $I_0 = I$. Consider the chain of short exact sequences of the form

we have,

By using [19,Theorem 2.2.21]

hence by Lemma 3.1, Proposition 4 and Theorem 3.3, we get

By [19,Theorem 2.2.21]

by Lemma 3.1 and Theorem 3.3, we get

Hence by Lemma 2.14, we get

2. Let $z\geq 4$. We consider the following subcases:

(a) Let $k = 2$. Let $u$ be a variable corresponding to the vertex of $C_{z}$ in $C_{z, 2}$. Consider the following short exact sequence

we have $S/(I:u)\cong K[V(P_{z-3, 2}\circ G)]/I(P_{z-3, 2}\circ G)\underset{j = 1}{\overset{3}{ \otimes_{K}}}K[V(G)]/I(G)$

$\underset{j = 1}{\overset{2}{ \otimes_{K}}}K[V(T\circ G)]/I(T\circ G){\otimes_K} K[e],$

Hence by using Lemma 3.1, [19,Theorem 2.2.21] and Theorem 3.1, we have

Thus by Depth Lemma we have $\text{depth}(S/I) = z(1+t)$.

(b) Let $k\geq 3$. Let $e_{1}, e_{2}, \dots, e_{k-1}$ be leaves attached to $u_z$ in $C_{z, k}$ and $I = I(C_{z, k}\circ G)$. For $0\leq i\leq k-2$, $I_i: = (I_{i}, e_{i+1})$ where $I_0 = I$. Consider the chain of short exact sequences of the form

By using [19,Theorem 2.2.21]

by Lemma 3.1, Proposition 4 and Theorem 3.1, we get

by Lemma 3.1, [19,Theorem 2.2.21] and Theorem 3.1, we have

Hence by Lemma 2.14, we will have the required result

For Stanley depth the result follows by Lemma 2.13 instead of [19,Theorem 2.2.21] and Lemma 2.15 instead of Lemma 2.14.

Corollary 3.4. Stanley's inequality holds for $S/I(C_{z, k}\circ G)$ if it holds for $K[V(G)]/I(G)$.

Theorem 3.3. Let $\alpha\geq 2$ and $k\geq3$ be integers and $G$ be a connected graph with $|V(G)|\geq2$ and $S: = K[V(F_{\alpha, k}\circ G)]$. Then

where $t = \mathit{\text{depth}}((K[V(G)])/I(G))$ and

where $s = \mathit{\text{sdepth}}((K[V(G)])/I(G))$ and $\lceil\alpha\rceil = \{n\in \mathbb{Z} : n\geq \alpha\}$; see Figure 8.

Proof. We consider the following cases:

$1.$Let $\alpha = 2$. Let $e_{1}, e_{2}, \dots, e_{k-1}$ be leaves attached to $u_{2}$ in $F(2, k)$ and $I = I(F_{2, k}\circ G)$. Consider the short exact sequence of the form

where $e_{1}$ is leave of second star that is attached to the previous star.

By [19,Theorem 2.2.21]

hence by Lemma 3.1 and Proposition 4, we get

and similarly

So by using Depth Lemma, we have

$2.$Let $\alpha\geq3$. Let $e_{1}.e_{2}, ..., e_{k-1}$ be leaves attached to $u_{\alpha}$ in $F(z, k)$ and $I = I(F_{\alpha, k}\circ G)$.

Consider the short exact sequence of the form

where $e_{1}$ is leave of last star that is attached to the previous star in $F_{\alpha, k}$. We have

By [19,Theorem 2.2.21]

hence by Lemma 3.1, Proposition 4 and induction on $\alpha$, we get

and similarly

So by using Depth Lemma, we have

For Stanley depth the result follows by Lemma 2.13 instead of [19,Theorem 2.2.21] and Lemma 2.9 instead of Depth Lemma.

Corollary 3.5. Stanley's inequality holds for $S/I(F_{\alpha, k}\circ G)$ if it holds for $K[V(G)]/I(G)$.

Theorem 3.4. Let $\alpha\geq3$ and $k\geq3$ be integers and $G$ be a connected graph with $|V(G)|\geq2$. Consider $S: = K[V(CF_{\alpha, k}\circ G)]$. Then

where $t = \mathit{\text{depth}}((K[V(G)])/I(G))$ and

where $s = \mathit{\text{sdepth}}((K[V(G)])/I(G))$; see Figure 9.

Proof. We consider the following cases:

$1.$Consider $\alpha = 3$. Let $e_{1}, e_{2}, ..., e_{k-1}$ be leaves attached to $u_{3}$ in $CF(3, k)$ and $I = I(CF_{3, k}\circ G)$.

Consider the short exact sequence of the form

where $e_{1}$ is leave of third star that is attached to the previous star and first star in $CF_{3, k}$. We have

By [19,Theorem 2.2.21]

hence by Lemma 3.1 and Proposition 4, we get

and similarly

So by using Depth Lemma 2.8, we have

$2.$Let $\alpha\geq3$. Let $e_{1}, e_{2}, \ldots , e_{k-1}$ be leaves attached to $u_{\alpha}$ in $CF(\alpha, k)$ and $I = I(CF_{\alpha, k}\circ G)$. Consider the short exact sequence of the form

where $e_{1}$ is leave of last star that is attached to the previous star and first star in $CF_{\alpha, k}$. We have

By using [19,Theorem 2.2.21]

hence by Lemma 3.1, Proposition 4 and Theorem 3.3, we get

and similarly

So by using Depth Lemma 2.8, we have

For Stanley depth the result follows by Lemma 2.13 instead of [19,Theorem 2.2.21] and Lemma 2.9 instead of Depth Lemma.

Corollary 3.6. Stanley's inequality holds for $S/I(CF_{\alpha, k}\circ G)$ if it holds for $K[V(G)]/I(G)$.

4.   Some special classes of caterpillar trees

In this section we calculate values of depth and Stanley depth of the quotient rings associated with edge ideals of some class of caterpillar graphs. We also prove that the values of both depth and Stanley depth for these classes of graphs are exactly the same. As a consequence the Stanley's inequality holds for the quotient ring of edge ideals of these classes of graphs.

Theorem 4.1. Let $z\geq3$ and $S = K[V(\mathcal{P}_z)]$. For $a\in\{1, 3, 5, \dots, z\}$, if $k_{a} > 1$ and $I = I(\mathcal{P}_z)$, then

Proof. The proof is done by induction on $z$. Let $z = 3$. Consider the following short exact sequence

We have $(I:u_{3}) = (x: x\in N(u_{3}))+I(S_{k_{1}})$ and $S/(I:u_{3}) \cong K[V(S_{k_1})\cup \{u_{3}\}]/I(S_{k_{1}}),$ thus by Lemma 2.10 and Proposition 3, $\text{depth} S/(I:u_{3}) = \text{sdepth} S/(I:u_{3}) = 1+1 = 2.$ Clearly $(I, u_{3}) = (I(S_{k_{1}+1}), u_{3})$ and $S/(I, u_{3})\cong K[V(S_{{k_1}+1})\cup\{u_{3}\}\cup\{e_1, e_2, \dots, e_{k_3}\}]/I(S_{{k_1}+1})$ by Lemma 2.3 and Proposition 3, $\text{depth} S/(I, u_{3}) = \text{sdepth} S/(I, u_{3}) = 1+k_{3}-1 = k_{3}$, by using Depth Lemma, Lemma 2.9 and Proposition 2 we have

Now assume that $z\geq 5$, consider a short exact sequence of the form

it is easy to see that $(I:u_{z}) = (x: x\in N(u_{z}))+I(\mathcal{P}_{z-2})$ and $S/(I:u_{z})\cong K[V(\mathcal{P}_{z-2})\cup \{u_{z}\}]/I(\mathcal{P}_{z-2})$ so by Lemma 2.3 and induction on $z$, we get

Since $(I, u_{z}) = (I(\mathcal{P}_{z-2}), u_{z})$ and

therefore by using Lemma 2.10 and induction on $z$, we get

Hence by Depth Lemma we have $\text{depth} S/I = \frac{z+1}{2}$ and by Lemma 2.9 $\text{sdepth} S/I \geq\frac{z+1}{2}.$ Now for the upper bound by Proposition 2 we have $\text{sdepth} S/(I)\leq \text{sdepth} S/(I:u_{z}) = \frac{z+1}{2}$ and hence $\text{sdepth} (S/I) = \frac{z+1}{2}.$

Theorem 4.2. Let $z \geq 2$, $k \geq 3$ and $S: = K[V(\mathcal{P}_{z, k})]$. If $I = I(\mathcal{P}_{z, k})$, then

Where $\lfloor \alpha \rfloor = \{ n\in \mathbb{Z}: n\leq \alpha \}.$

Proof. The proof is done by induction on $z$. Let $z = 2$. Consider the following short exact sequence

we have $(I:u_2) = (x :x \in N(u_2))$ and $S/(I:u_2) \cong K[\mathcal{L}(u_1) \cup \{u_2\}],$ where $N(u_2)$ are the neighbours of $u_2$ and $\mathcal{L}(u_1)$ represent the number of leaves at $u_1$. Thus by Lemma 2.10, $\text{depth}(S/(I:u_2)) = 1+k-1 = k$. Also $(I, u_2) = (I({S}_{k}), u_2)$ and $S/(I, u_2) \cong K[V({S}_{k})\cup \mathcal{L}(u_2)]/I({S}_{k})$, therefore by Proposition 2.10, $\text{depth}(S/(I, u_2)) = 1+(k+1-1) = k+1$ thus by Depth Lemma $\text{depth}(S/I) = k$. Now by Lemma 2.9 $\text{sdepth}(S/I) \geq k$ and by using Proposition 2 and Lemma 3 we have $\text{sdepth}(S/I) \leq k$. Thus $\text{sdepth}(S/I) = k$. Let $z = 3$. Consider the following short exact sequence

we have $(I:u_3) = I({S}_{k})+(x:x \in N(u_3))$ and $S/(I:u_3) \cong [V(\mathcal{S}_{k})\cup \mathcal{L}(u_2) \cup \{u_3\}]/I(\mathcal{S}_{k})$. Thus by Lemma 2.10 and Proposition, 3, $\text{depth}(S/(I:u_3)) = \text{sdepth}(S/(I:u_3)) = 1+(k+1-1)+1 = k+2$. Further $(I, u_3) = (I(\mathcal{P}_{2, k}), u_3)$ and $S/(I, u_3) \cong K[V(\mathcal{P}_{2, k})\cup \mathcal{L}(u_3)]/I(\mathcal{P}_{2, k})$. Therefore by Lemma 2.10, and the above case we have $\text{depth}(S/(I, u_3)) = \text{sdepth}(S/(I, u_3)) = k +(k+2-1) = 2k+1$. Applying Depth Lemma we get $\text{depth}(S/I) = k+2.$ Now by Lemma 2.9 and Proposition 2 we get $\text{sdepth}(S/I) = k+2.$ Let $z \geq 4$. Consider the following short exact sequence

it is easy to see that $(I:u_z) = (x:x \in N(u_z)) + I(\mathcal{P}_{z-2, k})$ and $S/(I: u_z) \cong K[V(\mathcal{P}_{z-2, k})\cup \mathcal{L}(u_{z-1}) \cup \{u_z\}] / I(\mathcal{P}_{z-2, k})$ also $(I, u_z) = (I(\mathcal{P}_{z-1, k}), u_z)$ and $S/(I, u_z) \cong K[V(\mathcal{P}_{z-1, k})\cup \mathcal{L}(u_{z})] / I(\mathcal{P}_{z-1, k})$.

Thus by using induction on $z$ and Lemma 2.10

introducing the transformation $j: = m+1$ we get $\text{depth}(S/(I:u_z)) = \big \lfloor\frac{z}{2} \big \rfloor (k-2)+z + \sum_{j = 1}^{\lceil\frac{z}{2}\rceil-1} (z-2j),$ where $j$ is dummy variable so by replacing $j$ with $m$ we get

Now by considering the inequality $\big \lceil x+y \big \rceil \geq \big \lceil x \big \rceil +\big \lceil y \big \rceil-1,$ we get

Thus by Depth Lemma

For Stanley depth the result follows by Lemma 2.9 and 2 instead of Depth Lemma. Clearly, one can see that Stanley's inequality holds for these classes of graphs.

Conflict of interest

All authors declare no conflicts of interest in this paper.