On the Burr XII-Power Cauchy distribution: Properties and applications

1.   Introduction

Data analysis is imperative in every aspect of statistical analysis. The statistical characteristics such as skewness, kurtosis, bimodality, monotonic and non-monotonic failure rates are obtained from datasets. The selection of a suitable model for data analysis is challenging task because it depends on the nature of the dataset. However, if a wrong model is applied to analyze the dataset it leads to loss of information and invalid inferences. It is necessary to search and identify the most suitable model for the given dataset.

In the recent decade, many continuous distributions have been introduced in statistical literature. Some of these distributions, however, are not flexible enough for data sets from survival analysis, life testing, reliability, finance, environmental sciences, biometry, hydrology, ecology and geology. Hence, the applications of the generalized models to these fields are clear requisite. The generalization techniques such as either inserting one or more shape parameters or transform of the parent distribution are useful to (ⅰ) increase the applicability of a parent distribution; (ⅱ) explore skewness and tail properties and (ⅲ) improve the goodness-of-fit of the generalized distributions. The Cauchy distribution is the ratio of two independent normal variables if the denominator variable has mean zero. The Cauchy distribution has wide applications in stochastic modeling of decreasing failure rate life components, clinical trials and finance risks.

During the recent years, the Cauchy distribution has been shown great interest in literature such generalized Cauchy ^[1], truncated Cauchy ^[2,3,4], beta-Cauchy ^[5,6,7], Marshall-Olkin half Cauchy ^[8], beta-half Cauchy ^[9], Kumaraswamy-half Cauchy ^[10], Weibull power Cauchy ^[11] and modified skew-normal-Cauchy distribution ^[12].

The Burr-XII (BXII) distribution among Burr family ^[13] is widely applied to model insurance data and failure time data. Many generalizations of the BXII distributions are available in the literature such as Burr XII power series ^[14], generalized Burr XII power series ^[15], Burr XII system of densities ^[16], Burr XII inverse Rayleigh ^[17] and Burr XII- moment exponential ^[18].

The idea is to incorporate Cauchy distribution into a larger family through an application of the Burr XII cdf. In fact, based on the T-X transform defined by ^[19], we construct the BXII-PC distribution. The new model has flexible shapes to model various lifetime data sets. The moments of the Cauchy distribution do not exist, but the BXII-PC distribution has moments. Additionally, its special models produce better fits than other well-known models.

This study is based on the following motivations: (ⅰ) to generate distributions with symmetrical, left-skewed, right-skewed, J and reverse-J shaped as well as high kurtosis; (ⅱ) to have monotone and non-monotone failure rate function; (ⅲ) to derive mathematical properties such as ordinary moments, incomplete moments, inequality measures, conditional moments, reliability measures and characterization; (ⅳ) to estimate the precision of the maximum likelihood, maximum product spacings, least squares, weighted least squares, Cramer-von Mises and Anderson-Darling estimators by means of Monte Carlo simulations; (ⅴ) to reveal the potentiality of the BXII-PC model; (ⅵ) to deliver better fits than other models and (ⅶ) to infer empirically.

The content of the article is structured as follows. Section 2 derives the BXII-PC model from (ⅰ) the T-X family technique and (ⅱ) linking the exponential and gamma variables. We study basic structural properties, random number generator and sub-models for the BXII-PC model. Section 3 presents certain mathematical properties such as ordinary moments, incomplete moments, inequality measures, conditional moments, reliability measures and characterization. Section 4 is devoted to parameter estimation methods. Section 5 presents simulation studies on the basis of graphical results to see the performance of maximum likelihood, maximum product spacings, least squares, weighted least squares, Cramer-von Mises and Anderson-Darling estimators of the BXII-PC distribution. In Section 6, we consider an application to illustrate the potentiality and utility of the BXII-PC model. We test the competency of the BXII-PC model via various model selection criteria. In Section 7, we offer some conclusions.

2.   The BXII-PC distribution

We derive the BXII-PC distribution from the T-X family technique. We also obtain this model by linking the exponential and gamma variables. We discuss basic structural properties. We highlight the shapes of the density and failure rate functions.

2.1.   T-X family technique

The cumulative distribution function (cdf) and probability density function (pdf) of the Power-Cauchy distribution ^[20] are given, respectively, by

and

The cumulative hazard rate function of the Power Cauchy distribution is

The cdf of the T-X family ^[19] of distributions has the form

where $r\left(t \right)$ is the pdf of the random variable (rv) $T$, where $T \in \left[ {a, {\rm{ b}}} \right]$ for $- \infty \le a\, {\rm{ < b }} < {\rm{ }}\infty$ and $W\left[ {G\left({x; \xi } \right)} \right]$ is a function of the baseline cdf of a rv $X$ with the vector parameter $\xi$, which satisfies the conditions:

ⅰ) $W\left[ {G\left({x; \xi } \right)} \right] \in \left[ {a, {\rm{ b}}} \right]$, ⅱ) $W\left[ {G\left({x; \xi } \right)} \right]$ is differentiable and monotonically non-decreasing and ⅲ) $\mathop {\lim }\limits_{x \to - \infty } W\left[ {G\left({x; \xi } \right)} \right] = a$ and $\mathop {\lim }\limits_{x \to \infty } \, W\, \left[ {G\left({x; \xi } \right)} \right] = b$.

The pdf of the T-X family can be expressed as

We derive the cdf of the BXII-PC distribution from the T-X family technique by setting

and

The cdf of the BXII-PC distribution takes the form

where $\, \, \alpha \, ,\, \, \beta, \kappa, \theta > 0$ are the parameters.

The BXII-PC density can be expressed as

Hereafter, a rv with pdf (2.4) is denoted by $X$ $\mathrm{\sim}$BXII-PC$\left(\alpha, \beta, \kappa, \theta \right).$ (ⅰ) For $\kappa = 1$, the BXII-PC distribution reduces to Burr XII Half Cauchy (BXII-HC) distribution; (ⅱ) For $\beta = 1$, the BXII-PC distribution reduces to the Lomax Power Cauchy (Lomax-PC) distribution; (ⅲ) For $\kappa = \beta = 1$, the BXII-PC distribution reduces to the Lomax Half Cauchy (Lomax-HC) distribution; (ⅳ) For $\alpha = 1$, the BXII-PC distribution reduces to the log-logistic Power Cauchy (Log-Log-PC) distribution and (ⅴ) For $\alpha = \kappa = 1$, the BXII-PC distribution reduces to the log-logistic half Cauchy (Log-Log-HC) distribution.

2.2.   Nexus between the exponential and gamma variables

We derive the BXII-PC distribution from nexus between the exponential and gamma variables.

Lemma 2.2.1. If $W_{1} \sim \exp \left(1\right)$ and $W_{2} \sim gamma\left(\alpha, 1\right)$ are independent, then for

$W_{1} = \left\{-\log \left[1-\frac{2}{\pi } \tan ^{-1} \left(\left(\frac{X}{\theta } \right)^{\kappa } \right)\right]\right\}^{\beta } W_{2}, \,$ we have that $X$ has the density (2.4).

Proof. If $W_{1} \sim \exp \left(1\right)$, i.e. $f\left(w_{1} \right) = {\rm e}^{-w_{1} } \, ,\, w_{1} > 0$,

$W_{2} \sim gamma\left(\alpha, 1\right)$, i.e. $f\left(w_{2} \right) = \frac{w_{2} {}^{\alpha -1} {\rm e}^{-w_{2} } }{\Gamma \left(\alpha \right)}, \, \, \, w_{2} > 0$,

then, the joint distribution of the two rvs is $f\left(w_{1}, w_{2} \right) = \frac{w_{2} {}^{\alpha -1} {\rm e}^{-w_{2} } {\rm e}^{-w_{1} } }{\Gamma \left(\alpha \right)}, \, \, \, w_{1} > 0, \, \, w_{2} > 0$.

Let $W_{1} = \left\{-\log \left[1-\frac{2}{\pi } \tan ^{-1} \left(\frac{X}{\theta } \right)^{\kappa } \right]\right\}^{\beta } W_{2}$, the joint density of the rvs $X$ and $W_{2}$ has the form

The marginal density of $X$ takes the form

After simplification, we arrive at

which is the BXII-PC density.

The survival, failure rate and cumulative failure rate functions of $X$ are given, respectively, by (for x>0)

and

The quantile function of $X$ (for $0 < q < 1$) follows from

and its random number generator with $Z \sim$ Uniform (0, 1) is the solution of the nonlinear equation

2.3.   Shapes of the BXII-PC density and hazard rate functions

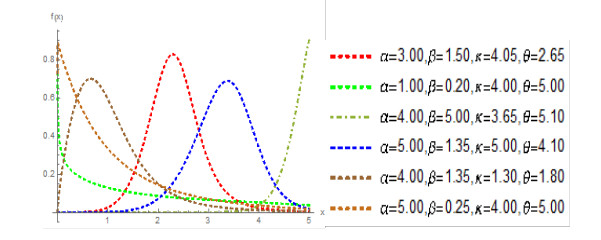
We plot the density and failure rate functions of the BXII-PC distribution for selected parameter values. The BXII-PC density can display numerous shapes such as symmetrical, right-skewed, left-skewed, J, reverse-J and exponential (as Figure 1). The failure rate function can highlight shapes as modified bathtub, inverted bathtub, increasing, decreasing; increasing-decreasing and decreasing-increasing-decreasing (as Figure 2). Therefore, the BXII-PC distribution is quite flexible and can be applied to numerous data sets.

3.   Mathematical properties

Here, we present certain mathematical and statistical properties such as the ordinary moments, incomplete moments, inequality measures, conditional moments, reliability measures and characterization.

3.1.   Moments

The moments are significant tools for statistical analysis in pragmatic sciences. The r${}^{th}$ ordinary moment of $X$, say $\mu '_{r} = E\left(X^{r} \right)$, can be expressed from (2.4) as

Letting $w = \left[-\log \left(1-2\pi ^{-1} \tan ^{-1} \left(\left(\frac{x}{\theta } \right)^{\kappa } \right)\right)\right]$, we have

The following power series (^[21]) can be obtained from Mathematica

where $a_{0} \left(s\right) = 1, a_{1} \left(s\right) = -s/3, \, \, \, a_{2} \left(s\right) = s\left(5s-7\right)/90,$ etc.

Using this expression we have

where $\exp \left[\left(\frac{r}{\kappa } -2i\right)w\right] = \sum _{j = 0}^{\infty }\frac{\left(\frac{r}{\kappa } -2i\right)^{j} }{j!} w^{j}$.

The r${}^{th}$ ordinary moment of $X$ with BXII-PC distribution is

Letting $w^{\beta } = y, w = y^{\frac{1}{\beta } }, \, \, dw = \frac{1}{\beta } y^{\frac{1}{\beta } -1} dy$, we have

where $\alpha \beta > j$ and $B\left(., . \right)$ is the beta function.

The r${}^{th}$ central moment $\left(\mu _{r} \right)$, coefficients of skewness ($\gamma _{1}$) and kurtosis ($\gamma _{2}$) of $X$ are

$\mu _{r} = \sum _{\ell = 1}^{r}\left(-1\right)^{\ell } \left({}_{\ell }^{r} \right)\, \mu '_{\ell } \, \mu '_{r-\ell }$, $\, \gamma _{1} = \mu _{3}/\sqrt[{3}]{\mu _{2} }$ and $\beta _{2} = \mu _{4} / (\mu _{2})^2$.

The numerical values for the mean $\left(\mu '_{1} \right)$, median $\left(\tilde{\mu }\right)$, standard deviation $\left(\sigma \right)$, skewness $\left(\gamma _{1} \right)$ and kurtosis $\left(\gamma _{2} \right)$ of the BXII-PC distribution for selected values of $\alpha, \beta, \kappa, \theta$ are listed in Table 1.

3.2.   Conditional moments

Life expectancy, mean waiting time and inequality measures can be obtained from the incomplete moments. The $s$th incomplete moment for the BXII-PC distribution is

Setting $w^{\beta } = y, w = y^{\frac{1}{\beta } }, \, \, dw = \frac{1}{\beta } y^{\frac{1}{\beta } -1} dy$, we have

where $B_{z} \left(., .\right)$ is incomplete beta function.

The mean deviation about the mean $\left(\delta _{1} = E\left|X-\mu \right|\right)$ and about the median $\left(\delta _{2} = E\left|X-\tilde{\mu }\right|\right)$ can be written as $\delta _{1} = 2\mu F\left(\mu \right)-2\mu \, M'_{1} \left(\mu \right)$ and $\delta _{2} = \mu -2M'_{1} \left(\tilde{\mu }\right)$, respectively, where $\mu = E\left(X\right)$ and $\tilde{\mu } = x_{0.5}$. The quantities $M'_{1} \left(\mu \right)$ and $M'_{1} \left(\tilde{\mu }\right)$ can be obtained from (3.2). For specific probability p, Lorenz and Bonferroni curves are computed as $L(p) = \frac{M'_{1} \left(q\right)}{\mu '}$ and $B(p) = \left. L(p)\right|p$ where $q = Q\left(p\right)$.

The r${}^{th}$ conditional moment $E\left(\left. X^{r} \right|X > z\right)$ is

The r${}^{th}$ reversed conditional moment $E\left(\left. X^{r} \right|X\le z\right)$ is

3.3.   Stochastic ordering

Stochastic orders are widely used in reliability, survival analysis, economics and operations research for judging the comparative behavior of distributions. Here, we present a result on the stochastic order for the BXII-PC distribution with $\beta, \kappa, \theta$ as common parameters. A random variable $X_{1}$ with a pfd denoted by $f_{1} (\alpha _{1}, \beta, \kappa, \theta)$ is said to be smaller than another random variable $X_{2}$ with a pfd denoted by $f_{2} (\alpha _{2}, \beta, \kappa, \theta)$ in likelihood ratio order, denoted by $X_{1} \le _{lr} X_{2}$, if $\frac{f_{1} (\alpha _{1}, \; \beta, \kappa, \theta)}{f_{2} (\alpha _{2}, \beta, \kappa, \theta)} \le 0$.

Proposition 3.3.1. Let $X_{1} \sim {\rm BXII}-{\rm PC}\left(\alpha _{1}, \beta, \kappa, \theta \right)\,$ and $X_{2} \sim {\rm BXII}-{\rm PC}\left(\alpha _{2}, \beta, \kappa, \theta \right).\, \,$ If $\alpha _{2} \le \alpha _{1},$ then the ${\rm BXII}-{\rm PC}$ distribution is ordered according to likelihood ratio ordering.

Proof. For $X_{1} \sim {\rm BXII}-{\rm PC}\left(\alpha _{1}, \beta, \kappa, \theta \right)\,$,

and for $X_{2} \sim {\rm BXII}-{\rm PC}\left(\alpha _{2}, \beta, \kappa, \theta \right)$,

Thus

If $\alpha _{2} \le \alpha _{1},$ we have $X_{1} \le _{lr} X_{2}$, i.e., $\frac{f_{1} (\alpha _{1}, \beta, \kappa, \theta)}{f_{2} (\alpha _{2}, \beta, \kappa, \theta)} \le 0$ is decreasing. Therefore for the BXII-PC distribution, random variable $X_{1}$ is said to be smaller than a random variable $X_{2}$ in likelihood ratio order $X_{1} \le _{lr} X_{2}$, since $\frac{f_{1} (\alpha _{1}, \beta, \kappa, \theta)}{f_{2} (\alpha _{2}, \beta, \kappa, \theta)} \le 0$.

3.4.   Reliability estimation of multicomponent stress-strength model

Consider a system that has $m$ identical components out of which s components are functioning. The strengths of m components are $X_{i}, i = 1, 2, ..., m$ with common cdf $F$ while, the stress $Y$ imposed on the components has cdf $G$. The strengths $X_{i}, i = 1, 2, ..., m$ and stress $Y$ are i.i.d. The probability that the system operates properly is reliability of the system i.e.

Let ${\rm X}\, {\rm \sim }\, {\rm BXII}-{\rm PC}\left(\alpha _{1}, \beta, \kappa, \theta \right)$ and ${\rm Y}\, {\rm \sim }\, {\rm BXII}-{\rm PC}\left(\alpha _{2}, \beta, \kappa, \theta \right)$ with common parameters $\beta, \kappa, \theta$ and unknown shape parameters $\alpha _{1}$ and $\, \alpha _{2}$. The reliability that the system operates properly in multicomponent stress- strength for the BXII-PC distribution is

where $v = \frac{\alpha _{1} }{\alpha _{2} }$ and $u = \left\{1+\left[-\log \left(1-2\pi ^{-1} \tan ^{-1} \left(\frac{y}{\theta } \right)^{\kappa } \right)\right]^{\beta } \right\}^{-\alpha _{2} }$.

Letting $u^{v} = w$, we have

where $B\left(., .\right)$ is the beta function. The probability in (3.4) is known as the reliability of multicomponent stress-strength model. For s$= m$ = 1, the multicomponent stress-strength model reduces to the stress-strength model (^[23]) as

which is independent of the parameters $\beta, \kappa \,$ and $\theta$.

3.5.   Characterizations based on truncated moment of a function of the random variable

In this subsection, we first present a characterization of the BXII-PC distribution in terms of a simple relationship between truncated moment of a function of $X$ and another function. This characterization result employs a version of a theorem due to ^[24]; see Theorem 7.1 of Appendix A. Note that the result holds also when the interval $H$ is not closed. Moreover, as mentioned above, it could be also applied when the cdf $F$ does not have a closed form. As shown in ^[25], this characterization is stable in the sense of weak convergence.

Proposition 3.5.1. Let ${\rm X:}\, \Omega \to \left(0, \infty \right)$ be a continuous rv and let

$q\left(x\right) = \left(1+\left\{-\log \left[1-2\pi ^{-1} \tan ^{-1} \left(\frac{x}{\theta } \right)^{\kappa } \right]\right\}^{\beta } \right)^{-1}, \, x > 0$. The rv $X$ has pdf (2.4) if and only if the function $\eta$ defined in Theorem 7.1 has the form

Proof. If $X$ has pdf (2.4), then for (x >0),

or

and

Conversely, if $\eta$ is given as above, then

and hence

and

In view of Theorem 7.1, $X$ has density (2.4).

Corollary 3.5.1. Let ${\rm X:}\, \Omega \to \left(0, \infty \right)$ be a continuous rv. The pdf of $X$ is (2.4) if and only if there exist functions $\eta \left(x\right)$ and $q\left(x\right)$ defined in Theorem 7.1 satisfying the differential equation

Remark 3.5.1. The general solution of the differential equation in Corollary 3.5.1 is

where D is a constant. Note that a set of functions satisfying the above differential equation is given in Proposition 3.5.1 with D = 0. However, it should also be noted that there are other pairs $\left(\eta, q\right)$ satisfying conditions of Theorem 7.1.

4.   Different estimation methods

In this section, we propose various estimators for estimating the unknown parameters of the BXII-PC distribution. We discuss maximum likelihood, maximum product spacings, least squares, weighted least squares, Cramer-von Mises and Anderson-Darling estimation methods and compare their performances on the basis of a simulated sample from the BXII-PC distribution. The details are as follows.

4.1.   Maximum likelihood estimation

We address parameters estimation using maximum likelihood method. The log-likelihood function for the vector of parameters $\xi = \left(\alpha, \beta, \kappa, \theta \right)$ of the BXII-PC distribution is

4.2.   Maximum product spacing estimates

The maximum product spacing (MPS) method is an alternative method to MLE for parameter estimation. This method was proposed by ^[26,27] as well as independently developed by ^[28] as an approximation to the Kullback-Leibler measure of information. This method is based on the idea that differences (spacings) between the values of the cdf at consecutive data points should be identically distributed. Let $X_{(1)}, X_{(2)}, \ldots, X_{(n)}$ be ordered sample of size n from the BXII-PC distribution. The geometric mean of the differences is given by

where, the difference $D_{i}$ is defined as

The maximum product spacing (MPS) estimates, say $\hat{\alpha }_{MPS}, \hat{\beta }_{MPS}, \hat{\theta }_{MPS}$ and $\hat{\kappa }_{MPS}$, of $\alpha, \beta, \theta$ and $\kappa$ are obtained by maximizing the geometric mean of the differences. Substituting cdf of BXII-PC distribution in Eq (4.2) and taking logarithm of the above expression, we have

where, $F\left(x_{(0)} \right) = 0$ and $F\left(x_{(n+1)} \right) = 1$. The MPSEs $\hat{\alpha }_{MPS}, \hat{\beta }_{MPS}, \hat{\theta }_{MPS}$ and $\hat{\kappa }_{MPS}$ are obtained by maximizing $MPS\left(\xi \right)$.

4.3.   Least squares estimates

Let $X_{(1)}, X_{(2)}, \ldots, X_{(n)}$ be ordered sample of size ${\rm n}$ from the BXII-PC distribution. Then, the expectation of the empirical cumulative distribution function is defined as

The least square estimates (LSEs) say, $\hat{\alpha }_{{\rm LSE}}, \hat{\beta }_{LSE}, \hat{\theta }_{LSE}$ and $\hat{\kappa }_{LSE}$, of $\alpha, \beta, \theta$ and $\kappa$ are obtained by minimizing

4.4.   Weighted least squares estimates

Let $X_{(1)}, X_{(2)}, \ldots, X_{(n)}$ be ordered sample of size ${\rm n}$ from the BXII-PC distribution. The variance of the empirical cumulative distribution function is defined as

Then, the weighted least square estimates (WLSEs) say, $\hat{\alpha }_{{\rm WLSE}}$, $\hat{\beta }_{WLSE}$, $\hat{\theta }_{WLSE}$ and $\hat{\kappa }_{WLSE}$, of $\alpha$, $\beta$, $\theta$ and $\kappa$ are obtained by minimizing

4.5.   Anderson-Darling estimation

This estimator is based on Anderson-Darling goodness-of-fits statistics which was introduced by ^[29]. The Anderson-Darling (AD) minimum distance estimates, $\hat{\alpha }_{{\rm AD}}$, $\hat{\beta }_{{\rm AD}}$, $\hat{\theta }_{{\rm AD}}$ and $\hat{\kappa }_{AD}$, of $\alpha$, $\beta$, $\theta$ and $\kappa$ are obtained by minimizing

4.6.   The Cramer-von mises estimations

The Cramer-von Mises (CVM) minimum distance estimates, $\hat{\alpha }_{{\rm CVM}}$, $\hat{\beta }_{{\rm CVM}}$, $\hat{\theta }_{{\rm CVM}}$ and $\hat{\kappa }_{{\rm CVM}}$, of $\alpha$, $\beta$, $\theta$ and $\kappa$ are obtained by minimizing

We refer the interested readers to ^[30] for AD and CVM goodness-of-fits statistics. To solve the above equations, Eqs (4.1)–(4.6) can be optimized either directly by using the R (optim and maxLik functions), SAS (PROC NLMIXED) and Ox package (sub-routine Max BFGS) or the non-linear optimization methods such as the quasi-Newton procedure to numerically optimize $\ell (\xi)$, $MPS\left(\xi \right)$, $QLSE\left(\xi \right)$, $QWLSE\left(\xi \right)$, $AD\left(\xi \right)$ and $CVM\left(\xi \right)$ functions.

5.   Simulation experiments

In this Section, we perform the simulation studies by using the BXII-PC to see the performance of the above estimators corresponding to this distribution and obtain the graphical results. We generate N = 1000 samples of size n = 20, 30, ${\dots}$, 800 from the BXII-PC distribution with true parameter values $\alpha = 15, \beta = 5, \theta = 0.5$ and $\kappa = 2$. The random numbers generation is obtained by its quantile function. In this simulation study, we calculate the empirical mean, bias and mean square errors (MSEs) and the mean relative estimates (MREs) of all estimators to compare in terms of their biases, MSEs and MREs with varying sample size. The empirical bias, MSE and MRE are calculated by (for $h = \alpha, \beta, \theta, \kappa$)

and

respectively. We expect that the empirical means are close to true values. MREs are closer to one when the MSEs and biases are near zero. All results related to estimations were obtained using optim-CG routine in the R programme.

The results of this simulation study are shown in Figures 3–6. These figures show that all estimators are to be consistent, since the MSE and biases decrease with increasing sample size and the values of MREs tend to one as expected. It is clear that the estimates of parameters are asymptotically unbiased. For all parameters estimations, the performances of all estimators are close except the MPS method.

6.   Application of the BXII-PC distribution

We consider an application to successive failures of the air conditioning system ^[31] for authentication the flexibility, utility and potentiality of the BXII-PC distribution. For this data set, we compare the BXII-PC distribution with BXII-HC, L-PC, LL-PC, Burr III power Cauchy (BIII-PC), Burr III half Cauchy (BIII-HC), Kumaraswamy half Cauchy (K-HC), beta half Cauchy (B-HC), Marshal Olkin power Cauchy (M-PC), Marshal Olkin half Cauchy (M-HC), BXII, PC and HC distributions. For selection of the optimum distribution, we compute the estimate of "likelihood ratio statistics ($-2\hat{\ell }$), Akaike information criterion (AIC), corrected Akaike information criterion (CAIC), Bayesian information criterion (BIC), Hannan-Quinn information criterion (HQIC), Cramer-von Mises (W*), Anderson Darling (A*), and Kolmogorov-Smirnov statistic with p-values [K-S (p-values] statistics" for all competing and sub distributions. We compute the MLEs and their standard errors (in parentheses). Table 2 reports the MLEs, their standard errors (in parentheses) and goodness of fit statistics such as W*, A*, KS (p-values). Table 3 displays the values of $-2\hat{\ell }$, AIC, CAIC, BIC and HQIC.

We infer from the Tables 2 and 3 that BXII-PC distribution is best model, with the smallest values for all criteria of goodness of fit statistics (except BIC).

Figure 7 infers that the BXII-PC distribution is best fitted to empirical data.

7.   Conclusions

We propose a new probability distribution, named BXII-PC distribution, based on Cauchy and Burr XII distribution via T-X family method. Its pdf and hrf shapes are seen as very flexible forms. To illustrate the importance of the BXII-PC distribution, we establish various mathematical properties such as random number generator, sub-models, moments related properties, inequality measures, reliability measures and characterizations. We estimate the model parameters by six different methods. We perform a simulation study on the basis of graphical results to evaluate the performance of maximum likelihood, maximum product spacings, least squares, weighted least squares, Cramer-von Mises and Anderson-Darling estimators of the BXII-PC distribution. We demonstrate the potentiality and utility of the BXII-PC distribution by considering an application to successive failures of the air conditioning system. We apply various model selection criteria and graphical tools to examine the adequacy of the proposed distribution. We infer that the BXII-PC model is empirically suitable for the lifetime applications (successive failures analysis). Therefore, the BXII-PC model is a flexible, reasonable and parsimonious to other existing distributions. Hence it should be included in the distribution theory to assist the researchers. Further, as perspective of future projects, we may consider several intensive subjects (ⅰ) unit BXII-PC; (ⅱ) Burr III-PC; (ⅲ) log-Burr XII-Power Cauchy regression; (ⅳ) various characteristics of the bivariate and the multivariate extensions of the BXII-PC; (ⅴ) Bayesian estimation of the BXII-PC parameters via complete and censored samples under different loss functions and (ⅵ) the study of the complexity of the BXII-PC via Bayesian methods.

Appendix A

Theorem 7.1. Let $\left(\Omega, F, P\right)$ be a given probability space and let $H = [a_{1}, a_{2} ]$ be an interval with $a_{1} < a_{2}$ ($a_{1} = -\infty, \, a_{2} = \infty$). Let $X:\Omega \to [a_{1}, a_{2} ]$ be a continuous random variable with distribution function $F$ and Let $g\left(x\right)$ be a real function defined on $H = [a_{1}, a_{2} ]$ such that $E[\left. g\left(X\right)\right|X\ge x] = h\left(x\right)$ for $x\in H$ is defined with some real function $h\left(x\right)$ should be in simple form. Assume that $g\left(x\right)\, \varepsilon \, C\left([a_{1}, a_{2} ]\right)$, $h\left(x\right)\varepsilon \, C^{2} \left([a_{1}, a_{2} ]\right)$ and $F$ is twofold continuously differentiable and strictly monotone function on the set $[a_{1}, a_{2} ]$. We conclude, assuming that the equation $g\left(x\right) = h\left(x\right)$ has no real solution in the inside of $[a_{1}, a_{2} ]$. Then $F$ is obtained from the functions $g\left(x\right)$ and $h\left(x\right)$ as $F\left(x\right) = \int _{a}^{x}k\left|\frac{h'\left(t\right)}{h\left(t\right)-g\left(t\right)} \right| \exp \left(-s\left(t\right)\right)dt$, where $s\left(t\right)$ is the solution of equation $s'\left(t\right) = \frac{h'\left(t\right)}{h\left(t\right)-g\left(t\right)}$ and k is a constant, chosen to make$\int _{a_{1} }^{a_{2} }dF = 1.$

Acknowledgments

The authors would like to thank the Editorial Board and two reviewers for their constructive comments that greatly improved the final version of the paper.

Conflicts of interest

The authors declare no conflict of interest.