Existence results for nonlinear fractional-order multi-term integro-multipoint boundary value problems

1.   Introduction

In general, microscopic particles spread out in a random manner. This occurs in a large number of phenomena in engineering, biology, ecology and medicine (see ^{[4,5,7,14,19,22,23,26,31,34,36]}). They have been studied by many researchers. Several formulations of diffusion exist in the market, and there are several types of treatments as well. Anomalous diffusion (unlike the classical one) cannot be elucidated by the standard ways, as the corresponding mean square displacement does not adhere to the linear growth law assumed in the classical problems. It is found that fractional derivatives are better suited for these disordered phenomena. They outperform by far the nonlinear models which suffer from high complexity and high computational cost.

In this paper, we are interested in structures described by Timoshenko models. This type of model, in the integer-order case (second order time derivative), has been investigated by a fairly large number of researchers, and several results have appeared in the literature. The basic model is described as follows:

where $\varphi$ stands for the transverse movement and $\psi$ stands for the angle of rotation of the beam. The constant $\rho _{1}$ stands for the mass density, $\rho _{2}$ represents the moment of mass inertia, $k$ is the shear modulus of elasticity and $b$ is the rigidity coefficient of the cross-section.

The system is conservative. Several kinds of damping devices have been utilized to stabilize these structures. First, two frictional dampings (based on velocity feedback) have been added, one in each equation ^[32]:

This is the most favorable situation after the case of structural dampings (based on the Laplacian of the velocity feedback). Of course, these are stronger than the mere frictional dampings. Quickly, it has been realized that only one damping process (in either the first or second equation) is enough to stabilize the system in an exponential manner. Undoubtedly, from the application point of view, this is more convenient because it is less costly and easier to implement. However, from the point of view mathematics, the problem becomes more challenging. Indeed, in this case we lost one nice term, which is responsible for the dissipation of that component. That is to say, one needs to show that only one damping in one component may not only force that component to go to zero exponentially, but also the other (undamped) one (in the energy norm). Researchers will then need to come up with new arguments to overcome this loss. For instance, the frictional damping term $\varphi _{t}$ has been dropped and the problem given by

is discussed in ^[25]. A much weaker damping namely, a viscoelastic damping in the rotational direction was considered first in ^[3]:

The authors proved that the system is exponentially (polynomially) stable depending on whether the involved relaxation function $\omega$ is exponentially (polynomially) decaying to zero. Subsequently, many extensions, improvements and generalizations, in several directions, have appeared in the literature (for example, ^{[10,15,20,21,24,35,37,38,39]} and the references therein). In particular, boundary dampings, nonlinear dampings and coupling with thermal equations have been considered. Moreover, the class of admissible relaxation functions has been extensively enlarged.

As mentioned above, when the structure operates in a complex medium, integer-order derivatives are no longer appropriate to describe the phenomena. The mean square displacement is not linear. It is nonlinear and proportional to "$t"$ to some power $\gamma \geq 0.$ The system is then classified according to the ranges or values of $\gamma$ whether they are equal to $0,$ between $0$ and $1,$ between $1$ and $2,$ equal to $2,$ above $2,$ etc. The combination of the balance law and the constitutive relationship between the stress and the strain will then involve a nonlocal term in time containing a singular kernel. This suggests fractional calculus as an adequate platform to study such phenomena.

We shall consider a viscoelastic damping which may be embodied in the material of the structure or added as a controller. It will act in the rotational direction to slow down the vibrations or absorb shocks that can reduce the lifetime of the structure, damage it or completely destroy it. Similar dampers are called "rotary" dampers in the market. We will address the fractional problem:

with the following Dirichlet boundary conditions and initial values:

where $^{C}D^{\beta }$ denotes the Caputo fractional derivative operator (defined below). To the best of our knowledge, the present analysis of this problem, has not been discussed so far.

Let $\mathcal{U} = \left(\varphi, \psi \right) ^{T}$ and $\mathcal{U}_{0} = \left(\varphi _{0}, \psi _{0}\right) ^{T};$ our system may be recast into the form

where

and

We consider the space

and the domain

In ^[9], the authors proved the existence and uniqueness for a similar abstract problem. We report here briefly this result. Let $(X, \left\Vert.\right\Vert)$ be a Banach space and $\mathcal{P},$ $\left(\mathcal{S} (t)\right) _{t\geq 0}$ be closed linear operators defined on the domains $D(\mathcal{P})$ and $D(\mathcal{S}(t))\supseteq D(\mathcal{P})$ dense in $X,$ respectively. We denote by $\left\Vert.\right\Vert _{G}$ the graph norm in $D(\mathcal{P}),$ $R(\nu, \mathcal{P}): = (\nu I-\mathcal{P})^{-1}$ and $\rho (\mathcal{P})$ is the resolvent of $\mathcal{P}.$ The problem

with the initial data $w(0) = w_{0}$ and $w^{\prime }(0) = 0$ in $D(\mathcal{P})$ (see also [1, 30]) admits the classical solution

such that $\frac{t^{1-\beta }}{\Gamma (2-\beta)}\ast (w-w_{0})\in C^{2}((0, \infty); X),$ provided that the following conditions hold:

(A1) For some $0 < \theta _{0}\leq \pi /2$ and every $\theta < \theta _{0},$ there is a constant $U > 0$ such that

and $\left\Vert R(\nu, \mathcal{P})\right\Vert < U/\left\vert \nu \right\vert,$ $\nu \in \Sigma _{0, \beta \omega }$ with $\omega = \theta +\pi /2.$

(A2) For each $w\in D(\mathcal{P}),$ $\mathcal{S}(.)w$ is strongly measurable on $(0, \infty).$ There exists a locally integrable function $f(t)$ with Laplace transform $\hat{f}(\nu),$ ${Re}(\nu) > 0$ and $\left\Vert \mathcal{S}(t)w\right\Vert \leq f(t)\left\Vert w\right\Vert _{G},$ $t > 0,$ $w\in D(\mathcal{P}).$ In addition, $\mathcal{S}^{\ast }:\Sigma _{0, \pi /2}\rightarrow \mathcal{L}(D(\mathcal{P}); X)$ has an analytic extension $\mathcal{\tilde{S}}$ to $\Sigma _{0, \omega },$ verifying the relations $\left\Vert \mathcal{\tilde{S}}(\nu)w\right\Vert \leq \left\Vert \mathcal{\tilde{S}}(\nu)\right\Vert \left\Vert w\right\Vert _{G},$ $w\in D(\mathcal{P})$ and $\left\Vert \mathcal{\tilde{S}}(\nu)\right\Vert = O\left(\frac{1}{\left\vert \nu \right\vert }\right)$ as $\left\vert \nu \right\vert \rightarrow \infty.$

(A3) There exists a subspace $F$ that is dense in $(D(\mathcal{P}), \left\Vert.\right\Vert _{G})$ and $C > 0$ such that $\mathcal{P} (F)\subseteq D(\mathcal{P}),$ $\mathcal{S}^{\ast }(\nu)(F)\subseteq D(\mathcal{P}),$ $\left\Vert \mathcal{PS}^{\ast }(\nu)w\right\Vert \leq C\left\Vert w\right\Vert,$ $w\in F$ and $\nu \in \Sigma _{0, \omega }.$

Assuming that $\mathcal{U}_{0}\in D(M),$ it follows from the above result that we have a classical solution in

such that $\frac{t^{1-\beta }}{\Gamma (2-\beta)}\ast (\varphi -\varphi _{0}), \frac{t^{1-\beta }}{\Gamma (2-\beta)}\ast (\psi -\psi _{0})\in C^{2}((0, \infty); L^{2}(0, 1)).$

In fractional calculus, it is known that $^{C}D^{\alpha }\left(^{C}D^{\alpha }\varphi (t, x)\right) \neq ^{C}D^{2\alpha }\varphi (t, x).$ Consequently, rewriting our system using $^{C}D^{\alpha }\left(^{C}D^{\alpha }\varphi \right)$ and $^{C}D^{\alpha }\left(^{C}D^{\alpha }\psi \right)$ will result in additional terms. Actually, the relationship between both forms is given by

We shall consider, rather the simplified system given by

for $0 < x < 1, \; t > 0$ with the initial and boundary conditions (1.2). Clearly, the two fractional derivatives coincide when $\varphi ^{\prime }(0, x) = 0.$ The existence and uniqueness are then guaranteed by ^[9] (see also Section 3 below). Regarding the stability, it will not be affected, as $1-2\alpha < 0.$

For this problem (1.2) and (1.3), we shall first finalize the discussion on the existence and uniqueness of a solution by using the notion of resolvents (instead of semi-groups). Then, we will highlight the difficulty of treating the stability for this problem. The utilization of a fractional chain rule version gives rise to a problematic term in the fractional derivative of the "energy" functional. Even though we found a way to control it, a smallness condition on the involved kernel is still imposed. We obtain a Mittag-Leffler- type stability provided that the kernel itself decays somehow in a similar manner.

Various other fractional systems modeling Timoshenko beams have been derived under different conditions and in different circumstances. The governing equations often involve either Caputo or Riemann-Liouville fractional derivatives. They have been tackled mostly from the engineering (response determination, resonance, free vibrations, influences on mechanical responses, parametric analyses, steady-state response, transient response, etc.) or numerical analysis perspective. A number of analytical and semi-analytical approaches have been employed (see ^[6,27,28] and the references therein). This involves, for instance, Galerkin schemes, central difference schemes, direct numerical integration schemes, averaging methods and various kinds of approximations of fractional derivatives. The utilized methods were compared to the traditional ones (extended actually to the fractional case), such as the Laplace transform, Fourier integral transform and Mellin transform, which have been very instrumental. Error estimates and numerical experiments have been conducted to justify the usefulness, effectiveness and accuracy of fractional models in describing the dynamics of beams. On the other hand, integer-order (with second-order time-derivatives of the states as leading terms) Timoshenko models with fractional damping have also been investigated in many research papers (see ^[16,18] and the references therein). The fractional damping may be weak (described by a fractional derivative of the state) or strong (described by a fractional derivative of the Laplacian of the state). In the latter case, it may be looked at as a viscoelastic damping process with a singular kernel. More precisely, it takes the form of the convolution of a singular kernel (power type) with the time-derivative of the Laplacian of the state.

In the next section, we prepare some preliminaries. Section 3 contains the existence and uniqueness results. It is followed by a section in which we prove two useful identities and define our "energy" functional. Section 5 is devoted to the introduction of several functionals. In Section 6, we treat the stability issue. Section 6 is concerned with some numerical simulations. A conclusion is provided in the last section.

2.   Definitions and propositions

In this section, we present the definition of the Riemann-Liouville fractional derivative, the Caputo fractional derivative and the Mittag-Leffler functions (see also ^{[13,17,29,33]} for more on fractional calculus). Some useful formulas are also given.

Definition 1. The Riemann-Liouville fractional integral of order $\gamma > 0$ is given by

for any measurable function $\mathcal{\chi }$ provided that the right-hand side exists. Here, $\Gamma (\gamma)$ is the usual gamma function.

Definition 2. The fractional derivative of order $\gamma$ in the sense of Caputo is given by

whereas the fractional derivative of order $\gamma$ in the sense of Riemann-Liouville is defined by

provided that the right-hand sides exist.

The passage to and from the Riemann-Liouville fractional derivative and the Caputo fractional derivative is given by

We recall the definitions of the one-parametric and two-parametric Mittag-Leffler functions, respectively:

and

Clearly, $E_{\alpha, 1}(z)\equiv E_{\alpha }(z)$.

Proposition 1. ^[40] If $\mathcal{\chi }(t)$ is a differentiable function satisfying

for some $\gamma > 0,$ then $\mathcal{\chi }(t)\leq \mathcal{\chi } (0)E_{\alpha }(-\gamma t^{\alpha }),$ $t\geq 0.$ When the derivative is of the Riemann-Liouville type, we obtain $t^{\alpha -1}E_{\alpha, \alpha }(-\gamma t^{\alpha })$ rather than $E_{\alpha }(-\gamma t^{\alpha }).$

Proposition 2. ^[13] For $\alpha, \beta > 0,$ the identity

holds.

Proposition 3. [13, p. 61] For $\mu, \alpha, \beta > 0,$ we have the relation

Proposition 4. [29, p. 99] If $I^{1-\gamma }\mathcal{\chi }(t)\in C^{1}([0, \infty)),$ $0 < \gamma < 1$ and $f(t)$ is a continuous function, then it holds that

We shall utilize repeatedly the following fractional product rule.

Proposition 5. ^[2] Let $f(t)$ and $g(t)$ be absolutely continuous functions on $[0, T],$ $T > 0$. Then, for $t\in \lbrack 0, T]$ and $0 < \alpha < 1,$ we have

Taking $f(t)\equiv g(t)$ will result in the well-known inequality (instead of the ordinary chain rule)

The vector version also holds.

3.   Existence and uniqueness

Here, we delineate the assumptions on the initial data and the kernel. Moreover, the existence and uniqueness issue is finalized. We shall assume that our initial data satisfy $\mathcal{U}_{0}\in D(M)$ (this is defined below and involves the knowledge of fractional derivatives of the states at zero). The kernel $\omega$ is assumed to satisfy the following condition:

(A) The kernel $\omega :(0, \infty)\rightarrow (0, \infty)$ is a nonnegative continuous function satisfying $I^{1-\alpha }\omega (t)\in C^{1}([0, \infty)),$

and

for some positive constant $C_{\omega }.$

Proposition 6. Assuming (A), we have

$\omega (t)$ is summable and

for some $\tilde{\omega} > 0.$

Proof. The proofs follow by a direct application of Propositions 1–3.

Our problem (1.2) and (1.3) may be rewritten as a system of fractional order $\alpha,$ $1/2 < \alpha < 1.$ As a matter of fact, letting $\mathcal{U} = \left(\varphi, \tilde{\varphi}, \psi, \tilde{\psi}\right) ^{T},$ $\tilde{\varphi} = ^{C}D^{\alpha }\varphi,$ $\tilde{\psi} = ^{C}D^{\alpha }\psi$ and $\mathcal{U} _{0} = \left(\varphi _{0}, \tilde{\varphi}_{0}, \psi _{0}, \tilde{\psi} _{0}\right) ^{T},$ it is evident that

where

and

We set

and

Assuming that $\mathcal{U}_{0}\in D(M),$ it follows from the theorem in ^[30] that we have the classical solution

satisfying $t^{-\alpha }\ast \varphi _{t}\in C^{1}\left((0, \infty), L^{2}(0, 1)\right)$ and $t^{-\alpha }\ast \psi _{t}\in C^{1}\left((0, \infty), L^{2}(0, 1)\right).$

It is proved in ^[8] that the abstract problem given by

possesses a unique solution under the above assumptions (A2), (A3) and

(A1)'For some $\pi /2 < \phi < \pi,$ there exists a constant $C = C(\phi) > 0$ such that

and $\left\Vert R(\nu, \mathcal{P})\right\Vert < C/\left\vert \nu \right\vert,$ $\nu \in \Sigma _{0, \phi }.$

The function $f:(0, \infty)\times X\rightarrow X$ was assumed to be continuous and locally Lipschitz in the second variable uniformly, with respect to the first variable.

The following resolvent operator notion was employed.

Definition 3. The family of bounded linear operators $\left(R_{\gamma }(t)\right) _{t\geq 0}$ determines a $\gamma$-resolvent for (3.2) if the following is true

(a) The mapping $R_{\gamma }(t):[0, \infty)\rightarrow \mathcal{L}(X): = \mathcal{L}(X; X)$ is strongly continuous and $R_{\gamma }(0) = I.$

(b) $\forall w\in D(\mathcal{P)},$ $R_{\gamma }(.)w\in C\left([0, \infty); D(\mathcal{P)}\right) \cap C^{\gamma }\left((0, \infty); X\right)$ ($C^{\gamma }\left((0, \infty); X\right)$ is the space of continuous functions $w$ for which $^{C}D^{\gamma }w$ exists and is continuous), and

It is shown that the family

is a $\gamma$-resolvent for (3.2). Here, $\Gamma : = \{te^{i\theta }:t\geq r\}\cup \{re^{i\zeta }:-\theta \leq \zeta \leq \theta \}\cup \{te^{-i\theta }:t\geq r\}$ is oriented counterclockwise, where $\pi /2 < \theta < \phi$ and $r > r_{1}$ (a positive number determined in the proofs). □

Theorem 1. For $U_{0}\in D(M\mathcal{)}$ and $f(t, U(t))\equiv 0,$ the function

is a solution of (3.2).

Bearing in mind that, in our case, the Laplacian is the infinitesimal generator of an analytic semigroup, the conditions (A1), (A2) and (A3) are fulfilled. We deduce the existence of a unique (strong) solution in the space

where

4.   Two useful identities

Before tackling the stability issue, we need to prove two identities, define the "energy" functional and compute its fractional derivative. The superscript $C$ in $^{C}D^{\alpha }$ will be dropped for notation convenience. Moreover, we will denote

and $\left\Vert.\right\Vert$ the $L^{2}$-norm.

The analysis below is valid on arbitrary intervals $[0, T],$ $T > 0.$ Since the evaluations are independent of time, they will be valid on all $[0, +\infty).$

Proposition 7. Assume that $I^{1-\alpha }\omega (t)\in C^{1}([0, \infty)),$ $0 < \alpha < 1$ and $\chi \in H_{0}^{1}(0, 1)$ is a differentiable function. Then, it holds that

Proof. Using Proposition 5 and the identity

we find that

By virtue of Proposition 4 and the summability of $\omega$, we see that

and

Therefore,

Having in mind that

we infer that

for $t\geq 0.$ This finishes the proof. □

Proposition 8. For absolutely continuous functions $\chi$ and $\omega$ such that $I^{1-\alpha }\omega,$ $0 < \alpha < 1$ is absolutely continuous, we have

Proof. Clearly, from Propositions 4 and 5, we can write

The conclusion follows.

The following energy functional is dictated by Proposition 7:

Employing (4.1), we have the following along the solutions of (1.3) and (1.2)

On the other hand, from the equations of the system (1.3), we have

Therefore,

As the last term in (4.2) may be estimated by

it is clear that, for $t > 0,$

where we have used the Assumption (A). This is a delicate situation because we do not know the sign of the right-hand side of (4.3). Actually, even if we know that the sign is negative, we cannot deduce dissipativity. □

5.   Several lemmas

Several functionals, with which we will modify our energy functional, will be introduced in this section, and their fractional derivatives will be evaluated.

Lemma 1. The $\alpha$-fractional derivative of the functional

satisfies

Proof. Proposition 5 allows us to write

for $t\geq 0,$ and the relationship between the Riemann-Liouville fractional derivative and the Caputo fractional derivative gives

Moreover, the summability of $\omega$ and Proposition 4 lead to

and by the definition of the Riemann-Liouville fractional derivative, it follows that

From Proposition 3, we have

and using

the relation (5.1) leads to

The announced estimation is obtained by noticing that

The proof is complete. □

Our second functional is given in the next lemma.

Lemma 2. For the functional

and $\delta _{2} > 0,$ it holds that

Proof. Applying the operator $D^{\alpha }$ to the functional $U_{2}(t),$ we obtain

Next, the estimations

and

imply that

Finally, by virtue of the relation

we get

□

Our third functional is defined below.

Lemma 3. If

then, for $t > t_{0} > 0,$

where $\omega _{0} = \int\nolimits_{0}^{t_{0}}\omega (s)ds$ and $\delta _{i} > 0,$ $i = 1, 2, 3.$

Proof. Differentiating $U_{3}(t)$ and using Problem (1.2) and (1.3), we find that

Next, we integrate by parts and use Proposition 8 to get

By assumption (A), relation (5.3) and the Young inequality, we infer that

for $\delta _{1} > 0,$ and

Next, observing that $E_{\alpha }(-C_{\omega }t^{\alpha })\leq C_{1}t^{-\alpha }$ (for some positive constant $C_{1}$) away from zero, we have

where $C_{2}: = C_{1}\Gamma ^{2}(1-\alpha)/\alpha.$ Therefore,

Our last evaluation is as follows:

for $\delta _{3} > 0.$ The relations (5.6)–(5.11), when inserted in (5.5), yield

for $t > t_{0} > 0.$ This ends the proof. □

The role of our fourth functional is to control the last term in the evaluation of $D^{\alpha }U_{3}(t).$ We set

Lemma 4. The Caputo fractional derivative of the above functional $U_{4}(t)$ fulfills the following for $\delta _{1}, \delta _{2} > 0$ and $t > t_{0} > 0:$

Proof. A simple fractional differentiation of order $\alpha$ shows that

and in view of Proposition 8, we see that

This identity (5.12) can be evaluated by Young's inequality and a similar argument as for relation (5.10) above, as follows:

for $\delta _{1}, \delta _{2} > 0$ and $t > t_{0} > 0.$ The proof is completed. □

The fractional derivative of our fifth functional gives rise to the useful term $-\left\Vert \varphi _{x}+\psi \right\Vert ^{2}.$

Lemma 5. Let

Then, for $\delta _{2}, \delta _{3} > 0$,

Proof. Clearly, from Proposition 5 and the equations of the system, we have

and after integration by parts,

Repeated use of Young's inequality leads to

Observe that

and

Therefore,

for $\delta _{2}, \delta _{3} > 0.$ The proof is complete. □

To deal with some of the boundary terms in (5.13), we need the functional

where $m(x) = 2-4x,$ so that $m(0) = -m(1) = 2.$

Lemma 6. The functional $U_{6}(t)$ verifies along the solutions of (1.2) and (1.3)

for $t\geq 0$ and $\delta _{i} > 0, \; i = 2, 3, 4.$

Proof. Clearly, a direct application of Proposition 5 gives

and using the second equation of our system gives

Notice that, employing the relations (5.2) and (5.3), integrations by parts and Young's inequality gives

and

It suffices now to apply the previous estimations (5.15)–(5.18) in (5.14) to obtain the following for $\delta _{i} > 0$, $i = 2, 3, 4$:

The proof is over. □

The derivative of the next functional provides us with the boundary terms needed to control the other remaining corresponding boundary terms in Lemma 5. Let

Lemma 7. The above functional $U_{7}(t)$ satisfies

Proof. Proceeding similarly to the previous lemmas, it appears that

or

Next, we employ the inequality $\left\Vert \varphi _{x}\right\Vert ^{2}\leq 2\left\Vert \varphi _{x}+\psi \right\Vert ^{2}+2\left\Vert \psi _{x}\right\Vert ^{2}$ to reach

The proof is complete. □

Consider the problem

The last functional is

Lemma 8. The above functional $U_{8}(t)$ satisfies the following for $\delta _{2}, \delta _{5} > 0$ and $t\geq 0:$

Proof. Proposition 5 implies that

Considering the solutions of (1.3), this relation may be estimated by

and because $\left\Vert D^{\alpha }w\right\Vert ^{2}\leq \left\Vert D^{\alpha }\psi \right\Vert ^{2}$ (by applying $D^{\alpha }$ to both sides, multiplying by $D^{\alpha }w$ and integrating by parts), we find that

Therefore,

or

The proof is complete. □

6.   Stability

We are now ready to state and prove our first theorem. Let

where $N$ and $M_{i}$ are positive constants to be determined inside the proof.

6.1.   Equal speed of propagation

In this subsection, we consider the case when the wave speeds of propagation are equal.

Theorem 2. Assume that the initial data satisfy $\mathcal{U} _{0}\in D(M)$ and $\omega$ satisfies assumption (A). If $\frac{ \rho _{1}}{k} = \frac{\rho _{2}}{b},$ then the solution of (1.2) and (1.3) goes to rest in a Mittag-leffler manner provided that $\tilde{\omega}$ is small enough, i.e., there exist two positive constants $\mu$ and $L$ (depending on $E(0)$) such that

Proof. With the help of all previous lemmas above, we compute $D^{\alpha }U(t).$ The idea of the proof is to reach a fractional differential equation of the form

Proposition 1 then allows one to conclude the estimation in the theorem but only on $(t_{0}, \infty).$ Employing a continuity argument, we obtain a similar one on $[0, t_{0}].$

Observe first that we can make the terms in $E_{\alpha }(-C_{\omega }t^{\alpha })$ as small as we wish by increasing the time $t_{0}$. Consequently, the parameter $\delta _{1}$ may be ignored for the time being. Second, take $M_{1} = \frac{2N}{b},$ $M_{6} = \frac{3M_{5}}{k},$ $\delta _{4} = \frac{k}{26}$ and $M_{7} = \frac{M_{5}}{12}$. For small $\tilde{\omega}$ (and therefore small $\delta _{2}),$ we are left with two sets of conditions:

and

Take $N$ large enough ($\delta _{3}$ may also be large) so that the first set of conditions of (6.2) holds. For a large value of $\delta _{3},$ there remains

Next, choosing $M_{3}$ large so that the second relation is verified (with $\delta _{5}$ large), we are left only with

Proceeding backward, we can select the ignored terms so as to verify all of the conditions. Thus, we get a relation of the form (6.1). The proof is complete. □

6.2.   Non-equal speed of propagation

In practical problems, the speeds of propagation are not necessarily equal. We will need the following result for the basic fractional differential equation:

with $0$ as the equilibrium. Let $\mathcal{K}$ be the class of strictly increasing continuous functions $h:[0, +\infty)\rightarrow \lbrack 0, +\infty)$ satisfying $h(0) = 0.$

Proposition 9. ^[11] Assume that $f$ is a nonnegative bounded function such that $I^{\alpha }f,$ $0 < \alpha < 1$ is also bounded. Then, $\lim \inf_{t\rightarrow \infty }f(t) = 0.$

Proposition 10. ^[12] If there exist a Lyapunov function $Z(t, x(t))$ and two functions $\vartheta _{1}(.)$ and $\vartheta _{2}(.)$ in $\mathcal{K}$ such that, for all $x\neq 0,$ $\vartheta _{1}(\left\Vert x(t)\right\Vert)\leq Z(t, x(t))\leq \vartheta _{2}(\left\Vert x(t)\right\Vert)$ and $D^{\alpha }Z(x(t), t)\leq 0,$ $0 < \alpha \leq 1,$ then the equilibrium is Lyapunov uniformly stable.

Theorem 3. Assume that $\mathcal{U}_{0}\in D(M)$ and the speeds of propagation are not necessarily equal. Then, we have that $\lim \inf_{t\rightarrow \infty }E(t) = 0.$ If $\psi _{x}(0) = 0,$ then the system is Lyapunov uniformly stable for small values of $\tilde{\omega}$.

We need to come up with a Lyapunov function whose fractional derivative is non-positive. We recall, from the previous section, that after putting back the non-zero term

in $U_{5}(t),$ as follows

we pass to the higher-order energy. Rewriting $E(t)$ in the form $E(t) = E(t, \varphi, \psi)$ to account for the dependence on $\varphi$ and $\psi,$ we define the `$2\alpha$-order' energy by

that is,

We find that

From Proposition 7, we have the following for $t\geq 0$:

Therefore, for $\delta _{6} > 0,$ it follows that

Proposition 11. Assume that $k, f$ are two continuous functions on $(0, +\infty)$ such that

Then,

Proof. Clearly, for $t\geq 0$,

On one hand, by Proposition 4, we find

and on the other hand, the relationship between both derivatives gives

Therefore,

and

The proof of the proposition is complete. □

Multiplying the relation (6.4) by $g(t),$ then integrating over $(0, 1)$ and applying Young's inequality, we obtain the following:

Corollary 1. Assume that $k, f$ are two continuous functions on $(0, +\infty)$ such that

and $f, D^{\alpha }f, g\in L^{2}(0, 1).$ Then,

In the case that $g = D^{\alpha }f$, this corollary gives the following:

Corollary 2. Assume that $k, f$ are two continuous functions on $(0, +\infty)$ such that $I^{1-\alpha }k(t), f(t)\in C^{1}(0, \infty).$ Then,

Proof of Theorem 3. (Sketch) As in the previous section, we suggest using the new functional

to deal with the problematic term

and proceed similarly. Combining (6.3), $D^{\alpha }U$ and the above corollaries, for

we arrive at

for small $\tilde{\omega}$ and large $t_{0}$ for some $C_{5}$, $C_{6} > 0.$ Applying $I^{\alpha }$ to both sides gives

Notice that, by the continuity of $D^{\alpha }V(s)$ (below, all constants $C_{i},$ $i = 7, ..., 12$ are positive),

Thus,

and by Proposition 3, for $t\geq t_{0}$, we have

Hence,

The first conclusion follows from Proposition 9 and the second one from Proposition 10. □

7.   Numerical simulations

In this section, we shall present some numerical examples to validate the results obtained for both the equal speed of propagation and non-equal speed of propagation cases.

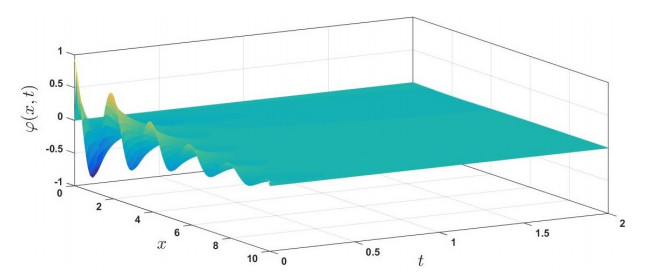
Example 1. Consider the system (1.2) and (1.3) with the following selected functions and parameters: $\varphi _{0}(x) = e^{- \frac{x}{4}}\cos (\pi x),$ $\psi _{0}(x) = 2e^{-\frac{x}{4}}\sin (2\pi x),$ $\varphi _{1}(x) = \psi _{1}(x) = 0,$ $\omega (t) = e^{-2t},$ $\beta = 1.96,$ $k = b = 2,$ $\rho _{1} = \rho _{2} = 2,$ $x\in \lbrack 0, 10],$ $t\in \lbrack 0, 2].$

The condition (A) and the equality $\frac{k}{\rho _{1}} = \frac{b}{\rho _{2}}$ are satisfied. By means of Theorem 2, the solutions $\varphi (x, t)$ and $\psi (x, t)$ go toward zero in a Mittag-Leffler manner. This finding is illustrated in Figures 1 and 2, depicting the variation of $\varphi (x, t)$ and $\psi (x, t)$ as functions of spatial and temporal variables in the range $[0, 10]\times \lbrack 0, 2].$ Figures 3 and 4 show the dissipativity of the vibrations relative to the $x$-axis as the time variable rises.

Example 2. Consider the system (1.2) and (1.3) involving the functions and parameters that are taken as $\varphi _{0}(x) = 0.5\sin (\frac{7}{4}\pi x),$ $\psi _{0}(x) = 2x\cos (\pi x),$ $\varphi _{1}(x) = \psi _{1}(x) = 0,$ $\omega (t) = e^{-4t},$ $\beta = 1.96,$ $k = 2,$ $b = 1.5,$ $\rho _{1} = \frac{2}{3},$ $\rho _{2} = 1,$ $x\in \lbrack 0, 10],$ $t\in \lbrack 0, 2].$

The conditions (A) and $\frac{k}{\rho _{1}}\neq \frac{b}{\rho _{2}}$ are met. Thus, Theorem 3 can be applied, which means that the solutions $\varphi (x, t)$ and $\psi (x, t)$ go toward zero as a Mittag-Leffler function. This may be visualized in Figures 5 and 6, representing the behavior of solutions $\varphi (x, t)$ and $\psi (x, t)$ in $[0, 10]\times \lbrack 0, 2].$ The oscillations of $\varphi (x, t)$ and $\psi (x, t)$ with regard to the spatial variable, decrease as the temporal variable increases, as illustrated in Figures 7 and 8.

8.   Conclusions

In this work, we have examined the dynamics of a Timoshenko beam operating in an anomalous media. It is derived from the classical Timoshenko model by replacing the integer-order derivatives with fractional ones between one and two. Actually, sequential fractional derivatives are better suited for the multiplier technique. It is shown that a viscoelastic damping process acting on the rotational component is capable of driving the structure to equilibrium with a Mittag-Leffler rate in the case of equal speed of propagation and a relaxation function satisfying a fractional inequality whose solutions are bounded above by Mittag-leffler functions. This generalizes a similar case of exponential stability which happens in the classical (integer-order) case. When the speeds of propagation are not equal, the situation is much more complicated and differs from the classical situation. We have obtained only a uniform Lyapunov stability without a specific rate.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are very grateful for the financial support and the facilities provided by King Fahd University of Petroleum and Minerals (Interdisciplinary Research Center for Intelligent Manufacturing & Robotics) through project number INMR2300. They are also very grateful to the anonymous referees, whose comments and suggestions helped to improve the original version of this work.

Conflict of interest

The authors declare no conflict of interest.