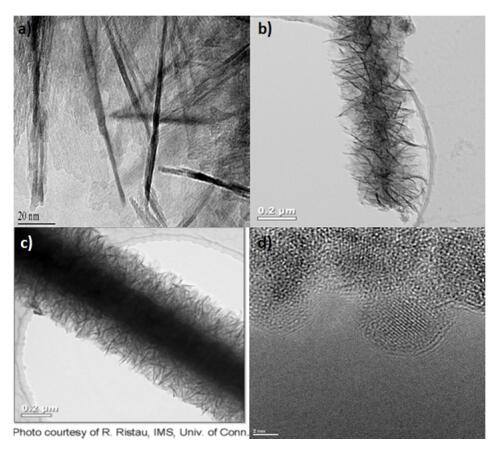
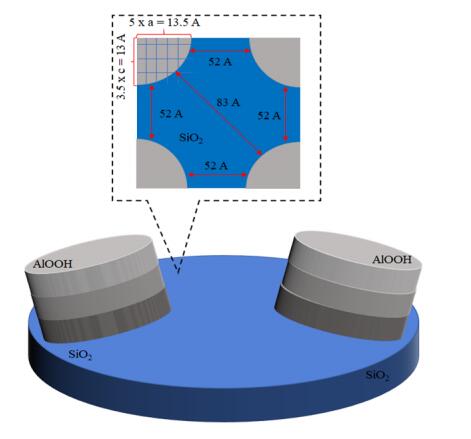
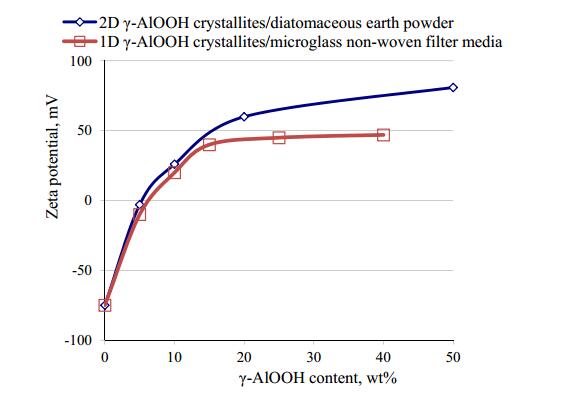
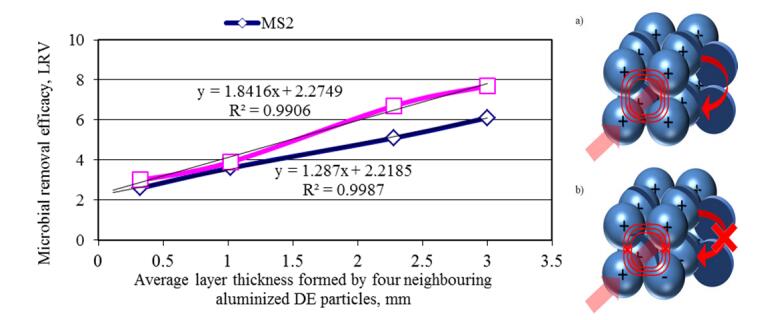
Two-dimensional (2D) and one-dimensional (1D) quantum-sized γ-AlOOH structures were deposited onto siliceous and cellulosic substrates in a one-step, aqueous, and moderate temperature process. Low cost, large scale manufacturing of siliceous and cellulosic substrates coated with 2D and 1D arrays of γ-AlOOH crystallites of 2.7 ± 0.5 nm in diameter, with an average height of 3 ± 2 nm and 250 ± 50 nm, respectively was demonstrated. Direct measurement of streaming potentials in NaCl aqueous electrolyte was accomplished in order to characterize the zeta potentials of the as mentioned surfaces. It was shown that the isoelectric point value of rough nanostructured surface is three pH units higher as compare to the flat crystalline γ-AlOOH surface, resulting in a high removal efficacy of submicron particles from aqueous suspension by the surfaces with combined microscale and nanoscale structures. Furthermore, ageing characteristics of the 2D and 1D γ-AlOOH crystallites were presented, which showed great removal efficiencies after seven to fourteen years of manufacturing.
1.
Introduction
With the rapid development of e-commerce platforms, the current order-driven reactive distribution model is increasingly failing to meet the requirements of e-commerce logistics for timeliness under the increasingly fierce competition. How to design an effective dynamic demand response strategy to alleviate the conflict between distribution efficiency and cost has become an urgent problem for e-commerce logistics. The massive historical demand data accumulated by digital business enterprises in the development process can be employed to generate prior knowledge of dynamic customer demand and integrate it with the optimization process of the vehicle routing problem, which is useful for the realization of dynamic proactive response to customer demand and to improve the quality of city logistics distribution efficiency.
In the context of a "sharing economy", the development of information technology and mobile communication networks has created favorable conditions for the employment of sharing services. Collaboration services allow participators to capture revenue from underutilized information resources. Nevertheless, the city distribution may exacerbate road traffic congestion and carbon emissions in urban areas. On this basis, some big retailers, such as Walmart, Tesco and Amazon, have begun to make new attempts to attract various resources participating in distribution [1,2,3]. Therefore, it is of great practical significance to consider collaborative services to design "last-mile" distribution in vehicle routing problems. At the same time, the importance and competitive value of "last-mile" and same-day delivery has led many companies to seek new solutions. One novel solution proposed by Walmart and Amazon is "crowdsourcing", which involves using their customers to transport packages on the way to their destinations rather than hiring many drivers or using third-party logistics firms (e.g., UPS or FedEx).
With the increase of e-tailing, orders are delivered through the fleets of retailers composed of capacitated vehicles or picked up by customers in physical stores. Compared with picking up in physical stores, higher distribution costs are required in the delivery of retailers, especially in the case of small numbers and scattered orders. However, with the unwillingness or insufficient time of some customers to pick up goods in physical stores, a new solution is required to motivate some customers picking up in physical stores to make a single delivery through their private cars, which requires that the delivery location is not too far from their destination and they are willing to make a single delivery given a small compensation. On this basis, a real-life application related to the PDVRPCS model occurs. Therefore, this paper focuses on the modeling and treatment of PDVRPCS. To deal with such routing optimization problems of collaboration services, this paper designs a highly accurate proactive forecasting method, order matching algorithm and a hybrid Genetic Algorithm (GA) and Simulated Annealing (SA) to minimize the transportation cost of logistic enterprises.
The remaining parts of this paper are organized as follows. In Section 2, the relevant literature is summarized, and the innovation points of this paper are clarified. Section 3 introduces the problem studied in this paper in detail. In Section 4, a mathematical model of PDVRPCS is described, and the detailed implementation of the GA-SA for solving the model is proposed in Section 5. A case study is conducted to verify the validity of the algorithm and mathematical model in Section 6. Finally, this study concludes in Section 7.
2.
Literature review
The literature review starts with proactive vehicle routing problems. Next, the existing results of vehicle routing problems based on capacity sharing are introduced, which is relevant for the research topic of this paper. Then, existing algorithms for solving vehicle routing problems are introduced briefly. Finally, the innovations of the models and algorithms proposed in this paper are emphasized.
The proactive vehicle routing problem is rooted in dynamic vehicle routing problems, referring to the vehicle routing problem with prediction and response strategies, and the possibility of demand is predicted in advance by the logistic enterprise through the customers' history of demand, attributes, etc. The distribution center of the enterprise can quickly respond to customer demand, decreasing the response time of demands. Thomas [4] designed a real-time heuristic algorithm to predict information in potential customer location and probability of demand occurrence, which can reduce the customer service delay rate. Lima et al. [5] improved the flexibility of customer response by using historical data and online data monitoring to anticipate the customer's requests from both customer needs and the enterprise itself. Based on the real-time, shared point-of-sale data, Hartzel and Wood [6] predicted future sales by using a single exponential smoothing method. Ma and Fildes [7] used a promotional decision support system to forecast demand and inventory levels by using the operational (store-level) data only. Zhu et al. [8] employed historical data to predict the demand for spare parts proactively using extreme value theory. Since the data change dynamically in real cases, Belka and Godlewski [9] focused on the aspect of geopositioning updates and their impact on the effectiveness of optimization algorithms. Ferrucci and Bock [10] proposed a space-time Poisson distribution model to cluster various customer demand patterns and realized proactive real-time control of distribution vehicles. Fathollahi-Fard et al. [11] optimized the home healthcare routing and scheduling problem considering patients' satisfaction under uncertainty by applying Jimenez's method and a modified multi-objective metaheuristic. Although all of the above papers have adopted prediction methods, there is a lack of appropriate response strategies. Therefore, fuzzy and deterministic indicators representing customers' attributes from multiple dimensions are selected in this paper. Then, the prospect value theory is used to predict the potential demands of dynamic customers, and the predicted results are employed for routing optimization.
In recent years, capacity sharing pattern design has become a hot topic in routing optimization. Fernández et al. [12] introduced the shared customer collaboration vehicle routing problem and established an integer programming model to minimize the total cost under the shared framework. The results showed that the ultimate cost savings depend on the number of shared customers and their location. Paul et al. [13] considered capacity sharing among different sales channels. Capacity sharing strategies were formulated mainly by determining transfer customers and using traditional idle capacity to reduce transportation cost. The outsourcing of 3rd Party Logistics (3PL) is a relatively mature logistics service mode, which can provide low-cost logistics services for enterprises. However, this mode requires a large number of orders as the basis of cooperation. Collaborative delivery of online orders by willing in-store customers (occasional drivers) is a low-cost solution when dealing with small, scattered orders. Archetti et al. [14] studied the vehicle routing problem with occasional drivers in logistics networks and established a static mixed integer programming model. The model is solved by the multi-start heuristic. Later, Macrina et al. [15] proposed two mixed integer programming models to extend the vehicle routing problem with occasional drivers, one allowing multiple deliveries per occasional driver and the other one allowing batch deliveries. Arslan et al. [16] studied the crowdsourcing distribution problem by proposing a variant that considers dynamic pickup and delivery options. The authors assumed that one driver can complete one or more deliveries from different sources. Mojtahedi et al. [17] proposed a sustainable vehicle routing problem by using the concept of triple bottom line for coordinating solid waste management based on the financial, environmental and social goals. Numerical experiments show that framing the coordinated logistics problem across several echelons can lead to potential overall waste disposal cost savings through increased recycling. Fathollahi-Fard et al. [18] developed a bi-level programming model for a home health care supply chain. To solve the model, three modified versions of algorithms and two hybrid meta-heuristics were presented to solve the model. For the first time, the authors proposed outsourcing for patients' demand to receive direct services from a hospital. Wang et al. [19] presented a Genetic Algorithm and Particle Swarm Optimization (GA-PSO) heuristic for the optimization of two-echelon cooperative logistics networks and designed a negotiation process for profit allocation. Dayarian and Savelsbergh [20] proposed a crowdsourcing and same-day delivery problem under a highly dynamic and stochastic delivery environment. To address the resource sharing in two-echelon logistics networks, Luo et al. [21] proposed an improved Non-dominated Sorting Genetic Algorithm-Ⅱ (NSGA-Ⅱ) for minimizing the total operational cost and vehicles used. Ren et al. [22] established a multi-center joint distribution optimization model for the low-carbon vehicle routing problem with time windows and developed a modified ant colony algorithm to solve the model by using the elite strategy and three further recombination rules. Gdowska et al. [23] modeled the crowdsourcing distribution problem as a double-level stochastic problem and assumed that occasional drivers can choose to accept or reject possible assignments. In order to solve the problem, the authors designed a heuristic method to find a subset of customers to be proposed to be occasional drivers. Research on capacity sharing focuses more on how to use cooperative vehicles for transportation instead of how to match between cooperative vehicles and online orders. In this paper, a low-cost capacity sharing strategy is achieved by matching the time window and destination relevance.
The Vehicle Routing Problems Cooperation Service (VRPCS) belongs to the Nondeterministic Polynomial-hard (NP-hard) problem. In addition to the basic constraints, the time window constraints of online customers, the time window constraints of cooperative drivers and the service scope should also be satisfied, which increases the complexity of PDVRPCS [24]. Russell and Chiang [25] employed a scatter search framework to solve the vehicle routing problem with time windows. For the same problem, Zhang et al. [26] established a mathematical model of vehicle routing problems with time windows and designed a hybrid intelligent algorithm to solve it. Cheng and Wang [27] decomposed the original vehicle routing problem into a clustering problem and a set of sub-problems with time window constraints. Meanwhile, a genetic algorithm and a simple heuristic algorithm have been developed to solve the two problems. Vidal et al. [28] designed a hybrid genetic algorithm with adaptive diversity control which provides a new neighborhood movement choice and restriction method to solve time-constrained vehicle routing problems. Belhaiza et al. [29] designed a hybrid tabu search with variable neighborhood algorithm to solve the vehicle routing problem with multiple time windows. In order to deal with multiple time windows, a minimum backward time slack algorithm is designed. Aiming at minimizing the total transportation distance, Shi et al. [30] designed a novel sector combination optimization algorithm to deal with waste collection problems in urban areas. Pasha et al. [31] studied a vehicle routing problem with a factory-in-a-box in multi-objective settings and proposed to compromise the conflicting cost components. A novel customized nature-inspired evolutionary algorithm is developed to solve the problem. Fathollahi-Fard et al. [32] studied a multi-objective robust optimization of the home healthcare model, which could present multi-depot, multi-period and multi-service. Baños et al. [33] considered a multi-objective vehicle routing problem with time windows, whose objective function not only considered distance and time window punishment, but also workload balance. Finally, a Pareto-based hybrid algorithm was designed to solve the model.
In order to solve the conflict between the demand and supply imbalance of terminal distribution, which aims to reduce the distribution cost and improve the distribution efficiency, scholars have carried out a lot of research on the mode of terminal collaborative distribution and introduced the concept of sharing into the field of distribution [34]. The public who are willing to participate receive small rewards. Jaller et al. [35] believe that crowdsourcing is a logistics mode in which traditional cargo transportation enterprises allocate the task of delivery of goods to the public who are willing to integrate it with their own schedules. This model is driven by the popularity of smartphones and the widespread adoption of mobile devices.
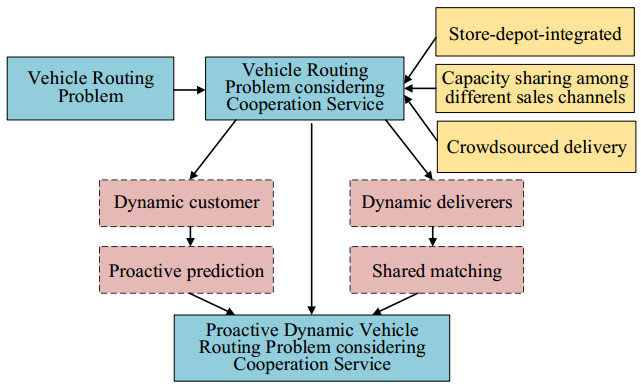
In a market where order arrival rates fluctuate greatly throughout the day, the advantages of crowdsourcing collaborative delivery are obvious and provide a new research perspective on collaborative vehicle routing problems. However, the volatility of customers and deliverers is an important exogenous variable in collaborative vehicle routing problems based on crowdsourced delivery. At present, a review of the relevant literature implies that few publications consider both dynamic proactive demand forecasting and order match simultaneously. Based on the studies of [13,14,36], the PDVRPCS was proposed in this paper (Figure 1), and this paper has the following four-fold scientific contributions:
1) Formulating a proactive dynamic vehicle routing problem considering a cooperation service model minimizing the total operational cost;
2) Designing a proactive customer demand forecasting method based on customer's historical data;
3) Developing a matching algorithm for collaborative temporary drivers and online orders;
4) Integrating the simulated annealing algorithm into a genetic algorithm framework to solve the PDVRPCS model.
3.
Problem development
In this section, the basics of PDVRPCS are described. The proactive prediction method is used based on the historical data of dynamic customers, and then the matching method is designed to realize capacity sharing.
3.1. Problem description
The research object of this paper is the store-depot-integrated retail enterprise with physical stores and online stores (the location of physical stores is denoted as depot below). This kind of enterprise has two types of customers, namely, Store Customer (SC) and Online Shopping Customer (OSC). The shared transportation service platform provided by the enterprise can achieve the resources match between SC and OSC. Store customers are willing to provide shared transportation resources to fulfill the OSC's orders by using compensation or preferential options. Capacity sharing vehicles of a SC will provide transportation services for a part of the OSC based on customer matching considering the time windows and destinations while the unserved OSC will be delivered by the enterprise's vehicles. Each capacity sharing vehicle arrives at its destination and enterprise-owned vehicles return to the warehouse after completing the service. The capacity-sharing mode considering time windows may reduce the usage frequency of enterprise-owned vehicles for serving an OSC. Therefore, distribution cost can be significantly reduced, especially for the scenario with many remote OSCs and SCs.
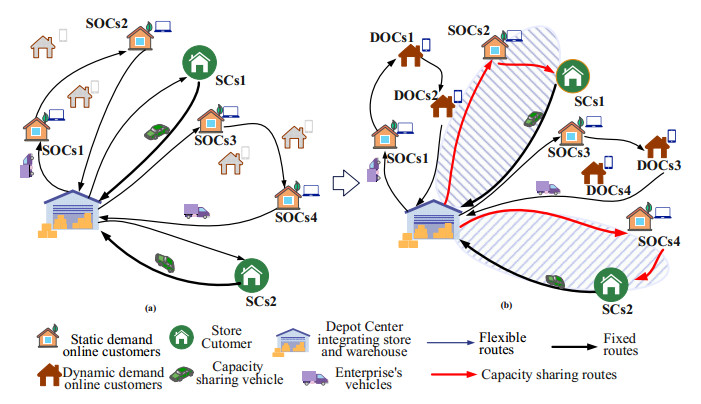
As shown in Figure 2, assuming that a retail enterprise has eight customers, among which customers SOC1 to SOC4 are OSCs, which are named static online customers. DOC1 to DOC4 are possible OSCs, which are called dynamic online customers. Customers SC1 and SC2 belong to SCs that can provide capacity sharing vehicles to provide a distribution service for dynamic online customers. Figure 2(a) shows the delivery path without the customer-matching strategy. The static online customers need to be delivered by two vehicles, and dynamic online customers have not been added to the delivery task. After predicting demands of online dynamic customers DOC1 to DOC3, the routings obtained by combining the customer matching strategy are shown in Figure 2(b), i.e., the orders of SOC2 and SC4 are distributed by SOC4 and SC2 respectively, and the remaining static and dynamic OSC are served by two vehicles.
3.2. Symbol description
The PDVRPCS model is defined as follows: a completely undirected graph G=(N,A) is used to represent the distribution network with node set N and arc set A. The node set N={o}∪NC∪NH consists of three parts, where o represents the location of the warehouse, NC means the location of the OSC and NH denotes the location of the SC's destination. The parameters and variables used in this model are presented in Table 1.
3.3. The conception of proactive predication
In order to meet the dynamic customer demands, the concept of proactive distribution is introduced. Meanwhile, the prospect theory [37] is employed to make a proactive evaluation of the dynamic customer's demands, and then judge whether to serve a dynamic customer, based on the predicted value pik, which denotes the customer's demand, and aik, which denotes the mean of distance matrix for the historical demand data. Assume that the customer historical demand data m dimensions, and all customers n can be expressed as matrix(a11,a12,...,a1m;a21,a22,...,a2m;an1,an2,...,anm). The triangular fuzzy number [38] and the deterministic attribute are used to describe definite and indefinite attributes in the customer demand matrix. The purpose of this expression is characterized as the dynamic customer's demand more precisely.
If the customer's attributes are determined, the logical distance dik between the average historical data and the predicted value of customer demand is:
Using the triangular fuzzy number to describe a customer demand [36], Eq (1) can be further formulated as Eq (2):
In Eq (2), pik can be calculated by [39]:
where l is the interval of the customer's attributes. A threshold is predefined by decision makers to select dynamic customers that need to be serviced, and then the selected static customers and dynamic customers will be composed into a new organization.
According to prospect theory, if the predicted value of the customer demand attribute is greater than the actual value of customer demand (pik>mik), decision makers are prone to choose the option with higher risk and return. Otherwise, decision makers are prone to avoid possible risks and choose the option with low risk and stable revenue. To cope with different situations, decision makers have different degrees of understanding the risk avoidance when making decisions. Therefore, two risk factors μ1 and μ2 are predefined, representing the decision makers' different risk preferences. The calculation method of the prospect value considering the two risk factors is shown in Eq (4):
Finally, according to the prospect value of dynamic online customers, a threshold has to be set to select the dynamic online customers that meet the decision maker's preference. Combined with the unserved static online customers, a total unserved customer set C as shown in Eq (5):
3.4. Customer matching strategy
Firstly, it has to be determined whether the cooperative SCs travel time meets the OSCs time window constraints according to Eqs (6)–(8):
Equations (6) and (7) indicate that the departure time of the cooperative SC from the warehouse and the travel time to the OSC should not be earlier than the opening time and should not be later than the closing time of the OSC's time window. Equation (8) indicates that the collaborative SC can return to its destination no later than its acceptable latest arrival time.
Secondly, it has to be determined whether the distance between the collaboration SC and the OSC meets the collaboration requirements according to Eqs (9)–(13).
Equation (9) indicates that the cooperating SCs will only accept orders from the OSC's if the distance traveled from the warehouse to the OSC and to its destination is less than or equal to ε times the direct distance traveled from the warehouse to the cooperating SC's destination, and ε⩾1. Equation (10) ensure that an OSC is assigned to a collaborative SC. Equation (11) ensure that a collaborative SC can serve at most one OSC. Thus, the matching results of cooperative SCs and OSC's orders can be obtained. Equations (12) and (13) are binary variables for the match.
3.5. The PDVRPCS model
The total cost includes vehicle variable cost, vehicle initial cost, soft time window penalty cost and compensation cost, denoted as: Z=C1+C2+C3+C4, where
Based on Table 1 and the previous description, a PDVRPCS model for minimizing the total cost can be established. The objective function is defined as:
s.t.
The objective function (18) is to minimize the total cost, including Z and the penalty cost for denial of service. Constraint (19) guarantees that each customer is served only once. Constraint (20) guarantees the balance of vehicle flow in each customer. Constraint (21) guarantees that all vehicles start from and return to the depot. Constraint (22) guarantees that each customer is served by a vehicle at most once. Constraint (23) ensures that all vehicles must return to the depot without load. Constraint (24) represents the relationship between the departure time of vehicles from the customer, the arrival time and service time. Constraint (25) represents the penalty cost of a vehicle violating the soft time window. Constraint (26) ensures that customer requirements are met on a route. Constraint (27) defines the capacity constraint of the vehicles. Constraint (28) indicates that the number of OSCs served by each vehicle cannot exceed the total number of OSCs. Because of complexity of the PDVRPCS model, the GA-SA algorithm is designed for large-scale instances to solve this problem in the next section.
4.
Solution framework of PDVRPCS
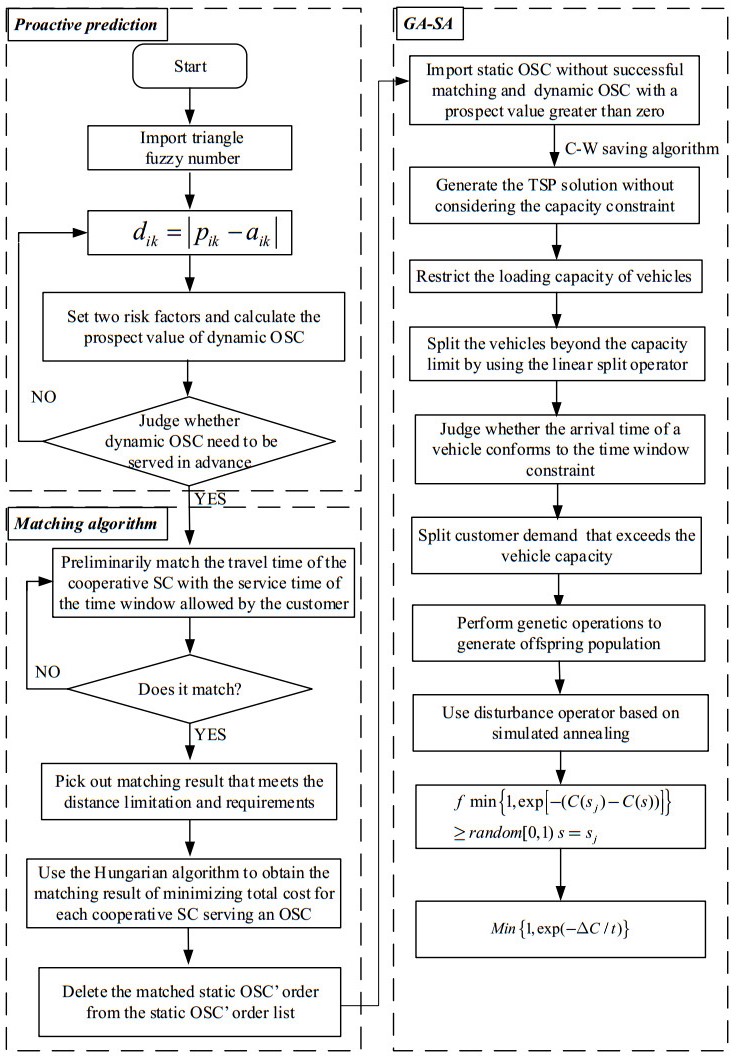
Different from other collaborative vehicle routing problems, this paper proposes a three-stage hybrid meta-heuristic algorithm to solve PDVRPCS. The first stage is a proactive prediction of dynamic OCSs, judging whether to provide the delivery service to customers according to their prospect value. In the second stage, the matching between cooperative SCs and static OCSs is solved by the Hungarian algorithm [40,41,42]. In the last stage, the designed GA-SA is employed to solve the static OSC that fails to match and the dynamic OSC whose prospect value is greater than zero. A special feature of the hybrid meta-heuristic algorithm is that the dynamic complexity problem is preprocessed statically by fuzzy theory before starting the meta-heuristic algorithm. When solving the main model of the vehicle routing problem, the advantages of two meta-heuristic algorithms, which are GA and SA based on neighborhood search, are used to establish a hybrid heuristic algorithm to effectively identify high-quality solutions. This algorithm is designed to balance the exploration behavior of the solution space. Figure 3 provides an overview of the framework of the hybrid algorithm.
4.1. Proactive prediction
By mining the demand regularity hidden in the demand information in the past, a proactive method can predict customer demand in advance by using correlation analysis methods and means of mathematical statistics. The method determines whether to deliver for customers based on their probability of appearing. The specific steps are as follows:
Step 1. Use triangle fuzzy number Eq (2) to calculate the logical distance of customer demand attributes;
Step 2. Judge the relationship between the predicted value of customer demand attributes and the actual value of customer demand, and determine the risk preference of decision makers;
Step 3. According to different risk preferences, set two risk factors and calculate the prospect value of dynamic OCSs considering risk factors according to Eq (4);
Step 4. Judge whether dynamic OCSs need to be served in advance according to the prospect value obtained by Eq (5).
4.2. Matching algorithm
The Hungarian algorithm is used to implement shared matching. It is a combinatorial optimization algorithm to solve the task assignment problem in polynomial time, which is widely used in the field of operations research. The specific steps are as follows:
Step 1. Preliminarily match the travel time of the cooperative SC with the service time of the time window allowed by the customer;
Step 2. Pick out matching results that meet the distance limitation and requirements;
Step 3. Use the Hungarian algorithm to obtain the matching result of minimum total cost for each cooperative SC serving an OSC;
Step 4. Delete the matched static OCS's order from the static OCS's order list.
4.3. Hybrid algorithm
SA is a simple and powerful single-point algorithm, inspired by the reduction of temperature during annealing, which is widely used to improve the search space of group-based algorithms. The hybrid GA-SA) is designed to solve the model, since the GA has strong global optimization ability and the SA has the ability to escape the local optimum. Unlike other meta-heuristics that only accept solutions that are better than the current one, the GA-SA hybrid algorithm offers the opportunity to accept new solutions that may be worse than the current one, and it initializes the search using the Chahla and Wagman (C-W) saving algorithm. The key operations of the GA-SA include the generation of an initial solution, genetic operators and a disturbance operator.
4.3.1. Solution representation and search space
In the proposed hybrid algorithm, a chromosome encoded with natural numbers is defined to represent the solution of a given optimization problem. Each natural number that codes for a chromosome is called a gene, where the number of the gene represents the number of the customer. The number of genes on the chromosome indicates the number of customers, and the order of genes indicates the order in which customers are visited. 0 indicates a garage, warehouse, or distribution center. The search space of the algorithm consists of all possible chromosomes. In order to determine the solution space, the cost function Eqs (14)–(18) and the Constraints (19)–(28) in the optimization model are defined by five binary decision variables (xijk, zik, ωih, βih, xok). In each iteration, search operators (including crossover, mutation, destruction and repair) randomly select chromosomes from the search space to further explore the solution space.
4.3.2. Initial solution
The initial solution is generated by the following three steps:
Step 1. For static OCSs without successful matching and for dynamic OCSs with a prospect value greater than zero, use the saving method to generate the travelling salesman problem (TSP) solution without considering the capacity constraint;
Step 2. Restrict the loading capacity of the vehicles, and split the vehicles beyond the capacity limit by using the linear split operator;
Step 3. Further constrain the time window of OCSs, judge whether the arrival time of vehicles conforms to the time window constraint and, if so, generate the initial solution.
4.3.3. Design genetic operator
In heuristic algorithms, crossover, mutation, destruction and repair operators are often used to explore and exploit the search space. The traditional roulette operator is used as the selection operator [43]. Meanwhile, the strategy of retaining the best substring is employed by crossover operators. The mutation operator is to randomly select a chromosome, and randomly select a mutation position in the chromosome. If the position is not zero, a new gene will be randomly generated to replace the original gene. If the mutation location gene is zero, the mutation location is selected again.
1) Crossover operator
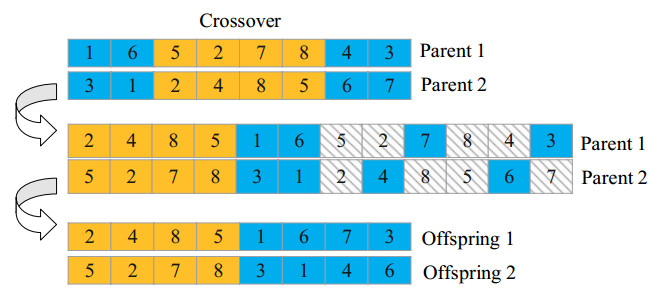
To explore the search space for solutions, gene segments with random min-max values are used to cross the operator to generate progeny chromosomes. For example, based on the crossover probability, two parental chromosomes are randomly selected to cross, which are parent 1: {1, 6, 5, 2, 7, 8, 4, 3} and parent 2: {3, 1, 2, 4, 8, 5, 6, 7}. Before crossing, two cross-indexed integer values 3 and 6, unequal and smaller than chromosome length, are first generated. Based on this, two gene segments {5, 2, 7, 8} and {2, 4, 8, 5} are generated by randomly selecting positions 3 to 6 from both the parent 1 and the parent 2. When crossing is performed, {5, 2, 7, 8} and {2, 4, 8, 5} are moved to the parental chromosome header, respectively. In the crossover operation, {5, 2, 7, 8} and {2, 4, 8, 5} are moved to the head of the parental chromosome, respectively, and the individuals with the same genes as {5, 2, 7, 8} and {2, 4, 8, 5} are deleted in the parents, resulting in two new individuals named offspring 1: {2, 4, 8, 5, 1, 6, 7, 3} and offspring 2: {5, 2, 7, 8, 3, 1, 4, 6} (Figure 4).
2) Mutation operator
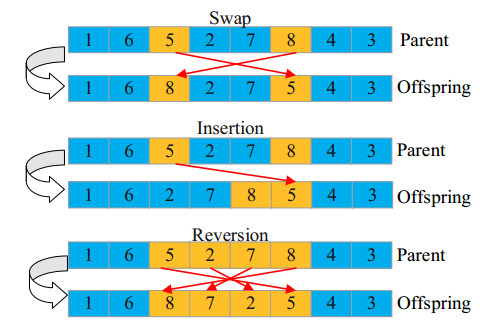
In order to perform the mutation operation, a part of the population is selected using the roulette selection method and a chromosome is selected as the parent. In our study, we used three different mutation operators: two-point, insertion, reversal and two-end interval reversal operators, as shown in Figure 5. For all three operators, we use the same parent p: {1, 6, 5, 2, 7, 8, 4, 3} to mutate. For a selected chromosome, one of the mutation operators is randomly selected to produce two new offsprings. By using the Swap mutation operator, two mutation index integer values 3 and 6, which are unequal and smaller than the length of the chromosome, are randomly generated, and the third and sixth genes are exchanged to generate a new daughter chromosome {1, 6, 8, 2, 7, 5, 4, 3}. A new progeny {1, 6, 2, 7, 8, 5, 4, 3} is generated by inserting the third gene into the sixth gene through Insertion operators. In addition, a new solution {1, 6, 8, 7, 2, 5, 4, 3} is created by using the Reversion operator to reverse the sequence of genes between the 3rd and 6th.
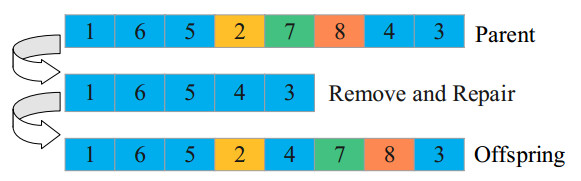
3) Damage and repair operators
In order to explore the space better, the damage repair operator is used to repair the chromosome {1, 6, 5, 2, 7, 8, 4, 3}. Three gene loci 2, 7 and 8 are removed according to certain rules to get the removed missing chromosome {1, 6, 5, 4, 3}, and then the removed points are inserted into the missing chromosome according to certain rules to get a better chromosome {1, 6, 5, 2, 4, 7, 8, 3} (Figure 6).
4.3.4. Disturbance operator based on simulated annealing
In the simulated annealing algorithm, the random perturbation operator is adopted, with the following steps:
Step 1. Generate new status sj=Generate(s);
Step 2. ifmin{1,exp[−(C(sj)−C(s))]}⩾random[0,1)s=sj;
Step 3. Accept Min{1,exp(−ΔC/t)} as a state function.
4.4. Benchmark test
In order to verify the solving quality of the GA-SA algorithm, the well-known Solomon benchmark instance is used to test it. The number of nodes in the tested instances is 50 and 100. The numbers of available vehicles and vehicle capacity vary with the different instances. The data files for all the instances can be downloaded from http://web.cba.neu.edu/~msolomon/problems.htm, and the Best Known Solution (BKS) can be obtained from http://web.cba.neu.edu/~msolomon/heuristi.htm. The result is used to compare with GA-SA, which is represented by Chen and Shi (C & S), and column C & S shows the optimal value [44]. The performance of GA-SA is measured in terms of gap percentage, which is defined by Eqs (29)–(31).
Since the benchmark instances are only simulations of realistic distribution scenarios, when applying GA-SA, the Euclidian distance is used to calculate the distance between nodes, and the travel time is assumed to be equal to the corresponding total distance, that is, the vehicle speed is 1. In addition, since the objective function designed in this paper represents the total cost and is designed for real cases, it needs to be changed to minimize the total distance. The algorithm is run 5 times on each benchmark instance, and the best results are summarized in Table 2 (N = 50) and Table 3 (N = 100).
As can be seen from Table 2, the average Gapa between the results obtained by the GA-SA and the BKS for N = 50 is 2.10%, and the average Gapb between the results obtained by the C & S and the BKS is 4.26%. The average Gapc between the results obtained by the Gapa and the Gapb for the three types of instances is 2.16%. In the bold value of Table 2, the total distance of 8 instances, such as C101–50 and C102–50, is better than that of C & S.
As can be seen from Table 3, the average Gapa between the results obtained by the GA-SA and the BKS for N = 100 is 2.92%, and the average Gapb between the results obtained by the C & S and the BKS is 5.68%. The average Gapc between the results obtained by the Gapa and the Gapb for the three types of instances is 2.76%. In the bold value of Table 3, the total distance of 9 instances, such as C201–100 and C202–100, is better than that of C & S.
5.
Computational study
5.1. Simulation instances
In order to verify the applicability and effectiveness of the established PDVRPCS model and the designed solving framework, the data of 60 customers are randomly generated, as shown in the Appendix Tables A1–A3. For dynamic OCSs, the system first predicts whether it will generate service requests and plan delivery routes in advance. The first index depot represents the distribution center, the numbers SOC1-SOC30 represent the static OCSs that need service, and the indexes DOC1-DOC15 represent the dynamic customer that could request service.
The three parameters of customer's dependence on the enterprise a1, time windows of user a2 and customer's historical demand a3 are used to compute the prospect value for proactive evaluation of customer's demand in the current horizon. Each of them has a weight λi,i∈{1,2,3}, correspondingly. The value of the three fuzzy parameters is divided into five grades: poor, fair, satisfactory, good and excellent. The specific values are computed according to Eq (29), which is an exceptional case of Eq (3).
Using the customer evaluation indicator, the prospect value of customers can be calculated by Eq (33):
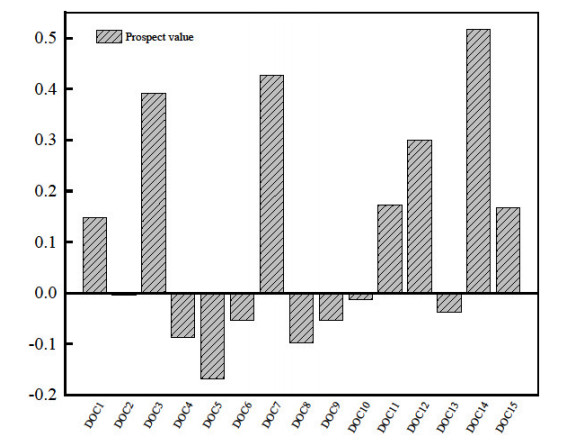
According to the above three indicators, the prospect value of dynamic customers can be evaluated by Eq (33). The calculated results are normalized in Figure 7 (λ={0.4,0.3,0.3}).
The normalized data in Figure 7 show that eleven customers (DOC1, DOC3, DOC7, DOC11, DOC12, DOC14 and DOC15) have a positive prospect value. Therefore, these customers will be prioritized for planning distribution services.
The necessary parameters need to be introduced before using the proposed algorithm. Given that the capacity of the vehicle is 200, the initial cost of each vehicle is 200 Chinese Yuan (CNY), the unit variable cost is 5 CNY, the unit penalty cost of the vehicle violating the time window is 2 CNY and the driving speed is 30 km/h. If the cooperative distribution service is not considered (Scenario Ⅰ), the routing plan of static OCS is carried out by GA-SA. The algorithm was run ten times, and the total cost of the optimal result is 4461 CNY. A total of five vehicles are needed to complete the task for thirty static OCSs, and the distribution plan is shown in Table 4.
The collaborative service is not considered in Scenario Ⅱ. Seven dynamic customers with positive proactive value (DOC1, DOC3, DOC7, DOC11, DOC12, DOC14 and DOC15) are renumbered SOC31, SOC32, SOC33, SOC34, SOC35, SOC36 and SOC37 as static customers, and their distribution services are fulfilled using enterprise vehicles. The total cost is 4659 CNY, and the distribution scheme is shown in Table 5.
If collaborative services are not used, delivery services cannot be provided to customers who appear in the service process or fail in prediction. Therefore, collaborative services should be considered for the requirements of dynamic OCSs (Scenario Ⅲ). Firstly, thirty static OCSs are matched with fifteen cooperative SCs. The matching algorithm is used under the conditions of compensation coefficient ρ=0.1 and cooperation flexibility ε=1.5. The result shows that eight orders of static OCSs can be served by cooperative SC. For the remaining 22 static OCS orders and the 11 dynamic OCSs with a prospect value greater than zero are renumbered 1–29. Then, GA-SA is run ten times, and the optimal distribution scheme obtained only needs four vehicles to complete the delivery tasks of these 29 customers, with a total delivery cost of 4043 CNY. The distribution plan is shown in Table 6.
The collaboration SCs are used to service new service requests that fail to predict or arise during the service process. Service is denied for new requests that cannot be successfully matched with the collaborating SCs. Assume that the system has new service requests numbered D2, D5, D8, D9 and D13. Four new requests and cooperative SC are successfully matched.
Compared with the above three scenarios, the use of collaborative services can reduce the number of vehicles on the basis of meeting the temporary requests of dynamic OCSs and better respond to the new requests generated in the delivery process. The comparison of cost for the three scenarios is shown in Table 7.
Denial of service may reduce customer satisfaction and dependency, which is harmful to the long-term development of enterprises. Compared to these three scenarios, collaborative services can reduce distribution cost and improve delivery timeliness based on proactive predication.
In order to verify the influence of different compensation coefficients and different cooperative flexibility on the cost, multiple combinations of the two coefficients are used in the simulation case of Scenario Ⅲ, As shown in Table 8, the matching number of cooperative vehicles and online orders increases if the cooperation flexibility value increases, resulting in the reduction of vehicle numbers used and total cost. In addition, the compensation cost of the cooperative vehicle increases along with the compensation coefficient increase, leading to an increase in the total cost. When that happens, total cost can no longer decrease, if ρ = 0.3.
5.2. Real-world case study
To assess the potential savings of the collaborative service strategy, the proposed model and solution framework are applied for the distribution network of a large store-depot-integrated retailer in Chongqing city in the southwest of China. The retailer has 51 static OCSs, 24 dynamic OCSs that may make service requests and 37 SCs that are willing to collaborate. The detailed information has been listed in the Appendix Tables A4–A6, where the encoding of nodes is the same as in the previous section.
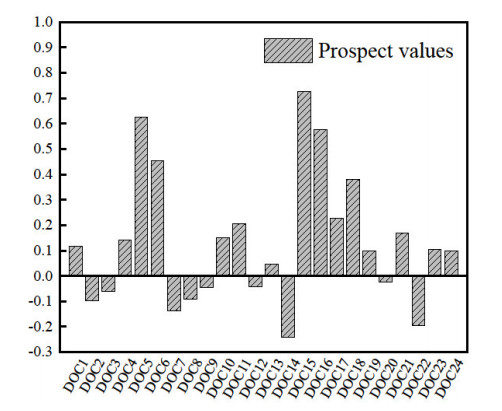
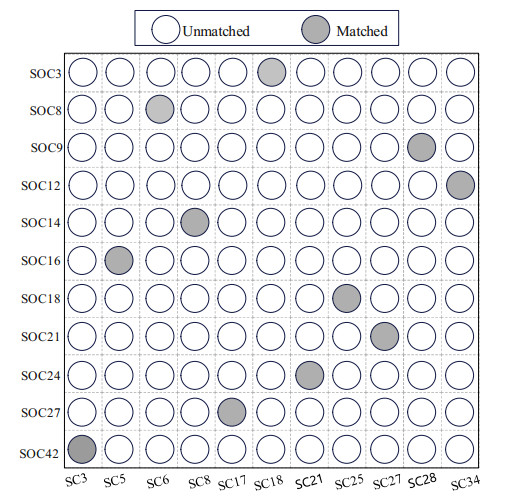
Similar to the result in Figure 3, the prospective value of customers is calculated from the predicted data as well as historical data for the three attributes of dynamic OCS. The results are shown in Figure 8, the customers (DOC1, DOC4, DOC5, DOC6, DOC10, DOC11, DOC13, DOC15, DOC16, DOC17, DOC18, DOC19, DOC21, DOC23 and DOC24) have a positive prospect value, and the customers (DOC2, DOC3, DOC7, DOC8, DOC9, DOC12, DOC14, DOC20 and DOC22) have a negative prospect value. Therefore, these customers will be prioritized for planning distribution services. A total of eleven static OCSs were successfully matched with cooperative SCs, namely SOC3, SOC8, SOC9, SOC12, SOC16, SOC18, SOC21, SOC24, SOC27 and SOC42, after matching between the static OCS and cooperative SC. The matching results are illustrated in Figure 9. Finally, the matched customers are removed from the static OSC set.
Considering the static distribution strategy of cooperative services (Scenario Ⅳ), all dynamic OCSs demands are rejected, and the penalty cost for rejections are included in total cost. The matching algorithm is employed on static customers (Figure 9) and cooperative SCs. The unmatched OCSs (renumbered 1–40) are serviced using the enterprise vehicles.
Running GA-SA 10 times, an average of four vehicles is needed to complete the service for the 40 customers, and the average cost is 983 CNY. The total cost of the optimal result is 959 CNY, including 129 CNY of collaboration cost. The optimal distribution routes are shown in Table 9.
In Scenario Ⅲ, 40 static OCSs and 15 dynamic OCSs with positive prospect value are renumbered as 1–55. The solutions can be obtained by using GA-SA, in which the average number of vehicles is five, the average cost is 1124 CNY and the optimal cost is 1031 CNY. The optimal plan is shown in Table 10.
During the distribution process, the dynamic OCSs that could not be predicted successfully are DOC2, DOC7, DOC8, DOC14, DOC20 and DOC22. The match algorithm is used between these nine customers and cooperative SCs, and the matching result shows that DOC8, DOC14 and DOC22 are successfully matched. Therefore, the matched customers are served by collaborative SC with a compensation cost of 39 CNY. Dynamic customers (DOC2, D7 and DOC20) failed to match with cooperative SC and are rejected to be served. Finally, the total compensation cost in the real-world case is 168 CNY under Scenario Ⅲ. The comparison of cost for the two scenarios is shown in Table 11.
1) Gapd = (ScenarioIV−ScenarioIII)ScenarioIV×100%
As can be seen from Table 8, Scenario Ⅳ has low cost related to vehicles, because the number of vehicles used in this scenario decreases when all dynamic customers are rejected. In addition, because 21 dynamic customers are rejected in this scenario, the penalty cost is high, resulting in a higher total cost than in Scenario Ⅲ. In the case that the denial cost is set to 50 CNY per customer, Scenario Ⅲ saves 34.64% of the cost compared to Scenario Ⅳ, which can solve the problem of customer satisfaction and loyalty reduction caused by service rejection.
In this study, sensitivity analyses for uncertainties and key parameters have been performed in mathematical formulas. With different degree of collaboration flexibility Ɛ of cooperative vehicle and compensation factors ρ of the cooperative vehicle, the average of all target cost functions is calculated to prove their effect. Table 12 shows the results of the analysis under different conditions, in which the variation range of cooperation flexibility degree is 1.1–1.5, and the variation range of compensation factors is 0.05–0.2. When the degree of cooperation increases, the total cost of the objective function decreases, and when the compensation factor increases, the total cost of the objective function increases. This is because when the degree of collaboration increases, more customers participate in the collaboration, resulting in cost savings. When the compensation factor increases, the subsidy to temporary deliverers will increase, which will also increase the total cost.
6.
Managerial insights
Under the trend of the rapid development of a sharing economy, information technology and intra-city express business, crowdsourcing intra-city delivery decreases the distance of serving customers by integrating goods into stores and warehouses, compared with the traditional intra-city delivery problem. Due to the unpredictability of when orders will arrive, logistics companies struggle to plan ahead. To meet customers' needs as much as possible during peak demand periods, logistics companies may compensate crowd delivery workers on platforms to share the delivery pressure. However, even with this approach, the delivery capacity remains insufficient. As a result, challenges such as insufficient capacity during peak demand periods, difficulties in meeting customer time windows and balancing subsidy amounts for different stakeholders remain obstacles faced by integrated store-warehouse crowd delivery. In this situation, this paper proposes a new linear programming model to solve the problems of order demand prediction, line and time matching and compensation distribution of crowdsourcing deliverers in the process of crowdsourcing collaborative distribution.
This study raised a new mechanism for cooperative routing planning, especially for crowded cities with intense last-mile transport effort. The "crowdsourcing" approach was expected to exploit tacit capacities at low additional cost, simultaneously saving expenses and contributing to reduce traffic and, thus, congestion. At the same time, the authors proposed a suitable forecasting method, an order matching algorithm to coordinate the different participants, and a genetic simulated annealing algorithm for the system's optimization. The approach is relevant and also up to date with current distribution developments. The solution approach, especially in its combination of methods, is novel.
7.
Conclusions and future works
With the rapid development of the digital economy, online shopping has become a habit of the public. The demand for small-batch, low-weight and multi-frequency distribution has witnessed explosive growth. At the same time, distribution price, service quality and timeliness are facing unprecedented tests. To reduce the distribution cost of store-depot-integrated retailers, this study presented a PDVRPCS model and proposed a novel solution framework considering the cooperation service provided by scattered SCs. The solution framework includes three stages, i.e., customers' prospect value prediction based on historical data, a matching algorithm and a hybrid GA-SA heuristic algorithm. Finally, the feasibility and effectiveness of the model and solution framework are verified under different scenarios.
However, there are still some weaknesses in this work, and more research could be done in the future to overcome these weaknesses. First, the proposed model only considers the economic objective. Multi-objective models (e.g., carbon emissions, considering the balance between the number of deliverers and customer satisfaction) could be developed by splitting the single objective into multiple objectives. Second, more prediction algorithms (e.g., statistics-based approaches, machine learning-based approaches or deep learning-based approaches) should be considered to accurately predict the customers' demand. Third, multiple depots and heterogeneous fleets could be considered for more flexibility. When electric vehicle riders or electric private cars participate in the distribution, how to cooperate with their own fleet is worth considering.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research was funded by the humanities and social science research project of Chongqing Education Commission [grant number 20JD059] and the Chongqing Jiaotong University graduate scientific research innovation project [grant number 2022S0069]. The authors are grateful to the support of the general project of Chongqing Natural Science Foundation [grant number cstc2020jcyj-msxmX0108], and the key scientific and technological innovation project of "Construction of Chengdu-Chongqing Economic Circle" [grant number KJCXZD2020031].
Conflict of interest
The authors declare there is no conflict of interest.
Appendix









 DownLoad:
DownLoad: