Nomenclature

Subscripts i and j are used to label particle size or as indices for general sequences. Other subscripted variables are defined separately below.

Boldface characters are used to denote sequences, as in ${\bf{a}} = \left ({{a_{ij}}} \right)_{j = 1}^\infty$;

L(a) or ${\tilde a}$ is used to denote the discrete Laplace transform of the sequence a;

$\left| {\bf{a}} \right|$ Equivalent to the series $\sum\limits_{j = 1}^\infty {{a_j}}$;

The discrete convolution operator is denoted by *.

---

Main Roman Symbols

---

Greek Symbols

---

1. Introduction

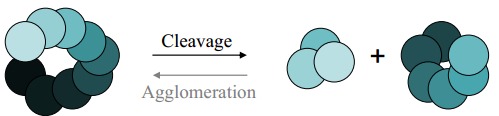
The processes of particle agglomeration and cleavage have important applications in many fields including the combustion of solid polymers, the development of atmospheric pollutants and water droplets, soot formation, the evolution of snow particles in blizzards and also astrophysics. Cleavage (or scission) occurs when large particles (or groups of smaller particles) split to form smaller particles. Agglomeration is the reverse of cleavage: smaller particles join to form larger particles. These processes are illustrated in Figure 1.

Population balance (PB) approaches to modelling these phenomena are based on statistical arguments applied to large ensembles of particles. In certain circumstances, this leads to a system of equations that describe the evolution of particle number distributions. In other circumstances, a purely computational approach based on the Monte-Carlo method is either required (through the complex nature of the particular process being analysed) or preferred. The Monte-Carlo (MC) method computes multiple samples (or realisations) of the outcome space, which are averaged to obtain numerical estimates. A simple example of a MC algorithm to estimate π might consist of the following. Randomly select N co-ordinates (x, y) such that x and y are uniformly distributed in the interval [0, 1]. Then compute the fraction α of points with the property that ${x^2} + {y^2} < 1$. Repeat the calculation a few times and average the results. As the number of points N increases, the fraction α will approach π/4. MC methods may be used to obtain approximate solutions of PB equations or used to explore processes for which it may not be possible (or at least exceedingly difficult) to formulate PB equations directly.

PB methods may be further divided into two categories that depend on how a particle is viewed: either as an infinitely divisible entity that can exist in a continuous spectrum of sizes or as a discrete collection of individual sub-particles (or monomers) of specified sizes. PB methods have the disadvantage that there are usually assumptions made in the derivation of the basic equations regarding the probabilities of individual particles interacting, which MC methods need not employ. This contribution focuses on the discrete PB case.

The first population balance formulation is usually accredited to Smoluchowski ^[1], who derived the equations that today bear his name for particle coagulation. One of the most recent reviews, featuring the derivations of various distinct types of PB equation, is given by Solsvik & Jakobsen ^[2]. Since its conception the PB method has been applied to a vast array of phenomena in science and engineering. The review by Ramkrishna & Singh ^[3] gives an indication of the variety of fields where PB models have been applied together with a selection of new applications. Indeed, in recent years, there have been several reviews of this subject and a selection are to be found in ^[4,5,6]. A useful review concentrating on one of the more popular applications in recent years is provided by Blum ^[7] who discusses agglomeration in atmospheric physics and also gives a discussion of the applications in astrophysics. Some of the first Monte-Carlo simulations involving cloud formation are those presented by Gillespie ^[8]. More recent contributions involving Monte-Carlo simulations include ^[9] and ^[10].

The author's motivation for studying the processes of agglomeration and cleavage stems from the wish to provide new mathematical models for polymer pyrolysis to improve prediction of the behaviour of these materials in fires. During the pyrolysis of a solid polymer the action of heat on the polymer molecule results in bond breakage (cleavage) and new bond formation as smaller, lighter, molecules are formed ^[11,12,13]. In some cases, additional reactions occur that result in bond formation, creating larger molecules. Although the reaction pathways involved in the pyrolysis of a given polymer may be complex ^[12,13], consisting of a number of steps, there are four main mechanisms involved: random scission, end-chain scission, chain stripping and recombination. Random scission occurs when a bond at a random location along the main polymer chain breaks, ultimately leading to the formation of two lighter molecules. End-chain scission occurs when bonds break only at the end points of the polymer molecule leading to the formation of a monomer and a molecule with one fewer bonds than the original specimen. Chain-stripping occurs in branched polymer molecules and is a process whereby groups that are attached to the main polymer chain are removed, leaving the polymer backbone intact. Finally, recombination is the process of bond formation between two or more molecules creating larger species. The thermal decomposition of a solid polymer in a fire occurs mainly in the absence of oxygen—it is only when volatile species are formed that oxidation plays a major role. Hence, the processes listed above, occurring in the condensed phase prior to volatile species being formed, may be assumed to be anaerobic. At some point, species light enough to be volatile are formed. In a diffusion flame, which is the main type of flame in most fires of engineering interest, these species are advected away from the decomposing solid and then subsequently react with oxygen. The overall process of forming volatile species from a solid fuel is generally referred to in fire engineering as gasification. One of the primary goals of fire modelling is predicting the rate at which heat is released when a solid fuel is exposed to heat and this in turn depends on the production rate of volatile species together with their composition.

Traditionally, kinetic rate equations are used to model the gasification rate of a solid fuel, but there are two significant problems associated with this approach. Firstly, there is no physical justification for the use of kinetic rate equations of this type for degradation reactions in the condensed phase. Also assumptions have to be made concerning the composition of the products—these are not predicted. In an alternative approach, the author and others ^{[14,15,16,17,18,19,20,21,22,23,24,25,26,27]} have attempted to use PB methods to model pyrolysis of polymers. This approach provides a rigorous framework for the analysis of a particular degradation process and the products of degradation may also be predicted. It also has the potential to model the effect of other important reactions occurring during gasification, so that mechanisms of flame retardancy can, at least in principle, be modelled in detail. However, there are considerable computational overheads involved in its implementation and simple closed-form expressions for direct application in typical engineering situations are difficult to obtain. A review of the application of PB methods in polymer fire retardancy is given in ^[27]. The goal of this work is to investigate two fundamental processes occurring during pyrolysis (random cleavage and random recombination) with a view to developing more detailed models of the behaviour of polymers in fires in subsequent work.

For practical purposes in what follows, a particle (or polymer) of a given size is considered as being composed of a finite collection of identically sized sub-particles (or monomers) connected by linkages, isomorphic to a linear chain. Consider an i-mer, a polymer comprised of i monomers with i – 1 links. During random cleavage, any of the i – 1 links is equally likely to break creating new molecules of smaller size. If link j breaks, then a j-mer and an (i − j)-mer are created. Recombination or agglomeration is viewed as the reverse of this process: an i-mer and j-mer combine to form an (i + j)-mer.

Application of the PB method to the processes of random cleavage and agglomeration to discretely-sized particles involves employing statistical arguments to predict the evolution of an initially large population of linear polymer molecules. This results in a system of ordinary differential equations describing the time dependence of each i-mer concentration. Evolution of the moments of the distribution, as well as the individual molecular concentrations, is also of interest and expressions for these will be derived via the construction of moment generating functions. For the purposes of this work, we shall assume that the total mass of the system remains constant, which is equivalent to stating that the first moment of the population is constant.

---

2. Continuous Models of Scission and Agglomeration

Although we shall be concentrating on discrete models, it is worth spending a brief moment reviewing the continuous case, as it provides helpful insight into solution methods for the discrete case. The processes of simple scission and agglomeration in a population with a continuous range of sizes have been considered by the author in an earlier paper in the context of an approximate model of polymer pyrolysis ^[25]. In that approach, it was assumed that a linear polymer molecule of length x may be cleaved at any point along its length creating two smaller molecules. Thus, if ξ is a continuous random variable uniformly distributed on the interval [0, 1], random cleavage of a molecule of size x will result in molecules of size ${x_1} = \xi x$, ${x_2} = \left ({1 -\xi } \right) x$. For the simplest case of random scission, it was assumed that the rate of cleavage was directly proportional to the molecule size and so the rate of cleavage of specimens of size x was taken as xk_c, where k_c is a rate function that depends on temperature alone. Thus, if $f\left ({x, t} \right)$ is the continuous probability density function for the population, defined such that the probability of encountering species of size in the range x to x + dx is $f\left ({x, t} \right)$, these assumptions lead directly to the continuous random scission equation

$\frac{{\partial f}}{{\partial t}} = - {k_c}\left( {xf + 2\int\limits_x^\infty {f\left( {\xi ,t} \right)d\xi } } \right).$

(1)

For the case of recombination it was assumed that there is a size-independent rate k_a, at which species combine to produce new larger species. Thus if a specimen of size ${x_1}$ encounters another of size ${x_2}$, then it was assumed that these will combine to produce a specimen of size ${x_1} + {x_2}$. It transpired that the evolution of f for pure agglomeration was determined by the equation

$\frac{{\partial f}}{{\partial t}} = \frac{{{k_a}}}{2}\left( {f * f - f} \right)$

(2)

where, the continuous convolution operator * is defined as $\left ({f*g} \right)\left ({x, t} \right) = \int\limits_0^x {f\left ({\xi, t} \right) g\left ({x -\xi, t} \right) d\xi }$.

If random scission and recombination occur together with the same assumptions for each process as described above, then the evolution of the probability density function f will be determined by the equation

$\frac{{\partial f}}{{\partial t}} = - {k_c}\left( {xf + 2\int\limits_x^\infty {f\left( {\xi ,t} \right)d\xi } } \right) + \frac{{{k_a}}}{2}\left( {f * f - f} \right).$

(3)

It was discovered that the solutions to both problems of continuous scission and recombination could be found by Laplace transform and this fact lends inspiration to our approach to the solution of the discrete problem below.

---

3. Discrete Agglomeration

Consider a population of discretely-sized particles. We assume that particles can have distinct sizes, which we label 1, 2, 3, …. Furthermore, we assume that each particle is equally likely to react with any other. Adopting the notation in the appendix, we use the sequence ${\bf{n}} = \left ({{n_j}\left (t \right)} \right)_{j = 1}^\infty = {n_1}$, ${n_2}$, $\ldots$ to define the population, where ${n_j}\left (t \right)$ is the ratio of number of particles in the population of size j to the initial number of particles in the population. Thus, if $N\left (t \right)$ is the number of particles in the population at time t, it follows that the ratio $N\left (t \right)/N\left (0 \right)$ corresponds to the zeroth moment of the population, ${\mu _0}\left (t \right) = \sum\limits_{i = 1}^\infty {{n_i}}$. Furthermore, the product $j{n_j}\left (t \right)$ will be proportional to the mass of particles of size j and consequently the sum $\sum\limits_{j = 1}^\infty {j{n_i}\left (t \right)}$, corresponding to the first moment ${\mu _1}\left (t \right)$, will be proportional to the total mass of the population and so will be constant.

Now consider the process of agglomeration where two particles of size i and j join to create a new particle of size i + j. We assume that the total recombination rate is directly proportional to the number of particles, so the rate at which particles combine is $N{k_a}$, where ${k_a}$ is a rate function that depends on temperature alone. Hence in time step Δt, $N{k_a}\Delta t$ particles combine to form larger species. Thus, $N{k_a}\Delta t$ particles will be removed from the population and $N{k_a}\Delta t/2$ new particles will be created (since two particles combine to form a new particle). It then follows that the number of particles in the distribution will evolve according to $dN/dt = -N{k_a}/2$ and accordingly the zeroth moment will be given by ${\mu _0}\left (t \right) = {e^{ -{k_a}t/2}}$. If we assume that the particle sizes are randomly distributed, and that each particle is equally likely to react, then the probability of selecting a particle of size j from the population is ${n_j}/{\mu _0}$. In order to generate a new particle of size i > 1, it is necessary for particles of size j and i − j, j = 1, .., i − 1, to combine. Thus the probability of generating a new particle of size i in the population by random agglomeration of particles of size j and i − j will be given by the ith. component of $\left ({{\bf{n}}*{\bf{n}}} \right)/\mu _0^2$, where * is now used to denote the discrete convolution operator (see appendix). Hence it follows that the discrete equations defining the evolution of the population by agglomeration alone can be written as

$\frac{{d{\bf{n}}}}{{d\tau }} = - {\bf{n}} + \frac{1}{{2{\mu _0}}}\left( {{\bf{n}} * {\bf{n}}} \right)$

(4)

where τ is defined implicitly by the equation $d\tau /dt/{k_a}$.

Now, setting $z = 1 -{\rm{exp}}\left ({ -\tau /2} \right)$ (which is equivalent to the fraction of particles that have undergone recombination, or conversion) and ${\bf{n}} = {e^{ -\tau }}{\bf{p}}$, the discrete agglomeration equations (4) may be recast in simpler form

$\frac{{d{\bf{p}}}}{{dz}} = {\bf{p}} * {\bf{p}}$

(5)

Taking the discrete Laplace transform (see appendix) of the equation above, using the results and notation of the appendix and remembering that the discrete Laplace transform (DLT) of p will now be a function of both s and z gives $\partial \tilde p/\partial z = {{\tilde p}^2}$. This last equation may be readily solved to give

$\tilde p\left( {s,z} \right) = \frac{{{{\tilde p}_0}\left( s \right)}}{{1 - z{{\tilde p}_0}\left( s \right)}}$

(6)

Here, ${{\tilde p}_0}$ is the DLT of ${\bf{p}}\left( 0 \right)$, which is identical to the DLT of ${\bf{p}}\left (0 \right)$ and is therefore a function of s only. Now, since $z < 1$ when $\tau > 0$, it follows that we can write the solution for $\tau > 0$ as $\tilde p = \sum\limits_{j = 1}^\infty {\tilde p_0^j{z^{j -1}}}$ and so it follows that we can write the inverse transform (corresponding to the solution for p in terms of z) as

${\bf{p}}\left( z \right) = \sum\limits_{j = 1}^\infty {{\bf{p}}_0^{j*}{z^{j - 1}}}$

(7)

Here, ${\bf{p}}_0^{j*}$ denotes j − 1 applications of the convolution operator * to the vector ${\bf{p}}0$, so that ${\bf{p}}_0^{1*} = {\bf{p}}0$, ${\bf{p}}_0^{2*} = {\bf{p}}0$, ${\bf{p}}_0^{3*} = {\bf{p}}0*{\bf{p}}0*{\bf{p}}0$, etc.

Now to pick a simple example, suppose that the initial distribution consists only of particles of size 1, so that ${\bf{p}}0 = \left ({{\delta _{1, j}}} \right)_{j = 1}^\infty$, where ${{\delta _{i, j}}}$ is Kronecker's delta. Then it is a simple matter to verify that ${\bf{p}}_0^{i*} = \left ({{\delta _{i, j}}} \right)_{j = 1}^\infty$ and so Eq. (7) implies that ${\bf{p}} = \left ({{z^{j -1}}} \right)_{j = 1}^\infty$ and hence

${n_i} = {e^{ - \tau }}{\left( {1 - {e^{ - \tau /2}}} \right)^{i - 1}}$

(8)

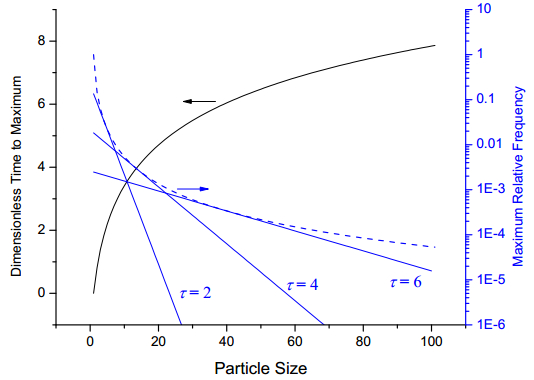
It follows that the maximum value of ${n_i}$ when i > 1 is achieved at ${\tau _{\max }} = -2\ln \left ({2/\left ({i + 1} \right)} \right)$ and is given by $\max \left ({{n_i}} \right) = 4{\left ({i -1} \right)^{i -1}}/{\left ({i + 1} \right)^{i + 1}}$. Figure 2 shows the time taken to achieve the maximum particle concentration (dark curve), the maximum particle concentration (dashed lighter curve) and concentration distributions at τ = 2, 4, 6 (solid lighter curves).

This solution may be extended readily to the general mono-disperse case where ${{\bf{p}}_0} = \left ({{\delta _{k, j}}} \right)_{j = 1}^\infty$. In this case, only species that are multiples of k will evolve and the solution is

${n_i} = \left\{ \begin{array}{l} {e^{ - \tau }},i = k,\\ I\left( {i/k} \right){e^{ - \tau }}{\left( {1 - {e^{ - \tau /2}}} \right)^{i/k - 1}},{\rm{otherwise}} \end{array} \right.$

(9)

Here the function $I\left (x \right)$, where x is a real number, returns 1 if x is an integer and 0 otherwise.

Returning to the general solution (7), it transpires that re-writing this expression component-by-component yields a more useful incarnation of the solution for any initial distribution of relative particle frequencies ${{\bf{n}}_0}$, which may be written as

${n_i} = \left\{ \begin{array}{l} {e^{ - \tau }}{\left( {{{\bf{n}}_0}} \right)_1},i = 1\\ {e^{ - \tau }}\sum\limits_{j = 1}^i {{{\left( {{\bf{n}}_0^{j*}} \right)}_i}{{\left( {1 - {e^{ - \tau /2}}} \right)}^{i - 1}},i > 1} , \end{array} \right.$

(10)

where ${\left ({{{\bf{n}}_0}} \right)_i}$ denotes the ith. component of ${{{\bf{n}}_0}}$.

Returning to the expression for ${\tilde p}$ in Eqn. (6), it follows that the DLT of the particle population is

$\tilde n = \frac{{{{\left( {1 - z} \right)}^2}{{\tilde n}_0}}}{{1 - z{{\tilde n}_0}}}$

(11)

As described in the appendix, it is possible to find the distribution moments from Eqn. (11) above. Proceeding as described in the appendix, on setting $s = 0$ and noting that ${{\tilde n}_0}\left (0 \right) = 1$, the zeroth moment ${\mu _0} = 1 -z$ is recovered as expected. Differentiating Eqn. (11) with respect to s gives

$\frac{{\partial \tilde n}}{{\partial s}} = {\left( {\frac{{1 - z}}{{1 - z{{\tilde n}_0}}}} \right)^2}\frac{{d{{\tilde n}_0}}}{{ds}},\frac{{{\partial ^2}\tilde n}}{{\partial {s^2}}} = {\left( {\frac{{1 - z}}{{1 - z{{\tilde n}_0}}}} \right)^2}\frac{{{d^2}{{\tilde n}_0}}}{{d{s^2}}} + \frac{{2z{{\left( {1 - z} \right)}^2}}}{{{{\left( {1 - z{{\tilde n}_0}} \right)}^3}}}{\left( {\frac{{d{{\tilde n}_0}}}{{ds}}} \right)^2}$

(12)

Setting $s = 0$, it follows from the first of these expressions that $\partial \tilde n/\partial s{|_{s = 0}} = d{{\tilde n}_0}/ds{|_{s = 0}}$, which confirms that the first moment ${\mu _1}$ is constant as expected from the fact that total particle mass must be conserved. The second expression yields the second moment

${\mu _2}\left( z \right) = {\mu _2}\left( 0 \right) + \frac{{2z}}{{1 - z}}\mu _1^2$

(13)

from which it follows that the coefficient of variation (see appendix for definition) is given by

$\frac{{{c^2}\left( \tau \right) - {c^2}\left( 0 \right)}}{{1 - {c^2}\left( 0 \right)}} = 1 - {e^{ - \tau /2}}$

(14)

Hence, we have the interesting result that no matter what the initial distribution, the coefficient of variation approaches 1 as $\tau \to \infty$.

---

4. Discrete Cleavage

As particles combine forming larger particles, there is also the possibility of that large particles may break apart to form smaller particles. The discrete cleavage problem has already been partly considered by the author and others in the context of random depolymerisation ^{[14,15,16,17,18,19,20,21,22,23,24,25,26,27]}; however, we revisit it here giving complete exact solutions for moments and general initial distributions.

Let us consider a large linear particle (with no branches for simplicity) of size j as comprising of j smaller particles with j − 1 discrete linkages or bonds, each link being equally likely to break. Let ${n_j}$ denote the ratio of the number of particles of size j to the initial number of particles as in the previous section. Since the total number of j-mers in the population is $N\left (0 \right){n_j}$, there will be $\left ({j -1} \right) N\left (0 \right){n_j}$ bonds, each of which is equally likely to break. Thus in time step $\Delta t$, we assume that $\Delta {n_j} = \left ({j -1} \right){n_j}N\left (0 \right){k_c}\Delta t$ bonds will break for each group of particles of size j, where ${k_c}$ is a rate function that depends only on temperature. If the time step is very small then it may be assumed that 1 link per particle breaks and so this will remove $\Delta {n_j}$ particles of size j from the population and create $2\Delta {n_j}$ smaller particles. If each link is equally likely to break then the $2\Delta {n_j}$ new particles created by cleavage will be uniformly distributed with sizes ranging from 1 to j − 1. Thus the equations for discrete cleavage are

$\frac{{d{n_i}}}{{d\tau }} = - \left( {i - 1} \right){n_i} + 2\sum\limits_{j = i + 1}^\infty {{n_j},i = 1,2, \cdots }$

(15)

Here, τ is defined implicitly by the equation $d\tau /dt = {k_c}$. The problem of general bond-weigthed scission has been discussed by the author in an earlier contribution ^[26]. In that case the probability of bond j breaking within a i-mer is denoted by $w_j^{\left (i \right)}$, with $\sum\limits_{j = 1}^{i -1} {w_j^{\left (i \right)}} = 1$, and the summation term of Eqn. (15) is replaced by $\sum\limits_{j = i + 1}^n {\left ({j -1} \right)\left ({w_{j -i}^{\left (j \right)} + w_i^{\left (j \right)}} \right){n_j}}$. When each bond is equally likely to break we have $w_i^{\left (j \right)} = 1/\left ({j -1} \right)$ and Eqn. (15) is recovered.

Summing these equations and using the result that $\sum\limits_{i = 1}^\infty {\sum\limits_{j = i + 1}^\infty {{n_j}} = \sum\limits_{j = 1}^\infty {\left ({j -1} \right){n_j}} }$, gives the equation for the zeroth moment as $d{\mu _0}/d\tau = {\mu _1} -{\mu _0}$. Multiplying by i and summing, noting the fact that $2\sum\limits_{i = 1}^\infty {i\sum\limits_{j = i + 1}^\infty {{n_j}} = \sum\limits_{j = 1}^\infty {j\left ({j -1} \right){n_j}} }$, gives $d{\mu _1}/d\tau = 0$ as expected. Hence, we see readily that the first moment is constant and solving the equation for the zeroth moment gives ${\mu _0} = {\mu _1} + \left ({1 -{\mu _1}} \right){e^{ -\tau }}$. Note that if ${\mu _1} = 1$ the zeroth moment is constant for all τ, which implies that there is no change in the number of particles as τ increases. Since cleavage can only increase population size, the only possible way that this can come about is that the initial particle distribution corresponds to a steady state of the system. It is obvious that the only steady state corresponds to a mono-disperse population $\left ({{\delta _{1, i}}} \right)_{i = 1}^\infty$, which of course, given the general observations in the appendix, is the only initial distribution with first moment ${\mu _1} = 1$.

It transpires that taking the DLT in this case does not prove helpful in constructing the solution. However, since the random cleavage problem is linear, the general solution can be constructed by superposition of solutions with initially mono-disperse distributions $\left ({{\delta _{j, i}}} \right)_{i = 1}^\infty$. Without going into detail for brevity, it transpires that, if ${n_i}\left (0 \right) = {\alpha _i}$, the general solution to the discrete cleavage equations may be written as

$\left. \begin{array}{l} {n_i} = {e^{ - i\tau }}\left( {{a_i}{e^\tau } - {b_i} + {c_i}{e^{ - \tau }}} \right)\\ {a_i} = \sum\limits_{j = i}^\infty {\left( {j - i + 1} \right){\alpha _j}} ,\\ {b_i} = 2\sum\limits_{j = i}^\infty {\left( {j - i} \right){\alpha _j}} ,\\ {c_i} = {\alpha _i} + \sum\limits_{j = i}^\infty {\left( {j - i - 1} \right){\alpha _j}} . \end{array} \right\}$

(16)

In order to compute solutions, the expressions (16) above are not convenient because each coefficient involves evaluating an infinite sum. This issue can be circumvented by defining ${\bf{1}} = \left (1 \right)_{i = 1}^\infty$ and ${\bf{I}} = \left (i \right)_{i = 1}^\infty$. Then it may be shown that the coefficients become

$\left. {\begin{array}{*{20}{c}} {{\bf{a}} = \left( {{\mu _1} + 1} \right){\bf{1}} - {\bf{I}} - \left( {{\bf{1}} - {\bf{I}}} \right)*{{\bf{n}}_0},}\\ {{\bf{b}} = 2\left( {{\mu _1}{\bf{1}} - {\bf{I}} + {\bf{I}}*{{\bf{n}}_0}} \right),}\\ {{\bf{c}} = {{\bf{n}}_0} + \left( {{\mu _1} - 1} \right){\bf{1}} - {\bf{I}} + \left( {{\bf{1}} + {\bf{I}}} \right)*{{\bf{n}}_0}.} \end{array}} \right\}$

(17)

Now, if Eqns. (16) are multiplied by ${e^{ -is}}$ and summed, it follows that the DLT of the solution is

$\tilde n\left( {s,\tau } \right) = {e^\tau }\tilde a\left( {s + \tau } \right) - \tilde b\left( {s + \tau } \right) + {e^{ - \tau }}\tilde c\left( {s + \tau } \right)$

(18)

Noting that the DLT of 1 is $E\left (s \right) = {e^{ -s}}/\left ({1 -{e^{ -s}}} \right)$ and the DLT of I is $-E' = {e^{ -s}}/{\left ({1 -{e^{ -s}}} \right)^2}$, the DLTs of a, b and c are found readily from Eqns. (17) as

$\left. {\begin{array}{*{20}{c}} {\tilde a = {\mu _1}E + \left( {1 - {{\tilde n}_0}} \right)\left( {E + E'} \right)}\\ {\tilde b = 2\left( {{\mu _1}E + \left( {1 - {{\tilde n}_0}} \right)E'} \right) = 2\left( {\tilde a - \left( {1 - {{\tilde n}_0}} \right)E} \right),}\\ {\tilde c = {{\tilde n}_0} + {\mu _1}E + \left( {1 - {{\tilde n}_0}} \right)\left( {E + E'} \right) = \tilde a + {{\tilde n}_0} - 2\left( {1 - {{\tilde n}_0}} \right)E.} \end{array}} \right\}$

(19)

It follows from the appendix that the second moment is given by ${\mu _2}\left (\tau \right) = {e^\tau }\tilde a''\left (\tau \right) -\tilde b''\left (\tau \right) + {e^{ -\tau }}\tilde c''\left (\tau \right)$ and using the expressions in Eqns. (19) above we have that when $\tau > 0$,

${\mu _2}\left( \tau \right) = \frac{1}{{{e^\tau } - 1}}\left\{ {{\mu _1}\left( {{e^\tau } + 1} \right) - \frac{{2{e^\tau }\left( {1 - {{\tilde n}_0}\left( \tau \right)} \right)}}{{{e^\tau } + 1}}} \right\}$

(20)

Note that this formula cannot be used to compute the second moment when τ = 0: this must be done directly from the initial distribution. To take the simple example of an initially mono-disperse distribution, where ${\alpha _j} = {\delta _{m, j}}$, we have

${a_i} = \sum\limits_{j = i}^\infty {\left( {j - i + 1} \right){\alpha _j}} = \left\{ {\begin{array}{*{20}{c}} {m - i + 1,i \le m,}\\ {0,i > m,} \end{array}} \right.$

(21)

${b_i} = 2\sum\limits_{j = i}^\infty {\left( {j - i} \right){\alpha _j}} = \left\{ {\begin{array}{*{20}{c}} {2\left( {m - i} \right),i < m,}\\ {0,i \ge m,} \end{array}} \right.$

(22)

${c_i} = {\alpha _i} + \sum\limits_{j = i}^\infty {\left( {j - i - 1} \right){\alpha _j}} = \left\{ {\begin{array}{*{20}{c}} {m - i - 1,i < m,}\\ {0,i \ge m.} \end{array}} \right.$

(23)

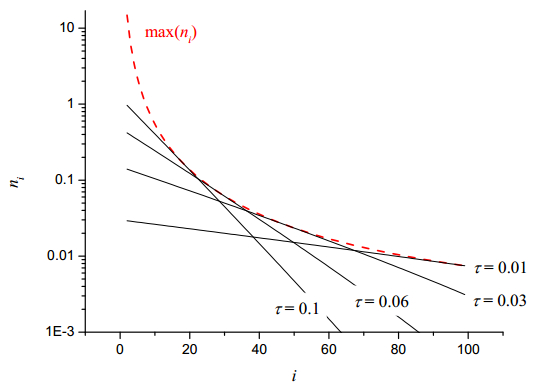
Thus, for $1 < i < n$, it may be shown that ${n_i}$ will achieve a maximum of $\max \left ({{n_i}} \right) = \left\{ {\frac{{\left ({m -i} \right)\sqrt {{{\left ({m -i} \right)}^2} + {i^2} -1} + {{\left ({m -i} \right)}^2} + i -1}}{{{{\left ({i -1} \right)}^2}\left ({m -i + 1} \right)}}} \right\}{\left\{ {\frac{{i\left ({m -i} \right) + \sqrt {{{\left ({m -i} \right)}^2} + {i^2} -1} }}{{\left ({i -1} \right)\left ({m -i} \right) + 1}}} \right\}^{ -\left ({i + 1} \right)}}$ at time ${\tau _i} = \ln \left ({\frac{{i\left ({m -i} \right) + \sqrt {{{\left ({m -i} \right)}^2} + {i^2} -1} }}{{\left ({i -1} \right)\left ({m -i + 1} \right)}}} \right)$. The graph in Figure 3 illustrates these results for m = 100. The dashed curve corresponds to the maximum particle concentration $\max \left ({{n_i}} \right)$ and the solid curves are particle distributions for $1 < i < m$ at different τ values.

It is apparent that ${\mu _0}\left (\tau \right) = m -\left ({m -1} \right){e^{ -\tau }}$, ${\mu _1} = m$, ${{\tilde n}_0}\left (\tau \right) = {e^{ -m\tau }}$, ${\mu _2}\left (0 \right) = {m^2}$ and so the coefficient of variation is

${c^2}\left( \tau \right) = \left\{ {\begin{array}{*{20}{c}} {0,\tau = 0}\\ {\left( {1 - \frac{{m - 1}}{m}{e^{ - \tau }}} \right)\left( {\frac{{{e^\tau } + 1}}{{{e^\tau } - 1}} - \frac{{2{e^\tau }\left( {1 - {e^{ - m\tau }}} \right)}}{{m{{\left( {{e^\tau } - 1} \right)}^2}}}} \right) - 1,\tau > 0.} \end{array}} \right.$

(24)

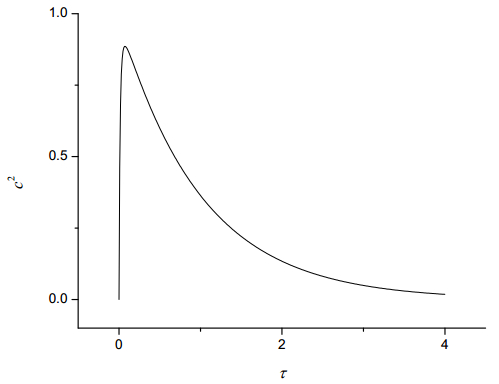
The graph in Figure 4 plots the coefficient of variation as a function of τ for m = 100. For a distribution that is initially mono-disperse, it follows that the coefficient of variation should be initially zero. As time progresses, random scission produces species of smaller size and so the variation of size will increase in the distribution, implying that ${c^2}$ will increase. However, since monomers are the smallest species that can exist in this model, as time progresses further the spectrum of sizes will approach a final mono-disperse distribution located on $m = 1$, implying that ${c^2}$ must approach 0 as $\tau \to \infty$. Hence, we would expect a peak in the graph of ${c^2}\left (\tau \right)$, as confirmed in Figure 4.

The composition of smaller species is of particular interest in the case of polymer combustion. Consider the initially mono-disperse case ${\alpha _j} = {\delta _{m, j}}$ when $m \gg 1$. It may be shown from Eqns. (16), (21), (22), (23) above that, when m is large, ${n_i}/m \approx {e^{ -\left ({i -1} \right)\tau }}{\left ({1 -{e^{ -\tau }}} \right)^2}$ for $i \ll m$. This result may be extended for particles of arbitrary initial distribution but with large first moment ${\mu _1}$. If this is the case, then it follows that the numbers of smaller particles will be ${n_i}/{\mu _1} \approx {e^{ -\left ({i -1} \right)\tau }}{\left ({1 -{e^{ -\tau }}} \right)^2}$. This is interesting because it shows that when the initial average particle mass is high, the distribution of evolved lighter species does not depend on the initial distribution. This observation has an important consequence for polymer flammability. If a given polymer P_m of molecular mass m degrades by random cleavage, then the evolved species will not depend on m, provided that it is large. This in turn implies that the effective heat of combustion of P_m (an important engineering quantity in flammability related to the rate of heat released per unit mass consumed) will not depend on initial molecular mass.

---

5. Combined Agglomeration and Cleavage

Naturally, it is reasonable to expect that both agglomeration and cleavage may occur at different rates as time progresses. If $\varepsilon = {k_a}/{k_c}$ is the ratio of agglomeration rate function to cleavage rate function (both of which are assumed to depend on temperature alone), then it follows directly from the preceding two sections above that the PB equations for particle concentrations may be written as

$\frac{{d{n_i}}}{{d\tau }} = - \left( {i + 1 + \varepsilon } \right){n_i} + 2\sum\limits_{j = i}^\infty {{n_j}} + \frac{\varepsilon }{{2{\mu _0}}}{\left( {{\bf{n}}*{\bf{n}}} \right)_i},$

(25)

where, τ is defined implicitly by the ordinary differential equation $d\tau /dt = {k_c}$ and ${\mu _0}$ is the zeroth moment.

Here we consider only cases where ε is constant. In general, especially in the case of polymer degradation, the agglomeration and cleavage rates will depend on temperature and so the assumption that ε = constant is consistent only with isothermal conditions. This restriction is not a problem if we seek to compare solutions of Eqn. (25) with experimental data obtained under constant temperature conditions, or where degradation occurs under quasi-steady conditions. However, if temperature is not constant, as would be the case for combustion of a polymer in a real fire, then ε would, in general, be a function of temperature. In order to close the model in this case, an appropriate expression for energy conservation must be formulated to give an equation describing the evolution of temperature together with expressions defining the temperature dependence of the rate functions ${k_a}$ and ${k_c}$.

Now, since cleavage increases population size and agglomeration reduces it, we have the possibility of solutions to the combined agglomeration-cleavage problem evolving on to steady states and these will be discussed in detail below.

Again from the preceding two sections, it follows that the first moment ${\mu _1}$ is constant and also that the equation for the zeroth moment is $d{\mu _0}/d\tau = {\mu _1} -\left ({1 + \varepsilon /2} \right){\mu _0}$. Employing the initial condition ${\mu _0}\left (0 \right)$, the solution is

${\mu _0}\left( \tau \right) = \frac{{{\mu _1}}}{{1 + \varepsilon /2}} + {e^{ - \left( {1 + \varepsilon /2} \right)}}\left( {1 - \frac{{{\mu _1}}}{{1 + \varepsilon /2}}} \right)$

(26)

Now, if one were to attempt a numerical solution of the combined agglomeration and cleavage equations, the term $2\sum\limits_{j = i}^\infty {{n_j}}$ would obviously prove troublesome. However, given the fact that we now know ${{\mu _0}}$, we are free to write $\sum\limits_{j = i}^\infty {{n_j}\sum\limits_{j = 1}^\infty {{n_j}} } -\sum\limits_{j = 1}^{i -1} {{n_j}} = {\mu _0} -\sum\limits_{j = 1}^{i -1} {{n_j}}$, which simplifies matters. Hence we may equally seek solutions of

$\frac{{d{n_i}}}{{d\tau }} = - \left( {i + 1 + \varepsilon } \right){n_i} + 2{\mu _0} - 2\sum\limits_{j = 1}^{i - 1} {{n_j} + \frac{\varepsilon }{{2{\mu _0}}}{{\left( {{\bf{n}}*{\bf{n}}} \right)}_i}}$

(27)

Now, as for the case of discrete cleavage, we have the situation that if ${{\mu }_{1}}=1+\varepsilon /2$, then the population size is invariant for all τ. However, this is different from pure cleavage as it is not necessarily the case that an initial population with ${{\mu }_{1}}=1+\varepsilon /2$ is a steady state for $\varepsilon >0$. For example, consider the case $\varepsilon =2$ and the initial population ${{\alpha }_{i}}={{\delta }_{2, i}}$. It is clear that this initial population has ${{\mu }_{1}}=1+\varepsilon /2=2$ and also that it is not a steady state since particles of size 2 will agglomerate forming larger species and also cleave forming species of size 1. Furthermore, from the observations of the appendix, since ${{\mu }_{1}}$ is always greater than or equal to 1, if $1\le {{\mu }_{1}} < 1+\varepsilon /2$, then ${{\mu }_{0}}/{{\mu }_{1}}$ will monotonically reduce to $1/\left (1+\varepsilon /2 \right)$ as $\tau \to \infty$ and if ${{\mu }_{1}}>1+\varepsilon /2$, then ${{\mu }_{0}}/{{\mu }_{1}}$ will monotonically increase to $1/\left (1+\varepsilon /2 \right)$ as $\tau \to \infty$. It also follows from these observations that for finite $\varepsilon >0$, ${{\mu }_{0}}/{{\mu }_{1}}$ will remain in the interval (0, 1] for all $\tau >0$.

Given the analysis of earlier sections above, it seems sensible to attempt to seek a solution of the form ${{n}_{i}}=f\left (\tau \right){{\Lambda }^{i-1}}\left (\tau \right)$, where f and $\Lambda$ are functions of τ alone to be found and $\Lambda \left (\tau \right) < 1$. For this to be valid we must have that both $f\sum\limits_{i=1}^{\infty }{{{\Lambda }^{i-1}}}={{\mu }_{0}}$ and $f\sum\limits_{i=1}^{\infty }{i{{\Lambda }^{i-1}}}={{\mu }_{1}}$. It is a straightforward matter to verify that these conditions imply that $f/\left (1-\Lambda \right)={{\mu }_{0}}$ and $f/{{\left (1-\Lambda \right)}^{2}}={{\mu }_{1}}$, thereby fixing the forms of f and $\Lambda$ as $f=\mu _{0}^{2}/{{\mu }_{1}}$ and $\Lambda =1-{{\mu }_{0}}/{{\mu }_{1}}$. We have seen above that $0 < {{\mu }_{0}}/{{\mu }_{1}}\le 1$ for all $\tau >0$, which implies that $\Lambda$ will remain in the interval [0, 1). Direct substitution of this candidate reveals that Eqns. (27) are satisfied and thus we see that solutions to the combined problem of the form

$\frac{{{n_i}}}{{{\mu _i}}} = {\left( {\frac{{{\mu _0}}}{{{\mu _i}}}} \right)^2}{\left( {1 - \frac{{{\mu _0}}}{{{\mu _i}}}} \right)^{i - 1}}$

(28)

are valid, where ${{\mu }_{0}}$ is given by (26) and ${{\mu }_{1}}$ can take any value greater than or equal to 1. It is clear that as $\tau \to \infty$ these solutions evolve onto the steady states:

$\frac{{{n_i}}}{{{\mu _i}}} \to \frac{1}{{{{\left( {1 + \varepsilon /2} \right)}^2}}}{\left( {\frac{\varepsilon }{{2 + \varepsilon }}} \right)^{i - 1}}$

(29)

It is straightforward to calculate the second moment for this particular solution and it transpires that as $\tau \to \infty$ the coefficient of variation will approach $\varepsilon /\left (2+\varepsilon \right)$.

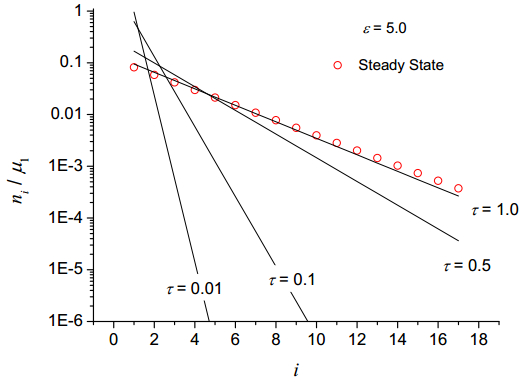
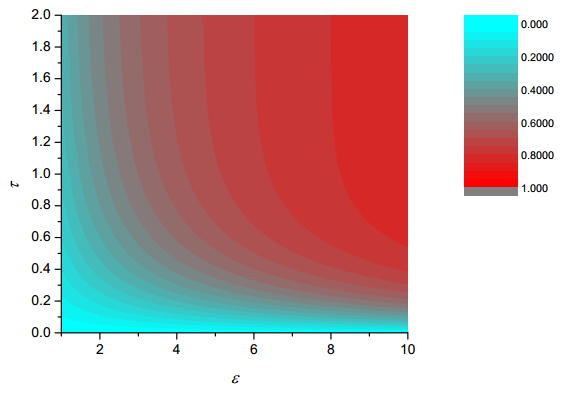
It is worth noting that if we take ${{\mu }_{1}}=1$, by the observations in the appendix, we recover the initially mono-disperse solution $\left ({{\delta }_{i, i}} \right)_{i=1}^{\infty }$. The solution is illustrated in Figure 5, where particle concentrations are plotted at different τ values for $\varepsilon =5.0$. Contours of the coefficient of variation are plotted against $\varepsilon$ and τ in Figure 6.

In general, as $\tau \to \infty$, solutions will approach steady-states given by the solutions of

$- \left( {i + 1 + \varepsilon } \right){n_i} + \frac{{2{\mu _1}}}{{1 + \varepsilon /2}} - 2\sum\limits_{j = 1}^{i - 1} {{n_j} + \frac{{\varepsilon \left( {1 + \varepsilon /2} \right)}}{{2{\mu _1}}}{{\left( {{\bf{n}}*{\bf{n}}} \right)}_i} = 0}$

(30)

Now, given the lower triangular form of these equations, it is possible to construct their solutions explicitly starting from the equation for i = 1. It further follows from this that there is a unique steady state. Since we have already found a steady state given by Eqn. (29) above, it must follow that this corresponds to the steady state of the general problem. It is interesting that up to a multiplicative constant, all solutions evolve onto the same steady state irrespective of the initial population.

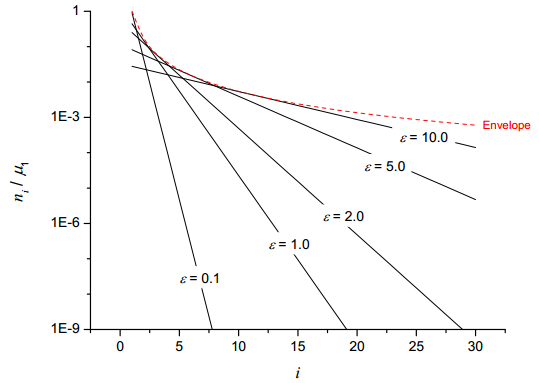
Figure 7 illustrates steady-state particle concentrations, ${{n}_{i}}/{{\mu }_{1}}$ taken from Eqn. (29), for various values of $\varepsilon$. The envelope ${{\text{E}}_{i}}$ of the steady-state solutions (shown by the dashed curve in Figure 7) may be readily calculated and is given by ${{\text{E}}_{i}}=4{{\left (i-1 \right)}^{i-1}}/{{\left (i+1 \right)}^{i+1}}$. Interestingly, this is identical to the maximum particle concentrations for discrete cleavage of an initially mono-disperse population given in the immediately preceding section above. Closer inspection of the mono-disperse example above reveals that this is to be expected since the curve giving the maximum particle concentration also corresponds to the envelope of solutions for this case and setting $\varepsilon =2\left ({{e}^{\tau /2}}-1 \right)$ in the steady state solution Eqn. (29) above recovers the maximum particle concentrations for the initially mono-disperse discrete cleavage case.

Now, to investigate stability of the steady state solution, set

$\frac{{{n_i}}}{{{\mu _i}}} = {v_i}\left( \tau \right){e^{ - \left( {i + 1 + \varepsilon } \right)\tau }} + \frac{1}{{1 + \varepsilon /2}}{\left( {\frac{\varepsilon }{{2 + \varepsilon }}} \right)^{i - 1}}$

(31)

We wish to investigate the behaviour of a small perturbation ${{u}_{i}}={{v}_{i}}{{e}^{-\left (i+4+\varepsilon \right)\tau }}$ to the steady state as $\tau \to \infty$. After substitution into Eqn. (27) and linearising, we find that for large τ, ${{v}_{i}}$ may be expressed as a linear combination of powers of ${{e}^{\tau }}$ up to a maximum power of ${{e}^{\left (i-1 \right)\tau }}$. Hence, up to a multiplicative constant, it follows that ${{u}_{i}}\sim {{e}^{-\left (2+\varepsilon \right)\tau }}$ as $\tau \to \infty$ and so the steady state is linearly stable to small perturbations.

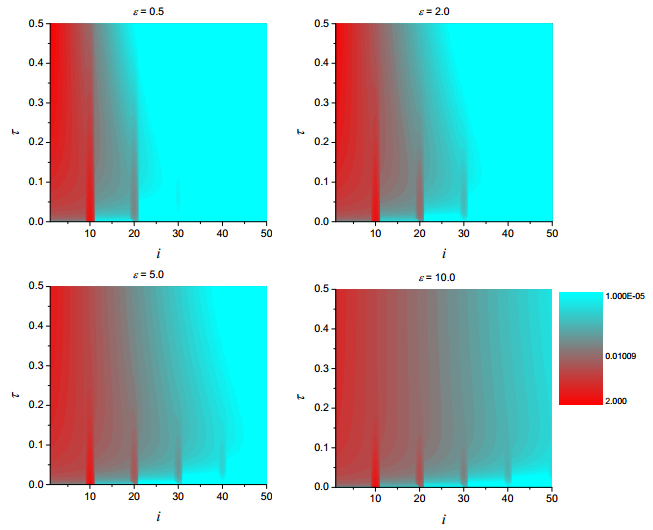
Figure 8 illustrates the results of numerical solutions of the combined agglomeration-cleavage problem for $\varepsilon$ = 0.5, 2.0, 5.0, 10.0. The solutions all start from a mono-disperse particle distribution located at i = 10. Note that particle concentrations peak at multiples of 10 due to agglomeration, but the peaks smooth out as τ increases and the steady state is approached. As $\varepsilon$ increases, the rate at which agglomeration occurs (compared with cleavage) increases and so we should expect to see more peaks at integer multiples of the initial molecule size being generated. As has been seen in Section 4, the effect of scission on an initially mono-disperse distribution is to reduce the peak in the size distribution located at the initial molecule size and generate an exponential distribution at smaller sizes. Hence as time progresses, the distribution peaks generated by agglomeration, located at increasingly large integer multiples of the initial molecule size, are re-distributed towards smaller molecule sizes. Thus we would expect that the tendency, as time becomes very large, is for the size distribution to evolve onto a smooth exponential distribution,

---

6. Conclusion

The problems of discrete random agglomeration and cleavage (together with the combined cleavage-agglomeration problem) have been investigated analytically. Whilst the main application from the author's view is polymer combustion, the results also have relevance in other fields. However, the main thrust of this work is aimed at producing solutions for random scission and agglomeration that may be incorporated into more comprehensive flammability models of polymer combustion.

Exact solutions for both problems were constructed and it was found that the discrete Laplace transform (DLT) was particularly useful for either obtaining solutions or distribution moments. The author failed to find an exact solution for the transient combined problem (cleavage with agglomeration), but it was demonstrated that a stable steady-state exists and a closed-form expression for this was found.

Two interesting results were observed for the discrete agglomeration and cleavage problems:

1. For large time, the coefficient of variation for discrete agglomeration ~1 and does not depend on the initial particle distribution.

2. For discrete cleavage, if the initial population is such that its first moment μ₁ is very large, then the evolving distribution of small particles (with masses much less than μ₁) does not depend on the initial distribution.

In future work, the solutions developed above will be implemented in a new complete pyrolysis model for an important class of polymers whose thermal degradation mechanism is dominated by random cleavage.

Direct comparison of PB predictions with experimentally determined molecular mass distributions of polymers during pyrolysis is exceedingly difficult, offering significant technical challenge, and most comparisons to date have been with derived quantities such as the rate of mass loss. However, it is hoped to provide direct comparison between PB predictions and molecular mass distributions in a future contribution.

---

Appendix: Notation and Fundamental Concepts

Let ${\bf{a}} = \left ({{a_j}} \right)_{j = 1}^\infty$, ${\bf{b}} = \left ({ = {b_j}} \right)_{j = 1}^\infty$ denote infinite sequences such that the sum of all their terms is finite. The discrete convolution operator * is defined such that ${\bf{a}}*{\bf{b}}$ is itself a sequence with ith. term given by

${\left( {{\bf{a}}*{\bf{b}}} \right)_i} = \left\{ \begin{array}{l} 0,i = 1\\ \sum\limits_{j = 1}^{i - 1} {{a_j}{b_{i - j}},i > 1} . \end{array} \right.$

(A1)

Furthermore, let $\left| {\bf{a}} \right| = \sum\limits_{j = 1}^\infty {{a_j}}$. It is well known 0 that * is both associative and commutative and also that

$\left| {{\bf{a}}*{\bf{b}}} \right| = \left| {\bf{a}} \right|\left| {\bf{b}} \right|$

(A2)

It immediately follows from this result that if $\left| {\bf{a}} \right|$ and $\left| {\bf{b}} \right|$ are finite then so is $\left| {{\bf{a}}*{\bf{b}}} \right|$.

The discrete Laplace transform (DLT) of a sequence a with $\left| {\bf{a}} \right|$ finite, denoted by either $L\left ({\bf{a}} \right)$ or ${\tilde a}$ is defined by

$\tilde a\left( s \right) = L\left( {\bf{a}} \right) = \sum\limits_{j = 1}^\infty {{e^{ - js}}{a_j}}$

(A3)

The DLT is analogous to the Z-transform ^[28] and if we put ${A_j} = {e^{ -js}}{a_j}$, ${B_j} = {e^{ -js}}{b_j}$, then it immediately follows from Eq. (A2) that the DLT has the property

$L\left( {{\bf{a}}*{\bf{b}}} \right) = L\left( {\bf{a}} \right)L\left( {\bf{b}} \right)$

(A4)

Statisticians will recognise the similarity between the DLT and the moment generating function of a discrete probability distribution ^[29]. The mth. moment of a sequence a, denoted by ${\mu _m}$, is defined as

${\mu _m} = \sum\limits_{j = 1}^\infty {{j^m}{a_j}}$

(A5)

and is given in terms of the DLT by

${\mu _m} = {\left( { - 1} \right)^m}\frac{{{d^m}\tilde a}}{{d{s^m}}}\left| {_{s = 0}} \right.$

(A6)

Note that $\left| {\bf{a}} \right|$ defined above is the same as the zeroth moment ${\mu _0}$. When dealing with discrete population dynamics, only species of a certain size (which may be labelled by an integer that is proportional to the particle size) exist and we shall consider sequences ${\bf{n}} = \left ({{n_j}} \right)_{j = 1}^\infty$, with finite $\left| {\bf{n}} \right|$, where ${n_j}$ is defined as the ratio of the number of particles of size j to the initial number of particles in the population. As time increases, the population evolves and so n will be, in general, a function of time. The population moments will also be functions of time with the exception of the first moment, since this is proportional to the total mass of particles, which is taken as constant.

Furthermore, if the initial particle distribution is ${{\bf{n}}_0} = \left ({{\alpha _j}} \right)_{j = 1}^\infty$, where $\left| {{{\bf{n}}_0}} \right| = 1$ and each ${\alpha _i} \ge 0$, then since $\sum\limits_{i = 1}^\infty {i{\alpha _i}} \ge \sum\limits_{i = 1}^\infty {{\alpha _i}}$, it follows that the first moment of the particle distribution will always be greater than, or equal to, 1. It is also apparent that the only initial population with first moment of 1 is the mono-disperse population ${\alpha _i} = {\delta _{i, 1}}$, where ${\delta _{i, j}}$ is Kronecker's delta. This last statement follows from the observation that if both $\sum\limits_{i = 1}^\infty {{\alpha _i}} = 1$ and $\sum\limits_{i = 1}^\infty i {\alpha _i} = 1$ for ${\alpha _i} = 0$, then subtracting these expressions implies that $\sum\limits_{i = 1}^\infty {\left ({i -1} \right)} {\alpha _i} = 0$, which is impossible unless ${\alpha _i} = 0$ for $i \ge 2$.

In many circumstances, we shall be interested in the second moment of the population, since it is central to definitions of dispersion such as the variance. For example, the population variance ${\delta ^2}$ and coefficient of variation ${c^2}$ respectively are defined by

${\sigma ^2} = \frac{{{\mu _2}}}{{{\mu _0}}} - \frac{{\mu _1^2}}{{\mu _0^2}},{c^2} = \frac{{{\mu _0}{\mu _2}}}{{u_1^2}} - 1.$

(A7)

Note that if the population is mono-disperse, then ${c^2}$; otherwise ${c^2}$ will be positive. It is also worthy of note that there is no guarantee that ${\mu _2}$ will always be well defined. To see this, consider the sequence ${\bf{a}} = \left ({1/{j^3}} \right)_{j = 1}^\infty$. Now clearly $\left| {\bf{a}} \right|$ is finite and the first moment is $\sum\limits_{j = 1}^\infty {\left ({1/{j^2}} \right)} = {\pi ^2}/6$ However the second moment is given by the harmonic series, which is divergent.

---

Conflict of Interest

There is no conflict of interest.

---