Citation: R.R.Bhargava, Kamlesh Jangid, Pavitra Tripathi. A Mode-III strip saturation model for two collinear semi-permeable cracks in a piezoelectric media[J]. AIMS Materials Science, 2016, 3(4): 1507-1519. doi: 10.3934/matersci.2016.4.1507
| [1] | Geoffrey E. Tupholme . Moving row of antiplane shear cracks within one-dimensional piezoelectric quasicrystals. AIMS Materials Science, 2016, 3(4): 1365-1381. doi: 10.3934/matersci.2016.4.1365 |
| [2] | N. Akhtar, S. Hasan . Assessment of the interaction between three collinear unequal straight cracks with unified yield zones. AIMS Materials Science, 2017, 4(2): 302-316. doi: 10.3934/matersci.2017.2.302 |
| [3] | Michael A. Stamps, Jeffrey W. Eischen, Hsiao-Ying Shadow Huang . Particle- and crack-size dependency of lithium-ion battery materials LiFePO4. AIMS Materials Science, 2016, 3(1): 190-203. doi: 10.3934/matersci.2016.1.190 |
| [4] | Hanh C. Nguyen, Shigeru Nagasawa, Kensei Kaneko . Strength estimation of silicon nitride ceramics using a round-notched specimen subjected to shearing-tool indentation. AIMS Materials Science, 2020, 7(5): 518-533. doi: 10.3934/matersci.2020.5.518 |
| [5] | Yanmei Zhang, Mu Fan, Zhongmin Xiao . Nonlinear elastic-plastic stress investigations on two interacting 3-D cracks in offshore pipelines subjected to different loadings. AIMS Materials Science, 2016, 3(4): 1321-1339. doi: 10.3934/matersci.2016.4.1321 |
| [6] | Mordechai Perl, Qin Ma, Cesar Levy . The influence of a non-aligned semi-elliptical surface crack on a quarter-circle corner crack in an infinitely large plate under uniaxial tension. AIMS Materials Science, 2016, 3(4): 1474-1492. doi: 10.3934/matersci.2016.4.1474 |
| [7] | Masanori Kikuchi . Study on multiple surface crack growth and coalescence behaviors. AIMS Materials Science, 2016, 3(4): 1623-1631. doi: 10.3934/matersci.2016.4.1623 |
| [8] | N. S. Biradar . Effect of transverse mechanical arc oscillation on hot cracking (solidification & liquation) and weld metal properties of AA2014 T6 TIG welds. AIMS Materials Science, 2016, 3(4): 1544-1560. doi: 10.3934/matersci.2016.4.1544 |
| [9] | Jian-Feng Wen, Yong Zhan, Shan-Tung Tu, Fu-Zhen Xuan . A combination rule for multiple surface cracks based on fatigue crack growth life. AIMS Materials Science, 2016, 3(4): 1649-1664. doi: 10.3934/matersci.2016.4.1649 |
| [10] | Bohdan Stasyuk . Interacting cracks 3D analysis using boundary integral equation method. AIMS Materials Science, 2016, 3(4): 1796-1810. doi: 10.3934/matersci.2016.4.1796 |
Due to intrinsic electro-mechanical coupling effect, piezoelectric materials have vast utility in many engineering devices, such as sensors, transducers, actuator components. But, under the action of electromechanical loadings, these piezoelectric materials could fail prematurely due to defects, e.g., cracks, holes, etc., arising during their manufacturing process over loads/fatigue/aging etc. This has made it important subject for study of their cracking/failure mechanics. Lots of research has been carried on a crack weakening a piezo-ceramic sensor etc., from 1990. Due to the tendency of developing multiple cracks in piezoelectric ceramics, the interaction amongst these cracks and their effects on the ceramic play an important role in fracture behavior of these ceramics and this makes the subject matter of the investigations of this paper.
The concept of strip-saturation model [1] was introduced by Gao for a cracked poled piezoelectric plate, based on the concept of Dugdale model for strip-yield model [2] for metals. The extended case of strip-saturation model for a semi-permeable and for a conductive crack face boundary conditions [3,4] was solved. Wang [5] gave a fully anisotropic analysis proposed by Gao et al. [1]. Li [6] re-examined the strip-saturation model for a permeable cracked piezoelectric ceramic to analyze fracture toughness of piezoelectric ceramic. Jeong et al. [7] proposed a strip-saturation model for cracked ferroelectric ceramic with perfect saturation under electrical loading.
Using complex function theory Beom et al. [8] analysed a strip-saturation model for an electro-strictive material under pure electric loading. Fan et al. [9] analysed a polarization saturation model for a non-linear semi-permeable crack in piezoelectric plane.
Bhargava and Jangid [10] were the first one to propose a strip-saturation model for two collinear cracks in a poled piezo-ceramic under mode-I conditions. They further extended [11] the strip-saturation when saturation zone developed at adjacent interior tips of the cracks get coalesced.
Zhang and Lee [12] investigated the problem of two collinear electrically dielectric cracks in a piezoelectric layer, within the frame work of linear piezoelectricity. Bui et al. [13,14,15] investigated the crack problems using BEM, DDM and XFEM methods for various crack face boundary conditions.
As we know, an analytic solution of the problem in closed form has some advantage over numerical and approximate solutions, which can serve a benchmark for the purpose of judging the accuracy and efficiency of various numerical and approximate methods.
Therefore, present paper deals with the problem of strip-saturation model for two collinear semi-permeable hairline cracks weakening a poled piezoelectric ceramic under mode-III conditions. Stroh formalism and complex variables employed to obtain the solution. Closed from analytic expressions are derived for various fracture parameters. A case study is presented for cracked piezo-ceramics PZT-5H, PZT-6B, PZT-7A under permeable, semi-permeable and impermeable crack face boundary conditions. Results obtained are presented graphically, discussed and concluded. It is seen that the model proposed is capable of crack arrest.
As are well known for out of plane problem, displacement components ui(i=x,y,z) are defined as
| ux(x,y,z)=0,uy(x,y,z)=0,and uz(x,y,z)=w(x,y) |
and for in-plane electric field problem, the electric field component Ei(x,y,z) may be defined as
| Ex(x,y,z)=Ex(x,y)=−ϕ,x,Ey(x,y,z)=Ey(x,y)=−ϕ,y and Ez(x,y,z)=0 |
where “ϕ” denotes the electric potential and comma after the function denotes the partial differentiation with respect to argument following it.
Gradient equations may be written as,
| ϵzi=w,i and Ei=−ϕ,i where i=x,y. | (1) |
Constitutive equations for stress components, σzi and electric displacement components, Di,(i=x,y) may be written as
| σzi=c44w,i+e15ϕ,i, Di=e15w,i−k11ϕ,i | (2) |
where c44, e15 and k11 are elastic, piezoelectric and dielectric constant, respectively.
Equilibrium equations for stresses in absence of body force and for electric displacement in absence of body charge may be written as
| σij,j=0,Di,i=0. | (3) |
The general solution of Eq. (2) may be expressed in terms of generalized stress function Φ and generalized displacement vector u=[w,ϕ]T, where superscript T denotes the transpose of the matrix.
| u,1=AF(z)+¯AF(z) | (4) |
| Φ,1=BF(z)+¯BF(z) | (5) |
where z=(x+iy=x1+ix2), F(z)=df(z)dz, f(z) being an analytic function and A, B stand for material constant matrix defined as,
| A=I,B=iB0=i(c44e15e15−k11). |
Let a piezoelectric material occupy the region oxy and is poled along oy direction. The plate is cut along ox direction forming two equal finite hairline straight cracks L1 and L2. These occupy the region y=0, [−d,−c] and [d,c] respectively. Out-of-plane stress, σzy=τ0, is applied at remote boundary as x2→∞ and also in-plane electric displacement, D2∞ applied along oy direction. Due to prescribed forces, the cracks open in self-similar fashion forming a small saturation zone in a strip ahead each tip of the cracks. To arrest the cracks from further opening, the developed zones are subjected to normal cohesive saturation limit electrical displacement D2=Ds. The schematic configuration of the problem is depicted in Figure 1.
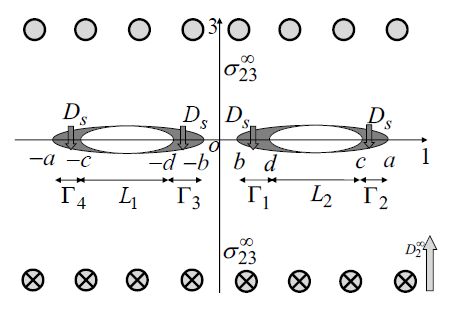 Figure 1. Schematic representation of the problem.
Figure 1. Schematic representation of the problem.Mathematically boundary conditions of the problem may be written as,
(i) σzi+=σzi−=0,D2=Dr,for d≤|x|≤c,
(ii) σzy=τ0,D2=D2∞,for |y|→∞,
(iii) σzi+=σzi−,D2+=D2−=Ds,for b≤|x|≤dand c≤|x|≤a,
(iv) Φ,1(x)+=Φ,1(x)−=−V,for d≤|x|≤c,
where, V=[0,0,τ0,D2∞]T and Dr denotes electric crack condition parameter which is of value 1 for permeable case, zero for impermeable case and lies between (0,1) for semi-permeable case.
From the condition of continuity of Φ,1 on the ox-axis barring the interval d≤|x|≤c yields vector Hilbert problem.
| [BF(x)−¯BF(x)]+−[BF(x)−¯BF(x)]−=0. |
Solution of which may be written as,
| BF(z)=¯BF(z)=h(z)(say) | (6) |
The boundary condition (iv) together with Eqs. (5), (6) yields
| h+(x)+h−(x)=−V, ford≤|x|≤c | (7) |
Introducing new complex function vector as,
| Ω(z)=[Ω1(z),Ω2(z),Ω3(z),Ω4(z)]T |
and
| h(z)=[HR]−1Ω(z)=ΛΩ(z) |
where
| HR=2Re[iAB−1] and Λ=(Λ33Λ34Λ43Λ44)=[HR]−1. |
Consequently Eq. (7) can be written as,
| Λ[Ω+(x)+Ω−(x)]=−V ford<|x|<c. | (8) |
Above equation in component form leads to the scalar Hilbert problem
| Λ33[Ω3+(x)+Ω3−(x)]+Λ34[Ω4+(x)+Ω4−(x)]=−τ0, | (9) |
| Λ43[Ω3+(x)+Ω3−(x)]+Λ44[Ω4+(x)+Ω4−(x)]=Dr−D2∞. | (10) |
Solving these equations for Ω3(z) and Ω4(z) together with boundary conditions (ii),(iii) and single-valuedness of displacement from Muskhelishvili [16], we obtain
| Ω3(z)=12△[τ0Λ44+(Dr−D∞2)]{z2−c2λ2√(z2−d2)(z2−c2)−1}, | (11) |
where, △=Λ33Λ44−Λ34Λ43, λ2=E(k)F(k) and k=(c2−d2)c2, E(k)and F(k) denote complete elliptic integral of first and second kind, respectively.
The general solution of Eq. (10) yields Ω4(z), once Ω3(z) is obtained.
| Ω4(z)=−Λ43Λ44Ω3(z)+Dr−D2∞2Λ44+1Λ44[P2(z)2X1(z)+Ds−Dr2πiX1(z)∫X1(t)t−zdt] | (12) |
where X1(z)=√(z2−a2)(z2−b2), P2(z)=G0z2+G1z+G2 and Γ=⋃4i=1Γi.
Here, Γi being the saturation zones occupying the interval b≤|x|≤d and c≤|x|≤a on ox-axis. Arbitrary constant, G0, determined using boundary condition at infinity; G1 and G2 are determined using single-valuedness condition of displacement around cracks. After a lengthy calculation, one finally obtain Ω4(z) as,
| Ω4(z)=−Λ43Λ44Ω3(z)+(D2∞−Dr)2Λ44{z2−a2λ12X1(z)−1}−(Ds−Dr)πΛ44X1(z)[(z2−a2λ12)(π2−ψ1+ψ2)−(a2−b2)(sinψ1cosψ1−sinψ2cosψ2)+ad{E(ψ1,k1)−λ12F(ψ1,k1)}−ac{E(ψ2,k1)−λ12F(ψ2,k1)}−X1(z)(π2−θ1+θ2)] | (13) |
where
| λ12=E(k1)K(k1),k1=(a2−b2)a2,sin2ψ=(a2−x12)(a2−b2),tan2θ=(b2−z2)a2−z2tan2ψsin2ψ1=(a2−d2)(a2−b2),sin2ψ2=(a2−c2)(a2−b2) |
In this section, we present various applications of the problem for finding crack sliding displacement, crack opening potential drop, intensity factors, saturation zone lengths and energy release rate.
The jump displacement vector Δu is defined as
| iΔu,1=HR[BF+(x)−BF−(x)]=Ω+(x)−Ω−(x) | (14) |
Crack sliding displacement is the relative crack face opening between the two surfaces of the crack. Crack sliding displacement can be used as a measure of the toughness of the materials under mode-III deformation. CSD, Δw, is determined substituting, Ω3(z), from Eq. (11) into Eq. (14) and noting Δw=0 at x=±d,±c, one obtains
| Δw,1=−i{Ω+3(x)−Ω−3(x)}. |
On integrating
| Δw=c{τ0Λ44+(Dr−D2∞)Λ34Λ33Λ44−Λ34Λ43}(E(χ,k)−λ2F(χ,k)) | (15) |
where, sin2χ=c2−x21c2−d2.
Crack opening potential drop is the electric potential difference between the two surfaces of the crack. Same as CSD, COP is used to measure the fracture and fatigue of materials. COP, Δϕ, can be obtained using,
| Δu4,1=−i{Ω4+(x)−Ω4−(x)} |
Integrating above equation, substituting Ω4(z) from Eq. (13) into Eq. (14), then taking limit x→c and x→d, we obtain
| Δϕ(d)=−Ds−DrπΛ44{R3−πaD∞2−DrDs−DrR4}, | (16) |
| Δϕ(c)=Ds−DrπΛ44{R5−πaD∞2−DrDs−Dr(E(ψ2,k1)−λ21F(ψ2,k1))}, | (17) |
where, R3, R4 and R5 can be found from appendix A.
Saturation zone length is obtained using Dugdale [2] hypothesis to be true for electric displacement to remain finite at every point of the body, consequently at the tips x=a and x=b yields following two non-linear transcendental equations.
| (b2a2−λ12)(π2D2∞−DrDs−Dr−π2+ψ1−ψ2)+k12(sinψ1cosψ1−sinψ2cosψ2)−da{E(ψ1,k1)−λ12F(ψ1,k1)}+ca{E(ψ2,k1)−λ12F(ψ2,k1)}=0, | (18) |
and
| (1−λ12)(π2D2∞−DrDs−Dr−π2+ψ1−ψ2)+k12(sinψ1cosψ1−sinψ1−sinψ2cosψ2)−da{E(ψ1,k1)−λ12F(ψ1,k1)}+ca{E(ψ2,k1)−λ12F(ψ2,k1)}=0. | (19) |
From these, a and b are determined and saturation zone lengths are then determined from (a−c) and (b−d).
In Piezoelectric materials, near the tip of the crack, each stress component is proportional to a constant K. And if this constant is known then the state of stress at the tip of crack can be determined. This constant is known as stress intensity factor. Stress and electric displacement intensity factors at the tip x=c and d are determined in this section.
Mode-III stress intensity factor Kdτ at the tip x=d can be determined by this formula,
| Kdτ=limx→d−√2π(d−x)σzy(x,0)=−{τ0+(Dr−D2∞)Λ34Λ44}√πd(d2−c2)(d2−c2λ2). | (20) |
Similarly, SIF at tip x=c is obtained as,
| Kcτ=limx→c+√2π(x−c)σzy(x,0)={τ0+(Dr−D2∞)Λ34Λ44}√πc(c2−d2)(c2−c2λ2). | (21) |
Mode-III, EDIF obtained at the tip x=b from
| KDb=limx→b−√2π(b−x)Dy(x,0)=√πb(a2−b2)[(D2∞−Dr)(b2−a2λ12)−2π(Ds−Dr){(b2−a2λ12)(π2−ψ1+ψ2)−(a2−b2)(sinψ1cosψ1−sinψ2cosψ2)+da(E(ψ1,k1)−λ12F(ψ1,k1))−ca(E(ψ2,k1)−λ12F(ψ2,k1))}] | (22) |
Analogously EDIF at the tip x=a is obtained as
| KDa=limx→a+√2π(x−a)Dy(x,0)=−√πa(a2−b2)[(D2∞−Dr)(a2−a2λ2)−2(Ds−Dr)π{(a2−a2λ12)(π2−ψ1+ψ2)−(a2−b2)(sinψ1cosψ1−sinψ2cosψ2)}+da(E(ψ1,k1)−λ12F(ψ1,k1))−ca(E(ψ2,k1)−λ12F(ψ2,k1))}]. | (23) |
While mode-III strain intensity factors Kdϵ and Kcϵ and mode-III electric field intensity factors, KbE and KaE factors are calculated from
| Kϵd=e15KDb+k11Kτde215+k11c44, | (24) |
| Kϵc=e15KDa+k11Kτce215+k11c44, | (25) |
| KEb=c44KDb−e15Kτde215+k11c44, | (26) |
| KEa=c44KDa−e15Kτce215+k11c44. | (27) |
ERR Gd and Gc at the tips x=d and x=c, respectively computed using,
| Gd=12[KdτKdϵ−KbDKbE], | (28) |
| Gc=12[KcτKcϵ−KaDKcE]. | (29) |
In order to verify the above derived results, let us consider a strip electric saturation model of single crack problem in piezoelectric material. The crack occupy the interval (−c,c) and developed saturation zone occupy the interval c<|x|<a; with semi-permeable electric boundary condition, then the above Eqs. (11) and (13) with b=d=0, reduces to the results of Wang [5].
A numerical case study is presented for various crack face boundary conditions for ceramics PZT-5H, PZT-6B and PZT-7A. The crack lengths are taken to be 10 mm each and Ds=0.03 C/m2.
The material parameter for piezo-ceramics given in Table 1 below taken from, Ou and Wu [17]
| Material/Constants | c44(1010 Nm-2) | e15(Cm-2) | k11(10-10C/Vm) |
| PZT-5H | 2.30 | 17.44 | 150.3 |
| PZT-6B | 2.71 | 4.60 | 36.0 |
| PZT-7A | 2.54 | 9.70 | 81.1 |
Figure 2 depicts the variation of CSD over the crack rims. It is observed that CSD is symmetrical and parabolically varying with respect to middle point and is maximum at the center point of crack and then reduces till it becomes zero at end points. Also CSD is maximum for impermeable boundary condition and almost three times less for semi-permeable case as compared to that for impermeable case. CSD further reduces for permeable crack face boundary conditions and crack opens least for this case.
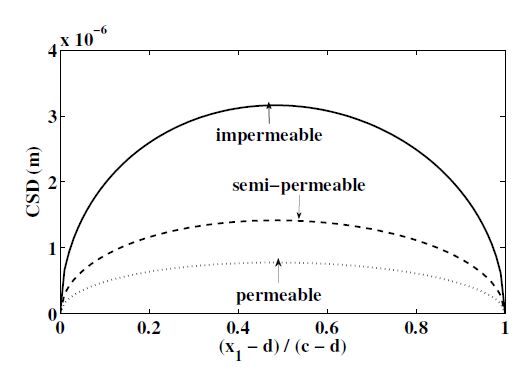 Figure 2. CSD over the crack surface.
Figure 2. CSD over the crack surface.The opening of crack on different piezoceramics is depicted in Figure 3. It is noted that crack opens least for PZT−5H ceramic and maximum for PZT−6B ceramic. It may assists the designers for the correct selection of the ceramic for desired purposes.
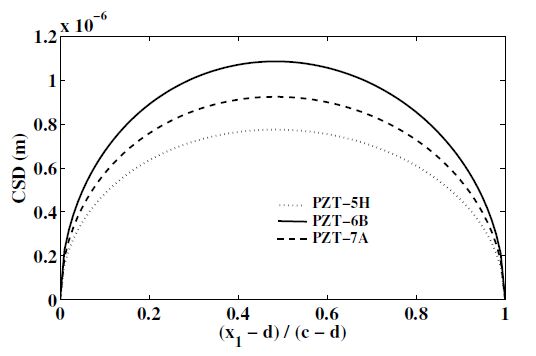 Figure 3. CSD for different piezoceramics.
Figure 3. CSD for different piezoceramics.Variation of electric displacement intensity factor KD versus prescribed electric displacement D2∞, for impermeable, semi-permeable and permeable crack face conditions is plotted in Figure 4 at interior and exterior tips of the crack. It is observed that KD decreases almost linearly as D2∞ is increased for all the cases. It is noted that KD is higher at inner tip for all three crack face boundary conditions. Also KD is maximum for impermeable case followed by semi-permeable case, and is minimum for permeable case. Same trend is followed at the interior tip of the crack.
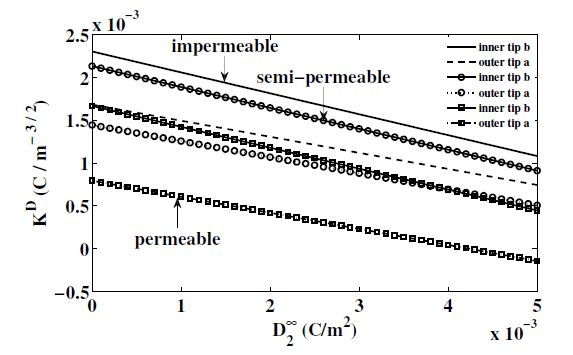 Figure 4. Variation of KD with respect to D2∞.
Figure 4. Variation of KD with respect to D2∞.Energy release rate versus D2∞ variation is presented in Figure 5. ERR decreases continuously with increasing D2∞. The decrease for impermeable boundary condition is more sharp as compared to that for semi-permeable and permeable case. At the outer tip d, the variation for semi-permeable and permeable cases, decrease in ERR is very close to each other while for impermeable case, variation is more steep and away from semi-permeable and permeable case.
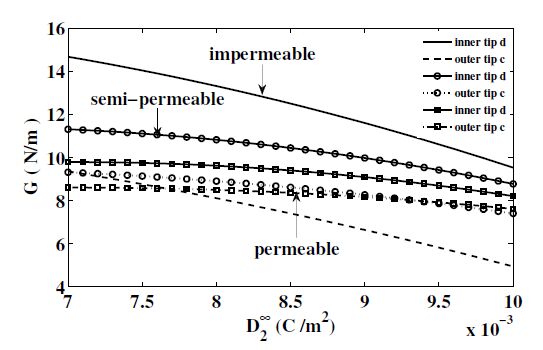 Figure 5. Variation of energy release rate versus D2∞
Figure 5. Variation of energy release rate versus D2∞Figure 6 presents the variation of SIF, Kτ at the inner tip x1=d and outer tip x1=c of the crack with respect to the inter-crack distance. It is observed that stress concentration is maximum for the case of impermeable crack face boundary condition followed by semi-permeable crack face boundary condition and least for permeable crack face boundary condition, as expected. For all the three cases the SIF variation at inner crack tip show a slight parabolic decrease for smaller values of inter crack distance to crack length ratio and then stabilizes to a uniform constant variation for d/a>1.5. The same is true for the variation at the outer tip but in this case, the variation is more flat as compared to that in the case of inner tip.
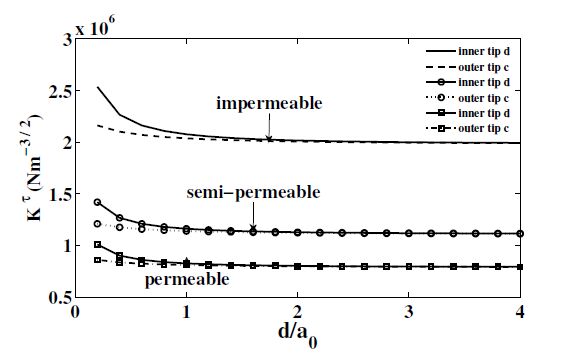 Figure 6. Variation of Kτ with respect to inter-crack distance.
Figure 6. Variation of Kτ with respect to inter-crack distance.· The proposed strip-saturation model is capable of crack arrest for small electric yielding case. The reduction in energy release rate confirms it.
· The study of CSD on different piezoceramic presented may assists the designers for the correct choice of the piezoceramic required for specific purpose.
· There is more stress concentration around crack tip for impermeable crack face boundary condition as compared to that for semi-permeable and permeable case and is least for permeable case.
Authors are grateful to Prof R. D. Bhargava {Senior Professor(retd.), Indian Institute of Technology Bombay, Mumbai, India} for continuous encouragement during course of this work. The second author wishes to gratefully acknowledge the support of RTU, Kota, India.
All authors declare no conflict of interest in this paper.
| R1=da(E(ψ1,k1)−λ21F(ψ1,k1))−ca(E(ψ2,k1)−λ21F(ψ2,k1))−k21(sinψ1cosψ1−sinψ2cosψ2), | (A.1) |
| R2=aλ21(π2−ψ1+ψ2)−aR1, | (A.2) |
| G(d,c)=−dln(√(d2−b2)(a2−c2)+√(a2−d2)(c2−b2)√(d2−b2)(a2−c2)−√(a2−d2)(c2−b2))+2b2a√a2−c2c2−b2II(ϑ1,c2k21c2−b2,k1), | (A.3) |
| sin2ϑ1=a2(d2−b2)d2(a2−b2), | (A.4) |
| H(c,d)=cln(√(c2−b2)(a2−d2)+√(a2−c2)(d2−b2)√(c2−b2)(a2−d2)−√(a2−c2)(d2−b2))−2a√(d2−b2)(a2−d2){F(ψ2,k1)+d2a2−d2II(ψ2,a2−b2a2−d2,k1)}, | (A.5) |
| R3=2b2a√a2−d2d2−b2{F(ϑ1,k1)−II(ϑ1,d2−b2d2,k1)}−dln(a2−d2a2−b2+a2(d2−b2)d2(a2−b2))+2a(π2−ψ1+ψ2){E(ϑ1,k1)−k21sinϑ1cosϑ1√1−k21sin2ϑ1}−2R2F(ϑ1,k1)−G(d,c), | (A.6) |
| R4=E(ϑ1,k1)−λ21F(ϑ1,k1)−k21sinϑ1cosϑ1√1−k21sin2ϑ1, | (A.7) |
| R5=−cln((a2−c2)(c2−b2)c2(a2−b2)+1)+2a√c2−b2a2−c2{a2F(ψ2,k1)−c2II(ψ2,a2−c2a2,k1)}+2a(π2−ψ1+ψ2)E(ψ2,k1)−2R2F(ψ2,k1)+H(c,d). | (A.8) |
| [1] |
Gao H, Zhang TY, Tong P (1997) Local and global energy release rates for an electrically yielde crack in a piezoelectric ceramic. J Mech Phy Solids 45: 491–510. doi: 10.1016/S0022-5096(96)00108-1

|
| [2] |
Dugdale DS (1960) Yielding of steel sheets containing slits. J Mech Phy Solids 8: 100–104. doi: 10.1016/0022-5096(60)90013-2

|
| [3] |
Ru CQ (1999) Effect of electrical polarization saturation on stress intensity factors in a piezoelectric ceramic. Int J Solids Struct 36: 869–883. doi: 10.1016/S0020-7683(97)00331-4

|
| [4] |
Ru CQ, Mao X (1999) Conducting cracks in a piezoelectric ceramic of limited electrical polarization. J Mech Phy Solids 47: 2125–2146. doi: 10.1016/S0022-5096(99)00007-1

|
| [5] |
Wang TC (2000) Analysis of strip electric saturation model of crack problem in piezoelectric materials. Int J Solids Struct 37: 6031–6049. doi: 10.1016/S0020-7683(99)00255-3

|
| [6] |
Li S (2003) On saturation-strip model of a permeable crack in a piezoelectric ceramic. Acta Mech 165: 47–71. doi: 10.1007/s00707-003-0038-1

|
| [7] |
Jeong KM, Kim IO, Beom HG (2004) E ect of electric displacement saturation on the stress intensity factor for a crack in a piezoelectric ceramic. Mech Res Comm 31: 373–382. doi: 10.1016/S0093-6413(03)00093-4

|
| [8] |
Beom HG, Kim YH, Cho C, et al. (2006) A crack with an electric displacement saturation zone in an electrostrictive material. Arch Appl Mech 76: 19–31. doi: 10.1007/s00419-006-0002-3

|
| [9] |
Fan CY, Zhao YF, Zhao MH, et al. (2012) Analytical solution of a semi-permeable crack in a 2D piezoelectric medium based on the PS model. Mech Res Comm 40: 34–40. doi: 10.1016/j.mechrescom.2012.01.001

|
| [10] | Bhargava RR, Jangid K (2014) A mathematical strip-saturation model for piezoelectric plate weakened by two collinear equal cracks. Math Mech Solids 19: 714–725. |
| [11] |
Bhargava RR, Jangid K (2013) Strip-saturation model for piezoelectric plane weakened by two collinear cracks with coalesced interior zones. Appl Math Modell 37: 4093–4102. doi: 10.1016/j.apm.2012.09.026

|
| [12] |
Zhong HC, Lee KY (2014) Electroelastic fields induced by two collinear and energetically consistent cracks in a piezoelectric layer. J Mech 30: 361–372. doi: 10.1017/jmech.2014.31

|
| [13] |
Sharma K, Bui TQ (2016) Numerical studies of an array of equidistant semi-permeable inclined cracks in 2-D piezoelectric strip using distributed dislocation method. Int J Solids Struct 80: 137–145. doi: 10.1016/j.ijsolstr.2015.10.030

|
| [14] |
Bui TQ (2014) Comparison of several BEM-based approaches in evaluating crack-tip field intensity factors in piezoelectric materials.Int J Fracture 189: 111–120. doi: 10.1007/s10704-014-9964-2

|
| [15] |
Sharma K, Bui TQ (2013) Analysis of a subinterface crack in piezoelectric bimaterials with the extended finite element method. Eng Fract Mech 104: 114–139. doi: 10.1016/j.engfracmech.2013.03.012

|
| [16] | Muskhelishvili NI (1963) Some basic problems of the mathematical theory of elasticity, The Netherlands, Nordhoff. |
| [17] |
Ou ZC, Wu X (2003) On the crack-tip stress singularity of interfacial cracks in transversely isotropic piezoelectric biomaterials. Int J Solids Struct 40: 7499–7511. doi: 10.1016/j.ijsolstr.2003.08.021

|
| 1. | Sandeep Singh, Kuldeep Sharma, Complex variable solution for mode-III quadratically varying PS model in piezoelectric media, 2021, 1033, 1757-899X, 012044, 10.1088/1757-899X/1033/1/012044 | |
| 2. | S. Singh, K. Sharma, R. R. Bhargava, Modified strip saturated models for two equal collinear cracks with coalesced zones in piezoelectric media, 2019, 40, 0253-4827, 1097, 10.1007/s10483-019-2507-6 | |
| 3. | Sandeep Singh, Kuldeep Sharma, R. R. Bhargava, Analytical solution for two equal collinear modified strip saturated cracks in 2‐D semipermeable piezoelectric media, 2019, 99, 0044-2267, 10.1002/zamm.201800244 | |
| 4. | Ashish Kumar, Kuldeep Sharma, Tinh Quoc Bui, Moving EMPS model for semipermeable two equal collinear interface cracks in dissimilar magneto-electro-elastic materials, 2024, 1537-6494, 1, 10.1080/15376494.2024.2356727 | |
| 5. | Sandeep Singh, Kuldeep Sharma, Closed form solution for generalized modified polarization saturation model in piezoelectric media, 2025, 1081-2865, 10.1177/10812865251317616 |
| Material/Constants | c44(1010 Nm-2) | e15(Cm-2) | k11(10-10C/Vm) |
| PZT-5H | 2.30 | 17.44 | 150.3 |
| PZT-6B | 2.71 | 4.60 | 36.0 |
| PZT-7A | 2.54 | 9.70 | 81.1 |